Functional Apparent Moduli (FAMs) as Predictors of Oral Implant Osseointegration Dynamics

Abstract

At present, limited functional data exists regarding the application and use of biomechanical and imaging technologies for oral implant osseointegration assessment. The objective of this investigation was to determine the functional apparent moduli (FAMs) that could predict the dynamics of oral implant osseointegration. Using an in vivo dental implant osseous healing model, two FAMs, functional bone apparent modulus (FBAM) and composite tissue apparent modulus (FCAM), of the selected peri-implant structures were calculated via microcomputed tomography (micro-CT) and finite element (FE) simulations in order to support this concept. Results showed significant sensitivity between FAMs and micro-CT parameters, especially between bone mineral density and FBAM, while at extraction defect sites the strongest correlations existed between bone-implant contact and FCAM. Significant enhancement of FCAM indicated progressive functional repair during early osseointegration. Further, the resultant interfacial resistance was predicted by bone mineral content (BMC) and FBAM within a ~200 μm peri-implant thickness, while the extraction defects gave zones of ~575 μm and 200 μm for BMC and FCAM, respectively. These results suggest that the function of dental implant support can be predicted from a peri-implant structural zone. We conclude that FAMs can be used to predict the dynamics of dental implant osseointegration in vivo.

1. INTRODUCTION

Dental implants have been a widely accepted alternative for tooth replacement, and the process of osseointegration has been extensively studied in preclinical and clinical investigations, with most of the information being derived from radiographic, histologic, and biomechanical analyses^1–4. As such, an uncertain relationship between the peri-implant structure and implant biomechanics creates challenges when evaluating the functional dynamics of dentoalveolar tissues during healing^5,6. This discrepancy might originate from the imprecision of the methodology as well as the information provided from the two-dimensional images^3,7. Micro-computed tomography (micro-CT) offers a comprehensive three-dimensional (3D) information of the dentoalveolar structures⁸, however, the potential physical artifacts due to the approach may still limit the application for dental implants^9,10.

Finite element (FE) analysis has previously been utilized to study the mechanical behavior of dental implants and bone tissues^11–13. However, the bone-implant interface has been considered as the boundary condition in FE models such that evaluating the in vivo process and progress of osseointegration via FE analysis alone has not been feasible¹⁴. Therefore, denser peri-implant structures and higher bone-implant contact surfaces tend to offer stronger contact stiffness^15,16. On the other hand, to eliminate the heterogeneity of bone tissues and simplify the iteration process, previous investigations on homogenizing the bone through FE optimization reported significant agreement between “effective stiffness” and experimental results^17–19. Thus, functional homogenization of peri-implant supporting tissue may be feasible to demonstrate the biomechanical dynamics of peri-implant supporting structures.

The primary aim of this study was to determine functional apparent moduli (FAMs) representing implant tissue-supporting biomechanical properties during osseointegration and bone regeneration. The interfacial stiffness (IS) between the peri-implant bone and implant was recorded during implant push-out, and FE analyses were performed to demonstrate that micro-CT was capable of providing precise 3D information of peri-implant structure after implant removal. Based on micro-CT images during osseointegration, FAMs were generated to homogenize the peri-implant structure through FE optimization, and the correlations between IS and peri-implant structure were evaluated to verify the functionally relevant peri-implant layer. Our results demonstrate that FAMs were capable of measuring dynamic functional change during early-stage implant osseointegration, and implant biomechanics can be predicted from a specific dimension of the functionally relevant peri-implant layer.

2. MATERIALS AND METHODS

2.1 Study materials and animal model

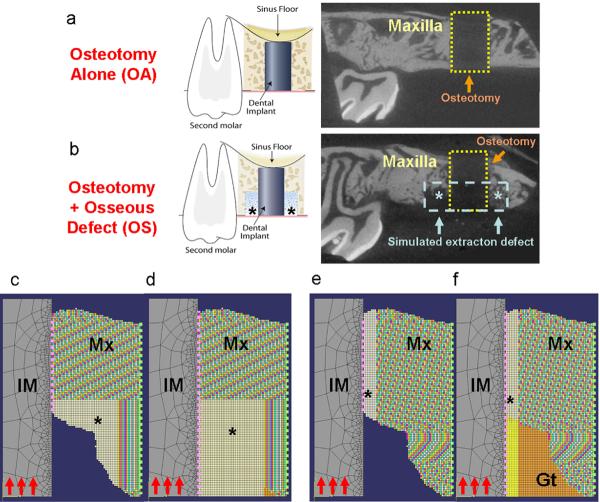
All animal surgical procedures followed the guidelines according to the Committee on Use and Care of Animals (UCUCA) at the University of Michigan. A modified small animal dental implant model was utilized in this study with a total of 38 adult Sprague-Dawley rats (Table 1, n=4–6 animals/time-point/group)²⁰. All the animals were anesthetized by intraperitoneal administration of ketamine and xyzaline, with subcutaneous administration of buprenex for analgesia. The maxillary first molars were extracted atraumatically and the alveolar ridges was allowed to heal for 30 days. To enable implant placement, a 0.95 mm diameter × 2 mm in length (reaching the maxillary sinus floor) osteotomy was created for the press-fit installation of a 1 mm × 2 mm cylindrical implant with SLActive® surface treatment (Institut Straumann AG, Basel, Switzerland). The control group constituted the osteotomy-alone defects (OA; Fig. 1a). The test group consisted of the creation of a simulated extraction socket defect at the coronal portion of the osteotomy with dimensions as shown in Figure 1b (osteotomy + osseous defect group (OS)). After defect creation and implant placement, the intra-oral wounds were closed by tissue glue (Periacryl®, Glustitch Inc., Point Roberts, WA, USA).

Table 1.

Study Design

	Osteotomy-Alone (OA)	Ostetomy + Osseous Defect (OS)
Day 7*	4
Day 10	6 (0)	6 (0)
Day 14	6 (2)	6 (0)
Day 21	4 (4)	6 (6)

Numbers in the table indicates specimens evaluated in each time point. Parentheses refer to the specimens unavailable for micro-CT examinations due to significant specimen fracture after implant push-out.

^*OS group was unavailable on day 7 due to no mineralization could be found from our preliminary study. One of the specimens in OA group without any significant bone destruction and microscopic fracture on day 7 was selected as the representative FE model for evaluating the radiographically detectable deformation.

Figure 1. In vivo dental implant osseointegration model for functional simulations.

The surgical model of osteotomy-alone and osseous-defect group are demonstrated in the left panels of (a, b). The right panels demonstrate a slice of micro-CT image from a 10-day specimen after implant removal (the 1×2mm area of osteotomy is marked by the yellow dashed line; the 0.6×1 mm area of simulated extraction defect is marked by blue dash line and asterisks). The optimized FE models are shown on (c) FBAM and (d) FCAM for evaluation of osseous wound repair, (e) FBAM and (f) FCAM of interfacial tissue for evaluating the correlation to interfacial biomechanics. Suspended boundary (dash lines in light green) was assumed, and the bone-implant interface (dash lines in pink) was assumed homogenous and simulated using cohesive elements. In each model, the Young's modulus of the mineralized tissue (Mx) was projected from the grayscale of micro-CT images, whereas the dental implant (IM) and granulation tissue (Gt) was obtained from a reference standard²⁹–³². The Young's modulus of the bone or tissue in the area of interest (asterisk) was calculated from the functional loading from the oral cavity (red arrows). The elasticity of interface was assumed equivalent to the peri-implant element nearby. Osteotomy-alone (OA) and osteotomy with osseous defect (OS) specimens were examined for each simulation (n=12–14 for each group).

Abbreviations: FE: finite element; FBAM: functional bone apparent modulus; FCAM: functional composite tissue apparent modulus

2.2 Bone-implant interfacial stiffness determination

Block biopsies from animals in the OA and OS groups were harvested at 7, 10, 14, or 21 days post-implant installation (Table 1) and secured in acrylic resin. The implants were pushed out of the maxillae using an MTS machine (Model 858, Mini-Bionix II, MTS Systems Corp., Eden Prairie, MN, USA) at a constant displacement rate of 0.1 mm/s (Fig. S1a). Maximal removing load (MRL) and interfacial stiffness (IS) were calculated from the load-displacement curves (Fig. S1b). An osseointegration index (OI) score was also determined after implant push-out (Table 2). The definitions of the biomechanical parameters are referred to in Appendix A.

Table 2.

Index of Osseointegration

Grade	Definition
0	Minimal contact. Interfacial stiffness < the value of day 7 OA specimens
1	Moderate contact. Interfacial stiffness > the value of day 7 OA specimens; no visible trabecular/cortical bone fracture
2	Trabecular bone fracture. No visible fracture or component loss on micro-CT, with macroscopically visible residual bone on the implant surface.
3	Mild cortical bone fracture. Fracture line on cortical bone detected on micro-CT; no significant bone component separation
4	Major cortical bone fracture. Separation of the bone components

Abbreviations: OA: osteotomy-alone defects

2.3 Micro-CT applications for peri-implant structures

Our preliminary study demonstrated a 120–150 μm zone on the CT phantom (Inner bone, Gammex Inc., Middletown, WI, USA) surrounding the border of the implant due to the metal scattering effect (Fig. S2) which limited the evaluation of the implant-supporting tissues^9,21,22, and this artifact may be eliminated after implant removal. Subsequently, the implant removal procedure could damage the peri-implant structure, but the comparison before and after the implant removal could not be evaluated directly from the experiments. Thus, we designed an in vivo FE model to evaluate potentially CT-detectable tissue damage after implant push-out.

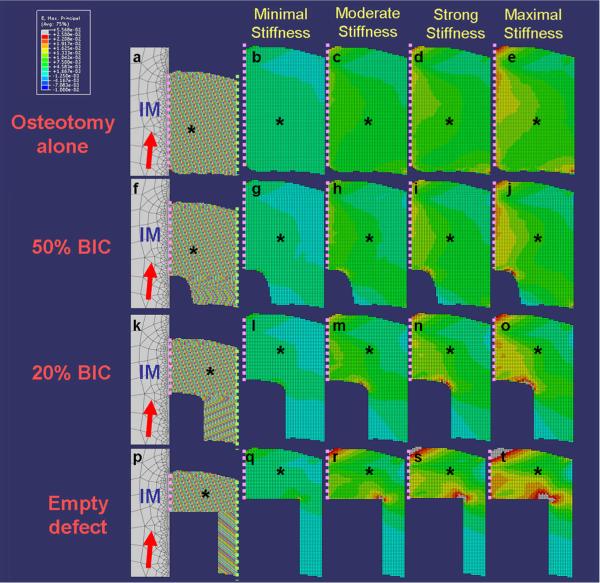
Our FE model was developed to simulate the implant push-out procedure using linear static analysis with ABAQUS™ v6.7-1 software (Simulia Inc., Northville MI, USA) based on micro-CT images from a representative in vivo specimen, and a 3-D image was homogenized to a plane and the axisymmetric model was established. Quadratic linear-isotropic elements were utilized to reconstruct the peri-implant bone, and the resultant properties were assigned by conversion of the mineral density data from micro-CT images. Cohesive elements were utilized to simulate the proteoglycan-rich zone of the bone-implant interface. Detailed model settings and assumptions are referenced in Appendix B. To investigate the influence of bone-implant contact (BIC), a 0.6 ×1mm circumferential peri-implant osseous defect was assumed, and based on observations from preliminary studies, several elements were removed to achieve 20% BIC (equivalent to wound healing at day 10) and 50% BIC (equivalent to day 14) models (Fig. 2). Then, the IS of cohesive elements was assigned by conversion of the measurements from micro-CT after implant push-out (section 2.2), in which `minimal' represented IS for day 7, `moderate' for day 10, `strong' for day 14, and `maximal' for day 21. The maximum principal strain was recorded after push-out. The visible deformation under micro-CT was set as 2.5% strain level²³, and elements exceeding this threshold were colorized by grey.

Figure 2. Finite element model and maximum principle strain distribution of implant-supporting tissues after implant removal.

Four axisymmetric models were generated to evaluate the effects of osseous wound repair over time (a, f, k, p). The maximum principle strain of the peri-implant tissue on the compression side (asterisks, and bone-implant interface referred to the dash line) after implant (IM) removal with 5° angulations (red arrows on a, f, k, p) was recorded (b–e, g–j, l–o, q–t). The osseous defect was set as 0.6mm-in-width and 1.0 mm-in-depth surrounding the dental implant (d), 20% bone-implant-contact (BIC) referred to normal healing wound at day 10 (k), 50% BIC referred to normal healing wound at day 14 (f), and osteotomy-only referred to no defect creating specimens (a). Suspended boundary (dash lines in light green on a, f, k, p) was assumed, and the bone-implant interface (dash lines in pink) was assumed homogenous and simulated using cohesive elements. Four different interfacial bonding situations were assigned for evaluations, whereas minimal, moderate, strong, and maximal stiffness was assigned according to the record from push out testing on the osteotomy-only group at day 7, 10, 14, and 21 (referred to Table 2). The elements with radiographically visible deformation (experienced more than 2.5% strain) were colorized by grey. The profile of minimal principle strain demonstrated a similar tendency, and fewer elements demonstrated radiographic deformation.

2.4 In vivo measurements

Micro-CT images were acquired (eXplore Locus SP, GE HealthCare) following implant removal (Fig. 1a-b, right panel) at an operating voltage of 80kV and reconstructed into voxels of 18 × 18 × 18 μm³, and then segmented with a threshold determined by an adaptive technique²⁴. BIC, bone volume fraction (BVF), tissue mineral density (TMD), and bone mineral density (BMD) were each evaluated to investigate the osseous wound healing within the osseous defect areas. The equivalent osseous defect areas were also segmented for the control group and they served as the reference for complete osseointegration.

To determine the correlation between interfacial resistance and the properties of concentric area, the peri-implant tissue was concentrically segmented in 18 μm intervals ranging from 18–720 μm and bone volume (BV), BMC, and BMD (Appendix A) from individual and cumulative peri-implant tissue layers from the bone-implant interface were calculated. The definition of all above abbreviated terms are referenced in Appendix A.

2.5 Functional Homogenization through FE optimization

FBAM and FCAM were generated (for definitions refer to Appendix A) for all available specimens from both OS and OA groups (Table 1). Micro-CT of the in vivo images was homogenized to establish axisymmetric FE models (Fig. 1c-f). Two models were generated for each specimen: the “microscopic” model which contained local mechanical properties from micro-CT, and the “optimizing” model, with the property within a specific area assumed homogenous and generated from FE optimization by applying a pre-yield load on the implant top surface (Appendix C). Correlations between functional apparent moduli and either mathematical moduli (MBM & MCM, mathematically averaged of Young's moduli within osseous defect, Appendix A) or micro-CT structural parameters (BIC, BVF, BMD, TMD) were examined to study the correspondence between radiographic and functional information from the osseous defect sites. FBAM and FCAM of the cumulative peri-implant concentric area (Fig. 1e,f) were also correlated to IS and MRL to investigate the functionally relevant peri-implant layer.

2.6 Statistical analysis

All the correlation analyses were performed using a Pearson Product Moment correlation test. Differences between the biomechanical, structural, and functionally-simulated parameters over time and between the OA and OS group were determined by paired t tests for continuous data, and by Mann-Whitney U tests for discontinuous data. A p value of <0.05 was considered as statistically significant.

3. RESULTS

3.1 Promotion of interfacial biomechanics during dental implant osseointegration

Overall results showed the interfacial stiffness significantly (p<0.01) increased from day 7 through day 10 then gradually leveled off by day 21. MRL and the mean OI score also demonstrated similar tendencies as IS, and most of the specimens at day 21 revealed visible cortical bone fracture (4 of 6 in OS group, and 6 of 6 in OA group). While osseointegration refers to the maximal bone-implant bonding capability, this situation indicated complete osseointegration occurred (Table 3).

Table 3.

Dynamic change of biomechanical, structural, and functional parameters over time

	Osteotomy-Alone (OA)				Ostetomy + Osseous Defect (OS)
	Day 7 (n=4)	Day 10 (n=6)	Day 14 (n=6)	Day 21 (n=4)	Day 10 (n=6)	Day 14 (n=6)	Day 21 (n=6)
Interfacial stiffness (N/mm)	67.66(42.57)	180.54 (30.79)#	229.16 (34.82)#	290.10 (57.97)$#	28.82 (25.79)*	77.74 (45.90)*	161.67 (100.96)&
Osseointegration index score	0.50	1.17	2.50#	4.00$#	0.17*	0.83*	3.33&
Maximal removal load (N)	2.52(1.69)	28.88 (7.93)#	44.65 (10.02)#	N.D.	5.29 (5.99)*	15.46 (7.09)*	N.D.
Bone-implant contact (mm2)	0.95(0.33)	1.13 (0.21)	1.04 (0.12)	N.D.	0.30 (0.15)*	0.44 (0.21)*	N.D.
Bone volume fraction	0.72(0.04)	0.74 (0.13)	0.77 (0.06)	N.D.	0.43 (0.15)*	0.57 (0.07)*	N.D.
Tissue mineral density (mg/cc)	667.35(63.37)	801.74 (94.12)	823.82 (80.07)#	N.D.	311.28 (80.40)*	383.40 (102.56)*	N.D.
Bone mineral density (mg/cc)	804.58(39.2)	1078.69 (196.32)#	1078.09 (120.03)#	N.D.	583.71 (55.82)*	668.32 (119.09)*	N.D.
MCM (GPa)	N.D.	3.362 (0.511)	3.687 (0.107)	N.D.	1.071 (0.125)*	1.506 (0.202)*	N.D.
FCAM (GPa)	N.D.	13.031 (1.807)	12.430 (2.965)	N.D.	3.801 (0.356)*	7.939 (1.318)*$	N.D.
MBM (GPa)	N.D.	11.889 (0.922)	12.176 (1.692)	N.D.	7.687 (0.348)*	7.993 (0.507)*	N.D.
FBAM (GPa)	N.D.	11.979 (1.670)	12.312 (2.775)	N.D.	7.752 (0.258)*	8.745 (0.662)*	N.D.

^*Significant difference to osteotomy-alone group at specific time points (p<0.001)

^$Significant difference to day 10 (p<0.01)

^#Significant difference to day 7 (p<0.01)

parentheses refers to standard deviation

N.D. Not determinable

Abbreviations: MCM: mathematical composite tissue modulus; FCAM: functional composite tissue apparent modulus; MBM: mathematical bone modulus; FBAM: functional bone apparent modulus

3.2 Interfacial damage is not a significant factor following implant removal during early healing

In our FE model for interfacial damage, no significant difference in strain distribution was noted among 0°, 3°, and 5°angulated loads, and the maximum principal strain occurred at a 5°angulated load, with the compression side illustrated in Fig. 2. Results revealed that the strain increased with elevations in interfacial stiffness, and greater defect fill led to more favorable strain distribution from fracturing. Although radiographically visible deformation of tissues was noted in several analyses (Table S1), those situations only occurred while the interfacial bonding was stiffer than the stiffness from our experiment in the non-defect condition at the relevant time points. Thus, the results of our FE analyses confirmed that implant removal did not lead to radiographically detectable deformation.

3.3 Correlations between functional apparent moduli and mathematical moduli or structural parameters during early healing

Within 14 days, both FBAM and FCAM were correlated to mathematical moduli for the OS and OA groups. Both FBAM and FCAM were more highly correlated to the micro-CT structural parameters (BIC, BVF, TMD, BMD) than mathematical bone and composite tissue modulus, especially to BMD in the OA group as well as to BIC in the OS group. Furthermore, FCAM demonstrated more correlation to all other structural parameters in the OS defects when compared to FBAM or both mathematical moduli (Table 4).

Table 4.

Correlations between micro-CT and functional/mathematical modulus

Parameters	Osteotomy-Alone (OA, n=14)		Osteotomy+Osseous Defect (OS, n=12)
	FBAM	FCAM	FBAM	FCAM
Functional/mathematical modulus
R square	0.8925	0.2780	0.5856	0.6762
P value	N.S.	<0.0001	<0.0001	<0.0001
R square to functional apparent modulus *
Bone-implant contact (BIC)	0.2755	0.2964	0.4243	0.7589
Bone volume fractions (BVF)	0.0869	0.0352	0.0057	0.4857
Tissue mineral density (TMD)	0.1203	0.0566	0.1113	0.4651
Bone mineral density (BMD)	0.8544	0.7364	0.3298	0.3708
R square to mathematical modulus *
Bone-implant contact (BIC)	0.0604	0.4140	0.1135	0.6204
Bone volume fractions (BVF)	0.1546	0.7168	0.0132	0.4062
Tissue mineral density (TMD)	0.3476	0.6458	0.1231	0.4081
Bone mineral density (BMD)	0.5003	0.1641	0.4937	0.0080

^*All the p value between micro-CT and functional/mathematical modulus were < 0.05

Abbreviations: FBAM: functional bone apparent modulus; FCAM: functional composite tissue apparent modulus

3.4 Biomechanical testing, micro-CT imaging, and FAMs of peri-implant wound repair

In the OS group, progressive increases for all of the biomechanical and structural parameters were noted (Table 3), and significant fracture of cortical bone after push-out testing on day-21 made the specimens unavailable for micro-CT structural evaluation (Table 1). However, those biomechanical and structural parameters were still significantly lower (p<0.05) compared to the OA group at day 10–14 (Table 3).

Among all the mathematical and functional apparent moduli, FCAM was the only one that demonstrated a significant difference over time in the OS group (p<0.01). There was a two-fold difference between FBAM and FCAM at day 10 but after accounting for an equivalent value at day 14 implied that the composite tissue in the osseous defect was able to offer equivalent functional support as the bone structure. However, FBAM changed dynamically in the OS group and continued to display significant differences from the OA group at day 14 (p<0.001), which also indicated that the functional resistance from the neogenic bone structure was still not as strong as the mature mineralized structures.

3.5 Correlations between interfacial resistance and micro-CT parameters/FAMs

In the OA group, BV and BMC from the innermost layer of the peri-implant area demonstrated the highest correlation to both IS and MRL when compared with all other concentric layers (Fig. 3 a, d). Using cumulative layer analysis, BMC better predicted IS at the 180 μm-thickness peri-implant layer (R=0.70, Fig. 3b). Although the micro-CT parameters and MRL were less correlated, BMD remained a better predictor of MRL at a 180 μm-thickness layer (R=0.501, Fig. 3e). In the OS group, BV exhibited a very weak correlation for both IS and MRL (R<0.2) in layer-by-layer analysis (Fig. 3 g, j). In the cumulative layer analysis, BMC displayed the highest correlation to both IS (R=0.66) and MRL (R=0.71) at the 576 μm-thickness level (Fig. 3 h, k). Those results implied that the tissue-implant interfacial biomechanics might be predicted from micro-CT imaging within 180 μm thickness peri-implant layer without any pre-existing osseous defect as well as 576 μm thickness with a 600 μm pre-existing defect.

Figure 3. Relationship between interfacial resistance and micro-CT/functional parameters.

Correlation coefficient of interfacial resistance (IS and MRL) and micro-CT parameters (BMD, BV, BMC) was evaluated by 18 μm thick individual concentric peri-implant tissue layer (a, d, g, j) and cumulative layer (b, e, h, k) in osteotomy-alone (OA) and osteotomy+osseous defect (OS) groups. While stronger correlation between micro-CT parameters and interfacial resistance was noted in the 0.180 mm thickness peri-implant region of OA group (b, e), and 576 μm in the OS group (h, k), further calculation of correlation coefficient of functional parameters (FBAM and FCAM) and interfacial resistance (IS and MRL) was performed within 200 μm concentric peri-implant area in the OA group (c, f), and 600 μm area in the OS group (i, l).

Abbreviations: IS: interfacial stiffness; MRL: maximal removal load; BMD: bone mineral density; BV: bone volume; BMC: bone mineral content; FBAM: functional bone apparent modulus; FCAM: functional composite tissue apparent modulus

Further examination of the FAMs within 200 μm-thickness peri-implant tissue in the OA group and 600 μm-thickness in the OS group demonstrated the highest correlation of FBAM to both biomechanical parameters in the OA group in the 180 μm concentric layer (R>0.8, Fig. 3 c, f) as well as FCAM in OS group from around 200 μm-thickness (Fig. 3 i, j). Thus, the functionally relevant peri-implant layer reduced to 200 μm thickness in the situation with and without a pre-existing defect as determined from the FAMs evaluations.

4. DISCUSSION

Although modern biomechanical assessments such as nanoindentation or scanning acoustic microscopy may provide microscopic mapping of the mechanical properties of bone^25,26, the properties at the implant interface still cannot be directly measured. Thus, in this study we generated functional apparent moduli (FAMs) by simulating the implant loading situation and extrapolation via FE modeling to match the microscopic data. This approach may be more clinically relevant and feasible as a methodology to assess the functional capability of the peri-implant tissue during osseointegration. As this approach is based on simplified assumptions of the axis-symmetric model, we also ran a 3-D finite element model and have determined that it demonstrates a similar distribution of strain as the axis-symmetric model although is much less practical (data not shown, Figs. S3, S4). We demonstrate that FAMs, both FBAM and FCAM, are correlated to mathematical moduli. FBAM is capable of expressing the biomechanical performance in the traditional osteotomy defects, while FCAM can better interpret the functional dynamics in the peri-implant defect situation. While physical artifacts surrounding the titanium implant do not reflect a reliable bone-implant interfacial relationship (Fig. S2), we also demonstrated that meticulous removal of the implant did not result in significant radiographically detectable deformation through FE analyses (Fig. 2).

Significant enhancement of the interfacial biomechanics and structural parameters from days 7 to 10 were later accompanied by a progressive increase in the OA group (Table 3), which could be explained histologically from the report of Franchi et al.²⁷. They demonstrated that bone trabeculae quickly invade the initial gap at the bone-implant interface and mature into a three-dimensional spongiosa to offer greater resistance for early implant stability. Therefore, correlations between FAMs and the structural parameters indicate that the function of tissues does not solely depend on any single parameter. FBAM relates to the extent of bone maturation, and FCAM signifies the composite tissue rigidity toward the implant. In the OS group, significant differences of FAMs and mathematical moduli at both day 10 and 14 indicated that healing was still so immature that could not offer as strong of a functional support as the OA specimens (Table 3). However, this significant difference between 10 and 14 days for FCAM in the OS group indicates rapid bone apposition towards the implant surface during osseous wound repair. While bone is the rigidity-dominant tissue within the defect, by 14 days FCAM reached an equivalent value as FBAM in OS group (Table 3) implying that although the defect was not completely filled by bone, the composite tissue could offer equivalent function as the neogenic bone. This finding suggests that the main response within the osseous defect was rapid expansion of mineralized tissue thus providing greater support of the dental implant during the early stage of osseointegration. Consistent with these findings, several of our later-stage (mostly day-21) specimens experienced cortical bone fracture during the implant push-out, due to high interfacial bonding of mature osseointegration resulting in trabecular structure failure prior to the interfacial failure.

Implant stability is clearly one of the critical factors for evaluating implant success and for determining the timing for loading or abutment connection⁴. However, a poor understanding of the relationship between structural parameters and implant stability and the subsequent range of peri-implant tissue properties can lead to a discrepancy between the peri-implant structure and implant functions^5,6,28. From our study, stronger correlations of the functional apparent moduli to interfacial resistance imply that integration of the peri-implant structural information is necessary to predict the functional performance of the implant system. The functionally relevant peri-implant layer was also identified as 180 μm in the OA situation, and around 200 μm in the OS situation. We interpret these findings to mean that integration of the 3D peri-implant structure within a range of a 200 μm concentric layer is capable of predicting the tissue-implant interfacial biomechanics.

These results lead us to conclude that micro-CT imaging can be used to provide 3-D information of implant-supporting tissues following cylinder-type implant removal, and both micro-CT imaging together with FAMs are capable of predicting the functional dynamics of implant-supporting osseous tissues and the interfacial biomechanics during osseointegration. Utilization of these functional and imaging methodologies may provide key biomechanical information for progression of peri-implant wound healing and determination of timing of dental implant loading in human patients.