Abstract
In the past decade, the development of synthetic gene networks has attracted much attention from many researchers. In particular, the genetic oscillator known as the repressilator has become a paradigm for how to design a gene network with a desired dynamic behaviour. Even though the repressilator can show oscillatory properties in its protein concentrations, their amplitudes, frequencies and phases are perturbed by the kinetic parametric fluctuations (intrinsic molecular perturbations) and external disturbances (extrinsic molecular noises) of the environment. Therefore, how to design a robust genetic oscillator with desired amplitude, frequency and phase under stochastic intrinsic and extrinsic molecular noises is an important topic for synthetic biology.
In this study, based on periodic reference signals with arbitrary amplitudes, frequencies and phases, a robust synthetic gene oscillator is designed by tuning the kinetic parameters of repressilator via a genetic algorithm (GA) so that the protein concentrations can track the desired periodic reference signals under intrinsic and extrinsic molecular noises. GA is a stochastic optimization algorithm which was inspired by the mechanisms of natural selection and evolution genetics. By the proposed GA-based design algorithm, the repressilator can track the desired amplitude, frequency and phase of oscillation under intrinsic and extrinsic noises through the optimization of fitness function.
The proposed GA-based design algorithm can mimic the natural selection in evolutionary process to select adequate kinetic parameters for robust genetic oscillators. The design method can be easily extended to any synthetic gene network design with prescribed behaviours.
Keywords: synthetic gene network, robust synthetic gene oscillator, genetic algorithm (GA), nature selection, evolutionary genetic repressilator
Introduction
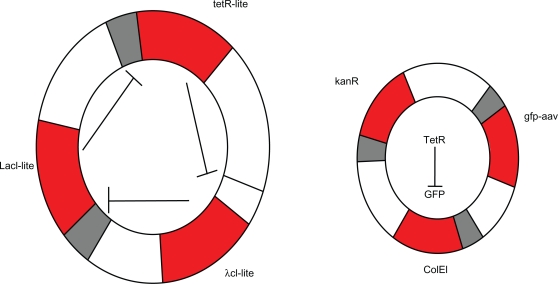
Although the molecular bases of cellular processes are already known, the behaviours of gene regulatory networks remain poorly understand due to the complexity of their components as well as their multiple specific interactions. The main goal of the nascent field of synthetic biology is to design and construct biological systems that present a desired behaviour.1,2 Synthetic biology is foreseen with important applications in biotechnology and medicine, and with significant contributions to a better understanding of the function of complex biological systems.3 Recently, several novel approaches to study the oscillatory interactions between genes and proteins of synthetic gene network have arisen.4–6 Two important designs of such networks advanced the study. One of them is the synthetic genetic toggle switch6 and the other is called the repressilator. In the present study, we focus on the design of a repressilator. The genetic network study of a repressilator was proposed by Elowitz and Leibler,4 consisting of three genes repressing each other in a closed chain (see Fig. 1). The repressilator can induce oscillation of the intracellular levels of three proteins encoded by the sequence of plasmid which is hosted by the unicellular bacterial microorganism Escherichia coli (E. coli).4
Figure 1.
Construction of the repressilator network in the host cell, E. coli. The repressilator is a cyclic negative-feedback loop composed of three repressor genes (the red regions) tetR, λcl, Lac and their corresponding promoters (the gray regions) in plasmid. The compatible reporter plasmid expresses an intermediate-stability GFP variant (gfp-aav) on the ring.
Although the repressilator can show oscillations in its protein concentrations, the design of a repressilator with desired amplitude, frequency and phase is a challenging problem in gene oscillator design. Moreover, the effects of thermal dynamic noise,7,8 mutation, cell division, undefined interactions with the cellular context,2 and changing extracellular environments can perturb oscillatory properties such as amplitude, frequency and phase. These stochastic behaviours are the consequence not only of current technological limitations but also of internal molecular fluctuations and external noise in the environment of the host cell. Therefore, designing a reliable gene oscillator with a desired amplitude, frequency and phase under these intrinsic parameter fluctuations and extrinsic disturbances on the host cell is another important topic for the design of robust synthetic gene oscillators.4,5,9,10 Robustness to intrinsic and extrinsic noises limits the range of possible circuits to only a few designs that can function properly in the synthetic gene network.11 Ko et al have proposed a constrained optimization method for system identification of biochemical network.12 Batt et al13 have proposed a piecewise-multi-affine method for a desired steady input/output of synthetic gene network and Chen et al14–16 and Lin et al17 have proposed a robust design to achieve a desired steady state of synthetic gene network. However, these desired steady state design methods can not be applied to transient oscillatory behaviours for a robust gene oscillator design problem. Indeed, these oscillatory behaviours could be represented as limit cycles in phase planes, which are more complex than steady state behaviours with a fixed equilibrium point. Therefore, how to design a robust oscillator around a desired limit cycle is more difficult than a robust synthetic gene network design with a desired constant steady state (i.e. to a desired equilibrium point) by the conventional system stabilization methods.14–16 The reason is that engineering a synthetic gene network with desired oscillatory behaviours is a tracking design problem, and more effort is needed to resolve it. To achieve the design objective of robust gene oscillator, we propose a genetic algorithm approach to imitate the adaptive design mechanisms via natural selection in the real evolutionary process.
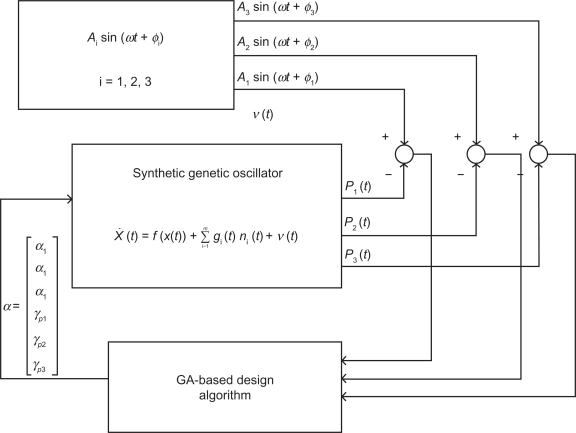
Unlike the conventional trial and error methods in gene oscillator designs, a systematic approach is developed for the robust design of oscillatory gene networks with desired amplitude, period, and phase that is robust against internal parameter fluctuations and external disturbances. At first, the desired oscillation is modeled by periodic reference signals with desired amplitudes, frequencies, and phases which are prescribed by the designer beforehand. Then, the robust gene oscillator design problem is transformed to a stochastic optimal tracking design problem, i.e. to specify the kinetic parameters of a gene oscillator to optimally track a reference periodic signal with desired amplitude, frequency and phase despite intrinsic fluctuation and external noise. Finally, a genetic algorithm (GA) is employed to mimic natural selection in an evolutionary process, which is faster than the adaptive design rules by natural selection in the real evolutionary process.18 This GA-based algorithm enables us to select adequate kinetic parameters to achieve optimal tracking of a repressilator on the host cell (see Fig. 2). GAs have been extensively applied in solving global optimization searching problems.19–26 Since GAs are parallel global search techniques that simulate natural genetic operators,20–22 they are useful when the closed-form optimization technique can not be applied. Further, because the GA-based design algorithm can simultaneously evaluate many points in the kinetic parameter space, it is more likely to converge toward the globally optimal tracking solution. The proposed GA-based design algorithm is inspired by the mechanics of natural selection to a population of binary strings encoding the parameter space. At each generation, it explores different areas of the parameter space, and then directs the search to regions where there is a high probability of finding improved tracking performance (fitness). By working with a population of tracking solutions, the design algorithm can search in effect for many local maximums of the fitness function, and thereby increase the likelihood of finding the global maximum of fitness function (or the optimal tracking performance). Global optimal tracking can be achieved via a number of genetic operators, e.g. reproduction, mutation, and crossover.
Figure 2.
Robust synthetic gene oscillator design process. Robust synthetic gene oscillator design process based on stochastic optimal reference tracking via GA searching. Based on the tracking error, the GA-based algorithm can select the design parameter vector α for synthetic genetic oscillator according to the three specifications (i)–(iii) to achieve the optimal tracking of any desired periodic signal in eq. (14).
After specifying kinetic parameters in feasible ranges by the proposed GA-based design algorithm for robust optimal tracking design, the robust synthetic gene oscillator could be realized with the recently advanced biological techniques. Combinatorial promoters with multiple TF binding sites, or operators, can assist in the programming gene expression to carry out the designed optimal transcription rates.5,27–29 Another characteristic method of protease modification is to control the degradation rates of protein by fusing ssrA- tagged proteins with corresponding protein, which can reduce the protein degradation of corresponding gene.5,30–32 Recently, a simple method to select adequate biological parts or devices from biological device datasheets (or libraries) to construct a gene network with desired kinetic parameters and decay rates has been proposed.33–35 In this way, synthetic biologists can increase the efficiency of gene circuit design through registries of biological parts from standard datasheets so that these biological parts or devices with desired parameters can be efficiently assembled into a desired synthetic gene oscillator.33–35
Gene oscillators have many useful applications. For instance, gene oscillators can be applied to control the dosage of drugs, e.g. melatonin can be released at night to aid sleeping.36 Moreover, oscillators are also essential for many biochemical networks which require synchronization among circuit elements.4,37 Further, since all these techniques can be effectively applied to any synthetic gene network design, in the future there should be many potential applications of robust synthetic gene networks.
Finally, a design example is given to describe the design procedure for a desired synthetic gene oscillator using the proposed GA-based design algorithm and to confirm its robust performance under intrinsic parameter fluctuation and extrinsic disturbance.
Methods
Stochastic model for repressilator under intrinsic and extrinsic molecular noises
In the previous repressilator design, the repressilator consists of two plasmids (see Fig. 1),4 one of which is a plasmid containing three in-chain repressor genes. The other plasmid consists of the reporter gene which encodes the green fluorescence protein (GFP). Because the GFP sequence is coupled to a promoter corresponding to one of proteins in the repressilator, if this protein is produced, it will repress the production of the GFP. That is to say, the oscillation expressions of the repressilator encoded proteins would be presented by the expression level of reporter gene. Hence, the oscillations of the system can be detected by measuring the fluorescence emitted by the cells.
In the repressilator shown in Figure 1, the first repressor protein, lacI from E. coli, inhibits the transcription of the second repressor gene, tetR from the tetracycline- resistance transposon TN10, whose protein product in turn inhibits the expression of the third gene, cI from the λ phage. Finally, cI inhibits lacI repression, completing the cycle. The negative feedback loop in the following transcriptional regulatory model can lead to temporal oscillations in the concentration of each component for us to design the repressilator and study its robust dynamic behaviour.4
| (1) |
| (2) |
where mi is the concentration of messenger RNA (mRNA) and pi and pj are concentrations of proteins for i = 1, 2, 3 corresponding to lacI, tetR, and cI; and j = 3, 1, 2 corresponding to cI, lacI, and tetR, respectively. Parameters γmi, and γpi are the decay rates of mRNAs and proteins. αi is the transcription rate of mRNA. α0i is the effect of leakiness and is usually zero for stable state. βi accounts for the number of translated protein molecules per mRNA molecule. Ki is the number of the jth proteins for a half repression of the ith promoter.
In this model, the network behaviour depends on the transcription rate of repressor concentration, the translation rates and decay rates of protein and mRNA. Depending on the values of these parameters, the network may be stable, chaotic or leading to sustained limit-cycle oscillations. Oscillations are favored by gene regulatory networks with strong promoters containing an efficient ribosome-binding site, tight transcriptional repression (low ‘leakiness’), cooperative repression characteristics, and comparable protein and mRNA decay rates.4 A further obstacle to the design of oscillatory biochemical networks is internal uncertainty, e.g. the thermal fluctuation and the stochastic effects due to the small number of particles involved, characterized as the fluctuations of parameters, and external disturbance on the host cell from the environment. These intrinsic parameter fluctuations and extrinsic molecular noises also may lead sustained oscillations to stable steady states or chaos. Although synthetic oscillators are much simpler than the real biological oscillations, at present these synthetic oscillators still can not work reliably for a long time and need further tuning before application.1,2 It is still difficult to systematically design a synthetic gene oscillator with desired amplitude, frequency and phase specified beforehand by the user. In practical applications, a robust synthetic gene oscillator with the desired amplitude, frequency and phase under intrinsic and extrinsic molecular noises is more useful. More efforts are still needed to achieve this kind of robust synthetic gene oscillator in vivo design.
Therefore, a robust synthetic oscillator network with desired amplitude, frequency and phase is more appealing for synthetic biologist. Before further discussion on the robust design of synthetic biological oscillators, a stochastic model for synthetic biological oscillator with intrinsic fluctuations and extrinsic disturbances in vivo is introduced as follows
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
where Δγmi, Δαi, Δβi, and Δγpi denote the kinetic parametric fluctuations and νk denotes the corresponding external stochastic disturbances with variance , for k = 1 … 6.
Suppose the parametric fluctuations are stochastic as follows
| (9) |
where δγmi, δαi, δβi, and δγpi denote the deterministic parts of parametric fluctuations, and n1, n2, n3, and n4 are independent standard white noises to denote the random fluctuation sources with unit variance.
i.e. δγmi, δαi, δβi, δγpi denote the standard deviations of the corresponding stochastic parametric fluctuations of Δγmi, Δαi, Δβi, Δγpi, respectively.
Substituting (9) into (3) to (8), we get the following stochastic synthetic oscillator in vivo
| (10) |
A more general form of stochastic system for synthetic biological oscillator (10) under intrinsic parameter fluctuations and external disturbances in the context of the host cell can be represented by the following nonlinear equation
| (11) |
where X = [m1 p1 … m3 p3]T denotes the state vector of the synthetic biological oscillator; ν = [ν1 … ν6]T denotes the external disturbance in vivo; f(X) denotes the nonlinear biochemical interactions of synthetic biological oscillator; and gi (X) denotes the effect of the ith random fluctuation source ni on the synthetic oscillator. In a real biological oscillator, the robust kinetic parameters are selected by natural selection in the evolutionary process to achieve robust oscillation under intrinsic and extrinsic molecular noises. In this study, we mimic the design rules of natural selection via genetic algorithm (GA) to select adequate kinetic parameters to achieve a robust genetic oscillator design via fast computer simulation.
Recent developed technique in synthetic biology may allow tuning promoter, ribosome binding and the protein degradation with relative ease and precision.5,27–32 Hence, we may select biological parts or devices with desired parameters to engineer gene circuits from biological device datasheets (or libraries) in future.33–35 Based on these biotechnologies or biological device datasheets, we want to design the transcription rates αi and the protein degradation rates γpi, i = 1, 2, 3 so that the protein concentrations pi, i = 1, 2, 3 of the synthetic oscillator in (10) have the desired amplitudes, frequencies and phases under stochastic intrinsic and extrinsic noises affecting the host cell. The transcription rates αi, i = 1, 2, 3 are dependent on the binding affinities of the corresponding transcription factors, which are related to the locations and lengths of binding sites inserted to the promoter regions of the target genes. The degradation rates γpi are dependent on their sequences and structures.30–32
Based on the analysis above, design specifications of robust synthetic gene oscillators are given as follows
- Give a desired oscillation with the following desired amplitudes, frequencies, and phases as followsa
i.e. Ai, ω, and φi, i = 1, 2, 3 in (12) are initially specified for the oscillatory behaviours of protein concentrations pi (t) in (10) by synthetic biologists.(12) Give the standard deviations δγmi, δαi, δβi, and δγpi, of intrinsic parameter fluctuations and the variances , k = 1 … 6 of extrinsic disturbances νi according to the in vivo situation of synthetic oscillators in the host cells.
- Give the ranges of feasible design parameters αi and γpi according to the feasible design condition
(13)
Then our design objective is to search for αi ∈ [αia αib] and γpi ∈ [γpia γpib], i = 1, 2, 3 such that the following mean-square tracking errors should be minimized to satisfy the requirement of the design specifications in (i)–(iii).
| (14) |
If the above mean-square tracking errors could be minimized by some design parameters and under the design specification (i)–(iii), then the amplitudes, frequencies and phases of the protein concentrations of synthetic genetic oscillator could be maintained as robustly as possible under the intrinsic and extrinsic molecular noises on the host cells.
Robust synthetic genetic oscillator design via GA-based design algorithm
It is generally not easy to get a closed-form solution to solve the optimal tracking design problem in (14) for a nonlinear stochastic oscillation system (11) to meet the robust synthetic oscillator design specifications (i)–(iii). In this study, the genetic algorithm (GA) is employed to mimic natural selection in the evolutionary process of a gene oscillator but with a faster evolutionary computation. Genetic algorithms are stochastic optimization algorithms that are originally motivated by the mechanisms of natural selection and evolutionary genetics.20–22 The underlying principles of GAs and mathematical frameworks were presented in Holland’s pioneering work, Adaptation in Natural and Artificial Systems.22 GAs have been proven to be efficient in many areas21 and more details about GAs can be found in.20
GAs are powerful searching algorithms based on the mechanics of natural genetic and are inherently parallel because they simultaneously evaluate many points in the parameter space (search space). Therefore, they are very suitable for the robust optimal design of synthetic gene oscillators. In the optimal tracking design problem (14), let us denote the cost function J
| (15) |
Our objective is to search for a set of design parameters αi and γpi, i = 1, 2, 3 by a genetic algorithm within the feasible parameter space in (13) to minimize J (αi, γpi), which should be assigned the smallest cost value. This is a highly nonlinear minimization problem, in which many local minima can be reached via conventional search algorithms, though they may not identify the global minimum. GA has been employed to solve the global minimization searching problem (15). Then the GA tries to generate better offspring αi and γpi, i = 1, 2, 3 to improve the fitness so we set a fitness function F (αi, γpi) ∝ 1/J (αi γpi). Therefore the fitness function plays the role of natural selection to select the parameters αi and γpi which will maximize the fitness function F (αi, γpi), or equivalently, minimize J (αi, γpi). Here we use the so-called the windowing mapping method to get the fitness function of natural selection as follows19
| (16) |
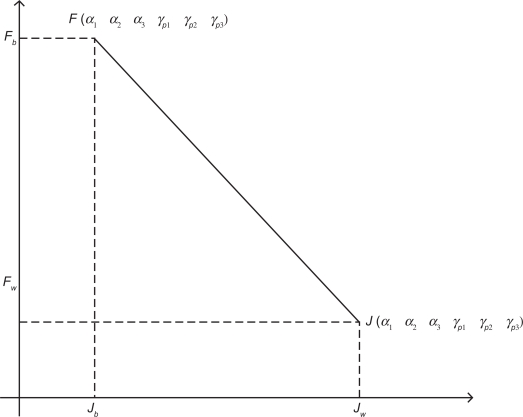
where the constants a and b are computed by Fb, Fw, Jb, and Jw in each generation according to (see Fig. 3)
i.e. the fitness function F (αi, γpi) is inversely proportional to J (αi, γpi). It means a small tracking error will lead to a large fitness, and vice versa.
Figure 3.
The inverse relation between the cost function J(α1 α2 α3 γP1 γP2 γP1) and fitness function F (α1 α2 α3 γP1 γP2 γP1) in eq. (16). This figure indicates that a large tracking error will lead to a small fitness, and vice versa.
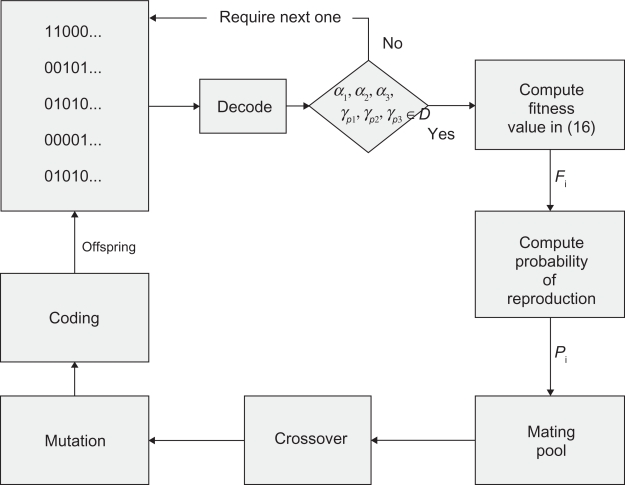
The GA-based deign algorithm is an iterative procedure to search for αi and γpi to maximize the fitness function in (16), which mimics the natural selection of the evolution process in the real world to select the optimal fit parameters for a robust synthetic gene oscillator. In each iteration or generation, these genetic operators (reproduction, crossover, and mutation) are performed to generate new populations (offsprings or new sets of parameters αi, γpi, i = 1, 2, 3), and the chromosomes of these new populations are evaluated via the fitness score (16). On the basis of these genetic operators and the evaluations, the better new populations of candidate solutions are formed in each genetic generation. A simple GA-based design algorithm is given as follows.
Generate a population (i.e. αi, γpi, i = 1, 2, 3) of binary strings randomly within feasible ranges in (13).
Calculate the fitness in (16) for each string in the population.
Create offspring by GA operators (i.e. reproduction, crossover, and mutation)
Evaluate the new strings and calculate the fitness of natural selection for each string.
If the searching goal is achieved, or an allowable generation is attained, stop and return; else go to (iii).
The convergence of genetic searching algorithm employed for our design problem has been discussed from the viewpoint of schema or similarity template scheme.20 It can be guaranteed that the optimal fitness function F ( , ) can be approached by genetic algorithm as t → ∞ and the corresponding optimal parameter set ( , ) is chosen as schema.20 We now describe the details in employing the proposed GA-based design algorithm to solve the robust design problem of synthetic gene oscillators. In order to introduce the design method more clearly, the following illustration is given with the description of αi only.
Chromosome coding and decoding
Since GAs work with a population of binary strings, not the parameters themselves, for simplicity and convenience, binary coding is used in this article. With the binary coding method to transform the phenotype space into a genotype space, the design parameters (phenotype) α1, α2, and α3 would be coded as binary strings (genotypes) of 0’s and 1’s with lengths B1, B2, and B3 (may be different), respectively. The choice of B1, B2, and B3 for the parameters is based on the resolution specified by the designer in the search space. In the binary coding method, the bit length Bi and the corresponding resolution Ri are related by
| (17) |
where the upper and lower bounds αib and αia are defined in (13). For example, suppose the feasible parameter domain of (α1, α2, α3) is
| (18) |
The resolution (R1, R2, R3) is specified by the designer as (0.25, 0.01, 0.2). From (17), we have(B1, B2, B3) = (4, 6, 5). Then the parameter set (α1, α2, α3) can be coded according to the following phenotype/genotype mapping
If (α1, α2, α3) is (0.25, 0.2, 8.7), then the chromosome for the parameter set is a binary string (0001 00000 11111). The decoding procedure is the reverse of the procedure for coding. Our design objective is to mimic natural selection in evolutionary process to search (α1, α2, α3) in D to achieve the maximization of the fitness function in (16) through GA via reproduction, crossover and mutation operators.
Reproduction
Reproduction is based on the principle of survival of the better fitness. The fitness of the ith string, Fi, is assigned to each individual string in the population where higher Fi means better fitness. These strings with large fitness would have a large number of copies in the new generation. For example, in roulette wheel selection, the ith string with high fitness value Fi is given a proportionately high probability of reproduction, Pi, according to the distribution
| (19) |
Once the strings are reproduced or copied for possible use in the next generation, they are reproduced in a mating pool where they await the action of the other two operators, crossover and mutation (see Fig. 4).
Figure 4.
Flow Chart for the design procedure via GA.
Crossover
By the second operator, the strings exchange information via probabilistic decision. Crossover provides a mechanism for strings to mix and match their desirable qualities through a random process. After reproduction, simple crossover proceeds in three steps. First, two newly reproduced strings are selected from the mating pool produced by reproduction. Second, a position along the two strings is selected uniformly at random. This is illustrated below where two binary coded strings, (α1, α2, α3)A and (α1, α2, α3)B with length l = 12 are shown aligned for crossover.
The third step is to exchange all characters following the crossing site. For example, the two strings (α1, α2, α3)A and (α1, α2, α3)B with a crossover at the 4th bit become.
Although crossover uses random choice, it should not be thought of as a random walk through the search space. When combined with reproduction, it is an effective means of exchanging information and combining portions of high-quality solutions.
Mutation
Reproduction and crossover give GAs most of their search power. The third operator, mutation, enhances an ability of GAs to find a near-optimal solution. Mutation is the occasional alternation of a value at a particular string position, an insurance policy against the permanent loss of any simple bit, and it is applied with a low probability such that it is chosen so that on average one string in the population is mutated. For example,
In the case of binary coding, the mutation operator simply flips the state of a bit from 0 to 1 at the 9th code or vice versa. Mutation should be used sparingly because it is a random search operator, and with high mutation rates, the algorithm could become a little more than a random search.
The convergence of a genetic search algorithm employed in our design problem can be shown by schema or a similarity template theorem20 to the maximization of fitness,b i.e. the optimal oscillation tracking for robust parameter design in (14) can be achieved under intrinsic parameter fluctuations and extrinsic disturbances in the design specifications (i)–(iii).
GAs are more suitable to the iterative synthetic gene oscillator design problem than other major searching methods such as gradient-based algorithms and random searching algorithms for the following reasons. First, the searching space may be very large. Second, the performance surface does not require a differentiability assumption with respect to changes in kinetic parameters of the repressilator. Hence, the gradient-based searching algorithms that depend on the existence of derivatives are inefficient. Third, the likely fit terms are less likely to be destroyed under a genetic operator, thereby often leading to faster convergence. Similarly, other synthetic gene networks with desired output responses can be obtained by the same design procedure.
Results
In order to illustrate the design procedure of the proposed robust synthetic gene oscillators, the following example with numerical simulation is given for the description of the design procedure.
Consider the synthetic gene oscillator example with the same parameters as,4 except that αi and γpi are to be designed. Suppose the desired phases of three proteins are uniformly distributed, e.g. φ1 = 2π/3, φ2 = 0, and φ3 = −2π/3. Then we give a prescribed reference model for the repressilator as follows (see Fig. 5a)
| (20) |
Figure 5.
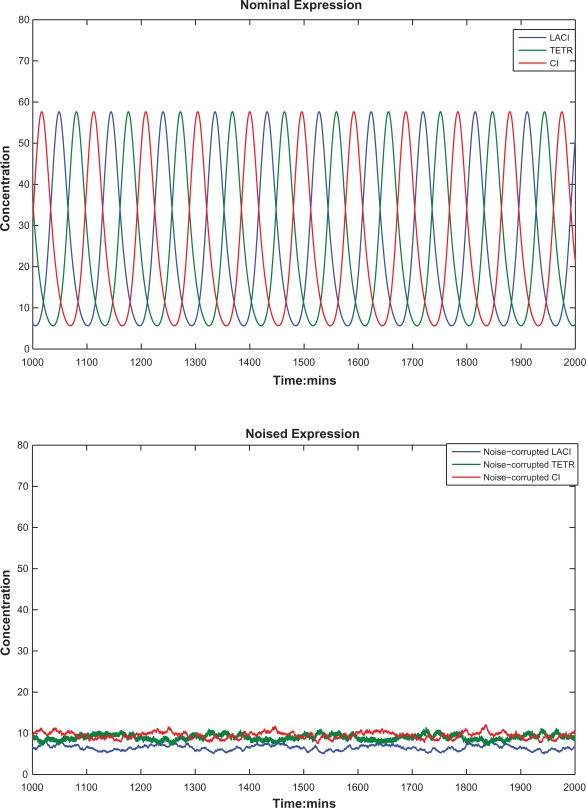
Time-responses of protein concentrations. (a) The nominal repressilator time-response with αi = 0.5, γpi 0.069 for i = 1, 2, 3 by the minute in.4 (b) The repressilator time-response under intrinsic parameter fluctuations and extrinsic disturbances on the host cell. These two time-responses show that the repressilator in4 suffers substantially from the effects of intrinsic parameter fluctuations and environmental noises on the host cell. Clearly, the corrupted repressilator does not have enough robustness to tolerate parameter fluctuations and extrinsic noises and loses its characteristics of oscillation.
Suppose the biochemical regulatory network is affected by the four random intrinsic parameter fluctuations from n1 to n4, and environmental disturbances ν1 (t), ν2 (t) and ν3 (t) as follows
| (21) |
where α0i = 0.001 αi for i = 1, 2, 3; and the random fluctuation sources n1, n2, n3, and n4 are independent standard white noises with unit variance from transcriptional noise, translational noise, and molecular diffusion noise etc. The standard deviations of stochastic parametric fluctuations in the host cell are assumed as
and the external noises νk for k = 1, 2, 3 are assumed to be uniformly distributed white noises on the concentrations of corresponding genes or proteins to show the ubiquitous intercellular and environmental disturbances.
Under the intrinsic fluctuations and extrinsic noises, the nominal and the noise-corrupted protein time-responses of a synthetic gene network with αi = 0.5 and γpi = 0.069 in4 are shown in Figures 5a and 5b, respectively. With intrinsic parameter perturbations and extrinsic disturbances, the parameter fluctuations of the repressilator can perturb the system away from the limit cycle region in,4 i.e. the bifurcation in parameters can perturb the synthetic genetic system away from limit cycle region and converge to some stable region with steady state values shown in Figure 5b. Obviously, the oscillatory character of synthetic repressilator in4 has been violated by intrinsic parameter fluctuations and extrinsic noises. Therefore, the repressilator in4 is not a robust oscillator. In this situation, a robust synthetic genetic oscillator design is necessary to guarantee the synthetic gene oscillator to function properly under intrinsic parameter fluctuations and extrinsic disturbances.
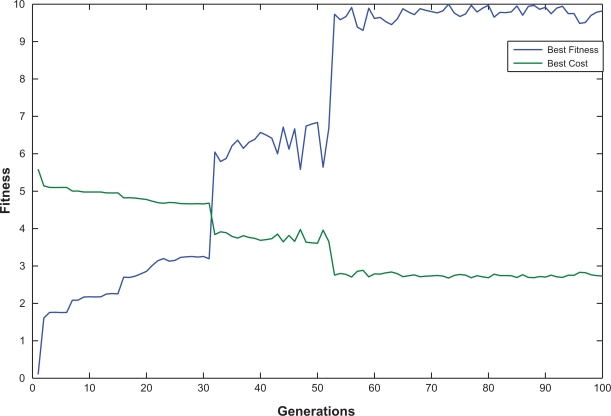
In order to solve the robust optimal tracking design problem of synthetic gene oscillator via the proposed GA-based design algorithm, we set the GA operators as follows: first, we use the roulette wheel selection to increase the selecting efficiency of the populations which have higher fitness score; second, the crossover rate is 0.8; third, the chromosome mutates uniformly with the mutation rate 0.05; and fourth, we set the constants a and b in (16) by choosing [Fb Fw Jb Jw] = [10 0.01 5.5869 2.6779]. In the binary coding process, we set the bit length in (17) as [Bα1 Bα2 Bα3 Bγp1 Bγp2 Bγp3] = [11 11 11 10 10 10], i.e. the corresponding resolutions of R αi and Rγpi are specified as [0.005 0.005 0.005 0.004 0.004 0.004] among the feasible parameter ranges given by αi ∈ [0 10] and γpi ∈ [0 5] for i = 1, 2, 3 (in,4 αi = 0.5 and γpi = 0.069 for all i). Via the help of Genetic Algorithm Toolbox in Matlab, from these feasible parameter ranges, we could solve the optimal tracking problem of robust synthetic oscillator in Figure 4 as [ ] = [0.515, 0.505, 0.505, 0.068, 0.068, 0.072], with fitness score 10. During the GA simulation, we record the course of evolutionary history in Figure 6. From the simulation result, we can see that the proposed GA-based design method could find the optimal oscillation tracking solution efficiently. Because of the random process of mutation and crossover, the average fitness score jumps up and down (Figure not shown). However, the best value is improved by employing the elite strategy with the best two populations in the evolution process. This can save the optimal solution until the crossover and mutation processes of the next generation. In Figure 6, we show both the evolutions of the best cost value and the best fitness score, with their relationship as shown in Figure 3. During the evolutionary process, because the repressilator system is a dynamic synthetic gene network, i.e. the parameter fluctuations and extrinsic disturbances vary stochastically in each generation, the fitness score of the best population in the new generation would be slightly different from the fitness score of the same population in the old generation. This is why the fitness score in Figure 6 is unsteady.
Figure 6.
Convergence of fitness value the best fitness score and best cost value evolve during the generations, whose relationship is shown in Figure 3. The vibrations of the best cost value and the best fitness score come from the stochastic intrinsic parameter fluctuations and extrinsic noises, which fluctuate in each generation and directly affect the reliability of the synthetic gene network.
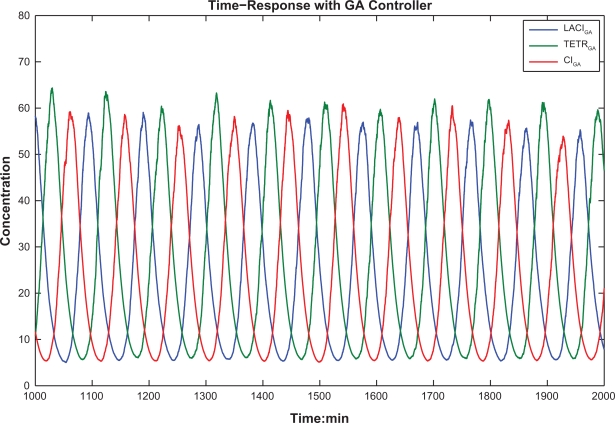
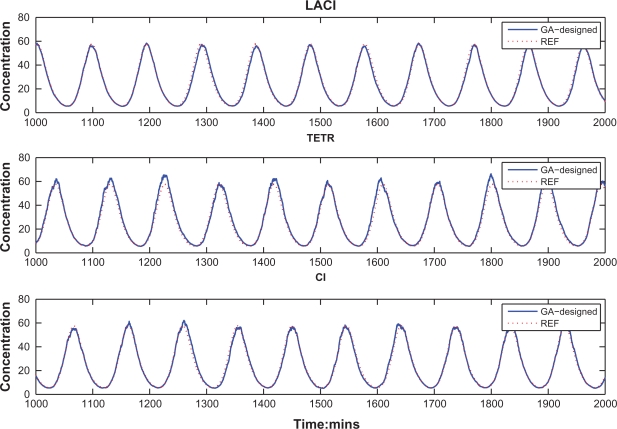
Based on the design parameters via the proposed GA-based design method, the time responses of robust synthetic gene oscillator under intrinsic parameter fluctuations and extrinsic noises are shown in Figure 7. Through the robust GA-based design method, we can obtain desired oscillatory behaviour in this repressilator system. In Figure 7(b), the repressilator system with GA optimal solutions shows the robust desired characteristics of oscillation under intrinsic parameter fluctuations and extrinsic disturbances. Although there are still some discrepancies between the desired oscillation signals and the protein concentrations of repressilator, mainly due to the intrinsic parameter fluctuations and extrinsic disturbances, these results are much better than the synthetic design in,4 as shown in Fig 5b. Clearly, the proposed robust synthetic gene oscillator design method has potential for practical applications in future.
Figure 7.
Time-response of the synthetic gene oscillator via the proposed GA-based design method solution. (a) Time-responses of these three proteins. (b) Time-response tracking of each protein and its reference. Under the parameter fluctuations and environmental noises, the designed repressilator can maintain its characteristics of oscillation and function properly. There are still some discrepancies between the desired reference signals and the protein concentrations of the repressilator, which are mainly due to parameter perturbations and environmental noises.
In this in silico robust repressilator design example, the robust design scheme could be realized with the specified robust mRNA transcription rates, , and protein decay rates, for i = 1, 2, 3, in the corresponding feasible parameter design ranges to satisfy the prescribed oscillatory characteristics of the synthetic gene oscillator. Several biotechnology methods have been proposed by adjusting the combinatorial polymerase binding boxes and integrating different ligations to generate a diverse promoter library and a diverse protein decay rate.27–32 Thus, we could synthesize the genetic repressilator with finetuned parameters, αi and γpi for i = 1, 2, 3 in (10) to confirm our design scheme. Although this method is direct, it is an inefficient method. To remedy this, synthetic biologists can increase efficiency of synthetic gene network design through registries of biological parts and standard datasheets of the Bio- Brick assembly standard, which are developed and concerned with proper packing and characterizing of ‘modular’ biological activities such that these biological parts or devices with some prescribed characters may be efficiently assembled into gene networks in the future.34,35
Comprehensive datasheets are used for quantitative descriptions of devices in many standardized engineering disciplines. A synthetic gene network designer can quickly and easily select some desired devices from biological device datasheets to meets their design requirements of a system.34 Thus, via the help of engineering theory and experience, a conceived system could be constructed by a set of devices with standard characteristics, which are typically reported on datasheets and are common across a wide range of devices type, such as sensors, logic elements and actuators. Recently, biological datasheets have been set as standards for the characterization, manufacture and sharing of information on modular biological devices to promote a more efficient, predictable and design-driven genetic engineering science.33–34 Because datasheets of biological parts or devices embody engineering standards for synthetic biology,34 a good device standard should show sufficient information about biological parts or devices to allow the design of synthetic gene networks with optimal parameters. Datasheets contain a formal set of context-dependent, input-output behaviours, tolerances, requirements and other details about a particular biological part or device.33–34 Since parameters αi represent the optimal transcriptional rates, these parameters could be measured from input-output behaviours of biological parts or devices. Moreover, through the combinations of one or more devices, a biological designer could assemble another well-defined physical device, such as a well-defined γpi, to achieve a desired oscillatory characteristic.34,35 From properly characterized input-output behaviours, the biological designer can estimate the corresponding parameters of biological parts or devices. Then, adequate devices can be rapidly selected from an extensive list of the parts to meet the design parameters. Adherence to the set of standard devices in datasheets ensures that each device and systems synthesized from them can satisfy the requirements of design specifications for a robust synthetic gene oscillator.
But there are many uncertainties about the behaviour of synthetic oscillators. For example, the cellular functions from devices will fluctuate and there are also many parasitic and unpredictable uncertainties among components as well as on the host cell. Since the transcriptional rate, αi, has a positive correlation with the promoter activity, it can been seen as a combinative presentation of promoter strength and ribosome binding site of the transcription. However, there are still some variations or uncertainties on the parameter value αi. In terms of a mathematic model, these variations or uncertainties of αi can be transformed to an equivalent uncertain disturbance δαi in equation (10), as can the other parameters δγmi, δβi, and δpi. The robust synthetic oscillator design can predict the most robust values of αi and γpi by the proposed GA-based design method under intrinsic fluctuations and extrinsic noise. In our design example, the proposed synthetic gene oscillator not only can achieve the desired oscillation tracking design but also can tolerate the worst-case effect due to these uncertain parameter fluctuations and external noises on the host cell.
Discussion
By using the GA-based design method along with Matlab, we can easily solve the design parameters for this optimal reference tracking problem of a robust synthetic gene oscillator under intrinsic and extrinsic noises. However, there are still some disadvantages in the GA method. First, this method requires a great deal of time for the coding and decoding process in the natural selection if the number of design parameters increases. Fortunately, there are many advanced GA methods, like Hybrid Genetic Algorithm (HGA)23,26,38 or the combination with Simulated Annealing Algorithm (SA),24,25 that can save time and increase the probability of finding the global optimum solution. Second, the solution may be only a near-optimum due to limitations of GA method, for example, the limitation of finite bit length Bi of chromosome coding and the finite generations in GA searching process. Therefore it is perhaps not surprising that the GA method may not converge to the truly global optimal tracking solution.
Despite these disadvantages of GA methods, their primary advantage is that the highly nonlinear constrained minimization problem in (14) can be solved for a robust synthetic gene oscillator, which does not have a closed-form solution. To avoid finding a local optimal solution, the proposed GA-based design method can help approach the global optimal solution by the ‘mutation’ and ‘crossover’ processes. Even though the GA method does not always find the global optimal solution, its solution is often close to the optimum, whereas other conventional searching algorithm can only obtain a local optimal solution. By the property of mimicking natural selection in the GA method, most optimal solutions are not reproducible in the repeated biological simulations. This is not surprising because the GA searching process contains not only the different initial conditions but also the different random mutations and crossovers, as in real world evolutionary processes. For example, in some in vivo experimental studies, E. coli changes its genotype to increase the survival opportunity when suffering intrinsic fluctuations and environmental noises like glucose fluctuation, glucose limitation, molecular thermal fluctuation or other environmental stresses.39–41 These random mutations and crossovers may be different in the GA searching process, but the evolutionary results from the GA method would be very similar due to mimicking the natural selection to maximize the fitness score in (16). This phenomenon is a form of convergent evolution and, clearly, our results by the GA-based design method in silico mirror what happens in these in vivo studies in parallel E. coli cultures.
From an engineering point of view, when we synthesize a prescribed biological oscillator as the repressilator, its function could suffer interference from the intrinsic fluctuations and environmental noises that affect the host cell. These fluctuations and noises will corrupt the synthetic gene oscillator so that it can not achieve the desired behaviour. In this study, we proposed a design procedure using the GA method which mimics the natural selection in the evolutionary process of the real world to optimize the desired reference tracking of synthetic gene oscillator and to tolerate parameter fluctuations and external disturbances on the host cell. In this respect, our design is a rapid selection scheme. This can save the evolution time for optimal selection in the revolutionary process for increasing the robust oscillation characteristics and for improving the reliability of a synthetic gene network. Thus, the time responses in Figure 7b compared with the time response in Figure 5b show that the robustly designed repressilator can efficiently eliminate the effect of uncertainties due to effects of intrinsic parameter fluctuation and the extrinsic noise on the oscillation.
Clearly, the proposed GA-based design method provides a systematic design method for a robust synthetic gene oscillator with desired amplitude, frequency and phase in a host cell with intrinsic parameter fluctuations and external disturbances. Therefore, combined with the recently advanced synthetic techniques such as promoter library, ssrA- tagged protein or the Biobrick assembly standard devices in biological device datasheets, the proposed design method has good potential for practical applications of robust synthetic genetic oscillators in future.
Recently, the synchronization problems of coupled biochemical oscillations have been widely studied.42–45 This is an important topic of synthetic gene oscillators for practical applications. Therefore, the robust synchronization design problem of a large number of coupling synthetic gene oscillators under intrinsic fluctuations and external disturbances will be our future work.
Conclusions
This study proposes a simple but efficient robust synthetic gene oscillator design method via a genetic algorithm. To mimic the natural selection in evolution in order to select adequate design parameters for obtaining a robust synthetic gene oscillator with desired amplitude, frequency and phase under intrinsic parametric fluctuations and extrinsic disturbances on the host cell, the proposed GA-based design method can search for design parameters to achieve the fitness maximization which is equivalent to the optimal tracking of desired oscillation under the effects of intrinsic and extrinsic noises on the host cell. The contributions of this study are given in the following. First, the intrinsic parametric fluctuations and environmental noises can be modelled as state-dependent noises and external disturbances of nonlinear stochastic oscillatory systems to mimic the stochastic behaviour of synthetic gene oscillators in a host cell. Second, the robust oscillator design problem can be formulated as an optimal tracking design problem and then transformed to a fitness maximization problem. Third, based on the fitness function, a GA-based design method is proposed to mimic natural selection in actual evolutionary processes to search for the design parameters of a synthetic oscillator to achieve the desired robust oscillation. The simulation results show that the robustness performance of the synthetic gene oscillator is guaranteed by the proposed design method. Therefore, the proposed GA-based design method has good potential for the practical design of robust synthetic gene oscillators. Further, it can also be extended to the robust design of other synthetic gene networks which could track their desired behaviours.
Acknowledgments
The study was supported by the Center for Fundamental Science Research of National Tsing Hua University in Taiwan and by the National Science Council of Taiwan under Grant no. NSC 97-2627-P-001-002.
Footnotes
Disclosures
This manuscript has been read and approved by all authors. This paper is unique and is not under consideration by any other publication and has not been published elsewhere. The authors and peer reviewers of this paper report no conflicts of interest. The authors confirm that they have permission to reproduce any copyrighted material.
The sinusoidal signal in (12) is given only for the convenience of the desired periodic signal. Actually, it can be any periodic signal to be designed for the synthetic genetic oscillator. For example, it could be any signal Yi (t) generated by the nonlinear differential equation Yi (t) = f (Yi (t)), Yi (0) = Yi,0, for i = 1, 2, 3.
In addition, in the genetic algorithm, the elitist strategy can be incorporated. This strategy directly copies the best chromosome from the old population into the next population to prevent losing the best solutions in the succeeding iteration to improve the genetic algorithm performance.
References
- 1.Endy D. “Foundations for engineering biology,”. Nature. 2005;438:449–53. doi: 10.1038/nature04342. [DOI] [PubMed] [Google Scholar]
- 2.Andrianantoandro E, et al. “Synthetic biology: new engineering rules for an emerging discipline,”. Mol Syst Biol. 2006;2:10.1038. doi: 10.1038/msb4100073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.McDaniel R, Weiss R. “Advances in synthetic biology: on the path from prototypes to applications,”. Current Opinion in Biotechnology. 2005;16:476–83. doi: 10.1016/j.copbio.2005.07.002. [DOI] [PubMed] [Google Scholar]
- 4.Elowitz MB, Leibler S. “A synthetic oscillatory network of transcriptional regulators,”. Nature. 2000;403:335–8. doi: 10.1038/35002125. [DOI] [PubMed] [Google Scholar]
- 5.Hasty J, et al. “Engineered gene circuits,”. Nature. 2002;420:224–30. doi: 10.1038/nature01257. [DOI] [PubMed] [Google Scholar]
- 6.Gardner TS, et al. “Construction of a genetic toggle switch in Escherichia coli,”. Nature. 2000;403:339–42. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- 7.McAdams HH, Arkin A. “It’s a noise business,”. Genetic regulation at the nanomolar scale Trends in Genetics. 1999;15:65–9. doi: 10.1016/s0168-9525(98)01659-x. [DOI] [PubMed] [Google Scholar]
- 8.Chen BS, Wang YC. “On the attenuation and amplification of molecular noise in genetic regulatory networks,”. BMC Bioinformatics. 2006;7:52. doi: 10.1186/1471-2105-7-52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kitano H. “Biological robustness,”. Nature Reviews Genetics. 2004;5:826–37. doi: 10.1038/nrg1471. [DOI] [PubMed] [Google Scholar]
- 10.Alon U. An introduction to systems biology: design principles of biological circuits. Chapman and Hall/CRC; 2007. [Google Scholar]
- 11.Alon U.“Biological networks: the tinkerer as an engineer,”vol. 301, ed:American Association for the Advancement of Science 20031866–7. [DOI] [PubMed] [Google Scholar]
- 12.Ko CL, et al. “Estimating parameters for generalized mass action models with connectivity information,”. BMC Bioinformatics. 2009;10:140. doi: 10.1186/1471-2105-10-140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Batt G, et al. “Robustness analysis and tuning of synthetic gene networks,”. Bioinformatics. 2007;23:2415. doi: 10.1093/bioinformatics/btm362. [DOI] [PubMed] [Google Scholar]
- 14.Chen BS, Chen PW. “Robust Engineered Circuit Design Principles for Stochastic Biochemical Networks With Parameter Uncertainties and Disturbances,”. IEEE Transactions on Biomedical Circuits and Systems. 2008;2:114–32. doi: 10.1109/TBCAS.2008.926728. [DOI] [PubMed] [Google Scholar]
- 15.Chen BS, et al. “Robust synthetic biology design: stochastic game theory approach,”. Bioinformatics. 2009;25(14):1822–30. doi: 10.1093/bioinformatics/btp310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chen BS, Wu CH. “A systematic design method for robust synthetic biology to satisfy design specifications,”. BMC Systems Biology. 2009;3:66. doi: 10.1186/1752-0509-3-66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lin YC, Lin CL. “Optimal control approach for robust control design of neutral systems,”. Optimal Control Applications and Methods. 2009;30 [Google Scholar]
- 18.Chen BS, Wu Ws. “Underlying principles of natural selection in network evolution: systems biology approach,”. Evolutionary Bioinformatics. 2007;3:245–62. [PMC free article] [PubMed] [Google Scholar]
- 19.Chen BS, et al. “A genetic approach to mixed H2/H∞ optimal PID control,”. Control Systems Magazine IEEE. 1995;15:51–60. [Google Scholar]
- 20.Goldberg DE. Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley Longman Publishing Co., Inc; Boston, MA, USA: 1989. [Google Scholar]
- 21.Grefenstette J. “Optimization of control parameters for genetic algorithms,”. IEEE Transactions on Systems, Man and Cybernetics. 1986;16:122–8. [Google Scholar]
- 22.Holland JH. Adaptation in natural and artificial systems. University of Michigan Press; Ann Arbor: 1975. [Google Scholar]
- 23.Katayama K, Narihisa H. “An Efficient Hybrid Genetic Algorithm for the Traveling Salesman Problem,”. Electronics and Communications in Japan, Part III: Fundamental Electronic Science (English translation of Denshi Tsushin Gakkai Ronbunshi) 2001;84:76–83. [Google Scholar]
- 24.Khan Z, et al. “Machining condition optimization by genetic algorithms and simulated annealing,”. Computers and Operations Research. 1997;24:647–57. [Google Scholar]
- 25.Kirkpatrick S. “Optimization by simulated annealing: Quantitative studies,”. Journal of Statistical Physics. 1984;34:975–86. [Google Scholar]
- 26.Renders JM, Flasse SP. “Hybrid methods using genetic algorithms for global optimization,”. Systems, Man and Cybernetics, Part B, IEEE Transactions on. 1996;26:243–58. doi: 10.1109/3477.485836. [DOI] [PubMed] [Google Scholar]
- 27.Basu S, et al. “A synthetic multicellular system for programmed pattern formation,”. Nature. 2005;434:1130–4. doi: 10.1038/nature03461. [DOI] [PubMed] [Google Scholar]
- 28.Cox RS, et al. “Programming gene expression with combinatorial promoters,”. Molecular Systems Biology. 2007;3 doi: 10.1038/msb4100187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hammer K, et al. “Synthetic promoter libraries–tuning of gene expression,”. Trends in Biotechnology. 2006;24:53–5. doi: 10.1016/j.tibtech.2005.12.003. [DOI] [PubMed] [Google Scholar]
- 30.McGinness KE, et al. “Engineering Controllable Protein Degradation,”. Molecular Cell. 2006;22:701–7. doi: 10.1016/j.molcel.2006.04.027. [DOI] [PubMed] [Google Scholar]
- 31.Solem C, Jensen PR. “Modulation of Gene Expression Made Easy,”. Applied and Environmental Microbiology. 2002;68:2397–403. doi: 10.1128/AEM.68.5.2397-2403.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wong WW, et al. “Single-cell zeroth-order protein degradation enhances the robustness of synthetic oscillator,”. Molecular Systems Biology. 2007;3 doi: 10.1038/msb4100172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Arkin A. “Setting the standard in synthetic biology,”. 2008 doi: 10.1038/nbt0708-771. [DOI] [PubMed] [Google Scholar]
- 34.Canton B, et al. “Refinement and standardization of synthetic biological parts and devices,”. 2008. [DOI] [PubMed]
- 35.Knight T, LAB Massachusetts Inst of Tech Cambridge Artificial Intelligence, “Idempotent vector design for standard assembly of biobricks,” ed: Massachusetts Inst of Tech Cambridge Artificial Intelligence LAB, 2003
- 36.Folkard S, et al. “Melatonin stabilises sleep onset time in a blind man without entrainment of cortisol or temperature rhythms,”. Neuroscience Letters. 113:193. doi: 10.1016/0304-3940(90)90302-p. [DOI] [PubMed] [Google Scholar]
- 37.McMillen D, et al. “Synchronizing genetic relaxation oscillators by intercell signaling,”. Proceedings of the National Academy of Sciences. 2002;99:679–4. doi: 10.1073/pnas.022642299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Katayama K, et al. “The efficiency of hybrid mutation genetic algorithm for the travelling salesman problem,”. Mathematical and Computer Modelling. 2000;31:197–203. [Google Scholar]
- 39.Cooper TF, et al. “Parallel changes in gene expression after 20,000 generations of evolution in Escherichia coli,”. Proceedings of the National Academy of Sciences. 2003;100:1072–7. doi: 10.1073/pnas.0334340100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Papadopoulos D, et al. “Genomic evolution during a 10,000-generation experiment with bacteria,” vol. 96(7), ed: National Acad Sciences. 1999:3807–12. doi: 10.1073/pnas.96.7.3807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Pelosi L, et al. “Parallel Changes in Global Protein Profiles During Long-Term Experimental Evolution in Escherichia coli,”. Genetics. 2006;173:1851. doi: 10.1534/genetics.105.049619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wang R, Chen L. “Synchronizing genetic oscillators by signaling molecules,”. Journal of Biological Rhythms. 2005;20:257. doi: 10.1177/0748730405275653. [DOI] [PubMed] [Google Scholar]
- 43.Wang R, et al. “Synchronizing a multicellular system by external input: an artificial control strategy,”. Bioinformatics. 2006;22:1775–81. doi: 10.1093/bioinformatics/btl182. [DOI] [PubMed] [Google Scholar]
- 44.Zhou T, et al. “Molecular communication through stochastic synchronization induced by extracellular fluctuations,”. Physical Review Letters. 2005;95:178103. doi: 10.1103/PhysRevLett.95.178103. [DOI] [PubMed] [Google Scholar]
- 45.Zhou T, et al. “Synchronization of genetic oscillators,”. Chaos: An Interdisciplinary Journal of Nonlinear Science. 2008;18:037126. doi: 10.1063/1.2978183. [DOI] [PubMed] [Google Scholar]