Choosing Statistical Tests

Abstract

Background

The interpretation of scientific articles often requires an understanding of the methods of inferential statistics. This article informs the reader about frequently used statistical tests and their correct application.

Methods

The most commonly used statistical tests were identified through a selective literature search on the methodology of medical research publications. These tests are discussed in this article, along with a selection of other standard methods of inferential statistics.

Results and conclusions

Readers who are acquainted not just with descriptive methods, but also with Pearson’s chi-square test, Fisher’s exact test, and Student’s t test will be able to interpret a large proportion of medical research articles. Criteria are presented for choosing the proper statistical test to be used out of the most frequently applied tests. An algorithm and a table are provided to facilitate the selection of the appropriate test.

Medical knowledge is increasingly based on empirical studies and the results of these are usually presented and analyzed with statistical methods. It is therefore an advantage for any physician if he/she is familiar with the frequently used statistical tests, as this is the only way he or she can evaluate the statistical methods in scientific publications and thus correctly interpret their findings. The present article will therefore discuss frequently used statistical tests for different scales of measurement and types of samples. Advice will be presented for selecting statistical tests—on the basis of very simple cases.

Statistical tests used frequently in medical studies

In order to assess which statistical tests are most often used in medical publications, 1828 publications were taken from six medical journals in general medicine, obstetrics and gynecology, or emergency medicine. The result showed that a reader who is familiar with descriptive statistics, Pearson’s chi-square test, Fisher’s exact test and the t-test, should be capable of correctly interpreting the statistics in at least 70% of the articles (1). This confirmed earlier studies on frequently used statistical tests in medical scientific literature (2, 3). There have however been changes over time in the spectrum of the tests used. A survey of the analytical statistical procedures used in publications of the journal Pediatrics in the first six months of 2005 found that the proportion of inferential methods had increased from 48 to 89% between 1982 and 2005 (4). There was also a trend towards more complex test procedures. Nevertheless, here too, the most frequent tests were the t-test, the chi-square test, and Fisher’s exact test. This article will accordingly discuss these tests and their proper application, together with other important statistical tests. If the reader is familiar with this limited number of tests, he/she will be capable of interpreting a large proportion of medical publications. Information about the rarer statistical tests can be found in the corresponding articles, in advanced literature (5– 7), or by consulting an experienced statistician.

What is the purpose of statistical tests?

Clinical studies [for example, [5, 8]) often compare the efficacy of a new preparation in a study group with the efficacy of an established preparation, or a placebo, in a control group. Aside from a pure description (9), we would like to know whether the observed differences between the treatment groups are just random or are really present. This is because differences can be due to chance variability (scatter) in a parameter, such as the success of the treatment in the study group.

Definition

If a scientific question is to be examined by comparing two or more groups, one can perform a statistical test. This means that a null hypothesis must be formulated, which can in principle be rejected. Moreover, a suitable test parameter must be identified (10, 11).

For example, a clinical study might investigate whether an antihypertensive drug works better than placebo. The test variable may then be the reduction in diastolic blood pressure, calculated from the mean difference in blood pressure between the active treatment and placebo groups. The null hypothesis is then: “There is no difference between the active treatment and the placebo with respect to antihypertensive activity” (effect = 0).

A statistical test then calculates the probability of obtaining the observed data (or even more extreme data), if the null hypothesis is correct. A small p-value means that this probability is slight. The null hypothesis is rejected if the p-value is less than a level of significance which has been defined in advance. A test variable (test statistic) is calculated from the observed data and this forms the basis of the statistical test. In our case, this might be the difference in mean blood pressure after six months. If specific assumptions are made about the distribution of the data (for example, normal distribution), the theoretical (expected) distribution of the test variable can be calculated.

The value of the test variable calculated from the observations is then compared with the distribution expected if the null hypothesis were correct (5). If this value is greater or less than a specific limit, it is unlikely that the null hypothesis is correct and the null hypothesis is accordingly rejected. The result is then “statistically significant at the level α”. The statistical test is thus a decision whether the observed value can be explained by chance, or whether it is greater than chance (statistically significant). The terms “level of significance” and the principle of the interpretation of p-values have already been discussed (10, 11). The underlying steps in a statistical test are shown once again in the Box.

Box. Steps in a statistical test.

• Statement of the question to be answered by the study

• Formulation of the null and alternative hypotheses

• Decision for a suitable statistical test

• Specification of the level of significance (for example, 0.05)

• Performance of the statistical test analysis: calculation of the p-value

• Statistical decision: for example

  • p<0.05 leads to rejection of the null hypothesis and acceptance of the alternative hypothesis

  • p≥0.05 leads to retention of the null hypothesis

• Interpretation of the test result

It is possible to be mistaken, either in the rejection or in the retention of the null hypothesis. The reason for this is that the values exhibit scatter, as, for example, not all patients react equally to a drug. An “error of the first type” is the mistaken rejection of the null hypothesis; the maximal probability of this error is the level of significance α. This is often chosen to be 5% (10, 11). An “error of the second type” is the mistaken retention of the null hypothesis; the probability of this is ß, which is the same as 1 minus the power of the study. The power of the study is specified before the study starts and depends on the sample size, as well as other factors. A power of 80% is often selected (10, 11).

Important steps in the decision for a statistical test

The decision for a statistical test is based on the scientific question to be answered, the data structure, and the study design. Before the data are recorded and the statistical test is selected, the question to be answered and the null hypothesis must be formulated. The test and the level of significance must be specified in the study protocol before the study is performed. It must be decided whether the test should be one-tailed or two-tailed. If the test is two-tailed, this means that the direction of the expected difference is unclear. One does not know whether there is a difference between the new drug and placebo with respect to efficacy. It is unclear in which direction the difference may be. (The new drug might even work less well than the placebo). A one-tailed test should only be performed when there is clear evidence that the intervention should only act in one direction.

The outcome variable (endpoint) is defined at the same time the question to be answered is formulated. Two criteria are decisive for the selection of the statistical test:

• The scale of measurement of the test variable (continuous, binary, categorical)

• The type of study design (paired or unpaired).

Scales of measurement: continuous, categorical, or binary

The different scales of measurement have already been discussed in the articles on study design and descriptive statistics, under the selection of suitable measures and methods of illustration (9, 12).

For example, in the comparison of two antihypertensives, the endpoint can be the antihypertensive activity in the two treatment groups. The reduction in blood pressure is a continuous endpoint. It is also necessary to distinguish whether a continuous endpoint is (approximately) normally distributed or not.

If however one only considers whether the diastolic blood pressure falls under 90 mm Hg or not, the endpoint is then categorical. It is even binary, as there are only two possibilities. If there is a meaningful sequence in the categorical endpoints, this can be described as an “ordinal endpoint.”

Paired and unpaired study designs

A statistical test is used to compare the results of the endpoint under different test conditions (such as treatments). There are often two therapies.

If results can be obtained for each patient under all experimental conditions, the study design is paired (dependent). For example, two times of measurement may be compared, or the two groups may be paired with respect to other characteristics.

Typical examples of pairs are studies performed on one eye or on one arm of the same person. Typical paired designs include comparisons before and after treatment. “Matched pairs,” for example in case-control studies, are a special case. This involves selecting persons from one group with the same specified characteristics as persons in another group. The data are then no longer independent and should be treated as if they were paired observations from one group (5).

With an unpaired or independent study design, results for each patient are only available under a single set of conditions. The results of two (or more) groups are then compared. There may be differences in the sizes of the groups.

Common statistical tests

The most important statistical tests are listed in the Table. A distinction is always made between “categorical or continuous” and “paired or unpaired.” If the endpoint is continuous, normal and non-normal distributions are distinguished (Table).

Table. Frequently used statistical tests (modified from [3]).

Statistical Test	Description
Fisher’s exact test	Suitable for binary data in unpaired samples: the 2 x 2 table is used to compare treatment effects or the frequencies of side effects in two treatment groups
Chi-square test	Similar to Fisher’s exact test (albeit less precise). Can also compare more than two groups or more than two categories of the outcome variable. Preconditions: sample size >ca. 60. Expected number in each field ≥5.
McNemar test	Preconditions similar to those for Fisher’s exact test, but for paired samples
Student’s t-test	Test for continuous data. Investigates whether the expected values for two groups are the same, assuming that the data are normally distributed. The test can be used for paired or unpaired groups.
Analysis of variance	Test preconditions as for the unpaired t-test, for comparison of more than two groups. The methods of analysis of variance are also used to compare more than two paired groups.
Wilcoxon’s rank sum test (also known as the unpaired Wilcoxon rank sum test or the Mann-Whitney U test)	Test for ordinal or continuous data. In contrast to Student’s t-test, does not require the data to be normally distributed. This test too can be used for paired or unpaired data.
Kruskal-Wallis test	Test preconditions as for the unpaired Wilcoxon rank sum test for comparing more than two groups
Friedman test	Comparison of more than two paired samples, at least ordinally scaled data
Log rank test	Test of survival time analysis to compare two or more independent groups
Pearson correlation test	Tests whether two continuous normally distributed variables exhibit linear correlation
Spearman correlation test	Tests whether there is a monotonous relationship between two continuous, or at least ordinal, variables

Group comparison of two categorical endpoints

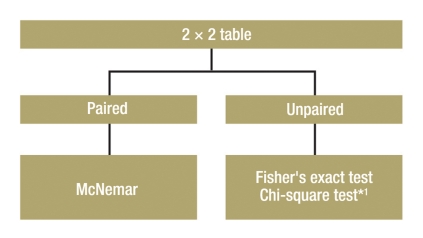
The group comparison for two categorical endpoints is illustrated here with the simplest case of a 2 x 2 table (four field table) (Figure 1). However, the procedure is similar for the group comparison of categorical endpoints with multiple values (Table).

Figure 1.

Test selection for group comparison with two categorical endpoints;

^*1 Preconditions: sample size

>ca. 60. Expected number in each field ≥5

• Unpaired samples:

  If the frequency of success in two treatment groups is to be compared, Fisher’s exact test is the correct statistical test, particularly with small samples (7). For large samples (about n >60), the chi-square test can also be used (Table).

• Paired samples:

  One example of the use of this test would be an intervention within a group at two anatomical sites, such as the implantation of two different sorts of IOL lenses in the right and left eyes, with the endpoint “Operation successful: yes or no.” The samples to be compared are paired. In such a case, one has to perform the McNemar test (7).

Continuous and at least ordinally scaled variables

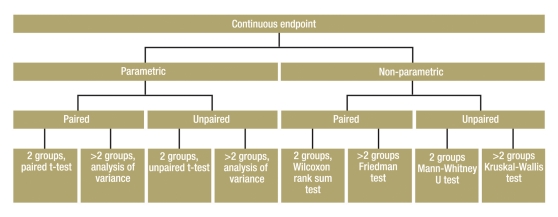
Figure 2 shows a decision algorithm for test selection.

Figure 2.

Algorithm for test selection for group comparison of a continuous endpoint

Normally distributed variables—parametric tests: So-called parametric tests can be used if the endpoint is normally distributed.

• Unpaired samples:

  Where subjects in both groups are independent of each other (persons in first group are different from those in second group), and the parameters are normally distributed and continuous, the unpaired t-test is used. If a comparison is to be made of a normally distributed continuous parameter in more than two independent (unpaired) groups, analysis of variance (ANOVA) can be used. One example would be a study with three or more treatment arms. ANOVA is a generalization of the unpaired t-test. ANOVA only informs you whether the groups differ, but does not say which groups. This requires methods of multiple testing (11).

• Paired samples:

  The paired t-test is used for normally distributed continuous parameters in two paired groups. If a normally distributed continuous parameter is compared in more than two paired groups, methods based on analysis of variance are also suitable. The factor describes the paired groups—for example, more than two points of measurement in the use of a therapy.

Non-normally distributed variables—non-parametric tests: If the parameter of interest is not normally distributed, but at least ordinally scaled, non-parametric statistical tests are used. One of these tests (the “rank test”) is not directly based on the observed values, but on the resulting rank numbers. This necessitates putting the values in order of size and giving them a running number. The test variable is then calculated from these rank numbers. If the necessary preconditions are fulfilled, parametric tests are more powerful than non-parametric tests. However, the power of parametric tests may sink drastically if the conditions are not fulfilled.

• Unpaired samples:

  The Mann-Whitney U test (also known as the Wilcoxon rank sum test) can be used for the comparison of a non-normally distributed, but at least ordinally scaled, parameter in two unpaired samples (5). If more than two unpaired samples are to be compared, the Kruskal-Wallis test can be used as a generalization of the Mann-Whitney U test (13).

• Paired samples:

  The Wilcoxon signed rank test can be used for the comparison of two paired samples of non-normally distributed, but at least ordinally scaled, parameters (13). Alternatively, the sign test should be used when the two values are only distinguished on a binary scale—for example, improvement versus deterioration (7). If more than two paired samples are being compared, the Friedman test can be used as a generalization of the sign test.

Other test procedures

Survival time analysis

If the point of interest is not the endpoint itself, but the time till it is reached, survival time analysis is the most suitable procedure. This compares two or more groups with respect to the time when an endpoint is reached (within the period of observation) (13). One example is the comparison of the survival time of two groups of cancer patients given different therapies. The endpoint here is death, although it could just as well be the occurrence of metastases. In contrast to the previous tests, it almost never happens that all subjects reach the endpoint in survival time analysis, as the period of observation is limited. For this reason, the data are also described as (right) censored, as it is still unclear when all subjects will reach the endpoint when the study ends. The log rank test is the usual statistical test for the comparison of the survival functions between two groups. A formula is used to calculate the test variable from the observed and the expected numbers of events. This value can be compared with the known distribution which would have been expected if the null hypothesis were correct—the chi-square distribution in this case. A p-value can thus be calculated. A rule can then be given for deciding for or against the null hypothesis.

Correlation analysis

Correlation analysis examines the strength of the correlation between two test variables, for example, the strength of the correlation between the body weight of a neonate and its body length. The selection of a suitable measure of association depends on the scale of measurement and the distribution of the two parameters. The parametric variant (Pearson correlation coefficient) exclusively tests for a linear correlation between continuous parameters. On the other hand, the non-parametric variant—the Spearman correlation coefficient—solely tests for monotonous relationships for at least ordinally scaled parameters. The advantages of the latter are its robustness to outliers and skew distributions. Correlation coefficients measure the strength of association and can have values between –1 and +1. The closer they are to 1, the stronger is the association. A test variable and a statistical test can be constructed from the correlation coefficient. The null hypothesis to be tested is then that there is no linear (or monotonous) correlation.

Discussion

The null hypotheses for these statistical tests described in this article are that the groups are equal. These commonly used tests are also known as “inequality tests”. There are however other types of test. “Trend tests” examine whether there is a tendency for increasing or decreasing values in at least three groups. There are also “superiority tests”, “non-inferiority tests,” and “equivalence tests.” For example, a superiority test examines whether an expensive new drug is better than the conventional standard medication by a specific and medically relevant difference. A non-inferiority test might examine whether a cheaper new medicine is not much worse than a conventional medicine. The acceptable level of activity is specified before the start of the study on the basis of expert medical knowledge. An equivalence test is intended to show that a medication has approximately the same activity as a conventional standard medication. The advantages of the new medication might be simpler administration, fewer side effects, or a lower price.

The methods of regression analysis and the related statistical tests will be discussed in more detail in the course of this series on the evaluation of scientific publications.

The present selection of statistical tests is obviously incomplete. Our intention has been to make it clear that the selection of a suitable test procedure is based on criteria such as the scale of measurement of the endpoint and its underlying distribution. We would like to recommend Altman’s book (5) to the interested reader as a practical guide. Bortz et al. (7) present a comprehensive overview of non-parametric tests (in German).

The selection of the statistical test before the study begins ensures that the study results do not influence the test selection. Moreover, the necessary sample size depends on the test procedure selected. Problems in planning sample size will be discussed in more detail later in this series.

Finally, the point must be made that a statistical test is not necessary for every study. Statistical testing can be dispensed with in purely descriptive studies (12) or when the interrelationships are based on scientific plausibility or logical arguments. Statistical tests are also usually not helpful when investigating the quality of a diagnostic test procedure or rater agreement (for example, in the form of a Bland-Altman diagram) (14). Because of the probability of error, statistical tests should be used “as often as necessary, but as little as possible.” The risk of purely chance results is especially high with multiple testing (11).