Using stylized agent-based models for population-environment research: A case study from the Galápagos Islands

Abstract

Agent Based Models (ABMs) are powerful tools for population-environment research but are subject to trade-offs between model complexity and abstraction. This study strikes a compromise between abstract and highly specified ABMs by designing a spatially explicit, stylized ABM and using it to explore policy scenarios in a setting that is facing substantial conservation and development challenges. Specifically, we present an ABM that reflects key Land Use / Land Cover (LULC) dynamics and livelihood decisions on Isabela Island in the Galápagos Archipelago of Ecuador. We implement the model using the NetLogo software platform, a free program that requires relatively little programming experience. The landscape is composed of a satellite-derived distribution of a problematic invasive species (common guava) and a stylized representation of the Galápagos National Park, the community of Puerto Villamil, the agricultural zone, and the marine area. The agent module is based on publicly available data and household interviews, and represents the primary livelihoods of the population in the Galápagos Islands – tourism, fisheries, and agriculture. We use the model to enact hypothetical agricultural subsidy scenarios aimed at controlling invasive guava and assess the resulting population and land cover dynamics. Findings suggest that spatially explicit, stylized ABMs have considerable utility, particularly during preliminary stages of research, as platforms for (1) sharpening conceptualizations of population-environment systems, (2) testing alternative scenarios, and (3) uncovering critical data gaps.

Introduction

Nearly a decade ago the US National Research Council identified an environmental research agenda that was published as the Grand Challenges in Environmental Sciences (2001). Central to the Council's research recommendations are the interactions of people, place, and environment. Human populations impact and respond to their environment in a variety of ways, and understanding these complex interactions is crucial to improving human and environmental well-being. More recently, the Millennium Ecosystem Assessment Report (2005) described the ways in which humans have transformed ecosystems, and how changes in ecosystem goods and services have affected human welfare and behavior. In the process, it drew attention to the feedbacks between people and the environment that operate across a range of scales in space and time.

Differences in the scale and measurement of social and ecological features are considerable obstacles to studying these complex interactions (Mather et al. 1998), making interdisciplinary work a challenge (Davis 1990). In response to this challenge, there has been a call to create a new interdisciplinary science devoted strictly to population-environment interactions, complete with its own standards and methods of inquiry (Lutz et al. 2002). Agent-based models are useful tools for advancing this interdisciplinary science due to their ability to integrate spatially explicit population and environmental data with information on how individual people make decisions.

In this paper, we draw on the insights and methods of complexity science to develop a stylized, spatially explicit agent-based model, which we use to investigate a set of population-environment interactions. The model incorporates feedbacks between alternate household livelihood strategies and land use/land cover (LULC) on Isabela Island in the Galápagos Archipelago of Ecuador. We develop a baseline model that resembles current trends in livelihood choice and guava cover on the Island, and then use it as a virtual laboratory to test a set of hypothetical interventions intended to decrease the percent of land cover occupied by an invasive species (common guava). We report the outcomes of these hypothetical interventions, and comment on how a stylized environment and simulated household agents that maintain key characteristics as well as social and spatial connections can guide the study of population-environment systems more generally.

Background

Complexity science provides unique and powerful insights for investigating population-environment interactions; in particular, the methodological approaches founded in the study of complex systems are directly relevant to this research. Broadly defined, a complex system is one that exhibits nonlinearity, heterogeneity, self-organizing properties, emergence of aggregate trends, interactions across scales, and sensitivity to initial conditions (Malanson et al. 2006; Portugali 2006). These systems self-organize to produce aggregate patterns that emerge from simple interactions between individual components (Holland 1996, Manson 2001; Abel and Stepp 2003). Complex systems can reproduce their state or transition between states due to interactions between individuals and positive and negative feedbacks with their environment (Blackman 2000).

Complex systems approaches have been applied in disciplines as diverse as climatology (Rind 1999), biology (Farmer et al. 1986), evolution (Kauffman 1993), and economics (Anderson et al. 1988, Arthur 1999, Beinhocker 2006), but it has particular relevance for the study of population-environment interactions (e.g., see the special issue on population-environment interactions in GeoForum (Walsh and McGinnis 2008)). The approaches of complexity science have informed studies of global environmental change (Janssen 1998), protected areas and their impact on human communities (Roberts et al. 2002), tropical deforestation (Soares et al. 2002; Deadman et al. 2004), climate change (Solecki and Oliveri 2004), and LULC change (Messina and Walsh 2001; Lambin et al. 2003; Evans and Kelley 2004). The varied applications of complexity science have underscored the importance of initial conditions, feedbacks, and interactions between heterogeneous agents.

Recognition of these key characteristics has spurred the development of computer-based research tools. Spatially explicit computer models built within the framework of complexity science generally consist of two main components: (1) a landscape or environment that represents the relevant physical and ecological aspects of the system, and (2) agents that act within that environment according to behavioral rules (Parker et al. 2003). These models are generally known as agent-based models (ABMs). With ABMs, the interactions between agents and the environment can be reproduced in order to examine the complex patterns that emerge, and to understand the processes that drive system dynamics (Axelrod 1997). ABMs have been promoted as viable tools for examining population-environment interactions (Hare and Deadman 2004; Batty and Torrens 2005; Rindfuss et al. 2007; Auchincloss and Diez Roux 2008; Evans and Kelley 2008; O'Sullivan 2008), as they are capable of modeling feedbacks among environmental conditions, human actions, and processes that change over time through agent learning and adaptation (O'Sullivan 2008). Unlike analytical or “state-variable” models, ABMs can incorporate individual variation that more effectively captures the heterogeneity in human-environment interactions (DeAngelis and Mooij 2005). Moreover, ABMs are capable of modeling spatially explicit phenomena. Overall, agent-based modeling has proven itself as a powerful tool for exploring interactions between people and the environment and for identifying ways in which systems may respond to human- and environmentally-induced perturbations (Bolte et al. 2007; Parker et al. 2003).

The proliferation of ABMs in recent decades has yielded models that range from abstract representations of reality to highly specified, place-specific models. Schelling's (1971) segregation model and Epstein and Axtell's (1996) Sugarscape exemplify the utility of abstract models as virtual laboratories for exploring the simple rules that underlie complex social patterns. In recent years, researchers have built increasingly complex models that attempt to reproduce key population-environment interactions specific to a particular place and time. These ABMs have provided important insights into the causes and consequences of landscape change, livelihood decision-making, and system outcomes under a variety of “what if” scenarios (Parker 2007; Walsh et al. 2006; Walsh et al. 2008b). For example, ABMs have been developed to examine human vulnerability in the Philippines through the responses of farming communities to change (Acosta-Michlik and Espaldon 2008); to assess the flows of information among fishing crews and their vessels in Australia to simulate the dynamics and resource exploitation of fisheries (Little et al. 2004); and to identify the most important decision-making inputs that affect land use in Texas and Venezuela (Acevedo et al. 2008). There is a clear and compelling precedent that justifies the use of ABMs to explore the relationships between human decision-making and system dynamics.

To date, there have been two major factors hindering the wider adoption of ABMs in population-environment research. First, the software environments in which these models have been developed typically have a steep learning curve. Many popular ABM platforms, including SWARM (Minar et al. 1996) and REPAST (Collier 2003) require the use of programming languages such as Java or C++. Researchers without extensive programming experience must rely on dedicated programmers for model implementation, slowing the model development process considerably (Railsback et al. 2006). For the present research, we use NetLogo (version 4.0.4), a comparatively user-friendly ABM development platform that integrates a graphical user interface with an intuitive scripting syntax based on the LOGO language (Papert 1972).

The second hindering factor is the extensive data that oftentimes is required to accurately represent specific agent and environmental attributes. For instance, ABMs that are used to evaluate the potential consequences of policy scenarios are often parameterized with considerable social and ecological data (e.g., Galvin et al. 2006; Brown et al. 2008). However, the more these models capture the complexity of the real world, the harder they are to develop, interpret, and validate (Grimm et al. 2005). In the words of Parker et al. (2003: 329): “whatever the goal of modeling efforts, balancing the utility of abstraction against the need to include the critical components of the system under study is a major challenge of modeling.”

Our model strikes a compromise between abstract and highly specified models. We develop a relatively simple, yet realistic, ABM with publicly available data, free software, and limited technical experience, in order to formulate and refine conceptualizations of an exemplary population-environment system. Specifically, we examine livelihood decision-making and LULC change on Isabela Island, Galápagos. We explicitly model inputs to human decision-making and feedbacks among interacting system components with remotely-sensed LULC data, demographic data from the Ecuadorian Instituto Nacional de Estadística y Censos (INEC), and with qualitative information about livelihood decision-making based on a small number of household interviews with Galápagos residents. We develop a baseline model in NetLogo that broadly reflects key patterns and processes of LULC dynamics and livelihood choices, and then perturb it by implementing two different hypothetical scenarios, which mimic two potential policies aimed at controlling the spread of invasive species.

The structure of the paper is as follows: first, we describe our study area and motivation for exploring population-environment interactions and hypothetical policy scenarios in this setting; second, we present a conceptual model of population-environment interactions on Isabela Island; third, we discuss the design, parameterization, verification, and validation of the Isabela Livelihoods and Land Use Model (ILLUM); fourth, we describe the fundamental characteristics of the baseline model; fifth, we present the results of different hypothetical policy scenarios implemented in our model; finally, we comment on model limitations and on the utility of ILLUM, and ABMs more generally, for sharpening conceptualizations of population-environment systems, and highlighting data and knowledge gaps.

Study Area

The Galápagos Archipelago is situated in the Pacific Ocean 600-miles off the western coast of South America. This archipelago straddles the equator and consists of 13 main islands, 113 smaller islands, islets and rocks, and the second largest marine reserve in the world. The largest (4,588 km²) of these islands, and the focus of our model, is Isabela Island, located in the western region of the archipelago. Our study area is in the southern portion of Isabela Island (Fig. 1) and encompasses a rainfall gradient that extends south from the southern flanks of Sierra Negra Volcano within Galápagos National Park (GNP) through the humid highland zone, including the household farms and the agricultural community of Santo Tomás, to the dry coastal lowlands where the community of Puerto Villamil is located. This site was selected for three main reasons: 1) it contains human communities whose livelihoods are intertwined with environmental conservation efforts and the maintenance of protected lands that are of international significance; 2) it exhibits relatively simple, large-scale spatial organization of the three primary economic sectors (i.e., tourism, fishing, and farming) and; 3) its relative isolation facilitates the identification of distal and proximate factors related to population-environment interactions (see Conceptual Framework). The demand for information on population-environment interactions, the importance of spatial structure, and the ability to identify the key system components make Isabela Island an attractive study site for exploring the utility of stylized ABMs. The Galápagos Islands have experienced significant social and ecological changes during the past 20-years as a result of human pressures on the fragile terrestrial and marine ecosystems of the archipelago (e.g., Ospina-Peralta 2004; Grenier 2007; Ospina and Falconí 2007; Watkins and Cruz 2007). Until recently, the Galápagos Islands remained relatively untouched by human influence, due in part to their geographic isolation from mainland South America. This geographic isolation has created a unique setting for the evolution of endemic species, many of which persist today (Gonzalez et al. 2008). In the past three decades, migration to the Galápagos Islands has increased, principally from the Ecuadorian mainland due to the relative economic prosperity of the Islands (INEC 1998).

Fig. 1.

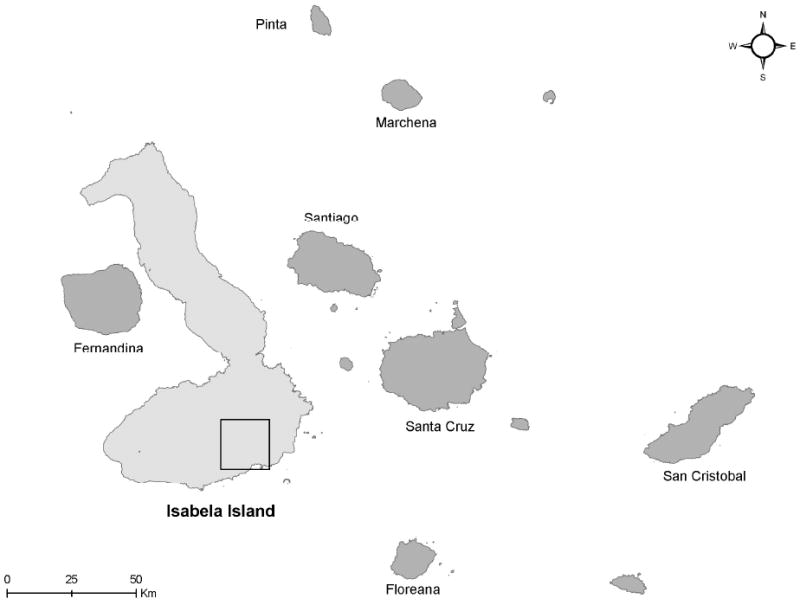
Map of the Galápagos Islands highlighting the study area on Isabela Island

This influx of migrants and visitors in recent years has been accompanied by many introduced plants and animals (Mauchamp 1997; Kerr et al. 2004; Watkins and Cruz 2007), some of which have become invasive and not only threaten endemic species, but also affect the local human population through changes in land use and shifts in livelihoods. The problem has become so widespread in the archipelago that introduced plants have been deemed one of the greatest threats to the terrestrial ecosystem of the islands (Kerr et al. 2004). One introduced species of particular interest, due to its introduction into protected areas and human-use zones alike, is common guava (Psidium guajava). Guava was introduced to the Galápagos for cultivation in 1858 and now covers more than 40,000 ha of land on Isabela Island, mostly within the agricultural zone and the adjacent protected area of GNP, nearly completely replacing a fern-sedge zone on the flanks of Sierra Negra Volcano (Hamann 1981; Walsh et al. 2008a). The spread of common guava in the agricultural zone can be an obstacle to cultivation and substantially reduce farm productivity. As a consequence, some households have decided to alter their land use patterns by allowing infested fields to lie fallow, effectively abandoning portions of the farm that are dominated by guava. These abandoned fields and farms act as source populations that promote the spread of guava into neighboring farms and the GNP. The spread of guava depresses household wealth and assets related to agriculture, and necessitates contract labor from the Ecuadorian mainland to eradicate problem populations in farm fields, as well as control measures within the GNP itself.

Farm abandonment is also related to the lucrative potential of tourism and fisheries for Galapagueños. These livelihood options can be seen as factors that “pull” people away from agricultural livelihoods. As more people switch from agrarian livelihoods to other opportunities with greater economic return, maintenance of land, usually driven by investment in the agricultural potential of farms, is at risk. The control of invasive species, particularly guava, is dependent upon farmers eradicating the guava that occupies their land, and diminishing the threat of invasion to adjacent farms and GNP. If the number, impact, and areal extent of non-native species in the Galápagos Islands continue to grow, the tourism industry, which relies heavily on continued conservation of the archipelago as a draw for visitors, could be negatively impacted through the loss of native and endemic species, abrupt changes in ecosystem goods and services, and increased vulnerability of local livelihoods.

The pattern-process relations and the feedback mechanisms between demographic, socioeconomic, and ecological sub-systems in the Galápagos Islands are driven in part by the livelihood and resource-use choices of individual residents. These choices play out in a landscape where outside entities (chiefly the GNP administration) exert strong regulatory control over land use, and residents make livelihood choices in the face of year-to-year uncertainty in the availability of resources (e.g., fish, precipitation, and tourists). Understanding these interactions between population and environment has immense consequences for articulating and mediating the often conflicting objectives of economic development and resource conservation in Galápagos. For these reasons, we use our ABM as a virtual laboratory for testing two hypothetical policy interventions (i.e., scenarios) aimed at reducing the percent of land covered by invasive species.

Conceptual Framework

We developed a conceptual framework (Fig. 2) to identify key population-environment interactions and to aid in operationalizing the model. This framework both guided model creation and was refined throughout the model development process. It proposes that distal factors influence more proximate, local landscapes, which affect agent characteristics, livelihood decisions, and ultimately land use patterns. Feedbacks among many of the factors are present in this framework and are specified in our model, which emphasizes the interactions between livelihoods and land use.

Fig. 2.

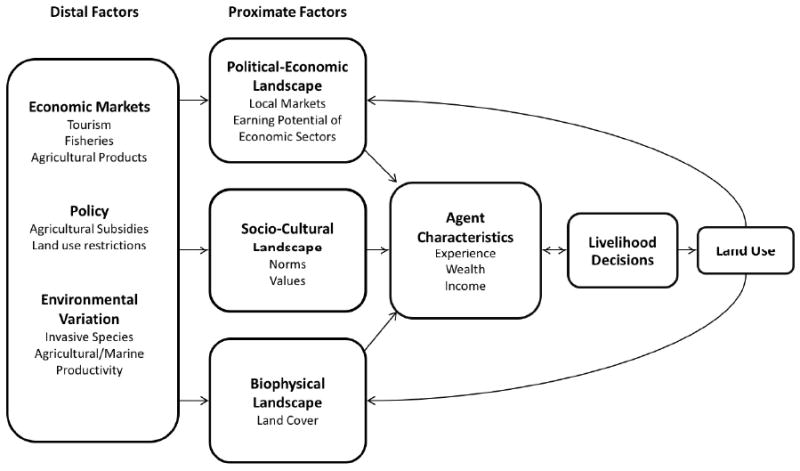
Conceptual framework for modeling livelihood decisions and land use/land cover processes

More specifically, distal factors such as global markets, public policies, and environmental variation influence agent characteristics by acting through more proximate or local factors. For instance, shifts in global markets could create a decline in tourism, or ocean-scale overexploitation could lead to a decline in fisheries productivity. Both of these events would affect the demand and earning potential for the associated livelihoods. The influence of global markets in our model is operationalized through the relative earnings potential of each of the different livelihoods. Also built into the model are policies dictating the fixed boundaries of the agricultural zone. Policy change is implemented by the model user through the introduction of different types of agricultural subsidization aimed at eradicating guava (described in detail below). We also include interannual variation in agent incomes in order to mimic variability in economic markets (e.g., tourist numbers) and environmental conditions (e.g., fish populations and rainfall).

We conceptualize the important proximate factors, or local environments as political-economic, socio-cultural, and biophysical landscapes. Encompassed in the political-economic landscapes are local markets and the earning potential for each economic sector. We operationalize each of these in our model mainly through the random assignment of a livelihood and appropriate income, and through the cost of switching occupations. The local socio-cultural landscape includes aspects such as values and norms. We attempt to indirectly model values and norms in our model through the “costs” associated with switching livelihoods, and through behavior rules that incorporate occupational experience. Experience is modeled as the number of consecutive years in an occupation, and is viewed as an asset due to the knowledge and social capital gained through time in a particular livelihood. The local biophysical landscape includes LULC, which we explicitly model as changes in guava land cover.

Agent characteristics influence both the livelihood options that are available and the livelihood decisions individuals make. The characteristics that we incorporate into the model are agent income dynamics, cost of living, wealth and assets, and experience as an indication of learning and the ability to adapt in the face of uncertainty and economic opportunities. The distal factors and proximate local landscapes affect livelihood decisions through agent characteristics and social-spatial interactions. Livelihood decision-making is limited to the selection of one of three options: agriculture, fisheries, or tourism. We focus on these three activities because they are the largest economic sectors on Isabela Island (Ospina-Peralta 2004) and they are tied to LULC change and environmental feedbacks. If the agent chooses to participate in the agricultural sector, the agent must decide whether or not to clear guava from the farm parcel, which directly influences LULC. There is a cost of eradicating guava from a farm, but eradication restores land productivity and land value, thus reducing the “push” to select another livelihood and potentially abandon one's land. Non-agricultural sectors also act as factors that “pull” agents away from farming; hence, off-farm employment, in this case through a full-time livelihood choice, indirectly influences LULC through farm abandonment and subsequent guava spread. In the resulting ABM, total guava coverage is the primary output that is used to measure land cover change. We include feedback mechanisms from the livelihood strategies and LULC conditions to the agents; these factors affect the decision-making of individuals via their changed wealth, assets, and land values.

Although this conceptual framework and model does not incorporate the entire suite of interactions among household livelihoods and LULC types on Isabela Island, we argue that it incorporates the key structural elements of the system necessary to explore livelihood decision-making and land use change on household farms in the highlands.

Model Design

We implemented our conceptual model as an ABM using NetLogo version 4.0.4 (http://ccl.northwestern.edu/netlogo/). NetLogo is a high-level platform that provides a user-friendly programming environment, without the need for expertise in standard programming languages such as Java or C++ (Railsback et al. 2006). NetLogo is designed to be an educational tool, readily implemented by researchers with little modeling background. While NetLogo lacks some of the speed, power, and extensibility of other ABM software, we chose the platform because of its ease of use and potential to support future modeling participation (e.g., model operation and extension through the development of new modules, scenarios, and agent characteristics and interactions) by various stakeholders, including park managers, researchers, and NGO representatives. NetLogo has been used previously to model a limited set of operations for a group of heterogeneous agents and to explore system processes (Le et al. 2008; An 2001; West 2009).

The ABM developed for Isabela Island, referred to as the Isabela Livelihoods and Land Use Model (ILLUM), is comprised of a “landscape” module and an “agent” module (Fig. 3) and is parameterized by a variety of social and biophysical data (Table 1). The landscape module consists of a stylized raster (gridded) representation of important landscape features such as land tenure, land cover, elevation, and guava distribution for a section of Isabela Island. The agent module consists of a collection of individual decision-making units (i.e., agents) that are a highly simplified characterization of the human inhabitants of Isabela. The model operates on an annual time-step. Each year every agent chooses a primary occupation, generates income, and makes land use decisions. The aggregate outcomes of these decisions influence LULC in the study area, which in turn affects decision-making and LULC for the following year. Controls and outputs are unified in a graphical display.

Fig. 3.

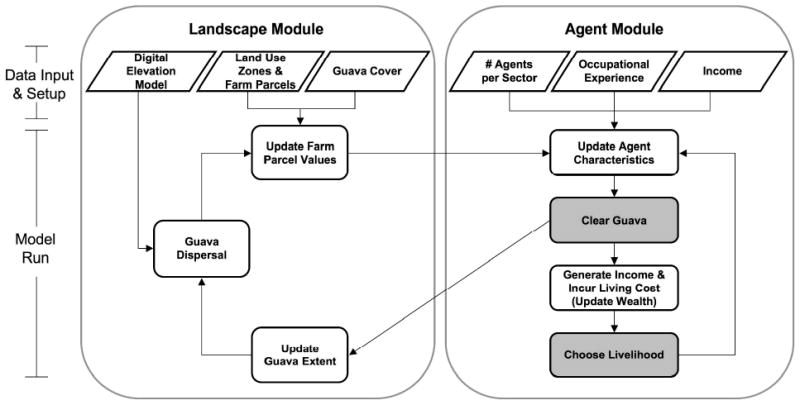
Flowchart of the Isabela Livelihood and Land Use Model setup and operation. The shaded boxes indicate the sub-models that are illustrated in detail in Fig. 4

Table 1.

Descriptions and sources of parameters of the Isabela Livelihoods and Land Use Model

Parameter	Description	Source
Landscape Module Inputs
Elevation	90m Digital Elevation Model (DEM) from the NASA Shuttle Radar Topography Mission (SRTM) V4 data	Available from http://srtm.csi.cgiar.org
Farm parcels	Farm parcel boundary layer based on actual land parcel data. Stylized to represent the number, size, and spatial distribution of farms.	Instituto Nacional Galápagos (INGALA)
Guava Cover	Raster layer of guava patches. LULC maps derived from 2.4m spatial resolution QuickBird Imagery acquired on October 2005	Details described in Walsh et al. 2008a
Guava Spread Rate	The probability of guava spreading to another cell	Estimated based on observed patterns of guava spread
Agent Module Inputs
Cost of living	Annual cost of living	Derived from study of standard of living and costs by Luna 2008
Experience	Initial values of agent experience in an occupation are based on the age distribution reported in the 2006 Census of the GalápagosMean (s.d.): 19 (12) years	Ecuador National Institute of Statistics and Censuses (INEC; available from http://www.inec.gov.ec/)
Guava Control Cost	The cost per hectare of clearing guava from a farm: 100 USD	Estimated based on field observation and interviews
Income	Initial incomes by economic sector. Mean (s.d.) in USD: Farming = 3300 (1800) Fishing = 4200 (3000) Tourism = 3600 (4200)	INEC, 2006 Census of the Galápagos
Number of agents	The numbers of farmers (86), fisherfolk (63), and tourism workers (140) are derived from the 2006 Census of the Galápagos	INEC, 2006 Census of the Galápagos

Landscape Module

We developed a stylized landscape in raster format to represent the four geographic zones of the southern portion of Isabela Island: the agricultural, urban, marine, and national park areas. A stylized farm parcel layer was created to approximate the number, size, and distribution of farms within the agricultural zone. Vector data for the agricultural zone boundary were converted into a raster format using ArcGIS 9.3. We also model the location and spread of guava in the agricultural zone and adjacent protected areas using an underlying cellular automata grid. The initial spatial pattern of guava is based on an analysis of satellite imagery and ground data described by Walsh et al. (2008a). Because the Walsh et al. analysis was performed at a much finer resolution than our modeled landscape (30m vs. 200m) we introduced limited local randomness into the distribution of guava in our model runs to account for uncertainty in how guava is represented. Elevation is based on a 90-meter spatial resolution digital elevation model (DEM) acquired by the Shuttle Radar Topography Mission (SRTM). This elevation surface constrains the spread of guava within appropriate elevation zones.

There are several factors that influence guava spread during each time-step. First, guava spreads by long-distance dispersal events and a neighborhood rule. Non-guava cells have a 10% chance of becoming guava if one of the adjacent cells is guava, and the probability of long distance dispersal events are inversely related to distance from the agricultural zone. These dispersal rates are also influenced by elevation, whereby guava spreads more readily in the wetter, higher elevations. Lacking data on the spread rate of guava on Isabela, this spread rate was calibrated to mirror observed rates of guava spread on the island. Farmer agents can remove guava during each time-step at a cost to their accrued wealth; this decision-making process is described in the agent module below. Park manager agents clear guava within in the GNP when they move within two cells of a guava cell. They move only within the GNP, but “patrol” near the boundaries of the agricultural zone.

Agent Module

Four different types of agents populate the four geographic zones of the stylized landscape: farmers act within the agricultural zone, fisher folk act within the marine zone, tourist industry workers act within the urban zone, and park employees act within the park zone. Farmers, fisher folk, and tourist industry workers make livelihood decisions, whereas park employee agents are only responsible for clearing guava from the park area that borders the agricultural zone. The initial number of agents in each of the three livelihoods is taken from the 2006 population census for the Galápagos.

The income of each agent is randomly selected from a livelihood-specific truncated normal distribution based on the 2006 census. Their gross income (I_gross) is a product of these values (Eq. 1).

$$I_{\mathit{gross}}=(I_{\mathit{base}}+V_o)+(I_{\mathit{base}}\ast ln(E)/ln(40)+V_o)$$ (1)

Where I_base is drawn from a livelihood-specific truncated normal distribution for each agent, V_o is random interannual variation that affects all agents in a particular occupation, and E is the occupational experience of each agent. Each agent's occupational experience (i.e., consecutive number of years in an occupation) is initially drawn from a truncated normal distribution; the mean, standard deviation, and shape of which are derived from the age distribution of working-age (i.e., 15 to 65 years old) residents of Isabela Island. Additionally, farmers' incomes are scaled in proportion to the amount of guava on their farm. Their income is multiplied by: 1 minus half of the proportion of guava on their farm. For instance, if 60% of a farm is covered in guava, then the farmer's income is multiplied by 0.70. Based on field observations and interviews, this is a conservative estimate of the effect of guava on farmer incomes; the proportional effect of guava on incomes would likely be larger if farmers' incomes were not also subject to a lack of reliable markets and other environmental risks (e.g., birds, rats, extreme rainfall events).

At every time-step, a baseline living cost (L, determined from Luna 2008) is deducted from each agent's income. For income greater than the baseline living cost, we assume that 95% of it is spent on maintaining the household across all occupations (Eq. 2).

$$I_{\mathit{net}}=I_{\mathit{gross}}-(L+0.95\ast (I_{\mathit{gross}}-L))$$ (2)

Net savings rates in developing countries vary widely over time (Hamilton and Clemens 1999), but here we assume a very conservative constant savings rate of 5%. Each agent retains this additional income as wealth, which can then be used to pay the costs of switching livelihoods or clearing guava.

Farmer agents evaluate a utility function to decide whether or not to clear guava on their parcel within each annual time-step (Fig. 4a). Farmers clear guava if the total control cost (proportion of the farm covered in guava multiplied by the control cost per hectare) is less than their wealth and is less than the expected income from their farm when guava is not present. Expected income is calculated in the same manner as I_gross but omits the influence of guava on income.

Fig. 4.

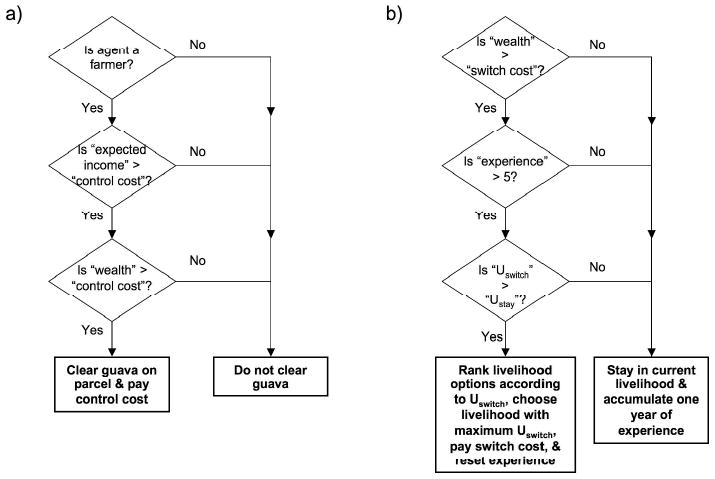
(a) Guava clearing and (b) livelihood choice sub-models. Livelihood options are limited by the availability of vacancies in the fishing and farming sectors, and switching is additionally constrained by a probabilistic control

During each time-step, all agents evaluate their livelihood options and decide whether to stay in their current livelihood or switch livelihoods (Fig. 4b). First, agents evaluate whether they have the option to switch livelihoods. Agents must be able to afford the switching costs associated with a change in livelihoods based on their accumulated wealth. The cost of switching to each livelihood was estimated based on direct observation and interviews with household representatives of each sector living on Isabela Island. The switch to fisheries and farming is additionally constrained by the number of vacancies available, simulating the limited availability of fishing licenses (as determined by GNP regulations of the number of fisher folk and boats) and farm parcels (as determined by the constraint on agricultural land area) respectively. We do not set vacancy limits on the tourism sector, because at present tourism growth is encouraged on Isabela Island. If an agent meets the switching cost and vacancy requirements, and has also been in its current occupation for more than 5 years, then it has a one-third probability of considering switching sectors in any given time-step. This rule ensures that the number of sector transitions is limited to a realistic proportion of the total population and mirrors rates of livelihood change observed on Isabela. If an agent is unable to maintain a livelihood or switch to a new one, then the agent exits the system.

If an agent has met the criteria to switch livelihoods, the agent chooses the new livelihood based on a series of functions that evaluate the utility of each livelihood option, including their current livelihood. The utility of staying in the current livelihood is calculated as a function of the past two year's net income in that occupation. The error terms are specified to incorporate non-economic factors and allow for “non-rational” decision-making. The utility of switching to one of the two other livelihoods (U_switch) is a function of the mean net income (I_net) of the alternative livelihood plus normally distributed error (Eq. 3).

$$U_{\mathit{switch}}=\mathit{mean}(I_{\mathit{net}(t)},I_{\mathit{net}(t-1)})+N(0,{\sigma }^2)$$ (3)

The switching options are ranked according to the calculated utility functions and the agent chooses the livelihood option with the highest utility. After choosing to switch or remain in the current livelihood, the wealth, income, and experience of the agents are updated. If an agent switches livelihoods, their occupational experience is set to zero, and the experience level will iterate the following year. Agents do not retain experience values from a previous livelihood for the sake of model simplicity and speed. Their income is also adjusted by drawing a value from the sector-specific income distribution of their new occupation.

Verification and Validation

Our verification and validation procedures follow those of An et al. (2005). We verified realistic model function both during and after model building, and then conducted validation to ensure that model outputs correspond to our conceptual model as well as real-world patterns. Specifically, verification involved model debugging, parameter calibration, and tests of extreme values, and validation included sensitivity analysis and pattern evaluation.

The development of ILLUM involved a progressive increase in model complexity, starting from a basic model involving one type of agent (i.e., farmers) with one task (i.e., clearing guava). We then added parameters with values based on available data (e.g., agents per sector), and values that were calibrated to match observed patterns on Isabela Island (e.g., guava spread rate). Probabilistic controls on agent livelihood switching were established in order to approximate observations of population shifts between sectors. We recognize that probabilistic controls are not ideal solutions for controlling agent behavior, but they are sometimes necessary to avoid extreme results and abnormal model operation. Attempts to remove the probabilistic control of livelihood switching through alterations of other model functions were met with limited success: increasing the cost of switching livelihoods was unrealistically selective of which agents could switch; lowering the experience requirement made the model more static; and the maximum capacity of each livelihood sector could not be changed because they match observed conditions. This process indicated that there is a need for further field-research on livelihood decision-making on Isabela Island.

Validation of ABMs remains a significant research challenge (Windrum et al. 2007), particularly for population-environment models that incorporate many parameters and integrate data from a variety of sources that contain various degrees of uncertainty. Our validation effort was limited by the stylized nature of ILLUM and by the lack of consistently collected social, ecological, and geographic data for the Galápagos. This paucity of data precluded empirical validation using outside data (i.e., data not used to parameterize the model); however, we implemented sensitivity analysis and pattern evaluation to check the validity of our model.

To test the robustness of ILLUM to parameter uncertainty, we performed sensitivity analysis by iterating the model with different parameter values. Following An et al. (2005) we perturbed parameter values by 50% and compared the resulting values of our primary outcome of interest, guava cover at time-step 50, to those of the baseline model. Guava cover was calculated as the mean of 100 model runs. The sensitivity index (Jørgensen 1986) is calculated as:

$$S_x=\frac{dx/x}{dp/p}$$ (4)

where p is the value of the independent variable, dp is the value for a change of p, x is the value of the dependent variable, and dx is the corresponding change in x in response to the change in p.

Varying one parameter at a time does not capture the full range of parameter uncertainty in complex models such as this one. To more fully explore the “parameter space” of these models we selected two extreme values (±100% variation from baseline) for three parameters that were identified in the sensitivity analysis as having a strong influence on model outcomes. We then ran 100 replicate models incorporating all possible combinations of extreme parameters (8 unique combinations).

Grimm et al. (2005) stress the importance of using ABMs to reproduce empirical patterns in real data at multiple spatial and temporal scales. In model development and testing we sought to reproduce the recent large-scale dynamics of population and environment interactions with the minimum number of assumptions about agent behavior and livelihood decision-making. The primary patterns of interest were the progressive increase in guava cover over time, and the switching of farmers to alternative livelihood options. These patterns are described in further detail in the Baseline Model section.

Results

Our primary outcome of interest is the percentage of land occupied by guava. We also assess the number of agents in each of the sectors and the median net income levels of each livelihood sector. We first present the results of the verification and validation tests, then describe the patterns of baseline model function to provide context for description of model behavior under hypothetical agricultural subsidy scenarios aimed at controlling guava spread.

Verification and Validation

Sensitivity analysis was used to evaluate the sensitivity of guava cover and the farming population to changes in other model parameters, including guava spread rate, cost of living, costs associated with switching livelihoods, guava control cost, occupational experience, the number of park rangers, and the income savings rate. We did not test model sensitivity to changes in the initial number of agents in each sector because this is currently unrealistic in the face of restrictions on fishing permits, as well as laws limiting immigration. Exploration of the parameter space of agent incomes is implemented in the agricultural subsidy scenarios.

The sensitivity analysis results (Table 2) demonstrate that guava cover at time-step 50 was highly sensitive to variation in the spread rate of guava on the landscape, the cost of its eradication, and the number of park rangers. The farming population was also marginally sensitive to the change in park rangers. Altering the cost of switching livelihoods significantly changed the number of farmer agents. The model was relatively insensitive to changes in baseline living cost, occupational experience, and savings rate. The fact that ILLUM was especially sensitive to guava spread rate and control measures indicates a need for more detailed data on guava spread and eradication patterns. These sensitivities also underscore the notion that the specific model results presented below, particularly those regarding projected parameter values, should not be interpreted as predictions of system outcomes; rather, we attempt to evaluate broad population and environment trends in the study area, as well as the utility of stylized ABMs for population-environment research in general.

Table 2.

ILLUM sensitivity analysis results

Parameter	Default Value	+ 50%a Perturbation	Guava Cover, Hectares	Guava Sensitivity	Farming Population	Population Sensitivity
Landscape Inputs
Guava Spread Rate (probability of spread to an adjacent cell)	10%	15%	2,396.5 (7.2)*	14.5%	24.2 (4.3)	N/A
Agent Inputs
Cost of Living (USD)	550	825	2,221.8 (-0.6)	N/A	21.9 (-5.5)	N/A
Cost of Switching to:	220	330	2,218.0 (-0.8)	N/A	25.1 (8.5)*	17.0%
Farming	570	855
Fishing	700	1,050
Tourism
Guava Control Cost (USD/hectare)	100	150	2,591.8 (16.0)*	31.9%	24.4 (5.4)	N/A
Mean Occupational Experience (years)	19	28.5	2,208.4 (-1.2)	N/A	23.7 (2.3)	N/A
Number of Park Rangers	14	21	1,926.1 (-13.8)*	27.6%	24.8 (7.0)+	14.0%
Savings Rate (% of net income)	5	7.5	2,219.6 (-0.7)	N/A	23.9 (3.2)	N/A

Guava cover and farming population values are means of 100 model runs with a 50% perturbation of the input variables, measured at time-step 50. Mean guava cover and population are compared to baseline model output using t-tests, and sensitivity values are reported for statistically significant differences. Percent changes from the baseline model are shown in parentheses

^*p< 0.05;

⁺p< 0.10 for the two-tailed distribution

^aResults of -50% perturbations are not shown for space considerations

Guava cover and farming population outcomes (at time-step 50) from the extreme parameter combinations are reported in Table 3. The parameter combinations are reported as a string of uppercase and lowercase letters. Uppercase letters indicate positively exaggerated extreme values (+100% of baseline), and lowercase letters indicate negatively exaggerated extreme values (0% of baseline). The parameters used are the number of park rangers (r,R), the control cost of guava(c,C), and the spread rate of guava (s,S). For instance, “rCs” indicates a small value for the number of park rangers, a large value for control cost, and a small value for spread rate.

Table 3.

ILLUM extreme parameter combination results

Parameters	Guava Cover, Hectares	Guava Cover Standard Deviation, Hectares	Farming Population	Farming Population Standard Deviation
rcs	1,419.7 (-35.7)	115.7 (-5.8)	28.0 (17.6)	7.0 (8.2)
rcS	2,303.5 (4.3)	138.8 (13.1)	26.7 (12.4)	6.4 (-0.1)
rCs	2,847.4 (29.0)	121.6 (-0.9)	23.5 (-1.3)	7.0 (8.3)
rCS	4,405.6 (99.6)	196.9 (60.4)	23.9 (0.3)	5.7 (-11.4)
Rcs	412.0 (-81.3)	411.4 (235.2)	27.4 (15.4)	6.6 (3.1)
RcS	651.3 (-70.5)	75.6 (-38.4)	28.7 (20.8)	7.4 (14.8)
RCs	1,768.7 (-19.9)	156.0 (27.1)	23.3 (-2.1)	6.2 (-3.4)
RCS	2,687.4 (21.7)	154.4 (25.8)	24.2 (2.0)	5.7 (-11.5)

Guava cover and farming population values are means of 100 model runs, measured at time-step 50. Percent changes from the baseline model are shown in parentheses

The model produces sensible results for combinations of extreme parameter values. For the most guava-promoting scenario (rCS) with no park rangers, $800 per hectare control costs, and a spread probability of 20%, the extent of guava is nearly doubled compared to the baseline scenario. For the least guava-promoting scenario (Rcs) with 24 park ranger agents, $0 per hectare control costs, and a spread probability of 0% the cover of guava is dramatically reduced. Notably, however, guava is not eradicated in this scenario, and the number of farmer agents increases only modestly. Overall, the number of farmer agents at the end of the scenario is relatively insensitive to even dramatic changes in the selected parameters.

Baseline Model

We ran the baseline model for 50 time-steps and averaged the values for each time-step over 1000 model runs. The baseline model broadly reflected current trends in livelihood choice and guava spread on Isabela Island (Fig. 5). When ILLUM ran unperturbed the number of farmers in the system declined as they transitioned to the other two sectors, particularly the tourism sector. The population of fisherfolk did not rise substantially due to limits on the vacancies in the fishing sector. The farming sector retained a small proportion of agents, and a small number of the farmer agents exited the system due to low accumulated wealth.

Fig. 5.

Baseline model output for (a) the total and agricultural guava cover, and (b) the human population in each economic sector. Points designate the means of 1000 model runs for each time-step and lines designate the bounds of 95% of the values from these runs

Mean agricultural guava cover increased during the period, also matching observed trends. Upon visual inspection of model output, much of the guava persisted in and dispersed beyond the agricultural zone. Guava spread in GNP remained stable due to the simultaneous processes of guava clearing by park rangers, and repopulation of guava from the agricultural zone. As evidenced by the sensitivity analysis results, this outcome is dependent on the number of park rangers and the spatial patterns of their activity. In reality, guava may be spreading between the two zones due to inadequate control in both areas.

Agricultural Subsidies

Given current trends on Isabela, it is reasonable to imagine a Galápagos future in which farming is an uncommon livelihood because of a lack of access to agricultural markets and the expansive nature of invasive species, such as guava, which effectively debilitate the ecological productivity of farms and further reduce the propensity of farmers to work the land and sustain an agrarian life-style. One proposed means of creating a more sustainable archipelago would be to provide subsidies that increase the maintenance of agricultural land by farmers and thereby control the spread of invasive guava. We take subsidies to mean the investment of non-household resources, generally by government and NGOs, to increase the productivity of the land. These subsidies could take many forms, but we focus on two potential scenarios: (1) direct income support for farmers; and (2) reduced guava eradication cost for farmers. These are expected to reverse the decline in farmer populations and concurrently decrease the areal extent of guava.

We separately tested four levels of direct income subsidy (increasing annual farmer incomes by $500, $1000, $1500, and $2000) and four levels of control cost subsidy (reducing the guava control cost per hectare by $25, $50, $75, and $100). The maximum income subsidy brought farmer incomes approximately in line with the other two economic sectors, and the maximum control cost subsidy eliminated the cost of clearing guava. Similar to the baseline model, we ran the model for 50 time-steps and averaged the outcome values for each time-step over 1000 model runs. The following comparisons refer to the mean guava cover and population values at the last time-step.

Compared to the baseline model, guava cover was reduced in all subsidy scenarios (Table 4). Total guava cover was inversely related to the level of subsidization, but this relationship was non-linear as evidenced by a non-significant reduction in guava between the $1000 and $1500 income subsidy levels, as well as the relationship between control cost and total guava cover shown in Fig. 6. Control cost subsidization yielded the greatest gains in guava control, both in terms of guava cover and the cost per hectare cleared. Compared to the baseline output at time-step 50, the elimination of guava clearing cost yielded a 59% decrease in total guava and 98% decrease in guava within the agricultural zone, with an associated cost of about $2000 for each hectare of guava reduction over the observation period. Even the second highest control cost subsidy led to a 91% decrease in agricultural guava cover. Combining the largest control cost subsidy with the highest income subsidy yielded an additional 26% decrease in guava within the agricultural zone (compared to only eliminating the control cost), but only decreased total guava by an additional 1% (9.68 hectares), with an associated increase in cost of $7,190,682 over the 50-year period.

Table 4.

Results of the ILLUM agricultural subsidy scenarios

Scenario	Guava Cover, Hectares	% Change in Guava Cover Relative to Baseline	Farming Population	% Change in Farmer Population Relative to Baseline	Total Subsidy Cost, USD	USD per Hectare of Guava Reduction
Baseline Model
	2,229.0 (125.9)	N/A	23.7 (6.3)	N/A	N/A	N/A
Income Subsidization [USD per farmer per year]
500	2,202.3* (125.2)	-1.2%	31.4* (6.9)	+32.7%	1,030,675.0 (126,391.6)	38,602.1
1000	2,176.3* (123.3)	-2.4%	40.3* (7.8)	+70.2%	2,354,411.0 (279,220.0)	44,719.9
1500	2,173.1 (117.8)	-2.5%	47.8* (8.7)	+101.6%	3,880,177.5 (447,285.0)	69,497.4
2000	2,151.0* (120.8)	-3.5%	57.1* (9.0)	+140.9%	5,769,352.0 (609,693.8)	74,038.2
Control Cost Subsidization [USD per hectare cleared]
25	1,938.8* (121.4)	-13.0%	24.0 (6.2)	+1.3%	245,236.7 (37,501.4)	845.2
50	1,501.1* (137.0)	-32.7%	25.4* (6.6)	+7.1%	750,134.2 (112,662.8)	1,030.6
75	1,004.8* (108.9)	-54.9%	26.9* (6.7)	+13.4%	1,693,917.9 (240,391.7)	1,383.8
100	916.6* (73.4)	-58.9%	27.9* (7.2)	+17.7%	2,633,309.6 (431,296.7)	2,006.5

Total guava cover, farming population, and total subsidy values are means of 1000 model runs, measured at time-step 50. Differences in mean guava cover and farming population between consecutive subsidy levels are compared using t-tests. Standard deviations are shown in parentheses

^*p< 0.05 for the two-tailed distribution

Fig. 6.

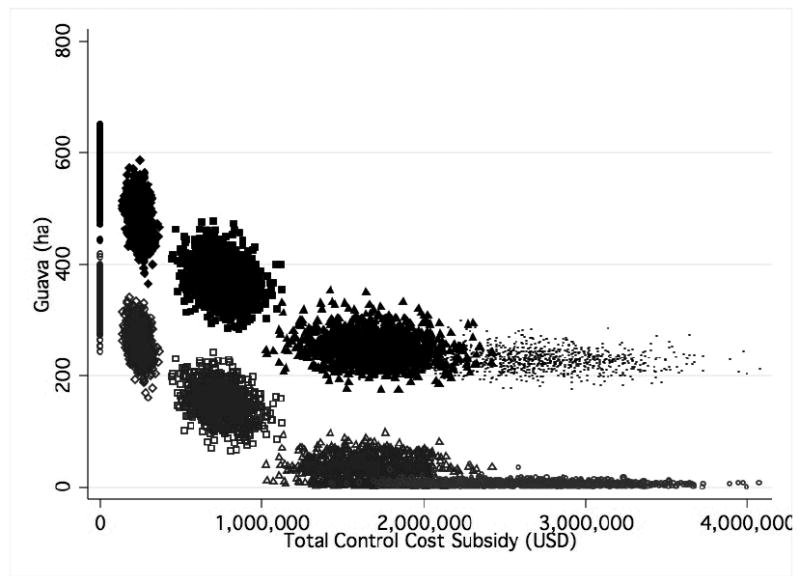
Total guava cover (solid black symbols) and agricultural guava cover (hollow grey symbols) at time-step 50 under five separate reductions in the per hectare guava control cost (circles=$0; diamonds=$25; squares=$50; triangles=$75; points=$100). “Total Control Cost Subsidy (USD)” represents the sum of 50 years of subsidization

Even under the most successful guava eradication subsidies, guava was not entirely eliminated from the landscape. This was due to the persistence of guava within the park zone, where a limited number of park agents were unable to eradicate it from the landscape. These guava reservoirs then repopulated the agricultural zone, possibly increasing the average per hectare cost of reducing guava cover over the 50-year period.

In all scenarios, the overall population of farmers increased (Table 4), largely due to agents coming from the tourism sector. The annual income subsidy scenarios had a larger effect on the farmer population compared to the control cost scenarios, with the $2000 income subsidy yielding a 141% increase in farmer population from baseline. Even when clearing costs were eliminated there was a relatively small (18%) increase in the number of farmers from the baseline population. Overall, the hypothetical intervention of reducing the cost of clearing the guava was not as effective for keeping farmers on the land but had the greatest impact on guava cover.

Discussion and Conclusions

Understanding the drivers of environmental change and the ways in which human populations impact and respond to the environment are central to the interdisciplinary study of population-environment interactions. Spatially-explicit models, particularly ABMs, are valuable analytical tools for the study of these and other complex systems. A wide variety of studies using ABMs with diverse model structures, inputs, processes, and outcomes have set the stage for our research; however, substantial challenges remain in finding compromise between abstraction and specificity.

In response to this challenge, we developed a stylized ABM that captures key interactions and feedbacks between human livelihood decisions and LULC change in the Galápagos Islands. Population-environment interactions were represented in ways that resemble current and projected conditions in guava cover and the farming population. We then used ILLUM as a virtual laboratory for exploring hypothetical interventions to control invasive species growth on Isabela Island.

Through model development we refined our conceptualization of the complex dynamics that emerge from the interactions of individual agents and a changing environment; in particular, the hypothetical scenarios highlighted the importance of interactions between livelihoods and LULC. Despite the real-world linkages between the farming population and guava cover, scenario testing demonstrated that they may not be dependent on one another: the control cost subsidies yielded the greatest decrease in guava, while the income subsidies yielded the greatest increases in the farming population. This result may be due to the ability of farmer agents' to maintain relatively high incomes without clearing guava when income subsidization is in place. The finding that large increases in farmer incomes had relatively little influence on the total area covered by the invasive plant indicates that factors other than income and the maintenance of agrarian populations are important aspects of invasive species control. Also, we found that guava persisted in the landscape, especially within the park zone, even under our largest and most effective control cost subsidy. Coordinated programs that link the protected area and farm households in a common goal of species control would likely be most effective means of reducing guava cover. Moreover, the complete elimination of control costs may not be necessary in order to achieve meaningful and cost-efficient gains in invasive species management, as even the second highest control cost subsidy eliminated over 90% of the guava in the agricultural zone. Assuming that ILLUM's decision-making rules and the parameters for guava spread sufficiently capture the key decision-making preferences of Galapagueños, this would suggest that reducing control costs – rather than an augmenting farmer incomes – would be a more effective intervention for controlling invasive guava. However, we acknowledge that current understandings of livelihood decision-making and guava spread are limited.

Although we believe that ILLUM is a useful analytical tool, like all models it suffers from simplifying assumptions that can lead to unreasonable system behavior and constrain the model in unintended ways. For instance, ILLUM does not include dynamic features of the socio-cultural environment such as cultural norms, values, social networks, status, and skills. Although we attempt to account for these factors through the use of occupational experience and the cost associated with switching occupations, we recognize that this is a limitation of our model. Further model development would benefit from better specification of switching costs, especially in light of the sensitivity analysis results. Other important features that we do not model are detailed demographic processes such as immigration/emigration, income sharing, household structure, age, and gender. We also acknowledge that the residents of the Galápagos often maintain more than one occupation, and livelihood diversification allows them to mitigate risk and avoid radical fluctuations in income or wealth. Modeling agent decision-making and livelihood choices would benefit from better information about the important factors that affect these decisions, and from detailed demographic, income, and standard of living information. Similarly, we were unable to include more nuanced treatments of LULC beyond guava. This was in part due to a general lack of available data with which to parameterize the model to reflect these complexities.

We view the limitations of our model as indicative of potential avenues for future data collection, research, and model extension. There is clearly a demand for more extensive data on the behavior and feedback effects of the environmental aspects of our model. The finding that the modeled system was highly sensitive to the rules of guava spread, the cost of its control, and the control measures of park personnel demonstrates the need for more detailed information on this invasive species. Not only is there a demand for research on guava's rate of spread over the landscape, but the spatial patterning of this species' dispersal patterns warrants further research as well. Our identification of these avenues for future research indicates that stylized models are useful during preliminary stages of research projects. In other words, ABM's are not only useful as tools for exploring population-environment interactions through the integration of large and varied datasets, but they can also serve as tools for directing data collection. The next iteration of ILLUM will be informed by more precise data on guava spread and by more household interviews and socioeconomic data to better capture human decision-making processes.

Models like ILLUM could be made more relevant to real-world problems by conducting exchanges between modelers and stakeholders (Ramanath and Gilbert 2004). Discussing the model and its findings with the residents of Isabela might be particularly informative. For instance, asking farmers about their views of, and probable reactions to, control cost subsidies would be a useful way to evaluate the accuracy of our modeling results. Participatory approaches have been considered problematic due to time, cost, stakeholder bias, and validation difficulties (Matthews et al. 2007); however, the refinement of participatory modeling approaches and the development of methods to allow non-specialists to participate in the modeling exercise is a promising area of research (Parker et al. 2003). The present study reinforces this optimism and indicates that stylized models may provide a particularly useful platform for combining local and scientific knowledge. In particular, the NetLogo software is consistent with this goal insofar as it is a free program with intuitive coding language that supports a user-friendly graphical interface. The benefits of stylized modeling outlined here, in combination with the NetLogo modeling platform, present a promising framework for implementing participatory modeling in the Galápagos and elsewhere.

This research demonstrates that even simple, stylized ABMs based on publicly available data can generate meaningful output that captures key patterns and processes of population-environment interactions. We suggest that stylized ABMs have considerable utility, even during preliminary stages of research, as platforms for (1) exploring alternative scenarios, (2), sharpening conceptualizations of complex systems and population-environment interactions and (3) uncovering critical data gaps. Such models can be implemented by non-specialists and they provide visual results that allow for discussions about population and environment interactions between multiple stakeholders, including researchers, policy-makers, and land managers (Erlien et al. 2006).