Abstract
Purpose: Estimating motion and deformation parameters from a series of projection radiographs acquired during arc therapy using a reference CT volume has become a promising technique for targeting treatment. The purpose of this work is to investigate the influence of rotational arc length on maximum achievable accuracy of motion estimation.
Methods: The projection-to-volume alignment procedure used a nonrigid model to describe motion in thorax area, a cost function consisting of a least-squared error metric and a simple regularizer that encourages local invertibility, and a four-level multiresolution scheme with a conjugate gradient method to optimize the cost function. The authors tested both small and large scale deformations typically found in the thorax of a radiotherapy patient at different breathing states and limited-angle scans of six angular widths (12°, 18°, 24°, 36°, 60°, and 90°) centered at three angles (0°, 45°, and 90°).
Results: The experiments illustrate the potential accuracy of limited-angle projection-to-volume alignment. Registration accuracy can be sensitive to angular center, tends to be lower along direction of the projection set, and tends to decrease away from the rotation center. The studies of small as well as large but realistically scaled deformations show similar dependencies. These trends appear to have fairly low sensitivity to quantum noise effects.
Conclusions: There is potentially sufficient information present in a small spread of projections to monitor the configuration of reasonably high contrast tumors without implanted markers.
Keywords: motion estimation, nonrigid image registration, cone-beam projection, arc therapy
INTRODUCTION
The rapid adoption of two technologies, arc therapies1, 2 and cone-beam CT,3, 4, 5, 6 have brought to the forefront a number of investigations about optimizing the use of projection radiographs and reference volumes for targeting treatment. While a significant number of investigations are ongoing into optimizing reconstruction and use of cone-beam CT, a smaller but highly relevant path of investigation is similarly being pursued in using subsets of projections from a rotational series for alignment and reconstruction.
Such experiments fall into two primary classes of operation. The first involves reconstructing volumetric images from subsets of projections acquired over rotational arcs of various lengths. For longer arcs, these backprojections yield volumetric images with fairly uniform resolution, while for shorter (typically 45°–90°) arcs, the reconstruction yields volumes with spatially varying resolution. Such reconstructions are generally termed tomosynthesis and have been evaluated from both kilovoltage as well as megavoltage projections for use in image guided radiotherapy.7, 8, 9, 10 There is a special case of tomosynthesis using a fixed set of projections (more complex than an arc) (see Refs. 11). These reconstructed volumes are typically aligned directly to the reference CT scan.
A different approach involves relating the new projections directly to the reference CT without reconstruction. Such projection-to-volume alignment experiments have been performed for some time.12, 13 More recently, the series of projections acquired during arc rotations has been used to estimate motion and deformation parameters.14, 15, 16, 17, 18, 19, 20, 21, 22
This area of research is highly promising. As the amount of information needed to estimate the position, pose, configuration, and finally motion of a patient is reduced, the temporal resolution of updates to the patient state improves. In this investigation, methods for estimating the local configuration of a lung tumor are tested, and an evaluation is made of the influence of rotational arc length on the maximum achievable accuracy.
MATERIALS AND METHODS
Projection-to-volume registration
We assume a static reference volume fref, such as a breath-hold planning CT, is available, the target anatomy ftar during rotational therapy is deformable from fref, and we record a sequence of cone-beam projection views of a limited-angle scan, denoted as ym for m=1,…,M, where M is the number of projection views. The current experiment assumes that movement during the limited projection arc is negligible. One can imagine that a continuous relationship exists between temporal resolution and spatial accuracy. The current investigation focuses on the spatial accuracy under ideal conditions (no movement between projections). While one can assume that movement during rotation would decrease the accuracy of measurements, it is our expectation that further studies will be able to extend prior models for estimating motion during rotational arcs (e.g., Refs. 19, 22), but that it is unlikely that such methods can recover spatial information at accuracies higher than the current motion-free estimations are capable of. We estimate the local configuration of a lung tumor using two sets of data: The reference volume fref and projection views ym.
Nonrigid transformation model
A nonrigid model is suitable to describe changes in the thorax configuration during breathing or as varying between breath-held states. Denote the operator T(ν;α):R3→R3 that represents a nonrigid transformation described by unknown parameters α≜(αx,αy,αz)∊Rnα as
| (1) |
where ν≜(x,y,z), x, y, and z denote the left-right (LR), posterior-anterior (AP), superior-inferior directions, respectively, and D(ν;α)=(Dx(ν;α),Dy(ν;α),Dz(ν;α)) is the deformation map vector modeled by a tensor product of cubic B-splines23 as
| (2) |
where c∊{x,y,z} and Δc is the knot spacing in the c direction.
Rather than operate on a continuous reference image fref, we represent it as a discretized object by a common basis function of cubic B-splines as follows:
| (3) |
where
| (4) |
u=(u1,…,unp) is the vector of basis coefficients computed from the sample values of fref by recursive digital filtering,23 and integer coordinates (xk,yk,zk) denote centers of basis functions. We denote the reference image coefficient vector as fref, whose jth component is
| (5) |
We next apply the same basis expansion model 3 to a target image ftar to obtain a target image coefficient vector ftar. Assuming that the target image ftar is deformable from fref, the geometric correspondence between them is
| (6) |
where W(α):Rnp→Rnp denotes the operator that maps fref to ftar and the expression for the jth element is
| (7) |
where νj=(xj,yj,zj) denotes the coordinates of the jth point.
Regularized least squares estimator
We estimate the deformation parameters α by minimizing the following regularized cost function:
| (8) |
where L(α) is the data fidelity term, R(α) is the regularization function, and scalar γ controls the trade-off between them.
We focus on the least-squared error metric because all the investigations in this paper are based on the same patient and imaging modality. The metric is expressed as
| (9) |
where Aφm denotes the system matrix with size of nd×np at projection angle φm that is the angle of the source point counterclockwise from the y axis (see Fig. 2) and ym≜(ym,1,…,ym,n,…,ym,nd) is the mth cone-beam CT projection view. In practice, ym is estimated from the transmitted intensity Ym, which is degraded by noise that dominated by the Poisson effect.27 For simplicity, assuming a monoenergetic model and ignoring the background signals such as Compton scatter, dark current, and noise, we describe the Poisson statistics as follows:
| (10) |
where Im,n denotes the incident intensity that incorporates the source spectrum and the detector gain. The projection view ym is estimated from Ym as follows:
| (11) |
Figure 2.
Schematic diagram of limited-angle scans centered at 0°, 45°, and 90°. p and o are the axes along and orthogonal to the ray connecting the X-ray source and the detector center for the limited-angle scan centered at 45°.
To encourage local invertibility and smoothness of changes due to local respiratory motion and its variations, we adopted a simple regularizer proposed by Chun and Fessler24 [see Eq. (10) in Ref. 24 for the expression of this regularizer]. This penalty method yields much more realistic deformation for breathing motion than unconstrained registration methods. Moreover, it is much simpler and faster than the traditional Jacobian determinant penalty and is more memory efficient. It is computationally expensive to calculate the Jacobian determinants or its gradient due to additional B-spline interpolations of the partial derivative of a deformation. This quadratic-like regularizer enforces a sufficient condition for invertibililty directly on the B-spline deformation coefficients, so it does not require additional B-spline interpolations beyond the interpolations needed for the data fitting term. It also encourages the smoothness of deformations inherently because it constrains the differences between adjacent deformation coefficients. In addition, its first and second derivatives are simple and convenient for use in optimization algorithms. In this investigation we used the same parameter settings as in Sec. IVD of Ref. 24, which used the prior knowledge that the deformation in the z direction is larger due to diaphragm motion, whereas the deformation in the x and y directions is small.
For optimization of the cost function 8, a conjugate gradient method was used. The line search step size was determined by one step of Newton’s method. To avoid local minima and accelerate the optimization procedure, we applied a four-level multiresolution scheme.25 We ran 100 iterations of conjugate gradient optimization for the first three levels of resolution and 150 iterations for the finest resolution. Large number of iterations were used to ensure convergence. Since this paper is a study of estimation accuracy, the computation time is not the major concern.
Investigating the influence of rotational arc length
Experimental setup
We acquired three 3D thorax volumes, two at different inhale states and one at exhale state, from a lung cancer patient by breath-held diagnostic CT. One inhale CT volume was chosen as the reference fref, while the other inhale and the exhale volumes were treated as different targets for evaluation. The volume size was 512×512×96 with spacing of 0.9375×0.9375×3 mm3 in the x, y, and z directions, respectively.
Two deformation maps were obtained by the regularized B-spline nonrigid registration24 between reference and each of the target volumes. The B-spline control knots were placed uniformly in CT volumes with a spacing of 8×8×4 voxels. Two synthetic CT volumes (see Fig. 1), one at inhale and another at exhale, were obtained by warping the reference volume with corresponding estimated deformation maps in a fashion similar to that applied in previous research (Ref. 22). These two synthetic CT volumes were used as new targets, denoted as and , for subsequent investigations of the influence of rotational arc length on the accuracy of the estimated local deformation around the tumor. The B-spline control knots were also placed uniformly in CT volumes with a spacing of 8×8×4 voxels, implying 64×64×24=98304 unknown deformation parameters to be estimated.
Figure 1.
Axial (left), sagittal (center), and coronal views (right) of the reference, target volumes, and reference volume within a ROI overlaid with example radial annuli for analysis.
We simulated an axial cone-beam flat-detector X-ray CT system with a detector size of 512×512 cells spaced by 1×1 mm2. The source to detector distance is 1500 mm, and the source to rotation center distance is 1000 mm.
Since our focus is the local configuration of a lung tumor (see Fig. 1), we set the tumor center in the reference volume as the rotation center to make sure that the local areas around it in the target volumes are always covered by X-rays emitting from the source at any projection angle. As a result, other structures away from the tumor, such as the scapular bones in the lower right or left sides (see Fig. 1), might be truncated at certain projection angles.
Investigation design
Typically, the X-ray source rotates around the patient, and 360° of projection views are acquired to perform projection-to-volume alignment. In this paper, we investigate deformation estimation accuracy with limited-angle scans (see Fig. 2). In addition, the angular center may affect the estimation accuracy. Without loss of generality, we chose three angular centers (0°, 45°, and 90°) and six angular ranges (12°, 18°, 24°, 36°, 60°, and 90°) with 2° angular spacing between projections. (We examined smaller angular spacings of 1° and 0.5°, and found performances very similar to that of 2°.) Using the case of 0° center and 12° range as an example, we performed projection-to-volume alignment between projection views from seven angles (−6°, −4°, −2°, 0°, 2°, 4°, and 6°) and the reference volume. Alignments on angular ranges of 360° and 180° ([−90°,90°]) were investigated too.
We also studied the influence of the extent of deformation. We considered the deformation between two different inhale volumes as small, and the deformation between inhale and exhale volumes large. We called the former as small deformation case and the latter as large deformation case. The experiments were executed on both cases.
In summary, we studied a total of 40 registration examinations. For each (small and large) deformation case, we tested 20 examinations that include the 360° and 180° scan and another 18 limited-angle scans (six angular ranges at three centers).
RESULTS AND DISCUSSION
In this section, we summarize the error of tumor center shift and deformation estimation within a region of interest (ROI) around the tumor. We computed the error using the true deformation maps between the reference and the synthetic target volumes in comparison to the experimental alignment estimates from various angular centers and ranges.
Noiseless projection views
We generated noiseless projection views of target volumes ( and ) at certain angles using a distance-driven (DD) forward projector26 for Aφ. The projection-to-volume registration described in Sec. 2A was performed between these generated projection views and the reference volume.
Accuracy of tumor center shift
We calculated the absolute error of estimated tumor center shift in the c direction by
| (12) |
where denotes the estimated motion parameters, denotes the estimated tumor center shift in the c direction, Dc(ν0;α) denotes the true tumor center shift in the c direction, and ν0 denotes the coordinates of the tumor center.
The true shifts of the tumor center are −2.21, −2.46, and 0.56 mm in the x, y, and z directions, respectively, for the small deformation case, and −0.92, 6.17, and 1.53 mm in the x, y, and z directions, respectively, for the large deformation. Table 1 shows the absolute errors of tumor center shift when the angular ranges are 360° and 180°. The absolute errors are all below 0.1 mm, except the error of 0.13 mm in the z direction for the large deformation case. Since the true shift is 1.53 mm for this case and the spacing is 3 mm in the z direction, this 0.13 mm error is small.
Table 1.
Absolute errors (mm) for angular ranges of 360° and 180° ([−90°,90°]).
| Direction | Small deformation | Large deformation | ||||
|---|---|---|---|---|---|---|
| x | y | z | x | y | z | |
| 360° | 0.06 | 0.08 | 0.03 | 0.09 | 0.06 | 0.08 |
| 180° | 0.08 | 0.07 | 0.001 | 0.08 | 0.05 | 0.13 |
The projection views are approximately line integrals along rays passing from the X-ray source to the detector cells.26 With limited-angle scans, the information about deformation along the projection direction is limited. Realizing this property, we used a 3D coordinate system with new axes to evaluate estimation accuracy. We rotated the 3D coordinate system around z by the central projection angle φ0, and denoted the axes as p, o, and z, where p and o are the axes along (parallel to) and orthogonal to the ray connecting the X-ray source and the detector center, respectively. Figure 2 shows the p and o directions when φ0=45°. The corresponding coordinates on the p and o axes are
| (13) |
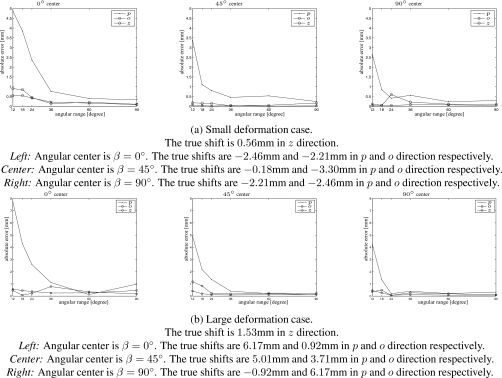
Figure 3 shows the absolute errors of tumor center shift with limited-angle scans centered at 0°, 45°, and 90° for both the small and large deformation cases. The error in the p direction is bigger than that in the o and z directions because only limited shape information can be extracted from projection views along the projection direction. The errors of the 0° center scans are larger than those of 45° and 90° center scans. When angular range is smaller than 36°, the estimation accuracy improves quickly with the increase in angular range, and the estimation errors of the large deformation case are slightly higher than those of the small deformation case. When the angular range exceeds 36°, the errors are within 1 mm for the 0° center scans, and within 0.5 mm for others.
Figure 3.
Absolute errors (mm) of tumor center shift.
Deformation accuracy within a ROI
Since the goal is to study estimation accuracy of the local configuration of a lung tumor, we chose a ROI centered at the tumor center and evaluated deformation estimation accuracy within this ROI. The ROI is a cylinder with height and radius of 6 cm, i.e., a diameter of 128 voxels and height of 20 voxels. The tumor center is also the rotation center, which guarantees the ROI is covered by the field of view (FOV) of radiation at any projection angle. Figure 1d shows the axial, sagittal, and coronal views of the reference volume within ROI.
We evaluated absolute errors of the estimated deformation of points in a set of S, such as the ROI, by mean , maximum , and standard deviation in the c direction as follows:
| (14) |
where denotes the estimated motion parameters, and Dc(νj;α) denote the estimated and true displacements at the jth point in S in the c direction, respectively, and νj denotes the coordinates of the jth point.
Table 2 shows the mean, max, and standard deviation of the estimated deformation for the angular ranges of 360° and 180°. The errors are very small, which demonstrates that the projection-to-volume method described in Sec. 2A works well.
Table 2.
Mean, maximum, and standard deviation σ of absolute errors of the estimated displacements with angular ranges of 180° ([−90°,90°]) and 360°.
| Direction | Small deformation | Large deformation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Angular range 180° | Angular range 360° | Angular range 180° | Angular range 360° | |||||||||
| x | y | z | x | y | z | x | y | z | x | y | z | |
| Mean | 0.08 | 0.07 | 0.09 | 0.05 | 0.05 | 0.07 | 0.06 | 0.07 | 0.08 | 0.05 | 0.06 | 0.06 |
| Max | 1.06 | 1.38 | 1.83 | 0.84 | 0.77 | 1.06 | 0.54 | 0.75 | 1.74 | 0.44 | 0.75 | 0.62 |
| σ | 0.10 | 0.10 | 0.11 | 0.06 | 0.06 | 0.08 | 0.07 | 0.07 | 0.09 | 0.05 | 0.07 | 0.06 |
Figures 456 show the mean, max, and standard deviation of the estimated deformation of all the studied limited-angle scan cases, respectively. In general, values of these measures decrease with increasing angular range. For 45° and 90° center cases, the errors and standard deviation in the p direction are bigger than those in the o and z directions and the errors of the large deformation case are slightly bigger than those of the small deformation case. The mean absolute error is below 0.5 mm for angular ranges greater than 36°. For the 0° center cases, the errors and standard deviation are larger than those of 45° and 90° center cases and the error in the z direction is larger than that in the p and o directions.
Figure 4.
Mean absolute errors (mm) of the estimated deformation within ROI. Left: Angular center is β=0°. Center: Angular center is β=45°. Right: Angular center is β=90°.
Figure 5.
Maximum absolute errors (mm) of the estimated deformation within ROI. Left: Angular center is β=0°. Center: Angular center is β=45°. Right: Angular center is β=90°.
Figure 6.
Standard deviation of absolute errors (mm) of the estimated deformation within ROI. Left: Angular center is β=0°. Center: Angular center is β=45°. Right: Angular center is β=90°.
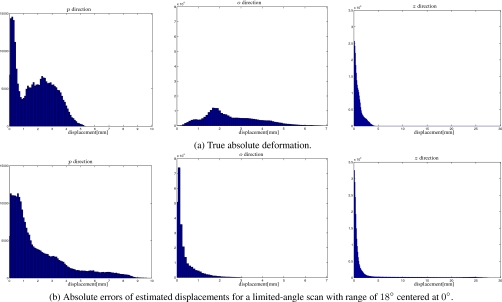
The maximum absolute error and standard deviation of the limited-angle scans centered at 0° are much larger than those of other cases, especially for the small deformation case with angular range smaller than 36°. We chose the scan with range of 18° centered at 0° for the small deformation case as an example to investigate more details about the estimated deformation.
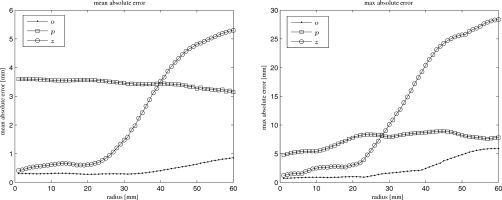
Figure 7a shows histograms of true absolute deformation within the ROI, and Fig. 7b shows histograms of absolute errors of estimated displacements within the ROI for a limited-angle scan with range of 18° centered at 0° for the large deformation case. Only a small percentage of voxels have large absolute errors in the z direction. For this case of a limited-angle scan, we also calculated mean and maximum errors among points within a sequence of cylindrical shells (with thickness of 1 mm) centered at the tumor center. The left panel of Fig. 1d shows an axial view of four such cylinders. Figure 8 shows these errors versus radial distance to the tumor center. With increasing radial distance, the errors in the z direction increase, especially when the radial distance is greater than 30 mm. The maximum errors in this direction happened at the bony portion inside the chest wall. The errors in the o direction are small and increase slowly. The errors in the p direction remain at the same level.
Figure 7.
Histograms in the o direction (left), p direction (center), and z direction (right) within the ROI for the small deformation case.
Figure 8.
Mean (left) and maximum (right) absolute errors of the estimated displacements within ROI for a limited-angle scan with range of 18° centered at 0°. The horizontal axis denotes radial distance to the tumor center. The errors were calculated among points within cylindrical shells centered at the tumor center.
The shape information that can be estimated from limited-angle projections depends on the angular center, especially when angular ranges are small. It appears that the truncation of 0° scans affects estimation accuracy more severely than scans at other centers. Since the deformation model covers the whole thorax, truncation outside the ROI still influences estimation accuracy in all regions. This influence becomes more obvious when radial distance from the rotation center (tumor center) increases, i.e., as the distance to truncated parts decreases. One reason for the large errors in z is that the voxel size in z is three times of those in x and y. The poor sampling (not truncation) associated with cone-beam CT geometry at the off-axis slices may also influence accuracy. Since the bony areas obey rigid motion instead of nonrigid movement, the nonrigid deformation model we used seems to cause errors in those areas. Adding a penalty that encourages rigid motion at bony areas may improve estimation accuracy.
Noisy projection views
We generated noiseless projection views ym of target volumes ( and ) using the DD method,26 generated transmitted intensities Ym using Eq. 10 with Im,n being 105 and 104 counts∕ray for all m and n, and then estimated noisy projection views using Eq. 11. The projection-to-volume registration described in Sec. 2A was performed between these estimated projections and the reference volume.
We tested estimation accuracy on noisy projections of a limited-angle scan with angular range of 24° centered at 45° of the small deformation case. Table 3 shows absolute errors (mm) of tumor center shifts for the tested limited-angle scan. Table 4 shows mean, maximum and standard deviation of absolute errors of estimated displacements within ROI for this scan. We denote noiseless experiments as Ia, noisy experiments with Im,n=105 counts∕ray as Ib, and noisy experiments with Im,n=104 counts∕ray as Ic in these tables. The errors of experiments Ia are smaller than those of Ib and Ic. The errors increase when incident intensity Im,n decreasing, but the errors in the p direction change very slowly. It appears that the errors in the p direction are dominated by limited shape information that can be extracted from limited-angle projections. The error differences between experiments Ia and Ib are smaller than those between experiments Ib and Ic.
Table 3.
Absolute errors (mm) of tumor center shifts for a limited-angle scan with range of 24° centered at 45° of the small deformation case. Ia stands for the case of no noise, Ib stands for the case when Im,n=105 counts∕ray, and Ic stands for the case when Im,n=104 counts∕ray.
| Intensity | p direction | o direction | z direction | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ia | Ib | Ic | Ia | Ib | Ic | Ia | Ib | Ic | |
| Error | 0.80 | 0.85 | 0.91 | 0.01 | 0.10 | 0.46 | 0.15 | 0.69 | 1.45 |
Table 4.
Mean, maximum, and standard deviation σ of absolute errors of the estimated displacements within ROI for a limited-angle scan with range of 24° centered at 45° of the small deformation case. Ia stands for the case of no noise, Ib stands for the case when Im,n=105 counts∕ray, and Ic stands for the case when Im,n=104 counts∕ray.
| Intensity | p direction | o direction | z direction | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ia | Ib | Ic | Ia | Ib | Ic | Ia | Ib | Ic | |
| Mean | 0.51 | 0.51 | 0.64 | 0.08 | 0.10 | 0.18 | 0.19 | 0.26 | 0.41 |
| Max | 4.31 | 4.14 | 4.23 | 1.08 | 1.25 | 1.17 | 2.60 | 3.27 | 3.76 |
| σ | 0.58 | 0.57 | 0.63 | 0.08 | 0.10 | 0.16 | 0.21 | 0.27 | 0.39 |
CONCLUSION
The experiments performed demonstrate the significant amount of information present to aid limited-angle projection-to-volume alignment. They also highlight some of the trends in degeneracy of such alignments from limited angular samples, both as a function of direction relative to the projection set as well as distance from the rotation center. It is hoped that such experiments can be used to guide optimal development of radiographic alignment and monitoring methods that maximize the prior knowledge available in radiotherapy targeting applications to minimize the time, radiographic dose, and computational resources needed for position monitoring during treatment.
This set of experiments presented both small as well as large scale deformations typically found in the thorax of a radiotherapy patient. While we used a deformation associated with variations in breathing states, we do not propose this methodology as a tool for tracking breathing. It is important to understand the information limits in rotational projection-to-volume registration as these will impact not only the complexity and operational parameters of positioning or tracking methodologies, but more importantly may indicate optimal design of radiographic localization technology integrated with linear accelerators. As a number of configurations have been proposed and introduced studies such as this may help determine the trade-offs associated with various parameters such as projection arrangement, noise∕dose, and temporal∕spatial accuracy limits.11, 28, 29, 30
ACKNOWLEDGMENTS
This work was supported in part by the NIH under Grant No. P01 CA59827. The authors would like to thank Dan Ruan for insightful discussions, Se Young Chun for the use of his registration code and GE for the use of DD code.
References
- Yu C. X., “Intensity-modulated arc therapy with dynamic multileaf collimation: An alternative to tomotherapy,” Phys. Med. Biol. 40(9), 1435–1449 (1995). 10.1088/0031-9155/40/9/004 [DOI] [PubMed] [Google Scholar]
- Otto K., “Volumetric modulated arc therapy: IMRT in a single gantry arc,” Med. Phys. 35(1), 310–317 (2008). 10.1118/1.2818738 [DOI] [PubMed] [Google Scholar]
- Cho P. S., Johnson R. H., and Griffin T. W., “Cone-beam CT for radiotherapy applications,” Phys. Med. Biol. 40(11), 1863–1883 (1995). 10.1088/0031-9155/40/11/007 [DOI] [PubMed] [Google Scholar]
- Mosleh-Shirazi M. A., Evans P. M., Swindell W., Webb S., and Partridge M., “A cone-beam megavoltage CT scanner for treatment verification in conformal radiotherapy,” Radiother. Oncol. 48(3), 319–328 (1998). 10.1016/S0167-8140(98)00042-5 [DOI] [PubMed] [Google Scholar]
- Jaffray D. A., Drakes D. G., Moreau M., Martinez A. A., and Wong J. W., “A radiographic and tomographic imaging system integrated into a medical linear accelerator for localization of bone and soft-tissue targets,” Int. J. Radiat. Oncol., Biol., Phys. 45(3), 773–789 (1999). 10.1016/S0360-3016(99)00118-2 [DOI] [PubMed] [Google Scholar]
- Jaffray D. A., Siewerdsen J. H., Wong J. W., and Martinez A. A., “Flat-panel cone-beam computed tomography for image-guided radiation therapy,” Int. J. Radiat. Oncol., Biol., Phys. 53(5), 1337–1349 (2002). 10.1016/S0360-3016(02)02884-5 [DOI] [PubMed] [Google Scholar]
- Kolitsi Z., Panayiotakis G., Anastassopoulos V., Scodras A., and Pallikarakis N., “A multiple projection method for digital tomosynthesis,” Med. Phys. 19(4), 1045–1050 (1992). 10.1118/1.596822 [DOI] [PubMed] [Google Scholar]
- Tutar I. B., Managuli R., Shamdasani V., Cho P. S., Pathak S. D., and Kim Y., “Tomosynthesis-based localization of radioactive seeds in prostate brachytherapy,” Med. Phys. 30(12), 3135–3142 (2003). 10.1118/1.1624755 [DOI] [PubMed] [Google Scholar]
- Godfrey D. J., Yin F. -F., Oldham M., Yoo S., and Willett C., “Digital tomosynthesis with an on-board kilovoltage imaging device,” Int. J. Radiat. Oncol., Biol., Phys. 65(1), 8–15 (2006). 10.1016/j.ijrobp.2006.01.025 [DOI] [PubMed] [Google Scholar]
- Sarkar V., Shi C., Rassiah-Szegedi P., Eng T., Diaz A., and Papanikolaou N., “A feasibility study on the use of digital tomosynthesis with individually-acquired megavoltage portal images for target localization,” Journal of B.U.ON. 14(1), 103–108 (2009). [PubMed] [Google Scholar]
- Maltz J. S., Sprenger F., Fuerst J., Paidi A., Fadler F., and Bani-Hashemi A. R., “Fixed gantry tomosynthesis system for radiation therapy image guidance based on a multiple source X-ray tube with carbon nanotube cathodes,” Med. Phys. 36(5), 1624–1636 (2009). 10.1118/1.3110067 [DOI] [PubMed] [Google Scholar]
- Kim J., Fessler J. A., Lam K. L., Balter J. M., and Ten Haken R. K., “A feasibility study of mutual information based set-up error estimator for radiotherapy,” Med. Phys. 28(12), 2507–2517 (2001). 10.1118/1.1420395 [DOI] [PubMed] [Google Scholar]
- Adler J. R., Chang S. D., Murphy M. J., Doty J., Geis P., and Hancock S. L., “The cyberknife: A frameless robotic system for radiosurgery,” Stereotact. Funct. Neurosurg. 69(1–4), 124–128 (1997). 10.1159/000099863 [DOI] [PubMed] [Google Scholar]
- Ren L., Godfrey D. J., Yan H., Wu Q. J., and Yin F. -F., “Automatic registration between reference and on-board digital tomosynthesis images for positioning verification,” Med. Phys. 35(2), 664–672 (2008). 10.1118/1.2831903 [DOI] [PubMed] [Google Scholar]
- Ren L., Zhang J., Thongphiew D., Godfrey D. J., Wu Q. J., Zhou S. -M., and Yin F. -F., “A novel digital tomosynthesis (DTS) reconstruction method using a deformation field map,” Med. Phys. 35(7), 3110–3115 (2008). 10.1118/1.2940725 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maurer J., Godfrey D., Wang Z., and Yin F. -F., “On-board four-dimensional digital tomosynthesis: First experimental results,” Med. Phys. 35(8), 3574–3583 (2008). 10.1118/1.2953561 [DOI] [PubMed] [Google Scholar]
- Yoo S., Wu Q. J., Godfrey D., Yan H., Ren L., Das S., Lee W. R., and Yin F. -F., “Clinical evaluation of positioning verification using digital tomosynthesis and bony anatomy and soft tissues for prostate image-guided radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys. 73(1), 296–305 (2009). 10.1016/j.ijrobp.2008.09.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Q. J., Godfrey D. J., Wang Z., Zhang J., Zhou S., Yoo S., Brizel D. M., and Yin F. -F., “On-board patient positioning for head-and-neck IMRT: Comparing digital tomosynthesis to kilovoltage radiography and cone-beam computed tomography,” Int. J. Radiat. Oncol., Biol., Phys. 69(2), 598–606 (2007). 10.1016/j.ijrobp.2007.05.045 [DOI] [PubMed] [Google Scholar]
- Li T., Schreibmann E., Yang Y., and Xing L., “Motion correction for improved target localization with on-board cone-beam computed tomography,” Phys. Med. Biol. 51(2), 253–267 (2006). 10.1088/0031-9155/51/2/005 [DOI] [PubMed] [Google Scholar]
- Pang G., Bani-Hashemi A., Au P., O’Brien P. F., Rowlands J. A., Morton G., Lim T., Cheung P., and Loblaw A., “Megavoltage cone beam digital tomosynthesis (MV-CBDT) for image-guided radiotherapy: A clinical investigational system,” Phys. Med. Biol. 53, 999–1013 (2008). 10.1088/0031-9155/53/4/012 [DOI] [PubMed] [Google Scholar]
- Zeng R., Fessler J. A., and Balter J. M., “Respiratory motion estimation from slowly rotating X-ray projections: Theory and simulation,” Med. Phys. 32(4), 984–991 (2005). 10.1118/1.1879132 [DOI] [PubMed] [Google Scholar]
- Rongping Z., Fessler J. A., and Balter J. M., “Estimating 3-D respiratory motion from orbiting views by tomographic image registration,” IEEE Trans. Med. Imaging 26(2), 153–163 (2007). 10.1109/TMI.2006.889719 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Unser M., “Splines: A perfect fit for signal and image processing,” IEEE Signal Process. Mag. 16(6), 22–38 (1999). 10.1109/79.799930 [DOI] [Google Scholar]
- Chun S. Y. and Fessler J. A., “A simple regularizer for B-spline nonrigid image registration that encourages local invertibility,” IEEE J. Sel. Top. Signal Process. 3(1), 159–169 (2009), special issue on digital image processing techniques for oncology. 10.1109/JSTSP.2008.2011116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Unser M., Aldroubi A., and Eden M., “The L2 polynomial spline pyramid,” IEEE Trans. Pattern Anal. Mach. Intell. 15(4), 364–379 (1993). 10.1109/34.206956 [DOI] [Google Scholar]
- De Man B. and Basu S., “Distance-driven projection and backprojection in three dimensions,” Phys. Med. Biol. 49(11), 2463–2475 (2004). 10.1088/0031-9155/49/11/024 [DOI] [PubMed] [Google Scholar]
- Erdogan H. and Fessler J. A., “Monotonic algorithms for transmission tomography,” IEEE Trans. Med. Imaging 18(9), 801–814 (1999). 10.1109/42.802758 [DOI] [PubMed] [Google Scholar]
- Berbeco R. I., Jiang S. B., Sharp G. C., Chen G. T. Y., Mostafavi H., and Shirato H., “Integrated radiotherapy imaging system (IRIS): Design considerations of tumour tracking with linac gantry-mounted diagnostic X-ray systems with flat-panel detectors,” Phys. Med. Biol. 49(2), 243–255 (2004). 10.1088/0031-9155/49/2/005 [DOI] [PubMed] [Google Scholar]
- Stutzel J., Oelfke U., and Nill S., “A quantitative image quality comparison of four different image guided radiotherapy devices,” Radiother. Oncol. 86(1), 20–24 (2008). 10.1016/j.radonc.2007.10.035 [DOI] [PubMed] [Google Scholar]
- Pouliot J., Bani-Hashemi A., Chen J., Svatos M., Ghelmansarai F., Mitschke M., Aubin M., Xia P., Morin O., Bucci K., and Roach M., “Low-dose megavoltage cone-beam CT for radiation therapy,” Int. J. Radiat. Oncol., Biol., Phys. 61(2), 552–560 (2005). 10.1016/j.ijrobp.2004.10.011 [DOI] [PubMed] [Google Scholar]