Quantitative polarized Raman spectroscopy in highly turbid bone tissue

Abstract

Polarized Raman spectroscopy allows measurement of molecular orientation and composition and is widely used in the study of polymer systems. Here, we extend the technique to the extraction of quantitative orientation information from bone tissue, which is optically thick and highly turbid. We discuss multiple scattering effects in tissue and show that repeated measurements using a series of objectives of differing numerical apertures can be employed to assess the contributions of sample turbidity and depth of field on polarized Raman measurements. A high numerical aperture objective minimizes the systematic errors introduced by multiple scattering. We test and validate the use of polarized Raman spectroscopy using wild-type and genetically modified (oim∕oim model of osteogenesis imperfecta) murine bones. Mineral orientation distribution functions show that mineral crystallites are not as well aligned (p<0.05) in oim∕oim bones (28±3 deg) compared to wild-type bones (22±3 deg), in agreement with small-angle X-ray scattering results. In wild-type mice, backbone carbonyl orientation is 76±2 deg and in oim∕oim mice, it is 72±4 deg (p>0.05). We provide evidence that simultaneous quantitative measurements of mineral and collagen orientations on intact bone specimens are possible using polarized Raman spectroscopy.

Introduction

Polarized Raman spectroscopy has long been used to study orientation in crystalline solids¹ and in both natural and synthetic fibers,² because it is possible to determine the most probable distributions of molecular orientations. Because diseases are frequently marked by changes in molecular organization of tissues, it is useful to have methodologies that can quantitatively report on molecular orientation. Bone is a composite tissue consisting of apatite mineral crystallites embedded within a predominantly collagen matrix. We focus on bone because maintenance of bone tissue organization at all hierarchical levels is important to its mechanical functioning. In long bones, the collagen fibers are preferentially aligned parallel to the long axis of the bone. The crystallographic c-axes of the crystals align along the long axis of the collagen fibrils.^{3, 4} Many disorders of bone are characterized, qualitatively, by changes in collagen and∕or mineral organization.^{5, 6} It is therefore imperative to quantitatively assess how this ordering is influenced by genetic defects, metabolic disorders, and other factors that affect bone quality.

Techniques such as X-ray diffraction,^{7, 8} and scanning small-angle X-ray scattering (SAXS)^{9, 10} have been used to measure quantitative orientation distributions for collagen and mineral crystallites in bone and other mineralized tissues. X-ray diffraction is limited to the crystalline regions within the tissue and involves harsh preparation techniques such as deproteination.¹¹ Hence, such orientation distributions have never been simultaneously obtained for collagen and mineral crystallites and never on fresh bone specimens.

Previous polarized Raman spectroscopy studies of dental enamel^{12, 13} and model apatite compounds¹⁴ have only been qualitative. Qualitative polarized Raman spectroscopic imaging has been used to study mineral and matrix orientation in cortical bone tissue by examination of the polarization components of phosphate ν₁ (P–O symmetric stretch) and amide I (carbonyl stretch).^{15, 16} Because the crystallites are oriented with their c-axes along the length of collagen fibrils, phosphate ν₁ scattering is more intense along this axis. Similarly, because collagen carbonyl groups are oriented perpendicular to the collagen chain, amide I scattering is more intense in the direction perpendicular to the collagen fibril orientation.

The polarized Raman data on bone confirm what was shown by polarized Fourier transform-infrared spectroscopic (FTIR) studies.¹⁷ It is widely understood that FTIR and Raman spectroscopies provide similar information. Spectral correspondences have recently been validated.¹⁸ Raman spectroscopy provides experimental advantages that include minimal specimen preparation and applicability to specimens of irregular shape or even intact bones. The problem of interference from fluorescence can be minimized by using excitation in the 650–800 nm range and by appropriate spectral processing methods, such as background subtraction. Polarized Raman spectroscopy yields both the second and fourth coefficients of the orientation distribution function, whereas IR spectroscopy yields only the second coefficient.² Both coefficients are needed to calculate the most probable orientation distribution function.

Bone tissue poses special challenges to the use of polarized Raman spectroscopy for measurement of quantitative orientation distribution functions because the tissue is turbid and birefringent. Standard theory assumes that the medium is completely transparent. However, multiple scattering in turbid media depolarizes light and introduces errors in the polarized Raman measurements.¹⁹ It is difficult or impossible to correct orientation functions for multiple scattering; thus, measurements must be made under conditions in which multiple scattering is negligible. Similarly, the simplest polarized Raman theory assumes that refractive index is the same in all Cartesian directions. Thus, a birefringence correction may be needed to describe bone tissue.²⁰

In this paper, we examine the conditions under which polarized Raman spectroscopy can be used to quantitatively measure mineral and matrix orientation in bone. We use objectives of increasingly higher numerical aperture (NA) to find the values at which polarized Raman measurements are independent of NA. We next test and validate the use of polarized Raman spectroscopy using genetically modified osteogenesis imperfecta (oim∕oim) murine bones for which mineral crystallite orientation distribution functions have been measured by SAXS.¹⁰ Finally, we use polarized Raman spectroscopy to compare mineral and matrix orientation distributions in cortical bone tissue from oim∕oim and wild-type mice.

Materials and Methods

Specimen Preparation

Both tibiae from four five-week-old wild-type and four oim∕oim female mice were used. The mice were part of a larger Institutional Animal Care and Use Committee (IACUC)-approved study at the Hospital for Special Surgery, New York. Specimens were harvested and immersed in phosphate-buffered saline (PBS) and frozen at −20°C until use. The specimens were thawed to room temperature before collection of spectra. They were kept moist throughout the experiment by a drip of PBS. Bone powders used to acquire isotropic Raman spectra were prepared from the mid-diaphyses of the wild-type specimens using a cryogenic impact grinder (Spex 6750 Freezer Mill, Spex CertiPrep, Metuchen, New Jersey). The age, bone, and background strain of the oim∕oim specimens used in this study match that of the specimens (tibiae from five-week-old oim∕oim mice) used in the SAXS study.¹⁰

Light-Scattering Measurements

To quantify the changes in elastic light scattering in wild-type versus oim∕oim bone specimens, an integrating sphere (RT-060-SF, Labsphere, North Sutton, New Hampshire) setup was used to extract the scattering coefficient of the wild-type and oim∕oim tibiae.²¹ A lamp attached to a Kohler Illuminator (KI-120, Labsphere) and powered by an LPS preset power supply (LPS-150-0660, Labsphere) was used to deliver a uniform beam of light to the mid-diaphysis of the bone specimens, with the beam diameter (1 μm) controlled by a 1:2 telescope and an adjustable iris. The specimens were placed between the telescope and the sphere such that diffusely transmitted light was sent into the sphere and ultimately detected by a spectrograph (HR 2000+, Ocean Optics, Dunedin, Florida, 200–1100 nm). All measured transmittance spectra were corrected for both dark current and the lamp spectrum. Because the wavelength regime of interest was in the near-infrared (800–896 nm), it was assumed that tissue absorption would have a negligible effect on the transmittance of the samples. The reduced scattering coefficient ${\mu }_s^{\prime }$ was calculated by setting the corrected measured transmittance of the samples equal to a Beer–Lambert factor of the form $\exp (-{\mu }_s^{\prime }d)$, where d is the thickness of the tissue (set equal to the cross-sectional diameter of the bone specimens: 1.37±0.06 mm for wild-type and 1.25±0.08 mm for oim∕oim specimens). For linearly polarized light depolarization length calculations, the anisotropy was taken to be 0.9.²²

Polarized Raman Spectroscopy

The locally constructed Raman microprobe has been described previously.²³ The system was constructed around a Nikon E600 microscope frame (Nikon USA, Melville, New York). The exciting laser was a 400-mW, 785-nm diode laser (Invictus, Kaiser Optical Systems, Inc., Ann Arbor, Michigan) from which the circularizing optics had been removed to allow line focusing. An axial transmissive imaging spectrograph (HoloSpec, Kaiser Optical Systems, Inc.) with 25-μm entrance slit (approximately 3–4 cm⁻¹ resolution) and a 1024×256 pixel deep depletion charge-coupled device detector (CCD) (Model DU 401-BR-DD, Andor Technology, South Windsor, Connecticut] were used to disperse and record the spectrum. The polarization direction of the beam was selected using a half-wave plate. The collected Raman scatter was passed through an analyzing polarizer and directed onto the slit of the spectrograph. A wedge depolarizer after the analyzer eliminated intensity artifacts caused by the polarization dependence of the grating transmission efficiency.

Polarized Raman spectra were collected from at least three mid-diaphyseal locations along the length of the bone in each of the eight wild-type and oim∕oim tibial bone specimens and from powdered bones. For comparisons of wild type to oim∕oim, each mouse was treated as an independent measure. In all experiments, the polarization of the incident laser beam was maintained either parallel (x) or perpendicular (y) to the long axis of the bones. The analyzer was adjusted to pass either the component of Raman scatter polarized parallel or perpendicular to the polarization direction of the incident laser. The intensities (I) of the four possible polarization components of the Raman scatter are described by their excitation and detection polarizations along the conventional directions: I_xx, I_xy, I_yy, and I_yx respectively.

Effect of Elastic Scattering on Polarized Raman Measurements

To assess the effect of light scattering on the molecular orientation measurements, the depth of field was varied using a series of objectives with differing NA. These were 4× (0.20 NA), 20× (0.50 NA), 20× (0.75 NA), and 40× (0.90 NA). The depth of field, z_min, was taken to be equal to the diffraction-limited axial resolution of an objective²⁴ and is given by

$$z_{\min }=2\lambda n∕{\left(\mathrm{NA}\right)}^2,$$

where n is the refractive index of bone tissue, NA is the numerical aperture of the objective, and λ is the laser wavelength (785 nm). Polarized Raman spectra (I_xx and I_yy) from the wild-type specimens measured using the different objectives were compared to define the NA needed for artifact-free polarization measurements independent of NA.

Data Analysis

The wavenumber scale of the spectrograph was calibrated against the emission lines of a neon lamp discharge. Intensities were corrected for polarization dependence of the optics by calibration against cyclohexane.²⁵ The spectra were corrected for spectrograph image curvature. Dark-current subtraction and white-light correction (flat-fielding) were performed using locally written scripts on Matlab (Mathworks Inc., Natick, Massachusetts). Spectra were analyzed using GRAMS∕AI 7.01 (Thermo Galactic, Waltham, Massachusetts).

For the wild-type and oim∕oim specimens, peak fitting was performed using GRAMS∕AI 7.01 (ThermoGalactic) and the intensities of the characteristic mineral band (phosphate ν₁ at 959 cm⁻¹) and the collagen band (amide I at 1665 cm⁻¹) were measured. Band intensities were used because they can be measured with less error from spectral background subtraction than areas. The Raman intensity ratios (R_x=I_xy∕I_xx and R_y=I_yx∕I_yy) for the mineral and amide I bands were corrected for the influence of sample birefringence (reflectivity, internal field, divergence) by assuming the typical collagen and mineral birefringence values of 3×10⁻³ and 7×10⁻³, respectively.^{18, 26} Statistical tests were performed on band intensities and intensity ratios using two-tailed unpaired t-tests to compare the effect of NA and to compare wild-type with oim∕oim specimens. A value of p<0.05 was considered significant.

Polarized Raman spectroscopy provides both the second- and fourth-order parameters, ⟨P₂⟩ and ⟨P₄⟩, which are the first two coefficients of the expansion in Legendre polynomials of the orientation distribution function.^{27, 28} The refractive index of the bone specimens was set as 1.55.^{29, 30} Assuming a uniaxial cylindrical symmetry, the orientational order parameters (henceforth referred to as P₂ and P₄) were calculated for both phosphate ν₁ and amide I components of the wild-type and oim∕oim groups from their respective intensity ratios, R_x and R_y, and the parameter a. The parameter a of the Raman tensor for both phosphate ν₁ and amide I was determined from their isotropic depolarization ratio, R_iso, using the bone powder. From P₂ and P₄, the most probable orientation distribution functions, N(θ), of the phosphate ν₁ and amide I groups for the wild-type and oim∕oim groups were estimated. As a uniaxial cylindrical symmetry is assumed, y and z directions are not distinguished in an x-y-z plane. Hence, the probability that these groups are oriented at an angle θ with respect to the axis of reference was calculated by multiplying N(θ) by sin(θ). The maximum position of this N(θ) sin(θ) distribution corresponds to the direction of preferred orientation with respect to the axis defined and the mean of the distribution calculated as the first moment characterizes the average orientation angle.¹⁰ The average orientation angle for the phosphate group obtained by Raman spectroscopy was compared to the typical tilt angle (i.e., distribution of orientation angles) of mineral crystals obtained using SAXS.^{9, 10}

Results

Representative peak fitted spectra of the mineral and collagen amide I bands are shown in Fig. 1. The reduced scattering coefficient, ${\mu }_s^{\prime }$, of the wild-type and oim∕oim specimens was obtained from integrating sphere measurements of diffuse transmittance in the 800–896 nm wavelength range. The mean ${\mu }_s^{\prime }$ for the wild-type and oim∕oim specimens using a flat slab model were calculated to be 14.7±0.5 and 12.3±0.8cm⁻¹, respectively (p<0.05). The lower scattering coefficient in oim∕oim bones is consistent with observations that molecular spacing in collagen fibrils from oim∕oim mice is larger than normal.³¹

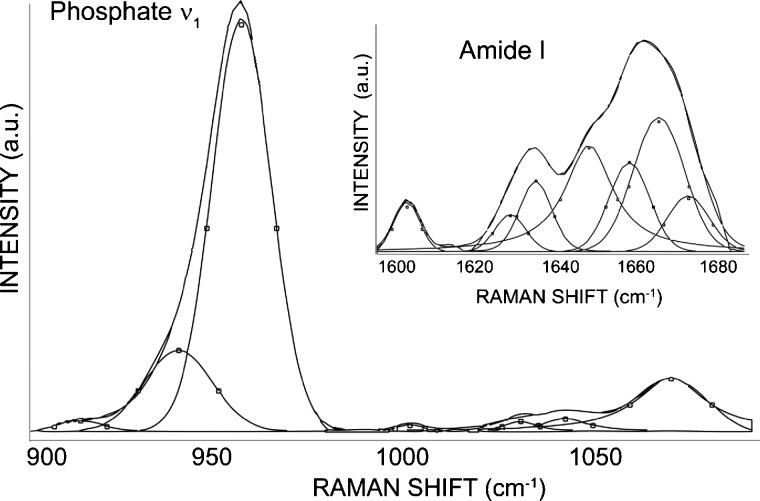
Figure 1.

Typical curve-fit spectra illustrating the sub-bands contributing to the overall contour of the mineral (phosphate ν₁ and carbonate) and amide I bands. The spectrum shown is from a wild-type specimen using a 0.90-NA objective.

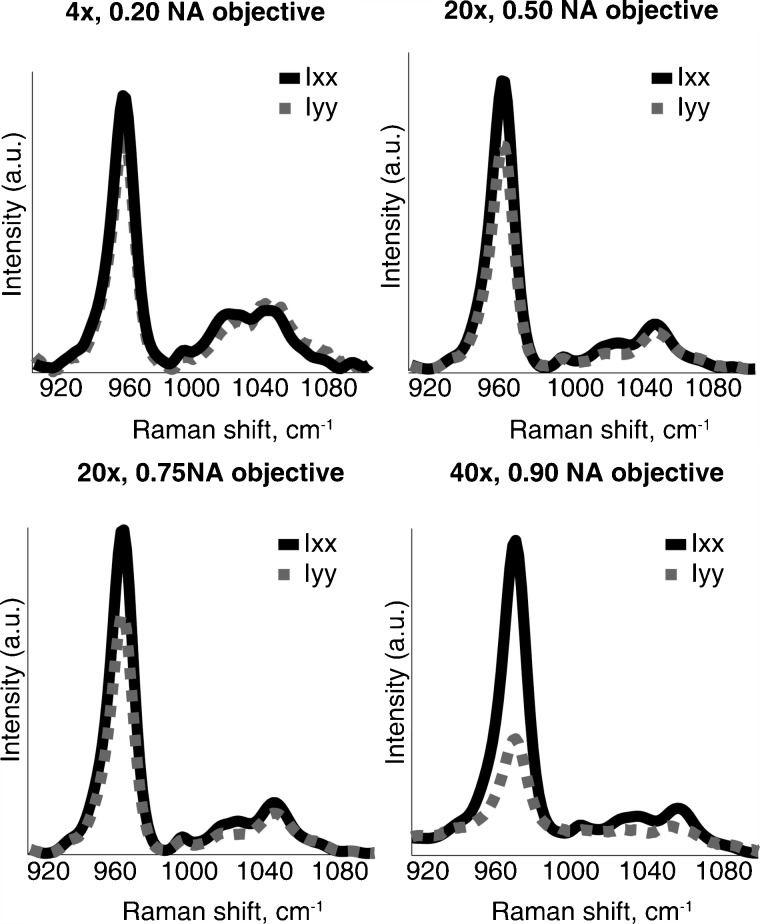
Polarized mineral spectra (I_xx and I_yy) from the wild-type specimens as functions of depth of field were measured using different objectives (Fig. 2). For the largest depth of field (0.2 NA), complete depolarization occurs and no polarization effects are observed (i.e., I_xx and I_yy are identical). As the depth of field decreases (NA increases to 0.90), the polarization effects in the phosphate ν₁ band become more prominent (i.e., I_xx is stronger).

Figure 2.

Mineral bands of the parallel-polarized bone spectra of a representative wild-type specimen as a function of depth of field. The polarization effects in the phosphate ν₁ band (I_xx>I_yy) are more prominent with the use of a high-NA objective.

Table 1 compares the intensity ratios and P₂ value of the phosphate ν₁ component of the wild-type specimens as a function of depth of field. The P₂ order parameter qualitatively defines the molecular orientation, with a value of −0.5 defining perfect perpendicular orientation and a value of +1 corresponding to perfect parallel orientation. A P₂ value of zero indicates random orientation with respect to the reference axis. With decreasing depth of field, depolarization decreases resulting in higher P₂ values. The 0.90 NA objective (i.e., smallest depth of field) gives P₂ values indicating parallel or near parallel orientation of mineral crystallites and therefore was found suitable for further quantitative polarized Raman measurements. Lower NA objectives (0.75 or 0.80 NA) could be employed for qualitative measures but are not suitable for quantitative estimations of molecular orientation. Higher NA objectives (water or oil immersion) might indeed give slightly higher P₂ values, but calibration and correction for partial depolarization by the high gathering angle would be challenging and laborious.

Table 1.

Measured intensity ratios and the calculated orientational order parameter, P₂, for the phosphate ν₁ component of wild-type specimens as a function of the depth of field (z_min) of the objective used.

Objective	Intensity Ratios		Order Parameter, P2
	Rx	Ry
4×, 0.20 NA (zmin=60.8 μm)	0.60±0.2	0.78±0.1	0.03±0.02
20×, 0.50 NA (zmin=9.7 μm)	0.26±0.1	0.36±0.11	0.06±0.01
20×, 0.75 NA (zmin=4.3 μm)	0.29±0.05	0.59±0.09	0.20±0.02
40×, 0.90 NA (zmin=3.0 μm)	0.06±0.03	0.74±0.1	0.72±0.06

Table 2 compares the order parameters, P₂ and P₄, of the 959 cm⁻¹ phosphate ν₁ band and the 1665 cm⁻¹ amide I band for the wild-type and oim∕oim specimens obtained using a 0.90 NA objective. The order parameters were calculated from the intensity ratios, R_x and R_y. The parameter a was calculated to be −0.04 for the phosphate ν₁ band and −0.48 for the amide I 1665 cm⁻¹ band using isotropic samples of murine cortical bone powder. Correcting for the effects of birefringence has a small effect (i.e., <1% change in the computed values of P₂ and P₄) and can be neglected for these samples.

Table 2.

The calculated orientational order parameters, P₂ and P₄, for the phosphate ν₁ and amide I components for wild type and oim∕oim groups. Polarized Raman measurements were made with a 0.90 NA objective.

Raman bands	Order parameters	Wild-type group (Mean+SD)	oim∕oim group (Mean+SD)
Phosphate ν1	P2	0.72±0.06	0.60±0.06a
	P4	0.58±0.08	0.48±0.06
Amide I	P2	−0.37±0.09	−0.32±0.05
	P4	0.15±0.05	0.06±0.03a

^ap<0.05

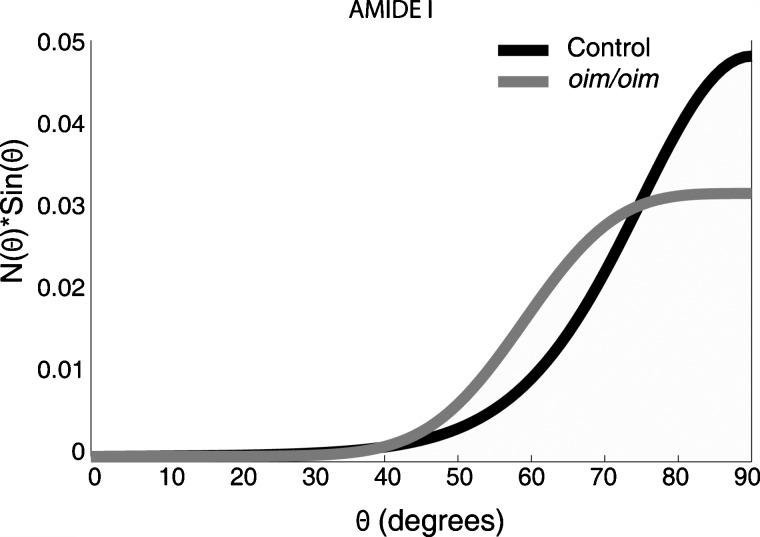
The N(θ) sin(θ) plot for amide I is shown in Fig. 3 for the wild-type and oim∕oim groups. For the wild-type group, the plot peaks at θ=90±19 deg, demonstrating that the amide I groups have a preferred orientation perpendicular to the longitudinal axis of the bone (x direction of the diaphysis in the nomenclature used here), although there is a distribution of ∼20 deg. For the oim∕oim group, the amide I N(θ) sin(θ) peaks at θ=90±32 deg. This indicates that although the preferred orientation is still perpendicular to the x direction of the diaphysis, collagen orientation is more variable in oim∕oim mice. The influence of uncertainty in the P₄-order parameter value on the orientation distribution function should be noted here. For example, at one standard deviation below the mean, the calculated amide I distribution for the oim∕oim group (Table 2) is an improbable asymmetric unimodal shape peaked at 69 deg, rather than the Gaussian shape that is expected.

Figure 3.

Rectangular coordinate plot of the orientation distribution function, N(θ) sin(θ), of amide I for wild-type and oim∕oim groups. The average orientation angles are 76±2 deg for the wild-type group and 72±4 deg for the oim∕oim group. The average orientation of collagen backbone can be calculated by subtracting the average orientation angle of amide I group from 90 deg.

Calculation of the first moments for these distributions for amide I give an average orientation angle of 76±2 deg for the wild-type group and that of 72±4 deg for the oim∕oim group. For comparison purposes, we have calculated the average orientation angles for the collagen backbone considering that amide I carbonyl groups are perpendicular to the collagen backbone. The average orientation angle for collagen backbone with respect to the x direction is 14 (90–76 deg) in the wild-type group. In the oim∕oim group, the average orientation angle is 18 (90–72 deg). There could be a tendency for a larger average orientation in oim∕oim, although the difference is not statistically significant. In the case of random orientation of the collagen backbone, the average orientation angle would be 57.3 deg.

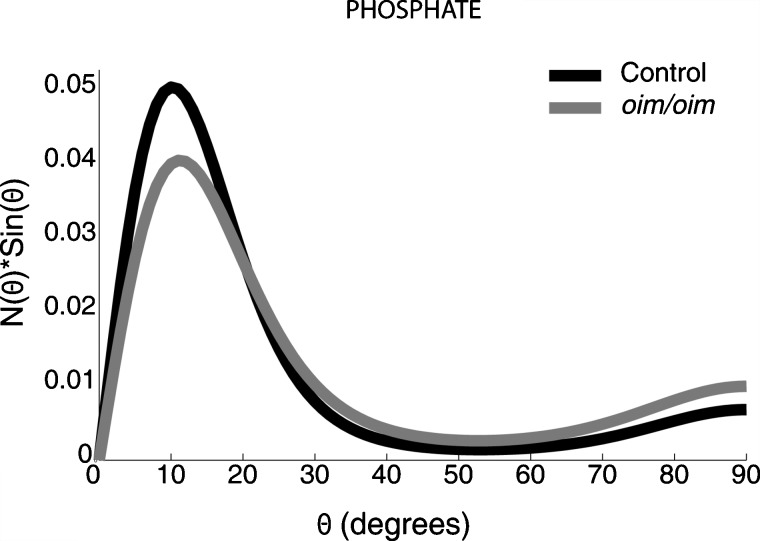
The N(θ) sin(θ) plot for phosphate ν₁ is shown in Fig. 4. The N(θ) sin(θ) distribution peaks at θ=10±8 deg for the wild-type group and at θ=11±11 deg for the oim∕oim group, indicating that the mineral crystallites are highly oriented along the x direction of the bone diaphysis and have a narrower distribution than collagen. Calculation of the mean of these distributions yields an average orientation angle of 22±3 deg for the mineral crystallites in the wild-type group. This is in agreement with values published in earlier X-ray scattering³² and electron microscopic tomography studies³³ on normal mice (typically around 20 deg). For the oim∕oim group, the mean of the distribution yields an average orientation angle of 28±3 deg for the mineral crystallites, which is significantly larger than that measured in the wild-type specimens (p<0.05). This average orientation angle is in agreement with the distribution of orientation angles of aligned crystals (25±3 deg with respect to the bone long axis) observed in a SAXS study on cortical bone samples also from five-week-old oim∕oim mice.¹⁰ These changes in the mineral crystallites could be due to the increased molecular spacing and reduced packing order of osteogenesis imperfecta-type collagen fibrils.³¹

Figure 4.

Rectangular coordinate plot of the orientation distribution function, N(θ) sin(θ) of phosphate ν₁ for wild-type and oim∕oim groups. The average orientation angles are 22±3 deg for the wild-type group and 28±3 deg for the oim∕oim group. Note that the carbonated apatite is preferentially aligned along the backbone axis of collagen (x direction).

Discussion

The orientation distributions of mineral crystallites and collagen fibers in the cortical regions of murine wild-type and oim∕oim bone specimens have been determined for the first time by polarized Raman spectroscopy. The orientation distribution functions for mineral and collagen in the wild-type group are in agreement with mineral and collagen orientation distributions obtained using SAXS and X-ray pole figure analysis on bone,^{32, 34} and X-ray diffraction on demineralized bone.³⁵ Furthermore, the average orientation angle of mineral crystallites in the oim∕oim group from our measurements agrees with that observed in an earlier SAXS study.¹⁰ These measurements provide validation for the use of Raman spectroscopy to assess mineral and matrix orientation simultaneously in intact normal and diseased or damaged tissues.

Using line illumination or point illumination requires trade-offs. A slit aperture has worse axial and lateral performance than a pinhole aperture, making the line illumination technique more vulnerable to artifacts rising from scattering effects.³⁶ However, line illumination has the advantage of power distribution, which limits thermal damage to the tissue specimen.³⁷ Furthermore, line illumination allows faster data acquisition over a wider region of interest. Hence, line illumination was the method of choice for this study. The line focus enabled the simultaneous collection of 126 spectra (one for each row of pixels on the CCD detector).

Systematic errors from elastic scattering in bone tissue can be reduced by the use of a high NA objective to minimize depolarization. In tissues with higher turbidity and an anisotropy factor of >0.9, an oil- or water-immersion objective might be required to limit depth of field. We caution that such objectives themselves partially depolarize Raman scatter because of their high gathering angles. Corrections for this effect are complicated. In soft tissues with a lower anisotropy factor and reduced turbidity, a lower NA objective might prove sufficient for quantitative polarized Raman measurements. Techniques such as spatially offset Raman spectroscopy and transmission Raman spectroscopy have been used to study bulk scattering materials, but it is unclear if they will be suitable for quantitative polarization analysis.

We caution that the mathematical description of orientation effects in Raman spectra has been derived for single fibers, not for extended arrays of fibers that are found in bone. We used a microscope objective with NA=0.90 with a nominal axial resolution of ∼3.0 μm. Taking the thickness of a lamella to be ∼300 nm, our microscope is integrating over almost 10 lamellae of intact bone. In the case of SAXS, the orientation information is averaged over a 200-μm thick section of demineralized bone.¹⁰ That we obtain agreement with SAXS orientation measurements in our wild-type and oim∕oim groups suggests that extension of polarization theory to bone is valid. The elastic scattering problem would have to be addressed in human bone specimens, such as those that have previously been used in polarized FTIR.¹⁷ In humans, the lamellae are about 2–9 μm thick³⁸ thus, confounding effects of multiple lamellae would be diminished, but multiple scattering would still occur.

In conclusion, the first simultaneous quantitative measurements of matrix collagen and mineral orientation in nondeproteinated, genetically disordered (OI) bone specimens have been reported. Systematic errors in the orientation distribution calculations due to contributions from sample turbidity and multiple elastic scattering effects have been minimized by employing a high NA objective. Mineral crystallite orientations in OI mouse bones calculated using polarized Raman spectroscopy have been validated against SAXS results. The techniques described in this paper may have widespread utility because the mechanical properties of calcified tissue are dependent on the molecular structure and the arrangement of the constituent mineral crystals within the organic matrix.³⁹ For example, in the SAMP6 mouse model for skeletal fragility, the reduced strength of the bone matrix is attributed to poorer organization of collagen fibers and reduced collagen content, although the animals have normal levels of collagen cross-links and normal mineral crystallite structure.⁴⁰ In biglycan-deficient mice, alterations in collagen and overexpression of noncollagenous proteins lead to an increase in mineralization, yet reduced mechanical properties.⁴¹ The ability to probe simultaneously mineral and matrix composition and orientation makes Raman spectroscopy a valuable tool to study such problems.