Skip to main content
PMC home page
Applied Physics Letters logoLink to Applied Physics Letters
. 2010 May 13;96(19):192903. doi: 10.1063/1.3430059

Piezoelectric activity of relaxor-PbTiO3 based single crystals and polycrystalline ceramics at cryogenic temperatures: Intrinsic and extrinsic contributions

Fei Li 1,2, Shujun Zhang 1,a), Zhuo Xu 2, Xiaoyong Wei 2, Jun Luo 3, Thomas R Shrout 1
PMCID: PMC2881932  PMID: 20531980

Abstract

The piezoelectric activity in [001] poled Pb(In1∕2Nb1∕2)O3–Pb(Mg1∕3Nb2∕3)O3–PbTiO3 crystals was investigated as a function of composition and temperature. The level of intrinsic and∕or extrinsic contribution to the total piezoelectric activity was analyzed using Rayleigh method. The results revealed that though 95% of the observed piezoelectric activity in rhombohedral crystals was intrinsic (lattice), the properties decreased significantly with decreasing temperature. At −150 °C, the piezoelectric response decreased by 40%–55% for the compositions close to a morphotropic phase boundary (rhombohedral-monoclinic or monoclinic-tetragonal), while decreasing only 20%–30% for the compositions in the rhombohedral region. The piezoelectric properties of Pb(Mg1∕3Nb2∕3)O3–PbTiO3 polycrystalline ceramics were found to decrease by 75%, showing both intrinsic and extrinsic contributions play important role in the reduction in piezoelectricity at cryogenic temperatures for ceramics.

Relaxor-PbTiO3 (PT) based crystals, such as (1-x)Pb(Zn1∕3Nb2∕3)O3–xPbTiO3 and (1-x)Pb(Mg1∕3Nb2∕3)O3–xPbTiO3 (PMN-PT), have attracted significant attention owing to their high piezoelectric activity (d33>1500 pC∕N) along the [001] crystallographic direction.1 In addition to high piezoelectric activity, rhombohedral ternary Pb(In1∕2Nb1∕2)O3–Pb(Mg1∕3Nb2∕3)O3–PbTiO3 (PIN-PMN-PT) crystals have been studied,2, 3, 4 offering expanded temperature usage range, >30 °C higher than that of commercial PMN-PT binary crystals. The ultrahigh piezoelectric activity in domain engineered relaxor-based crystals is believed to be primarily intrinsic (lattice) in nature. Two underlying intrinsic mechanisms, including “polarization rotation” (Ref. 5) and “high piezoelectric anisotropy (d15∕d33⪢1),”6 have been proposed as the origin of the high piezoelectric activity. Actually, an “easy” polarization rotation is directly related to the high piezoelectric anisotropy.7 Investigations of polycrystalline ceramics and single crystals at cryogenic temperatures8, 9, 10, 11, 12, 13 revealed a high reduction in piezoelectric response, being attributed to the clamping of domain wall motion and∕or mobility,8, 9 reflecting a high level of extrinsic contribution in ceramics∕crystals. However, based on a recent investigation,14 the extrinsic contribution was found to be less than 10% of the total piezoelectric response across the compositional range of 0.25<x<0.35 in (1-x)PMN-xPT crystals, owing to the stable domain engineered structure. Thus, it was deemed important to further investigate the intrinsic and extrinsic contributions to the piezoelectric response in relaxor-PT based crystals as a function of decreasing temperature.

Rayleigh law has been used to study the degree of intrinsic∕extrinsic contribution to dielectric and piezoelectric activity in ferroelectric crystals and ceramics.15, 16 In the present study, the Rayleigh analysis was used to delineate the level of the intrinsic and extrinsic contributions to piezoelectric activity in PIN-PMN-PT crystals from room temperature to −150 °C. To provide a contrast to crystals, a relaxor-PT based polycrystalline ceramic was also investigated.

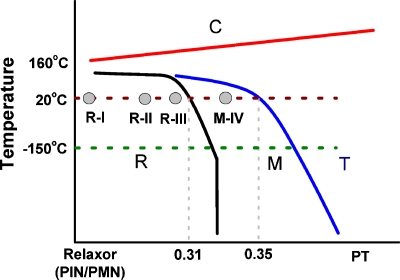
PIN-PMN-PT single crystals investigated in this study were grown along their crystallographic [001] direction using the modified Bridgman technique. Analogous to the binary systems (1-x)PMN-xPT and (1-x)PZN-xPT,17 a schematic phase diagram of the ternary composition PIN-PMN-PT system studied in this work is depicted in Fig. 1, where C, R, M, and T represent cubic, rhombohedral, monoclinic, and tetragonal phases, respectively. At room temperature, the PT content of the R-M and M-T phase boundaries were found to be 0.31 and 0.35, respectively. The composition and phase of the studied crystals were inferred by temperature-dependent-dielectric and electric-field-induced-strain behavior, and symbolized as R-I, R-II, R-III, and M-IV. The crystals were oriented by real-time Laue and cut to obtain longitudinal rods with dimensions of 2×2×8 mm3 for Rayleigh analysis. All the crystal samples were poled by applying a dc electric field of 15 kV∕cm at room temperature, while PMN-PT polycrystalline ceramic samples were poled at 25 kV∕cm. The electric-field-induced strain was measured at 1 kV∕cm and 1 Hz frequency, using a linear variable differential transducer driven by a lock-in amplifier (Stanford Research system, Model SR830), connected to a temperature chamber (Delta Design 2300).

Figure 1.

Figure 1

Open in a new tab

Schematic phase diagram for PIN-PMN-PT crystals, compositions studied in this work were labeled as R-I, R-II, R-III, and M-IV.

For the case of the converse piezoelectric response, the Rayleigh law can be expressed using the following formulae:18

S(E)=(dinit+αE0)E±α(E02−E2)∕2, (1)
d(E0)=(dinit+αE0)pC∕N, (2)

where S(E) is the electric-field-induced strain and E0 is the level of applied electric field. The coefficient “dinit” describes the reversible piezoelectric response, including intrinsic contribution and the contribution from reversible displacement of internal interfaces.15, 18 The latter one was related to the reversible domain wall motion in ferroelectric ceramics. However, in [001] poled domain engineered crystals, the contribution of domain wall motion is minimal due to the four energetically equivalent domains and stable domain configuration. In this investigation, therefore, the measured coefficient dinit is considered to arise from an intrinsic contribution. The coefficient “α” is the irreversible Rayleigh parameter, resulting from the irreversible motion of internal interfaces (e.g., domain wall, phase boundaries), and αE0 represents the extrinsic contribution to the total piezoelectric response. Equation 1 describes the Rayleigh hysteresis, where the signs “+” and “−” correspond to decreasing and increasing electric fields, respectively. The Rayleigh parameters dinit and α can be obtained by fitting Eq. 1.

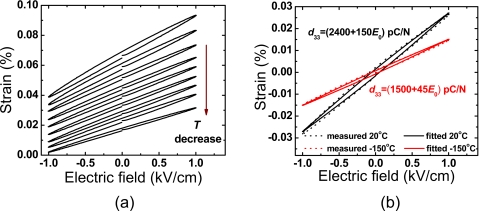
As an example, Fig. 2a shows the strain versus electric field (S-E) loops at temperatures from 20 to −150 °C for the [001] poled crystals with composition R-III. Using the Rayleigh law, Fig. 2b exhibits the good fitted results to the experimental data measured at room temperature and cryogenic temperature of −150 °C.

Figure 2.

Figure 2

Open in a new tab

(a) Strain vs electric field loops for PIN-PMN-PT crystals with composition R-III, at various temperatures (20, 0, −20, −40, −60, −80, −100, −130, and −150 °C); (b) the fitted results at 20 °C and −150 °C, respectively.

Table 1 presents a summary of the piezoelectric activity of PIN-PMN-PT crystals and PMN-PT ceramics at 20 and −150 °C. At room temperature, the maximum intrinsic piezoelectric response was found in PIN-PMN-PT crystals with composition R-III. In the rhombohedral phase region, the intrinsic piezoelectric response decreased for compositions being relative far from the R-M phase boundary. As expected, the parameter α was relatively small for crystals with compositions R-I (55 cm∕kV) and R-II (67 cm∕kV) when compared to PMN-PT ceramics (∼280 cm∕kV), due to a lack of domain wall motion in the stable domain engineered configuration (“4R”). The value of α in PIN-PMN-PT crystals was found to be relatively high for the compositions R-III (∼150 cm∕kV) and M-IV (∼280 cm∕kV), lying close to the morphotropic phase boundaries (R-M∕M-T). The high level of α at compositions close to the phase boundaries is a consequence of phase boundary motion. Phases at morphotropic phase boundaries (MPB) are energetically similar and easy to transform into one another when an electric∕stress field is applied, subsequently contributing to the extrinsic piezoelectric activity αE0.

Table 1.

The phase transition temperature and piezoelectric response of studied crystals and polycrystalline ceramics.

Material Tc (°C) TR(M)-T (°C) dinit α (cm∕kV) αE0+dinit dinit∕(αE0+dinit)
20 °C −150 °C 20 °C −150 °C 20 °C −150 °C 20 °C (%) −150 °C (%)
R-I 155 125 1080 860 55 25 1135 885 95 97
R-II 180 115 1700 1250 67 32 1767 1282 96 97.5
R-III 185 100 2400 1520 150 45 2550 1565 94 97
M-IV 195 55 1500 800 280 40 1780 840 85 95
Ceramic 165 ⋯ 750 220 285 42 1035 262 65 85
Open in a new tab

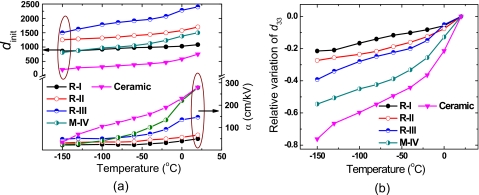
The temperature dependent dinit and α values obtained for PIN-PMN-PT crystals and PMN-PT ceramics are summarized in Fig. 3a. As expected, both parameters dinit and α decreased with decreasing temperature for all compositions.

Figure 3.

Figure 3

Open in a new tab

(a) The temperature dependent Rayleigh parameters; (b) relative variation in d33 as a function of temperature for [001] poled PIN-PMN-PT crystals and PMN-PT ceramics.

Based on thermodynamic analysis, the shear piezoelectric response (d15 or d24) of rhombohedral∕monoclinic single domain state will decrease as the testing temperature moves away from the ferroelectric-ferroelectric phase transition temperature (TF-F).19, 20 The reduction in shear piezoelectric response corresponds to an effective “hardening” of the polarization rotation process.7 Thus, the less polarization rotation contribution to the intrinsic piezoelectric activity in domain engineered crystals results in reduced piezoelectricity as the temperature shifts downward from TF-F. The extrinsic contribution αE0 in domain engineered crystals is believed to be related to an electric field induced phase transition (phase boundary motion).14 Therefore, as the temperature shifts downward from TF-F, the motion of phase boundary becomes “frozen,” leading to a decrease in the extrinsic parameter α. For PMN-PT ceramics, the parameter α drastically decreased from 280 to 40 cm∕kV as the temperature decreased from 20 to −150 °C, a result of domain wall motion clamping.8, 9 Of particular interest is that the α values for both crystals and ceramics were found to be on the same order at −150 °C, revealing minimal extrinsic contribution, which can be confirmed by the high intrinsic contribution, dinit∕(αE0+dinit), being on the order of 85%–97%, as listed in Table 1.

Figure 3b shows the relative variation in piezoelectric response, [d33(T)-d33(20 °C)]∕d33 (20 °C), as a function of temperature. At −150 °C, the piezoelectric response was found to decrease by 20%, 30%, 40%, and 55% for PIN-PMN-PT crystals with compositions R-I, R-II, R-III, and M-IV, respectively. The PMN-PT ceramic exhibited the largest decrease, ∼75% of the original value. For the rhombohedral PIN-PMN-PT crystals, as the composition approached the R-M phase boundary, the crystals became “softer” and the piezoelectric activity increase, and subsequently the temperature instability also increased.

In summary, the piezoelectric activity of relaxor-PT based crystals and ceramics was investigated from room temperature to −150 °C using the Rayleigh analysis. For [001] poled PIN-PMN-PT crystals, the decrease in piezoelectric activity at cryogenic temperatures was observed for rhombohedral to monoclinic compositions. The decrease in piezoelectric activity was mainly attributed to the reduction of the intrinsic piezoelectric response as the temperature moves away from the TF-F. For PMN-PT ceramics, the decreased piezoelectric activity observed at cryogenic temperature, was related both intrinsic (lattice) and extrinsic (domain clamping effects) contributions. From an application viewpoint, PIN-PMN-PT crystals with compositions far away from the R-M phase boundary (R-I and R-II) offer excellent potential applications at cryogenic temperatures, with high temperature stability and yet high piezoelectric activity at −150 °C, being four to five times larger than that of PMN-PT ceramics.

Acknowledgments

The authors from Xi’an Jiaotong University acknowledged the National basic research program of China under Grant No. 2009CB623306 and the National Natural Science foundation of China under Grant Nos. 50632030 and 10976022. The work supported by NIH under Grant No. P41-EB21820 and ONR under Grant Nos. N00014-09-1-01456 and N-00014-07-C-0858.

References

  1. Park S. -E. and Shrout T. R., J. Appl. Phys. 82, 1804 (1997). 10.1063/1.365983 [DOI] [Google Scholar]
  2. Hosono Y., Yamashita Y., Sakamoto H., and Ichinose N., Jpn. J. Appl. Phys., Part 1 42, 5681 (2003). 10.1143/JJAP.42.5681 [DOI] [Google Scholar]
  3. Tian J., Han P., Huang X., and Pan H., Appl. Phys. Lett. 91, 222903 (2007). 10.1063/1.2817743 [DOI] [Google Scholar]
  4. Zhang S., Luo J., Hackenberger W., and Shrout T., J. Appl. Phys. 104, 064106 (2008). 10.1063/1.2978333 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Fu H. and Cohen R. E., Nature (London) 403, 281 (2000). 10.1038/35002022 [DOI] [PubMed] [Google Scholar]
  6. Damjanovic D., Budimir M., Davis M., and Setter N., Appl. Phys. Lett. 83, 527 (2003). 10.1063/1.1592880 [DOI] [Google Scholar]
  7. Davis M., Budimir M., Damjanovic D., and Setter N., J. Appl. Phys. 101, 054112 (2007). 10.1063/1.2653925 [DOI] [Google Scholar]
  8. Zhang Q. M., Wang H., Kim N., and Cross L. E., J. Appl. Phys. 75, 454 (1994). 10.1063/1.355874 [DOI] [Google Scholar]
  9. Sabat R. G., Mukherjee B., Ren W., and Yang G., J. Appl. Phys. 101, 064111 (2007). 10.1063/1.2560441 [DOI] [Google Scholar]
  10. Paik D. S., Park S. E., and Shrout T. R., J. Mater. Sci. 34, 469 (1999). 10.1023/A:1004578225228 [DOI] [Google Scholar]
  11. Jiang X., Rehrig P. W., Hackenberger W. S., and Shrout T. R., Advances in cryogenic engineering: Transactions of the cryogenic engineering conference, AIP Conf. Proc. No. 823 (AIP, New York, 2006), p. 1783. [Google Scholar]
  12. Liu S., Park S. E., Cross L. E., and Shrout T. R., J. Appl. Phys. 92, 461 (2002). 10.1063/1.1486028 [DOI] [Google Scholar]
  13. Wang F., Or S., Zhao X., and Luo H., J. Phys. D: Appl. Phys. 42, 182001 (2009). 10.1088/0022-3727/42/18/182001 [DOI] [Google Scholar]
  14. Li F., Zhang S. J., Xu Z., Wei X., Luo J., and Shrout T. R. (unpublished).
  15. Davis M., Damjanovic D., and Setter N., J. Appl. Phys. 100, 084103 (2006). 10.1063/1.2358408 [DOI] [Google Scholar]
  16. Bernal A., Zhang S. J., and Bassiri-Gharb N., Appl. Phys. Lett. 95, 142911 (2009). 10.1063/1.3245316 [DOI] [Google Scholar]
  17. Noheda B., Curr. Opin. Solid State Mater. Sci. 6, 27 (2002). 10.1016/S1359-0286(02)00015-3 [DOI] [Google Scholar]
  18. Damjanvoic D., The Science of Hysteresis (Elsevier, New York, 2005), Vol. 3, p. 337. [Google Scholar]
  19. Budimir M., Damjanovic D., and Setter N., J. Appl. Phys. 94, 6753 (2003). 10.1063/1.1625080 [DOI] [Google Scholar]
  20. Budimir M., Damjanovic D., and Setter N., Phys. Rev. B 72, 064107 (2005). 10.1103/PhysRevB.72.064107 [DOI] [Google Scholar]

Articles from Applied Physics Letters are provided here courtesy of American Institute of Physics

RESOURCES