A Comparative Finite-Element Analysis of Bone Failure and Load Transfer of Osseointegrated Prostheses Fixations

Abstract

An alternative solution to conventional stump–socket prosthetic limb attachment is offered by direct skeletal fixation. This study aimed to assess two percutaneous trans-femoral implants, the OPRA system (Integrum AB, Göteborg, Sweden), and the ISP Endo/Exo prosthesis (ESKA Implants AG, Lübeck, Germany) on bone failure and stem–bone interface mechanics both early post-operative (before bony ingrowth) and after full bone ingrowth. Moreover, mechanical consequences of implantation of those implants in terms of changed loading pattern within the bone and potential consequences on long-term bone remodeling were studied using finite-element models that represent the intact femur and implants fitted in amputated femora. Two experimentally measured loads from the normal walking cycle were applied. The analyses revealed that implantation of percutaneous prostheses had considerable effects on stress and strain energy density levels in bone. This was not only caused by the implant itself, but also by changed loading conditions in the amputated leg. The ISP design promoted slightly more physiological strain energy distribution (favoring long-term bone maintenance), but the OPRA design generated lower bone stresses (reducing bone fracture risk). The safety factor against mechanical failure of the two percutaneous designs was relatively low, which could be improved by design optimization of the implants.

Introduction

Each year around 600 patients undergo transfemoral amputation in the Netherlands, which gives an average of 3.7 amputations per 100,000 inhabitants.23 The conventional prosthetic limb attachment is realized by a stump-fitting socket to which the artificial limb is fixed. Decades of development of socket technology have led to a more optimal coupling between stump and socket. However, performance of this fixation method is often reported as unsatisfactory.8 Pain, soft-tissue irritation and breakdown,28 and lack of appropriate control of the prosthetic limb10 arise due to the fact that the soft tissues of the residual limb are not appropriately suited for body weight support. Moreover, the fixation is affected by volumetric variations of the stump due to swelling.1

For two decades an alternative solution has been offered by attachment of the artificial limb directly to the femur via a percutaneous implant. Long-term fixation is achieved by osseointegration.3

Currently, two trans-femoral limb fixation devices are available on the market: the OPRA system (Integrum AB, Göteborg, Sweden) and the ISP Endo/Exo prosthesis (ESKA Implants AG, Lübeck, Germany). Both devices follow a similar general concept: a metal-based intramedullary stem is connected with a coupling element, which protrudes the soft tissue layer of the stump to provide an attachment for an external artificial limb. However, the fixation of the intramedullary stem with the bone is realized by different methods in both implants. The OPRA device has a form of titanium stem with a thread and the ISP implant uses a cobalt–chromium–molybdenum stem covered with a porous metal.2,26

The surgical procedure for implantation consists of two stages. First, the implant is introduced into the medullary cavity and left unloaded for 6–8 weeks for the ISP implant, and up to 6 months for the OPRA device.4,30 During that time bone–implant integration is expected to occur. In the second surgery, the skin penetrating shaft is attached to the intramedullary fixation. After wound healing, loading of the system is gradually increased and 3–6 months later full load bearing is allowed.30

Direct attachment of an artificial limb to the skeletal system allows overcoming the conventional socket system problems and provides a better control of the prosthetic limb including sensory feedback from the ground surface.30 Finally, the range of the hip joint motion is unrestricted and sitting comfort is increased relative to socket prostheses.9,10

However, infection problems may occur4,7,30 and there is a risk of fracture (either of the implant or the bone) or bone–implant interface disruption and implant loosening. Because the stiffness of the intramedullary stem is much higher than that of bone, high loads could cause bone fractures around the tip of the intramedullary stem or close to the osteotomy. The reported cases of failure include intertrochanteric femur fracture and bending fractures of the skin-penetrating part of the devices, usually as a result of a falling accident.4,28,30

Moreover, it is generally known in endoprosthetics that after implantation the local loading condition in the periprosthetic region changes considerably in comparison to the intact situation, leading to bone resorption around the implant. Obviously, direct skeletal attachment of prosthetic component is also expected to provoke a bone-remodeling response,7,33 which could promote bone fracture.

An obvious shortcoming of the percutaneous method is the length of the rehabilitation period, which spans up to 18 months. As a result, bone tissue stays unloaded for a considerable time. This, again, could promote bone resorption and thus lead to an increased risk of bone fracture.

Current protocols of patient selection for treatment with direct transfemoral prosthesis fixation include a body mass limit of 100 kg, as high loads as a consequence of high body mass are considered to be unsafe. All these restraining issues make percutaneous implants a secondary choice in transfemoral prosthetics, leaving only trauma-amputation patients, who have experienced major difficulties with socket-type prosthesis as the primary target group.8,28

If these restraining issues could be resolved, more patients could benefit from the advantages of direct fixation. In this study, we hypothesized that current percutaneous devices could be considerably improved when a thorough biomechanical analysis was available. Finite-element (FE) analyses techniques are highly suitable for this purpose. In the field of the transfemoral skeletal attachment, the FE modeling was previously used to study the influence of various geometric parameters on stress and strain distribution in the region of the bone–implant interface.32,34,35 More recently, FE modeling compared stress distribution within bone adjacent to the OPRA implant subjected to different loading conditions that may occur during weight-bearing exercises21 and searched for the correlations between FE simulated stress/strain distributions and the bone turnover observed on clinical radiographs.33 Helgason et al. 11 analyzed with a general model the failure risk of direct skeletal attachment.

However, none of these studies assessed the risk of bone–implant interface failure nor reported any results about the ISP device. So a more detailed mechanical analysis of both implants will improve our understanding of the biomechanical issues that are involved with respect to prosthetic limb attachment devices.

The purpose of this study was to assess the mechanical consequences of the changed loading pattern within the bone and its potential consequences on long-term bone remodeling. In particular, we analyzed if the normal walking activity can cause any risk to the femur of the amputee using direct prosthesis fixation. Furthermore, we investigated if the application of the porous metal on the cobalt–chromium–molybdenum alloy stem of the ISP prosthesis is more beneficial to the bone–implant load transfer than the titanium stem of the OPRA system either early post-operative (before bony ingrowth) or after bone ingrowth had occurred.

Materials and Methods

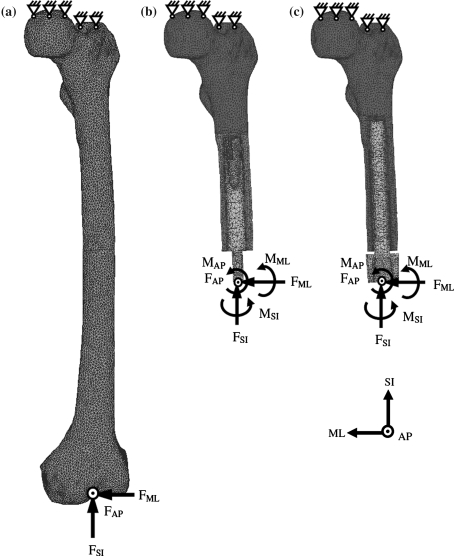
Three FE models were created, one representing a femur amputated at the metaphyseal level and provided with an OPRA prosthesis, one representing the same femur bone with an ISP device, and a third model representing the intact femoral bone (Fig. 1).

FIGURE 1.

FE mesh and boundary conditions applied to the intact bone (a), the OPRA implant (b), and the ISP implant model. The axes are denoted as antero-posterior (AP), medio-lateral (ML), and superior-inferior (SI)

The geometry of the bone was determined from CT scans (slice thickness 3 mm) of a male femur bone with normal bone mineral density (DEXA T-score: 0.1).

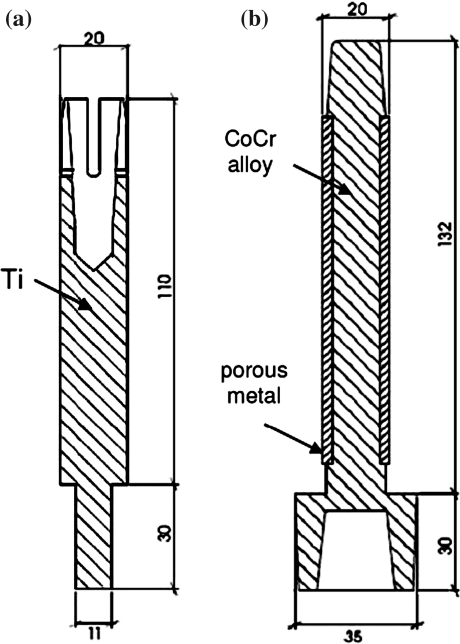
The amputated femur model represented the most common osteotomy level of 250 mm above the knee. The surface-shape contours of the two implants (Fig. 2) were fitted in the femoral bone and implemented into the FE models. The implants with the same outer diameter of the intermedullary part were assumed to be in close contact to the bone. Firstly, using frictional contact (friction coefficient of 0.425), which models the direct post-operative case. Secondly, the implant and bone were bonded to represent full osseointegration.

FIGURE 2.

Geometry of the OPRA (a) and the ISP implant (b), all dimensions in mm

The optimal mesh size for the bone model was determined by a mesh-refinement test with 5% convergence error for the peak equivalent von Misses stress. The edge length for all meshes was 3 mm except for the interface region where it was further refined, leading to meshes in the range 150,000–190,000 of 4-noded tetrahedral elements.

The Young’s moduli of the bone elements were derived from their ash densities16: 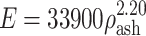for 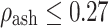(trabecular bone); 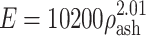for 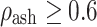(cortical bone); 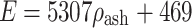for 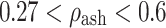(transition); where ρ _ash was calculated from calcium hydroxyapatite (CHA)-calibrated CT scan data using the relationship17: 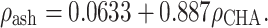Poisson’s ratio for all bone elements was 0.4. Characteristic elastic moduli for implant materials were taken as follows: ISP prosthesis stem (cobalt–chromium–molybdenum) 2.1 × 10⁵ MPa and the porous metal layer (Spongiosa metal with assumed partial bone ingrowth) 1.0 × 10³ MPa20; the OPRA implant (commercially pure titanium) 1.1 × 10⁵ MPa. Poisson’s ratio for all implant materials was set to 0.3.

Two loading cases from a normal walking cycle at 25% (heel strike) and 55% (shortly before toe-off) were considered. The loading of the implants was taken from the measurements performed with amputees using the OPRA device.22 The set of forces at the condyles of the intact femur were measured in vivo with an instrumented knee implant.6 The latter was used as a reference situation when all muscle forces were present, since a normal walking activity in this case is safe for the bone. Firstly, the intact loads6 were linearly scaled to correspond to the implant loads,22 reported for a patient with 61-kg body mass. Secondly, both loads were linearly rescaled to represent a body mass of 100 kg. The loading conditions are presented in Table 1. In all simulations, the bone was fixed at the proximal end and load was applied distally (Fig. 1.). 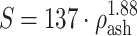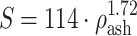Periprosthetic bone failure risk was evaluated by the von Mises stress (σ _VM) criterion, previously used in related research.15–17,19 The bone strength (S) was calculated for each bone element from ρ _ash 16: for ρ _ash < 0.317 (trabecular bone); for 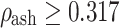(cortical bone).

Table 1.

Overview of two different load cases applied to the FE models

Load case	Intact knee joint			Implanted
	F SI (N)	F AP (N)	F ML (N)	F SI (N)	F AP (N)	F ML (N)	M SI (Nm)	M AP (Nm)	M ML (Nm)
1	1302	244	−180	780	100	−20	−2.0	30.8	−7.2
2	1170 (1914)	44 (73)	−60 (−99)	180 (295)	120 (196)	40 (66)	0.0 (0.0)	37.3 (61.0)	4.1 (6.7)

All values are given for body mass of 61 and 100 kg (values in brackets). F _SI, F _AP, F _ML are the superior-interior axis (superior being positive), antero-posterior (anterior being positive), and medio-lateral (lateral being positive), respectively

Bone failure risk was identified when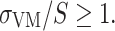

The assessment of interface stresses was taken from Huiskes et al. 13 Interface stresses were based upon nodal contact forces extracted from a contact algorithm provided by Marc (MSC Software Corporation, Santa Ana, CA, USA). The interface area associated with the node in contact was calculated by dividing the interface normal force by the interface normal stress. To relate interface stresses (normal and shear stresses) to the probability of mechanical failure, we used a criterion defined by Hoffman.12 Each nodal point at the interface was assigned a Hoffman number calculated from the normal and shear stress and the interface-bone density as:

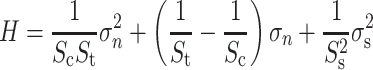where S _c, S _t, and S _s are the interface uniaxial compressive, tensile, and shear strength, respectively. All strengths depend on the apparent density of the interface bone as14,27: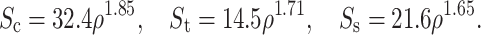

The regression equation relating apparent density to ash density was18: ρ = 1.79ρ _ash + 0.0119.

The Hoffman criterion transforms the local interface stresses to a value referred to as the Hoffman number (H), which represents the probability of interface failure. The interface disruption is assumed to occur when H > 1, for lower H no interface failure is expected.

According to the adaptive bone-remodeling theory,29,31 the bone mass is regulated by the elastic strain energy per unit mass.5 Following this theory, our study examined strain energy density (SED) distribution in the intact and amputated bones to predict the long-term bone remodeling.

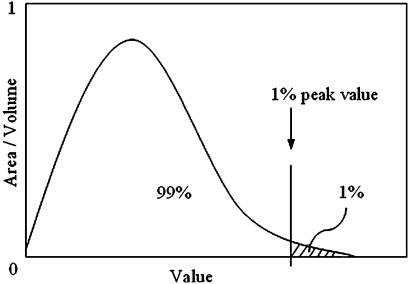
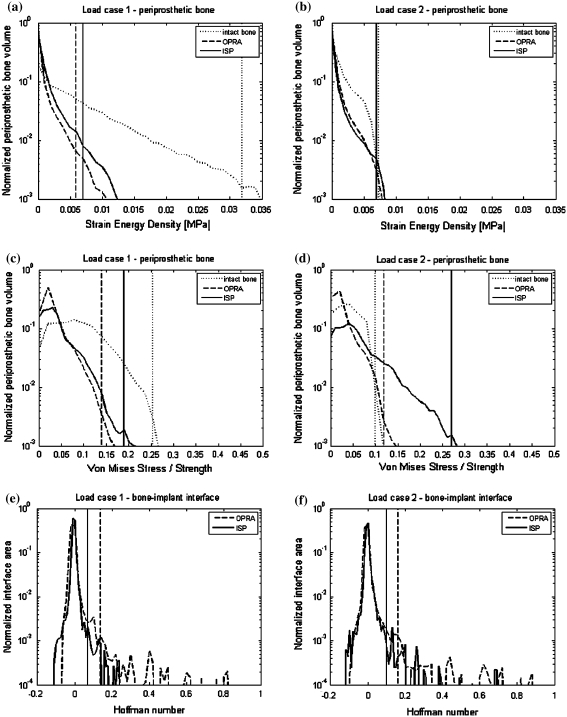
Comparing the peak values of any stress or strain quantity obtained with the FEM is often unreliable due to mesh dependency, especially in contact problems. In this study, we therefore chose to determine the peak stress threshold beyond which 1% of the interface area was exposed (Fig. 3). As the two different prosthetic systems led to a different interfacial area, the data on the plots were normalized with total interface area equal to 6.0 × 10³ mm² for the ISP and 6.4 × 10³ mm² for the OPRA implant. Similar analyses (1% peak threshold values) were performed to quantify peak values for SED and bone failure ratio values in the volumes of the bone adjacent to the implants. The bone volumes were selected from the osteotomy up to 10 mm above the proximal implants’ end and were 81.1 × 10³ and 62.7 × 10³ mm³ for the ISP and the OPRA implants, respectively.

FIGURE 3.

The 1% peak value determined from the volumetric/areal distribution of analyzed quantity

Results

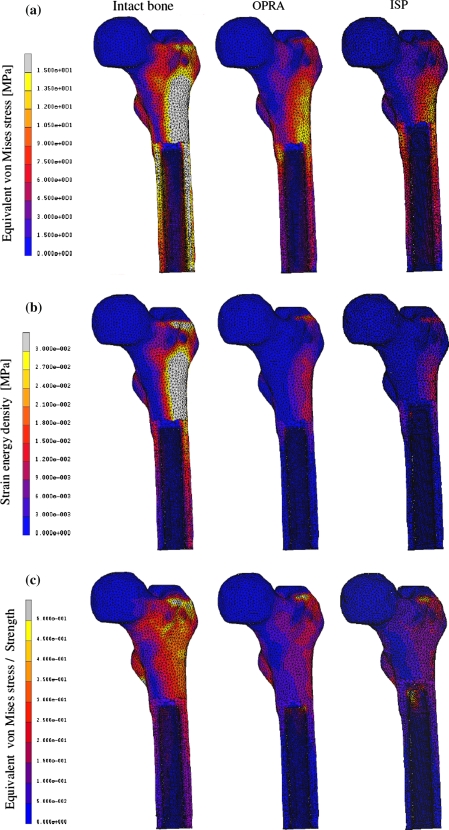
The stress pattern in the bone changed considerably after implantation of direct fixation prostheses. In both load cases, the equivalent von Mises stresses in the diaphysis of the intact femur were uniformly distributed along the cortex (Fig. 4a). After introduction of the implants, high stress concentration in the bone region close to the proximal end of the implant was found and much lower stresses were present in the distal part located close to the osteotomy. The stresses were slightly more evenly distributed in the bone around the ISP than the OPRA implant. Overall levels of the von Mises stress were higher in the intact than in the implanted bones.

FIGURE 4.

Von Mises stress (a), SED (b), and von Mises stress/strength distribution (c) in the periprosthetic bone obtained for the load case 1. Part of the bone removed to facilitate the direct comparison of intact bone with the implanted cases

Introduction of the direct fixation prostheses caused redistribution of the SED in the bone. Similarly as in the case of the von Mises stress, high values of the SED were present in the proximity of the implants’ proximal tips and relatively low values more distally. In both considered load configurations, the overall levels of the SED were higher in the intact bone; however, the difference was much larger in the first load case representing heel strike phase of the gait cycle (Figs. 5a and 5b). Relative to bone-remodeling stimulus, the ISP prosthesis induced higher SED levels than that of the OPRA design.

FIGURE 5.

Area/volume distribution of the SED (a, b), the von Mises stress/strength (c, d) in the periprosthetic bone region and the Hoffman number (e, f) at the bone–implant interface obtained from the simulations with bonded interface for the load case 1 (a, c, e) and load case 2 (b, d, f). Vertical lines mark 1% peak thresholds

Normal walking activity did not cause considerable risks to the bone fitted with the direct fixation implants. Loads for a person with the body mass of 61 kg (Table 1) did not indicate any direct bone damage (σ _VM/S < 1) neither directly post-operative nor after complete bone ingrowth. The highest failure ratio was always found in the bone region in contact with the proximal end of the implant (Fig. 4c). The probability of the bone failure was higher for the ISP than for the OPRA implant (Figs. 5c and 5d).

The interface load transfer varied between both studied implants. In the debonded simulation, the OPRA device showed higher compressive and shear stresses at the interface. When the implants were bonded to the bone, values of shear stresses were still higher for the OPRA prosthesis but tensile stresses as well as compressive stresses were lower than in the case of the ISP prosthesis. This was reflected in much lower Hoffman values found at the ISP implant–bone interface (Figs. 5e and 5f).

The increase in the body mass of the patient over the limit of 100 kg is assumed to be dangerous for the bone–implant integrity. As the second load case appeared to be more demanding for the interface, it was chosen for the additional simulation with the loads corresponding to the patient’s mass of 100 kg (Table 1). As expected, the increased failure risk of periprosthetic bone and bone–implant interface was found for both implants (Table 2). However, direct interface failure was indicated only for the OPRA prosthesis.

Table 2.

1% Peak values calculated for body mass of 61 and 100 kg (values in brackets)

	Load case 1			Load case 2
	Intact bone	OPRA	ISP	Intact bone	OPRA	ISP
Bonded
Bone volume
von Mises stress/strength	0.26	0.14	0.19	0.10 (0.18)	0.12 (0.20)	0.27 (0.44)
SED	0.032	0.006	0.007	0.007 (0.018)	0.006 (0.017)	0.007 (0.018)
Interface area
Hoffman value		0.14	0.07		0.16 (0.50)	0.11 (0.24)
Shear stress		7.20	3.66		5.20 (8.40)	4.42 (7.65)
Compressive stress		2.38	2.41		4.38 (4.20)	4.53 (5.90)
Tensile stress		2.00	3.25		2.40 (3.81)	4.86 (7.94)
Debonded
Bone volume
von Mises stress/strength		0.16	0.37		0.12	0.33
SED		0.009	0.008		0.008	0.008
Interface area
Shear stress		1.80	1.62		1.80	1.77
Compressive stress		5.03	3.45		5.40	4.92

Discussion

Our study aimed to identify the mechanical situation after implantations of direct skeletal fixations for upper-leg prostheses. For this purpose, we used the FE method to analyze the intact femur and transected femora fitted with two different implants. The normal bone density assumed for the implanted femora represented a case of a patient fitted with direct fixation prosthesis shortly after trauma amputation. In this way, the bone properties in both analyzed cases are the same and the results are not biased by any individual factors such as level of activity and time between amputation and prosthesis implantation. The FE modeling demonstrated considerable difference in magnitude and distribution of stresses between the healthy and implanted femora. This effect is induced by the altered loading conditions of the amputated bone as well as by the introduction of the intramedullary implant. The muscle activity in the amputated leg is considerably impaired; therefore, the remaining bone experiences less loading from the muscular system. This finding correlates well with lower bone mineral densities measured in post-amputation femora.24

The influence of the implant on the surrounding bone is an important aspect in contemporary endoprosthetics. The notable variation in stress patterns in the bone around both direct fixation implants originates from their different geometric and elastic properties. The ISP stem promotes slightly more uniform load transfer than the threaded OPRA device. The observed stress patterns for the latter prosthesis were similar to those recently reported by Xu and Robinson.33 The more favorable bone–implant interface stress transfer was found in the case of the ISP implant, in which the low stiffness porous structure at the stem appears to reduce shear stresses at the bone–implant interface.

The considerable difference of strain energy distribution between intact and implanted femora suggests new bone formation in the regions adjacent to the proximal end of the implants and bone resorption in the distal part of the bone. This stays in agreement with published clinical data of the OPRA patients.33 Bone stock preservation and minimization of the bone failure risk appear to be incompatible design goals. The direct comparison of the SED levels around both implants predicts less adverse bone remodeling around the ISP stem. On the other hand, analyzing the periprosthetic bone failure probability around fixations suggests that less bone damage is likely to appear around the OPRA device.

In our study, we used load data reported from two different measurement setups, that could also introduce inaccuracy in the analysis, but obviously it is very difficult to get a consistent loading data set (intact and amputated) of the same person. Furthermore, it should be realized that this loading configuration does not represent a worst case scenario; staircase climbing or stumbling would be better suitable for that. However, for the amputated patient, these loading configurations are unknown. Estimating these loads from the healthy situation is not possible due to the absence of muscle forces in amputated patients. However, we believe that the qualitative differences in both systems will remain as found in this study for these higher load cases.

For analyzing the two prosthetic systems analyzed in this study, some assumptions were made. The trabecular metal was assumed to have only some stiffening due to bone ingrowth and omitting the threading of the OPRA system was thought to be of minor influence for the global stress transfer patterns. Furthermore, bony ingrowth was assumed to be either fully absent or fully completed, which is obviously a simplification of reality. Nevertheless, we believe that we have simulated the most important features of the two prosthetic systems to an adequate degree in order to get an estimation of the load–transfer mechanisms that are involved in the short- and longer-term fixation of these types of implants. Based on these assumptions, we would like to emphasize that the results of this study should be considered from a global point of view rather than trusting the exact figures.

From a mechanical perspective loading of the implant directly post-operative does not considerably increase bone failure risk. Therefore, assuming an accurate fit between the implant and prosthesis, a shorter delay period between implantation and loading of the stem may be considered. However, whether early loading would jeopardize bony ingrowth due to dynamic motions at the implant–bone interface was not analyzed in this study and would require further analyses.

A considerable increase in the failure risk of the bone–implant integrity was found with a body mass increase to 100 kg, which justifies the limitation used in clinical practice. It furthermore highlights that the factor of safety against mechanical failure of these reconstructions is relatively low, which corresponds to the reported in vivo literature.4,28,30

In conclusion, we found some general differences between the two designs analyzed in this study. The ISP design seemed to have a slightly more physiological SED distribution (favoring long-term bone maintenance), whereas the OPRA design generated lower bone stresses (reducing the risk of bone fracture). The application of a low-stiffness porous layer on the ISP stem’s surface appears to be very favorable for bone–implant interface safety. With this respect we would recommend this method for the intramedullary fixation.

In a more general sense, implantation of a percutaneous amputation prosthesis had considerable effects on the stress and SED levels in the bone. This was not only caused by the implant itself, but also by the changed loading conditions. The safety factor against periprosthetic bone failure of the two percutaneous designs was relatively low. In order to increase it, we recommend to use a porous metal layer on the entire intramedullary part of a stem. The performed analysis is currently used to develop an alternative implant design with increased safety factor against mechanical failure.