Abstract
Purpose
To describe inter- and intra-observer reliability of 3D measurements of female pelvic floor structures.
Materials and Methods
Twenty reconstructed MR datasets of primiparas at 6–12 months postpartum were analyzed. Pelvic organ measurements were independently made twice by 3 radiologists blinded to dataset order. A “within-reader” analysis, a “between-reader” analysis, and the intraclass correlation (ICC), and standard deviation ratio (SDR) were computed for each parameter. Fifteen continuous variables and one categorical variable were measured.
Results
Eight continuous parameters showed excellent agreement (ICC >0.85/SDR <0.40), 5 parameters showed relatively good agreement (ICC >0.70/SDR ≥0.40, <0.60). Two parameters showed poor agreement (ICC ≤0.70 and/or SDR ≥0.60). The categorical variable showed poor agreement.
Conclusion
Agreement was best where landmark edges were well defined, acceptable where more “reader judgement” was needed, and poor where levator defects made landmarks difficult to identify. Automated measurement algorithms are under study, and may improve agreement in future.
Key words/phrases: 3D reconstruction, MRI, Pelvic floor muscles, 3D measurement reliability, Standard deviation ratio, Intraclass correlation
INTRODUCTION
Magnetic Resonance imaging has proven useful in evaluating the complex anatomy of the female pelvic floor structures(1) Data have suggested that linear measurements made on 2D MR images may be subject to measurement variations of up to 16%, depending on the angle of acquisition of the MR slices(2). This source of variability is believed to be reduced if a 3-dimensional model is used to make the measurements. This is because a 3D model allows for direct placement of the measurement markers on the model landmarks. For this reason, 3D MRI has been suggested as an optimal modality for obtaining more reliable measurements of complex female pelvic floor structures, compared to 2D imaging.
Furthermore, female pelvic surgeons have reported that magnetic resonance based three dimensional (3D) depictions of female pelvic floor anatomy have been useful in the study of the pelvic structures in nulliparous(3, 4) and symptomatic women(5). These MR-based 3D depictions have also proven helpful to pediatric and gynecologic oncology surgeons in planning and conduct of complex surgical cases (6, 7), as well as to gynecologists seeking to noninvasively diagnose complex mullerian anomalies(8). Hsu et al., reported that MR based 3D models help in visualizing complex posterior compartment pelvic floor anatomy(9).
In several pelvic floor imaging studies, MR-based 3D renderings have been used to evaluate quantitative linear, angular, and volumetric measurements of bony and soft tissue female pelvic organs in asymptomatic women, compared to those with prolapse and urinary incontinence(3, 10, 11). In another study, 3D renderings were used to quantify diminished levator ani muscle mass in women with pelvic floor dysfunction.(12)
Image based 3D reconstruction has proven to be useful as a research technique for localizing and measuring the volume of tumors in the brain, kidneys bladder(10, 13–15), and clinically for detecting tumors in the colon(16).
A 3D rendering is accomplished by manual segmentation, that is, serial outlining of each anatomic structure to be displayed in the 3D rendering. Subsequently, a series of advanced imaging processing techniques based on triangle decimation and the marching cubes algorithm is applied to form 3D objects that can be given color and opacity, and can be rotated and manipulated in space.(13, 17) With the aid of a software tool like the 3DSlicer(18) ( www.slicer.org ), the volume of any given 3D structure can be readily calculated, using voxel size information from the original 2D MR scan. Linear and angular measures can be easily made directly on the 3D model within the 3DSlicer by placing marks on the points of interest, without the need to resort to moving back and forth between multiple 2D slices. An example of an MRI 2D source image measurement of the intertuberous distance, and the corresponding 3D measurement is shown in Figure 1. The volume, linear, and angular measurements can then be used to study differences among different groups of women.
Figure 1.
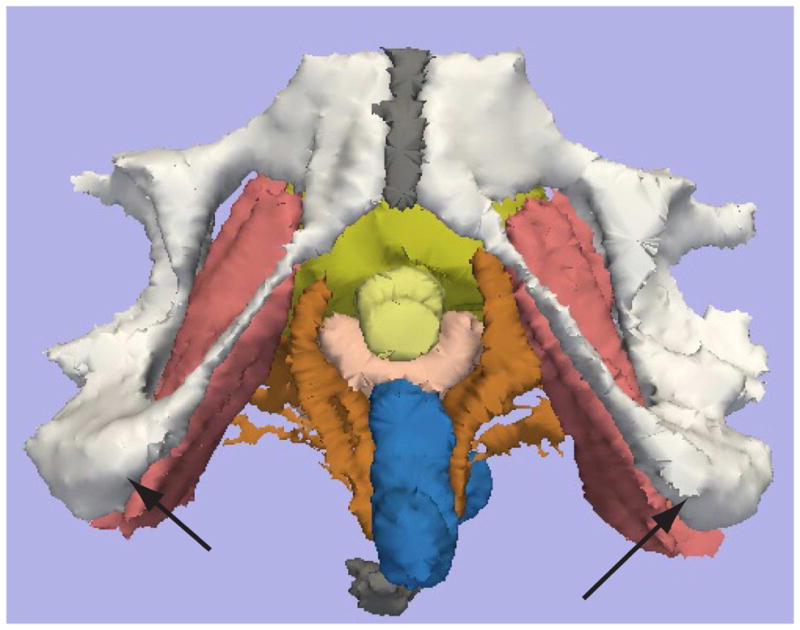
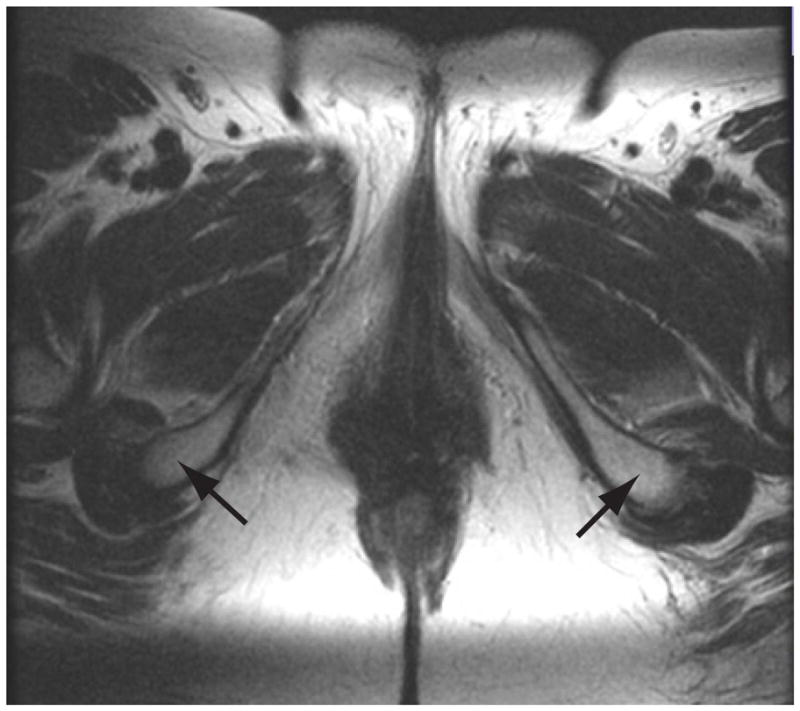
MRI 2D and 3D measurement of the intertuberous distance.
Figure 1a shows the MRI 2D axial source image is shown at the level of the iscial tuberosities (Arrowheads). Figure 1b shows the 3D reconstructed image, with the black arrowheads indicating the iscial tuberosities. Color legend: White: pubic bones, yellow- urethra, pink – vagina, brown – Levator ani, rose- Obturator internus, gray – symphysis bubis and coccyx.
It is hypothesized that evaluation of 3D renderings may improve understanding of anatomical and pathophysiologic changes in women with pelvic floor disorders, However, the research utility of such comparisons depends on a standardized and reproducible measurement technique.(17)
The present analysis describes the inter- and intra-observer reliability of a 3D measurement technique, applied to the bony and soft tissue structures of the female pelvis, as derived from MR images obtained using a standardized protocol.
MATERIALS AND METHODS
Source images for this study were acquired from a large cohort of women in a multicenter trial, the Childbirth And Pelvic Symptoms study of the Pelvic Floor Disorders Network. Data acquisition was prospectively acquired following IRB approval at all 6 sites. This study is HIPAA-compliant. Two hundred MR data sets were obtained from a multicenter study comparing MR-based reconstructed 3D pelvic models from newly primiparous women at 6–12 months postpartum, 88 of the women sustained an advanced perineal tear during vaginal delivery, 81 delivered vaginally without an advanced perineal tear, and 31 delivered by cesarean section prior to labor.
Imaging parameters were standardized across study centers in the original protocol, in order to minimize the effect of imaging variations on the final measurements. The source MR images of the pelvis were obtained in the axial plane, using a 1.5T magnet and a surface coil. Source imaging parameters were: T2 Turbo SE axial images with TR 5000 milliseconds, TE 132 milliseconds, FOV 200 cm, slice thickness 3millimeters/interleaved, no gap, flip angle180°, Matrix 270 × 256.
Twenty of the reconstructed MR data sets were chosen from the study group. The 20 datasets were chosen from a group of 200 3D reconstructed datasets. Each of the 200 original datasets were previously judged to have all landmarks present sufficient to allow for adequately performing measurements.
Three radiologists, all fellowship trained and experienced in abdominal imaging, were asked to independently perform measurements on each of the 3D datasets, on 2 separate occasions, using the 3DSlicer software(18) (www.slicer.org).
Prior to obtaining measurement data for study analysis, a dedicated training session was completed, and preliminary trial measurements were performed. For the training session, an expert 3D reader demonstrated the measurements to each of the readers individually, and as a group. Each reader was given time to practice making the measurements on a single test dataset that was not used in the final measurement tabulation. The readers jointly reviewed each other’s measurements on the test dataset and agreed on the principle behind each measurement. Each dataset required less than 10 minutes to perform all of the 3D measurements. This is thought to be comparable to the time required to make corresponding measurements on the 2D source images.
Each of the readers independently measured each of the study parameters on a single 3D dataset. All of the measurements on the 20 datasets were accomplished in a single day, composed of 2 sessions separated by a 1 hour break. The datasets were presented to the readers, one at a time as an ordered list of 40 datasets, representing 2 copies of each of the 20 datasets. The datasets were shuffled, and ordering of the datasets was not known to the reader. Each reader was required to perform the measurements on the datasets in the order they were presented. Each reader was allowed to work at their own pace, making all measurements on each dataset, before moving on to the next one on the list.
The measured parameters included linear and angular bony and soft tissue measurements related to the pelvic floor and levator ani muscles. The parameters are detailed in Table 1. The H-Line measurement familiar to readers of 2D pelvic images(19) is approximated by the 3D measurement of levator hiatus (Table 1). The M-line 2D measurement does not have a correlate in the present 3D analysis. Volume measurements were not performed because they are automatically calculated by the 3DSlicer and require no operator input to determine. Because of this, they are not subject to operator derived variability. In the training session, the readers then compared results, discussed, and refined the measurement technique for each parameter until all readers were in agreement regarding measurement methodology.
Table 1.
Overall Means and SDs and Results of Individual Readers Relative to the Mean. (all linear measurements are in millimeters, and angular measurements are in degrees)
| Tissue Type | Tissue Structure | N | Mean | SD | Difference between reader and overall mean | ||
|---|---|---|---|---|---|---|---|
| Reader 1 | Reader 2 | Reader 3 | |||||
| Primarily soft | Bladder neck to pubococcygeal line | 118 | 17.37 | 4.61 | 1.03 | −1.58 | 0.47 |
| Levator hiatus width | 88 | 31.22 | 3.20 | −0.10 | 0.11 | −0.01 | |
| Urethral length | 118 | 27.96 | 4.59 | 0.17 | 0.46 | −0.61 | |
| Primarily bony | Interacetabular distance | 118 | 129.83 | 7.69 | −0.79 | −2.04 | 2.73 |
| Interspinous distance | 117 | 111.27 | 8.45 | 0.50 | 0.72 | −1.21 | |
| Intertuberous distance | 112 | 127.54 | 9.73 | 0.77 | −1.05 | 0.19 | |
| Pubic arch angle | 115 | 94.25 | 6.99 | −0.59 | 0.72 | −0.07 | |
| Pubococcygeal line | 118 | 104.35 | 8.98 | −0.28 | 1.01 | −0.67 | |
| Involve both soft and bony tissue | Bladder neck to symphysis | 118 | 18.49 | 4.21 | 1.05 | −0.88 | −0.22 |
| Levator hiatus height | 118 | 60.17 | 7.12 | −0.46 | −0.85 | 1.27 | |
| Levator symphysis gap on left | 118 | 24.73 | 8.08 | 0.93 | −0.78 | −0.19 | |
| Levator symphysis gap on right | 118 | 21.54 | 6.34 | 0.66 | −0.88 | 0.18 | |
| Puborectalis attachment width on left | 94 | 17.67 | 7.68 | −1.64 | 2.05 | −0.28 | |
| Puborectalis attachment width on right | 106 | 17.12 | 7.27 | −2.30 | 1.92 | 0.48 | |
| Urethral angle | 118 | 51.23 | 10.70 | −0.25 | 0.25 | 0.01 | |
Subsequently, a series of forty 3D datasets (not including the training dataset) was created by randomly ordering 20 different datasets twice and labeling the datasets with new research IDs. Each of the 40 datasets was measured by each radiologist. The protocol for review of the study datasets was strictly defined. The readers were informed that two copies of each dataset were included in the group of 40, but were blinded to the order of the datasets.
The readers were not permitted to confer with each other during the measurement of the datasets. As a result, each parameter was measured two times by each individual, yielding six measurements per parameter per dataset. The readers were told that when a landmark could not be observed, they should not record a value for the structure; agreement on the presence or absence of a landmark would lead to either six (all) or zero readings for a structure. If the readers did not agree on whether a landmark was observed, there would be between one and five readings for that structure.
Statistical Methods
A total of 16 structures were measured from the 3D reconstructions of 20 pelvic MRI examinations. There were three readers, and each reader measured each dataset on two separate occasions. The 16 structures include four that primarily involved soft tissues, five that primarily involved bony tissues, and seven that involved both types of tissues. Only two of the structures had left and right components, namely levator symphysis gap and puborectalis attachment width. The levator shape parameter was categorical. All other structures were measured on a continuous scale.
The statistical analysis consisted of a “within-reader” analysis, a “between-reader” analysis, and a calculation of the intraclass correlation (ICC) (20) and the standard deviation (SD) ratio for each parameter (structure). The within-reader analysis is performed as follows: for each parameter (e.g., intertuberous distance), the mean value for all 20 subjects is computed, and a correlation between values from the first and second readings is computed. The within-reader analysis compares the mean value between the first and second reading for each reader, and also the correlation between the first and second reading.
The between-reader analysis is performed as follows: for each parameter, the mean value for all 20 subjects, (i.e., from first and second readings), is computed for each reader. In addition, correlation of values between each pair of readings (e.g., reader #1/first read and reader #2/first read, and all other combinations) is performed. The between-reader analysis compares the mean of each parameter between the three readers, as well as the correlation between each pair within the six readings.
In order to assure good reproducibility, there should be both good “within-reader” and “between-reader” reliability. Good within-reader reliability requires that the two sets of readings from the same reader have similar mean values and a high correlation. Similarly, good between-reader reliability requires that the mean values of readings from the three readers be similar, and that the correlations between any pairs of the six readings must be high.
The ICC can be conceptualized as the ratio of variance between subjects to variance on an individual subject; this ratio is high when the values from the readings of each subject clusters in a narrow range compared to the range compared to the range over which all the subjects are measured. A high ICC value indicates good reliability.
For any given structure, the “SD ratio” is the ratio of the standard deviation (SD) computed between the readings from the same subject (within subject SD) to the SD computed from all the subjects. It compares measurement variability in an individual subject against variability across all subjects in the study. Variability across different subjects should be expected due to anatomic differences, but variability within a single subject would be due to measurement error. Therefore, a small SD ratio is desirable and indicates a good reliability, whereas a large SD ratio would indicate poor reliability, because it means that measurement variability between readers is similar in magnitude to the anatomic variability between subjects. The SD ratio and ICC are closely related: ICC is approximately 1 – (SD ratio)2. For simplicity, we calculated both of the above statistics based on a model in which the 6 readings for each image were treated as if they were replicates from 6 independent readers.
One measurement was more than 7 times the standard deviation away from its mean; this measurement was treated as an outlier and omitted from the analysis..Except for this observation all recorded measurements are included in the analysis. The readers were told not to provide a measurement if in their opinion one of the landmarks defining the measurement could not be observed.
Since measurements for each subject are repeated on the same image volume, a high correlation between readers was expected; therefore, we set a threshold for the ICC of 0.85 to be considered reliable and a lower limit of 0.7 to be considered acceptable. These thresholds are approximately equivalent to SD ratios of 0.4 and 0.55 respectively; however, since the relationship between ICC and SD ratio is only approximate, the ICC thresholds will be used for classification.
To determine the source of variance and bias for the parameters with ICC scores less than 0.85, we fitted each parameter by a three-way analysis of variance (ANOVA) where the 3 factors were reader, image (subject) and replicate. Within-reader correlations were also calculated for each parameter where the factors were image (subject), reader and replicate (i.e., first versus second reading). An extreme p-value for readers indicates a selection bias by the reader; one reader has either a higher or lower mean value than the other readers – this may be caused by choosing a different landmark as a starting or ending point. An extreme p-value for replicate indicates a learning curve; there is a difference in the measurement between the first and second reading. An extreme p-value for the interaction between reader and replicate indicates that there was a learning curve, but the learning curve differed by reader. An extreme p-value for the interaction between image and reader indicates that the readers differed between themselves, but that the difference depended on the image and the difference may not have been a consistent direction.
RESULTS
Continuous variables
Intraclass Correlation coefficients ranged from 0.62 in the case of the Levator hiatus width, to 0.95 in the case of the interspinous distance. Of the 3 soft tissue parameters, 2 had ICC >0.7, and one (Levator hiatus width), had an ICC <0.7. Of the 5 bony parameters, all had ICC >0.7, and of these 3 had ICC >0.85. Of the 7 measurements involving bony and soft tissues, 6 had ICC >0.7, of these 4 had ICC >0.85, and one had ICC <0.7.
Table 2 and Figure 2 present the ICC’s and SD ratios for all the parameters; in addition, Table 2 contains the correlation between the re-reads for each reader. Eight of the 15 continuous parameters showed excellent agreement among readers (ICC >0.85 and SD ratio <0.40): urethral length, interspinous distance, pubic arch angle, pubococcygeal line, levator hiatus height, levator symphysis gap on left and right, and urethral angle. Five parameters showed relatively good agreement among readers (ICC >0.70 and SD ratio <0.60, and ≥0.40): bladder neck to pubococcygeal line, interacetabular distance, intertuberous distance, bladder neck to symphysis, and puborectalis attachment width on right. Levator hiatus width and puborectalis attachment width on left showed poor agreements among readers (ICC ≤0.70 and/or SD ratio ≥0.60).
Table 2.
Intraclass correlations (ICC), within-reader correlations and SD ratios.
| Tissue Type | Tissue Structure | Within-Reader Correlations | ICC | SD Ratio | ||
|---|---|---|---|---|---|---|
| Reader 1 | Reader 2 | Reader 3 | ||||
| Primarily soft | Bladder neck to pubococcygeal line | 0.81 | 0.91 | 0.81 | 0.73 | 0.53 |
| Levator hiatus width | 0.96 | 0.40 | 0.76 | 0.62 | 0.63 | |
| Urethral length | 0.98 | 0.99 | 0.99 | 0.92 | 0.28 | |
| Primarily bony | Interacetabular distance | 0.86 | 0.80 | 0.86 | 0.75 | 0.52 |
| Interspinous distance | 0.98 | 0.97 | 0.97 | 0.95 | 0.22 | |
| Intertuberous distance | 0.85 | 0.84 | 0.93 | 0.77 | 0.48 | |
| Pubic arch angle | 0.95 | 0.91 | 0.95 | 0.90 | 0.31 | |
| Pubococcygeal line | 0.96 | 0.94 | 0.99 | 0.88 | 0.35 | |
| Involve both soft and bony tissue | Bladder neck to symphysis | 0.74 | 0.94 | 0.91 | 0.80 | 0.46 |
| Levator hiatus height | 0.98 | 0.95 | 0.95 | 0.93 | 0.27 | |
| Levator symphysis gap on left | 0.93 | 0.89 | 0.98 | 0.91 | 0.31 | |
| Levator symphysis gap on right | 0.97 | 0.98 | 0.97 | 0.94 | 0.25 | |
| Puborectalis attachment width on left | 0.88 | 0.96 | 0.95 | 0.64 | 0.61 | |
| Puborectalis attachment width on right | 0.87 | 0.93 | 0.95 | 0.76 | 0.50 | |
| Urethral angle | 0.91 | 0.92 | 0.85 | 0.86 | 0.38 | |
Figure 2.
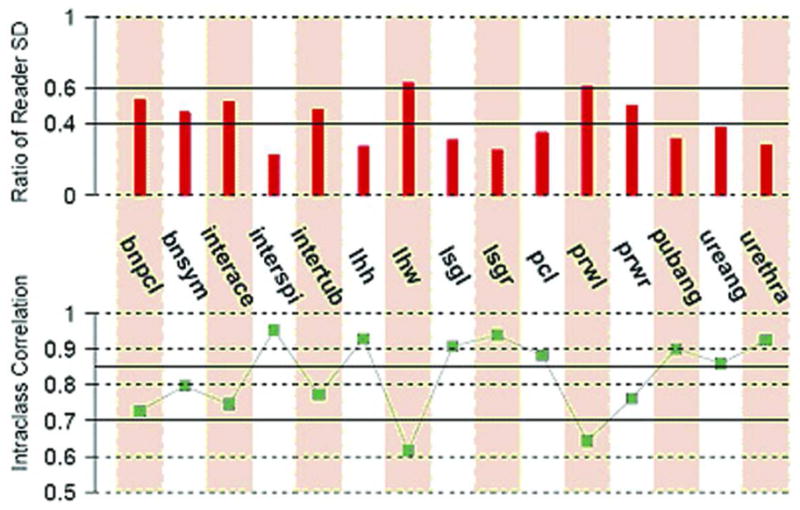
Intraclass correlations and SD ratio.
The top plot is the ratio of the standard deviation (SD) between readers to the SD of the measurement. A short line indicates good reproducibility and a long line indicates poor reproducibility. The short lines correspond to high IntraClass Correlation (ICC). Levels below 0.4 are considered reliable, and those less than 0.6 are considered acceptable. The bottom panel is the intraclass correlation for each measured parameter. Values above the 0.7 level are considered acceptable, and those above 0.85 are considered reliable. Both levels are illustrated on the lower graph.
For the seven parameters with an ICC value less than 0.85, the 3-way ANOVA analysis is presented in Table 3. The measurements on bladder neck to symphysis showed selection bias among readers (p < 0.0001); i.e. reader No. 1 tended to report greater values than the other two readers (Table 1). The corresponding within-reader correlations are 0.74, 0.94, and 0.91 for readers 1, 2, and 3, respectively. This suggests that reader 1’s low within-reader correlation and selection bias on this measure are the main causes for the relatively low ICC.
Table 3.
p-values of the tests of significance from a 3-way ANOVA
| Tissue Type | Tissue Structure | P-Values | |||
|---|---|---|---|---|---|
| Reader | Replicate | Reader × Replicate Interaction | Reader × Image Interaction | ||
| Primarily soft | Bladder neck to Pubococcygeal line | <.0001 | 0.32 | 0.0003 | 0.063 |
| Levator hiatus width | 0.89 | 0.79 | 0.24 | 0.43 | |
| Primarily bony | Interacetabular distance | <0.0001 | 0.0036 | 0.43 | 0.38 |
| Intertuberous distance | 0.042 | 0.064 | 0.054 | 0.0072 | |
| Involve both soft and bony tissue | Bladder neck to symphysis | <0.0001 | 0.34 | 0.067 | 0.68 |
| Puborectalis attachment width on left | 0.078 | 0.65 | 0.022 | <0.0001 | |
| Puborectalis attachment width on right | 0.0005 | 0.17 | 0.017 | <0.0001 | |
The measurements on intertuberous distance showed an image-dependent reader difference (p=0.0072). Within-reader correlations for the three readers are 0.84, 0.85, and 0.93.
Puborectalis attachment width on right and left both have very good within-reader correlations (0.88, 93, and 0.95 on right, and 0.88, 0.95, and 0.97 on left). However, both of them showed very significant image-dependent reader difference (p <0.0001 for both). The differences among readers are so large for the measurements on the left, such that the corresponding ICC value is 0.64.
The within-reader correlations for the interacetabular distance are 0.80, 0.86 and 0.86. The ANOVA showed significant selection bias among readers (p <0.0001) and difference between the first and second readings (p = 0.0036). Reader 3 tended to report larger values than the two other readers. In addition, on average the second readings are smaller than the first readings.
Measurements on bladder neck to pubococcygeal line have reader dependent difference between the first and second readings (p = 0.0003). Reader 1’s first readings are significant larger than the second reading. In addition, both readers 1 and 3 have relatively low within-reader correlations (0.81 and 0.81).
Measurements on levator hiatus width had the worst over all quality (ICC = 0.62, within-reader correlation = 0.96, 0.40, 0.76). Further investigations found two problematic readings. The first reading is from reader 2 with a value much larger than the rest of the five readings (43.27 vs. 31.06 – 32.9). The second reading is from reader No. 3, and similarly its value is much larger than the rest of the five readings (41.56 vs. 28.51 – 29.1). If there two problematic points were deleted, the corresponding within-reader correlation for readers 2 and 3 both would increase to 0.97, and the ICC would increase to 0.92.
Correlations were considered marginal at best for bladder neck to pubo-coccygeal line, bladder neck to symphysis, interacetabular distance, intertuberous disctance, and puborectalis attachment width on right. Margins of anatomic structures selected for 3 dimensional segmentation had already been chosen prior to this study, thereby eliminating potential error in structure identification.
Levator shape
The three readers showed poor agreement on whether a levator is U-shaped or V-shaped. Of the 20 reconstructions, one had only 4 readings and therefore was deleted from the analysis. In the remaining 19 reconstructions, only two were unanimously identified as U-shaped and three as V-shaped. In four other reconstructions, five of the readings agreed. The remaining nine reconstructions were split either 4:2 or 3:3, i.e. there was little agreement about the shape among readers.
The maximum number of measurements reported for any parameter was 118; the minimum number was 88 (levator hiatus width). This was likely the case because the levator hiatus measurement depended on the presence of an intact puborectalis muscle approaching the symphysis bilaterally. In those subjects with marked deficiency or absence of the puborectalis muscle, the measurement landmarks were not available, and the measurement was not made. Nine parameters were each measured 118 times. The other parameters with fewer than 118 reported measurements were: puborectalis width left (n=94) and right (n=106), intertuberous distance (n=112), pubic arch angle (n=115), and interspinous distance (n=117). Because of absence of landmarks, puborectalis width measurements could not be made in cases where one or more arms of the puborectalis were absent from the original MR images, and thus the 3D reconstructions. The intertuberous distance, and pubic arch angle were likely not measured because the original MR scans did not reach inferiorly enough to capture these landmarks. The interspinous distance was sometimes not captured on the 3D models, owing to poor definition of this bony landmark on the original MR images.
DISCUSSION
Magnetic based 3D reconstruction is evolving into a valuable research tool for quantitative study of female pelvic floor anatomy. However, to permit good comparison of measurement parameters, interoperator measurement reliability is essential.
The present measurement reliability analysis demonstrated that eight of the 15 continuous parameters showed excellent agreement among readers (ICC 0.85 or better), five showed relatively good agreement (ICC 0.7 or greater), and two showed poor agreement (ICC less than 0.7). It is possible that the parameters with good or poor agreement can be improved with the aid of software algorithms designed to automate placement of the measurement markers for each parameter, in order to improve consistency. Such algorithms are currently being investigated.
The best agreement was seen in cases where the landmark edges were sharp and well defined e.g., ischial spines (interspinous distance), urethral ends (urethral length), lower symphysis edge and puborectalis edge (Levator symphysis gap, left, right), and symphysis edge to coccyx (pubococcygeal line). Excellent agreement was also seen in angular measurements (urethral angle and pubic arch angle), where it is possible that the arms and vertices of the angles are sufficiently well defined so as to reduce the measurement error.
The five parameters with acceptable level of agreement required a “judgement call” on the part of each reader to determine where to place the measurement markers. In case of the bladder neck to pubococcygeal line, the reader was obliged to identify an area of the urethra as the bladder neck. It is possible that this location on the 3D models was simply too subtle to reliably identify. For the interacetabular distance, the reader was obliged to identify points outlining the closest aspects of the acetabular concavities, which are on opposite sides of the bony pelvis, and therefore difficult to visualize together in the same view. Regarding the intertuberous distance, readers are required to identify the middle of each ischial tuberosity, and this could have introduced variability because this landmark has a relatively large surface from which the marking point must be chosen. It is possible that an automated algorithm for marking the points of each parameter in this “acceptable agreement” group may yield markedly improved reliability; this possibility is under investigation.
The worst agreement was seen in the levator hiatus width and puborectalis width on the left. Levator hiatus width reliability was poor probably because of the difficulty in specifying good landmarks for this measurement, especially in cases where the puborectalis is damaged or markedly attenuated. The poor agreement shown in the puborectalis width on the left may be related to difficulty in standardizing the cross-sectional level at which puborectalis width is to be measured. However, it is unclear why the right sided version of this parameter produced better measurement agreement than the left. It is likely that these measurements may simply not be feasible in all subjects.
The present analysis did not include a measurement correlate of the M-Line measurement familiar to 2D pelvic image readers. A correlate of this measurement was not considered at the time of our analysis, and will be included in future analyses. The Levator hiatus parameter is the 3D correlate of the familiar “H-Line” 2D parameter, and was included in the present analysis.
For the evaluation of pelvic floor structures by MRI, there is a high ratio of excellent or adequate correlation (13/15 parameters) between readers of 3D measurements based upon 2D source data. The 3D tool forces placement of the measurement cursor on a surface closest to the pointer thus reducing variability when compared with free placement of cursors on a routine 2D data set. Therefore, it is reasonable to expect higher levels of correlation between measurements than is found in the 2D literature. Our findings support this concept.
Because only 20 studies were chosen for review, it is possible that the appearance of the measured structures is not representative of the entire study population. Women of different ages or races may have anatomic landmarks that are more difficult or easier to identify, which may alter interobserver reliability. Because of the time required to create and review these 3D datasets however, a 20 subject sample was considered reasonable. These results may not be generalizeable to the general physician population. This is because of the specialized experience and training required of each measurer. However, using computer image analysis techniques, it may be possible to fully automate the measurement process in the future, thus making the capability more reliable and widely available.
The resolution of specific 3D structures is dependent upon the source data resolution and reconstruction algorithms. Use of 3D reconstructions is unlikely to improve detection of small defects or abnormalities, but may help show differences in overall morphologic structure and volume. This might be particularly valuable in measuring muscle volume and for planning of complex pelvic surgical interventions.
The use of 3D has the possibility to improve diagnosis by presenting the conventional data in a new perspective, easier to assimilate and use by pelvic floor surgeons and researchers. Imagers are beginning to routinely evaluate the body in multiple planes. Multiplanar visualization of structures has added diagnostic benefit in other areas such as CT urography and colonography, and in fetal ultrasound.
In clinical practice or research, the variability of the measurements cannot be considered in a vacuum. The variability in the acquisition of the data set and in the creation of a 3D model each contribute to the overall variability of the technique. However, if these components of the process can be standardized and automated, the present results suggest promise for this technique.
Acknowledgments
Supported by grants from the National Institute of Child Health and Human Development (U01 HD41249, U10 HD41268, U10 HD41248, U10 HD41250, U10 HD41261, U10 HD41263, U10 HD41269, and U10 HD41267).
Footnotes
Reprints are not available.
References
- 1.Fielding JR, Griffiths DJ, Versi E, Mulkern RV, Lee M-LT, Jolesz FA. MR Imaging of Pelvic Floor Continence Mechanisms in the Supine and Upright Positions. Amer J Radiol. 1998;171:1607–1610. doi: 10.2214/ajr.171.6.9843296. [DOI] [PubMed] [Google Scholar]
- 2.Hoyte L, Ratiu P. Linear measurements in 2-dimensional pelvic floor imaging: The impact of slice tilt angles on measurement reproducibility. Am J Obstet Gynecol. 2001;185(3):537–44. doi: 10.1067/mob.2001.116751. [DOI] [PubMed] [Google Scholar]
- 3.Hoyte L, Thomas J, Foster RT, Shott S, Jakab M, Weidner AC. Racial differences in pelvic geometry among asymptomatic nulliparas as seen on three-dimensional MR images. Am J Obstet Gynecol; 2005 Annual Meeting, Soc. Gynecologic Surgeons; California: Rancho Mirage; 2005. [DOI] [PubMed] [Google Scholar]
- 4.Cornella JL, Hibner M, Fenner DE, Kriegshauser JS, Hentz J, Magrina JF. Three-dimensional reconstruction of magnetic resonance images of the anal sphincter and correlation between sphincter volume and pressure. Am J Obstet Gynecol. 2003;189(1):130–5. doi: 10.1067/mob.2003.545. [DOI] [PubMed] [Google Scholar]
- 5.Singh K, Jakab M, Reid WM, Berger LA, Hoyte L. Three-dimensional magnetic resonance imaging assessment of levator ani morphologic features in different grades of prolapse. Am J Obstet Gynecol. 2003;188(4):910–5. doi: 10.1067/mob.2003.254. [DOI] [PubMed] [Google Scholar]
- 6.Norwitz ER, Hoyte LPJ, Jenkins K, van der Velde M, Ratiu P, Rodriguez-Thompson D, Wilkins-Haug L, Tempany CMC, FSJ Conjoined twins with twin reversed arterial perfusion sequence: A novel technique for antenatal surgical planning. New England Journal of Medicine. 2000;343(6) doi: 10.1056/NEJM200008103430604. [DOI] [PubMed] [Google Scholar]
- 7.Hoyte L, Lu K, Muto M, Nucci M, Versi E, Kikinis R, FJR Magnetic Resonance Imaging based three dimensional modeling of a complex vulvar tumor as a component of presurgical planning. J Women’s Imaging. 2000;2:138–140. [Google Scholar]
- 8.Hundley AF, Fielding JR, Hoyte L. Double cervix and vagina with septate uterus: an uncommon mullerian. Obstet Gynecol. 2001;98(5 Pt 2):982–5. doi: 10.1016/s0029-7844(01)01559-9. [DOI] [PubMed] [Google Scholar]
- 9.Hsu Y, Lewicky-Gaupp C, DJO Posterior compartment anatomy as seen in magnetic resonance imaging and 3-dimensional reconstruction from asymptomatic nulliparas. Am J Obstet Gynecol. 2008;198(6):651. doi: 10.1016/j.ajog.2007.11.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fielding JR, Dumanli H, Schreyer A, Okuda S, Gering D, Zou K, Kikinis R, Jolesz F. MR-Based Three dimensional Modeling of the Normal Pelvic Floor in Women: Quantification of Muscle Mass. Amer J Radiol. 2000;174:657–660. doi: 10.2214/ajr.174.3.1740657. [DOI] [PubMed] [Google Scholar]
- 11.Hoyte L, Schierlitz L, Zou K, Flesh G, Fielding JR. Two and 3 dimensional MRI comparison of Levator Ani structure, volume and integrity in women with stress incontinence and prolapse. Am J Obstet Gynecol. 2001;185(1):11–19. doi: 10.1067/mob.2001.116365. [DOI] [PubMed] [Google Scholar]
- 12.Chen L, Hsu Y, Ashton-Miller JA, DeLancey JO. Measurement of the pubic portion of the levator ani muscle in women with unilateral defects in 3-D models from MR images. Int J Gynaecol Obstet. 2006;92(3):234–41. doi: 10.1016/j.ijgo.2005.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kikinis R, Gleason PL, Moriarty TM, Moore MR, Alexander E, 3rd, Stieg PE, Matsumae M, Lorensen WE, Cline HE, Black PM, Jolesz FA. Computer-assisted interactive three-dimensional planning for neurosurgical procedures. Neurosurgery. 1996;38(4):640–9. discussion 649–51. [PubMed] [Google Scholar]
- 14.Schreyer AG, Fielding JR, Warfield SK, Lee JH, Loughlin KR, Dumanli H, Jolesz FA, KR Virtual Cystoscopy: Color Mapping of Bladder Wall Thickness. Invest Radiol. 2000;35:331–334. doi: 10.1097/00004424-200005000-00008. [DOI] [PubMed] [Google Scholar]
- 15.Stenzl A, Frank R, Eder R, Recheis W, Knapp R, zur Nedden D, Bartsch G. 3-Dimensional computerized tomography and virtual reality endoscopy of the reconstructed lower urinary tract. J Urol. 1998;159(3):741–6. [PubMed] [Google Scholar]
- 16.Kim DH, Pickhardt PJ, Taylor AJ, Leung WK, Winter TC, Hinshaw JL, Gopal DV, Reichelderfer M, Hsu RH, PPR CT colonography versus colonoscopy for the detection of advanced neoplasia. N Engl J Med. 2007;357:1403–12. doi: 10.1056/NEJMoa070543. [DOI] [PubMed] [Google Scholar]
- 17.Cline HE, Lorensen WE, Ludke S, Crawford CR, Teeter BC. Two algorithms for the three-dimensional reconstruction of tomograms. Med Phys. 1988;15(3):320–7. doi: 10.1118/1.596225. [DOI] [PubMed] [Google Scholar]
- 18.Gering DT, Nabavi A, Kikinis R, Hata N, O’Donnell LJ, Grimson WE, Jolesz FA, Black PM, Wells WM., 3rd An integrated visualization system for surgical planning and guidance using image fusion and an open MR. J Magn Reson Imaging. 2001;13(6):967–75. doi: 10.1002/jmri.1139. [DOI] [PubMed] [Google Scholar]
- 19.Handa VL, Lockhart ME, Fielding JR, Bradley CS, Brubaker L, Cundiff YWGW, Richter HE PFD Network. Racial differences in pelvic anatomy by magnetic resonance imaging. Obstet Gynecol. 2008;111(4):914–20. doi: 10.1097/AOG.0b013e318169ce03. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.SHROUT PE, FJL Intraclass correlations: Uses in assessing rater reliability. Psychological Bulletin. 1979;86:420–428. doi: 10.1037//0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]


