Cone Spacing and Waveguide Properties from Cone Directionality Measurements

Abstract

Reflectometric techniques estimate the directionality of the retinal cones, by measuring the distribution of light at the pupil plane of light reflected off the bleached retina. The waveguide-scattering model [Marcos et al. (1998), J. Opt. Soc. Am A] predicts that the shape of this intensity distribution is determined by both the waveguide properties of the cone photoreceptors and by the topography of the cone mosaic (cone spacing). We have performed two types of cone directionality measurements. In the first type, cone directionality estimates are obtained by measuring the spatial distribution of light returning from the retina with a single entry pupil position (single-entry measurements). In the second type, estimates are obtained by measuring the total amount of light guided back through the pupil as a function of entry pupil position (multiple-entry measurements). As predicted by the model, single-entry measurements provide narrower distributions than the multiple-entry measurements, since the former are affected by both waveguides and scattering and the latter primarily by waveguides. Measurements at different retinal eccentricities and at two different wavelengths are consistent with the model. We show that the broader multiple-entry measurements are not accounted for by cone disarray. Results of multiple-entry measurements are closer to results from measurements of the psychophysical Stiles-Crawford effect (although still narrower), and the variation with retinal eccentricity and wavelength is similar. By combining single- and multiple-entry measurements we can estimate cone spacing. The estimates at 0 and 2 deg retinal eccentricities are in good agreement with published anatomical data.

Introduction

It is widely accepted that the cone-photoreceptors in the human retina exhibit directional sensitivity¹. If the cones are pointing toward the center of the pupil, light entering through the center of the pupil (or equivalently, entering the cones along their axis) is perceived as brighter than the same light coming from the edge of the pupil (i.e. at a larger angle). The Stiles-Crawford effect of the first kind (SCE), as this effect is known, is typically measured using psychophysical techniques^2,3. Since normal photoreceptor directionality requires a normal cone morphology and relation to the extracellular space, photoreceptor directionality has been of clinical interest^4,5,6,7,8. Unfortunately, the long experimental sessions and high degree of cooperation required for the psychophysical measures have restricted the availability of these measurements.

Recently developed reflectometric techniques allow a much more rapid estimation of cone directionality^9,10,11,12. The common principle of these techniques is that, when the photopigment is bleached, part of the light entering the cone inner segments is guided along the outer segment, and then scattered back toward the region of the pupil corresponding to the axis of the cones. The relative luminous efficiency (in psychophysical measurements) or the distribution of the directed or guided reflectance (in the reflectometric measurements) are typically fit at the plane of the pupil by a gaussian function I_max10^{−ρ[(x−x₀)2+(y−y₀)2]}, where x₀ and y₀ represent the coordinates of the peak location for which either the luminous efficiency or the guided reflectance are highest (i.e. the location at the pupil plane where the cones are aimed), and ρ is a measure of directionality (the higher ρ, the more narrowly tuned the function). It has been reported that reflectometric techniques provide the same estimate for the location at the pupil plane to which the photoreceptors are oriented, although directionality is, in general higher (higher rho values) in reflectometric measurements than in psychophysical measurements^9,13,14.

Predictions of the waveguide-scattering model

We have proposed a more complete model¹⁵ of the intensity distributions measured at the plane of the pupil obtained in Burns et al.'s reflectometric technique¹¹. In this technique, the distribution at the pupil plane of light reflected off the retina is imaged on a CCD camera, while a small patch of the bleached retina is illuminated in maxwellian view. In our model, we propose that the light distribution at the pupil plane is affected by both the waveguide properties of the photoreceptors and the interference of light re-emitted from the cones. Our assumption is that since the photoreceptors have slightly different lengths, light emerges from each cone with a different phase and interferes at the plane of the pupil. For the dimensions of the eye and cone mosaic, the effect is similar to that produced at the far-field plane by light scattered from a rough surface¹⁶. The scattering alone produces a gaussian distribution at the pupil plane and the rho value (ρ_scatt) depends on the spatial distribution of the cones¹⁵: ρ_scatt = k(fλ)⁻² s², where f is the axial length of the eye, λ is the wavelength, k is a constant and s is the row-to-row cone spacing.

As a result, the overall intensity distribution at the plane of the pupil is the product of two gaussian distributions¹⁵: the angular distribution of light emitted by the cones (ρ_wg) and the gaussian distribution caused by scattering. The rho value for the final distribution is then the sum of the rho values from the two components: ρ=ρ_scatt+ρ_wg

The waveguide-scattering model¹⁵ predicts that techniques measuring the waveguide properties of the cones alone should produce lower rho values (ρ_wg) than the rho value in Burns et al.'s reflectometric technique¹¹. In addition, according to the model, if the waveguide properties can be measured independently, both ρ_wg and ρ_scatt can be determined, and the cone spacing of the retinal mosaic can be calculated. In the current paper, we present a technique to separate these components and show that the resulting cone spacing agrees with anatomical estimates in normal subjects, supporting our model. In addition, we show that different reflectometric techniques are differentially sensitive to ρ_wg and ρ_scatt. This differential sensitivity can explain some of the differences in measurements of cone directionality between laboratories.

Single-entry and multiple-entry photoreceptor directionality measurements

In Burns et al.'s technique¹¹, typically a single image is measured for the entry pupil position that produces the highest directional intensity. This distribution is used to determine rho. If the entry location is moved away from this optimal entry pupil, less light is coupled into the photoreceptors, and consequently the amount of guided light reflected back from the photoreceptors decreases. According to our model¹⁵, while the shape of the light distribution depends on both waveguides and scattering, the total amount of guided light at each entry pupil location depends only on the angular tuning of the cones. As a result, the total amount of light guided as a function of entry pupil position represents a measure of the waveguide properties of the cones, and should be more similar to psychophysical estimates of cone directionality than to the estimates from the conventional reflectometric technique. We will refer to the measurements based on a single intensity distribution at the pupil as single-entry reflectometric measurements. The measurements based on the estimation of the total guided intensity as a function of entry pupil will be referred to as multiple-entry reflectometric measurements, since they are derived from multiple images.

In this paper, we present single- and multiple-entry measurements of photoreceptor directionality for a group of subjects. As predicted by the model¹⁵, multiple-entry measurements (that depend on the waveguide properties alone) provide consistently lower estimates of rho (broader functions) than the single-entry measurements. In the Discussion, we study the potential role of cone disarray^17,18,20 on the measurements and we compare these results to previous measurements of the Stiles-Crawford effect in the same subjects¹⁴. We also present cone spacing estimates obtained by applying the model to directionality measurements. We finally reinterpret the results from other reflectometric measurements^9,10,12 by applying the waveguide-scattering model.

Methods

Apparatus

We used an imaging reflectometer to measure the spatial distribution of the guided light reflected off the retina (single-entry measurements), as well as to measure the total amount of guided light reflected off the retina as a function of entry pupil position (multiple-entry measurements). The apparatus has been described previously^11,18,15. Briefly, a 1-deg area of the retina is illuminated in Maxwelliam view by projecting a 0.18 μm laser spot at the pupil plane. Green or red illumination light is provided by two He-Ne lasers respectively (543 nm and 632 nm). A diode-pumped laser (532 nm) provides a wide bleaching field (∼6%10⁵ Td). The position of both the entrance pupil and the retinal fixation location is under computer control. Light returning from the retina through a 2 deg- retinal field stop is collected at the plane of the pupil by means of a high resolution, scientific grade, cooled CCD camera (Princeton Instruments), located in a pupil conjugate plane. A separate channel allows infrared viewing of the pupil, and is used for centration and alignment of the subject to the instrument throughout the session. Subjects' head positions are stabilized by means of a bite bar and forehead rests.

Single-entry reflectometric measurements are based only on the spatial distribution of light guided towards the pupil within a single image. However, the new multiple-entry measurements require accurate measurements of relative intensity for all images within a session. To ensure that fluctuations in either the light source or the detector did not cause artifacts, the tip of a fiber optic collecting part of the output of the laser source was placed at a plane conjugate to the pupil and imaged together with light coming from the retina. Fluctuations were not detected within any single session, so we present unnormalized data.

Subjects and conditions

Single- and multiple-entry reflectometric measurements were collected on three normal subjects (SM, JH, and SB), ages 27, 38 and 48, one female and two males. JH had deuteranomalous color vision. Subjects were dilated with 0.5% Mydriacil after informed consent was obtained.

Two retinal locations (0 and 2 deg temporal) were tested in all subjects. Measurements were made typically using green light (543 nm); for subject JH data were also collected using red light (632 nm).

Experimental Procedure

Previous measurements^13,18,15 on each subject provided an estimate of the entry location that produced the highest directionality. This location was taken as the optimal entry pupil for each subject: (0, -1) for subject SM, (-1,1) for subject JH and (0, -2) mm for subject SB. Positive coordinates stand for temporal and superior coordinates at the pupil plane, respectively, and negative coordinates for nasal and inferior coordinates at the pupil plane.

Series of images were obtained while moving the entry pupil in 0.5-mm steps along the horizontal and vertical axis. Five consecutive images were obtained at each entry pupil position and 6 to 11 entry positions were tested per axis. For a given wavelength, the intensity of the illuminating beam was kept constant throughout the experiment. For each condition, the entire series was repeated at least once on a different day.

Data analysis

Figure 1 sketches the basic idea of both single-entry and multiple-entry measurements and how to extract cone directionality information from the two types of measurements. The top panel represents a series of images obtained with the imaging reflectometer as the illumination beam moves nasally or temporally across the pupil.

Fig. 1.

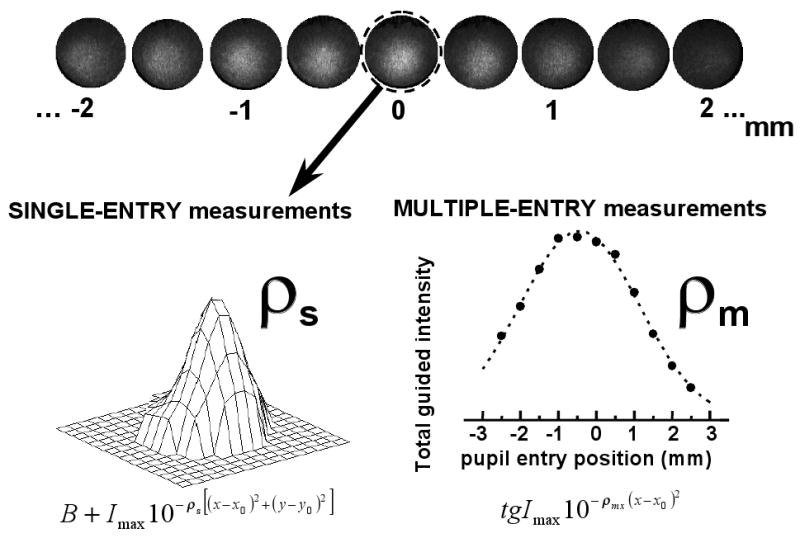
Theory of single- and multiple-entry reflectometric measurements. The intensity distribution at the pupil plane of light returning from a small area of bleached retina is imaged on a CCD camera for a series of entry pupil locations (top panel, data from subject SM, 0 deg, 543 nm, horizontal axis). The total amount of guided light is maximum for the location in the pupil toward which the photoreceptors are pointing. The circled image corresponds to the optimal entry pupil location, and is the image used for single entry reflectometric measurements. Since these measurements are based on a single image, we refer to them as single-entry measurements (left bottom panel). The intensity distribution for this image is fit to a constant added to a 2-D gaussian function, from which we obtain rho value : ρ_s. As the entry position of the illuminating beam moves away from the optimal entry pupil, less light is captured by the cones and guided back. The measurements based on a series of images across the pupil are referred to as multiple-entry measurements (right bottom panel). The total amount of guided light as a function of entry pupil position is fit with a gaussian function, with rho value: ρ_mx. The final rho, ρ_m, is computed as the mean of the estimates for the horizontal and vertical axis (ρ_mx and ρ_my).

For the single-entry estimates of cone directionality (see Fig. 1, left panel), images at the optimal entry pupil are processed as described elsewhere^11,18. First, the corneal reflexes corresponding to the first and 4^th Purkinje images are eliminated. The intensity distribution at the pupil plane is fit with the following equation: B + I_max10^{−ρ_s[(x−x₀)2+(y−y₀)2]}, where B is a constant that accounts for light diffusely reflected, forming a constant background that fills the pupil) and the second term is a 2-dimensional gaussian function that represents the light directly guided from the photoreceptors; I_max is the intensity at the peak, and it is highest for images obtained when illuminating through the optimal entry pupil; ρ_s is the directionality factor. For each session and each condition (retinal eccentricity and wavelength), we select the ρ_s corresponding to the best fit (the lowest rms between measurement and fit). Final ρ_s's are averages across sessions.

For the multiple-entry estimates of cone directionality (see Fig. 1, right panel) we did not use the same fitting procedure, since the quality of the fit is poor when I_max is small. Instead, we obtained estimates of the total guided intensity by analyzing the images directly. As before, corneal reflexes are eliminated. We select a small region of the pupil far from the distribution of guided light. The average intensity over that region is taken as an estimate of the diffuse background. The background is then subtracted from the image. The remaining total intensity in the image is used as an estimate of the total guided intensity. The total guided intensity (average over 5 measurements) as a function of entry pupil position is fit to a gaussian: tgI_max10^{−ρ_mx(x−x₀)2} and tgI_max10^{−ρ_my(y−y₀)2}, for the horizontal and vertical axes respectively. If the spatial distribution of the guided light at the pupil plane fits a gaussian whose rho value does not change with entry pupil position, then fitting the total guided intensity or the maximum guided intensity should be equivalent. We confirmed this by analyzing sample data both ways. We decided to use the total guided intensity instead of the maximum guided intensity because the first one is based on the entire image, and is therefore a more robust estimate.

For each session and each condition, ρ_m is obtained as the average of the rho values obtained by fitting the total guided intensity estimates across the horizontal and vertical axis (ρ_m=(ρ_mx+ρ_my)/2). Except for one case (SB, 0 deg) we did not find significant asymmetry between the estimates for the horizontal axis and vertical axis respectively. Final ρ_m's are averages across sessions. The peak locations (x₀ and y₀) obtained from the fit to the multiple-entry measurements [(-0.15, -1.08) for SM, (-1.09, 0.79) for JH and (-0.54,-2.24) mm for SB, on average] are similar to those obtained from single-entry measurements: (-0.28, -1.29) for SM, (-1.01, 0.77) for JH, and (-0.07,-2.24) mm for SB, on average. These peak locations are very close to the horizontal and vertical coordinates chosen for the multiple-entry measurements. The reader should note that even if the sample transverse does not pass through the true peak location, the values of ρ and coordinates of the maximum would be constant, because of the nature of the gaussian function we are using in our analysis¹⁹.

Results

Single-entry and multiple-entry directionality measurements

Figure 1 (top panel) shows a typical example of the intensity distribution at the pupil plane for a series of entry pupil positions (subject SM, 0 deg, horizontal axis). Single-entry rhos (ρ_s) are extracted from images obtained at the optimal entry pupil.

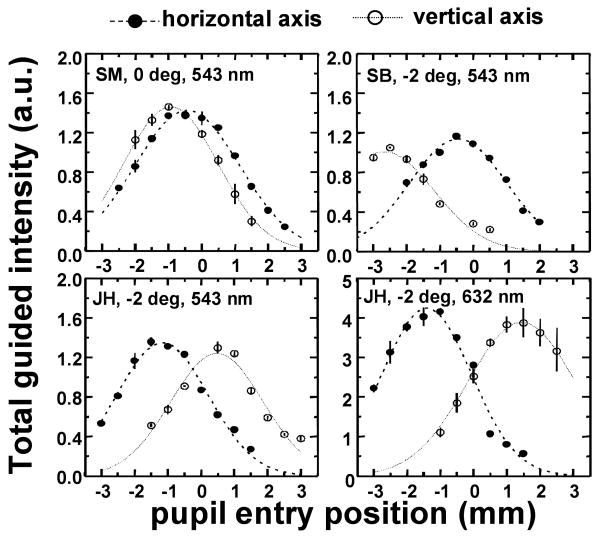
Figure 2 shows various representative examples of multiple-entry reflectometric functions for different subjects and conditions, obtained in separate sessions. Filled symbols represent measurements across the horizontal axis of the pupil, and open symbols measurements across the vertical axis. Each symbol is the average of five measurements, obtained consecutively. Reproducibility within a session is high (in most cases the error bars, !1 standard error of the mean, are smaller than the size of the symbols). The measurements were well fit by gaussian functions (represented by dashed and dotted lines for the fits to measurements across the horizontal and vertical axes respectively). Variability is highest for red illumination, probably because the background component is generally higher than the guided component, and slight errors in the determination of the background have a higher impact on the estimate of the total guided component than for green illumination.

Fig. 2.

Example of multiple-entry reflectometric functions (total guided intensity as a function of entry pupil position), for different subjects (SM, SB and JH), retinal eccentricities (0 deg and 2 deg temporal) and wavelengths (543 and 632 nm). Each panel represents results from a single session. Circles are averaged across five consecutive measurements at the same pupil location. Filled circles stand for measurements across the horizontal axis, and open circles across the vertical axis. (Error bars stand for !1 standard error of the mean). Positive entry pupil positions stand for temporal and superior locations, and negative for nasal and inferior locations. Dashed and dotted curves represent the best fit to the measurements across horizontal and vertical axis respectively.

Variation of rho value as a function of retinal eccentricity and wavelength

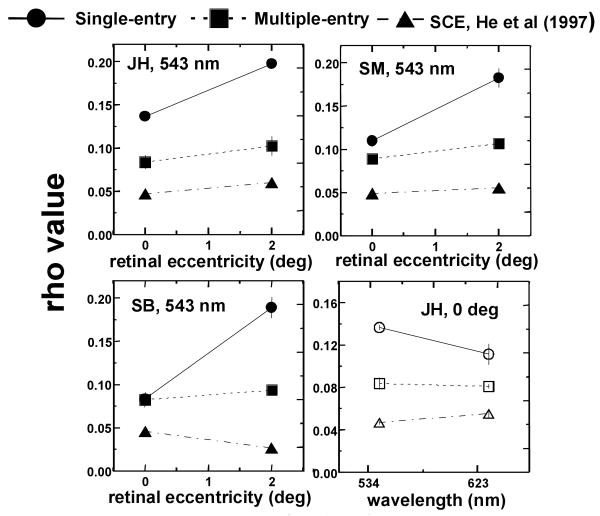
As our model predicts¹⁵, multiple-entry reflectometric functions are systematically broader (lower rho) than single-entry reflectometric distributions (higher rho). The difference is particularly clear at 2 deg, although at the center of the fovea, it is significant in 2 of the 3 subjects. Also, the increase of rho with retinal eccentricity is steeper for single-entry measurements than for multiple-entry measurements. Figure 3 (a) shows rho derived from the two types of measurements as a function of retinal eccentricity for the three subjects, using green (543 nm) light. Filled symbols represent single-entry measurements (ρ_s) and open symbols represent multiple-entry measurements (ρ_m). Each symbol is the average of estimates of rho values from at least two sessions. For the sake of clarity, error bars are not shown in the figure, but standard errors never exceeded 0.0166 mm^-2 for ρ_s and 0.0108 mm^-2 for ρ_m. Table 1 shows ρ_s and ρ_m values for 0 and 2 deg for the three subjects, as well as the standard deviations of the measurements.

Fig. 3.

Rho value as a function of retinal eccentricity for single-entry measurements, ρ_s (filled symbols) and multiple-entry measurements, ρ_m (open symbols). (a) Results for the three subjects. Symbols with the same shape correspond to the same subject. Single-entry measurements are in all cases narrower than multiple-entry measurements. (b) Results for subject JH for two wavelengths: 543 nm (filled symbols) and 632 nm (open symbols). Circles represent single-entry measurements and squares represent multiple-entry measurements. Single-entry measurements in green light are narrower than in red light, although there is no significant difference across wavelengths for multiple-entry measurements. Standard errors are smaller than 0.0166 mm^-2 for single-entry measurements and smaller than 0.0108 mm^-2 for multiple-entry measurements.

Table 1. ρ_dir and ρ_ind for 0 and 2 deg retinal eccentricity (3 subjects and average) for the experiments in the present study.

	ρdir (±1 SD)		ρind (±1 SD)
	0 deg	2 deg	0 deg	2 deg
JH	0.136±0.004	0.197±0.004	0.111±0.012	0.102±0.015
SM	0.110±0.014	0.182±0.023	0.089±0.010	0.106±0.017
SB	0.083±0.002	0.189±0.020	0.082±0.015	0.093±0.007
average	0.110	0.189	0.094	0.100

Single-entry measurements as a function of wavelength (in JH, 0 and 2 deg) are markedly broader for red light than for green light, as shown elsewhere¹⁵. However, multiple-entry measurements in the same subject are not significantly different for the two wavelengths. Figure 3 (b) shows rho value as a function of retinal eccentricity for the two wavelengths for subject JH. Circles represent single-entry measurements, and squares multiple-entry measurements. Filled symbols stand for 543 nm and open symbols stand for 632 nm. Whereas for single-entry measurements, rho (ρ_s) decreases as the wavelength increases, for multiple-entry measurements rho (ρ_m) is very similar for the two wavelengths.

Discussion

Our model predicts that the spatial distribution of light guided back through the pupil is controlled by two factors: waveguide properties and interference effects arising from the retinal cone mosaic¹⁵. We have separated these two factors by measuring cone directionality using two different approaches (measuring the spatial intensity distribution at the plane of the pupil for the optimal entry position, and computing the total amount of light guided as a function of entry pupil position). As expected, multiple-entry measurements produce lower estimates of rho values than single-entry measurements, since the former should depend only on the waveguide properties, whereas the latter incorporates the additional contribution of scattering.

In the next section we discuss the potential effects of photoreceptor disarray and show that they are not responsible for the differences that we find between the two measurements.

Effect of cone-photoreceptor disarray

Photoreceptor disarray can potentially broaden the multiple-entry measurements with respect to single-entry measurements: if there are cones at an angle away from the group mean, those cones will return relatively more light at an angle of illumination along their own axis, corresponding to an entry pupil away from the optimal location. As a consequence the multiple-entry measurements will broaden. Previous measurements show that cone disarray is small in the human fovea and parafovea^17,18. McLeod¹⁷ calculated that the acceptance angle of an individual cone is only two percent less than the global tuning of a group of photoreceptors when a realistic amount of disarray is considered.

To calculate possible influence of disarray on our measurements, we simulated the differences between single-entry and multiple-entry measurements in the presence of cone disarray (assuming the extreme case of no scattering being involved). Figure 4 shows the rational that we followed in the computer simulation. We assume the cones with a given distribution of orientations²⁰ or distribution of pupil intercepts, using the same terminology used by McLeod¹⁷: G_dis. In our calculations, G_dis is a gaussian function, but for simplicity in Fig. 4 we represent it as three delta functions. The emission angle of a single cone is also represented as a gaussian function at the pupil plane, G_wg. For convenience, we suppose that both G_dis and G_wg are concentric with the geometrical center of the pupil: 10^{−ρ_dis(x2+y2)} and 10^{−ρ_wg(x2+y2)}. We then compute the intensity distribution at the pupil plane for different entry pupils across the horizontal axis, by performing the following convolution: (G_wg(x − x_i) × G_dis)⊗ G_wg, where x_i represents the entry pupil position of the illuminating beam. G_dis is multiplied by G_wg since the amount of light captured by cones not oriented along the direction of illumination is proportional to both the number of cones oriented toward a specific location at the pupil and the intensity of the ‘tail’ of the angular tuning at that particular pupil location. Significant disarray predicts two findings¹⁸ (Fig. 4): First, the location of the peak of the intensity distribution should move toward the direction of the entry pupil location; second, the total guided intensity vs entry pupil position should be broader than the spatial intensity distribution from a single image. Both functions are affected by cone disarray, but single-entry measurements to a lesser extent than multiple-entry measurements. From our simulations, and given values of G_dis and G_wg, we computed the displacement of the peak position, and rho values for single- and multi-entry measurements (ρ_s and ρ_m respectively).

Fig. 4.

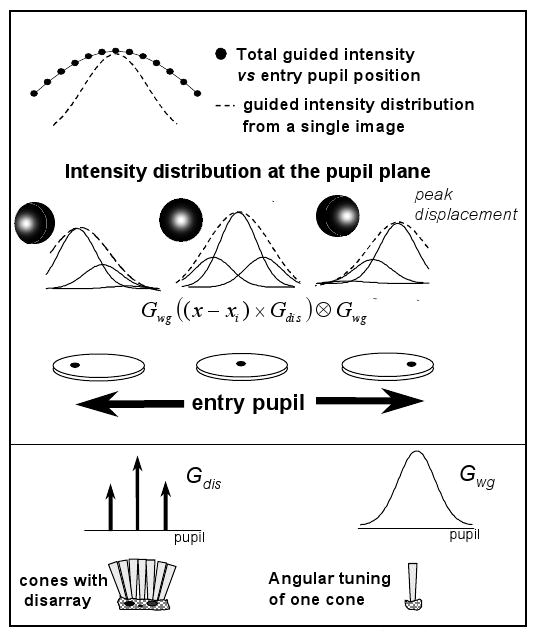
Scheme of computer simulations showing the effect of cone disarray. G_dis stands for the cone disarray distribution (a gaussian distribution in the simulation, represented as three delta functions for graphical purposes); G_wg represents the angular tuning of a cone (bottom panel). The middle panel represents the convolution process to compute the intensity distribution at the pupil plane for different entry pupil positions (shown for entry pupil positions coincident with the location of the delta functions). Cone disarray has two consequences: displacement of the peak of the intensity distribution and broadening of the function calculated as the total guided intensity vs pupil position, with respect to the distribution computed from a single image.

The actual measured variation in the location of the maximum in light exiting the eye was smaller than 0.5 mm when the entry location varied as much as 2.5 mm from the optimal entry pupil. We found similar peak displacements for both 0 and 2 deg retinal eccentricities, and for both horizontal and vertical axes.

The simulations did not find a combination of waveguide properties and disarray that are consistent with both the peak displacements and broadening. We simulated single- and multiple-entry functions for different cases. For example, if we choose ρ_wg=0.22 mm^-2 and ρ_dis=1.3 mm^-2, we can compute single-entry intensity distributions (ρ_s=0.19 mm^-2) to match our experimental estimates (ρ_s=0.189 mm^-2 on average) at 2 deg; these conditions generate also peak displacements close to our experimental estimates (∼0.5 mm). However, for these conditions the computed values for multiple-entry measurements (ρ_m=0.18 mm^-2) do not match the experimental multiple-entry estimates (ρ_m=0.106 mm^-2). In the example just shown, disarray would only be responsible for ∼10% of the broadening that we found experimentally. If we choose ρ_wg=0.12 mm^-2 and ρ_dis=0.8 mm^-2, we can compute multiple-entry functions (ρ_m =0.10 mm^-2) that match our experimental estimates for ρ_m and peak displacements. However, the predicted single-entry rho value (ρ_s =0. 11 mm^-2) is much lower than the experimental value. We conclude that another factor (scattering) must be involved in the differences between single- and multiple-entry measurements.

Reflectometric measurements and the Stiles-Crawford effect

Various studies show that estimates of the point in the pupil toward which the photoreceptors are optimally aligned agree well with measurements of the psychophysical Stiles-Crawford effect^10,12,13,14. However, the directionality factor rho is consistently higher for reflectometric measurements than for psychophysical measurements. He et al.¹⁴ compared in the same subjects the directionality factors obtained using Burns et al.'s reflectometric technique¹¹ (single-entry measurements, using the terminology coined in the current paper) with psychophysical Stiles-Crawford measurements (using a criterion of flicker thresholds, and bleaching adaptation fields to avoid self-screening and to isolate as much as possible the waveguide properties). On average rho for reflectometric measurements was ∼2% rho for the psychophysical measurements at the center of the fovea, and ∼4% at -2 deg retinal eccentricity. Several causes are pointed to in that study to explain the narrowing of the single-entry reflectometric measurements¹⁴. Gorrand and Delori²¹ proposed a model that explained the differences between psychophysical and reflectometric measurements, that suggested that some modes guided within the photoreceptors are poorly excited backwards, giving rise to a narrowing of the reflected distribution. While in some animals it is possible to image waveguides in vivo²², in humans it has not been possible; so although a very plausible explanation, this hypothesis is not proven. Our model also predicted that single-entry reflectometric measurements should be broader than the psychophysical SCE, since according to the model, the former are affected by both waveguide properties and scattering, and the latter are affected primarily by the waveguide component¹⁵. According to our reasoning, multiple-entry measurements are also not affected by scattering from the cones, and depend only on the waveguide properties of the photoreceptors. A question then arises: do the Stiles-Crawford effect and the multiple-entry reflectometric measurements reflect the same waveguide properties of the photoreceptors?

Results from the three types of measurements for the three subjects are displayed in Figure 5. Fig. 5 (a), (b) and (c) show rho value as a function of retinal eccentricity for the single- and multiple-entry reflectometric measurements from the present study, and SCE measurements from He et al.¹⁴, for subjects JH, SM and SB (who participated in both studies). ρ_SCE values are more similar to ρ_m than to ρ_s values. The slight increase of SCE directionality with retinal eccentricity is consistent with previous data in the literature^23,24 and with predictions from waveguide models^25,15. For all subjects both SCE and multiple-entry measurements vary with eccentricity more slowly than do the single-entry measurements. Fig. 5 (d) compares rho values as a function of wavelength for the three types of measurements, for subject JH. Whereas single-entry measurements decrease markedly with wavelength, both SCE measurements and multiple-entry measurements barely change. We had shown in a previous paper that the decrease of ρ_s with λ supports the presence of scattering^15,16: the scattering component should decrease with wavelength since it is inversely proportional to λ². In addition, our finding that both ρ_SCE and and ρ_m change minimally with wavelength is consistent with the waveguide properties of the photoreceptors. Waveguide models predict a non-systematic variation of rho as a function of wavelength, very dependent upon the specific cone dimensions and indices of refraction^25,26. In the bleached state²⁷ the SCE change little with wavelength²⁸. Also, recent computer simulations of light propagation within the vertebrate retinal rod have shown a flat dependence of directionality with wavelength²⁹.

Fig. 5.

(a) (b) (c) Rho value as a function of retinal eccentricity for single-entry measurements, ρ_s (filled circles); multiple-entry measurements, ρ_m (filled squares); and Stiles-Crawford effect measurements, from He et al. (1997)¹⁴, ρ_SCE (filled triangles). Subjects JH (a), SM (b) and SB (c). The variation of ρ_m and ρ_SCE with retinal eccentricity is similar; both increase more slowly with increasing retinal eccentricity than ρ_s. However SCE measurements are still broader than multiple-entry measurements. (d) Rho value as a function of wavelength for subject JH: ρ_s (open circles); multiple-entry measurements, ρ_m(open squares); and Stiles-Crawford effect measurements, ρ_SCE (open triangles). ρ_s decreases markedly with wavelength, whereas ρ_SCE and ρ_m do not change significantly. Error bars represent !1 standard error of the mean.

Despite the parallel behavior of SCE and multiple-entry measurements as a function of retinal eccentricity and wavelength, we found that SCE functions are still broader than multiple-entry functions (ρ_SCE is shifted toward lower values). Such a discrepancy cannot be explained by our model. Chen and Makous³⁰ suggested cross-talk (light escaping one cone and being absorbed in adjacent cones) as a potential reason for the broadening of the SCE with respect to the acceptance angle of a single cone. However, as it has been pointed out^{14, 30}, cross-talk is more likely at the foveal center where the cones are more tightly packed than at 2 deg, where the cone coverage is smaller. From Gorrand and Delori's model²¹ differences could arise also from differences between the angular dependence of the absorption and emission of light by the photoreceptors. Finally, as demonstrated in the previous subsection, cone-photoreceptor disarray seems a negligible factor. Also, it should contribute to a broadening of both SCE and multiple-entry measurements.

Estimates of cone spacing

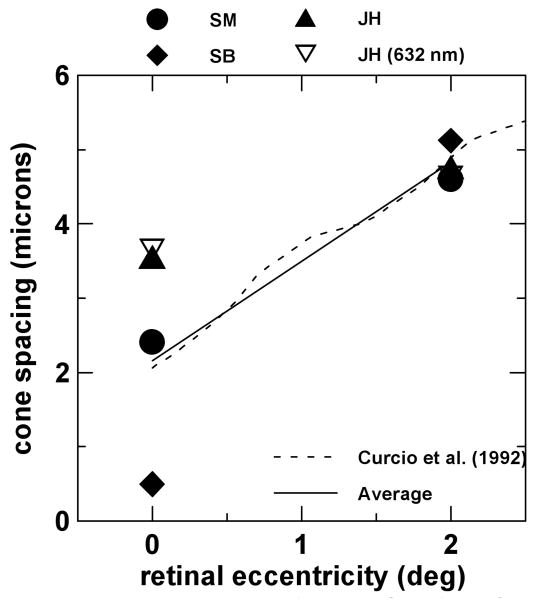
Our model predicts that ρ_s =ρ_wg + ρ_scatt, where ρ_wg is the angular tuning of the cone (assuming no disarray) and ρ_scatt is given by scattering theory¹⁶. Since, assuming no disarray, ρ_m =ρ_wg., the scattering component can be derived combining the two techniques: ρ_scatt =ρ_s-ρ_m. As we mentioned above, the scattering component (ρ_scatt) and row-to-row cone spacing (s) are linked by the following expression¹⁵: $s=k\cdot \text{f}\cdot \lambda \sqrt{{\rho }_{\mathit{scatt}}}$, where k= 1.20753, assuming cone apertures equal to 80% of the cone spacing, f is the axial length of the eye and λ is the wavelength used in the experiments (0.543 μm and 0.632 μm). Figure 6 shows the calculated row-to-row cone spacing as a function of retinal eccentricity for the three subjects. The axial length of the eye was measured for each of the three subjects using A-scan ultrasonography (f= 25.30 mm for SB, f=25.52 mm for SM and f=23.60 mm for JH). Filled symbols represent cone spacing estimates for the three subjects with green light. Open symbols are independent measurements using red light, for JH. The solid line represents an average across our subjects and the dashed line is an average from Curcio et al.'s data³¹, very close to our average data. Note that, as from previous anatomical³¹ and in vivo³² cone spacing estimates, intersubject variability is higher at the foveal center than at 2 deg eccentricity.

Fig. 6.

Derived cone spacing as a function of retinal eccentricity for the three observers. Filled symbols are results using green light and open symbols using red light. Solid line is the average across the three subjects, and the dashed line is the average of Curcio et al.'s³¹ anatomical data.

In its present form, obtaining cone spacing is slower and more indirect than alternative imaging techniques^32,33,34. However, the fact that we obtain consistent estimates of cone spacing provides further support for the waveguide-scattering model, suggesting that more information can be extracted from reflectometric directionality measurements than had been assumed.

Interpretation of other cone directionality techniques using the waveguide-scattering model

While reflectometric techniques used to measure cone directionality are all based on the measurement of light reflected back from the cones with bleached photopigment, the particular design of each approach yields somewhat different rho directionality factors. By taking into account the particular optical configuration and experimental conditions, our model allows us to improve the comparability of the different techniques.

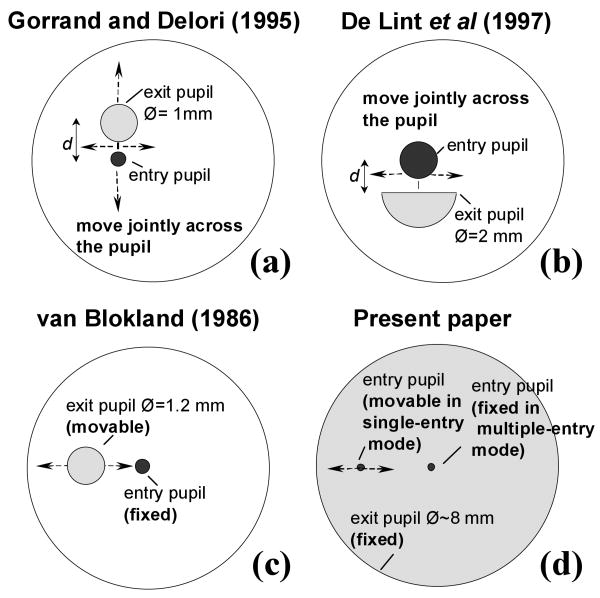
Figure 7 compares the pupil configurations for Gorrand and Delori's¹⁰, de Lint et al.'s¹², van Blockland's⁹ and the single- and multiple-entry techniques presented in the current paper. The sampled retinal area is 1 deg in our measurements as well as in Gorrand and Delori's; 1.5 deg in van Blokland's and 2 deg in de Lint et al.'s³⁵. Wavelengths are also comparable: 543 nm in Gorrands and Delori's and ours; 514 nm in Lint et al.'s and 568 nm in van Blokland's.

Fig. 7.

Entry and exit pupil configurations in different cone directionality reflectometric techniques: (a) Gorrand and Delori's¹⁰; (b) de Lint et al.'s¹²; (c) van Blokland's⁹, and (d) Burns et al.¹³ and present paper.

Gorrand and Delori¹⁰ scanned the exit and entry circular pupils across the eye's pupil. De Lint et al.¹² also used a double scanning configuration, with the exit pupil being a half aperture of bigger radius than Gorrand and Delori's (2 mm instead of 1 mm); however they only scanned across the horizontal axis and measure the intensity distribution at a plane conjugate to the retina instead of in the pupil plane. These two techniques should yield similar rho values (as in fact they do in different sets of subjects). Apart from the difference in the exit pupil sizes and distance between entry and exit pupils, the main difference must arise from the size of the sampled retina: de Lint's et al. averaged over 2 deg, providing higher estimates of rho value³⁵. Compared to our measurements, both approaches represent intermediate conditions between single- and multiple-entry measurements (ignoring the effects of instrumental anisotropy, and design details such as finite size of the sampling exit pupil aperture) the directionality is given by ρ_s +ρ_m. That is, according to our model these two techniques are affected twice by the waveguide properties (owing to the double scanning) as well as by cone spacing. Increasing the exit pupil aperture should decrease rho –with the limiting case being a sampling aperture which fills the dilated pupil at all locations, as we have in our multiple-entry measurements. Van Blokland⁹ scanned the exit pupil with a 1.2 mm pupil aperture while the illumination beam entered the eye through a fixed location. This configuration is equivalent to our single-entry measurements. In our case, we image the pupil all at once, whereas van Blokland obtained sequential measurements along one axis.

Table 2(a) shows simulated rho values derived from the measurements on our subjects (using the rho values of Table 1) for other group's configurations: Gorrand and Delori's¹⁰, de Lint et al¹², and van Blokland⁹. Table 2(b) shows the corresponding rho values reported from these groups^9,10,12. We have used our fitted rhos and translated the maximum intensities to the center of the pupil. In addition, we simulated Gorrand and Delori's technique¹⁰ only for a scan along the horizontal axis instead of scanning the entire pupil. The predictions from the simulations of the results from techniques (Table 2a) agree well with the experimental findings (Table 2b). As expected, the simulations of Gorrand and Delori's measurements¹⁰ are slightly narrower than the simulations for deLint et al.'s measurements¹² (unlike the experimental measurements, which are most likely narrowed by the increase in retinal area) and both sets of data are narrower than our single- and multiple-entry measurements, as well as van Blockland's⁹.

Table 2. (a) Simulated ρ_{Gorrand-Delori}, ρ_{deLint et al} and ρ_vanBlokland (0 and 2 deg) based on results from our experiments (3 subjects and average).

	simulated ρGorrand-Delori		simulated ρdeLint et al		simulated ρvanBlokland
	0 deg	2 deg	0 deg	2 deg	0 deg	2 deg
JH	0.250	0.298	0.229	0.261	0.134	0.189
SM	0.202	0.288	0.187	0.256	0.198	0.176
SB	0.175	0.281	0.165	0.246	0.083	0.182
average	0.209	0.289	0.194	0.254	0.108	0.182
Table 2 (b) Experimental ρ values reported from Gorrand and Delori (1995), deLint et al. (1997) and van Blokland (1986)
	experimental ρGorrand-Delori		experimental ρdeLint et al		experimental ρvan Blokland
	0 deg	2 deg	∼0 deg35	2 deg	0 deg	2 deg
average	0.204	0.279	0.226	not reported	0.103	not measured

Conclusions

From the single- and multiple-entry reflectometric measurements of cone directionality we can conclude the following:

1. Single-entry reflectometric measurements (based on a single image) depend on waveguide properties and scattering from the photoreceptors.

2. Multiple-entry reflectometric measurements (based on a series of images with different pupil entry locations) depend primarily on the waveguide properties of the cones, and thus are fit by broader functions than the single-entry measurements.

3. The differences between single- and multiple-entry measurements cannot be accounted for by photoreceptor disarray.

4. The estimates of cone spacing obtained by applying the model to the two sets of measurements agree well with anatomical data.

5. Multiple-entry reflectometric measurements are more similar to Stiles-Crawford measurements than single-entry reflectometric measurements. They follow similar dependencies with retinal eccentricity and wavelength. However, the Stiles-Crawford functions are still broader than the multiple-entry functions.

6. The waveguide-model can be used to explain differences between estimates of cone directionality obtained with different reflectometric techniques.