“Some,” and possibly all, scalar inferences are not delayed: Evidence for immediate pragmatic enrichment

Abstract

Scalar inferences are commonly generated when a speaker uses a weaker expression rather than a stronger alternative, e.g., John ate some of the apples implies that he did not eat them all. This article describes a visual-world study investigating how and when perceivers compute these inferences. Participants followed spoken instructions containing the scalar quantifier some directing them to interact with one of several referential targets (e.g., Click on the girl who has some of the balloons). Participants fixated on the target compatible with the implicated meaning of some and avoided a competitor compatible with the literal meaning prior to a disambiguating noun. Further, convergence on the target was as fast for some as for the non-scalar quantifiers none and all. These findings indicate that the scalar inference is computed immediately and is not delayed relative to the literal interpretation of some. It is argued that previous demonstrations that scalar inferences increase processing time are not necessarily due to delays in generating the inference itself, but rather arise because integrating the interpretation of the inference with relevant information in the context may require additional time. With sufficient contextual support, processing delays disappear.

INTRODUCTION

The sensorimotor systems involved in producing language have limited informational capacity. Even generous calculations estimate that spoken language carries phonetic information at less than 100 bits per second (Calvert 1992, Pollack & Ficks 1954). Nonetheless, linguistic communication is remarkably efficient. One way in which speakers might overcome limits on channel capacity is by conveying information indirectly via tacit conventions of cooperative communication (Grice 1975, 1989; Levinson 2000). A paradigmatic example is (1):

• (1)Ditte has some of the balloons.

Whereas (1) asserts that Ditte has at least two balloons, its utterance typically implies that Ditte does not have all of the balloons. The assertion is not dependent on context, but the implied (or pragmatic) content is. As a result, the pragmatic meaning can be canceled by additional linguistic material (2a), while the literal meaning cannot (2b) (Sadock 1978).

• (2a)Ditte has some of the balloons. In fact, she has all of them.
• (2b)*Ditte has some of the balloons. In fact, she has none of them.

The “not-all” interpretation associated with (1) is a scalar inference. Scalar inferences occur along multiple semantic dimensions, including number, logical relations, frequency, and epistemic status, and can be triggered by different types of syntactic constituents, including quantifiers, adjectives, adverbials, modals, verbs, and nouns (Hirschberg 1985; Horn 1972, 1989). They arise when a speaker produces a less specific (hence less informative) expression than a salient alternative. This follows from a convention that speakers should make the strongest statement compatible with their knowledge (Grice 1975, 1989). All is stronger than some in contexts like (1) because some can be uttered truthfully in any situation in which all is true, but it is not the case that all is true in every situation where some is true. This asymmetric entailment permits one to view these quantifiers as elements of a scale (<some, many, most, all>) (Horn 1972). A speaker who uses a weaker expression on the scale signals she was not in a position to use a stronger expression, which implies that the corresponding stronger statement is false. Thus uttering (1) implies (1a).¹

• (1a)It is not the case that Ditte has all of the balloons.

The foregoing provides a normative account of the contextual triggers and linguistic environments in which scalar inferences emerge (Geurts 2009; Horn 1989; Russell 2006; Sauerland 2004; but see Chierchia 2004, 2006; Chierchia, Fox & Spector in press), but does not address how and when perceivers compute these inferences as an utterance unfolds. Recent investigations into this process have centered on two related but logically independent questions. The first is the extent to which the computation of the scalar inference is dependent on the conversational context. At one extreme lies the defaultist view, which holds that scalar inferences are automatically triggered upon encountering scalar expressions. From the standpoint of computational efficiency, this could explain the seeming speed and automaticity with which scalar interpretations arise. Levinson argues that a default mechanism would obviate “too much calculation of the speakers’ intentions, encyclopedic knowledge of the domain being talked about, or calculations of others’ mental processes” (2000 p.4). The defaultist view predicts that scalar inferences would initially be computed mandatorily, though they might later be rescinded in cases like (2a) where they are incompatible with the context.

Alternatively, computing scalar inferences may be influenced by various aspects of the context. Relevance Theorists adopt a particularly strong contextualist position (Carston 1998, Sperber & Wilson 1995). This account claims that all pragmatic content, and much semantic content, is inherently underspecified and must be actively constructed according to the exigencies of the immediate context. On this view scalar inferences would arise only when licensed in a given context (Noveck & Sperber 2007).

Several recent results support a contextually flexible inferencing mechanism. Breheny, Katsos and Williams (2006, Experiments 1 & 3) found that individuals took longer to read scalar expressions when preceding contexts supported a pragmatically enriched compared to a literal interpretation. If the enriched meaning had been computed by default, then the opposite pattern should have been observed: there should have been a cost for rescinding the inference in the literal-supporting contexts. Similar results were found by Bott and Noveck (2004, see also Noveck & Prasada 2003, Rips 1975), who had participants judge the truth of under-informative sentences such as Some elephants have trunks. In their Experiment 3, mean response times were over 600ms slower and significantly more error-prone when subjects were encouraged to interpret some pragmatically as “some but not all” rather than literally as “some and possibly all.” Moreover, when participants were required to respond within either 900ms or 3s after the sentence ended (Experiment 4), the rate of literal interpretations was reliably higher in the shorter response condition. The opposite pattern would be predicted by the defaultist position. Namely, there should have been more time and error associated with rescinding the inference in the literal condition. These results thus indicate that scalar inferencing is somewhat dependent on the context.

The present study addresses a second question that has been the focus of recent inquiry: When do scalar interpretations arise relative to literal content? One possibility is that perceivers initially decode the literal or context-independent meaning of the triggering expression in order to determine whether the inference should be generated (Huang & Snedeker 2009). Analogous claims have made for initial activation of context-independent features of words prior to emergent features in modifier-noun conceptual combinations (Swinney, Love, Walenski & Smith 2007). The basic claim is that recognition of an encoded meaning makes available its core sense or features (literal or logical some), with the scalar inference arising later when the word is integrated into context. This sort of psychological mechanism is a direct translation of the prevailing Gricean explanation for the inference, whereby the semantic content of what is said feeds into pragmatic reasoning about what was meant.

It is important to stress that the timing of the scalar inference is independent of its contextual dependency. On the one hand, it is logically possible that the inferential interpretation arises by default, but that it takes time for this interpretation to become sufficiently activated to influence behavior (see Horn 2006 and Huang & Snedeker 2009 for similar suggestions). On the other hand, there are at least two context sensitive mechanisms of inferencing that predict the pragmatic meaning will be available immediately. One is that scalar expressions are systematically ambiguous between literal and enriched meanings (Chierchia 2006; Chierchia et al in press). Candidate meanings of ambiguous lexical items are activated in parallel (Swinney 1979; Tanenhaus, Leiman, Seidenberg 1979), which would provide immediate access to both interpretations. A second, more radical, possibility assumes that context immediately interacts with, or even directs, interpretation of an expression. This is similar to the non-modular interaction that has been proposed to exist between context and incremental syntactic interpretation (Chambers, Magnuson & Tanenhaus 2004; Grodner, Gibson & Watson 2005).

The extra time taken to read and verify pragmatically enriched meanings provides prima facie support for the view that the inference arrives after the literal interpretation. However, because reading and verification provide indirect indications of the actual interpretation than an individual entertains moment-by-moment during incremental processing, they do not settle the question of when the pragmatic and literal interpretations arise. Reading times, for instance, are influenced by many factors including the complexity of the discourse model associated with an interpretation (Grodner et al. 2005; Murphy 1985; Ni, Crain & Schankweiler 2002). The pragmatic reading of some A are B evokes both a referent set (those A that are B) and a complement set (those A that are not B). The discourse associated with the literal interpretation is simpler because it contains only the referent set. Though, the longer reading times Breheny et al. found in the pragmatic supporting conditions could have been caused by a late-arriving inference, they could also reflect the additional work of constructing the more complex discourse associated with a pragmatic inference. Thus, even if the inference arrived immediately, it could have led to elevated reading times

Likewise, verification requires not just computing a given meaning from the input, but evaluating the truth of that meaning. The delay for pragmatic verification in Bott and Noveck’s task may have arisen because evaluating the literal meanings was easier than evaluating the pragmatic meaning. Note that judging the truth of either interpretation of Some elephants are mammals requires searching long-term memory to establish whether there is overlap between the set of elephants and the set of mammals. However, establishing the falsity of the pragmatic interpretation further requires seeking, and failing to find, a subset of elephants that are not mammals. This additional step is potentially time consuming. Thus complexity differences in evaluating the truth of the pragmatic and literal interpretations may have obscured the relative timing of the inference.

Huang and Snedeker (2009) conducted the most direct investigation of the timing of the scalar inference associated with some. In an ingenious study using the visual-world eye-tracking paradigm (Cooper 1974, Tanenhaus, Spivey-Knowlton, Eberhard & Sedivy 1995), they found striking support for delayed inference. Participants viewed a display with four quadrants. In a typical trial the two left quadrants each contained a picture of a boy: one with two socks and one with nothing. The two right quadrants each contained a girl: one with two socks (pragmatic target) and one with three soccer balls (literal target). Participants were asked to Point to the girl with some of the socks.

If the literal interpretation is computed prior to the inference, then, upon hearing some of, participants should initially fixate both the literal and pragmatic targets equally because both are consistent with the literal interpretation. If, however, the inference is immediate, then the literal target should be rejected as soon as some of is recognized, resulting in rapid fixation of the pragmatic target.² Huang and Snedeker’s results strongly indicated that the literal interpretation was computed first. Participants did not favor the pragmatic target prior to the noun’s phonetic point of disambiguation (POD; e.g., -ks of socks). In fact, target identification did not occur until 1000–1200ms after the quantifier onset. In contrast, participants converged on the correct referent 200–400ms after the quantifier, and well before POD, for commands containing non-scalar all (e.g., Point to the girl with all of the soccer balls) and commands using number (e.g., Point to the girl with two/three of the soccer balls). The authors concluded that “even the most robust pragmatic inferences take additional time to compute.” (p. 33)

Huang and Snedecker’s results demonstrate that under some conditions referent identification for pragmatic some is delayed relative to all. However, there are several aspects of the study that might have conspired against finding earlier effects of the inference. First, some in this context is not unambiguously associated with a scalar inference, especially when fully articulated. Intuition suggests that Click on the girl with some socks does not imply that other socks are in the discourse as strongly as Click on the girl with some of the socks does.³ Indeed in a recent study, Judith Degen and her colleagues (Degen, Reeder, Carbary & Tanenhaus 2009) provided empirical evidence for a difference between some and some of. They measured verification times using a “gumball” paradigm in which the top chamber of a two-chamber virtual gumball machine began with 13 gumballs. The screen then turned blank, there was a “kachunk” sound, and between 0 and 13 of the gumballs appeared in the lower chamber, with the remainder in the upper chamber. Participants verified descriptions, such as You got some of/some/all/none of/ or X gumballs, where X was a number. Crucially, when the lower chamber contained all of the gumballs, participants nearly always responded “yes” to you got some gumballs, but often responded “no” when the description was you got some of the gumballs. This raises the possibility that in the Huang and Snedeker studies convergence on the pragmatic target for some of might be delayed until after identification of the partitive construction at of. This could have resulted in a delay relative to all of, two of, and three of, for which the quantifier was sufficient to disambiguate the target on its own.

Second, in the Huang and Snedecker studies commands containing exact numbers were used more often than some of. Degen et al.’s work also suggests that using some of with small countable quantities, which are within the subitizing range, and thus rapidly accessed and verified is dispreferred to exact number. If so, the frequent use of exact numbers may have reduced the acceptability of some of. Finally, participants might have had a bias to initially look at the picture with the most objects. This is consistent with recent models of human visual attention, which indicate that the visual system employs bottom up and top down scene characteristics to direct fixations to regions with the highest probability of containing objects (Kanan, Tong, Zhang & Cottrell in press). These models predict that entities with more objects would attract more fixations and increase the time it takes to make a saccade to an area with fewer objects.

The present experiment exploits the referent identification method of Huang and Snedeker in the visual world paradigm, modifying the design and materials to reduce the effects of the aforementioned factors. We provide evidence that scalar interpretations can emerge without delay relative to literal interpretations of similar quantifiers, and indeed during the earliest moments of interpretation. Below we present the experiment and its findings. We then present survey evidence to further elucidate which differences between our study and previous work are most likely responsible for the disparate timing of scalar effects in our study compared to Huang and Snedeker. In addition to finding a set of boundary conditions under which scalar inferences can be observed without delay, this work supports Degen et al.’s conclusion that inferential effects are strongly influenced by the form of the triggering expression, and further suggests that inferential effects are influenced by the salience of relevant alternative expressions.

EXPERIMENT

To examine whether the scalar inference is universally delayed, Huang and Snedeker’s basic design was modified in five ways. First, we replaced some of with summa. Listeners use the duration of the first syllable to distinguish between monosyllabic and polysyllabic words as a vowel unfolds (Salverda, Dahan & McQueen 2003; Salverda, Dahan, Tanenhaus, Crosswhite, Masharov, McDonough 2007; Magnuson, Dixon, Tanenhaus & Aslin 2007). Therefore a shortened first syllable provides an earlier phonetic signal for the partitive, making the timing more comparable to literal controls. Second, we did not use any instructions with exact number. Third, each trial began with a prerecorded statement that described the types and quantity of objects in the display (e.g., There are four balls, four planets, and four balloons) in order to draw attention to the total cardinality of each type of item. This was to enhance the salience of the full set of each object type as a means of identifying a referential candidate. This potentially makes the contrast between full sets and subsets more prominent and could thus facilitate the comparison of alternatives that leads to the scalar inference. Fourth, we included a Nunna condition, as well as Alla, as literal controls. Fifth, we included a Late-Summa condition, in which two characters had some, but not all, of different sets of objects in the display. This provided a baseline for the time course of fixations to a pragmatic-some target when the scalar inference alone is insufficient to disambiguate. If pragmatic some is delayed under these conditions, it would provide strong support for the generality of the claim that computation of a scalar inference is delayed relative to retrieval of a core meaning. If instead, these conditions yield evidence that the inference is not delayed, it would indicate that computing the pragmatic interpretation need not involve initially computing the literal interpretation.

METHOD

Participants

Twenty-five members of the University of Rochester community, who were naive with respect to the goals of the experiment, were paid participants. Each was a native speaker of English and had normal or corrected-to-normal vision.

Materials and Design

For each trial, participants saw six cartoon figures, three males and three females, surrounding a collection of at least three groups of objects. Two of the object types were phonological cohorts (e.g., balls and balloons). A prerecorded statement described the types and quantity of objects (e.g., There are four balls, four planets, and four balloons) in order to draw attention to the total cardinality of each type of item. This also served to ensure that participants knew the identity and names for each object type. Four seconds after the description began, the objects were distributed among the individuals. For the Early-Summa, Alla, and Nunna conditions, displays were configured as in Figure 1a. One individual had all tokens of one cohort (e.g., all four balloons); another same-gender individual had a proper subset of the other cohort (e.g., two of four balls); the third same-gender competitor had no items. These were designated the Alla, Early-Summa, and Nunna targets, respectively. After 2.5 seconds, a dot appeared in the center of the display, which participants clicked to hear instructions. Instructions corresponding to Figure 1a are given in (3).

• (3)Click on the girl who has…

    Early-summa:   …summa the balls.

    Alla:        …alla the balloons.

    Nunna:     …nunna the items.

Figure 1.

The displays for (A) the Early-Summa, Alla, and Nunna conditions, and (B) the Late-Summa condition

For the Late-Summa condition, the instruction was identical to Early-Summa, but displays were configured as in Figure 1b: two individuals of the target gender each had a proper subset of one cohort; the third had all tokens of a non-cohort object. Therefore, the correct target among the candidates with some but not all of an item remained unidentifiable until POD.

We constructed 32 stimulus items. Test stimuli were separated into four lists, where each condition was equally represented, and each item appeared once. Across lists, each item appeared in each condition an equal number of times. Test stimuli were presented in random order and intermixed with 40 fillers, designed so that throughout the experiment, all six individual types in a display were equally likely to be a target, and each quantifier was equally likely to designate a member of the target or opposite gender. The distribution of objects in the fillers was like the early and late-summa target displays, but a member of the opposite gender was identified (the boys in Figure 1). This was so the perceiver could not predict beforehand which of the six individuals was the correct target. Fourteen fillers contained alla, eight nunna, and eight summa. An additional ten items used the definite determiner “the” to refer to a target with a proper subset of objects.

For the main eye-tracking experiment, commands were recorded with the nuclear accent on the sentence-final noun, and secondary (H*) prominence on the quantifier. Care was taken to insure that the quantifier did not receive contrastive stress. To ensure this, the commands were coded according to the ToBI system (Silverman, Beckman, Pitrelli, Ostendorf, Wightman, Price, Pierrehumbert & Hirschberg 1991). Ninety-three of the 96 stimulus quantifiers received H* accenting; three were ambiguous between H* and L+H*. The lengths of critical regions are reported in Table 1. Two-tailed comparisons between the Alla and Summa conditions revealed that the interval between the onset of the quantifier and noun was marginally shorter for the Alla commands (F(1,31)=3.1, p=.09) as was the interval between the noun onset and POD (F(1,31)=2.9, p=.10). Thus, if anything, the identifying acoustic information was delivered earlier in the Alla condition.

Table 1.

Duration (in ms) of critical speech regions. Standard errors in parentheses.

Condition	Quantifier to Noun Onset	Noun Onset to Disambiguation
Summa	348 (5.4)	257 (14.8)
Alla	338 (5.1)	230 (13.6)
Nunna	418 (2.8)	N/A

To determine whether the quantifier + partitive region of our items was phonetically reduced, we compared our auditory stimuli to those used by Huang and Snedeker. Three research assistants who were naïve to the hypotheses being tested hand coded the length of the interval from quantifier onset to determiner onset. Their judgments were highly correlated (all rs>.89, all ps < .0001). Quantifier lengths are given in Table 2. Both summa and alla were reliably shorter in our stimuli (summa: F(1,46)=141.2, MSE=.5, p < .001; alla: F(1,46)=173.9, MSE=.4, p<.001). To be sure that this was due to selective reduction of the quantifier, and not merely a faster speaking rate in the present study, the duration of this segment was normalized by dividing it by the interval length from the onset of the verb to the onset of the determiner. This region was chosen because it contained an equivalent number of syllables for all stimuli. Even as a proportion, the quantifier was reliably reduced in our items (summa: F(1,46)=122.6, MSE=.006, p < .001; alla: F(1,46)=168.1, MSE=.006, p<.001). If the reduction of the first syllable was sufficient to identify the partitive in the present items, but not in Huang and Snedeker’s items, then the phonetic cue to the presence of the partitive construction would have been postponed from the onset of the quantifier until the onset of the vowel in of. This corresponds to a mean delay of 226ms (SD=32ms).

Table 2.

Duration (in ms) between quantifier onset to determiner onset and for critical stimuli for this study and Huang and Snedeker. Standard errors in parentheses.

Condition	Present Study	Huang and Snedeker
Summa/Some of	243(33)	328(78)
Alla/All of	183(39)	267(39)

APPARATUS AND PROCEDURE

Eye-movements were monitored using an Eyelink II head-mounted eye-tracker from SR Research. Fixations were sampled every 4ms and binned into 20ms windows for analysis. Stimuli were presented on a PC running the ExBuilder software package (Longhurst, 2006). Participants completed three practice trials, were given the opportunity to ask questions about the procedure, and then completed the main experiment. Participant responses were recorded via mouse-click.

RESULTS AND DISCUSSION

We excluded one participant whose mean response times were more than one standard deviation greater than the next-slowest participant’s. We also excluded trials where participants selected the wrong target (.9%) and trials with response times slower than three standard deviations from the grand mean (1.2%). To establish when the correct referent was identified, we calculated the proportion of fixations to the target over the combined fixations to the target and the Alla-competitor (For the Alla condition, the denominator included fixations to the Summa target.). For Early-Summa, this provides a direct measure of when the pragmatic interpretation is sufficiently active to drive fixations to the correct target: an increase in the ratio reflects a selective increase in looks to the pragmatic-some target.

Figure 2 depicts target proportions and Figure 3 depicts fixations to each same gender competitor for each of the critical conditions. For the first set of analyses, target proportions were calculated for three windows: (1) from 400ms before the quantifier until quantifier onset (gender interval); (2) from the onset of the quantifier until POD (quantifier interval) and (3) from 400ms after POD (post-disambiguation interval). Analysis intervals were offset by 200ms to accommodate the time required for planning and launching a saccade (Matin, Shao & Boff 1993). The central question addressed in these analyses was whether target proportions would be above chance for each condition in the region after the quantifier but before phonetic disambiguation of the noun.

Figure 2.

Fixations to the target as a proportion of combined fixations to the target and critical competitor. For Alla, the competitor was the Summa target. For the other conditions the competitor was the Alla target. The top panel depicts target proportions over the gender interval, the quantifier interval, and the post-disambiguation interval. The lower panel depicts target proportions over each 100ms window from the beginning of the quantifier.

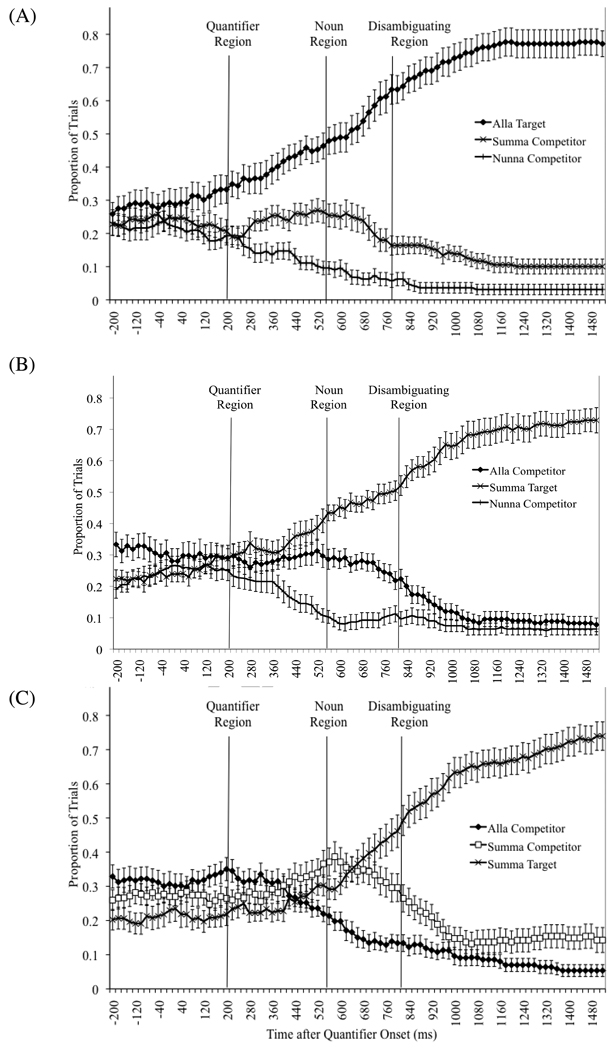
Figure 3.

The proportion of trials for which each correct gender competitor was fixated for each 20ms window after quantifier onset for the (A) Alla, (B) Early-Summa, and (C) Late-Summa conditions. Region indicators occur 200ms after the corresponding phonetic cue.

To establish the region where target identification occurred for each condition, target proportions were compared to chance (50%) over the gender, quantifier, and post-disambiguation intervals.⁴ No conditions were reliably above chance in the gender interval. However, the Alla condition was numerically above chance. This likely reflects a bias to look at the target with the most objects. This trend was visible in all conditions prior to the quantifier (Figure 3), and is consistent with patterns reported in all three Huang and Snedeker experiments (2009). Correspondingly, fixations to targets in the Late-Summa and Nunna conditions were reliably below chance (Late-Summa: F1(1,23)=7.91, MSE=.15, p<.01; F2(1,31)=8.8, MSE=.20, p <.01; Nunna: F1(1,23)=6.95, MSE=.18, p<.05; F2(1,31)=4.75, MSE=.57, p <.05). In the quantifier interval, target-proportions for all conditions were reliably above chance (Early-Summa: F1(1,23)=8.9, MSE=.07, p<.01; F2(1,31)=5.15, MSE=.19, p <.05; Late-Summa: F1(1,23)=3.33, MSE=.20, p<.05; F2(1,31)=3.9, MSE=.31, p <.05; Alla: F1(1,23)=11.53, MSE=.25, p<.01; F2(1,31)=16.86, MSE=.21, p <.001; Nunna: F1(1,23)=39.28, MSE=.12, p<.001; F2(1,31)=45.69, MSE=.15, p <.001). Note that target proportions in the quantifier interval for Late-Summa were numerically slightly lower than for Early-Summa. This is expected because participants’ fixations were divided between the two targets consistent with pragmatic-some; however, the target ratio for this analysis only included fixations to the correct target.

To more precisely determine when the pragmatic interpretation emerged, we analyzed each 100ms interval after the onset of the quantifier. Unlike the preceding analyses, intervals were not offset by 200ms. A main effect of condition for the 200ms before the quantifier was significant by items (F2(3,93)=2.81, MSE=.60, p<.05) but not by participants (F1(3,69)=2.15, MSE=.42, p =.10), reflecting more fixations to the Alla target than to Summa and Nunna targets. We compensated for differences in initial looking preference by using this 200ms interval as the baseline rate of target fixations. Target convergence was defined as the first 100ms interval for which the proportion of target fixations exceeded the baseline. For the Alla condition, target proportions were reliably higher than baseline 200–300ms after quantifier onset in the participants analysis (F1(1,23)=5.73, MSE=.12, p < 05), but only marginally reliable by items (F2(1,31)=2.46, MSE=.33, p =.06). For Early-Summa and Nunna, convergence also occurred in the 200–300ms interval (Early-Summa: F1(1,23)=3.13, MSE=.36, p < .05; F2(1,31)=4.46, MSE=.31, p < .05; Nunna: F1(1,23)=5.93, MSE=.09, p < .05; F2(1,31)=6.52, MSE=.24, p < .01). In contrast, convergence was delayed for Late-Summa: it was marginally reliable 400–500ms after the quantifier (F1(1,23)=1.76; MSE=.28, p =.098; F2(1,31)=2.13, MSE=.42, p =.078), and fully reliable in the 500–600ms interval (F1(1,23)=7.75; MSE=.26, p < .01; F2(1,31)=7.6, MSE=.45, p < .01). To summarize, the quantifier generated increased fixations to the target rather than the Alla or Summa competitor 200–300ms after onset for all conditions except Late-Summa, where the target could not be identified based on the quantifier alone.

The Late-Summa condition also provides evidence about the time course of the upper-bounded interpretation. When the pragmatic interpretation is computed, fixations should shift away from the Alla-competitor toward the two individuals that are temporarily consistent with pragmatic-some. Indeed, as can be seen in Figure 3C, Figure 400ms after the onset of the quantifier, fixations to the individual with all of an object (the girl with the hats in Figure 1b) begin to fall, whereas fixations to the two characters with a subset of the objects (the girl with the balls and the girl with the balloons) begin to increase. In order to quantify when the shift away from the Alla-competitor became significant, we computed the ratio of fixations to the Alla-competitor to all three same-gender competitors. The ratio for each 100ms interval after quantifier onset was compared to the 200ms interval preceding the quantifier. Fixations to the Alla-competitor were marginally below baseline in the 400–500ms interval (F1(1,23)=2.2; MSE=.38, p =.08; F2(1,31)=2.6, MSE=.59, p = .06) and fully reliable in the 500–600ms interval (F1(1,23)=8.4; MSE=.44, p <.01; F2(1,31)=8.9, MSE=.68, p < .01).⁵

Though we see target identification for both the critical Early-Summa and Alla conditions occurs 200–300ms after the quantifier, it is possible that convergence was more robust for the Alla conditions. This might have been the case if inferential cues to target identity were weaker or delayed for some proportion of trials relative to literally conveyed cues. To investigate this possibility, we examined whether there was an interval for which target proportions were reliably higher for the Alla condition than the Early-Summa condition after normalizing for target biases revealed during the 200ms interval prior to quantifier onset. Target proportions were submitted to a series of 2 × 2 ANOVAs crossing condition with analysis interval (baseline vs. current). These analyses are summarized in Table 3.

Table 3.

Comparison of Summa-Early and Alla conditions. Each column reports analyses for the 100 ms interval beginning X ms after quantifier onset. X is listed in the column header.

Participants analysis
	0	100	200	300	400	500	600
Main effect of condition (early-summa vs. alla)
F(1,23)	1.89	2.76	2.73	4.68	5.27	3.64	3.29
p	.09	.06	.06	*	*	*	*
Main effect of interval (baseline vs. current)
F(1,23)	1.86	2.02	6.55	5.33	8.82	13.4	38.2
p	.09	.08	*	*	**	**	***
Interaction
F(1,23)	.53	.04	.11	.05	.06	.16	.02
p	.47	.84	.74	.82	.81	.69	.90
Items analysis
Main effect of condition (early-summa vs. alla)
F(1,31)	2.90	4.94	3.87	4.25	4.73	3.61	5.76
p	*	*	*	*	*	*	*
Main effect of interval (baseline vs. current)
F(1,31)	2.65	2.23	9.07	6.06	10.6	14.4	32.5
p	.06	.07	**	*	**	***	***
Interaction
F(1,31)	.60	.07	.10	.11	.06	.32	.06
p	.45	.79	.76	.75	.81	.57	.81

^*p < .05,

^**p < .01,

^***p < .001

Consistent with earlier analyses, target proportions were significantly higher than baseline beginning at 200–300ms. Additionally, the Alla condition induced reliably more fixations to the target. In the items analysis this was present from the earliest analysis interval, in the participants analysis, this trend was not reliable until 300–400ms. Thus, this analysis provides further evidence that the Alla target is visually preferred to the Early-Summa target. Crucially, there was no interaction between interval and condition (all Fs<.6). Therefore there is no indication that the Alla condition evoked earlier or stronger target convergence than the Early-Summa condition when baseline visual biases are taken into account.

The preceding ANOVA analysis does not license us to accept the null hypothesis that target convergence occurred with an identical time-course for the Alla and Early-Summa conditions. Ideally, we would like to establish whether this null hypothesis does a better job of accounting for the data than the hypothesis that target convergence was faster in the Alla condition. To this end, we employed the Bayesian method outlined by Gallistel (2009) for comparing the likelihood of the null hypothesis to a reasonably specified alternative hypothesis. To compensate for visual biases, target convergence was defined as the difference between target proportions during the baseline interval and target proportions during the interval 200–300ms after quantifier onset where convergence was first observed. To license modeling hypotheses using a normal distribution, proportions were submitted to a log odds transform prior to calculating target convergence values. These values were calculated for each subject in the Alla and Early-Summa conditions. We evaluated whether the mean target convergence values for Alla and Early-Summa were the same or whether the mean for the Alla condition was larger for each interval. The method requires determining a plausible range of effect sizes for the alternative hypothesis. At the lower bound, it might be that the there is no difference between target convergence in the Alla and Early-Summa conditions. At the higher bound, the alternative hypothesis might predict target proportions could increase from chance levels in the baseline interval (1/2) to complete convergence on the target for the Alla condition (1, which was converted to .99 in this analysis to avoid division by zero), but zero target convergence for Early-Summa. The maximally vague alternative hypothesis is one in which any effect size in between these bounds is equally likely. Figure 4a depicts the prior probability density functions for the null hypothesis and maximally vague alternative hypothesis. These were derived from the target convergence data from the Early-Summa condition and can be thought of as predictions for the data in the Alla condition. Figure 4a also depicts the likelihood function of the mean derived from the Alla data. The posterior likelihood of each hypothesis given the Alla data can be computed from crossproduct of the prior probability and the likelihood function. The ratio of hypothesis likelihoods reflects the odds that the data supports the hypothesis in the numerator. For the maximally vague alternative hypothesis, the odds in favor of the null hypothesis are 20.74:1. However, this analysis method penalizes vague hypotheses relative to specific ones. Thus it is important to determine the range of possible effect sizes for which the null hypothesis is still favored. Figure 4b plots the odds ratio for alternative hypothesis with effect sizes ranging from an increase in Alla target proportions of 0 to 1/2. Note that there is no range of effect size for which the odds ratio favors the alternative hypothesis. Except for very small effect size ranges, the odds favor the null hypothesis by over 3:1. There is no fixed convention, but some sources suggest regarding odds ratios over this criterion as providing “substantial” support for one hypothesis (Kass & Raftery 1995). Thus the evidence supports the conclusion that the rate of convergence in the two conditions was equivalent.

Figure 4.

Panel A: The prior probability density functions of the null hypothesis and the maximally vague alternative hypothesis along with the likelihood function of the Alla data. The high degree of overlap between the null and likelihood functions indicate that it does a superior job of predicting the data. Panel B: The odds in favor of the null as a function of the upper limit on the possible size of the effect. The dotted line indicates where the odds ratio reverses (from favoring the null to favoring the alternative). For all effect sizes great than zero, the odds ratio favors the null hypothesis.

DISCUSSION

The results demonstrate that the scalar inference associated with pragmatic-some was not delayed relative to expressions that do not require a scalar inference. Most strikingly, effects of the pragmatic interpretation were observed 200–400 ms after the onset of the quantifier. Two hundred ms is the earliest point at which effects on eye-movements are expected from any information made available during word recognition. Moreover, even with simpler displays, signal-driven effects of phonetic information in word recognition typically do not become statistically reliable until nearly 300 ms after word onset (Allopenna, Magnuson & Tanenhaus 1998; Dahan, Magnuson & Tanenhaus 2001; Dahan, Magnuson, Tanenhaus & Hogan 2001). The present study provides the earliest evidence yet observed for a scalar inference. It is logically possible that the lower-bounded literal interpretation preceded the upper-bounded pragmatic interpretation for a period too brief to be observed (0–100ms). This would still be far sooner than either the ∼600ms delay that might be inferred from the difference in verification times to pragmatic and logical some (Bott & Noveck 2004, Experiments 1 & 3; Noveck & Prasada 2003) or the 800–1000ms delay in referent identification observed by Huang and Snedeker (Experiments 1 & 2).

The results of this study are consistent with immediate computation of the inference. It is however, important to address two non-pragmatic explanations for these early effects. One possibility is that participants may have encoded targets with a proper subset of one item type as summa prior to the command because this was the most common label used in the course of the experiment. This strategy would not have been helpful in Huang and Snedeker’s Experiments 1 and 2, because the numerical quantifier two of was used to refer to subset targets as often as some of. We are skeptical of this pre-coding explanation for two reasons. First, in order to develop this strategy participants would have had to learn a co-occurrence pattern between the type of display and the summa instruction during the experiment. If the rapid effects of the pragmatic interpretation were strategic, then target identification should have been weaker in the quantifier region for the early trials of the experiment, before the strategy developed. In fact the average target proportion in the quantifier region was higher in the first half compared to the second half of the experiment (Early-Summa:.603 versus .528; Late-Summa:.561 versus .557). Crucially, Summa conditions were still above chance in the quantifier interval for the first half of the experiment when analyzed on its own. For Early-Summa this difference was significant (F(1,23) = 5.61, MS=.39, p < .05). For Late-Summa it was only a trend (F(1,23)=2.34, MS=.41, p=.07).⁶ Recall, that this measure of target convergence is biased against the Late-Summa condition because it does not take into account looks to the subset competitor, which is consistent with pragmatic some until POD.

Second, predictive-encoding would not have not been an optimal strategy for a large proportion of trials. For ten trials, the subset target was labeled with a simple definite determiner rather than summa (e.g., the girl who has the scissors). Further for half the trials with subset targets, the quantifier was insufficient to identify the target because there was another subset target of the same gender. Third, the complexity and variability of our displays likely discouraged pre-encoding. Though the subset targets were usually picked out with summa, this target was visually variable in that it could have either two or three items. Guessing the appropriate referential label was made still more difficult because targets with three items were as likely to possess all of an object group as a subset of that group. Further, each display consisted of six individuals and three distinct object types distributed in a variety of ways among at least four of them. Each individual was equally likely to be the correct target and five possible determiners were used to quantify the objects associated with the target. This variability was intended to make it difficult to consistently predict the label to be used with each target.

Another non-pragmatic factor that might have influenced this study is that the nouns provided by the speaker occurred at multiple levels of abstraction. In the Nunna condition the speaker always used the noun items, but for all other determiners, the speaker used a more specific basic level term. This may have created some confusion as to what taxonomic level of description the perceiver should anticipate. Though plausible, this taxonomic confusion account cannot explain the present results. Such confusion should have led to delayed target convergence for the Summa and Nunna conditions. In the Summa conditions, the perceiver would have been led to anticipate the superordinate term on some proportion of trials. If so, then the Alla-competitor, who has all of a particular object class, but not all of the items, would have been as compatible with the scalar interpretation as the subset targets. Hence, the noun would be required to disambiguate the target. Similarly, taxonomic confusion would have led the perceiver to sometimes expect a basic level term in the Nunna condition. If so, then every same gender target would have been compatible with the command prior to the noun. In contrast, taxonomic confusion should not have led to a delay for Alla. This is because there was never a target who possessed all of the items in the display. The superordinate term could be ruled out immediately upon hearing the quantifier because a basic level term was always required for successful reference. Note that these predictions are radically different than what was observed. The Summa and Nunna conditions elicited rapid target convergence and were no slower than the Alla condition. Hence, the taxonomic confusion account is at odds with the present results.

Our results clearly differ from those of Huang and Snedeker (2009) and lead to very different conclusions. Without a systematic parametric exploration of potential differences between the two sets of studies, which would require dozens of additional experiments, we cannot conclude which factor or combination of factors account for the differences. If we set aside, the potential impact of including a late POD baseline and a Nunna control, we believe that there are four likely candidates. First, our baseline analyses adjusted for possible perceptual biases to targets with more objects and hence revealed effects that might have been obscured by direct comparison to chance.⁷ This alone cannot account for the different patterns observed by Huang and Snedeker because they observed faster target convergence in response to two of compared to some of, which corresponded to the same targets. However, it might have exaggerated observed rate of convergence differences between the scalar some of and the literal all of and three of controls.

Second, because we used the phonetically reduced form of the partitive construction, the phonetic cue to the partitive occurred over 200ms earlier in our stimuli. If the partitive provides a stronger cue to the scalar inference than the bare quantifier this would account for some of the delay observed by Huang and Snedeker. It is therefore important to verify the intuition that Click on the girl with some of the socks is more likely to engender the not-all inference than Click on the girl with some socks. To this end we conducted a survey to evaluate how natural the partitive and bare quantifier were to pick out a target with all tokens of an item type compared to a subset of a particular item type. If the partitive is more strongly associated with the inference as found by Degen et al. (2009), then it should be a less natural means of identifying an all target. Twenty-four of the critical items in our displays were used for this purpose and presented along with the remainder of our items. Full methodological details and results are provided in Appendix A. Naturalness judgments are depicted in Figure 5.

Figure 5.

Perceived naturalness of command type for picking out targets with a subset of an item type and all of an item type (N=35). Error bars represent one standard error of the mean.

There was a reliable interaction between quantifier type (partitive vs. bare quantifier) and target type (subset vs. all target). Pairwise comparisons confirmed that this arose because the partitive was significantly less natural than the bare quantifier for picking out a target with all of an item type. This demonstrates that upper-bounded reading is more strongly associated with the partitive than with the bare quantifier for these materials, replicating the initial finding reported by Degen et al. (2009).

The third and perhaps most important difference between our study and Huang and Snedeker is that we did not include numbers in our commands. Exact numerals may be favored for picking out cardinalities that can be identified quickly via pre-attentive subitizing processes (Degen et al. 2009). The speaker in Huang and Snedeker (2009) used exact number terms 50% of the time –twice as often as some of. The salience of these preferred alternatives might have reduced the felicity of some of for referring to the upper bounded targets. To investigate this possibility we conducted a second survey to assess the acceptability of the commands used in the present study when no number terms were used compared to when exact number terms were frequently used (for 22.2% of all trials). Survey details are presented in Appendix B. Results are presented in Figure 6.

Figure 6.

Acceptability of critical command types when numbers were absent (N=30) or frequently used in filler trials (N=29)

There are two striking aspects of the results. First, number commands were judged as reliably more natural than some of commands whether number commands were present or not. Second, including numbers marginally reduced the naturalness of some of commands and reliably increased the discrepancy in the naturalness between some of and all of. The relative felicity of some of and all of in the presence and absence of salient number terms, mirrors the different patterns in target identification obtained in the present study compared to Huang and Snedeker (2009).

A fourth difference between the present study and previous work is that the total cardinality of each item type contained in the display was announced at the beginning of each trial. There are two ways that this could have accelerated the emergence of the inference. First, it could have strengthened the inference by increasing the relevance of the full collection of each item type. As a result, when the speaker used a vague term like some, the accessibility of the more restrictive term all would have been enhanced. This might have encouraged listeners to consider why the speaker did not use the more specific term giving rise to the scalar inference. Second, this may have made computing and recognizing subsets easier. Because the participants already knew how many of each item type there were they did not need to search the display to see if a given individual had all of or a subset of the set of each item type.

In sum, there are a number of potential factors that singly or in combination allowed the inference to arise and be observed rapidly. Unearthing the wide range of potential pragmatic influences and the mechanisms by which they operate promises to be an exciting arena of future research. However, we do not believe it is fruitful to parametrically manipulate the many potential confounding variables that separate our work from Huang and Snedeker (2009) in the present paradigm. Rather this work and that of Huang and Snedeker should be viewed as establishing sets of boundary conditions: one set under which the scalar inference is not observable immediately and another set where pragmatic some emerges without delay. Comprehensive understanding of these conditions will likely require research that examines the conditions of use for pragmatic some. This will likely require detailed corpus analyses alongside on-line research that manipulates contextual variables, including the goals of the speaker and listener, that are likely to control the salience and importance of potential inferences. This will demand using situations that go beyond those investigated in the paradigms that we and Huang and Snedeker have used.

CONCLUSION

The current study contributes to the literature in two ways. First and foremost, our on-line results are inconsistent with the hypothesis that that literal content must be computed prior to any pragmatic inferences. This is compatible with models in which pragmatic constraints can affect the earliest moments of interpretation. We propose that when a scalar inference increases processing time, it is because integrating its interpretation with relevant information in the context may require additional time and not because generating the inference itself is time consuming. This would serve to explain the processing delays observed by Bott and Noveck (2004), Breheny et al. (2006) and Huang and Snedeker (2009). Pickering, McElree, Frisson, Chin and Traxler (2006) have made a similar proposal for processing difficulty associated with coercing the aspect of a semantic event.

Second, we have established that the naturalness of pragmatic some is affected by the salience of alternative forms that a speaker has used in the context. It may well be that the structure of the context itself plays a similar role. For example Degen and Tanenhaus (2010) found that when the context makes a potential contrast salient--a gumball machine delivered all, some, or some number of prizes and/or gumballs)--pragmatic some was interpreted as rapidly as all even though the instructions included exact number and the cardinality of the sets were within the subitizing range. This suggests that understanding the role of enabling conditions in a context will be central to understanding both when generalized implicatures are used by speakers and how they are processed by listeners. In particular, we believe that it will be important to better understand the notion of contrast, and well as what aspects of a situation make contrast or potential contrast salient.

APPENDIX A: SURVEY TO ESTABLISH NATURALNESS OF THE PARTITIVE WITH AN ALL TARGET

Participants

Thirty-five native English speakers were recruited from the Swarthmore College community to participate in the present survey. They were paid for their participation.

Materials

Twenty-four of the 32 critical stimuli from the eye-tracking experiment were assigned to be critical stimuli in this study. Half of these used the Late-Summa display and half used the Early-Summa display. The design was 2 × 2 crossing quantifier type (some of vs. some) with target type (a target with all of an item vs. a target with a subset of an item). Four versions of each item were created (one for each cell in the design). Four presentation lists were created according to a balanced Latin square design so that both participants and items were potential random variables using repeated measures tests. The fillers for this study were identical to the fillers for the main study with the addition of the eight unused critical stimuli. For these filler items the command contained all of and picked out an all target. Half of them used a Late-Summa display, and half used an Early-Summa display. A pseudorandom presentation order was created. Each participant saw only one list presented in that order or the reverse.

Procedure and Apparatus

Data were collected using an online survey administered with the open source Lime Survey package v1.80 (www.limesurvey.org). Participants were asked to judge how natural a command was for identifying a single individual in a display. For each item, a written description of the number and types of objects in the display was presented above a picture of the display. Underneath the display the critical command was presented. Beneath that was the following prompt: “How naturally does this command identify a particular individual? (7 is the most natural fit, 1 is the least).” Beneath this was a series of radial buttons labeled 1–7. Participants were given instructions, two example items, and then completed the survey.

RESULTS

One item was omitted from analyses because its display failed to load due to a typographical error. The means for each condition are reported in Figure 4. There were no reliable effects or interactions with list or order (Fs<1) so these variables are omitted from the analyses below. The judgment data were subjected to a 2 × 2 ANOVA. There was a reliable interaction between quantifier type (partitive vs. bare quantifier) and target type (subset vs. all target) (F1(1,34)=20.4, MSE=.32, p < .001; F2(1,23)=23.9, MSE=.21, p < .001). In addition there was a main effect of quantifier type because the partitive was judged less natural than the bare quantifier (F1(1,34)=12.6, MSE=.45, p <.01; F2(1,22)=15.8, MSE=.25, p < .001), and a main effect of target type because all-targets were less natural than subset-targets (F1(1,34)=36, MSE=1.9, p <.001; F2(1,22)=215.4, MSE=.2, p < .001). Pairwise comparisons confirmed that the interaction arose because the partitive was rated significantly less natural than the bare quantifier for picking out a target with all of an item type (F1(1,34)=18.3, MSE=.66, p < .001; F2(1,23)=37.7, MSE=.23, p < .001). Thus the upper-bounded reading is more strongly associated with the partitive than the bare quantifier. Notably, identifying the all target with a partitive was the only mapping that was not reliably judged as more natural than the midpoint of our seven-point scale. Indeed, in the participants analysis, this condition was reliably below the midpoint.

Both quantifier types were judged as reliably less natural referring to an all-target compared to a subset-target (partitive: F1(1,34)=47.4, MSE=1.2, p <.001; F2(1,22)=538.9, MSE=.07, p< .001; bare: F1(1,34)=15.4, MSE=.99, p <.001; F2(1,22)=27.2, MSE=.33, p< .001). This may indicate that the scalar inference was triggered as strongly by the bare quantifier as it was for the partitive. However this explanation is confounded with another factor –the fact that all of was frequently used to pick out an all-target (sixteen times across both fillers and stimuli). All of items were judged as more natural than any of the other commands to pick out an all-target (mean=6.3, SE=.15, all Fs>32, ps< .001). The salient availability of this preferred label might have decreased the naturalness of identifying an all target with either some or some of. Thus, on the basis of the present data it is not possible to tell whether some was weakly associated with the scalar inference on its own. We can, however, conclude that the scalar inference is more strongly associated with the partitive than the bare quantiifer.

APPENDIX B: SURVEY TO DETERMINE WHETHER THE PRESENCE OF NUMBERS ALTERS FELICITY OF SCALAR QUANTIFIERS

Participants

Fifty-nine native English speakers were recruited from the Swarthmore College community to participate in the present survey. They were either paid or received course credit for their participation.

Materials

Participants were divided into two groups. One group judged the acceptability of the commands for the critical displays that were used in the main eye-tracking experiment. The second group judged these items when a subset of the fillers and some of the critical items contained numbers in the commands. Eight critical items and eight fillers were assigned commands containing numbers. Half of these commands picked out subset targets with two items and half with three items. Thus for the numbers group, the quantifier some of was equally likely to pick out a subset target as two of or three of. To minimize differences with the main experiment, the same four presentation lists were used in this study. All lists were presented in the same pseudorandom order.

Procedure and Apparatus

The procedure was the same as the previous survey.

RESULTS

The means for critical conditions are given in Figure 5. Two analyses were conducted. The first analysis was to establish whether number terms were preferred to some of for picking out subsets. This pattern turned out to be reliable both when responses to the number commands were compared to responses to some of in the numbers present condition (F1(1,28)=38.8, MSE=.30 p < .001; F2(1,70)=39, MSE=.33, p < .001), and when compared to some of in the numbers absent condition (F1(1,57)=4.4, MSE=1.2, p < .05; F2(1,70)=23.1, MSE=.25, p < .001).

To examine whether the presence of numbers affected judgments in the other conditions, A 2 × 3 ANOVA crossing quantifier type (some of, all of, none of) with the presence of number commands (present vs. absent) was conducted. This revealed a main effect of quantifier (F1(2,114)=37.3, MSE=.51, p < .001; F2(2,62)=120.9, MSE=.17, p < .001) but not of the presence of number commands (F1(1,57)=.15, MSE=2.5, p=.7; F2(1,31)=6.7, MSE=.10, p<05). There was, however a reliable interaction between numbers commands and quantifier type F1(2,114)=3.6, MSE=.51, p < 05; F2(2,62)=5.4, MSE=.35, p <.01). The interaction resulted because the presence of numbers marginally decreased the acceptability of some of (F1(1,57)=1.84, MSE=1.5, p = .09; F2(1,31)=6.1, MSE=.3, p < .01), but marginally increased the acceptability of none of (F1(1,57)=1.7, MSE=1.1, p = .10; F2(1,31)=14.9, MSE=.15, p < .001) and numerically increased the acceptability all of (F1(1,57)=1.17, MSE=.79, p=.14; F2(1,31)=4.8, MSE=.22, p < .05). Even when the none of conditions were excluded from this analysis, including numbers reliably increased the discrepancy in the naturalness between just the some of and all of conditions (F1(1,57)=4.05, MSE=.52, p < .05; F2(1,31)=4.01, MSE=.52, p = .05).