Abstract
In a series of experiments, Semal and Demany [(2006). J. Acoust. Soc. Am. 120, 3907–3915] demonstrated that some normally hearing listeners are unable to determine the direction of small but detectable differences in frequency between pure tones. Unlike studies demonstrating similar effects in patients with brain damage, the authors used stimuli in which the standard frequency of the tones was highly uncertain (roved) over trials. In Experiment 1, listeners were identified as insensitive to the direction of pitch changes using stimuli with frequency roving. When listeners were retested using stimuli without roving in Experiment 2, impairments in pitch-direction identification were generally much less profound. In Experiment 3, frequency-roving range had a systematic effect on listeners’ thresholds, and impairments in pitch-direction identification tended to occur only when the roving range was widest. In Experiment 4, the influence of frequency roving was similar for continuous frequency changes as for discrete changes. Possible explanations for the influence of roving on listeners’ insensitivity to pitch-change direction are discussed.
INTRODUCTION
In the classic experiments measuring difference limens for frequency (DLFs; e.g., Harris, 1952a, 1952b , Moore, 1973, 1974, Nordmark, 1968, and Wier et al. 1977), listeners were presented with two successive pure tones on each trial. These tones differed slightly in frequency, and listeners indicated which tone had the higher frequency, or whether the second tone was higher or lower than the first. It is reasonable to assume that successful performance in these kinds of experiments is achieved through the percept of a difference in pitch, usually defined as “that attribute of auditory sensation in terms of which sounds may be ordered on a scale extending from low to high” (ANSI, 1994).
The DLFs measured in these experiments can be remarkably small. For instance, in Moore’s (1974) study, the mean DLF across three listeners for 200-ms tones at a test frequency of 1000 Hz was 1.8 Hz—a frequency difference of less than 0.2%. Clearly these experiments require listeners to be—and indeed demonstrate that they often are—sensitive to the direction or sign of very small frequency changes. However, three more recent studies have suggested that in certain circumstances some listeners can detect the presence of a small frequency difference, but are unable to identify the direction of the resulting percept (Johnsrude et al., 2000; Tramo et al., 2002; Semal and Demany, 2006).
Two of the studies cited above involved listeners with cortical lesions. Johnsrude et al. (2000) tested patients with unilateral temporal lobe excisions and healthy controls using two frequency discrimination tasks: a two-interval, two-alternative forced-choice (2I-2AFC) task similar to those used in classic studies of frequency discrimination, and a same-different (SD) task in which the second tone was equiprobably identical to or higher in frequency than the first tone. For the 2I-2AFC task, which required listeners to be sensitive to the direction of frequency changes, they found that a group of patients with right-hemisphere lesions that encroached Heschl’s gyrus had much larger DLFs than the other groups of patients and controls. In contrast, the DLFs measured using the SD task, which did not require listeners to be sensitive to frequency change direction, were not elevated for any patient group compared to controls. Similarly, Tramo et al. (2002) reported that a single patient with lesions including bilateral Heschl’s gyri had much larger DLFs in a 2I-2AFC task than in an SD task. These findings have been interpreted as indicating that successfully identifying the direction of frequency changes recruits cortical networks that are not necessary for simply detecting frequency differences (Foxton et al., 2009).
Semal and Demany (2006) used a dual-pair paradigm to measure DLFs for frequency-change detection and frequency-direction identification for the same listeners under directly comparable stimulus conditions. In their main experiment, listeners heard two pairs of pure tones on each trial. In one pair the tones were identical, and in the other pair the tones differed in frequency. In the “detection” task, listeners indicated which pair (first or second) contained the change in frequency. In the “identification” task, listeners indicated the direction (up or down) of the change. For three of their listeners, identification DLF (IDLF) was considerably larger than detection DLF (DDLF). Follow-up experiments showed that the discrepancy between detection and identification abilities observed for frequency in these listeners did not generalize to other sound dimensions (level or the rate of amplitude modulation), and remained even after extensive practice in both tasks.
What makes Semal and Demany’s (2006) findings particularly intriguing is that their listeners, unlike those in the studies of Johnsrude et al. (2000) and Tramo et al. (2002), appeared to be audiologically and neurologically normal. The elevation in IDLFs—though similar in magnitude to that observed by Johnsrude et al.—was not symptomatic of any obvious real-world hearing problems, such as congenital amusia (Peretz et al., 2003). An important difference between Semal and Demany’s study and those involving clinical patients is that the former employed frequency roving—on each trial, the frequencies of the first tones in each pair were randomly varied over a wide range (400–2400 Hz). This raises the question of whether the specific deficit observed for some of Semal and Demany’s listeners would also occur under conditions in which the stimuli are not roved in frequency over a wide range.
A number of previous studies have demonstrated that frequency roving is deleterious to normally hearing listeners’ sensitivity to frequency differences (Amitay et al., 2005; Demany and Semal, 2005; Harris, 1952a; Jesteadt and Bilger, 1974). For instance, Jesteadt and Bilger measured discriminability (d′) for frequency differences between pure tones using a 2I-2AFC task and several variants of the SD task for four listeners. The standard frequency of the tones within a run of trials was either fixed, “jittered” (varied randomly over a 40-Hz range), or roved (varied randomly over a 465-Hz range). For their listeners—who had no apparent difficulty in identifying frequency-change direction1—roving resulted in smaller d′ than for the fixed and jittered conditions.
Amitay et al. (2005) measured DLFs using a 2I-2AFC task for three groups of listeners. The groups differed in the training they received: the first was trained using stimuli in which the standard frequency was fixed; the second with stimuli roved over a 200-Hz range; and the third with stimuli roved over a 1580-Hz range. Large individual differences in DLFs were found initially within all three groups. For the fixed-stimuli group, the individual differences were considerably reduced by training. In contrast, the individual differences within the roving-stimuli groups remained pronounced after extensive training, and both groups had larger DLFs on average than the fixed-stimuli group2. These results suggest that frequency roving increases DLFs overall, but to different extents for different listeners. Since Amitay et al. only measured DLFs using a 2I-2AFC task, and DLFs with and without roving were not measured for the same listeners, it is not known if the influence of roving on DLFs is greater in individuals who have difficulty identifying the direction of frequency changes.
Here we report four experiments which aimed to investigate if the difficulty in identifying the direction of frequency changes between pure tones observed in some listeners is influenced by stimulus roving. We follow Semal and Demany (2006) in assuming that the primary cue listeners used in these experiments was pitch, and therefore that, although cues other than pitch may have sometimes been available, it is appropriate to refer to them as pitch discriminations (other possible cues on which the discriminations could have been based are considered later). Experiment 1 was primarily a replication of Semal and Demany’s (2006) main experiment. As in that study, DDLFs and IDLFs were measured using a dual-pair paradigm with frequency roved both between and within trials. In Experiment 2, most of the same individuals were retested in a similar procedure without frequency roving. In Experiment 3, frequency-roving range was manipulated systematically, and additional conditions including level roving but no frequency roving were added. Finally, in Experiment 4 listeners were tested using continuous frequency-modulated tones rather than discrete tone pairs, both with and without carrier-frequency roving.
EXPERIMENTS 1 AND 2
Methods
Listeners
Sixteen listeners (13 females; 12 right-handed; age range 18–26 years) took part in Experiment 1, of whom 13 also took part in Experiment 2 (11 females; 10 right-handed; age range 18–24 years). In what follows, individual listeners are identified by number (L1, L2, etc). L1 was author SRM, and only L1–3 had considerable prior experience in psychoacoustical experiments involving frequency and∕or pitch discrimination.
L4–16, who were paid for their participation, were undergraduates selected using a short pre-test experiment similar to that used by Semal and Demany (2006). For the pretest a total of 355 undergraduates were presented with 60 dual-pair trials (30 detection, 30 identification) with various magnitudes of frequency change, via the loudspeaker system in a large lecture room. For each participant, the proportion of correct trials (PC) was calculated from pen-and-paper responses. Listeners for the main experiment were chosen from the 61 individuals (17.2%) whose PC for identification trials was lower than their PC for detection trials, and for whom this difference exceeded one standard deviation of the mean difference across the whole group. L1–3 took part in a web-based version of the pre-test and their results did not indicate a difficulty with pitch-direction identification. Listeners varied in their musical experience, but none was a professional musician or performed music regularly.
Hearing levels were measured for frequencies between 250 and 4000 Hz in octave steps using pure tone audiometry. For all listeners except three, hearing levels did not exceed 20 dB hearing level (HL) at any frequency. For L4, hearing level was 25 dB HL for 250 and 500 Hz in the right ear, and 30 dB HL for 250 and 500 Hz in the left ear. For L12 and L16, hearing levels were 25 dB HL for 250 and 500 Hz in their right ears. For all listeners, worst-ear averages over all frequencies were <20 dB HL.
Stimuli
All tones were 250-ms sinusoids presented at 60 dB sound pressure level (SPL) with random starting phases and 20-ms cosine-squared on∕off ramps. Stimuli were generated digitally and delivered diotically through headphones (Sennheiser HD580) using a 24-bit digital-to-analog converter (LynxONE) at a sampling rate of 22500 Hz.
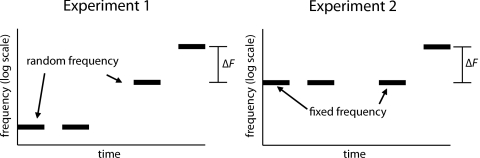
In both experiments, the stimuli were four successive tones arranged temporally into two pairs, with a 700-ms silent interval (ISI) between pairs, and a 250-ms ISI between the tones in each pair (illustrated in Fig. 1). In one of the pairs, selected randomly, the second tone was equiprobably higher or lower in frequency than the preceding tone by an amount (ΔF) expressed in musical cents (1 cent equals 1∕100th of a semitone or 1∕1200th of an octave). In the other pair, the two tones were identical. In Experiment 1, the frequencies of the first tones in each pair were independently drawn from a rectangular distribution defined on a log-frequency (cents) scale with limits of 0 and 3102 cents above 400 Hz (400 and 2400.1 Hz). In Experiment 2 there was no frequency rove; the first tone in each pair always had the same frequency, 979.8 Hz (1551 cents above 400 Hz), which corresponds to the center of the roving range in Experiment 1.
Figure 1.
Illustrations of example trials in Experiments 1 (left-hand panel) and 2 (right-hand panel). Solid lines represent pure tones. In both cases the correct response would be “second” (for detection) or ‘‘up’’ (for identification).
Procedure
Prior to testing, hearing levels were measured and each listener completed two questionnaires: the Speech, Spatial and Qualities of Hearing Scale questionnaire (SSQ; Gatehouse and Noble, 2004)4 and a questionnaire about their musical experience and expertise. Following these assessments, listeners took part in Experiment 1. DLFs were measured using two tasks in separate runs of trials: in the detection task, listeners indicated which tone pair contained the frequency change (first or second); and in the identification task, listeners indicated the direction of the change (up or down) that occurred in the pair containing different tones, without specifying which pair this was. Listeners first completed a few trials in each condition to familiarize themselves with the stimuli and procedure. Testing was carried out individually in a sound-attenuating booth (IAC) in three sessions lasting approximately 1 h each, on different days. Responses were made using a keyboard, and were followed by visual feedback and a 600-ms pause before the start of the next trial.
The magnitude of ΔF in a run of trials was set initially to 100 cents, and was manipulated within the run using a weighted one-up one-down adaptive procedure that estimates DLFs corresponding to 75% correct on the psychometric function (Kaernbach, 1991). Up to the fifth reversal in the direction of the staircase, ΔF was decreased by a factor of following a correct response and increased by a factor of 2.25 following an incorrect response. At the fifth reversal onwards, down and up step sizes were and 1.5, respectively. In each run, ΔF was limited to a maximum of 600 cents. A run ended after the 14th reversal. DLF for a run was defined as the geometric mean of all ΔF values used from the fifth reversal onward.
During testing, instructions for the current task were presented on the computer screen, together with the current trial number and current ΔF. The task alternated from one run to the next, with the order of task presentation counterbalanced across listeners. Twenty DLFs were measured for each task and for each listener.
Thirteen of the 16 listeners who had taken part in Experiment 1 subsequently took part in Experiment 2. The procedure for this experiment was similar to that for Experiment 1, except that 15 DLFs were measured for each task and for each listener, using the non-roved stimuli described above. Testing for this experiment was carried out in two 1-h sessions on different days.
Results
Experiment 1: Wide frequency roving
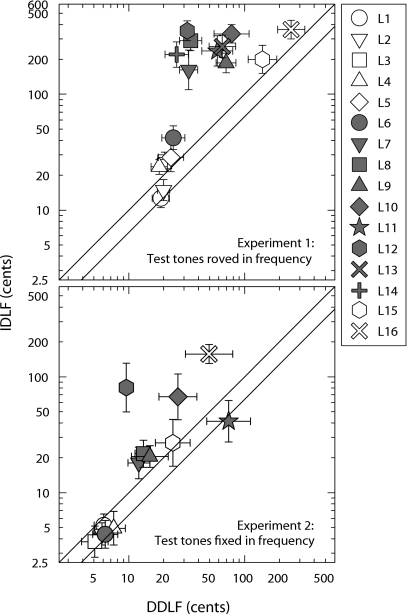
DLFs for Experiment 1 are shown in the upper panel of Fig. 2, in which listeners’ geometric mean DDLFs and IDLFs are plotted as abscissae and ordinates, respectively. Mann–Whitney tests with a Bonferroni-corrected significance criterion (α=0.003125) were used to compare DDLFs and IDLFs on a listener-by-listener basis. The results indicated that L7–14—whose data form a visible cluster in Fig. 2 (top panel)—all had significantly larger IDLFs than their DDLFs (U≤24.00, z≤−4.76, p<0.001, r≤−0.75). IDLF was also significantly larger than DDLF for L6, whose data fell outside of this cluster, but the effect was considerably smaller for this listener (U=76.00, z=−3.35, p≤0.001, r=−0.53) than for L7–14. The data for these individuals, whom we refer to hereafter as “direction-impaired” listeners, are shown as gray symbols in Fig. 2.
Figure 2.
Results of Experiments 1 (upper panel) and 2 (lower panel). Each listener is represented by a unique symbol and number. Listeners represented by gray symbols are those deemed to be direction-impaired listeners in Experiment 1 (see text). The abscissa and ordinate of each symbol represents that listener’s geometric mean DDLF and IDLF, respectively, with error bars representing geometric 95% confidence intervals, on logarithmic axes. Error bars are smaller than the symbol if not shown. The upper diagonal line in each panel represents the locus of equivalent performance. The lower diagonal line represents the locus of performance predicted by a model, discussed by Semal and Demany (2006), in which IDLFs and DDLFs are limited only by the same internal noise (see also Micheyl et al., 2008).
As in Semal and Demany’s (2009) study, impairments in pitch-direction identification observed here persisted after (in this case, approximately 3) hours of task practice with feedback after each trial. Comparisons between the DLFs measured for direction-impaired listeners in the two studies should be made with some caution, because those measured here may have been limited by the 600-cents cap imposed on ΔF, which was not present in Semal and Demany’s study. The DLFs were also based on fewer threshold estimates in this study (20 per listener per condition) than in Semal and Demany’s study (50 per listener per condition).
None of the other listeners showed a difference between their DDLF and IDLF that was significant at the corrected level (U≥121.00, z≥−2.13, p<0.033, r≥−0.34). L1 and L2, who achieved the smallest DLFs overall, had IDLFs that were approximately 5 to 6 cents smaller than their DDLFs. Though counterintuitive, smaller IDLFs than DDLFs were also observed for some listeners by Semal and Demany (2006), and this pattern of performance is broadly consistent with the predictions of a model they propose in which both detection and identification tasks are limited solely by the same internal noise (this point is revisited in the general discussion). For L3–5, IDLFs were slightly larger than their DDLFs. This pattern of performance was also seen by Semal and Demany, and overall DLFs for L1–5 are reasonably similar to those of their counterparts in that study.
Two listeners in Experiment 1 did not fit neatly into any of the groups identified by Semal and Demany (2006). L15 and L16 had very large DDLFs (143 and 253 cents respectively), yet relatively their IDLFs were not elevated significantly. This combination of large IDLF and large DDLF in the same individual was not observed for the smaller sample of listeners tested by Semal and Demany. L15 exhibited a bias for better performance on both tasks when the frequency difference was in the second pair, responding correctly on only 62% of first-pair trials compared to 85% of second-pair trials. Contrastingly, L16 was not able to perform either task at the accuracy targeted by the adaptive procedure (75% correct), with an overall accuracy of 63% correct across all trials. The DLFs measured for this listener are therefore likely to be underestimates of her true thresholds for frequency discrimination.
Experiment 2: No frequency roving
DLFs for Experiment 2 are shown in the lower panel of Fig. 2. Overall, DLFs were smaller than those measured in Experiment 1. Bonferroni-corrected Mann–Whitney tests (α=0.003846) were used to compare listeners’ DDLFs and IDLFs in Experiment 2. Four listeners had significantly larger IDLFs than their DDLFs (L8, L10, L12, and L16; U≤42.00, z≤−2.92, p<0.003, r≤−0.46), and none of the remaining listeners exhibited a significant difference between their DDLF and IDLF (U≥65.00, z≥−1.97, p≥0.050, r≥−0.31).
Of the nine listeners who had significantly larger IDLFs than DDLFs in Experiment 1 (L6–14), only three showed a similar effect in Experiment 2 (L8, L10, and L12). For L6, L7, L9, and L11, IDLFs were no longer significantly larger than their DDLFs at the corrected level. L16 was the only listener whose IDLF was significantly elevated relative to DDLF in Experiment 2 and not in Experiment 1, probably as a result of DLFs being underestimated in Experiment 1. L13 and L14 were unavailable for re-testing in Experiment 2.
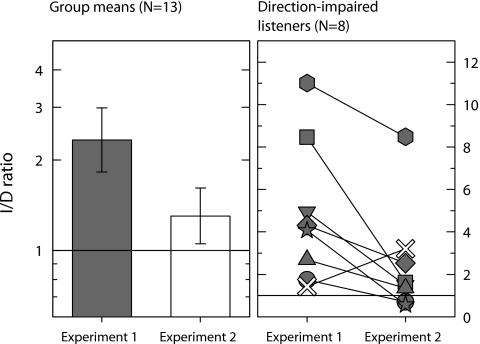
Influence of roving on I∕D ratios
A listener’s relative ability to identify pitch-change direction can be quantified by dividing their IDLF by their DDLF. Figure 3 (left-hand panel) shows the geometric mean “I∕D ratios” for the group who took part in both experiments. A paired-samples t-test performed on listeners’ log-transformed I∕D ratios confirmed that they were reliably smaller in Experiment 2 for the group as a whole [t(12)=2.81, p<0.050, r=−0.63]. The effect remained significant when only the listeners who showed the pitch-direction impairment in either or both experiments (L6–12 and L16) were included in the analysis [Fig. 3, right-hand panel; t(7)=2.63, p<0.050, r=−0.70].
Figure 3.
I∕D ratios in Experiments 1 and 2 for the listeners taking part in both experiments. The left-hand panel shows geometric mean ratios for the group as a whole, with bars representing 1 geometric standard error of the mean, on a logarithmic axis. The right-hand panel shows the I∕D ratios for the eight individuals showing the pitch-direction impairment in either or both experiments, with symbol and color combinations consistent with Fig. 2, plotted on a linear axis so that the individual points can be seen clearly. Solid horizontal lines in both panels represent an I∕D ratio of 1 (i.e., equal DDLFs and IDLFs).
Discussion
The observed tendency for some listeners to be poorer at pitch-direction identification than pitch-change detection has been suggested by Foxton et al. (2004) to be a characteristic of people with congenital amusia. Although the present study did not involve testing for amusia in a standardized way (Peretz et al., 2003), our questionnaires did not reveal any gross differences between direction-impaired and non-impaired listeners in terms of their musical ability or experience, and none of the listeners reported any difficulty in appreciating music. Moreover, the result that relative impairments in pitch-direction identification tended to disappear when fixed-frequency stimuli were used suggests that the impairment observed here is different in origin to that seen in patients with cortical lesions (Johnsrude et al., 2000; Tramo et al., 2002).
Consistent with previous studies (Amitay et al., 2005; Demany and Semal, 2005; Harris, 1952a; Jesteadt and Bilger, 1974), Experiment 2 revealed that when frequency roving was removed, DLFs were usually reduced considerably. One possible reason why DLFs were smaller in the absence of roving is that it was no longer necessary for listeners to compare directly the pitches of the two tones within each pair for correct task performance. Instead, in Experiment 2 listeners could compare each tone individually against an internal representation of the standard tone (979.8 Hz), which occurred three times on every trial. In a preliminary theory of intensity discrimination, Durlach and Braida (1969) referred to these two strategies as “trace coding” and “context coding,” respectively. The repeated presentation of the standard tone in Experiment 2 may have provided listeners with the opportunity to build a relatively more precise and stable referent than the evanescent echoic memory trace of the tones in Experiment 1. Thus, in Experiment 2 the variance of the internal noise associated with context coding would be less than that associated with trace coding, which could explain why DLFs were generally smaller in that experiment. However, Experiment 2 also revealed that impairments in pitch-direction identification relative to pitch-change detection were reduced when roving was not used. Since context coding does not eliminate the need for the listener to be sensitive to pitch-change direction, it is unclear why a switch from trace coding to context coding should improve thresholds so much more for the identification task than for the detection task.
Another interpretation of the results is that removing frequency roving simply decreased stimulus uncertainty. The effects of uncertainty have been modeled previously in different ways for different psychophysical experiments, for example by varying the width of listening bands in probe-signal detection (Schlauch and Hafter, 1991), the ensemble variance at the output of auditory channels in informational masking (Lutfi, 1993; Durlach et al., 2005), or the number of noisy templates in visual discrimination (Pelli, 1985). However, in general, more uncertainty is thought to lead to an increase in internal noise and consequently poorer task performance. In the present experiments, any model of performance that assumes that the effects of roving are due to stimulus uncertainty would additionally have to assume that, for some listeners, uncertainty results in a larger proportional increase in internal noise for the identification task than for the detection task. As with the coding-strategy hypothesis, why this would be the case is not presently clear.
While removal of the frequency roving is the most likely explanation for the reduction in IDLFs between Experiments 1 and 2, other explanations are conceivable. Since Experiment 2 was performed after Experiment 1, the improvement in DLFs could reflect learning. This potential confound was addressed in Experiment 3, in which a new sample of direction-impaired listeners completed runs of fixed- and roving-frequency conditions in random order.
Other possible explanations for the differences between Experiments 1 and 2 follow from the fact that the nominal level of the tones in those experiments was fixed. There are at least two conceivable strategies by which listeners may have exploited this feature of the stimuli. First, as discussed by Semal and Demany (2006), differences in the output level of a single auditory channel could provide a cue other than pitch for successful task performance. This strategy would be useful in the detection task, but for it to be useful in the identification task, the listener would have to choose an appropriate channel. The optimal frequency of the channel would have to be consistently higher or lower than the frequency of the first tone in each pair, so that the direction of the excitation-level change co-varied consistently with the direction of the frequency change. This listening strategy might have been more difficult to achieve when the stimuli were roved in frequency than when they were fixed, because in the former case it would require constant re-selection of the listening channel, and in the latter case the same channel could be used for all trials.
Listeners may have also used differences in loudness associated with changes in frequency (Mauermann et al., 2004; Moore et al., 2006) as a cue for successful task performance. Equal-loudness contours over the range 400–2400 Hz are not monotonic (Suzuki and Takeshima, 2004), so for tones roved over this range the direction of the loudness cue would not always be concordant with the direction of a frequency change. If tones were fixed in frequency, however, loudness-change direction and frequency change direction could co-vary systematically because the standard tone would occupy a single point on the loudness-frequency function. Use of either or both of the strategies highlighted above could have contributed to the smaller DDLFs than IDLFs in Experiment 1, and to the reduced differences between DLFs for the two tasks in Experiment 2. This issue was also investigated in Experiment 3.
EXPERIMENT 3
Rationale
The first aim of Experiment 3 was to test if the results of Experiments 1 and 2 could be replicated while controlling for the potential confounds highlighted in the previous section. A new sample of direction-impaired listeners completed runs of different conditions in random order, and most conditions included random changes in level from tone to tone. The second aim was to test whether the impairment in pitch-direction identification depends critically on the use of a very wide roving range (3102 cents, as in Experiment 1), or if significant impairments can also be observed with smaller roving ranges.
Method
Listeners
The 10 listeners who took part in Experiment 3 formed two subgroups: “experts” and “novices.” The expert group consisted of four listeners (four males; three right-handed; age range 24–61 years): L1, L2, and two new listeners, L17 (author PJB) and L18. All of these had taken part in many previous psychoacoustical experiments involving frequency and∕or pitch discrimination. The novice group consisted of six new listeners (L19–L24; six females; four right-handed; age range 18–22 years) who were selected from the cohort of undergraduates as having particular difficulty with identifying pitch-change direction using the pre-test described previously, and who had no prior experience in such experiments. None of the listeners in either group was a professional or practicing musician.
Stimuli and procedure
The new listeners first underwent preliminary assessments as in Experiments 1 and 2. For five of the new listeners, hearing levels did not exceed 20 dB HL at any frequency. For the remaining listener (L19), hearing level at 250 Hz was 30 dB HL in one earn3. For all listeners, worst-ear averages over all frequencies were <20 dB HL. As before, in the main part of the experiment listeners heard two pairs of tones on every trial. The frequency of the first tone in each pair was either fixed or randomly selected from a rectangular probability distribution. There were four levels of frequency-roving range: a “wide” range of 3102 cents (400–2400.1 Hz, as in Experiment 1); a “medium” range of 310 cents (895.9–1071.6 Hz); a “narrow” range of 31 cents (988.9–971.4 Hz); and “none,” corresponding to the absence of frequency roving (as in Experiment 2). For each roving range, the level of each tone in every trial was randomly set within a 7-dB range (±3.5 dB around 60 dB SPL). To assess if these level differences influenced DLFs, two more stimulus arrangements without frequency roving were included: in the first, all tones were presented at 60 dB SPL (as in Experiments 1 and 2); and in the second, tone level was roved between pairs but was fixed for the two tones within each pair.
For each of the six stimulus conditions, 20 DDLFs and 20 IDLFs were obtained from each listener, resulting in 240 threshold measurements per listener in total. Listeners completed 11 sessions on different days. The initial session involved gathering the questionnaire and audiometric data, followed by a short practice block. The remaining sessions contained two experimental blocks, and each block contained one run of each condition in a random order.
The adaptive procedure in Experiment 3 was similar to that used previously, but included the following modifications. If listeners made an error within the first three trials, two additional first-phase reversals were added to the run; in such cases, the measurement phase started on the seventh rather than the fifth reversal. The maximum allowed ΔF was 2400 cents. If listeners did not make an error within the first three trials, each adaptive run lasted for 12 rather than 14 reversals. Again, the DLF was defined as the geometric mean of all values visited during the measurement phase.
Results and discussion
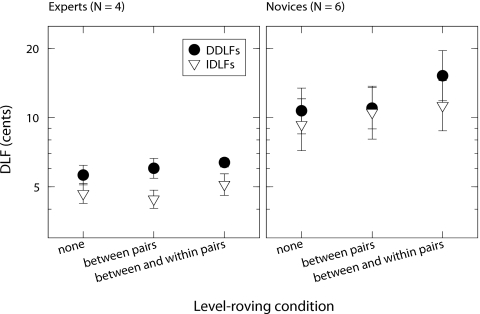
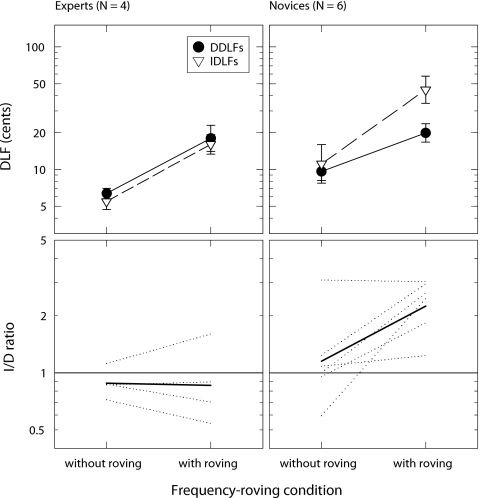
Effects of level roving
DLFs for the conditions in which level was roved and test frequency was fixed are shown in Fig. 4. The data for the expert and novice groups are shown in the left- and right-hand panels, respectively. These data were analyzed using two repeated-measures analyses of variance (ANOVAs) with task (detection, identification) and level roving (none, between pairs, between and within pairs) as factors, and the log-transformed DLFs measured in each group as the dependent variable. In these and following ANOVAs, Greenhouse–Geisser corrections have been applied where the assumption of sphericity (determined with Mauchly’s test) was violated. Neither ANOVA revealed a significant main effect of task [experts: F(1,3)=9.86, p=0.052, η2=0.77; novices: F(1,5)=5.85, p=0.060, η2=0.54], although for the experts the trend for IDLFs to be smaller than DDLFs was close to being significant. Level roving also had no significant effect for the expert group [F(2,6)=1.72, p=0.256, η2=0.37].
Figure 4.
Results of Experiment 3 for expert (left-hand panel) and novice (right-hand panel) listener groups in conditions with level roving and without frequency roving. The ordinate of each symbol represents that group’s geometric mean DLF for that condition on logarithmic axes, with bars representing 1 geometric standard error.
For the novice group, a main effect of level roving was observed [F(2,10)=12.29, p<0.010, η2=0.71]. Planned comparisons revealed that this effect was driven by a difference between the two forms of roving: roving level between and within pairs resulted in significantly larger DLFs than roving level between pairs only [F(1,5)=14.60, p<0.050, r=0.86]. No significant interaction was found for either group [experts: F(2,6)=0.51, p=0.625, η2=0.15; novices: F(2,10)=3.62, p=0.066, η2=0.42].
The effects of level roving on frequency discrimination have been explored in previous studies. Emmerich et al. (1989) found that DLFs measured for fixed-frequency tone pairs were larger when the tones were roved independently in level over a 12-dB range than when they were fixed in level (see also Henning, 1966). Conversely, Moore and Glasberg (1989) did not find a significant difference between DLFs measured for tones that were either fixed or roved over a 6-dB range. The non-significant (experts) and modest (novices) effects of level-roving reported here are perhaps not surprising given that our level-roving range (7-dB) was closest to the one used by Moore and Glasberg.
Importantly, although the novice listeners had slightly elevated DLFs when level was roved between and within pairs, their IDLFs were not larger than their DDLFs in these conditions, which did not involve any frequency roving. This is consistent with the results of Experiment 2, where impairments in pitch-direction identification were far less profound than in Experiment 1. The results also suggest that the differences between the results of Experiments 1 and 2 are not likely to be due to the use of cues other than pitch, which were available in Experiment 2 but not in Experiment 1.
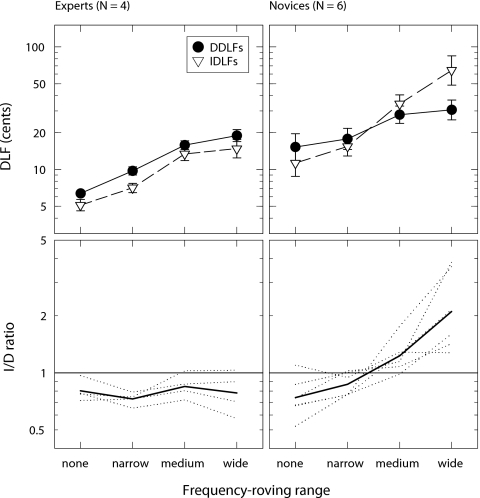
Effects of frequency roving
Figure 5 shows DLFs and I∕D ratios for the conditions in which test frequency was roved and for the corresponding no-rove control. All these conditions involved level roving both within and between pairs in a trial. These data were analyzed using two repeated-measures ANOVAs with task (detection, identification) and frequency-roving range (none, narrow, medium, wide) as factors, and the log-transformed DLFs from each group as the dependent variable. For the expert group, the results showed significant main effects of roving range [F(3,9)=44.47, p<0.001, η2=0.94] and task [F(1,3)=12.84, p<0.050, η2=0.81], but no significant interaction [F(3,9)=1.15, p=0.382, η2=0.28]. This corresponds to the observation that DLFs in both tasks increased with roving range, and that IDLFs were generally smaller than DDLFs. Planned comparisons revealed that the narrow roving range yielded larger DLFs than the no roving condition [F(1,3)=92.07, p<0.010, r=0.98], and that the medium roving range yielded larger DLFs than the narrow roving range [F(1,3)=44.71, p<0.010, r=0.97]. DLFs did not differ significantly between medium and wide roving.
Figure 5.
Upper panels: same as Fig. 4, for the no-rove condition and the three conditions in which test frequency was roved, in each case including level roving both within and between tone pairs in a trial. Lower panels: each dotted line represents a single listener’s I∕D ratios and the thicker lines represent geometric group mean I∕D ratios, on logarithmic axes. Horizontal reference lines represent an I∕D ratio of 1.
There was a significant main effect of frequency-roving range for the novice listeners [F(1.20,6.00)=34.11, p<0.050, η2=0.87]. Planned comparisons revealed that each increment in roving range yielded significantly larger DLFs than the previous range [F(1,5)≥9.43, p<0.050, r≥0.81]. Although there was no significant main effect of task [F(1,5)=3.45, p=0.122, η2=0.41], there was a significant interaction [F(3,15)=16.13, p<0.001, η2=0.76]. The result of this interaction is seen more clearly in the I∕D ratios plotted in the lower-right panel of Fig. 4: the novice listeners became poorer at identification than at detection—and therefore more direction-impaired—as frequency-roving range increased. I∕D ratios generally only exceeded 1 for the medium or wide roving ranges.
It is important to point out that, on the whole, the impairments in pitch-direction identification observed for the new listeners in this experiment (L19–L24) turned out to be less severe than those observed for the previous pre-selected group (L4–16). In the wide frequency-roving range conditions in Experiment 3, L19–L24 had a group geometric mean I∕D ratio of 2.10, compared to 3.48 for L6–14 in Experiment 1. Moreover, unlike L10, L12, and L16 in Experiment 2, none of the listeners in Experiment 3 had elevated IDLFs in conditions without frequency roving. Because Experiment 3 was considerably longer than Experiments 1 and 2 combined (12 versus 3 h), the smaller I∕D ratios could have come about because of more task practice; Semal and Demany (2006) noted that the pitch-direction impairment improved over time for one of their three direction-impaired listeners. Although the severity of selective impairments in pitch-direction identification—and the dependence of these impairments on frequency-roving range—varied appreciably across listeners in Experiments 1–3, overall the results show that such impairments are far more likely to be observed under conditions in which the standard frequency of the stimuli is roved over a wide range than under conditions in which this frequency is fixed.
EXPERIMENT 4
Rationale and method
In a recent series of experiments, Demany et al. (2009a) measured DDLFs and IDLFs for discrete and continuous frequency changes. They found that DLFs for both tasks were improved when the tones within a pair were connected by a frequency glide compared to when they were separated by a silent ISI (see also Sek and Moore, 1999; Lyzenga et al., 2004). Although the data reported in that study only included listeners who did not experience difficulty identifying pitch-change direction, the authors mentioned in a footnote that four additional listeners did have larger IDLFs than DDLFs in the discrete and continuous conditions. This observation suggests that the impairment in pitch-direction identification is not specific to the use of discrete tones. However, Demany et al.’s experiments always involved frequency roving over a wide range. Experiment 4 assessed whether the effects of frequency roving on DLFs and I∕D ratios observed in our previous experiments were specific to the particular stimuli employed or generalized to a second stimulus arrangement in which the target frequency change was continuous.
The listeners from Experiment 3 were retested after the final session of the previous experiment. The stimuli in Experiment 4 were similar to those used above, except that the pair of same frequency tones was replaced by a constant-frequency tone, and the pair of different-frequency tones was replaced by two 250-ms steady-state plateaux connected by a frequency sweep. The sweep was a half-cycle sinusoidal frequency-modulation function with no change in amplitude and with phase continuity. The two tones had durations of 750 ms and were separated by a 700-ms silent ISI. Thus, instead of hearing four discrete tones on every trial, listeners heard two tones with one containing a continuous frequency sweep. The sweep could occur in either the first or the second tone, and could be upward or downward. The level of each tone was independently varied over a 7-dB range centered on 60 dB SPL.5 DDLFs and IDLFs were measured using two stimulus conditions: the starting frequency of the tones was fixed at 979.8 Hz for a run of trials, or roved independently from 400–2400.1 Hz. Six DLFs were measured per condition for each listener.
Results
The group geometric mean DDLFs and IDLFs (and the corresponding I∕D ratios) measured in Experiment 4 are shown in Fig. 6. A repeated-measures ANOVA with expert group DLFs as the dependent variable, and with frequency roving (roving, no roving) and task (detection, identification) as factors, revealed a main effect of frequency roving only [F(1,3)=43.72, p<0.050, η2=0.94]. The effect of task was not significant [F(1,3)=0.76, p=0.448, η2=0.20], and there was no significant interaction [F(1,3)=0.36, p=0.862, η2=0.12]. A corresponding ANOVA for the novice group revealed significant main effects of frequency roving [F(1,5)=179.46, p<0.001, η2=0.97] and task [F(1,5)=10.14, p<0.050, η2=0.67]. As in Experiment 3, there was a significant interaction [F(1,5)=9.22, p<0.050, η2=0.65], suggesting that roving mediated the relative difficulty in pitch-direction identification using continuous stimuli also. In this experiment, the geometric mean I∕D ratio observed for the novice group with roved stimuli was 2.25, which is similar to the ratio observed for the same listeners in the maximum-roving condition in Experiment 3 (2.10).
Figure 6.
Same as Fig. 5, for the conditions in Experiment 4.
GENERAL DISCUSSION
Summary of the findings
(1) Experiment 1 replicated the finding that some listeners have difficulty identifying the direction of small but detectable frequency changes between pure tones when the standard frequency is roved widely. Other listeners showed no such deficit in pitch-direction identification, and consistent with previous results their IDLFs were roughly equal to or smaller than their DDLFs.
(2) When frequency roving was removed in Experiment 2, the large discrepancies between IDLFs and DDLFs (reflected in large I∕D ratios) were reduced. Many of the listeners who had been identified as direction-impaired in Experiment 1 no longer had significantly larger IDLFs than DDLFs in Experiment 2.
(3) Experiment 3 revealed that DLFs tended to increase monotonically with frequency-roving range for all listeners. For direction-impaired listeners, I∕D ratios also increased with frequency-roving range. These listeners appeared to be direction-impaired only when a relatively wide frequency-roving range (3102 cents) was used, and not when level was roved and frequency was fixed.
(4) In Experiment 4, listeners were tested with continuous instead of discrete frequency changes. Again, the results showed generally larger DLFs—and larger I∕D ratios in direction-impaired listeners—under wide frequency roving than under no roving.
Implications for the origin of the impairment
Why are some listeners unable to reliably identify the direction of small yet detectable frequency changes? Based on earlier findings, which suggest that the human auditory system contains neural populations that are selectively sensitive to the direction of small frequency changes (Demany and Ramos, 2005; Demany et al., 2009b) Semal and Demany, (2006) proposed that such frequency-shift detectors (FSDs) may not respond to small shifts in the brains of direction-impaired listeners. The result that insensitivity to pitch-change direction is greatly reduced or eliminated when wide frequency roving is not used suggests either that this explanation is incorrect, or that when the stimuli are not roved widely in frequency, listeners’ ability to identify pitch-change direction no longer relies on FSDs. As mentioned earlier, when the standard frequency of the tones is fixed, listeners may be able to compare the frequencies evoked by the tones to a standard referent stored in long-term auditory memory (context coding) instead of comparing directly the echoic traces of the two tones (trace coding). If FSDs are necessary for successful task performance only when listeners use trace coding and not context coding, less or no impairment may be observed with fixed-frequency stimuli. This explanation rests on several assumptions that need to be tested further.
A second possible explanation for the findings is that, when performing the identification task with stimuli that were not roved widely in frequency, direction-impaired listeners were able to make more effective use of the detailed feedback provided after every trial. According to this explanation, direction-impaired listeners could not perceive a small pitch change as upward or downward per se in these conditions, but could perceive a difference between tone pairs containing upward and downward changes, simply because the second element in the sequence was perceived as different in the two cases. Owing to the provision of feedback after each trial, and to the fact that the stimuli did not vary widely across trials, listeners could have learned to correctly label the two different-sounding cases as either “up” or “down,” allowing for more successful task performance. Since this strategy requires that the tones forming the up and down cases do not vary widely across trials, this could explain why IDLFs were considerably elevated relative to DDLFs when the frequency-roving range of the stimuli was wide.
If this “learning” hypothesis is correct, in conditions without wide frequency roving, direction-impaired listeners might show an initial impairment in pitch-direction identification that decreases over trials. This was investigated by examining how threshold estimates obtained in Experiment 2 for L6, L7, L9, and L11 changed over time. The data did not show learning over the course of the experiment (i.e., there was not a monotonic decrease in thresholds), nor did they show differences in learning between the detection and identification tasks. Although this analysis does not support the learning hypothesis it does not rule it out completely, because the listeners may have learned to utilize feedback in Experiment 2 very rapidly (within the first run of trials). A stronger test of the hypothesis would involve measuring IDLFs in direction-impaired listeners using fixed-frequency stimuli without trial-by-trial feedback. In this circumstance, the listeners should not be able to learn to label upward and downward changes appropriately, and they should remain direction-impaired regardless of the frequency-roving range used. This could not be assessed with the present data, since feedback was included in all four experiments.
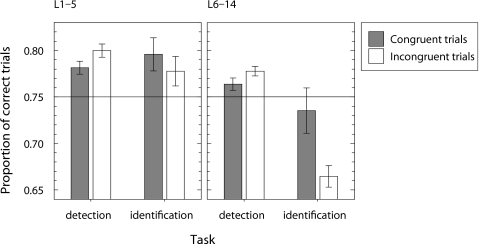
A third explanation for the results is that direction-impaired listeners were more easily confused or distracted by the irrelevant—and sometimes much larger—pitch changes that occurred between the last and the first tones from adjacent trials, or between pairs within a trial. In order to test this hypothesis, we performed a trial-by-trial analysis of the data from Experiment 1. For each listener and each task (detection and identification), trials completed during the course of the experiment were sorted into two groups depending on whether or not the direction of the frequency change between the second and third tones in the trial (the between-pair frequency change) was in the same direction as the target (within-pair) frequency change on that same trial. The results are shown in Fig. 7. For the detection task, the congruence of between- and within-pair changes did not have a significant effect on performance [direction-impaired listeners: t(8)=−1.53, p=0.166, r=0.48; non-impaired listeners: t(4)=−1.33, p=0.255, r=0.55]. However, for the identification task, direction-impaired listeners performed more poorly on trials in which the direction of the between-pair change was opposite to that of the within-pair change [t(8)=2.87, p<0.050, r=0.71]. This effect was not found for the non-impaired listeners in that experiment [t(5)=0.59, p=0.586, r=0.28]. A similar pattern was observed for the data from the wide frequency-roving conditions in Experiment 3—frequency-direction incongruence also resulted in poorer performance in identification trials for the novice listener group [t(5)=5.73, p<0.050, r=0.93]. This exploratory analysis suggests that pitch-direction judgments are susceptible to sequential interference by task-irrelevant pitch changes that occur within the stimulus ensemble.
Figure 7.
Results of the trial-by-trial analysis performed on the data from Experiment 1. Bars represent the group mean PC for the non-impaired listeners (left-hand panel) and the direction-impaired listeners (right-hand panel). PC is shown separately for congruent and incongruent trial types, and for trials in the detection and identification tasks. Error bars represent 1 standard error of the mean. Horizontal reference lines represent 75% correct, which was measured by the adaptive routine in the experiment. Data from L15 and L16 have been excluded because of these listeners’ unusual performance. Since this analysis was performed post-hoc, the number of trials in each average and ΔF for any given trial is not controlled.
If confirmed, the inability of some listeners to ignore irrelevant stimulus variations when making pitch-direction judgments would be similar in some respects to findings from the informational masking literature. In those experiments, listeners’ ability to hear out a target stimulus—usually a single pure tone of known frequency or a short sequence of tones—is impaired when the target is presented in a background of spectrally distant, task-irrelevant masker tones (for reviews, see Kidd et al., 2008 and Watson, 2005). A clear aspect of informational masking is that listeners often attend to a frequency region that is wider than the region occupied by the target, such that random variability of the maskers which fall within the attended region affects performance. A second aspect is that susceptibility to informational masking is subject to large individual differences; some listeners are greatly affected by masker uncertainty, while others are able to listen “analytically” and largely ignore the maskers (Neff and Callaghan, 1988; Neff and Dethlefs, 1995). The individual differences in pitch-direction identification are similar to individual differences in informational masking in that greater susceptibility to masker uncertainty does not appear to be symptomatic of any real-world hearing deficits (Neff and Dethlefs, 1995), and the differences remain pronounced despite extensive task practice (Neff and Callaghan, 1988). It would be interesting to determine if those individuals who are relatively insensitive to pitch-change direction are also relatively more susceptible to informational masking.
Finally, it is important to note again that three of the listeners tested still had significantly larger IDLFs than their DDLFs in Experiment 2, in which frequency roving was not used, and in which the potential for interference from irrelevant pitch changes was rather small. This suggests that while sequential interference appears to have contributed to the impairment, it may not be the sole cause of the difficulties experienced by these listeners. It is plausible that greater susceptibility to sequential interference could actually result from a genuine difficulty in identifying the direction of small pitch changes even under conditions in which this interference is minimal. In this case, listeners who were unable to perceive the direction of the within-pair frequency change may have indicated the direction of the most salient frequency change occurring in the trial (i.e., the between-pair change), hence making more errors when the directions of the two changes were incongruent. However, it is equally noteworthy that most direction-impaired listeners tested here were not direction-impaired in the absence of frequency roving, which suggests that impairments in pitch-direction identification may have more than one cause.
Implications for psychophysical models
The findings of this series of experiments present several challenges for psychophysical models of frequency discrimination. One challenge is to account for the general influence of frequency roving—for all listeners, DDLFs and IDLFs tended to increase monotonically with increasing frequency-roving range. Arguably the simplest models that can be applied to the present data are phenomenological models based on signal detection theory (SDT), such as those described by Semal and Demany (2006) and Micheyl et al. (2008). These models make few assumptions as to how pitch is determined in the auditory system, merely that listeners’ decisions in a frequency discrimination task are based on noisy internal representations (“observations”) of the pitch of the stimuli presented. The decision variable in these models is based on the differences between observations within each stimulus pair. Specifically, the listener is assumed to select whichever pair yields the largest difference (for detection trials), or to respond upward or downward depending on whether the sign of this difference is positive or negative (for identification trials). This so-called “differencing strategy” has often been utilized in psychophysical models of frequency and intensity discrimination, and forms the basis of the SDT analysis of the popular 2I-2AFC paradigm (Green and Swets, 1966; Macmillan et al., 1977; Noreen, 1981; Macmillan and Creelman, 2005). When frequency is roved widely across pairs, the differencing strategy is actually the optimal strategy in the dual-pair detection and identification tasks (Micheyl and Messing, 2006; Micheyl and Dai, 2009). However, models that use solely a differencing strategy cannot account for changes in DLFs as a function of roving range. Mathematically, the application of across-pair roving corresponds to adding the same quantity (drawn from a random distribution) to the two observations within a pair. This quantity cancels out when one takes the difference between the pairs, yielding no difference in predicted DLFs whether roving is applied or not. For differencing models to account for the effects of roving, the variance of the internal noise that limits sensitivity to frequency differences must be assumed to increase with frequency-roving range. This could correspond to assuming different coding strategies depending on roving range, as in Durlach and Braida’s (1969) model, or increases in internal noise with increasing stimulus uncertainty, as outlined earlier.
A second challenge is to account for the large individual differences observed in listeners’ I∕D ratios. While direction-impaired listeners have elevated IDLFs relative to their DDLFs, listeners without such impairment have IDLFs that are equal to or smaller than their DDLFs. Semal and Demany (2006) and Micheyl et al. (2008) demonstrated that the latter outcome can be explained by SDT models in which the same source of internal noise limits performance in both detection and identification tasks. Under the traditional, equal-variance Gaussian noise assumption, SDT predicts that IDLFs should be smaller than DDLFs by a factor of 1.56 (corresponding to an I∕D ratio of 0.64). However, the ratio measured for real listeners who show no specific deficit in the identification task is often different from this value. Micheyl et al. (2008) pointed out that I∕D ratios between 0.64 and 1 can be predicted by models in which observations are discretized into a variable number of categories, or by assuming Poisson-rather than Gaussian-distributed noise. In short, if it is assumed that the same internal noise limits both pitch-change detection and pitch-direction identification, listeners’ IDLFs should be the same as or slightly smaller than their DDLFs.
Arguably the most pressing challenge is to account for the relationship between DDLFs and IDLFs in direction-impaired listeners, and for the influence of frequency roving on this relationship. One way to account for the relationship without throwing away existing models of frequency discrimination is to abandon the parsimonious—but clearly not generally correct—assumption that sensitivity in pitch-change detection and pitch-direction identification tasks is limited by the same internal noise, and assume instead that, for some reason, the internal noise is greater in the latter than the former. Consider frequency discrimination as a two-step decision process: first the listener must detect a change in frequency, and then assign the correct direction (up or down) to the change. In the present experiments, the detection task would require only the first step, while the identification task would require both steps. The first step involves comparing sensory observations and so would be limited by internal sensory noise. When listeners are required additionally to perform the second step, a novel source of internal noise could be introduced. For listeners with no difficulty identifying pitch-change direction, this additional noise could be assumed to be minimal, and therefore the phenomenological models provided by Micheyl et al. (2008) would be applicable. For direction-impaired listeners, one potential source of additional noise has been identified above, namely sequential interference effects between across- and within-pair pitch changes. However, at least one other source is needed in order to account for the observation that some listeners still had significantly larger IDLFs than DDLFs in Experiment 2. At present, the origin of this additional source of identification-specific internal noise is not clear.
While formulating a new psychophysical model of listeners’ behavior in pitch-change detection and pitch-direction identification tasks is beyond the scope of this empirical report, it is clear that current models will need to be enhanced if they are to account for the range of individual differences and the effects of roving observed in the experiments reported above.
ACKNOWLEDGMENTS
We thank Brian Moore, Catherine Semal, and an anonymous reviewer for their comments on earlier drafts of this article. S.R.M. is supported by a studentship from the UK Biotechnology and Biological Sciences Research Council. C.M. is supported by NIH under Grant No. R01 DC 05216.
Footnotes
For three of the listeners in that study, d′ was larger on average for the 2I-2AFC task than for the SD tasks for equivalent magnitudes of frequency difference. This suggests that the frequency differences were no less discriminable in the 2I-2AFC task than they were in the SD tasks. For the remaining listener, d′ was small (<1) in all conditions, suggesting that this listener had difficulty discriminating small frequency differences regardless of task.
In that study DLFs were largest on average for the group trained with the more narrowly roved stimuli.
Since all the stimuli in the experiments were clearly audible to all listeners, we think that it is very unlikely that the minor audiometric abnormalities observed in some individuals influenced the results. Therefore we have chosen to include the data for all listeners in the results reported here.
The SSQ was administered to explore the relationship between listeners’ reports of any difficulties with hearing in real-world situations and their ability to detect or identify the direction of frequency changes. These data are not included in the present article.
The level roving used in this experiment could not control for potential loudness or excitation-pattern cues—as in Experiment 3—because the level was always constant within each tone. However, the results of Experiment 3 suggest that it was very unlikely that listeners actually made use of such cues.
References
- Amitay, S., Hawkey, D. J. C., and Moore, D. R. (2005). “Auditory frequency discrimination learning is affected by stimulus variability,” Percept. Psychophys. 67, 691–698. [DOI] [PubMed] [Google Scholar]
- ANSI (1994). American National Standards Acoustical Terminology (American National Standards Institute, New York: ). [Google Scholar]
- Demany, L., Carlyon, R. P., and Semal, C. (2009a). “Continuous versus discrete frequency changes: Different detection mechanisms?,” J. Acoust. Soc. Am. 125, 1082–1090. 10.1121/1.3050271 [DOI] [PubMed] [Google Scholar]
- Demany, L., Pressnitzer, D., and Semal, C. (2009b). “Tuning properties of the auditory frequency-shift detectors,” J. Acoust. Soc. Am. 126, 1342–1348. 10.1121/1.3179675 [DOI] [PubMed] [Google Scholar]
- Demany, L., and Ramos, C. (2005). “On the binding of successive sounds: Perceiving shifts in nonperceived pitches,” J. Acoust. Soc. Am. 117, 833–841. 10.1121/1.1850209 [DOI] [PubMed] [Google Scholar]
- Demany, L., and Semal, C. (2005). “The slow formation of a pitch percept beyond the ending time of a short tone burst,” Percept. Psychophys. 67, 1376–1383. [DOI] [PubMed] [Google Scholar]
- Durlach, N. I., and Braida, L. D. (1969). “Intensity perception: I. Preliminary theory of intensity resolution,” J. Acoust. Soc. Am. 46, 372–383. 10.1121/1.1911699 [DOI] [PubMed] [Google Scholar]
- Durlach, N. I., Mason, C. R., Gallun, F. J., Shinn-Cunningham, B., Colburn, H. S., and Kidd, G., Jr. (2005). “Informational masking for simultaneous nonspeech stimuli: Psychometric functions for fixed and randomly mixed maskers,” J. Acoust. Soc. Am. 118, 2482–2497. 10.1121/1.2032748 [DOI] [PubMed] [Google Scholar]
- Emmerich, D. S., Ellermeier, W., and Butensky, B. (1989). “A reexamination of the frequency discrimination of random-amplitude tones, and a test of Henning’s modified energy-detector model,” J. Acoust. Soc. Am. 85, 1653–1659. 10.1121/1.397953 [DOI] [Google Scholar]
- Foxton, J. M., Dean, J. L., Gee, R., Peretz, I., and Griffiths, T. D. (2004). “Characterization of deficits in pitch perception underlying ‘tone deafness’,” Brain 127, 801–810. 10.1093/brain/awh105 [DOI] [PubMed] [Google Scholar]
- Foxton, J. M., Weisz, N., Bauchet-Lecaignard, F., Delpuech, C., and Bertrand, O. (2009). “The neural bases underlying pitch processing difficulties,” Neuroimage 45, 1305–1313. 10.1016/j.neuroimage.2008.10.068 [DOI] [PubMed] [Google Scholar]
- Gatehouse, S., and Noble, W. (2004). “The speech, spatial and qualities of hearing scale (SSQ),” Int. J. Audiol. 43, 85–99. 10.1080/14992020400050014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green, D. M., and Swets, J. A. (1966). Signal Detection Theory and Psychophysics (Wiley, New York: ). [Google Scholar]
- Harris, J. D. (1952a). “The decline of pitch discrimination with time,” J. Exp. Psychol. 43, 96–99. 10.1037/h0057373 [DOI] [PubMed] [Google Scholar]
- Harris, J. D. (1952b). “Pitch discrimination,” J. Acoust. Soc. Am. 24, 750–755. 10.1121/1.1906970 [DOI] [Google Scholar]
- Henning, G. B. (1966). “Frequency discrimination of random amplitude tones,” J. Acoust. Soc. Am. 39, 336–339. 10.1121/1.1909894 [DOI] [PubMed] [Google Scholar]
- Jesteadt, W., and Bilger, R. C. (1974). “Intensity and frequency discrimination in one- and two-interval paradigms,” J. Acoust. Soc. Am. 55, 1266–1276. 10.1121/1.1914696 [DOI] [PubMed] [Google Scholar]
- Johnsrude, I. S., Penhune, V. B., and Zatorre, R. J. (2000). “Functional specificity in the right human auditory cortex for perceiving pitch direction,” Brain 123, 155–163. 10.1093/brain/123.1.155 [DOI] [PubMed] [Google Scholar]
- Kaernbach, C. (1991). “Simple adaptive testing with the weighted up-down method,” Percept. Psychophys. 49, 227–229. [DOI] [PubMed] [Google Scholar]
- Kidd, G., Jr., Mason, C. R., Richards, V. M., Gallun, F. J., and Durlach, N. I. (2008). “Informational masking,” Auditory Perception of Sound Sources, edited by Yost W. A., Popper A. N., and Fay R. R. (Springer, New York: ), pp. 143–189. [Google Scholar]
- Lutfi, A. (1993). “A model of auditory pattern analysis based on component-relative-entropy,” J. Acoust. Soc. Am. 94, 748–758. 10.1121/1.408204 [DOI] [PubMed] [Google Scholar]
- Lyzenga, J., Carlyon, R. P., and Moore, B. C. J. (2004). “The effects of real and illusory glides on pure-tone frequency discrimination,” J. Acoust. Soc. Am. 116, 491–501. 10.1121/1.1756616 [DOI] [PubMed] [Google Scholar]
- Macmillan, N. A., and Creelman, C. D. (2005). Dection Theory: A User’s Guide (Lawrence Erlbaum Associates, Mahwah, NJ: ). [Google Scholar]
- Macmillan, N. A., Kaplan, H. L., and Creelman, C. D. (1977). “Psychophysics of categorical perception,” Psychol. Rev. 84, 452–471. 10.1037/0033-295X.84.5.452 [DOI] [PubMed] [Google Scholar]
- Mauermann, M., Long, G. R., and Kollmeier, B. (2004). “Fine structure of hearing threshold and loudness perception,” J. Acoust. Soc. Am. 116, 1066–1080. 10.1121/1.1760106 [DOI] [PubMed] [Google Scholar]
- Micheyl, C., and Dai, H. (2009). “Likelihood ratio, optimal decision rules and relationship between proportion correct and d′ in the dual-pair AB-versus-BA identification paradigm,” Percept. Psychophys. 71, 1426–1433. 10.3758/APP.71.1.5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micheyl, C., Kaernbach, C., and Demany, L. (2008). “An evaluation of psychophysical models of auditory change perception,” Psychol. Rev. 115, 1069–1083. 10.1037/a0013572 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micheyl, C., and Messing, D. P. (2006). “Likelihood ratio, optimal decision rules and correct response probabilities in a signal detection theoretic, equal-variance Gaussian model of the observer in the 4IAX paradigm,” Percept. Psychophys. 68, 725–735. [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J. (1973). “Frequency difference limens for short-duration tones,” J. Acoust. Soc. Am. 54, 610–619. 10.1121/1.1913640 [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J. (1974). “Relation between critical bandwidth and frequency-difference limen,” J. Acoust. Soc. Am. 55, 359–359. 10.1121/1.1914512 [DOI] [PubMed] [Google Scholar]
- Moore, B. C. J., and Glasberg, B. R. (1989). “Mechanisms underlying the frequency discrimination of pulsed tones and the detection of frequency modulation,” J. Acoust. Soc. Am. 86, 1722–1732. 10.1121/1.398603 [DOI] [Google Scholar]
- Moore, B. C. J., Glasberg, B. R., Low, K. E., Cope, T., and Cope, W. (2006). “Effects of level and frequency on the audibility of partials in inharmonic complex tones,” J. Acoust. Soc. Am. 120, 934–944. 10.1121/1.2216906 [DOI] [PubMed] [Google Scholar]
- Neff, D. L., and Callaghan, B. P. (1988). “Effective properties of multicomponent simultaneous maskers under conditions of uncertainty,” J. Acoust. Soc. Am. 83, 1833–1838. 10.1121/1.396518 [DOI] [PubMed] [Google Scholar]
- Neff, D. L., and Dethlefs, T. M. (1995). “Individual-differences in simultaneous masking with random-frequency, multicomponent maskers,” J. Acoust. Soc. Am. 98, 125–134. 10.1121/1.413748 [DOI] [PubMed] [Google Scholar]
- Nordmark, J. O. (1968). “Mechanisms of frequency discrimination,” J. Acoust. Soc. Am. 44, 1533–1540. 10.1121/1.1911293 [DOI] [PubMed] [Google Scholar]
- Noreen, D. (1981). “Optimal decision rules for some common psychophysical paradigms,” Mathematical Psychology and Psychophysiology: Proceedings of the Symposium in Applied Mathematics of the American Mathematical Society and the Society for Industrial and Applied Mathematics, edited by Grossberg S. (American Mathematical Society, Providence, RI: ), Vol. 13, pp. 237–279.
- Pelli, D. G. (1985). “Uncertainty explains many aspects of visual contrast detection and discrimination,” J. Opt. Soc. Am. A 2, 1508–1532. 10.1364/JOSAA.2.001508 [DOI] [PubMed] [Google Scholar]
- Peretz, I., Champod, S., and Hyde, K. (2003). “Varieties of musical disorders: The Montreal battery of evaluation of amusia,” Ann. N. Y. Acad. Sci. 999, 58–75. 10.1196/annals.1284.006 [DOI] [PubMed] [Google Scholar]
- Schlauch, R. S., and Hafter, E. R. (1991). “Listening bandwidths and frequency uncertainty in pure-tone signal-detection,” J. Acoust. Soc. Am. 90, 1332–1339. 10.1121/1.401925 [DOI] [PubMed] [Google Scholar]
- Sek, A., and Moore, B. C. J. (1999). “Discrimination of frequency steps linked by glides of various durations,” J. Acoust. Soc. Am. 106, 351–359. 10.1121/1.427061 [DOI] [PubMed] [Google Scholar]
- Semal, C., and Demany, L. (2006). “Individual differences in the sensitivity to pitch direction,” J. Acoust. Soc. Am. 120, 3907–3915. 10.1121/1.2357708 [DOI] [PubMed] [Google Scholar]
- Suzuki, Y., and Takeshima, H. (2004). “Equal-loudness-level contours for pure tones,” J. Acoust. Soc. Am. 116, 918–933. 10.1121/1.1763601 [DOI] [PubMed] [Google Scholar]
- Tramo, M. J., Shah, G. D., and Braida, L. D. (2002). “Functional role of auditory cortex in frequency processing and pitch perception,” J. Neurophysiol. 87, 122–139. [DOI] [PubMed] [Google Scholar]
- Watson, C. S. (2005). “Some comments on informational masking,” Acust. Acta Acust. 91, 502–512. [Google Scholar]
- Wier, C. C., Jesteadt, W., and Green, D. M. (1977). “Frequency discrimination as a function of frequency and sensation level,” J. Acoust. Soc. Am. 61, 178–184. 10.1121/1.381251 [DOI] [PubMed] [Google Scholar]