Integration of auditory and vibrotactile stimuli: Effects of frequency

Abstract

Perceptual integration of vibrotactile and auditory sinusoidal tone pulses was studied in detection experiments as a function of stimulation frequency. Vibrotactile stimuli were delivered through a single channel vibrator to the left middle fingertip. Auditory stimuli were presented diotically through headphones in a background of 50 dB sound pressure level broadband noise. Detection performance for combined auditory-tactile presentations was measured using stimulus levels that yielded 63% to 77% correct unimodal performance. In Experiment 1, the vibrotactile stimulus was 250 Hz and the auditory stimulus varied between 125 and 2000 Hz. In Experiment 2, the auditory stimulus was 250 Hz and the tactile stimulus varied between 50 and 400 Hz. In Experiment 3, the auditory and tactile stimuli were always equal in frequency and ranged from 50 to 400 Hz. The highest rates of detection for the combined-modality stimulus were obtained when stimulating frequencies in the two modalities were equal or closely spaced (and within the Pacinian range). Combined-modality detection for closely spaced frequencies was generally consistent with an algebraic sum model of perceptual integration; wider-frequency spacings were generally better fit by a Pythagorean sum model. Thus, perceptual integration of auditory and tactile stimuli at near-threshold levels appears to depend both on absolute frequency and relative frequency of stimulation within each modality.

INTRODUCTION

Recent anatomical and neurophysiological research has shown evidence of interaction between the auditory and somatosensory systems at various levels of the central nervous system in both animals (e.g., Zhou and Shore, 2004; Cappe and Barone, 2005; Schroeder et al., 2001) and in humans (Foxe et al., 2002; Schürmann et al., 2006). Perceptual studies also provide evidence for auditory-somatosensory interactions. For example, facilitative interactions between audition and touch have been observed using subjective techniques such as loudness matching (e.g., Schürmann et al., 2004; Gillmeister and Eimer, 2007; Yarrow et al., 2008) as well as objective measurements of detection and discrimination (e.g., Schnupp et al., 2005; Wilson et al., 2009; Yau et al., 2009; Ro et al., 2009). Other studies (Gescheider et al., 1969; Gescheider, 1970), however, have reported inhibitory results for the detection of a tactile stimulus in the presence of a suprathreshold auditory tone.

Background

Our previous research in this area (Wilson et al., 2009) examined the perceptual integration of auditory and vibrotactile 250 Hz tones in an objective detection task as a function of the relative phase and temporal asynchrony of 500 ms tone pulses. Our results showed that performance increased significantly over unimodal detection when the auditory and tactile signals were presented synchronously, and that the combined performance increase was not affected by the relative phase between the auditory and tactile stimuli. The lack of a phase effect suggests integration operates on the slowly varying envelopes of the auditory and tactile stimuli rather than on their temporal fine structure, the cycle by cycle variation in the auditory and tactile waveforms. The effects of presenting the auditory and tactile stimuli with no temporal overlap (i.e., asynchronously) were consistent with time constants deduced from single-modality masking experiments. For example, when the tactile signal preceded the auditory signal, a significant increase in performance was observed for temporal separations up to 100 ms between the offset of the tactile stimulus and the onset of the auditory stimulus. On the other hand, when the auditory stimulus was presented before the tactile stimulus (with no temporal overlap), performance on the combined condition was not significantly different from performance on either the auditory- or tactile-alone conditions.

The current study extends our previous work by examining the effects of stimulus frequency on auditory-tactile integration when stimuli in both modalities are presented simultaneously at signal levels near the threshold of detection. Given that both of these sensory systems respond differentially to frequency (auditory: Fletcher and Wegel, 1922; Fletcher, 1940; Dadson and King, 1952; Watson et al., 1972; Romani et al., 1982; Bilecen et al., 1998; Schreiner et al., 2000; Talavage et al., 2000; Talavage et al., 2004; somatosensory: Bolanowski et al., 1988; Francis et al., 2000;Gescheider et al., 2002; Gescheider et al., 2001; Harrington and Downs, 2001; Harris et al., 2006; Hegner et al., 2007; Iguchi et al., 2007) and that the frequency region to which both systems are responsive is limited, it is possible that frequency of stimulation may be an important variable in auditory-tactile perceptual interactions. Specifically, we hypothesize that if the auditory and tactile systems integrate into a common neural pathway, then interaction effects should be greater than when they integrate in different pathways. Furthermore if the same frequency is conveyed by a common pathway and different frequencies are conveyed by different pathways, then integration effects should be greater when both modalities are stimulated by the same frequency than by different frequencies.

This paper explores the frequency relationship between audition and touch in a signal detection task in three experiments. In Experiment 1, the frequency of the auditory component assumed values in the range of 125–2000 Hz while the frequency of the tactile component was held constant at 250 Hz. In Experiment 2, the frequency of the tactile signal assumed values in the range of 50–400 Hz while the frequency of the auditory component was held constant at 250 Hz. In Experiment 3, the frequencies of the auditory and tactile stimuli were equal to each other and assumed values in the range of 50–400 Hz. For comparison purposes, we tested purely auditory detection with a 250 Hz narrowband noise (NBN) that was combined with a tone of frequency ranging from 125 to 2000 Hz (Appendix0). These experiments were designed (a) to test the effects of frequency separation between the auditory and tactile components on multisensory integration and (b) to test the effects of frequency of stimulation when the auditory and tactile stimulating frequencies were equal to one another and covarying. Measurements of d^′ (and % correct) were obtained for auditory-alone, tactile-alone, and combined auditory-tactile presentations. The observed performance in the combined condition was then compared to predictions of multimodal performance derived from observed measures of detectability within each of the two separate sensory modalities.

Theory

Green (1958) and Marill (1956) considered a variety of models to relate the detectability of individual tones to the detectability of auditory two-tone complexes. Green considered a “statistical decision model” by analyzing linear combinations of the observations made on the two tones of the complex [X(f₁) and X(f₂)]:

$$Z=aX\left(f_1\right)+bX\left(f_2\right).$$

He showed that (i) under the assumption that X(f₁) and X(f₂) are uncorrelated Gaussian random variables, the optimal choice of a and b leads to a detectability index

$$d^{\prime }{}_Z={\left({\left(d^{\prime }{}_1\right)}^2+{\left(d^{\prime }{}_2\right)}^2\right)}^{1∕2},$$

where d^′₁ and d^′₂ are the detectability indices of the two tones separately and (ii) when X(f₁) and X(f₂) are perfectly correlated, the optimal choice of a and b leads to a detectability index

$$d^{\prime }{}_Z=d^{\prime }{}_1+d^{\prime }{}_2.$$

Thus when the observations are contaminated by independent noise, the Pythagorean sum applies, whereas when they are contaminated by correlated noise, the arithmetic sum applies. Green’s (1958) “no-summation model” assumed that the detectability of the complex was equal to the detectability index of the more detectable of the tones:

$$d^{\prime }{}_Z=\text{max}\left(d^{\prime }{}_1,d^{\prime }{}_2\right).$$

Green (1958) also considered a form of “probability summation” that assumes that in the detection of a single tone, a decision variable must exceed a threshold value. In the particular probability summation model considered, the “two independent thresholds model,” when two tones are presented and the decision variables associated with them are independent, a detection response will result if either or both tones exceeds the threshold value of the decision variable.

Green (1958) measured the detection of pure tones of frequency 500, 1000, 1823, and 2000 Hz as well as all pairs made up from these tones. Green tested three listeners on the detection of 50, 200, and 1000 ms tone bursts in 60 dB spectrum level noise using a four-alternative forced choice procedure. He rejected the no-summation model because the percentage of correct detections of the two-tone complex was greater than the percentage of correct detections of the most detectable component in the complex in 53 out of 54 cases. Green (1958) rejected the two independent thresholds model because it had an average error of roughly 5% whereas the Pythagorean form of the statistical decision model had an average error of only 1.5%. He did not consider the arithmetic sum form of the statistical decision model, although it seems unlikely to have made good predictions for these data.

Marill (1956) tested two listeners on the detection of 1 s bursts of 500 and 1100 Hz tones in 57 dB spectrum level noise as a function of signal level in a two-interval, two-alternative forced choice (2I, 2AFC) experiment. He then measured the detection of pairs of tones (500, 540), (1060, 1100), and (500, 1100) Hz. Marill (1956) compared his results to models similar to Green’s (1958) no-summation model and the arithmetic sum form of the statistical decision model. He found that the no-summation model predicted the detectability of the (500, 1100 Hz) pair whereas the arithmetic sum form of the statistical decision model predicted the detectability of the (1060, 1100 Hz) pair. The detectability of the (500, 540 Hz) pair fell between the predictions of these two models, and would likely been explained by the Pythagorean form of the statistical decision model.

Recently, Grose and Hall (1997) tested eight listeners using a three-alternative forced choice adaptive procedure with a masker consisting of 20 Hz wide bands of noise presented at 35 dB spectrum level. They found that a Pythagorean sum type model accounted for the detection of pairs consisting of 870 and 1125 Hz tones of duration 400 ms.

In previous work on multimodal auditory-tactile detection (Wilson et al., 2009), we compared results to three different models that were similar to those considered by Green (1958). The optimal single channel model (OSCM) is similar to Green’s no-summation model; the Pythagorean sum model (PSM) is similar to the Pythagorean sum form of Green’s statistical decision model; and the algebraic sum model (ASM) is similar to the arithmetic sum version of Green’s statistical decision model. The OSCM assumes that the observers’ responses are based on the better of the tactile or auditory input channels; the PSM assumes that integration occurs across channels (e.g., as in audiovisual integration, Braida, 1991) and that the combined auditory-tactile response is the Pythagorean sum of the separate channels; and the ASM assumes that integration occurs within a given channel and that the combined response is the linear sum of the scores for the separate channels. We did not consider models based on probability summation based on Green’s finding that the predictions of such models were inferior to the Pythagorean sum version of the statistical decision model. We found that on average, the observed scores tended to be greater than the prediction of the OSCM and the PSM but less than the prediction of the ASM. The same models of integration were applied in the current research to determine the manner in which properties of integration are affected by frequency of stimulation in each modality.

METHODS

Stimuli

The auditory stimuli were pure tones presented in a background of pulsed 50 dB sound pressure level (SPL) Gaussian broadband noise (bandwidth of 0.02–11.0 kHz). The frequency of the auditory stimulus across the three experiments was 50, 125, 250, 400, 500, 1000, and 2000 Hz. The tactile stimuli were sinusoidal vibrations with a frequency of 50, 125, 250, and 400 Hz across the three experiments. The background noise was used to mask possible auditory cues arising from the tactile device and was present in all auditory (A), tactile (T), and combined auditory plus tactile (A+T) test conditions. Sinusoidal signals in both modalities were generated digitally (using MATLAB 7.1 software) to have a total duration of 500 ms that included 20 ms raised cosine-squared rise∕fall times.

The digitized signals were played through a D∕A sound card (Lynx Studio Lynx One, Costa Mesa, CA) with a sampling frequency of 24 kHz and 24 bit resolution. The auditory signal was sent through channel 1 of the sound card to a programmable attenuator (TDT PA4) and headphone buffer (TDT HB6) before being presented diotically through headphones (Sennheiser HD 580). The tactile signal was passed through channel 2 of the sound card to a programmable attenuator (TDT PA4) and amplifier (Crown D-75) before being delivered to an electromagnetic vibrator (Alpha-M Corporation, model A V-6, Dallas, TX). The subject’s left middle fingertip made contact with the vibrator (0.9 cm diameter) which was housed inside a wooden box for visual shielding and sound attenuation. A heating pad was placed inside the box to keep the box and tactile device at a constant temperature. A laser accelerometer was used to calibrate the tactile device so that displacement could be measured from input voltage.

Subjects

Eight subjects ranging in age from 18 to 45 years (four females) participated in this study. Audiological testing was conducted on the first visit to the laboratory. Only those subjects who met the criterion of normal audiometric thresholds (20 dB hearing level or better at frequencies of 125, 250, 500, 1000, 2000, 4000, and 8000 Hz) were included in the studies. All subjects were paid an hourly wage for their participation in the experiments and signed an informed-consent document prior to entry into the study. All subjects except S₁₃ were right handed. Five subjects participated in Experiment 1 (S₁, S₆, S₁₀, S₁₃, and S₁₄), four in Experiment 2 (S₁, S₆, S₁₀, and S₁₁), and four in Experiment 3 (S₆, S₁₀, S₁₈, and S₂₂). Three of the subjects participated in multiple experiments (S₁: Experiments 1 and 2; S₆ and S₁₀: Experiments 1, 2, and 3). These three subjects also participated in experiments conducted by Wilson et al. (2009) and subject identification is consistent with that used in our previous paper.

Experimental conditions

The experiments examined the perceptual integration of sinusoidal auditory and vibrotactile signals with different values of frequency, which were presented near the threshold of detection. Within a given test session, threshold measurements were first obtained under each of the two single-modality conditions (A and T separately). Then the detectability of the combined A+T signal was measured at levels established for threshold within each of the two individual modalities. The experimental conditions examined the effects of frequency under different relative conditions: Auditory frequency varied, tactile frequency constant (Experiment 1); tactile frequency varied, auditory frequency constant (Experiment 2); and auditory and tactile frequency equal and covaried (Experiment 3).

For all A+T conditions, the auditory and tactile sinusoids were presented in sinusoidal phase with equal onset and offset times.

Baseline condition. A baseline condition employing an equal frequency of 250 Hz for both A and T stimulation was included in each of the experiments.1

Experiment 1. Experiment 1 examined the effect of varying the frequency of the auditory stimulus while holding the tactile stimulus frequency constant. The frequency of the tactile stimulus was held constant at 250 Hz while the frequency of the auditory stimulus took on five different values: 125, 250, 500, 1000, and 2000 Hz resulting in five separate experimental conditions: A125+T250, A250+T250, A500+T250, A1000+T250, and A2000+T250. The order of the five experimental A+T conditions was randomized for each of four replications for each of the five subjects. Subjects S₁, S₆, S₁₀, S₁₃, and S₁₄ participated in this experiment. Subjects required a total of 5 days (S₆) to 12 days (S₁) of testing to complete the experiment.

Experiment 2. Experiment 2 examined the effect of varying the frequency of the tactile stimulus while holding the auditory stimulus frequency constant. The frequency of the auditory stimulus was held constant at 250 Hz while the frequency of the tactile stimulus took on four different values: 50, 125, 250, and 400 Hz resulting in four separate experimental conditions: A250+T50, A250+T125, A250+T250, and A250+T400. The order of the four experimental A+T conditions was randomized for each of four replications for each of the four subjects. Subjects S₁, S₆, S₁₀, and S₁₁ participated in this experiment. One subject (S₁₁) required 6 days to complete the repetitions of the four combined runs, while the remaining three subjects (S₁, S₆, and S₁₀) required 10 days.

Experiment 3. Experiment 3 examined the effect of covarying the frequencies of both the tactile and auditory stimulus while holding them equal to one another. The frequencies of the auditory and tactile stimuli were 50, 125, 250, and 400 Hz resulting in four separate experimental conditions: A50+T50, A125+T125, A250+T250, and A400+T400. The order of the four experimental A+T conditions was randomized for each of four replications for each of the four subjects. Subjects S₆, S₁₀, S₁₈, and S₂₂ participated in this experiment. Two subjects (S₁₀ and S₂₂) required 9 total days, while S₆ and S₁₈ required 11 and 12 days of testing, respectively, to complete the experiment.

Experimental procedures

For all experimental conditions, subjects were seated in a sound-treated booth and were presented with 50 dB SPL broadband noise diotically via headphones. For testing in conditions that involved presentation of the tactile stimulus (T and A+T), the subject placed the left middle finger on the electromagnetic vibrator. In each experimental session, testing was first conducted for A-alone and T-alone separately to establish a signal level for single-modality performance in the range of 63% to 77% correct. Performance was then measured in the A+T conditions for a given experiment. The number of experimental A+T conditions that could be completed within a given test session was generally dependent on the time required to establish signal levels that met the single-modality performance criterion. Each experimental session lasted no more than 2 h on any given day and subjects were required to take frequent breaks throughout the session. For each subject, three training sessions identical to the experimental sessions were provided before data were recorded.2

In Experiments 1 and 2, certain single-modality conditions were retested in the fixed-level procedure before the end of each session to ensure that thresholds remained stable throughout the session. For Experiment 1, only T-alone was retested and for Experiment 2, only A-alone was retested. No post-session test was performed for Experiment 3 because the thresholds were measured immediately preceding each combined run. If single-modality thresholds were less than 56% correct or greater than 84% correct (±2 standard deviations assuming an original score of 70% correct), the data for that session were discarded. If a subject’s threshold shifted more than 2 standard deviations in three nontraining sessions, our policy was to terminate that subject from the study; however, all subjects met the qualification for threshold stability and none was disqualified on these grounds.

2I, 2AFC tests. The threshold estimates under the single-modality A and T conditions employed a 2I, 2AFC fixed-level procedure with 75 trials per run. Stimulus levels were adjusted and runs were repeated until scores of 63% to 77% correct were obtained. These stimulus levels were then used in testing the combined A+T conditions with the fixed-level 2I, 2AFC procedure.

On each presentation, the stimulus (A, T, or A+T) was presented with equal a priori probability in one of the two intervals. The interval duration was 1.1 s for all experiments. Each observation interval was marked by a visual cue that appeared on a computer terminal located in front of the subject. Noise was presented diotically over headphones starting 500 ms before the first interval, and played continuously throughout a trial (including the durations of the two intervals and the 500 ms duration between intervals) before being turned off 500 ms after the end of the second interval. Each trial had a fixed duration of 3.7 s, plus the time it took subjects to respond. The onset of the stimulus (A, T, or combined A+T) was always coincident with the onset of the observation interval in which it appeared. Subjects responded between trials by selecting the interval in which they thought the stimulus was presented (using either a mouse or keyboard) and were provided with visual correct-answer feedback after each trial. Attention to the combined A+T stimulus was encouraged by having subjects count the number of times they perceived a signal.

Data analysis

A two-by-two stimulus-response confusion matrix was constructed for each 75-trial experimental run, and was used to determine percent-correct scores and signal-detection measures of sensitivity (d^′). These measures were averaged across the repetitions of each experimental condition within a given subject. Statistical tests performed on the data included analyses of variance (ANOVAs) on the arcsine-transformed percent-correct scores, with statistical significance level defined for probability (p-values) less than or equal to 0.01. For statistically significant effects a post hoc Tukey–Kramer analysis was performed with alpha=0.05.

Models of integration

The results of the experiments were compared with three different models of integration: OSCM, PSM, and ASM. The OSCM assumes that the observers’ responses are based on the better of the tactile or auditory input channels. The predicted D^′_OSCM3 for the combined A+T condition is the greater of the tactile (d^′_T) or auditory (d^′_A), D^′_OSCM=max(d^′_T,d^′_A). The PSM assumes that integration occurs across channels (e.g., as in audiovisual integration, Braida, 1991) and that the d^′ in the combined auditory-tactile condition is the Pythagorean sum of the d^′ values for the separate channels, $D^{\prime }{}_{\text{PSM}}=\sqrt{d^{\prime }{}_A{}^2+d^{\prime }{}_T{}^2}$. The ASM, on the other hand, assumes that integration occurs within a given channel and that the combined d^′ is the linear sum of the d^′ values for the separate channels, D^′_ASM=d^′_A+d^′_T. For example, if the auditory d^′_A was 1.0 (69% correct) and the tactile d^′_T was 0.8 (66% correct), the OSCM would predict a D^′_OSCM of 1.0 (69% correct), the PSM would predict a D^′_PSM of 1.28 (74% correct), and the ASM would predict a D^′_ASM of 1.8 (82% correct). The OSCM prediction is never greater than the PSM prediction, which in turn is never greater than the prediction of the ASM.

Chi-squared goodness-of-fit calculations were employed to compare observed with predicted values from each of the three models. The predictions of the models were evaluated as follows: First, d^′ values were determined for each auditory (d^′_A) and tactile (d^′_T) experiment, on the basis of 75 total trials. Second, predicted d^′ values were computed for the three models according to the formulas given above. Third, predicted % correct scores were computed for each of the models in the following manner: % correct=100ϕ((D^′_A+T)∕2), where ϕ is the cumulative of the Gaussian distribution function, and D^′_A+T is the predicted D^′. Fourth, the observed A+T confusion matrix was analyzed to estimate d^′_A+T and the “no bias” estimate of % correct score was computed as %_A+T=100ϕ((d^′_A+T)∕2). This relatively small adjustment (1.6 percentage points on average, 13 points maximum) was necessary because the predictions of the models assumed that the observer is not biased. Predictions (D^′_OSCM, D^′_PSM, and D^′_ASM or %_OSCM, %_PSM, and %_ASM) were compared with observations (d^′_A+T or %_A+T). The proportion of the observations that agreed with predictions was judged by having a chi-squared value less than 3.841 (the 95% criterion) between predicted and observed scores (corrected as discussed above) using a contingency table analysis (Neville and Kennedy, 1964). This analysis allows for errors in both the observed score and the predicted score.

RESULTS

Signal levels employed in single-modality conditions

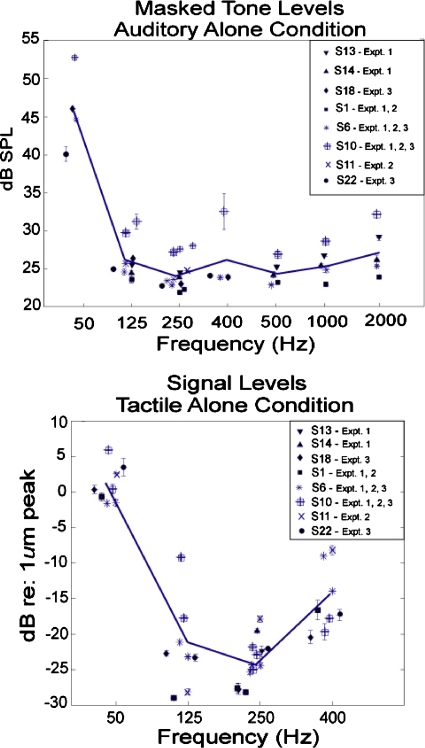
Levels for auditory-alone conditions. The mean signal levels that yielded performance in the range of 63% to 77% correct for auditory pure tones in 50 dB SPL broadband noise are shown in the upper panel of Fig. 1. Frequencies measured in these experiments included 50, 125, 250, 400, 500, 1000, and 2000 Hz. Mean levels are plotted for each individual subject for the frequencies tested in each of the three experiments. Each data point depicted in the plot is based on an average of at least 4 and as many as 11 measurements per frequency. Averaged across subjects and experiments, the mean threshold level for each of the tones is shown as a solid line. Within a given subject, levels for all frequencies tested were highly stable for measurements made within a given experiment and across experiments. For all but one subject, values of ±2 standard error of the mean (SEM) (accounting for 96% of the measurements) ranged from 0.0 to 1.92 dB across subjects and experiments. For that subject (S₁₀), variability was slightly higher (2.77 dB) in the 400 Hz condition in Experiment 3.

Figure 1.

Single-modality signal levels employed for individual subjects tested in each of the four experiments. Auditory levels are for detection of pure tones in 50–dB SPL broadband noise. Tactile levels are for detection of sinusoidal vibrations presented to the fingertip. Different symbols represent results obtained in different experiments. Some subjects participated in more than one experiment. Solid line indicates the average across subjects and experiments for each frequency. Error bars are 1 SEM.

Critical ratios (CRs) were calculated for the tone-in-noise levels shown in Fig. 1 by subtracting the spectrum level of the noise from the presentation levels of the different tones employed in these experiments. The spectrum level was flat from approximately 100 Hz to 11 kHz (7.4 dB) but was 20 dB at 50 Hz. The magnitude of the CR was consistent with the values reported by Hawkins and Stevens (1950) in the range of 125–2000 Hz, and with values reported by Houtsma (2004) for 50 Hz tones. These results indicate that subjects were listening to tones at levels near masked threshold.

Levels for tactile-alone conditions. The mean signal levels that yielded performance in the range of 63%–77% correct for a sinusoidal vibration (50, 125, 250, and 400 Hz) to the left middle fingertip are shown in the lower panel of Fig. 1. All threshold measurements were obtained in the presence of a diotic 50 dB SPL broadband noise presented over headphones. Mean levels are shown for individual subjects who participated in each of the three experiments. Each data point is based on 4–20 measurements per frequency across individual subjects and experiments. The average level across subjects is represented by the solid line in the lower panel of Fig. 1. Within-subject values of ±2 SEM (accounting for 96% of the measurements) ranged from 0 to 2.2 dB across subjects and experiments.

Mean thresholds measured across the three experiments were 1.0 dB re 1 μm peak at 50 Hz, −21.7 dB at 125 Hz, −24.2 dB at 250 Hz, and −14.6 dB at 400 Hz. These threshold values are consistent with previous measurements using contactor areas in the range of 28–150 mm² (e.g., Gescheider et al., 2002; Verrillo et al., 1983; Lamoré et al., 1986; Rabinowitz et al., 1987; Verrillo, 1963) and show a similar frequency dependence. Specifically, maximal sensitivity is obtained at 250 Hz and thresholds increase at frequencies above and below this value.

Baseline experiment

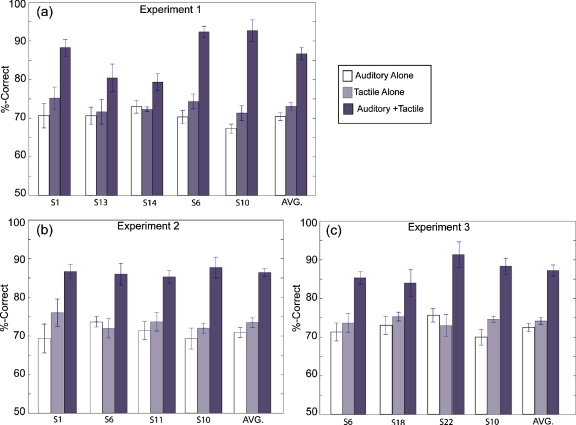
Results from the baseline experiment are shown for individual subjects in Experiments 1–3 in the three panels of Fig. 2 [Figs. 2a, 2b, 2c, respectively]. The mean % correct scores with error bars depicting ±1 SEM are plotted for the three conditions of A-alone, T-alone, and A+T (auditory and tactile frequency=250 Hz across the three experiments) for each subject within each experiment. Averages across subjects are provided as the rightmost data bars within each panel. For each of the three experiments, there is a substantial increase in the % correct score for the A+T condition compared with the A-alone and T-alone conditions. The mean scores on each condition, averaged over subjects, were similar across experiments: A-alone values were 70.5, 71.5, and 72.9% correct (Experiments 1–3, respectively); T-alone values were 70.9, 72.6, and 74.3% correct (Experiments 1–3, respectively); and A+T values were 86.6, 86.3, and 87.9% correct (Experiments 1–3, respectively). Variability on the combined A+T condition was generally low, with values of ±2 SEM ranging from 2.8 to 7.0 percentage points across subjects and experiments. These results are consistent with values previously reported by Wilson et al. (2009) for the baseline experiment.

Figure 2.

Summary of results for the baseline condition in Experiments 1–3. Percent-correct scores for the individual subjects in each experiment are averaged across multiple repetitions per condition; number of repetitions varies by subject, and is equal to or greater than four per subject. AVG is an average across subjects and repetition in each experiment. White bars represent auditory-alone conditions, gray bars represent tactile-alone conditions, and black bars represent the A+T baseline condition with auditory and tactile frequencies=250 Hz, simultaneous presentation. Error bars are 1 SEM.

A two-way ANOVA was performed on the arcsine-transformed percent-correct scores of the baseline experiment to examine the main effects of condition (A, T, and A+T) and subject (eight different subjects across experiments). The results indicate a significant main effect for condition [F(2,111)=88.5, p<0.01] but not for subject [F(7,111)=2.09, p>0.01] or for their interaction [F(14,111)=1.99, p>0.01]. A post hoc analysis of the main effect of condition showed that scores on the A+T condition were significantly greater than on the A-alone and T-alone conditions and that the A-alone and T-alone conditions were not significantly different from one another.

Experiment 1: Auditory frequency varied, tactile frequency constant

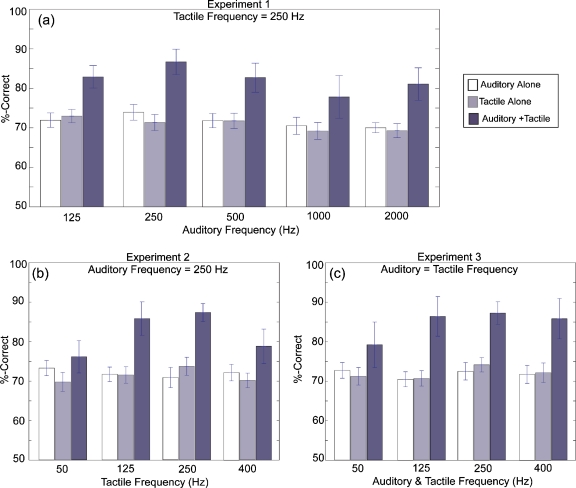
The results of Experiment 1 are shown in Fig. 3a. Percent-correct scores averaged across five subjects and four repetitions per condition are shown for each of the five experimental conditions: A-alone, T-alone, and combined A+T with five different values for the frequency of the auditory tone (125, 250, 500, 1000, and 2000 Hz) while the frequency of the tactile tone remained constant at 250 Hz. The average score for T-alone was 70.9% correct. The average score for A-alone ranged from 69.1% correct (2000 Hz) to 72.3% correct (125 Hz). Variability in terms of ±2 SEM was small and ranged from 1.3 (A=2000 Hz) to 2.3 (A=1000 Hz) percentage points across all single-modality conditions. Average scores for the A+T conditions changed as a function of auditory stimulus frequency. The highest score of 86.6% correct was obtained with A=250 Hz. The A+T conditions with other auditory frequencies resulted in lower scores: 125 Hz=82.5% correct, 500 Hz=82.0% correct, 1000 Hz=77.5% correct, and 2000 Hz=80.6% correct. Variability was small, with ±2 SEM values ranging from 2.9 (A=125 Hz) to 5.0 (A=1000 Hz) percentage points.

Figure 3.

Summary of results for Experiment 1 (3a), Experiment 2 (3b), and Experiment 3 (3c). Percent-correct scores are averaged across subjects and sessions. Scores are shown for A-alone (white bars), T-alone (light gray bars), and for combined A+T conditions (dark gray bars). In Experiment 1, scores are shown as a function of auditory frequency with tactile frequency=250 Hz. In Experiment 2, scores are shown as a function of tactile frequency with auditory frequency=250 Hz. In Experiment 3, scores are shown as a function of frequency where auditory=tactile. Error bars are 1 SEM.

A two-way ANOVA was performed on the arcsine-transformed percent-correct scores with main factors of condition (A, T, and A+T) and subject. The A condition includes A-alone measures at the five auditory frequencies, the T condition includes T-alone measures at 250 Hz, and the A+T condition includes five auditory-tactile frequency combinations. The results of the ANOVA indicate significant main effects for condition [F(14,225)=27.41, p<0.01] and subject [F(4,225)=7.71, p<0.01] as well as a significant interaction between them [F(56,225)=3.67, p<0.01]. The post hoc analysis of the condition effect indicated that all of the A-alone scores and T-alone scores were statistically equivalent and that the scores on each of the five A+T frequency combinations were significantly higher than each of the unimodal scores. Within the five A+T frequency combinations, the post hoc analysis indicated that the A250+T250 score was significantly greater than the scores for A500+T250, A1000+T250, and A2000+T250 but was not significantly different from the score for A125+T250; no other significant differences were found among the remaining A+T frequency combinations. The mean performance of the subjects was ordered as S₁₄<S₁₃<S₆<S₁<S₁₀. A post hoc analysis of the main effect for subject indicated that the following differences among subjects were significant: the scores of S₁₄ were significantly less than those of S₁ and S₁₀, the scores of S₁₃ were significantly lower than those of S₁₀, and the scores of S₆ were not significantly different from those of any other subject. The interaction effect arises in part from different patterns of performance for individual subjects on the A2000+T250 condition.

Experiment 2: Tactile frequency varied, auditory frequency constant

The results of Experiment 2 are shown in Fig. 3b. Percent-correct scores averaged across four subjects and four repetitions per condition are shown for each of the four experimental conditions: A-alone, T-alone, and combined A+T with constant auditory stimulus frequency (250 Hz) and four different values of the tactile stimulus frequency (50, 125, 250, and 400 Hz). The average score for A-alone was 71.3% correct. T-alone scores ranged from 69.8% correct (at T=50 Hz) to 73.4% correct (at T=250 Hz). Variability in terms of ±2 SEM was small and ranged from 1.6 (A=250 Hz) to 2.4 (T=250 Hz) percentage points across all single-modality conditions. Average scores for the A+T conditions changed as a function of tactile stimulus frequency. The highest score of 86.4% correct was obtained with a tactile frequency of 250 Hz. Lower scores were obtained with other tactile frequencies: 50 Hz=76.2% correct, 125 Hz=85.8% correct, and 400 Hz=78.8% correct. Variability was small, with ±2 SEM values ranging from 2.1 (T=250 Hz) to 4.4 (T=400 Hz) percentage points.

A two-way ANOVA was performed on the arcsine-transformed percent-correct scores with main factors of condition (A, T, and A+T) and subject. The A condition includes A-alone measures at 250 Hz, the T condition includes T-alone measures at 50, 125, 250, and 400 Hz, and the A+T condition includes the four auditory-tactile frequency combinations. The results of the ANOVA indicate a significant main effect for condition [F(11,144)=21.03, p<0.01] but not for subject [F(3,144)=1.96, p>0.01], and a significant interaction effect [F(33,144)=2.12, p<0.01]. The post hoc analysis of the condition effect indicated the following: All of the A-alone scores and T-alone scores were statistically equivalent; the A250+T50 score was not statistically different from any of the A-alone and T-alone scores or from the A250+T400 score, the A250+T400 score was significantly higher than six of the eight unimodal scores (including those at A250 and T400) but significantly lower than the A250+T125 and A250+T250 scores, and that the scores on A250+T125 and A250+T250 were not statistically different but were significantly higher than all the other unimodal and bimodal scores. The subject×condition interaction arises primarily from the superior performance of S₁₀ on the A250+T125 condition.

Experiment 3: Auditory and tactile frequency equal and covaried

The results of Experiment 3 are shown in Fig. 3c. Percent-correct scores averaged across four subjects and four repetitions per condition are shown for each of the four experimental conditions: A-alone, T-alone, and combined A+T with four different values of frequency where A=T (50, 125, 250, and 400 Hz). Average scores for A-alone ranged from 70.5% correct (at 125 Hz) to 72.5% correct (at 50 and 250 Hz) and the T-alone scores ranged from 70.6% correct (at 50 Hz) to 74.1% correct (at 250 Hz). Variability in terms of ±2 SEM was small and ranged from 1.9 (A=50 Hz) to 2.4 (T=50 Hz) percentage points across all single-modality conditions. Average scores for the A+T conditions were 78.3%, 86.47%, 87.25%, and 85.8% correct for auditory-tactile frequencies of 50, 125, 250, and 400 Hz, respectively. Variability was smallest on the 250 Hz condition, with a ±2 SEM value of 2.8 percentage points, while that of other frequencies ranged from 5.0 (125 Hz) to 5.6 (50 Hz) percentage points.

A two-way ANOVA was performed on the arcsine-transformed percent-correct scores with main factors of condition (A, T, and A+T) and subject. The A condition includes A-alone measures at four frequencies, the T condition includes T-alone measures at four frequencies, and the A+T condition includes the four auditory-tactile frequency combinations. The results of the ANOVA indicate significant main effects for condition [F(11,141)=31.38, p<0.01] and subject [F(3,141)=10.15, p<0.01] as well as a significant interaction effect [F(33,141)=5.92, p<0.01]. The post hoc analysis of the condition effect indicated that all of the A-alone scores and T-alone scores were statistically equivalent, that scores on A50+T50 were significantly higher than seven of the eight unimodal scores (including A50 and T50) but significantly lower than those of the remaining three A+T conditions, and that scores on A125+T125, A250+T250, and A400+T400 were statistically equivalent and significantly higher than all remaining conditions. The post hoc analysis of the subject effect indicated that the scores of S₁₀ were significantly higher than those of the remaining three subjects (whose scores were not significantly different from each other). The interaction effect arises primarily from differential performance among subjects on the A50+T50 condition.

Comparisons to model predictions

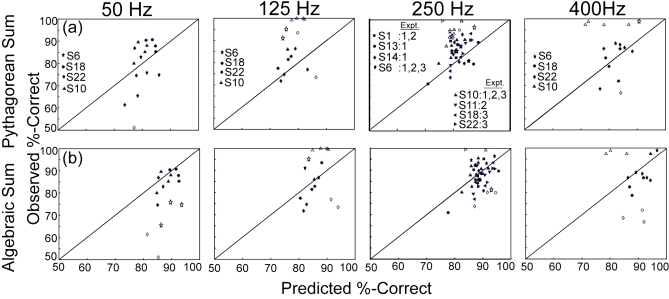
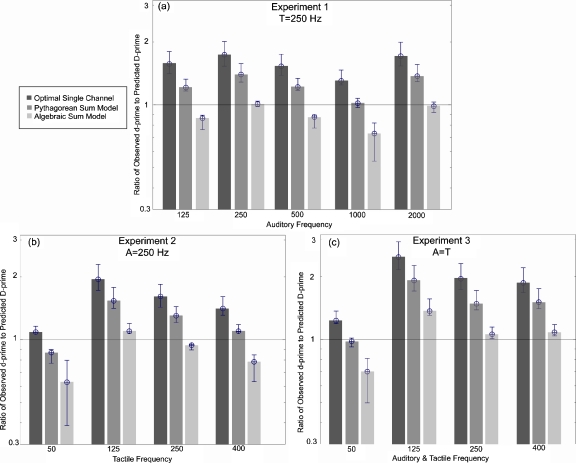
Chi-squared goodness-of-fit tests were performed on the data in order to examine which model, the OSCM, the PSM, or the ASM, best fit the measured percent-correct scores (Sec. 2F). The proportion of observations in agreement with predictions, i.e., having a chi-squared value less than 3.841, is summarized in Table 1. Figures 4a, 4b show plots of the observed versus predicted percent-correct scores for PSM and ASM, respectively, for the data set from Experiment 3 (auditory and tactile frequencies equal and covaried). These conditions were chosen because they represent an extension of the baseline data from Wilson et al. (2009) and because they demonstrate the best fits to the PSM and ASM models. [For the original Baseline condition (250 Hz panel), data are also included from Experiments 1 and 2.] The remaining conditions (i.e., in which the frequency of the auditory and tactile stimuli were different from one another) are summarized in Table 1, but not displayed. In Figs. 5a, 5b, 5c, the ratio of observed d^′ to predicted D^′ is plotted as a function of stimulus frequency for each of the three experiments (Experiments 1–3, respectively).

Table 1.

Chi-squared tests: predicted vs observed. This table enumerates the number of observations that have passed∕failed the chi-squared goodness of fit test for each of the three models (i.e., optimal single channel, Pythagorean sum, and algebraic sum).

Expt.	Auditory freq.	Tactile freq.	Total	Optimal single channel			Pythagorean sum			Algebraic sum
				Pass	Fail	Under-predict Fail	Pass	Fail	Under-predict Fail	Pass	Fail	Under-predict Fail
1	250	250	21	11 (52%)	10	10	14 (67%)	7	7	17 (81%)	4	1
2	250	250	16	10 (63%)	6	6	13 (81%)	3	3	15 (94%)	1	0
3	250	250	16	9 (57%)	7	7	13 (81%)	3	3	14 (88%)	2	1
Totals			53	30 (57%)	23	23	40 (76%)	13	13	46 (87%)	7	2
1	125	250	22	15 (68%)	7	7	19 (86%)	3	3	15 (68%)	7	1
1	500	250	22	15 (68%)	7	7	17 (77%)	5	4	13 (59%)	9	1
1	1000	250	22	11 (50%)	11	8	16 (73%)	6	2	14 (64%)	8	0
1	2000	250	22	12 (55%)	10	10	13 (59%)	9	6	12 (55%)	10	3
2	250	50	16	15 (94%)	1	1	15 (94%)	1	0	9 (56%)	7	0
2	250	125	16	10 (63%)	6	6	11 (69%)	5	5	14 (88%)	2	2
2	250	400	16	12 (75%)	4	4	12 (75%)	4	2	11 (69%)	5	0
3	50	50	16	10 (63%)	6	5	15 (94%)	1	0	11 (69%)	5	0
3	125	125	16	8 (50%)	8	8	8 (50%)	8	7	9 (57%)	7	5
3	400	400	16	10 (63%)	6	6	10 (63%)	6	5	10 (63%)	6	3

Figure 4.

Predicted vs observed values for the two models of integration, showing data for conditions in which the auditory and tactile frequencies are equal to one another. The top row (4a) represents the results of the Pythagorean sum model for the four equal-frequency conditions across experiments (from left to right: 50, 125, 250, and 400 Hz). The 250 Hz panel pools data across Experiments 1–3, while the remaining panels show data from Experiment 3. The bottom row (4b) represents the results of the algebraic sum model for the four equal-frequency conditions across experiments (from left to right: 50, 125, 250, and 400 Hz). The 250 Hz panel pools data across Experiments 1–3, while the remaining panels show data from Experiment 3. Results for each subject are delineated by shape (see legend) in each panel. Open symbols indicate that the observed value failed the chi-squared test and filled symbols indicate the observed value passed the chi-squared test.

Figure 5.

Ratio of the observed d^′ values to the Predicted D^′ values for each of the three models averaged across subjects and repetitions of each experimental condition. (a) Ratios for Experiment 1, in which the tactile frequency=250 Hz and the auditory frequency was varied between 125 and 2000 Hz. (b) Ratios for Experiment 2, in which the auditory frequency=250 Hz and the tactile frequency was varied between 50 and 400 Hz. (c) Ratios for Experiment 3, in which the auditory and tactile frequencies were equal and covaried between 50 and 400 Hz. The horizontal bar on each graph indicates a ratio of 1.0 (i.e., observed=predicted values). The dark gray bars represent the optimal single channel model, the gray bars represent the Pythagorean sum model, and the light gray bars represent the Algebraic sum model. Error bars are 1 SEM.

The baseline condition [250 Hz panels of Figs. 4a, 4b] was included in all experiments and involved a total of 53 comparisons. Of these, 30 (57%) agreed with OSCM predictions, 40 (76%) agreed with PSM predictions, and 46 (87%) agreed with ASM predictions. All of the OSCM and PSM prediction failures are due to under-prediction while the ASM under-predicted only two out of seven failures. It can be seen that most of the data points that do not satisfy the chi-squared test are higher than the predictions of the PSM [Fig. 4a, 250 Hz panel] and lower than the predictions of the ASM [Fig. 4b, 250 Hz panel], consistent with results found previously in Wilson et al., 2009. Of the eight subjects tested, two (S₁₃ and S₁₈) had more than 95% of measurements passing the chi-squared test for the PSM, while two had more than 95% of measurements passing the chi-squared test for the ASM (S₁₁ and S₁₈). The “extended baseline” conditions will be discussed below in the context of results from Experiment 3.

The results of Experiment 1 indicated a change in best-model fit as a function of auditory frequency. When the auditory and tactile frequencies were equal (250 Hz, baseline condition), the ASM model (81%) outperformed the PSM and OSCM (67% and 52%, respectively). When the auditory and tactile stimuli were not equal in frequency, however, the PSM outperformed the ASM and OSCM by 4–18 percentage points. The largest prediction difference between models was measured at 125 Hz, and the three models predicted observations almost equally well at 2000 Hz (resulting in the smallest prediction difference). The OSCM did not accurately model any conditions of Experiment 1 (between 50% and 68% of observations passing the prediction criterion). Even though the 2000 Hz condition had the same percentage of observations passing the model prediction using the OSCM and ASM (55%), all of the failures of the OSCM were under-predictions, while only 30% of the failures of the ASM were under-predictions. Figure 5a shows that the ratio of observed d^′ to predicted D^′ values was close to 1 for the ASM when the auditory frequency was 250 and 2000 Hz, and close to 1 for the PSM when the auditory frequency was 1000 Hz. For the 125 and 500 Hz conditions, the ratios fell between the PSM and ASM predictions.

For Experiment 2, a frequency-dependent trend was also observed. When the tactile frequency was 125 or 250 Hz, the ASM model best fit the observations (88% and 94% passing the chi-squared tests, respectively). In the 50 Hz tactile frequency condition, both the OSCM and PSM best fit the observations (94% passing the chi-squared test in each model). Similarly, in the 400 Hz tactile frequency condition, both the OSCM and PSM fit the observations equally well (75% passing chi-squared tests in each model). Again, the same trend occurred such that the OSCM and PSM tended to under-predict the observations, while the ASM tended to over-predict observations. Figure 5b shows that the ratio of observed d^′ to predicted D^′ values is consistent with the percentages passing the chi-squared test. Tactile frequency conditions of 125 and 250 Hz were best predicted by the ASM (with ratios close to 1) while conditions in which the tactile frequency was equal to 50 or 400 Hz were best predicted by the OSCM or PSM, respectively.

For Experiment 3, in which the auditory and tactile frequencies were equal and covaried [Figs. 4a, 4b], the ASM best fit the observations for the 125 and 250 Hz conditions, with 57% and 88% passing the chi-squared tests, respectively. In the 125 Hz condition, five out of seven of the failures are due to ASM under-prediction. In the 50 Hz condition, the PSM best fit the data with 94% of observations passing the chi-squared test, with no under-predictions for either PSM or ASM. In the 400 Hz condition, each model scored the same percentage of observations passing the chi-squared test (63%). However, all three models under-predicted the observations and of the six ASM failures, three are due to model under-prediction. Figure 5c shows a similar trend such that the ASM was most accurate in predicting the observations when the auditory and tactile frequencies were equal to 125, 250, and 400 Hz, but that the PSM was the most accurate in predicting the observations when the stimulus frequencies were equal to 50 Hz.

DISCUSSION

Effects of frequency separation

Effects of the frequency of stimulation on auditory-tactile integration of signals presented at near-threshold levels were observed in each of the three experiments. Such effects were present both for signal detectability (as measured in percent-correct scores) of the combined A+T stimulus and for best fits to different models of integration. Generally, a tendency was observed for higher rates of detection of the combined-modality stimulus when the stimulating frequencies in the two modalities were equal or close to one another, and for lower rates of detection as the frequency separation of the auditory and tactile stimuli increased. Furthermore, the ASM (indicative of within-channel integration) provided a better fit to the data when the auditory and tactile stimulating frequencies were equal or close to one another compared to a better fit of the PSM (indicative of cross-channel integration) for larger frequency spacings. Measurements of the detectability of purely auditory stimulus pairs (Appendix0) gave similar results to our measurements of auditory-tactile stimuli, with the exception of the (125, 250) Hz condition. Apparently the auditory separation, roughly 3 equivalent rectangular bandwidths (ERBs) (Moore et al., 1990), is effectively greater than the tactile separation.

A baseline condition employing 250 Hz stimulation in both auditory and tactile modalities was included in each of the three experiments, as it was in Wilson et al., 2009. The results of this condition, which are in good agreement with those reported by Wilson et al. (2009), indicate a roughly 15 percentage-point increase in the percent-correct score for A+T compared with A-alone or T-alone. On average, A+T performance on the baseline condition was well modeled by the within-channel integration process of the ASM.

The baseline measurement was extended in Experiment 3 where the auditory and tactile stimulating frequencies were set equal to one another but took on values of 50, 125, and 400 Hz in addition to the original baseline value of 250 Hz. The results of this experiment indicate detection rates of the A+T stimulus at 125 and 400 Hz that are equivalent to those at 250 Hz (i.e., roughly 86% correct) and that are well modeled by the within-channel model of integration (ASM). At the 50 Hz frequency, however, average performance on the A+T condition (78% correct) was lower than for the remaining three frequencies and was best modeled by the cross-channel model of integration (PSM), with only two of the four subjects showing ASM-type integration. Whereas the three higher frequencies (125, 250, and 400 Hz) are well within the range of the Pacinian receptor system (Verrillo, 1963; Hamer et al., 1983), at 50 Hz it is likely that the non-Pacinian and Pacinian receptors may also convey aspects of the tactile stimulus: the non-Pacinian receptors respond robustly for frequencies less than 50 Hz (“flutter”) and Pacinian receptors respond robustly for frequencies greater than 50 Hz (“vibration”).

Intersubject differences observed at 50 Hz may be indicative of differences in tactile physiology. In fact, the observation that two of the four subjects (S₁₀ and S₁₈) showed sizable A+T scores (>85% correct), when both frequencies were equal to 50 Hz while two others (S₆ and S₂₂) did not, suggests that the cross-over point between the non-Pacinian and Pacinian receptors may be different across individuals. Those subjects with high A+T scores at 50 Hz may have a cross-over point lower in frequency than those subjects whose A+T scores at 50 Hz were similar to single-modality scores. Additional data collected on subject S₆ at 60 and 75 Hz corroborates this claim: at 50 and 60 Hz, responses to the combined A+T stimulus were approximately 77% correct, but at 75 Hz, combined responses were approximately 90% correct. This result suggests a cross-over frequency between non-Pacinian and Pacinian receptors somewhere in the range of 60–75 Hz for this subject.

When different auditory frequencies were combined with a 250 Hz tactile signal (Experiment 1), A+T scores were similar for auditory values of 125, 500, 1000, and 2000 Hz and, on average, were lower than that obtained for the equal-frequency 250 Hz auditory condition. For the nonequal frequency conditions (with the exception of 2000 Hz), multimodal performance was over-predicted by the PSM but under-predicted by the ASM, whereas the ASM provided an excellent fit to the baseline condition. Unexpectedly, average performance for the condition with an auditory frequency of 2000 Hz was also well modeled by the ASM. Individual-subject differences were observed on this condition, indicating that the results of one subject (S₁₄) were well modeled by the OCSM while that of two other subjects (S₁ and S₁₀) were well modeled by the ASM. No obvious explanation for these intersubject differences is apparent.

When different tactile stimulating frequencies were combined with an auditory frequency of 250 Hz (Experiment 2), integration of the two stimuli was similar for tactile frequencies of 125 and 250 Hz (indicating within-channel integration predicted by the ASM) but was less effective for tactile frequencies of 50 and 400 Hz. The integration effects with a 400 Hz tactile signal were fairly well modeled with the PSM whereas those with a 50 Hz signal were closer to the OSCM. In comparing the results of Experiments 1 and 2, one can conclude that the filtering in Experiment 1 is similar to auditory critical-band filtering whereas a broader tactile filter is implied by the results of Experiment 2.

Comparisons with previous studies

Other perceptual studies have explored the frequency relationship between the auditory and tactile stimuli through “roughness judgments.” For example, the “parchment-skin illusion” (Jousmäki and Hari, 1998; Guest et al., 2002) demonstrates that the percept of tactile roughness can be modulated by manipulating the high- frequency components of the auditory signal. The attenuation of high frequencies results in a “less rough” percept of the tactile stimuli compared to no manipulation, whereas the amplification of high-frequency components leads to a percept of greater roughness compared to the baseline condition.

Two recent perceptual studies have reported effects of frequency on auditory-tactile interactions in tactile frequency-discrimination tasks performed in the presence of auditory “distracter” tones (Ro et al., 2009; Yau et al., 2009). Ro et al. (2009) examined the ability to discriminate between 100 Hz and 200 Hz vibratory stimuli using a one-interval, 2AFC procedure for stimulus presentations that included tactile stimulation alone and tactile stimulation in conjunction with a synchronous auditory tone of 100 or 200 Hz. The tactile stimuli were 250 ms in duration and were presented at levels that were subjectively matched to produce a “moderately intense percept” through a piezoelectric element at the dorsal surface of the left hand. The auditory stimuli, which were also 250 ms in duration, were presented through a loudspeaker located in front of the subject’s left hand at a level of roughly 60 dB SPL. The mean hit rates were 0.62 for the tactile-alone stimulus presentations, 0.74 for presentations with equal-frequency auditory and tactile tones, and 0.43 for presentations with different-frequency auditory and tactile tones. Thus, performance was aided by the presence of auditory tones matched in frequency to the tactile sinusoids but declined in the presence of incongruous auditory tones. In fact, performance appears to be substantially worse than that expected on the basis of chance alone for the incongruous conditions. For the 200 Hz tactile, 100 Hz auditory condition, the hit rate was only 0.37, suggesting that subjects were able to discriminate the stimuli but reversed their corresponding response labels of “high” and “low.” Thus, the 100 Hz auditory tone appears to have lowered the perception of the higher-frequency tactile signal.

Yau et al. (2009) used a 2I, 2AFC procedure to measure frequency discrimination for 1 s sinusoidal tactile signals presented to the right index finger. For a 200 Hz standard tactile stimulus (delivered over a contactor with 1 mm diameter), tactile comparison stimuli were seven sinusoids that were equally spaced in frequency over the range of 100–300 Hz and whose levels were equated for perceived intensity with the 200 Hz standard (whose level was 11.2 μm). On most trials of the experiment, an auditory tone (one of eight values in the range of 100–1500 Hz with individual-tone levels in the range of 56.5–76.4 dB SPL selected to be equated for loudness) was presented synchronously with the comparison stimulus. (Although absolute thresholds for the tactile and auditory stimuli were not reported in this study, it is reasonable to assume that all signals were substantially above threshold—see discussion of tactile thresholds in Sec. 3A of the current paper.) The remaining trials, conducted without the auditory “distracter” tones, were used to establish baseline performance for the tactile frequency-discrimination task. The psychometric functions showed a significant reduction in sensitivity (i.e., ΔF for 73% correct performance) compared to baseline performance only for those auditory distracters that were less than or equal to 300 Hz and a significant change in bias (i.e., the point of perceived subjective equality) for auditory distracters of 100 Hz only. An analogous frequency-discrimination experiment conducted with a 400 Hz tactile standard stimulus (delivered over a contactor with 8 mm diameter at a level of 1 μm) indicated a significant reduction in sensitivity for auditory distracters in the range of 100–400 Hz and changes in bias for auditory tones of 100–300 Hz. Thus, these results suggest a significant interaction between auditory and tactile stimuli that are similar in frequency in performing a tactile frequency-discrimination task. No such effects of the frequency of auditory distracter tones were observed, however, in a tactile intensity-discrimination task employing either a 100 Hz standard (at a level of 14.2 μm and comparisons in the range of 7.1–21.4 μm) or a 200 Hz standard (at a level of 7.6 μm and comparisons in the range of 3.8 to 11.5 μm). The psychometric functions derived from trials with each of the auditory distracter frequencies were nondistinguishable from those of the baseline trials with no auditory distractors.

Substantial differences in approach exist between the detection experiments described in the current paper and the frequency-discrimination experiments of Ro et al. (2009) and Yau et al. (2009). In the detection experiments (conducted near threshold), both the auditory and tactile stimuli in the A+T condition are relevant to performing the task whereas in the tactile frequency-discrimination experiments (conducted at suprathreshold levels) only the T stimulus is task relevant during A+T presentations. However, both approaches suggest that the frequency of stimulation within each of the two modalities affects performance on A+T conditions. In the case of the tactile frequency-discrimination experiments conducted by Yau et al. (2009), performance on a 200 Hz tactile target was affected only by the presence of auditory frequencies in the range of 100–300 Hz and on a 400 Hz tactile target by auditory frequencies in the range of 100–400 Hz. Thus, similar to our results in Experiments 1 and 2, perceptual interactions appear to be greater when the frequencies of A and T are more closely spaced and furthermore when both frequencies are within the Pacinian range.

The results of Yau et al. (2009) indicate that subjects were able to effectively ignore interactions of the auditory and tactile tones in performing the intensity-discrimination task but not the frequency-discrimination task. In the case of intensity discrimination, Weber’s law predicts an increase in ΔI with an increase in the level of the standard stimulus that would arise from integration of the auditory and tactile stimuli; thus, subjects may choose to ignore the auditory intensity component in order to maximize their performance. In the case of tactile frequency discrimination, however, performance was strongly affected by the presence of auditory frequencies in the Pacinian range (i.e., below 300 or 400 Hz). In fact, our own analysis of the data of Yau et al. (2009) suggests that performance in the presence of these distracters closely matches what would be predicted from the baseline function for a comparison tone that is the average of the frequency of the tactile comparison tone and the auditory distracter. A similar averaging operation may also be inferred from the results of Ro et al. (2009), described above.

Tonotopy, filtering, and pathways in the auditory and tactile systems

Tonotopic mapping from the brainstem to the cortex has been demonstrated in neurophysiological studies with animals (for a review see Schreiner et al., 2000) as well as in imaging studies of the human auditory cortex (Romani et al., 1982; Bilecen et al., 1998; Talavage et al., 2000; Talavage et al., 2004). In the perceptual domain, a variety of experiments have shown that the auditory system exhibits critical-band filtering (e.g., Moore et al., 1990; Zwicker, 1961; Greenwood, 1961). Interaction of multiple auditory stimuli is greatest when those two stimuli fall within a single critical band, and decreases as the frequency separation between them increases (i.e., as they fall into separate critical bands).

The peripheral tactile receptor system has also been shown to respond to different ranges of frequencies: a “non-Pacinian” channel responding to frequencies ranging from less than 1 to approximately 50 Hz, and a Pacinian channel, responding to frequencies ranging from approximately 50–500 Hz (Verrillo, 1963; Verrillo et al., 1983; Hamer et al., 1983; Bolanowski et al., 1988; Morley and Rowe, 1990; Formby et al., 1992; Gescheider et al., 2001; Gescheider et al., 2002). There is also some evidence for possible frequency selectivity at the level of the somatosensory cortex. The primary somatosensory cortex responds to frequencies in the “flutter” range (i.e., frequencies less than 50 Hz: Harris et al., 2006; Hegner et al., 2007) while the secondary somatosensory cortex responds to frequencies in the “vibration” range (i.e., frequencies between 50 and 500 Hz: Francis et al., 2000; Harrington and Downs, 2001; Iguchi et al., 2007). The results of other studies, however, suggest that a frequency organization in S1 may not exist in humans (Hashimoto et al., 1999) or in animal models (Romo et al., 1998; Romo et al., 2000; Hernandez et al., 2000; Luna et al., 2005; de Lafuente and Romo, 2005). Psychophysical studies have also shown evidence of “critical-band” filtering in the tactile system although over a frequency range that is greatly compressed compared to that of the auditory system (Marks, 1979; Makous et al., 1995).

Given that recent anatomical studies have shown that the somatosensory system projects to the auditory system (Cappe and Barone, 2005) and that physiological studies have shown that these two sensory systems interact with one another in the auditory cortex (Schroeder et al., 2001; Foxe et al., 2002; Schürmann et al., 2006), our data suggest the possibility of a cross-modal tonotopic mapping. The results from Experiments 1–3 indicate that critical-band filtering is exhibited in both the auditory and somatosensory systems and that these filters interact with one another across the different sensory modalities. In comparing the results of Experiments 1 and 2, our data suggest that the auditory and somatosensory filters are of different shapes, with the auditory filters being more sharply defined than those of the tactile system.

Our modeling results are suggestive of different anatomical pathways for cross-modal integration depending on the frequencies of the A and T stimuli. When auditory and tactile stimulus frequencies are similar to each other and within the Pacinian range, cross-modal scores are well modeled by the ASM. A pathway for within-channel integration may occur through ascending somatosensory inputs to early auditory centers in the brainstem and thalamus. Auditory and tactile sensations may be integrated at these early levels before their combination reaches the auditory cortex. When auditory and tactile frequencies of stimulation are farther apart, cross-modal scores tend to be well modeled by the PSM, suggesting cross-channel integration. A potential anatomical pathway for this type of integration may be the ascending inputs to the somatosensory cortex, which then project to the auditory cortex. Interactions between auditory and tactile stimuli would take place at the level of the cortex using input derived from independent pathways for each modality.

It has been suggested that the inner ear evolved out of the skin as a highly frequency-specific responder (Fritzsch and Beisel, 2001; Fritzsch et al., 2007). The tactile system may thus serve to extend the range of low-frequency hearing where sensitivity to auditory signals is not as good as at higher frequencies. Recent research suggests that in large mammals such as elephants and lions, vibrational events in the ground may be used for communication (O’Connell-Rodwell et al., 2001). In this light, the tactile and auditory systems could represent a continuum of detectable frequencies, with one sense picking up where the other one leaves off.

SUMMARY AND CONCLUSIONS

Our experiments have shown that the detection of combinations of near-threshold auditory and tactile stimuli is dependent on the frequencies of stimulation employed within each modality. When stimulating frequencies in the two modalities are equal or close to one another, detection rates tend to be higher than for combinations employing larger differences in frequency. Observed auditory-tactile performance was compared to the predictions of three different models of integration using single-modality scores as input. Different types of integration were observed with different combinations of auditory and tactile stimuli. In particular, the within-channel integration of the ASM provided a close fit to data for conditions in which the auditory and tactile stimulating frequencies were equal or close to one another and were within the Pacinian frequency range. The cross-channel integration of the PSM tended to provide the best fit to conditions with larger frequency spacings. Little integration of any type was observed for 50 Hz stimulation in both modalities, suggesting that integrative effects may not extend to frequency regions conveyed by non-Pacinian receptors.

Further research is being conducted on auditory-tactile integration with suprathreshold stimuli and concerned in particular with the relation between frequency spacing and loudness. In the auditory domain, it is well established that two-tone stimuli that lie within a critical band are more effectively integrated as far as detection is concerned than two tones that lie in different critical bands. This effect is similar to that observed in our experiments with auditory and tactile stimuli: detection is higher when the frequencies of the auditory and tactile stimuli are equal or closely spaced than when they are farther apart. For loudness, on the other hand, two auditory tonal stimuli are louder when they occupy different critical bands than when they lie within the same critical band. It will be important to determine whether the frequency spacing of auditory and tactile stimuli has a similar effect on perceived strength of combined auditory-tactile stimuli.

APPENDIX: AUDITORY NARROWBAND NOISE COMBINED WITH AUDITORY PURE TONES

To test our methods we conducted a purely auditory experiment as a complement to Experiment 1, in which an auditory NBN of bandwidth 48 Hz and centered on 250 Hz was substituted for the tactile stimulus. This experiment was conducted on five audiometrically normal subjects (three females; age range of 19–59 years). Each subject completed four repetitions of the experimental conditions. One subject (S₁₂) was disqualified after testing because of abnormally high threshold levels for the pure tones. The auditory pure tone (PT) frequencies used were the same as in Experiment 1: 125, 250, 500, 1000, and 2000 Hz. The level of the narrowband noise was determined by the same procedure that was used to determine the levels of the tones (see Sec. 2D).

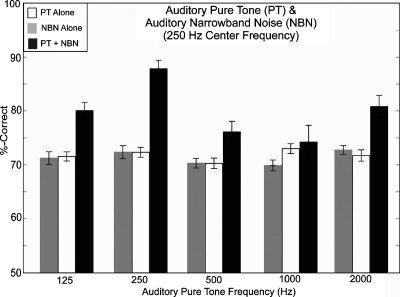
Figure 6 shows the results of the detection experiment. At threshold, percent-correct values for a single stimulus (PT-alone and NBN-alone) ranged from 69.8% correct (NBN) to 73% correct (1000 Hz tone). In the combined PT+NBN presentations, the highest percent-correct score was obtained when the tone was 250 Hz (87.8% correct), while the response levels were lower for other PT frequencies.

Figure 6.

% correct scores averaged across four subjects and four repetitions per condition. Scores are shown for auditory PTs alone (white bars), auditory NBN alone (light gray bars), and for combined PT+NBN (dark gray bars). Scores are shown as a function of auditory PT frequency with NBN centered at 250 Hz and bandwidth of 48 Hz. Error bars are 1 SEM.

A two-way ANOVA was performed on the arcsine-transformed percent-correct scores with main factors of condition (NBN-alone, PT-alone, and NBN+PT) and subject. The results of the ANOVA indicate significant main effects for condition [F(14,180)=18.04, p<0.01] and subject [F(3,180)=11.87, p<0.01] as well as a significant interaction between them [F(42,180)=2.65, p<0.01]. A post hoc Tukey–Kramer analysis of the condition effect indicated that (i) all of the NBN-alone and PT-alone scores were statistically equivalent, (ii) NBN+250 scores were significantly higher than scores on all other conditions, (iii) scores on the remaining four NBN+PT conditions were not significantly different from each other, and (iv) NBN+125 and NBN+2000 scores were significantly greater than scores on all NBN-alone and PT-alone conditions but that scores on NBN+500 and NBN+1000 were not significantly higher than the NBN-alone and PT-alone scores. A post hoc analysis of the main effect for subject indicated the following significant differences: the scores of S₆ were significantly lower than those of S₁₀ and S₁₉, the scores of S₁₅ were significantly lower than those of S₁₀, the scores of S₁₉ were significantly higher than those of S₆, and the scores of S₁₀ were significantly higher than those of all other subjects. The interaction effect arises in part from different patterns of performance among subjects on the NBN+1000 and NBN+2000 conditions.

The responses were analyzed in terms of the three models (OSCM, PSM, and ASM) discussed in Sec. 3F. The PSM best fit the results of conditions 125 and 500 Hz (both with 94% passing the chi-squared test). The ASM best fit the results of the 250 Hz condition (with 75% passing), while the OSCM best fit the 1000 and 2000 Hz conditions (with 69% and 81% passing, respectively).

The results of the three studies reviewed in Sec. 1B are fairly consistent with ours if one assumes that the ASM applies to frequency separations less than 0.3 ERB (Moore et al., 1990), the PSM to separations between 0.4 and 5 ERB, and the OSCM to separations greater than roughly 11 ERB. The studies give conflicting results for separations of 5.5–10.4 ERB, with the findings of Green (1958) supporting the PSM rule, while our results and those of Marill (1956) support the OCSM rule.