Abstract
We investigated the ordering of gold nanowires that settled from aqueous suspension onto a glass substrate due to gravity. The nanowires, ca. 300 nm in cross-sectional diameter and ca. 2, 4, or 7 microns in length, were coated with 2-mercaptoethanesulfonic acid to provide electrostatic repulsion and prevent aggregation. The layer of nanowires in direct contact with the substrate was examined from below using optical microscopy and found to exhibit smectic-like ordering. The extent of smectic ordering depended on nanowire length with the shortest (2 μm) nanowires exhibiting the best ordering. To understand the assembly in this system, we used canonical Monte Carlo simulations to model the two-dimensional ordering of the nanowires on a substrate. We accounted for van der Waals and electrostatic interactions between the nanowires. The simulations reproduced the experimental trends and showed that roughness at the ends of the nanowires, which locally increased electrostatic repulsion, is critical to correctly predicting the experimentally observed smectic ordering.
Keywords: Monte Carlo, self-assembly, electrostatic, van der Waals, particle, metal
Introduction
It is now possible to synthesize inorganic nano- and microparticles with controlled size, shape, composition, and surface coatings.1 These particles can have optical, magnetic, and electrical properties amenable to applications ranging from biomedical diagnostics2 to next-generation electronics.3–5 Many applications require control over particle organization in a larger structure. Although methods for particle assembly are much less well developed as compared with synthesis, a variety of strategies have been reported.6–8 These include: (1) adhesion-based assembly, in which particles are coated with molecular or biomolecular layers that enable them to bind to each other or to another surface;9–10 (2) drying, which concentrates particles via capillary forces and convection as the solution evaporates, often forming regions of high density assemblies;11–14 (3) Langmuir-Blodgett and related approaches, in which particles are floated and compressed on a liquid subphase using methods originally developed for surfactant monolayers;15–18 (4) external magnetic or electrical fields, which can be used to orient or move particles;19–23 and (5) fluid flow,24, 25 which is effective in orienting anisotropic particles such as nanowires. Any of these can be combined with assembly substrates that have been patterned with regions of differing height26 or chemical functionalization27, 28 to further direct particle assembly.
We are interested in the assembly of metallic nanowires that are prepared by templated electrodeposition in the pores of alumina membranes, a method pioneered by the groups of Martin Moskovits and Charles Martin.29, 30 The nanowire diameter is fixed by the pores of the template membrane, and the length can be controlled by the amount of current passed during electrodeposition. Multicomponent nanowires with segments of different metals or conducting polymers can be readily prepared; more elaborate molecular31 or intermetallic32 layers can also be incorporated.33, 34 These materials have potential as chemoresistors,35 nanoresonators,36 nanomotors,37 encoded particles for suspension arrays,38, 39 and components in electronic devices31, 40, 41.
Although the understanding of nanowire assembly is not yet as advanced as for spherical particles, many of the approaches listed above have been employed to control nanowire organization. Attachment of nanowires to a surface via electrostatic, hydrophobic, or biorecognition interactions provides selectivity but does not control orientation, which limits assembly densities.28, 42 Simple drying of CdSe or Au nanorod suspensions led to a variety of assemblies ranging from high-density smectic assemblies to more complex structures such as vortices or stripe patterns;14, 43, 44 the latter were interpreted as kinetically trapped structures.14 For anisotropic particles such as nanowires, orientation is particularly important. Thus, several methods based on alignment of the particles in fluid flow have been developed that are not routinely used for spherical particles. These include nanowire alignment in blown bubble films45 or microscale flow channels.25 Nanowire assemblies have also been prepared via Langmuir-Blodgett methods and transferred from the air/liquid interface onto a solid support.46 Close-packed assemblies can be formed; alternatively, stick-slip deposition can provide a range of particle spacings.15 Nanowires have also been assembled at liquid/liquid interfaces; chemical or biorecognition-driven crosslinking has been performed at these interfaces to help preserve the assemblies.47 External magnetic or electrical fields have been used extensively in the assembly of metallic and semiconducting nanowires. These methods provide control over nanowire orientation; when locally-defined fields provided by microscale electrodes/magnets are used, precise positioning of individual nanowires can be achieved.20, 22, 48 Locally-defined features such as chemical patterns or microwells have been used to increase spatial control over nanowire assemblies formed by many of the aforementioned techniques. Additionally, templates have been used to guide the assembly of elaborate nanowire superstructures,49 and printing/transfer approaches have been developed to fabricate oriented nanowire arrays50.
Regardless of the assembly strategy selected, inherent forces acting on the particles, for example, van der Waals attractions, electrostatic attractions and/or repulsions, entropy (i.e., depletion forces or confinement effects), thermal motions (for smaller particles), and gravity (for larger particles), will be present and may assist or hinder the formation of desired assemblies.6,7 For example, van der Waals attractions can lead to uncontrolled particle aggregation if not balanced by electrostatic repulsions.
Combining experimental work with theory will improve understanding of the forces that drive nanowire self-assembly. On the theoretical side, much work has been focused on understanding the phase behavior of hard rectangles51–53 and spherocylinders52, 54 in two dimensions. Both rectangles and spherocylinders exhibit the nematic phase.52, 54 Additionally, spherocylinders also exhibit a solid (smectic-like) phase at sufficiently high densities.54 These studies provide insight into entropy-driven assembly which is often used as a basis for understanding the assembly of rods with energetic interactions.55–65 Avendano et al. showed that short, hard spherocylinders with short-range repulsive interactions create an effectively larger spherocylinder and excluded volume, which shifts the nematic-to-smectic phase transition to lower densities.62 A similar conclusion was obtained by Earl et al. for a system of soft repulsive spherocylinders.59 A different behavior was found for soft repulsive spherocylinders at higher temperatures by Cuetos et al., where the nematic phase was found to be stabilized with respect to the smectic phase.60 The stabilization of the nematic phase was attributed to better sampling of high energy configurations that reduced the importance of excluded volume effects responsible for the smectic phase. A central longitudinal point dipole placed in the center of hard spherocylinders was found to stabilize the smectic phase over the nematic phase;65 whereas, spherocylinders with terminal longitudinal point dipoles were shown to destabilize the smectic phase in favor of the nematic phase.64
The effects of gravity are often negligible in colloidal systems. However, for large or very dense particles, the effects of gravity may lead to particle sedimentation from solution. Only a few theoretical studies have focused on understanding the sedimentation of rods.66–68 Simulations and theoretical calculations on the phase coexistence of short, hard spherocylinders revealed that in a semi-infinite container, the spherocylinders always pack with the densest phase at the bottom of the container and the least dense phase at higher altitudes.66 The presence of the smectic, nematic, and isotropic phases depended on the number of spherocylinders as well as the gravitational strength.
Making connections between experimental and computational work is valuable for improving understanding of the forces that drive particle assembly. For example, Titov and Král developed a model that takes the interactions due to van der Waals and dipole-dipole forces, both with and without polarization due to an external electric field, of small (5–40 nm long, 3–10 nm width) CdSe/CdS nanorods.69 Their work served to show that the experimentally observed phase diagrams can be matched with calculations that minimize the total energy. Unfortunately, studies that directly link the experimental results of nanowire assembly with specific calculations are limited in the literature.6, 7
In this work, we employed both theory and experiments to understand the self-assembly of gold nanowires derivatized with a negatively-charged monolayer and settled from suspension by gravity onto glass substrates in sealed chambers. This method allowed us to isolate and examine the effects of electrostatic repulsion and van der Waals attraction, while avoiding effects due to solvent evaporation (e.g., capillary forces and convective flow). The nanowire assemblies exhibited smectic ordering, the extent of which depended on nanowire length. Using Monte Carlo (MC) simulations, we investigated the origins of the experimentally observed phase behavior. This work provides a fundamental basis for examining the forces that affect self- and directed assembly of micro- and nanoparticles.
Experimental Materials and Methods
Materials
All water used in these experiments was purified to >18 MΩ, using a Barnstead Nanopure filtration system. All chemicals were used as received except where noted. Alumina membranes, nominal pore diameter 0.2 μm, were purchased from Whatman, and Orotemp 24 and Ag Cyless R plating solutions were from Technic Inc. 2-mercaptoethanesulfonic acid (MESA) was purchased from Sigma. The oligonucleotide used (5′ to 3′ HS-C6H12 AAA AAA AAA A) was purchased from Integrated DNA Technologies.
Optical Microscopy
Optical microscopy was performed on a Nikon Eclipse TE300 inverted microscope with a Xe lamp and a Photometrics CoolSNAP HQ camera. Plan Fluor 100× oil objective (NA 1.3) and a Plan Apo 60× oil objective (NA 1.4) were used. Reflected brightfield images were collected using white light with Image-Pro Plus software (version 4.5; Media Cybernetics).
Nanowire Synthesis
Gold nanowires were grown by electrochemical deposition in the pores of alumina membranes following previously reported methods.34, 38 The resulting nanowires were imaged by optical microscopy to determine lengths (≥50 nanowires measured). Three different lengths were used in this work, referred to throughout this manuscript as 2, 4, and 7 μm nanowires. Measured lengths and standard deviations for these particles were: L = 1.8 ± 0.2, 4.3 ± 0.3, and 7.0 ± 0.5 μm, respectively. Length polydispersities were nearly the same for the three batches, ranging from 7% for the 4.3 and 7.0 μm wires to 11% for the 1.8 micron wires. The nanowires were d = 318 ± 45 nm in diameter (previously determined by transmission electron microscopy30, 70), hence their aspect ratios were approximately 6, 12, and 22.
Nanowire Derivatization
Nanowires were functionalized with a coating of MESA to provide electrostatic repulsion. The thiol moiety of this molecule binds to the Au surface of the nanowires, resulting in a monolayer terminated with the negatively-charged sulfonate groups. To form the monolayer, the nanowire stock solution (~109 nanowires in 1 mL ethanol) was pelleted by centrifugation at 8100g for 1 min and, after rinsing 3× in water, was resuspended in a 10 mg/mL aqueous solution of MESA. The suspension was then vortexed for two hours followed by rinsing the nanowires 3× with 1 mL of H2O by centrifugation. Nanowires that were functionalized with DNA were incubated with 1 μM thiolated DNA for 30 min and washed 3× with water prior to use.
Self-Assembly of Nanowires
A silicone spacer (Invitrogen CoverWell™ perfusion chamber gasket) was cleaned with ethanol and placed onto a glass slide, forming wells 9 mm in diameter and 2.5 mm deep. A suspension of nanowires (100 μL), at the batch concentration, was sonicated and immediately added to a well and allowed to settle onto the glass slide. After addition of the nanowires, each cell was sealed with a glass cover slip, which prevented the evaporation of solution allowing the nanowires to form assemblies without being effected by an evaporation front. Each constructed well constituted one sample and at least six different samples were imaged for each nanowire length. After nanowire loading, the sample was allowed to rest on the stage of an inverted microscope for assembly. We observed that the nanowires nearly always deposited on the substrate as single nanowires, not higher order aggregates. Final configurations only formed once sufficient deposition time had passed, approximately 30 minutes. The bottommost layer of nanowires was observed on the microscope after letting the nanowires rest overnight.
Analysis of assemblies
The Fourier transforms (FTs) of sample images were obtained using the Image-Pro Plus software package. This software performs a fast Fourier transform of the images and the resulting transformation is plotted as the spectral form on a logarithmic scale. To enhance the features of the transformed images for analysis the brightness and contrast was uniformly enhanced to better show features.
Experimental Results
Figure 1(a) shows a representative image of 2-mercaptoethanesulfonic acid (MESA)-coated, 4 μm long, Au nanowires assembled from deionized water suspension onto a glass coverslip, and viewed from below via reflectance brightfield optical microscopy. Well-ordered rows of nanowires were observed. Individual nanowires remained mobile in these assemblies (Supporting Figure 1). In these experiments, the principal role of the negatively-charged MESA monolayer on the nanowires was to provide electrostatic repulsion, thereby inhibiting aggregation. Low ionic strength media were necessary to observe these highly ordered assemblies. At [NaCl] ≤ 100 μM, well-ordered assemblies similar to those in deionized water were observed. However, at [NaCl] ≥ 5 mM (Debye length = 4.3 nm), aggregation occurred immediately upon contact with other nanowires [Fig. 1(c)], forming an extended open network rather than the high-density assemblies seen at lower ionic strength. In principle any negatively-charged coating should provide the same benefits for assembly in low ionic strength solutions, and this has been our observation. Supporting Figure 2 shows assemblies of Au nanowires coated with a monolayer of single-stranded, 5′ thiolated DNA oligonucleotides. The DNA-coated nanowires formed well-ordered nanowire assemblies very similar to those formed from MESA-coated nanowires.
Figure 1.

Effect of suspension ionic strength on assembly. MESA-coated Au nanowires ca 4 μm long assembled from: deionized water (a), 0.1 mM (b), and 5 mM NaCl (c). Scale bar in (a) is 10 μm and applies to all images.
Based on the nanowire size and the area available for assembly within the cell, the experimental assemblies of 4 μm nanowires (prepared from 100 μL, 109 nanowires/mL suspension) should produce 2.16 monolayers. We observed areas within each assembly sample that had differing nanowire densities. While a few areas had almost no nanowires present, the majority of the surface was coated with high densities of nanowires.71 The experiments and simulations in this manuscript focus on these high-density regions of the samples. Nanowire surface coverages in some regions approached close-packed arrangements. For example, a high-density region of 4.3 μm long nanowires had 5.1 × 107 nanowires/cm2, as compared with a calculated maximum packing of 7.3 × 107 nanowires/cm2. It should be noted that these assemblies are three-dimensional, comprising several multilayers as expected based on the number of nanowires present, and confirmed by optical microscopy (Supporting Figure 3). The upper layers consist of nanowire rows positioned directly above and oriented in the same manner as the lower layers. Assemblies of nanowires produced with tenfold lower nanowire concentrations (108 nanowires/mL) display the same general properties as the assemblies discussed here, such as, regions of varying nanowire density with the highest densities having multilayered, well-ordered rows of nanowires. We note that although in general the regions of high nanowire density were formed by large numbers of wires falling from suspension, nanowires did not need to fall onto each other in order to assemble. Individual nanowires would eventually form small bundles over long times, 24–48 hr (Supporting Figure 1).
To evaluate the effect of nanowire length on assembly, we synthesized nanowires approximately 2, 4, and 7 μm in length and 300 nm in cross-sectional diameter (measured dimensions were 1.8 ± 0.2, 4.3 ± 0.3, and 7.0 ± 0.5 μm, respectively for the three lengths, and 318 ± 45 nm diameter for all lengths). Although each of these samples formed similar assemblies, the shorter nanowires produced larger domains with increased order (Figure 2). The 2 μm nanowires form well-defined rows with well-aligned ends. This high degree of orientational and positional order is consistent with the smectic phase. The 4 μm nanowires shown in Fig. 2(c) have many of the same features as the 2 μm nanowires, notably the distinct rows of nanowires, except that there is more disorder between the ends of the nanowires within a row. The 7 μm [Fig. 2(e)] nanowires exhibit a marked decrease in order. The rows persist over only short distances and the ends of the nanowires are disordered and penetrate into the gap between rows.
Figure 2.

Representative experimental microscope images of self-assembled Au nanowires with nominal lengths of 2 (a), 4 (c), and 7 μm (e). The corresponding FTs of the images in a, c, and e (b, d, and f, respectively) are included to the right of the corresponding microscope image. The FTs were cropped to magnify the features in the center. The scale bar in (a) is 10 μm and applies to images (c) and (e).
The FTs of the microscope images in Figure 2 provide information on the characteristic distances in the assemblies and confirm our qualitative visual assessment of nanowire ordering. Each of the experimental FT images shows concentric rings, which reflect the multidomain smectic alignment of the nanowires. The FT image of the 2 μm nanowires [Fig. 2(b)] shows two distinctly separate rings, the 4 μm nanowires show three rings [Fig. 2(d)], and the 7 μm nanowires have a single, vaguely visible ring [Fig. 2(f)]. The 2 and 4 μm nanowires exhibit equally spaced rings, with radii that are integer multiples of one another. The distance from the origin to the middle of the first ring is 2.1 μm for the 2 μm nanowires, 4.4 μm for the 4 μm nanowires, and 7.9 μm for the 7 μm nanowires. These distances represent the nanowire length plus the inter-row spacing. The width of the rings represents the nonuniformity of nanowires within a row. For the 2 and 4 μm nanowires, each of the rings within the respective FT image has a similar width. For the 2 μm nanowires, the width of the rings is 0.6 μm and for the 4 μm nanowires it is 1.8 μm. The width of the ring is 4.0 μm for the 7 μm nanowires. In the case of the 2 μm nanowires, the shortest distance represented by the innermost ring [i.e., the middle-of-the-ring distance (2.1 μm) minus one-half the ring width (0.3 μm)] is equal to the nanowire length. The longest distance is the middle-of-the-ring distance plus one-half the ring width, which is equal to the nanowire length plus inter-row spacing. This indicates that the 2 μm nanowires have highly uniform rows. For the 4 and 7 μm nanowires, the minimum distances represented by the innermost ring are 3.5 and 5.9 μm, respectively, which are less than the nanowire lengths, indicating interdigitation between rows of nanowires. Polydispersity of the nanowires can also contribute to broadening of the rings and could reduce the size of the smectic domains observed experimentally. We note, however, that all samples have a similar polydispersity as described in the Materials and Methods. We also note that there is anisotropy in the intensity of the rings in the FT in Fig. 2(b), which is due to the small sampling region for the FT analysis: a large number of randomly oriented smectic domains would produce uniform rings.
Unlike the shorter nanowires, the 7 μm nanowires exhibit only a single, vaguely visible ring about the center of the image. If disordering and interdigitation of the nanowire rows is significant, then the nanowires might be considered to be in the nematic phase. Our FT analysis of assembly pictures indicates that this is not the case and that ordering of the 7 μm nanowires can be considered to be smectic. Figure 3(a) shows a snapshot from a simulation where the nanowires are in a nematic phase.51 The nanowires shown in Fig. 3(a) have an aspect ratio of L/d=13, similar to the experimental nanowires’ value of 12, with a similar density, Af, wires=0.6, to that in the experiments. The nanowire density is calculated as the fractional surface coverage according to
Figure 3.
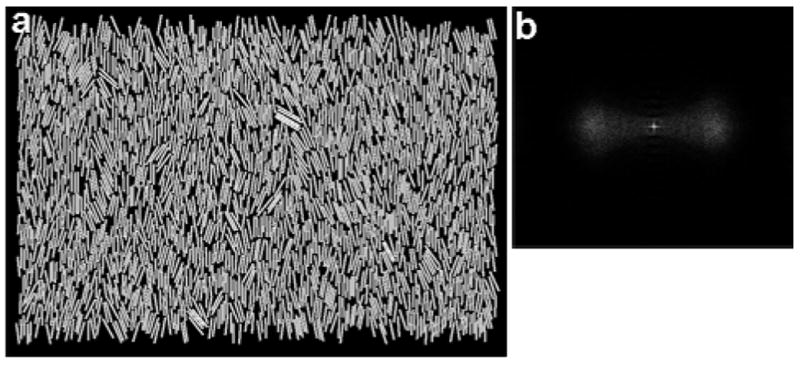
A nematic phase of nanowires is shown in (a) with the corresponding FT in (b).
| (1) |
where Nwires is the number of nanowires and Abox is the area of the simulation box. Unlike the experiments, the nanowires in Fig. 3(a) exist in a single domain. Thus, the FT of this snapshot [Fig. 3(b)] does not exhibit a ring—instead the FT exhibits diffuse clouds perpendicular to the director (the dominant direction of alignment of the nanowires’ long axis), that results from the collective alignment of the nanowires. While the length scale in the experimental FT in Fig. 2(f) represents the nanowire length plus inter-row spacing, the length scale associated with the blurry regions in Fig. 3(b) is consistent with the nanowire diameter plus intra-row spacing. Thus, ordering of the 7 μm nanowires can be considered to be smectic.
Model System
In an effort to understand nanowire ordering in the experiments, we created a model of the experimental systems. This model incorporates the three major interactions in the experimental system: gravity, van der Waals attraction, and electrostatic repulsion. Gravity is responsible for settling the nanowires from the aqueous solution onto the glass substrate and holding them there. van der Waals attraction would give rise to nanowire aggregation in the absence of the stabilizing MESA layer; however, the electrostatic interactions due to the MESA coating are repulsive and keep the particles from aggregating. As we will discuss below, the roughness of the nanowire ends creates additional electrostatic repulsion. Therefore, the balance of van der Waals and electrostatic interactions leads to the self-assembly of the nanowires on the surface.
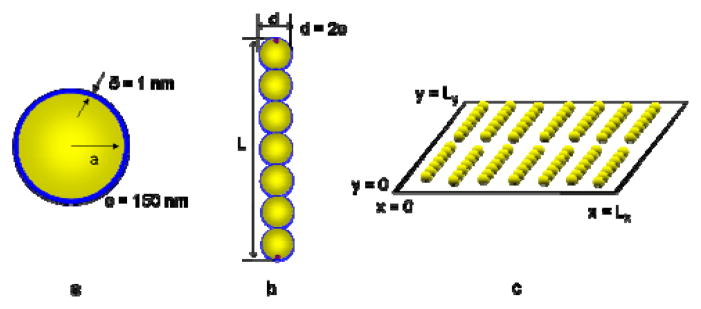
In our simulations, we represent the nanowires as rigid chains consisting of spherical segments. This model has been used previously to simulate systems of rods.55–57 The approximation of a rigid chain of spherical segments underestimates the van der Waals attraction as compared to two parallel aligned cylinders by approximately 30%.72 We adjust the nanowire length by varying the number of segments in the chain. Each of the segments is modeled as a core-shell sphere with a gold core and a MESA shell. The diameter and lengths of the nanowires in the simulations were selected to match the nominal dimensions for experimental nanowires, i.e., 2, 4, and 7 μm lengths and 300 nm diameter. The simulated nanowire diameter was 302 nm, which represents a 300-nanometer-diameter gold core with a one-nanometer-thick MESA layer. Thus, we adopt a total diameter of 302 nm for the spherical segments in the model. We simulated monodisperse nanowires containing seven, 13, and 23 segments, which resulted in nanowire lengths of 2.1, 3.9, and 6.9 μm. In the discussion below, we will refer to the nanowires as 2, 4, and 7 μm nanowires. As we will elaborate below, we simulated point charges on the end segments of each nanowire to represent the increase in electrostatic repulsion due to surface roughness at the nanowire ends. Figure 4(a) and (b) illustrate the essential elements of the model nanowires.
Figure 4.
Characteristics of the model nanowires. The core-shell configuration of the spherical segments is shown in (a) and an example nanowire composed of seven spherical segments with point charges on the terminal segments is shown in (b). A cartoon of the simulation box is shown in (c).
To model a layer of nanowires on the glass substrate, we consider a two-dimensional system. Our model neglects the nanowire sedimentation process, as it was determined from the experiments that nanowire ordering improves after the initial sedimentation; thus we are modeling only the post-sedimentation assembly (Supporting Figure S4). Because of their high densities in the experiments, we expect that the nanowires could exhibit either nematic ordering, in which nanowires adopt similar orientations but have disordered center-of-mass positions, or smectic ordering, where the nanowires exhibit order in both their orientation and centers of mass. Since orientational ordering occurs in both cases, we fix the nanowire orientations and we only consider displacement of the nanowire centers of mass. As shown in Fig. 4(c), the simulation box has dimensions of Lx and Ly and is periodic in the x and y directions.
The total energy of the system Utotal is given by
| (2) |
where UvdW and Useg-seg are the van der Waals attraction and electrostatic repulsion, respectively, between segments i and j separated by a distance of rij, Useg-end is the electrostatic repulsion between segment i and end-point charge k separated by rik, and Uend-end is the electrostatic repulsion between end-point charges k and l separated by rkl. In all the sums in Eq. (2), the interactions are pair-wise additive and intra-wire interactions are excluded. It should also be noted that overlap is prohibited between segments of different nanowires.
We model the core-shell van der Waals interaction UvdW using the potential developed by Vold,73 which is given by
| (3) |
with
| (4) |
Here, Aw, Am, and AAu are the Hamaker constants for water, MESA, and gold, respectively; r is the center-of-mass separation between segments; δ is the thickness of the MESA layer; and d is the Au core-particle diameter. The following values of the Hamaker constants were used: AAu=40×10−20 J, Aw=3.73×10−20 J, and Am=5.0×10−20 J.74, 75 In Eq. (3), the attraction between the gold segment cores is the dominant contribution because of the large value of the Hamaker constant of gold relative to MESA or water.
We model the segment-segment electrostatic interaction Useg-seg using the potential developed by Sader et al.,76 which has the form
| (5) |
with
| (6) |
Here, ε is the permittivity of water, kB is Boltzmann’s constant, T is the absolute temperature, e0 is the charge of a proton, a is the segment radius, κ is the Debye screening parameter, and ys is the reduced surface potential, which is determined from the zeta potential of the nanowires. We chose this form for the electrostatic potential because it is valid for moderate to high surface potentials (25–100 mV), over a large range of particle separations [κ(r-d-2δ)>0.2], and for modest values of κa (κa>3), making it the most appropriate choice for the systems in this study. The experimental inverse Debye screening length is κ−1=100 nm, which is based on 10 μM ionic strength.77 In the paper by Dougherty et al., the zeta potential of gold nanowires coated with MESA was determined to be ξAu=55 mV.78 The zeta potential is related to the reduced surface potential in Eq. (6) by .
Scanning electron microscope (SEM) images of nanowires that were synthesized with the technique employed here reveal that the sides of the nanowires are relatively smooth compared to the ends.29, 79 Structural irregularities can occur as protrusions or concavity of the nanowire ends. In previous work, it was found that such roughness can lead to an increase in electrostatic repulsion.80–84 Kostoglou and Karabelas discussed that electrostatic repulsion of two interacting surfaces can be up to three times stronger on a rough surface than on a smooth one.80 To address increased electrostatic repulsion associated with the rough ends of the nanowires, we placed point charges at the terminal segments of the nanowires. A similar technique has been used by Suresh and Walz to describe a rough spherical particle interacting with a flat, smooth surface.82 They modeled roughness as a uniform distribution of small hemispherical asperities on a larger spherical particle surface and calculated the increase in electrostatic repulsion as a sum of pairwise interactions between the asperities and the flat smooth surface. Here, the ends of the experimental nanowires are not uniform and it would be difficult to characterize and model the different ends. Thus, the point charge represents the effect of increased electrostatic repulsion in a general way.
We used a screened Coulomb potential to describe the interaction between segments and end charges Useg-end and between two end charges Uend-end. A screened Coulomb potential been used previously to simulate colloids with adsorbed polyelectrolyte,85 where it was shown to successfully capture charge non-uniformity. The screened Coulomb potentials have the forms
| (7) |
and
| (8) |
Here, zi and zseg are the number of elementary charges at the ends and segments, respectively. Based on the zeta potential of the nanowires, zseg=1282e0. As we will elaborate below, the value of the end-point charge was set to zi=50e0, which results in less than a 4% increase in the total charge of an end segment. It should be noted that zi is the only adjustable parameter in our model.
Metropolis MC simulations were used to determine the equilibrium configurations of nanowire assemblies. The simulations were performed in the canonical ensemble, where the number of nanowires Nwires, area of the substrate Abox, and temperature T=293K are constant. In all simulations of 4 and 7 μm nanowires, Nwires=1070, and for systems with 2 μm nanowires, Nwires=1177. Below, we will discuss results for 2, 4, and 7 μm nanowires simulated at densities of Af,wires=0.69, 0.70, and 0.65, respectively. These values are similar to average experimental fractional coverage of Af, wires=0.7 ± 0.2, which is the same for all wire lengths. The simulation box size (Abox = Lx × Ly) varied from a minimum of (37.9 × 24.9) μm2 to a maximum of (46.7 × 72.8) μm2 to achieve the desired surface coverage. To determine the influence of density on nanowire ordering, we studied a variety of additional surface coverages for each length. For values within the experimental uncertainty, we find the influence of density to be negligible.
In the MC simulations, a trial move is performed by randomly displacing the center of mass of a nanowire in the x or y direction. The displacements are uniformly distributed with a maximum value of 0.1d. The difference between the value of Utotal for the initial and trial configuration ΔU is obtained and the trial move is accepted with a probability given by
| (9) |
The acceptance rate of the trial moves varied from a minimum of 35% to a maximum of 43% for the various systems probed. Each simulation was equilibrated for a minimum of 50,000 MC steps (MCS), where a MCS is defined as an average of one attempted move per nanowire per step. By monitoring the convergence of the total energy, as well as sampled structural quantities, to a constant value, we confirmed that the simulated systems were successfully equilibrated. We also employed different initial nanowire configurations to verify that the final configuration of nanowires was independent of the starting configuration. Data production runs consisted of 50,000 MCS. The results are an average over a minimum of ten production runs for each length of nanowire, where the output of one production run was used as the input to the next one.
We used the pair-longitudinal distribution function g|| to quantify the smectic ordering of the nanowires. This quantity yields the probability of finding a pair of nanowires whose center of mass is separated by a distance y|| in the direction parallel to the long axis of the nanowire. It is defined by
| (10) |
where 〈N(y||, y|| + Δy||)〉 is an ensemble average of the number of nanowires that have their center of mass at a distance between y|| and y||+Δy|| and ρbulk = (Nwires/Abox) is the bulk density of nanowires. A smectic phase will exhibit peaks in g|| indicating layers of nanowires. The nematic phase, due to a lack of positional order to the nanowires, will not exhibit peaks but rather has a value of unity.
Additionally, we obtain FTs from snapshots of the simulated nanowire assemblies using the same Image-Pro Plus software package that is used to analyze the experimental images. We replicate the snapshots along the periodic y direction to provide a large enough image so we could obtain sufficient resolution with the FT to identify structural details.
Simulation Results
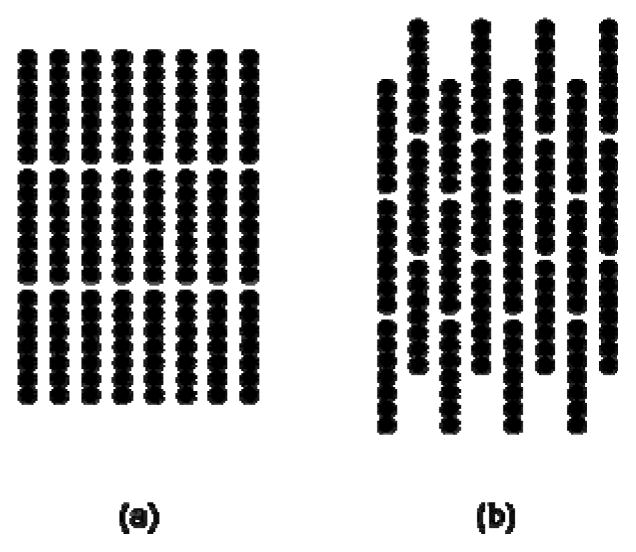
As discussed above, for the experimental and simulated nanowires, either nematic or smectic ordering could occur. To understand the preference for the smectic phase, we contrast it to a rectangular columnar phase, shown in Fig. 5, in terms of how various energies contribute to the total energy in Eq. (2). In the rectangular columnar phase, maximum interdigitation occurs between the nanowires so, in this sense, it is the opposite of the smectic phase. For our test calculations, nanowires are fixed and have uniform inter-wire spacings at the densities discussed above. van der Waals attraction UvdW favors aggregation of the nanowires, since this interaction is minimized at contact. Experimentally, individual nanowires retain mobility in the smectic rows, indicating irreversible aggregation has not occurred. To minimize the van der Waals energy in an assembly without aggregation, nanowires tend to align within a row. For the 4 μm nanowires, the van der Waals energy is 5% (0.3 kBT/nanowire) lower in the smectic phase than in the rectangular columnar phase. On the other hand, the segment-segment electrostatic repulsion Useg-seg is greatest when the nanowires are in the smectic phase. This repulsion is mitigated in the rectangular columnar phase. For the 4 μm nanowires, the segment-segment electrostatic repulsion is 3% (4.6 kBT/nanowire) higher in the smectic phase than in the rectangular columnar phase.
Figure 5.
The smectic phase is shown in (a) and the rectangular columnar phase is shown in (b).
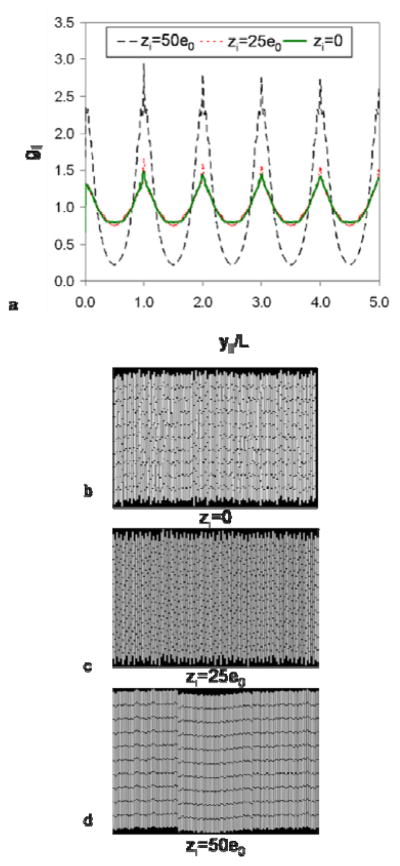
Considering only van der Waals attraction and segment-segment repulsion (i.e., no end charges), we expect that the dominant interaction would dictate the resulting phase. For all three lengths of nanowires, the van der Waals attraction accounts for approximately 3% of the total energy when only considering UvdW and Useg-seg. Since the segment-segment repulsion is much greater than the van der Waals attraction in these systems, a disordered phase is expected. This is observed in the MC simulation snapshot shown in Fig. 6(b), where the nanowires exhibit significant positional disorder when charges at the ends of the nanowires are neglected. The significant positional disorder results in the low peak values of g|| in Fig. 6(a).
Figure 6.
The pair-longitudinal distribution function, given by Eq. (10), is shown in (a) for 4 μm nanowires with various end charges. Simulation snapshots are shown for zi=0 (b), zi=25e0 (c), and zi=50e0 (d).
Adding a point charge to the terminal segments of the nanowires improves smectic ordering. To investigate this effect, we performed MC simulations with zi equal to 1e0, 5e0, 25e0, 50e0, and 100e0. Figures 6(c) and (d) show simulation snapshots of 4 μm nanowires with zi=25e0 (c) and zi=50e0 (d). The snapshot in Fig. 6(c) shows similar order to that for no end charge [Fig. 6(b)] and g|| is nearly identical for the two cases [Fig. 6(a)]. By increasing the end charge to zi=50e0, it is evident in Fig. 6(d) that there is an increase in smectic ordering. This increase is also evident in g|| in Fig. 6(a), which exhibits well defined peaks indicative of smectic layers. Each broad peak contains a sharp central peak which indicates the average position of the center of mass of the rows of wires. Thus, from our simulations, we find that zi=50e0 is the lowest value of the end-point charge to induce a smectic phase for all lengths of nanowires and we adopt this value in the simulations and analysis below. The end-point charge results in less than a 4% increase in the total charge of an end segment and the additional repulsion is within the range of values reported in the literature.80, 82 It should be noted that to some extent, the end charge may also compensate for phenomena not included in the model, such as nanowire polydispersity in length and diameter or the varying amounts of surface roughness present on the nanowires.
To understand how the end-point charge influences smectic ordering, we return to our analysis of the smectic and rectangular columnar structures in Fig. 5, assuming an end charge of zi=50e0. The electrostatic repulsion between end-point charges Uend-end favors the rectangular columnar phase over the smectic phase because end-end contact is minimized in this configuration. Uend-end is 14% (0.2 kBT/nanowire) lower when the nanowires are in the rectangular columnar phase than in the smectic phase for 4 μm nanowires. On the other hand, the electrostatic repulsion due to segments and end-point charges Useg-end is minimized in the smectic phase, where contact between ends and non-terminal segments is minimized. For the 4 μm nanowires, Useg-end is 20% (3.4 kBT/nanowire) lower in the smectic phase than in the rectangular columnar phase.
From the different contributions to Utotal, two interactions favor the smectic phase (UvdW and Useg-end) and two favor the rectangular columnar phase (Useg-seg and Uend-end). The two most significant contributions to the total energy are Useg-end and Useg-seg. We also note that Useg-seg and UvdW are proportional to the length of the nanowire. In contrast, the localized repulsion due to roughness at the end of the nanowires, Useg-end and Uend-end, is independent of nanowire length. Thus, Useg-end and Uend-end contribute less significantly to the total energy as the nanowire length increases and end roughness impacts ordering the most for the 2 μm nanowires and the least for the 7 μm nanowires. Useg-end and Uend-end contribute ~25% of the total electrostatic repulsion for the 2 μm nanowires, ~7% for the 4 μm nanowires, and ~2% for the 7 μm nanowires.
In addition to energetic factors, entropic factors also govern nanowire ordering. The effects of entropy can be inferred from related studies of hard rectangles51–53 and hard spherocylinders.52, 54 For the area fractions and aspect ratios of nanowires in this study hard rectangles exhibit only the nematic phase.52 The area fractions and aspect ratios of nanowires in this work are too low for the formation of the solid (smectic) phase in spherocylinders.54 Thus, based on these studies, for the aspect ratios and area fractions of nanowires in this study, the nematic phase is favored by entropy.
In addition to high density assemblies found in the experiments, low density suspensions of nanowires (1–10% of the typical starting concentration) have shown the ability of some nanowires to form well-aligned bundles (Supporting Figure 1), at long times. This would not be predicted by the simulations due to strong electrostatic repulsion between nanowires. These differences between the model and experiment can be rationalized as arising from additional effects between the nanowires in the experiments such as non-uniform MESA coatings or branched nanowire geometries.70, 79
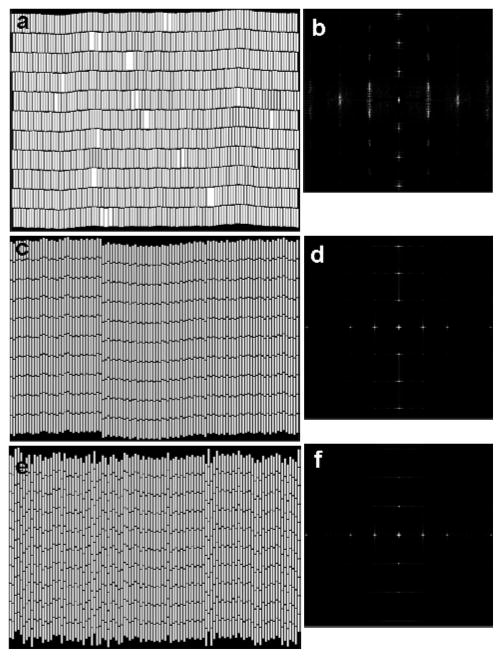
Through an analysis of the different interactions we have gained an understanding of why the smectic phase is energetically preferred in the adsorption of charged-stabilized, aqueous metallic nanowires. Our MC simulations reflect these energetic tendencies, which apparently dominate over entropy. Upon inspection of representative simulation snapshots for the 2 [Fig. 7(a)], 4 [Fig. 7(c)], and 7 μm [Fig. 7(e)] nanowires, we see that as the length of the nanowire increases, the degree of smectic ordering decreases. The 2 μm nanowires [Fig. 7(a)] are well aligned and the space between rows of nanowires is mostly free of nanowire ends. Figure 7(c) shows that the ends of the 4 μm nanowires interdigitate between the rows to a greater extent than the 2 μm nanowires and Fig. 7(e) shows that the 7 μm nanowires exhibit greater interdigitation than the 4 μm nanowires. The simulation snapshots are qualitatively consistent with the experimental images in Fig. 2.
Figure 7.
Simulation snapshots for the 2 (a), 4 (c), and 7 μm long nanowires (e). Corresponding FT images are shown to the right of each snapshot in (b), (d), and (f). FTs were cropped to enhance the features in the center.
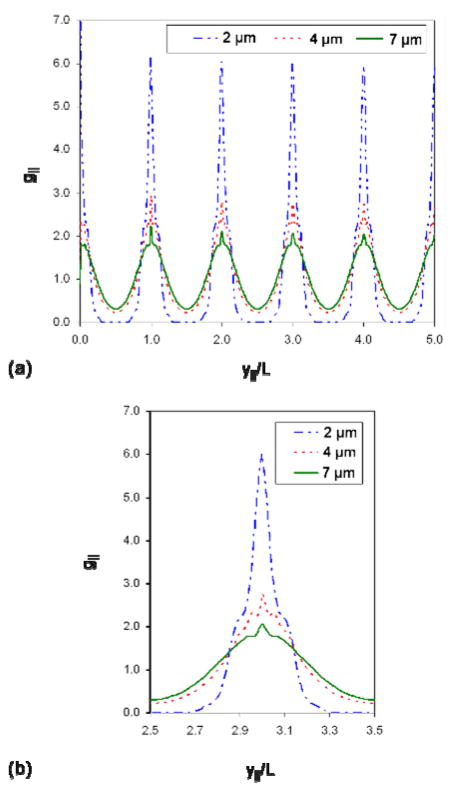
The visual observation of order is supported by the pair-longitudinal distribution function g|| shown in Fig. 8. Figure 8(a) shows the entire function and Fig. 8(b) highlights the features of a single peak. The 2 μm nanowires exhibit the best ordered rows and have the highest peak value of g||, as well as a zero value of g|| between the peaks. The zero value of g|| indicates that the rows of nanowires do not interdigitate. The 4 μm nanowires show a lower peak value than the 2 μm nanowires, which means the rows of nanowires are not as well aligned, as noted in the simulation snapshots of Fig. 7(c). The 7 μm nanowires have the lowest peak value, indicating the least amount of smectic order. This is supported by the simulation snapshot in Fig. 7(e).
Figure 8.
Pair-longitudinal distribution function, given by Eq. (10), for the different lengths of nanowires. The entire function is shown in (a) and a single peak centered around y||/L=3 is highlighted in (b). The features present in (b) are characteristic of all peaks.
Figures 7(b), (d), and (f) contain the FTs of the 2, 4, and 7 μm nanowires. Unlike the experiments (cf., Fig. 2), the FTs of the simulation snapshots do not show rings because the nanowires are aligned in a single direction and do not exhibit multiple ordered domains. The vertical dots in the center of the FT images are equally spaced and represent the same structure as the rings in the experimental FT images. The distances represented by the vertical dots is 2.2 μm for the 2 μm nanowires, 3.8 μm for the 4 μm nanowires, and 6.7 μm for the 7 μm nanowires. For the 2 μm nanowires [Fig. 7(b)], the vertical dots represent the nanowire length plus inter-row spacing because the ends of the nanowires within a row are well ordered and the rows are clearly separated. For the 4 and 7 μm nanowires [Figs. 7(d) and (f)], the vertical dots represent a distance that is less than the nanowire length because rows of nanowires are interdigitated. We note that the distances extracted from the locations of the vertical dots in the center of the FTs in Fig. 7 are consistent with the structure noted in g|| in Fig. 8. For the 4 and 7 μm nanowires, g|| exhibits side peaks to the left and right that flank the center of each main peak [cf., Fig. 8(b)], which represent the disorder of the nanowire ends between rows. The distance between the side peaks represents the deviation from perfectly aligned rows of nanowires, where a broader width indicates that the nanowires are more disordered. The distances between the vertical dots in the FTs in Fig. 7 are equal to the nanowire length plus inter-row spacing minus the distance between side peaks. The spacings between vertical dots in the simulation FTs and the rings in the experimental FTs are in good agreement.
The horizontal features in the simulation FTs in Fig. 7 provide a measure of the nanowire diameter plus intra-row spacing. These features represent the same structure as the edge of the large, circular, diffuse cloud that envelops the concentric rings in the experimental FTs in Fig. 2. The intra-row spacing is 100 nm and is equivalent for all three nanowire lengths in the simulations. This value can be compared to the experimental data in Figure 2. From Figure 2(b), (d), and (f), we estimated intra-row spacings of approximately 70, 80, and 100 nm for the 2, 4, and 7 μm nanowires, respectively.
Conclusions
We observed and quantified smectic ordering in charge-stabilized, colloidal Au nanowires that settle onto a glass substrate due to gravity. Our MC simulations indicate that these assemblies are brought about by a balance of electrostatic and van der Waals interactions and that a small degree of end charging, associated with roughness of the nanowire ends, can lead to well-aligned nanowire rows. Smectic ordering has been observed in previous experimental studies involving self-assembled nanowires on solid substrates.17, 44, 86–88 However, these studies involved liquid-vapor interfaces or drying of the nanowires, so that capillary forces were deemed significant. Here, we demonstrate that the balance of non-specific forces can lead to well-ordered nanowire arrays. This knowledge may be useful in the selective fabrication of devices.
Supplementary Material
Acknowledgments
The authors thank T. E. Mallouk for helpful discussions on Au nanowire assembly. This work was funded by the National Science Foundation (IGERT DGE-9987589, NIRT CCR-0303976), the DOE (DE-FG02-07ER46414), and National Institutes of Health (R01 EB000268). Undergraduates DHR and PG were supported by NSF grants DMR 0648837 and DMR 0820404.
Footnotes
Supporting Information Available: Additional micrographs of experimental nanowire assemblies, a close-up, image series of high- and low-density assemblies, and DNA coated nanowires, are available as supporting information. This material is available free of charge via the Internet at http://pubs.acs.org.
References and Notes
- 1.Burda C, Chen X, Narayanan R, El-Sayed MA. Chem Rev. 2005;105:1025–1102. doi: 10.1021/cr030063a. [DOI] [PubMed] [Google Scholar]
- 2.(a) Rosi NL, Mirkin CA. Chem Rev. 2005;105:1547–1562. doi: 10.1021/cr030067f. [DOI] [PubMed] [Google Scholar]; (b) Ming-Cheng Cheng M, Cuda G, Bunimovich YL, Gaspari M, Heath JR, Hill HD, Mirkin CA, Nijdam AJ, Terracciano R, Thundat T, Ferrari M. Curr Opin Chem Biol. 2006;10:11–19. doi: 10.1016/j.cbpa.2006.01.006. [DOI] [PubMed] [Google Scholar]; (c) Patolsky F, Zheng G, Lieber CM. Nanomedicine. 2006;1:51–65. doi: 10.2217/17435889.1.1.51. [DOI] [PubMed] [Google Scholar]
- 3.Ahn JH, Kim HS, Lee KJ, Jeon S, Kang SJ, Sun Y, Nuzzo RG, Rogers JA. Science. 2006;314:1754–1757. doi: 10.1126/science.1132394. [DOI] [PubMed] [Google Scholar]
- 4.Xia Y, Yang P, Sun Y, Wu Y, Mayers B, Gates B, Yin Y, Kim F, Yan H. Adv Mater. 2003;15:353–389. [Google Scholar]
- 5.(a) Lu W, Lieber CM. Nat Mater. 2007;6:841–850. doi: 10.1038/nmat2028. [DOI] [PubMed] [Google Scholar]; (b) Patolsky F, Timko BP, Yu G, Fang Y, Greytak AB, Zheng G, Lieber CM. Science. 2006;313:1100–1104. doi: 10.1126/science.1128640. [DOI] [PubMed] [Google Scholar]
- 6.Bishop KJ, Wilmer CE, Soh S, Grzybowski BA. Small. 2009;5:1600–1630. doi: 10.1002/smll.200900358. [DOI] [PubMed] [Google Scholar]
- 7.Min Y, Akbulut M, Kristiansen K, Golan Y, Israelachvili J. Nat Mater. 2008;7:527–538. doi: 10.1038/nmat2206. [DOI] [PubMed] [Google Scholar]
- 8.(a) Xia Y, Gates B, Yin Y, Lu Y. Adv Mater. 2000;12:643–713. [Google Scholar]; (b) Zhang H, Edwards EW, Wang D, Mohwald H. Phys Chem Chem Phys. 2006;8:3288–3299. doi: 10.1039/b604745a. [DOI] [PubMed] [Google Scholar]
- 9.(a) Lim SI, Zhong CJ. Acc Chem Res. 2009;42:798–808. doi: 10.1021/ar8002688. [DOI] [PubMed] [Google Scholar]; (b) Shenhar R, Norsten TB, Rotello VM. Adv Mater. 2005;17:657–669. [Google Scholar]
- 10.(a) Storhoff JJ, Mirkin CA. Chem Rev. 1999;99:1849–1862. doi: 10.1021/cr970071p. [DOI] [PubMed] [Google Scholar]; (b) Caswell KK, Wilson JN, Bunz UHF, Murphy CJ. J Am Chem Soc. 2003;125:13914–13915. doi: 10.1021/ja037969i. [DOI] [PubMed] [Google Scholar]; (c) Dillenback LM, Goodrich GP, Keating CD. Nano Lett. 2006;6:16–23. doi: 10.1021/nl0508873. [DOI] [PubMed] [Google Scholar]
- 11.(a) Jana NR. Angew Chem Int Ed. 2004;43:1536–1540. doi: 10.1002/anie.200352260. [DOI] [PubMed] [Google Scholar]; (b) He J, Zhang Q, Gupta S, Emrick T, Russell TP, Thiyagarjan P. Small. 2007;3:1214–1217. doi: 10.1002/smll.200700055. [DOI] [PubMed] [Google Scholar]
- 12.(a) Ming T, Kou X, Chen H, Wang T, Tam HL, Cheah KW, Chen JY, Wang J. Angew Chem Int Ed. 2008;47:9685–9690. doi: 10.1002/anie.200803642. [DOI] [PubMed] [Google Scholar]; (b) Sharma V, Park K, Srinivasarao M. Mater Sci Eng R. 2009;65:1–38. [Google Scholar]
- 13.(a) Malaquin L, Kraus T, Schmid H, Delamarche E, Wolf H. Langmuir. 2007;23:11513–11521. doi: 10.1021/la700852c. [DOI] [PubMed] [Google Scholar]; (b) Prevo BG, Kuncicky DM, Velev OD. Coll Surf A: Physicochem Eng Aspects. 2007;311:2–10. [Google Scholar]
- 14.Ghezelbash A, Koo B, Korgel BA. Nano Lett. 2006;6:1832–1836. doi: 10.1021/nl061035l. [DOI] [PubMed] [Google Scholar]
- 15.Tao AR, Huang J, Yang P. Acc Chem Res. 2008;41:1662–1673. doi: 10.1021/ar8000525. [DOI] [PubMed] [Google Scholar]
- 16.(a) Jin S, Whang D, McAlpine MC, Friedman RS, Wu Y, Lieber CM. Nano Lett. 2004;4:915–919. [Google Scholar]; (b) Acharya S, Efrima S. J Am Chem Soc. 2005;127:3486–3490. doi: 10.1021/ja044934p. [DOI] [PubMed] [Google Scholar]; (c) Pieranski P. Phys Rev Lett. 1980;45:569–572. [Google Scholar]; (d) Reculusa S, Ravaine S. Chem Mater. 2003;15:598–605. [Google Scholar]; (e) Tsai PS, Yang YM, Lee YL. Langmuir. 2006;22:5660–5665. doi: 10.1021/la053152m. [DOI] [PubMed] [Google Scholar]
- 17.(a) Kim F, Kwan S, Akana J, Yang P. J Am Chem Soc. 2001;123:4360–4361. doi: 10.1021/ja0059138. [DOI] [PubMed] [Google Scholar]; (b) Kwan S, Kim F, Akana J, Yang P. Chem Commun. 2001:447–448. doi: 10.1021/ja0059138. [DOI] [PubMed] [Google Scholar]
- 18.Lewandowski EP, Bernate JA, Searson PC, Stebe KJ. Langmuir. 2008;24:9302–9307. doi: 10.1021/la801167h. [DOI] [PubMed] [Google Scholar]
- 19.(a) Smith PA, Nordquist CD, Jackson TN, Mayer TS, Martin BR, Mbindyo J, Mallouk TE. Appl Phys Lett. 2000;77:1399–1401. [Google Scholar]; (b) Li M, Bhiladvala RB, Morrow TJ, Sioss JA, Lew KK, Redwing JM, Keating CD, Mayer TS. Nat Nanotechnol. 2008;3:88–92. doi: 10.1038/nnano.2008.26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Morrow TJ, Li M, Kim J, Mayer TS, Keating CD. Science. 2009;323:352. doi: 10.1126/science.1165921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.(a) Velev OD, Bhatt KH. Soft Matter. 2006;2:738–750. doi: 10.1039/b605052b. [DOI] [PubMed] [Google Scholar]; (b) Ryan KM, Mastroianni A, Stancil KA, Liu H, Alivisatos AP. Nano Lett. 2006;6:1479–1482. doi: 10.1021/nl060866o. [DOI] [PubMed] [Google Scholar]; (c) Gupta S, Zhang Q, Emrick T, Russell TP. Nano Lett. 2006;6:2066–2069. doi: 10.1021/nl061336v. [DOI] [PubMed] [Google Scholar]; (d) Raychaudhuri S, Dayeh SA, Wang D, Yu ET. Nano Lett. 2009;9:2260–2266. doi: 10.1021/nl900423g. [DOI] [PubMed] [Google Scholar]; (e) Gangwal S, Cayre OJ, Velev OD. Langmuir. 2008;24:13312–13320. doi: 10.1021/la8015222. [DOI] [PubMed] [Google Scholar]; (f) Mittal M, Lele PP, Kaler EW, Furst EM. J Chem Phys. 2008;129:064513. doi: 10.1063/1.2969103. [DOI] [PubMed] [Google Scholar]; (g) Lele PP, Mittal M, Furst EM. Langmuir. 2008;24:12842–12848. doi: 10.1021/la802225u. [DOI] [PubMed] [Google Scholar]
- 22.Liu M, Lagdani J, Imrane H, Pettiford C, Lou J, Yoon S, Harris VG, Vittoria C, Sun NX. App Phys Lett. 2007;90:103105. [Google Scholar]
- 23.(a) Tanase M, Bauer LA, Hultgren A, Silevitch DM, Sun L, Reich DH, Searson PC, Meyer GJ. Nano Lett. 2001;1:155–158. [Google Scholar]; (b) Yellen BB, Freidman G. Langmuir. 2004;20:2553–2559. doi: 10.1021/la0352016. [DOI] [PubMed] [Google Scholar]; (c) Ge J, Hu Y, Zhang T, Huynh T, Yin Y. Langmuir. 2008;24:3671–3680. doi: 10.1021/la7039493. [DOI] [PubMed] [Google Scholar]
- 24.(a) Kumacheva E, Garstecki P, Wu H, Whitesides GM. Phys Rev Lett. 2003;91:128301. doi: 10.1103/PhysRevLett.91.128301. [DOI] [PubMed] [Google Scholar]; (b) Cai Y, Newby B-mZ. J Am Chem Soc. 2008;130:6076–6077. doi: 10.1021/ja801438u. [DOI] [PubMed] [Google Scholar]
- 25.(a) Huang Y, Duan X, Wei Q, Lieber CM. Science. 2001;291:630–633. doi: 10.1126/science.291.5504.630. [DOI] [PubMed] [Google Scholar]; (b) Zheng G, Patolsky F, Cui Y, Wang WU, Lieber CM. Nature Biotechnol. 2005;23:1294–1301. doi: 10.1038/nbt1138. [DOI] [PubMed] [Google Scholar]; (c) Messer B, Song JH, Yang P. J Am Chem Soc. 2000;122:10232–10233. [Google Scholar]
- 26.(a) Xia Y, Yin Y, Lu Y, McLellan J. Adv Funct Mater. 2003;13:907–918. [Google Scholar]; (b) Cui Y, Bjork MT, Liddle JA, Sonnichsen C, Boussert B, Alivisatos AP. Nano Lett. 2004;4:1093–1098. [Google Scholar]; (c) Yin Y, Lu Y, Gates B, Xia Y. J Am Chem Soc. 2001;123:8718–8729. doi: 10.1021/ja011048v. [DOI] [PubMed] [Google Scholar]; (d) Dziomkina NV, Vancso GJ. Soft Matter. 2005;1:265–279. doi: 10.1039/b503145c. [DOI] [PubMed] [Google Scholar]; (c) Kraus T, Malaquin L, Schmid H, Riess W, Spencer ND, Wolf H. Nature Nanotechnol. 2007;2:570–576. doi: 10.1038/nnano.2007.262. [DOI] [PubMed] [Google Scholar]
- 27.(a) Zhang X, Imae T. J Phys Chem C. 2009;113:5947–5951. [Google Scholar]; (b) Heo K, Cho E, Yang JE, Kim MH, Lee M, Lee BY, Kwon SG, Lee MS, Jo MH, Choi HJ, Hyeon T, Hong S. Nano Lett. 2008;8:4523–4527. doi: 10.1021/nl802570m. [DOI] [PubMed] [Google Scholar]; (c) Ling XY, Malaquin L, Reinhoudt DN, Wolf H, Huskins J. Langmuir. 2007;23:9990–9999. doi: 10.1021/la701671s. [DOI] [PubMed] [Google Scholar]; (d) Cha N-G, Echegoyen Y, Kim T-H, Park J-G, Busnaina AA. Langmuir. 2009 doi: 10.1021/la901496s. ASAP. [DOI] [PubMed] [Google Scholar]; (e) Lenggoro IW, Lee HM, Okuyama K. J Colloid Inter Sci. 2006;303:124–130. doi: 10.1016/j.jcis.2006.07.033. [DOI] [PubMed] [Google Scholar]
- 28.(a) Martin BR, St Angelo SK, Mallouk TE. Adv Funct Mater. 2002;12:759–765. [Google Scholar]; (b) Sreeprasad TS, Samal AK, Pradeep T. Langmuir. 2008;24:4589–4599. doi: 10.1021/la703523s. [DOI] [PubMed] [Google Scholar]; (c) Pan B, Cui D, Ozkan C, Xu P, Huang T, Li Q, Chen H, Liu F, Gao F, He R. J Phys Chem C. 2007;111:12572–12576. [Google Scholar]
- 29.Almalawi D, Liu CZ, Moskovits M. J Mater Res. 1994;9(4):1014–1018. [Google Scholar]
- 30.Hulteen JC, Martin CR. J Mater Chem. 1997;7:1075–1087. [Google Scholar]
- 31.Cai L, Cabassi MA, Yoon H, Cabarcos OM, McGuiness CL, Flatt AK, Allara DL, Tour JM, Mayer TS. Nano Lett. 2005;5:2365–2372. doi: 10.1021/nl051219k. [DOI] [PubMed] [Google Scholar]
- 32.Anderson ME, Buck MR, Sines IT, Oyler KD, Schaak RE. J Am Chem Soc. 2008;130:14042–14043. doi: 10.1021/ja804743b. [DOI] [PubMed] [Google Scholar]
- 33.Hurst SJ, Payne EK, Qin L, Mirkin CA. Angew Chem Int Ed. 2006;45:2672–2692. doi: 10.1002/anie.200504025. [DOI] [PubMed] [Google Scholar]
- 34.Keating CD, Natan MJ. Advanced Materials. 2003;15:451–454. [Google Scholar]
- 35.(a) Cao Y, Kovalev AE, Xiao R, Kim J, Mayer TS, Mallouk TE. Nano Lett. 2008;8:4653–4658. doi: 10.1021/nl800940e. [DOI] [PubMed] [Google Scholar]; (b) Kolmakov A, Moskovits M. Annu Rev Mater Res. 2004;34:151–180. [Google Scholar]
- 36.(a) Li M, Bhiladvala RB, Morrow TJ, Sioss JA, Lew KK, Redwing JM, Keating CD, Mayer TS. Nat Nanotechnol. 2008;3:88–92. doi: 10.1038/nnano.2008.26. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Li M, Mayer TS, Sioss JA, Keating CD, Bhiladvala RB. Nano Lett. 2007;7:3281–3284. doi: 10.1021/nl071416e. [DOI] [PubMed] [Google Scholar]
- 37.(a) Paxton WF, Kistler KC, Olmeda CC, Sen A, St Angelo SK, Cao Y, Mallouk TE, Lammert P, Crespi VH. J Am Chem Soc. 2004;126:13424–13431. doi: 10.1021/ja047697z. [DOI] [PubMed] [Google Scholar]; (b) Burdick J, Laocharoensuk R, Wheat PM, Posner JD, Wang J. J Am Chem Soc. 2008;130:8164–8165. doi: 10.1021/ja803529u. [DOI] [PubMed] [Google Scholar]
- 38.Nicewarner-Peña SR, Freeman RG, Reiss BD, He L, Pena DJ, Walton ID, Cromer R, Keating CD, Natan MJ. Science. 2001;294:137–141. doi: 10.1126/science.294.5540.137. [DOI] [PubMed] [Google Scholar]
- 39.Brunker SE, Cederquist KB, Keating CD. Nanomedicine. 2007;2:695–710. doi: 10.2217/17435889.2.5.695. [DOI] [PubMed] [Google Scholar]
- 40.Peña DJ, Mbindyo JKN, Carado AJ, Mallouk TE, Keating CD, Razavi B, Mayer TS. J Phys Chem B. 2002;106:7458–7462. [Google Scholar]
- 41.Schierhorn M, Boettcher SW, Ivanovskaya A, Norvell E, Sherman JB, Stucky GD, Moskovits M. J Phys Chem C. 2008;112:8516–8520. [Google Scholar]
- 42.(a) Mbindyo JKN, Reiss BD, Martin BR, Keating CD, Natan MJ, Mallouk TE. Adv Mater. 2001;13:249–254. [Google Scholar]; (b) Stoermer RL, Keating CD. Smart Medical and Biomedical Sensor Technology II. In: Cullum B, editor. Proc SPIE. Vol. 5588. SPIE; Belingham, WA: 2004. pp. 51–58. [Google Scholar]; (c) Gole A, Murphy CJ. Chem Mater. 2005;17:1325–1330. [Google Scholar]
- 43.Ming T, Kou X, Chen H, Wang T, Tam HL, Cheah KW, Chen JY, Wang J. Angew Chem Int Ed. 2008;47:9685–9690. doi: 10.1002/anie.200803642. [DOI] [PubMed] [Google Scholar]
- 44.(a) Li LS, Alivisatos AP. Adv Mater. 2003;15:408–411. [Google Scholar]; (b) Jana NR, Gearheart LA, Obare SO, Johnson CJ, Edler KJ, Mann S, Murphy CJ. J Mater Chem. 2002;12(12):2909–2912. [Google Scholar]; (c) Murphy CJ, Sau TK, Gole AM, Orendorff CJ, Gao J, Gou L, Hunyadi SE, Li T. J Phys Chem B. 2005;109:13857–13870. doi: 10.1021/jp0516846. [DOI] [PubMed] [Google Scholar]
- 45.(a) Yu G, Li X, Lieber CM, Cao A. J Mater Chem. 2008;18:728–734. [Google Scholar]; (b) Yu G, Cao A, Lieber CM. Nat Nanotech. 2007;2:372–377. doi: 10.1038/nnano.2007.150. [DOI] [PubMed] [Google Scholar]
- 46.Whang D, Jin S, Wu Y, Leiber CM. Nano Lett. 2003;3:1255–1259. [Google Scholar]
- 47.(a) Helfrich MR, El-Kouedi M, Etherton MR, Keating CD. Langmuir. 2005;21:8478–8486. doi: 10.1021/la051220z. [DOI] [PubMed] [Google Scholar]; (b) St Angelo SK. PhD. Thesis. The Pennsylvania State University; University Park, PA: 2004. Assembly of metal nanowires: Fundamental studies and applications toward nanoelectronics. [Google Scholar]
- 48.Chien CL, Sun L, Tanase M, Bauer LA, Hultgren A, Silevitch DM, Meyer GJ, Searson PC, Reich DH. J Magen Magen Mater. 2002;249:146–155. [Google Scholar]
- 49.(a) Park S, Lim J-H, Chung SS-W, Mirkin CA. Science. 2004;303:348–351. doi: 10.1126/science.1093276. [DOI] [PubMed] [Google Scholar]; (b) Ciszek JW, Huang L, Wang Y, Mirkin CA. Small. 2008;4:206–210. doi: 10.1002/smll.200700840. [DOI] [PubMed] [Google Scholar]
- 50.(a) Fan Z, Ho JC, Jacobson ZA, Yerushalmi R, Alley RL, Razavi H, Javey A. Nano Lett. 2008;8:20–25. doi: 10.1021/nl071626r. [DOI] [PubMed] [Google Scholar]; (b) Yerushalmi R, Jacobson ZA, Ho JC, Fan Z, Javey A. Appl Phys Lett. 2007;91:203104. [Google Scholar]; (c) Kim YK, Kang PS, Kim DI, Shin G, Kim GT, Ha JS. Small. 2009;5:727–734. doi: 10.1002/smll.200801362. [DOI] [PubMed] [Google Scholar]
- 51.Triplett DA, Fichthorn KA. Phys Rev E: Stat Phys Plasmas Fluids Relat Interdisciplin Top. 2008;77:011707. doi: 10.1103/PhysRevE.77.011707. [DOI] [PubMed] [Google Scholar]
- 52.Martínez-Ratón Y, Velasco E, Mederos L. J Chem Phys. 2005;122:064903. doi: 10.1063/1.1849159. [DOI] [PubMed] [Google Scholar]
- 53.Donev A, Burton J, Stillinger FH, Torquato S. Phys Rev B: Condens Matter. 2006;73:054109. [Google Scholar]
- 54.Bates MA, Frenkel D. J Chem Phys. 2000;112:10034–10041. [Google Scholar]
- 55.Maier EE, Krause R, Deggelmann M, Hagenbuechle M, Weber R, Fraden S. Macromolecules. 1992;25:1125–1133. [Google Scholar]
- 56.(a) Schneider J, Hess W, Klein R. J Phys A: Math Gen. 1985;18:1221–1228. [Google Scholar]; (b) Schneider J, Hess W, Klein R. Macromolecules. 1986;19:1729–1732. [Google Scholar]; (c) Schneider J, Karrer D, Dhont JKG, Klein R. J Chem Phys. 1987;87:3008–3015. [Google Scholar]
- 57.Weyerich B, D’Aguanno B, Canessa E, Klein R. Faraday Discuss Chem Soc. 1990;90:245–259. [Google Scholar]
- 58.Kramer EM, Herzfeld J. Phys Rev E. 2000;61:6872–6878. doi: 10.1103/physreve.61.6872. [DOI] [PubMed] [Google Scholar]
- 59.Earl DJ, Ilnytskyi J, Wilson MR. Mol Phys. 2001;99:1719–1726. [Google Scholar]
- 60.Cuetos A, Martínez-Haya B, Rull LF, Lago S. J Chem Phys. 2002;117:2934–2946. doi: 10.1063/1.1830429. [DOI] [PubMed] [Google Scholar]
- 61.Wensink HH. J Chem Phys. 2007;126:194901. doi: 10.1063/1.2730819. [DOI] [PubMed] [Google Scholar]
- 62.Avendaño C, Gil-Villegas A, González-Tovar E. J Chem Phys. 2008;128:044506. doi: 10.1063/1.2823736. [DOI] [PubMed] [Google Scholar]
- 63.Martínez-Haya B, Cuetos A. J Phys Chem B. 2007;111:8150–8157. doi: 10.1021/jp0715171. [DOI] [PubMed] [Google Scholar]
- 64.McGrother SC, Gil-Villegas A, Jackson G. J Phys Condens Matter. 1996;8:9649–9655. [Google Scholar]
- 65.McGrother SC, Gil-Villegas A, Jackson G. Mol Phys. 1998;95:657–673. [Google Scholar]
- 66.Savenko SV, Dijkstra M. Phys Rev E: Soft Matter Biol Phys. 2004;70:051401. doi: 10.1103/PhysRevE.70.051401. [DOI] [PubMed] [Google Scholar]
- 67.Baulin VA, Khokhlov AR. Phys Rev E. 1999;60:2973–2977. doi: 10.1103/physreve.60.2973. [DOI] [PubMed] [Google Scholar]
- 68.Allen R, Goulding D, Hansen JP. PhysChemComm. 1999;2:30–33. [Google Scholar]
- 69.Titov AV, Král P. Nano Lett. 2008;8:3605–3612. doi: 10.1021/nl801530x. [DOI] [PubMed] [Google Scholar]
- 70.(a) Nicewarner-Peña SR, Carado AJ, Shale KE, Keating CD. J Phys Chem B. 2003;107:7360–7367. [Google Scholar]; (b) Martin CR. Chem Mater. 1996;8:1739–1746. [Google Scholar]
- 71.We postulate that the regions of low wire density result from a combination of repulsions from the edges of the sample well (as low density regions often occurred close to the walls), convective flow due to manual pipetting of the nanowire suspensions into the wells, and weak attractive forces between the wires; together these effects overcame the tendency for uniform nanowire densities across the entire sample area.
- 72.Russel WB, Saville DA, Schowalter WR. Colloidal Dispersion. Cambridge University Press; Cambridge, UK: 1989. [Google Scholar]
- 73.Vold MJ. J Colloid Sci. 1961;16:1–12. [Google Scholar]
- 74.Das S, Sreeram PA, Raychaudhuri AK. Nanotechnology. 2007;18:035501. doi: 10.1088/0957-4484/18/3/035501. [DOI] [PubMed] [Google Scholar]
- 75.Visser J. Adv Colloid Interface Sci. 1972;3:331–363. [Google Scholar]
- 76.Sader JE, Carnie SL, Chan DYC. J Colloid Interface Sci. 1995;171:46–54. [Google Scholar]
- 77.The deionized water used in the experiments was at a pH of 4.7, which should lead to a nominal ionic strength of slightly more than 10 μM.
- 78.Dougherty GM, Rose KA, Tok JBH, Pannu SS, Chuang FYS, Sha MY, Chakarova G, Penn SG. Electrophoresis. 2008;29:1131–1139. doi: 10.1002/elps.200700448. [DOI] [PubMed] [Google Scholar]
- 79.(a) Sioss JA, Keating CD. Nano Lett. 2005;5:1779–1783. doi: 10.1021/nl051370u. [DOI] [PubMed] [Google Scholar]; (b) Banholzer MJ, Li S, Ketter JB, Rozkiewicz DI, Schatz GC, Mirkin CA. J Phys Chem C. 2008;112:15729–15734. doi: 10.1021/jp805215j. [DOI] [PMC free article] [PubMed] [Google Scholar]; (c) O’Sullivan JP, Wood GC. Proc Roy Soc Lond A. 1970;317:511–543. [Google Scholar]
- 80.Kostoglou M, Karabelas AJ. J Colloid Interface Sci. 1995;171:187–199. [Google Scholar]
- 81.Martines E, Csaderova L, Morgan H, Curtis ASG, Riehle MO. Colloids Surf, A. 2008;318:45–52. [Google Scholar]
- 82.Suresh L, Walz JY. J Colloid Interface Sci. 1996;183:199–213. doi: 10.1006/jcis.1997.5216. [DOI] [PubMed] [Google Scholar]
- 83.Bhattacharjee S, Ko CH, Elimelech M. Langmuir. 1998;14:3365–3375. [Google Scholar]
- 84.Suresh L, Walz JY. J Colloid Interface Sci. 1997;196:177–190. doi: 10.1006/jcis.1997.5216. [DOI] [PubMed] [Google Scholar]
- 85.Granfeldt MK, Jonsson B, Woodward CE. J Phys Chem. 1991;95:4819–4826. [Google Scholar]
- 86.Chen H, Clarkson B, Sun K, Mansfield JF. J Colloid Interface Sci. 2005;288:97–103. doi: 10.1016/j.jcis.2005.02.064. [DOI] [PubMed] [Google Scholar]
- 87.Talapin DV, Shevchenko EV, Murray CB, Kornowski A, Föster S, Weller H. J Am Chem Soc. 2004;126:12984–12988. doi: 10.1021/ja046727v. [DOI] [PubMed] [Google Scholar]
- 88.Tao A, Kim F, Hess C, Goldberger J, He R, Sun Y, Xia Y, Yang P. Nano Lett. 2003;3:1229–1233. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.