Semi-Automatic Medical Image Segmentation with Adaptive Local Statistics in Conditional Random Fields Framework

Abstract

Planning radiotherapy and surgical procedures usually require onerous manual segmentation of anatomical structures from medical images. In this paper we present a semi-automatic and accurate segmentation method to dramatically reduce the time and effort required of expert users. This is accomplished by giving a user an intuitive graphical interface to indicate samples of target and non-target tissue by loosely drawing a few brush strokes on the image. We use these brush strokes to provide the statistical input for a Conditional Random Field (CRF) based segmentation. Since we extract purely statistical information from the user input, we eliminate the need of assumptions on boundary contrast previously used by many other methods, A new feature of our method is that the statistics on one image can be reused on related images without registration. To demonstrate this, we show that boundary statistics provided on a few 2D slices of volumetric medical data, can be propagated through the entire 3D stack of images without using the geometric correspondence between images. In addition, the image segmentation from the CRF can be formulated as a minimum s–t graph cut problem which has a solution that is both globally optimal and fast. The combination of a fast segmentation and minimal user input that is reusable, make this a powerful technique for the segmentation of medical images.

I. Introduction

The time required for manual delineation of organ tissues by radiologists and radiation oncologists is a major bottleneck in the treatment planning process. Expert oversight, however, is a necessity due to the legal and moral implications of any error in the process. While reliable automatic segmentation is a long-term goal, a semiautomatic method can have immediate and significant impact by improving productivity and consistency in the tasks. We present a semi-automatic segmentation approach to address these challenges. We focus on the case where the segmentation task is to separate normal organ tissue, referred to as the target, from non-target (background) tissue. User interactive input is used to extract statistics which determine an energy (cost) function with regional and boundary terms. The form of the energy function is based on the probabilistic graphical model: Conditional Random Fields (CRF) [9, 10]. Maximum-A-Posterior (MAP) estimation inference is given by minimizing this energy function. The solution is determined by a graph min s–t cut algorithm that rapidly provides a globally optimal segmentation. Unlike work that makes simplified assumption on structure boundary (Greig et al. [6], Boykov at el. [2, 3] and Wu et al [13]) or work that is prone to boundary leakage due to boundary contrast (snakes [1, 7, 14] and level set [12]) and sensitive to initialization of a seed point or contour, our work combines interactive expert user guidance to collect regional and boundary statistics in a probabilistic framework and a fast graph partition algorithm that provides a global solution for spatial consistency.

II. Methods

A. User Inputs

Initially the algorithm is provided training information from the expert user via a set of simple and intuitive brush strokes on one or a few of the images to be segmented trough an interactive GUI. As the user adjusts interactively and subsequently accepts a given segmentation, the training samples with observed image features are progressively collected. For subsequent slices to be segmented, the algorithm estimates the parameters of an energy function containing both boundary and regional components from the training samples as well as new brush strokes. The users can retrain the model at any time if the statistics is not applicable. The segmentation process is shown in Figure 1.

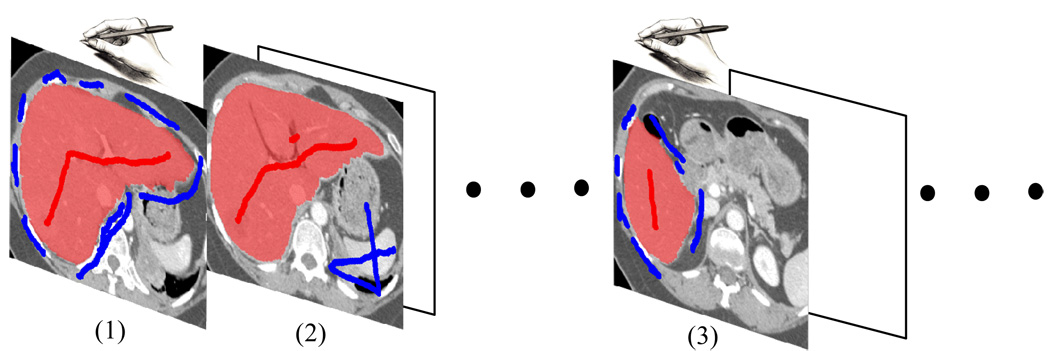
Figure 1.

The process of segmenting a stack of medical images in our method. (1) On one of the images, the user specifies the seed pixels interactively by using brush strokes. At this time no statistics is available for segmentation. Once the initial result is satisfactory, pixels along the boundary are sampled. (2) On the subsequent image slices, the boundary term is estimated from the samples on the training slice. The regional term is also estimated from the new brush strokes on the image slice being segmented. Note that the humane interactions (brush strokes) are significantly reduced. (3) Users can always re-train the model if the boundary statistics is no longer applicable.

B. Conditional Random Field (CRF)

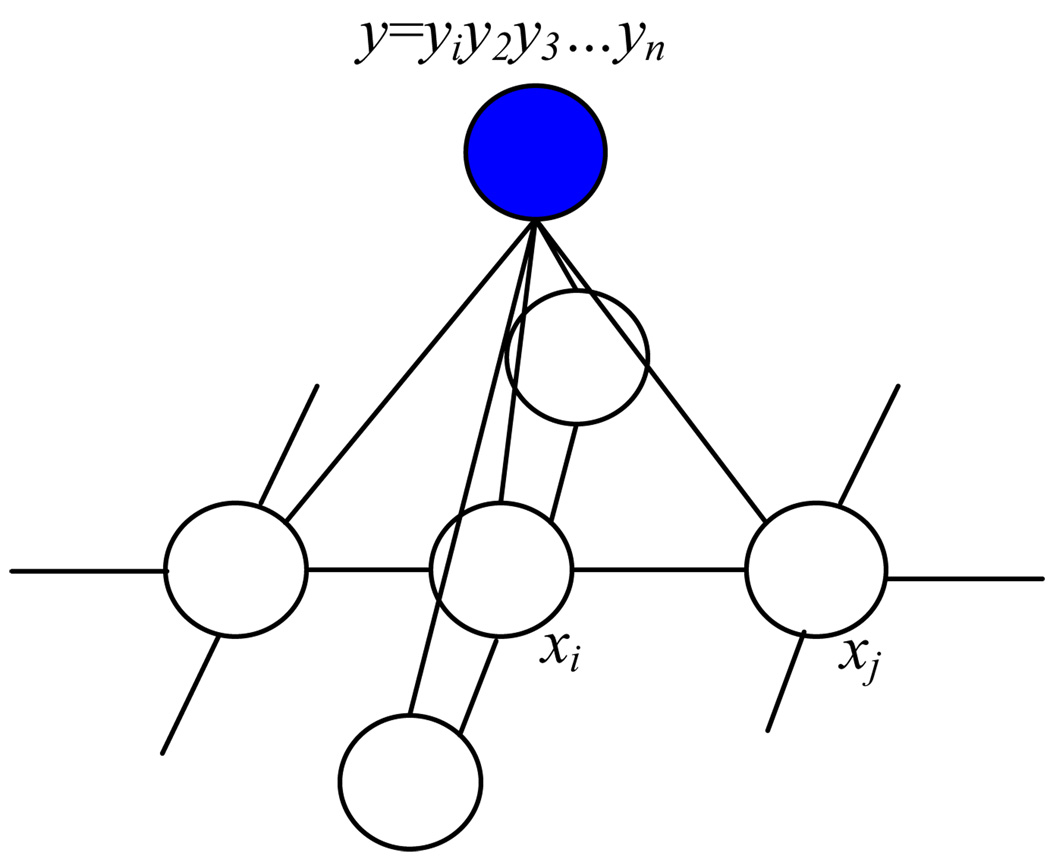
We begin by defining notation. We represent an image by a vector of random variables, Y = (Y₁, Y₂, …, Y_n), where Y_i is a random variable for the grey level intensity of the ith pixel. Let y denote an observed instance of Y with y_i the measured feature vector at pixel i. We will use a single dimension feature - gray level in this work. The segmentation is described by a vector X = (X₁, X₂, …, X_n), X_i ∈ {0, 1} of binary valued random variables. In any segmentation x pixel i must be classified as x_i = 0, if it represents the target anatomical structure, and as x_i = 1 if it is in the complement, a non-target tissue. The labeling sequence of X, given an observed image Y, can be modeled as a Conditional Random Field (CRF) [10] or more precisely, a Discriminative Random Field (DRF) [9]. The undirected graphical model is shown in Figure 2. CRF is a special type of Markov Random Field (MRF) globally conditional on Y. Using the Hammersley-Clifford theorem, the joint distribution over labels X, given image Y, is given by $p(x|y)=\frac{1}{Z}\text{exp}(-E(x,y))$, where Z is a normalization constant. E(x, y) is an energy function can be expressed in term of clique (maximum clique) potentials describing the local interactions in a neighborhood system. Here we use 4-connected neighborhood system in the graphical model and let N_i denote the neighborhood of site i, then

$$E(x,y)={\displaystyle \sum _i{r}_i(x_i,y)+\beta {\displaystyle \sum _i{\displaystyle \sum _{j,j\in N_i}{u}_{\mathit{\text{ij}}}(x_i,x_j,y)}}},$$ (1)

where r_i and u_ij are unary and pair-wise potentials respectively and β is a constant weight . We call r_i the regional term for association of a local site i with possible label class and u_ij the boundary term for potential of assigning x_i and x_j to different labels (a smoothness energy) when observing image y. Let f_i be a function that maps the observed image y to a feature vector at site i, that is f_i(y) = y_i. In this work we let the feature vector to be gray level value of image. We then choose

$$r_i(x_i,y)=-\text{ln}p(f_i(y)|x_i)$$ (2)

and

$$u_{\mathit{\text{ij}}}(x_i,x_j,y)=-\text{ln}p(f_i(y),f_j(y)|x_i\ne x_j)·\delta (x_i,x_j).$$ (3)

Figure 2.

The CRF graphical model for labeling x given 2D image y, where {y, x_i, x_j} is one of the cliques. The conditional probability p(x | y) can be factorized by clique potentials.

Here δ is a Kronecker delta function with δ(x_i,x_j) = 1 if, x_i ≠ x_j, and δ(x_i,x_j) = 0 otherwise. The pair-wise interaction term u_ij is obtained from well known general Potts Model. Then (1) can be rewritten to

$$E(x,y)=-{\displaystyle \sum _{i,x_i=0}\text{ln}p(f_i(y)|0)-{\displaystyle \sum _{i,x_i=1}\text{ln}p(f_i(y)|1)}-\beta {\displaystyle \sum _i{\displaystyle \sum _{j,j\in N_i}\text{ln}p(f_i(y),f_j(y)|x_i\ne x_j)}}}$$ (4)

C. Graph Cut

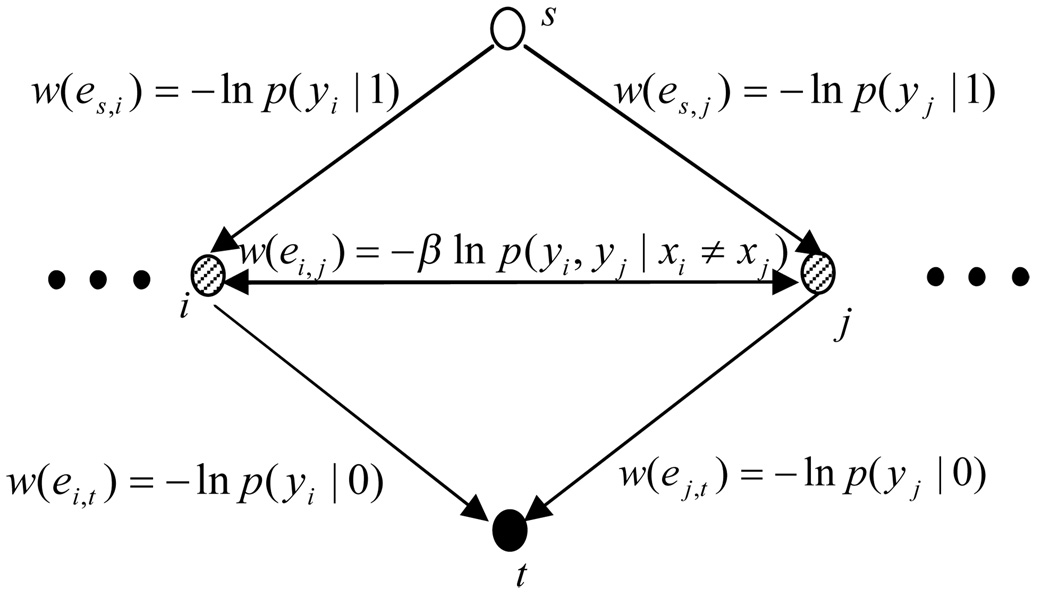
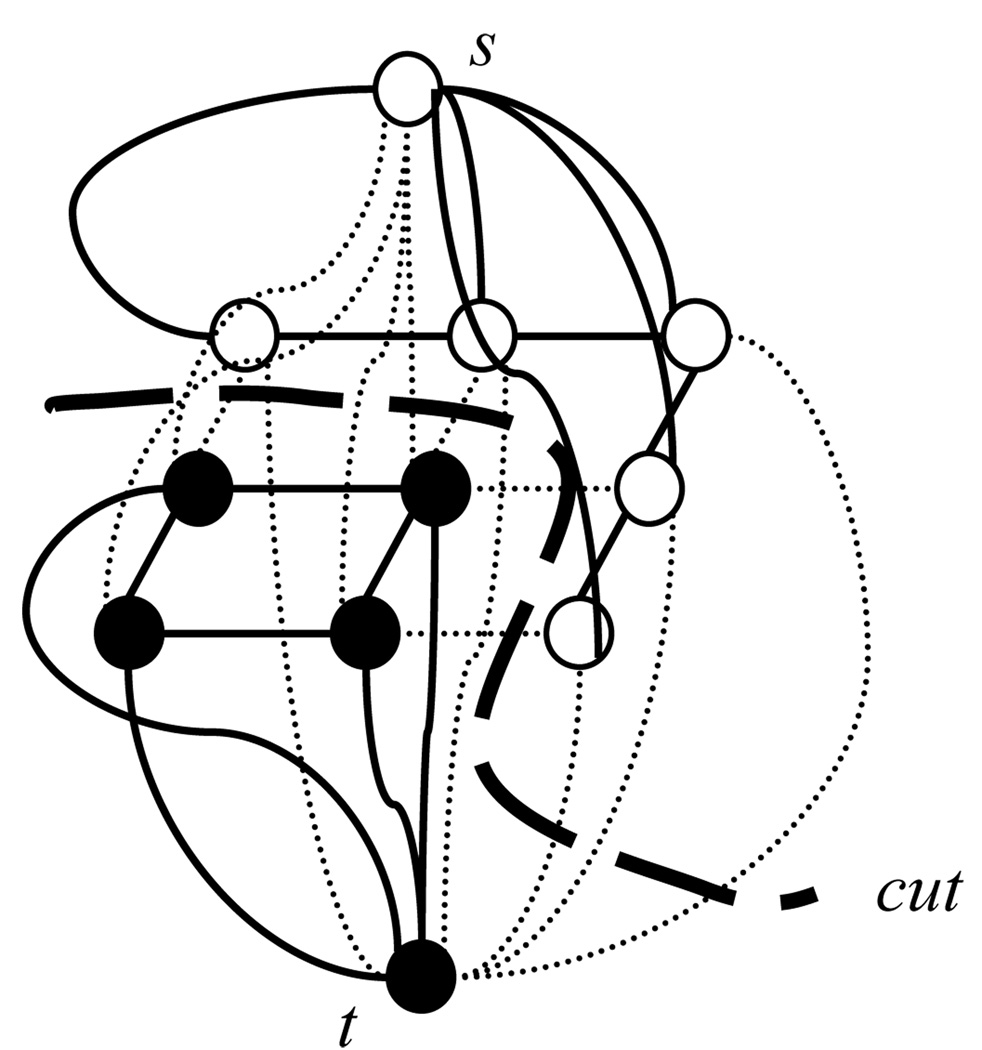
MAP inference is given by minimizing E(x, y). Further, E(x, y) is graph representable [8] and thus we can solve the minimization problem using a graph min-cut/max-flow algorithm in polynomial time [4, 5]. By finding the minimum s–t cut, the cost of the cut (sum of the edges’ cost being cut) is the minimum value of the energy function E(x, y). The graph construction for solving the minimization is shown in Figure 3 and Figure 4 shows an s–t cut example.

Figure 3.

The edge cost assignment. The cost of the min s–t cut in the graph minimizes our energy function E in (4).

Figure 4.

An s–t cut on a 3×3 image. White dots are target pixels and black dots are non-target pixels. The dotted lines are edges being cut. The cost of the cut is sum of the edges’ cost being cut.

D. Probability estimation

The major contribution of our method is not using a fixed value or any assumption on strength of the pair-wise interaction (boundary term) in CRF. The boundary term, as well as the regional term, is estimated from the observed samples specified by the user. We provide an interactive user interface similar to [2, 3] and [11.] The user specifies the seed pixels for the target and non-target by paint brushes.

Once the user determines that an agreeable result is obtained, we first obtain regional statistics from the seeds for both target and non-target regions. For each pixel i, if i is a target seed then y_i is added to the training set for target, otherwise if i is a non-target seed then y_i is added to the training set for non-target. We then sample along the boundary of segmented target accepted by the user for boundary statistics. Each pair of (y_i, y_j) where i, j are neighbors and i ∈ target, j ∈ non-target is added to the boundary training set. The sets of regional and boundary training samples are used for estimating the probabilities of r_i and u_i,j in (2) and (3) for the subsequence slices unless it is re-trained.

III. Results

A. Phantom

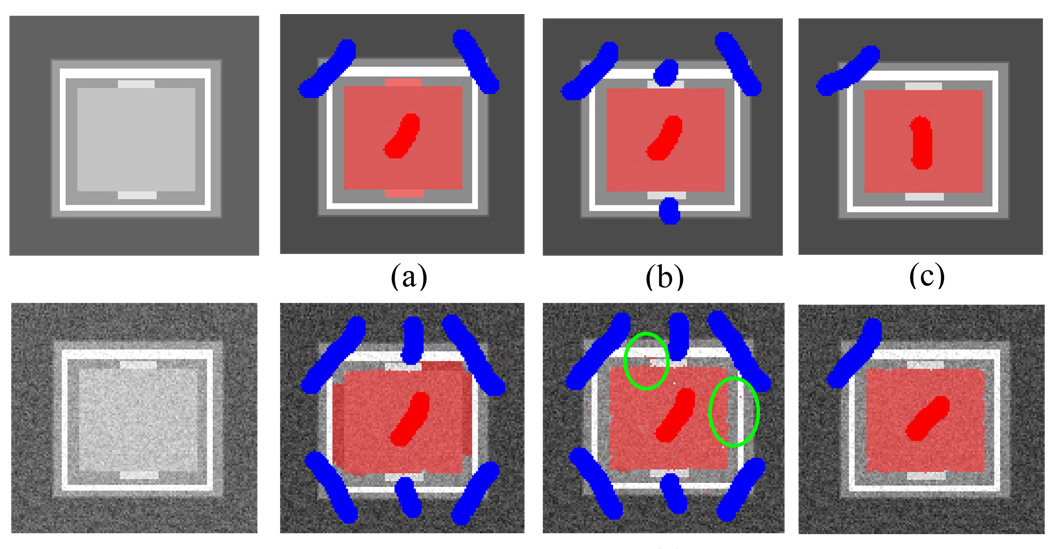
To show the advantage of our method using estimated probability for the pair-wise potential function u_i,j, we synthesize a phantom image and compare our method’s segmentation (referred to as graph cut with probability estimation, GCPE) with a method based on the assumption that favors a high contrast boundary (graph cut with high contrast, GCHC). The phantom image contains a rectangle target region and various surrounding regions. Some of the surrounding regions have higher contrast boundary than the target region. This design reflects some real situations in medial images and GCHC will usually mislabel the surrounding regions with high contrast boundary as target (Figure 5(a), (d)) and extra manual corrections are required (Figure 5(b), (e)). Addition of some Gaussian noise to the phantom image shows that, even with region terms, i.e. likelihoods for intensity of the target and non-target regions, GCHC cannot achieve a clean segmentation due to the noise pixels that are picked up by using stronger regional terms (Figure 5(e)). Note that the GCPE requires much fewer seed pixels to obtain good segmentation results (Figure 5(c), (f)).

Figure 5.

Segmentation results from the phantom image. The first row is clean image and the second row is the same image with Gaussian noises. The target is inner rectangle. (a) GCHC. (b)(d) GCHC with extra brushes. (e) GCHC with regional term. (c)(f) Our method GCPE.

B. CT Liver

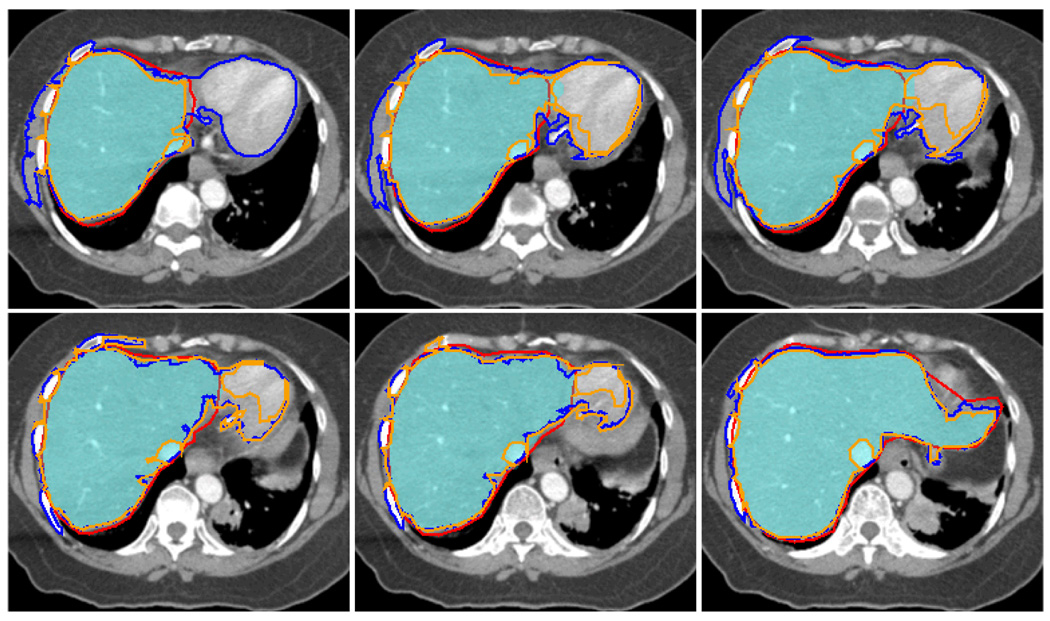
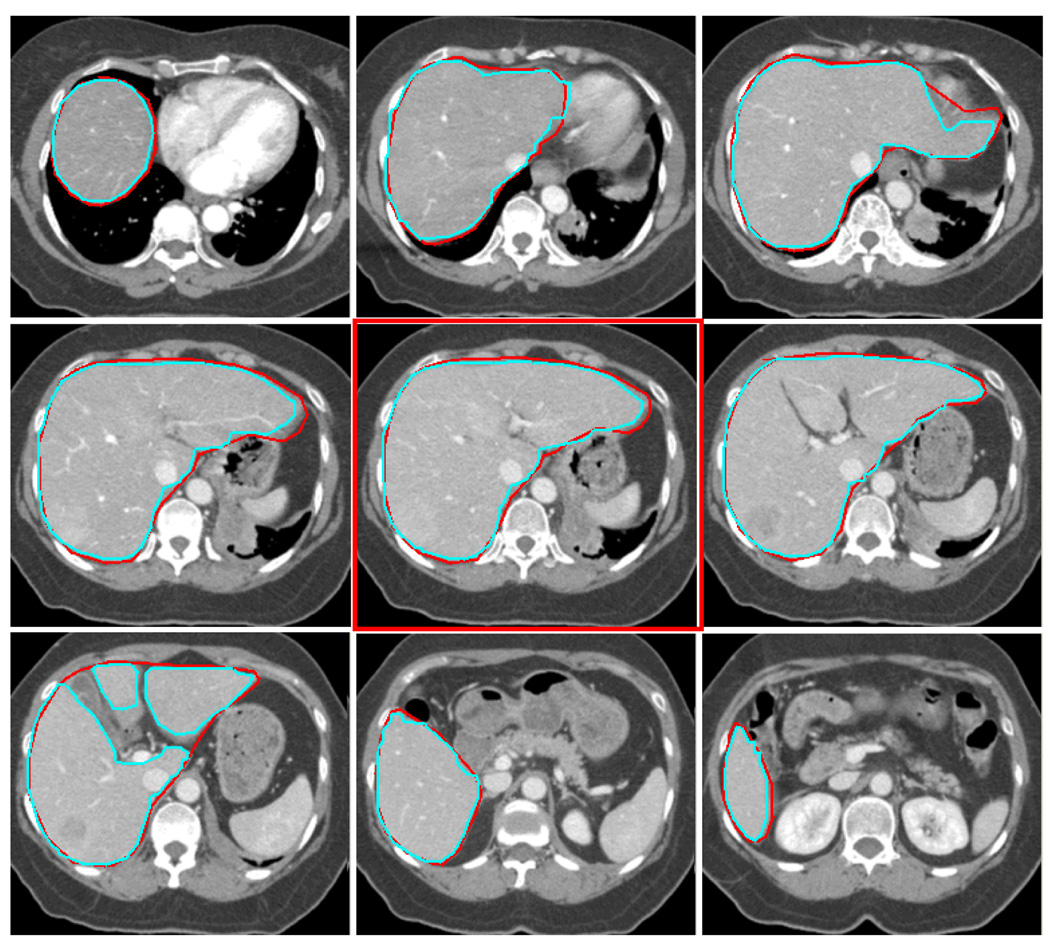
An experienced physician manually delineated a complete liver of a patient. The delineated contours are used as ground truth. There are total of 65 CT slices that intercept the liver. Each 2D slice’s dimension is 512×512. The single middle slice is first segmented with GCHC and the boundary of the resulting target region is sampled for training. Later this statistical information from this single slice is used by our method GCPE for estimating the clique potential for all other slices without retraining during the whole segmentation process for this case. Once the training is done, the GCPE segmentation can be done in 6 seconds for each slice, excluding the time needed for users to specify the seed pixels. For comparison, we also segment the liver by our in house application that implements Region Growing (RG) and by Level Set (LS) methods provided by the MIPAV package from NIH. Precision and Recall rates and F measure are calculated for each of the methods. The numbers are shown in Table 1 and Figure 7 shows some CT Slices with segmented contours along with the ground truth. Our analysis finds that most of the errors are from slices where the liver has several branches. The physician’s intent was to draw a contour that contained all the branches, rather than follow the boundary of individual branches, in order to consider the deformation and motion of the organ during the treatment (the lower left image in Figure 6.) In contrast to RG and LS, GCPE performs well on the slices where the liver boundary is not clearly defined (Figure 7.) On these slices, the precision is 0.99 and recall rate is 0.93 for GCPE while RG has precision 0.93 and recall 0.91 and LS has precision 0.79 and recall 0.93. The F-measure on these slices for GCPE, RG and LS are 0.96, 0.92 and 0.85 respectively.

Table 1.

The quantified error of the segmentation results against ground truth for the CT liver case containing 65 slices.

	TP	TN	FP	FN	Precision	Recall	F(1)
GCPE	525303	1871296	7365	58691	0.9862	0.8995	0.9408
RG	522730	1815425	63236	61264	0.9656	0.8889	0.9256
LS	519108	1860145	18516	64886	0.8921	0.8951	0.8936

Figure 7.

CT slices where the boundary of liver becomes blurred. Red: ground truth, Orange: RG, Blue: LS, Filled Cyan: GCPE. Boundary leakage is severe in RG and LS.

Figure 6.

The contours extracted from our method (cyan) and the contours drawn by an experienced physician (red) from 9 of 65 CT slices segmented. The middle slice in red frame is the slice used for training and its statistics for boundary is used for all 65 slices.

IV. Conclusion and future works

We have proposed a purely statistical semi-automatic 2.5D medical image segmentation method that obtains MAP estimation of segmentation in Conditional Random Field framework. Results of the liver case have shown that the boundary statistics from a single slice can be reused for the entire image stack without retraining to achieve high accuracy. The liver case also shows that our method is not prone to boundary leakage as is the case with region growing and level set methods. This is due to the global optimal solution in the graph cut and the smoothness weight in the CRF. By comparing our method to the original graph cut methods, the time required for manual interaction is significantly reduced. This is extremely important when the target anatomy volume is large and fast and accurate segmentation is very much desired. In our future work, we will extend our framework to 3D and explore more sophisticated image features to proved more accurate classification.