A novel platform for in situ investigation of cells and tissues under mechanical strain

Abstract

The mechanical micro-environment influences cellular responses such as migration, proliferation, differentiation, and apoptosis. Cells are subjected to mechanical stretching in vivo, e.g., epithelial cells during embryogenesis. Current methodologies do not allow high resolution in situ observation of cells and tissues under applied strain, which may reveal intracellular dynamics and the origin of cell mechanosensitivity. We have developed a novel polydimethylsiloxane (PDMS) substrate capable of applying tensile and compressive strain (up to 45%) to cells and tissues while allowing in situ observation with high resolution optics. The strain field of the substrate was characterized experimentally using digital image correlation (DIC) and the deformation was modeled with finite element method (FEM) using a Mooney-Rivlin hyperelastic constitutive relation. The substrate strain was found to be uniform for greater than 95% of the substrate area. As a demonstration of our system, we applied mechanical strain to single fibroblasts transfected with GFP-Actin and whole transgenic Drosophila embryos expressing GFP in all neurons during live imaging. We report three observations of biological responses due to applied strain: (1) dynamic rotation of intact actin stress fibers in fibroblasts; (2) lamellipodia activity and actin polymerization in fibroblasts; (3) active axonal contraction in Drosophila embryo motor neurons. Our novel platform may serve as an important tool in studying the mechanoresponse of cells and tissues including whole embryos.

1 Introduction

The mechanical micro-environment influences cellular responses such as migration, proliferation, differentiation, and apoptosis [1, 2, 3, 4]. When the natural state of the microenvironment is altered, cells often transit to a malfunctioning or diseased state [5, 6, 7]. Vascular cells such as smooth muscle cells or endothelial cells experience strain along their long axis as blood vessels expand and contract [8]. Striated muscle such as cardiac and skeletal muscle cells undergo strain upon every heartbeat and movement [9]. Epithelial cells are subjected to various types of strain throughout different regions of the body such as the lungs during breathing [10]. Recent literature highlights the influence of mechanical forces in cell and tissue development [11, 12, 13] and embryogenesis [14, 15, 16, 17].

To understand how cells and tissues respond to mechanical stretch it is important to investigate their morphological organization and subcellular structure. The combination of new imaging techniques and modern biosensors provide visualization tools for investigating subcellular dynamics previously unavailable for living cells [18, 19, 20], motivating the development of compatible experimental techniques. Cell stretching systems, which allow simultaneous application of strain and high resolution imaging, are needed to understand the role of stretch in cell functionality [21, 22, 23, 24]. Ideally such a system should be easily reproducible for use in many different laboratories, and be highly compatible with a wide variety of imaging systems and biological specimens. Additionally the applied strain field must be precise, well characterized, and highly uniform since it is known that strain gradients have varying affects on gene regulation, intracellular signaling, and alignment [25, 26, 27, 28]. Such a system would allow investigations probing different scales including: subcellular dynamics of single cells and large scale organization of cells in whole tissues in response to applied strain.

Earlier cell stretching systems, such as that offered by Flexcell International, utilize vacuum pressure to deform an elastomeric membrane that is stretched over a cell culture well [29], but these systems are primarily used with fixing and staining for biochemical studies. Furthermore, the strain field in the pressure driven system may not be uniform [30] which may lead to ambiguous experimental results. Most current systems grip and stretch the substrates in an attempt to achieve a more uniform strain field. However they do not allow live imaging with high numerical aperture optics because of the incompatibility with the short working distance (100–200 µm) objectives. This is typically due to either limitations of the stretching device itself [31, 32, 33, 34, 35] or the thickness of the stretchable substrate [36, 37, 38, 39]. Stretching systems, which are compatible with high resolution optics, tend to be complicated and require integration with a specific microscopy system [40, 41]. Additionally, most studies measure the strain field experimentally at discrete locations and assume uniformity over the substrate surface. This may not be adequate to precisely characterize the strain field since complicated boundary conditions due to clamping may lead to locally non-uniform strains, especially under large deformations.

2 Design of the Stretching System and Working Principle

We have designed and characterized a novel platform for precise application of mechanical strain to single cells and tissues while allowing in situ live imaging with high resolution optics. The system specifications are as follows: (a) portable and easily replicated, (b) compatible with various types of microscopes and imaging chambers, (c) uniform strain over a large area.

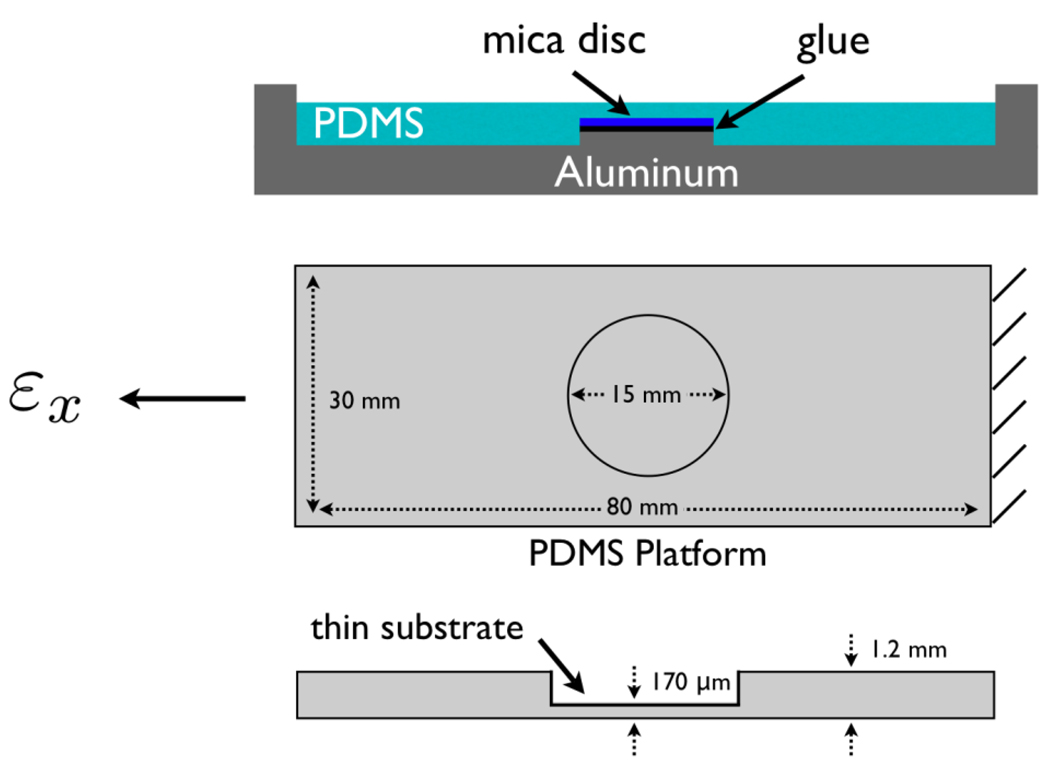
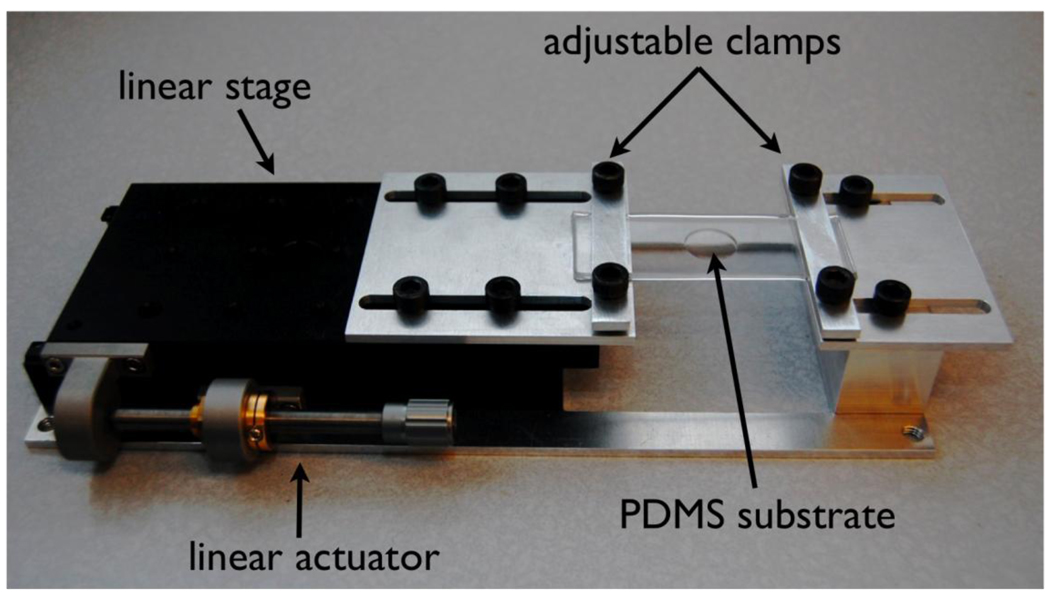
Our novel platform is a polydimethylsiloxane (PDMS) substrate with two thicknesses. A thin region (diameter = 15 mm, and thickness = 170 µm) serves as the culture surface and is surrounded by a thicker region (thickness = 1.2 mm) as shown in Figure 1. The thick substrate around the thin region provides structural support necessary for handling. The ends of the thick substrate are clamped and stretched and the strain is transferred to the thin culture surface (Figure 2). The PDMS substrate is supported by a linear stage and actuator (Newport Inc.) mounted on an aluminum base with adjustable clamps. Aluminum was chosen for its corrosion resistance in cell culture/incubator environments. Uniaxial stretch of the flexible substrate, which is unconstrained in the lateral direction, results in a Poisson’s contraction.

Figure 1.

Schematic diagrams of the aluminum mold and the flexible PDMS substrate.

Figure 2.

The stretching system consists of a flexible PDMS substrate mounted on a linear stage with an actuator. Adjustable aluminum plates are used to clamp the substrate. The system is approximately 10 inches long.

Thus as ε_x is applied, there is a lateral contraction of ε_x= −νε_y for the ideally linear elastic case (Poisson’s ratio, ν≈0.5 for PDMS). To adequately describe the material behavior under large deformations a nonlinear constitutive relation must be used which is discussed later.

Polymer Casting

PDMS substrates were prepared by thoroughly mixing a 10:1 ratio of Dow Corning Sylgard 184 silicone elastomer and curing agent resulting in a Young’s Modulus of E ≈ 1 MPa [42]. The mixture was cast in an aluminum mold and cured at 100° C for 12 hrs (Figure 1). The surface of the aluminum mold was coated with a thin layer of polytetrafluoroethylene (PTFE) prior to polymer casting to facilitate mold release.

Surface Roughness

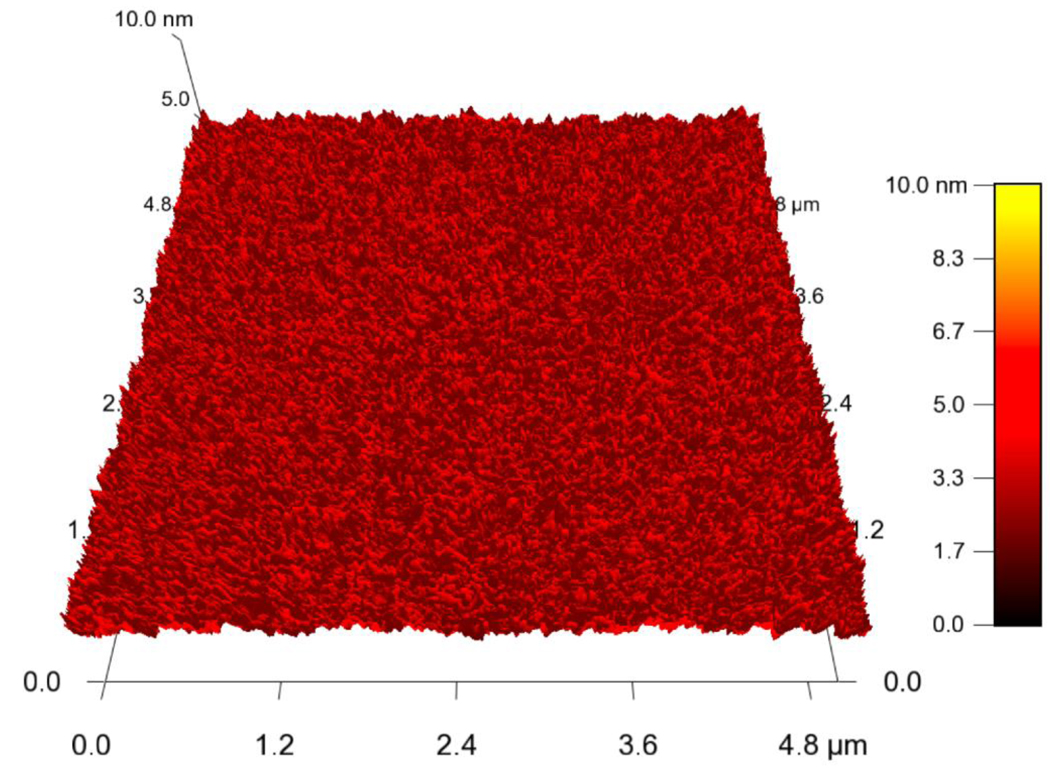
The surface of the culture reservoir is the mirror image of the surface of the polished aluminum mold. Thus, to ensure a smooth surface finish, the mold was polished with alumina nanoparticles and metal polish. The surface roughness of the resulting PDMS substrate was found to have an rms value of approximately 30 nm by atomic force microscopy (AFM). To achieve a smoother finish Mica discs were adhered to the surface of the aluminum mold and the PDMS was cured in contact with this surface as shown in Figure 1. The resulting surface roughness of the PDMS was found to have an rms value of less than 2 nm. The surface of the culture well was probed by AFM after plasma treatment and no irregular surface patterns were observed as shown in Figure 3.

Figure 3.

Surface roughness of the PDMS surface was measured by AFM after O2 plasma treatment and was found to be less than 2 nm.

Surface functionalization

PDMS can be functionalized in a variety of ways [43, 44, 45]. Here, we employed two different types of surface functionalization, using (1) silane for Drosophila embryos and (2) fibronectin for cell adhesion. (1) The silane based functionalization [46] involves a pretreatment with O₂ plasma (300 W, 500 mtorr, 3 min) followed by immediate incubation in 10% (3-Aminopropyl)triethoxysilane (APTES) for two hours. After incubation, the PDMS surface was washed with phosphate buffered saline (PBS) and allowed to air dry to make the surface hydrophobic [47]. (2) A fibronectin functionalization [48] involves sterilization of the PDMS substrates with ethanol and rinsing with PBS. The substrates were then exposed to low intensity ultraviolet (UV) light for 20 minutes to ensure sterilization and modify the surface [49]. Subsequently, the culture surface of the substrate was incubated in 0.5 mL of 50 µg/mL human derived fibronectin for at least two hours to allow uniform adsorption.

3 Characterization of Substrate Deformation

When studying the effect of mechanical strain on cells and tissues quantitatively, it is important to know the magnitude and the type of strain being applied. If the strain is applied by culturing the cell or the tissue on a stretchable substrate, then the substrate strain must be known at any point on the surface. In case the substrate strain is non-uniform, then, to determine the strain on the cell, the location of the cell with respect to a reference must also be known. The latter is non trivial when observing a cell that is orders of magnitude smaller than the substrate size. A non-uniform strain field also induces a strain gradient on the cell or the tissue, which may result in additional unwanted functionalities. As an example, the strain field for a circular film induced by a pressure differential is non-uniform, it varies radially [30]. A uniform strain field of the substrate is thus most desirable, which ensures that any cell or a tissue is subjected to a prescribed strain that is independent of their location. Such uniformity is particularly important when the applied strains are large and material behavior is nonlinear. In that case, small geometric non-uniformities of the substrate (due to fabrication) can result in large unaccounted variation in the strain field [50].

We investigate the substrate strain both experimentally and numerically using finite element analysis. The in-plane displacements and strains measured experimentally match well with the numerical simulation. The simulation reveals the uniformity of the strain field and the out of plane deformation of the substrate [51, 52].

3.1 Experimental observation of the strain field

To measure the strain field experimentally, markers were added to the substrate surface and stretch was applied incrementally using the stretching system. The surface was imaged using a Canon 5D Mark II Digital SLR camera with a 65 mm 1x to 5x macro lens mounted perpendicular to the substrate surface. Strains were calculated using the built in digital image correlation (DIC) function in Matlab. The DIC algorithm located multiple trackable points within each marker and tracked their displacement through sequential images. An example of the images used for the DIC analysis is shown in Figure 4. Strains were measured both at room temperature as well as at 37°C in a cell culture incubator. In the latter case, a fixed stretch was applied and strain was measured over 24 hrs later to check for any time dependent change in the strain field in the thin substrate.

Figure 4.

Images of substrate strain for DIC analysis. The DIC algorithm locates multiple trackable points within each marker and calculates their displacement through sequential images. ε_x denotes tensile strain in the horizontal direction and ε_y denotes the compressive strain in the vertical direction in the image plane. (scale bar = 5 mm)

The deformation of the PDMS substrate was found to be completely reversible and time independent even for large strains (ε_x > 45%). The strain field remained steady even after 24 hrs of applied stretch at elevated temperature (37°C). Thus it can be concluded that there is no slippage in the clamps and no strain redistribution in the substrate due to relaxation of higher stresses at the stress concentration regions (near the edges of the circular thin substrate). The lack of relaxation is an important observation for two reasons: (1) this is highly desirable for controlled experiments and (2) a time independent material model can be used for the finite element analysis. The stretching system has a resolution of approximately 0.1% substrate strain.

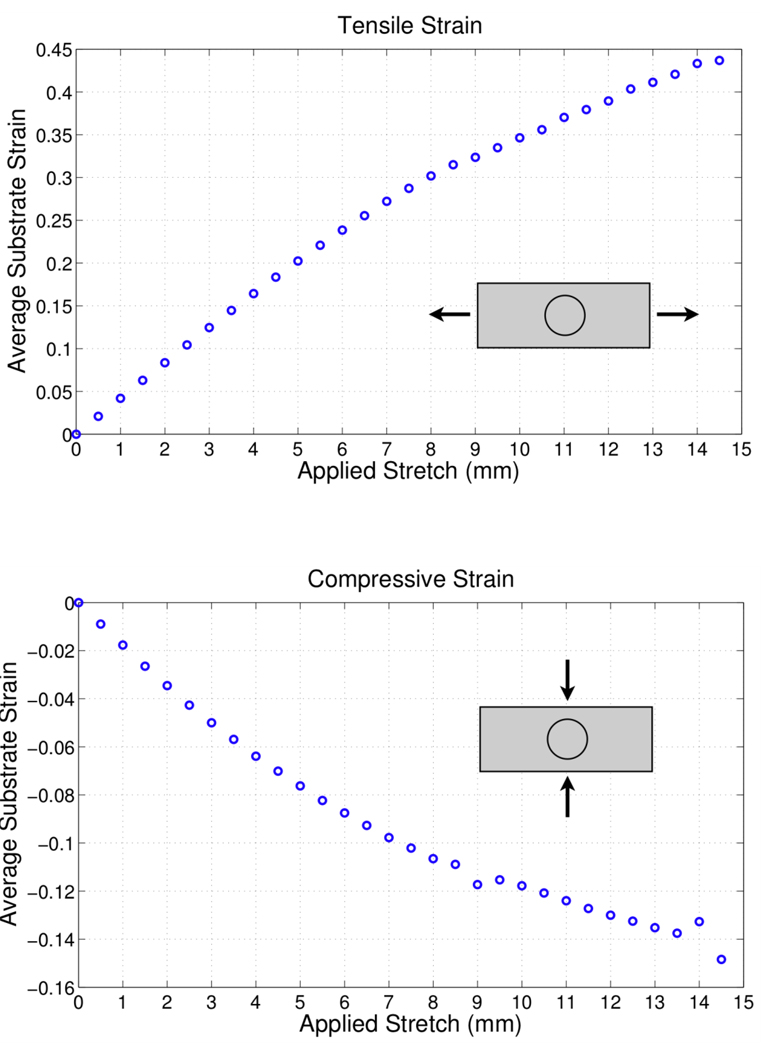
The DIC analysis yielded the experimentally observed substrate strain in Figure 5. When the substrate is stretched by 8 mm, the resulting tensile strain in the thin membrane is approximately 30% with a lateral contraction of 10%. When the substrate is stretched by 14.5 mm the resulting tensile strain is 45% with a lateral contraction of 15%.

Figure 5.

Average substrate strain as calculated by the DIC analysis. Where (a) is the tensile strain in the x direction and (b) is the compressive strain in the y direction.

3.2 Numerical Simulation of the strain field

3.2.1 Constitutive behavior of PDMS

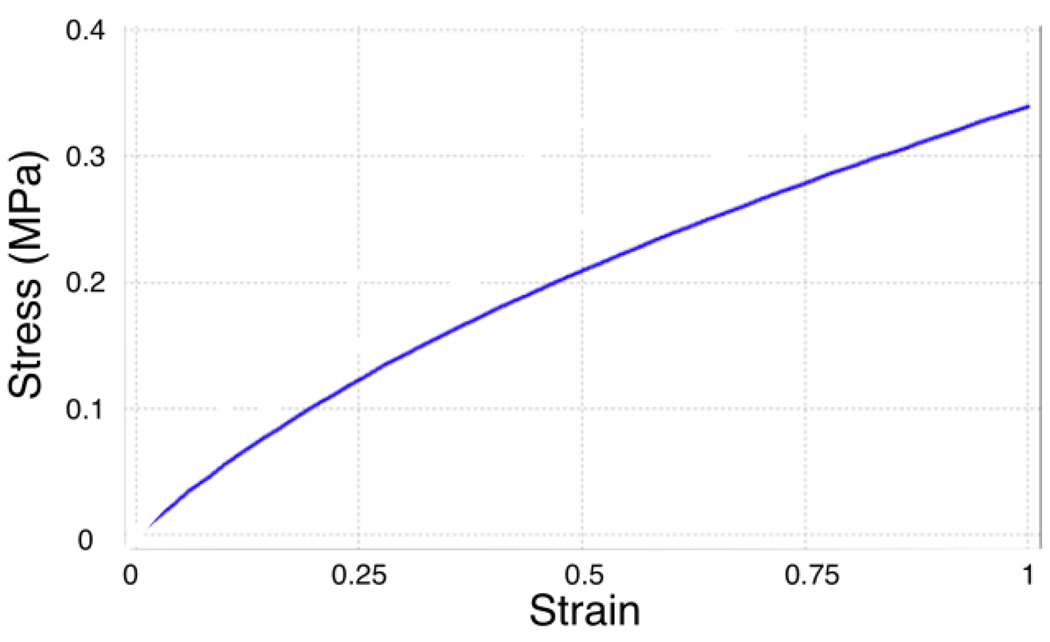
Rubber-like materials like PDMS are able to sustain large deformations with elastic recovery, and they exhibit a nonlinear stress-strain behavior (Figure 6). Here, we use the Mooney-Rivlin constitutive relation to describe the hyperelastic material behavior [53, 54, 55]. In this model PDMS is assumed to be ideally elastic, isotropic, and incompressible. The strain energy function, W, is a polynomial function of the strain invariants,

$$W={\displaystyle \sum _{i=0}^{\infty }{\displaystyle \sum _{j=0}^{\infty }{c}_{ij}{(I_1-3)}^i{(I_2-3)}^j}}$$ (1)

where c_ij are material constants, and I₁ = trC, $I_2=\frac{1}{2}\left({(\text{tr}\mathbf{C})}^2-\text{tr}{\mathbf{C}}^2\right)$ where C is the right Cauchy-Green deformation tensor, and the Green strain tensor is defined as $\mathrm{E}=\frac{1}{2}(\mathbf{C}-\mathbf{I})$ [56]. For strains of less than 100%, the first order terms of the strain energy is often used which is a linear function of the strain invariants [57],

$$W=c_{10}(I_1-3)+c_{01}(I_2-3)$$ (2)

where c₁₀ and c₀₁ are the two material constants required to completely specify the material behavior, the strain invariants are, $I_1={\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2$, $I_2={\lambda }_1^2{\lambda }_2^2+{\lambda }_2^2{\lambda }_3^2+{\lambda }_3^2{\lambda }_1^2$, and the principle stretch ratios are, λ_i = 1+ε_i, where ε_i is the principal value of engineering strain in the ith direction. The first order Mooney-Rivlin model for a hyperelastic material was used with c₁₀ = 90.35 kPa and c₀₁ = 12.82 kPa which were previously reported to be valid for strains up to 50% [58].

Figure 6.

Stress-strain plot for a Mooney-Rivlin material with c₁₀ = 90.35 kPa and c₀₁ = 12.82 kPa used for PDMS [58].

3.2.2 Boundary conditions for numerical simulation

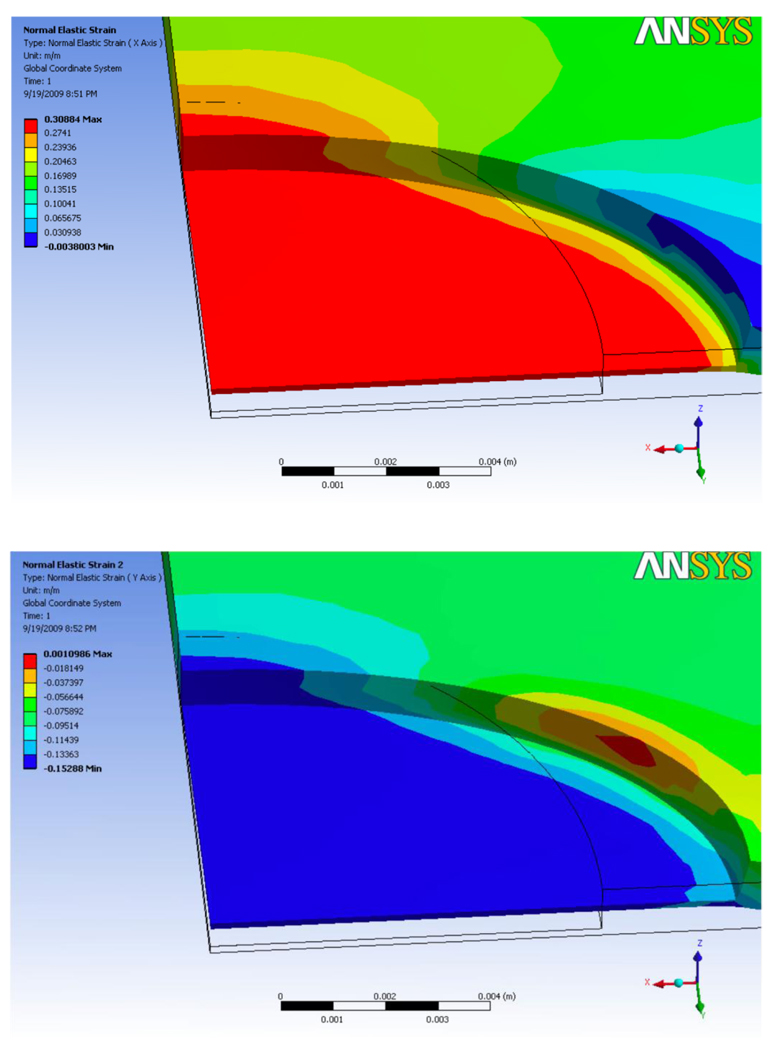
The PDMS substrate geometry was created in ANSYS and displacement boundary conditions were applied to the clamping area of the substrate to mimic application of strain by the stretching system. One quarter of the platform was modeled with symmetric boundary conditions: (1) all the nodes on the YZ surface were restrained against motion along the X direction, (2) all the nodes on the XZ surface were restrained against motion along the Y direction, and (3) the clamping surface was fixed in the Z direction, and an X displacement was applied to stretch the platform (refer to Figure 7 for axis orientation).

Figure 7.

Finite element method simulation of substrate deformation using the two parameter Mooney-Rivlin hyperelastic constitutive relation. Where (a) and (b) are the contour plots of ε_x and ε_y respectively. The average predicted tensile strain and lateral contraction are ε_x = 30% and ε_y = 14% respectively.

3.3 Simulation results

3.3.1 Uniformity of strain field

Most importantly, the FEM simulation shows that the strain in the thin substrate is uniform for the majority of the surface area as seen in Figure 7. In over 95% of the surface area of the thin substrate, the surface strain varies by approximately 1%. This verifies that the strain field is uniform and any biological specimen will be under approximately the same strain regardless of its location on the substrate. This allows a highly controlled experiment where the applied strain in known regardless of the location of the specimen on the substrate.

3.3.2 Out of plane deformation

The simulation shows that at 30% tensile strain the center of the thin membrane displaces upward by 400 µm above the surrounding edge. Relative to the diameter of the membrane (15 mm) this deformation is small and the resulting membrane curvature is low and thus does not affect imaging or the uniformity of the surface strain in the thin membrane.

3.3.3 Comparison with experiment

The FEM results (Figure 7) show close agreement with the measured experimental strains (Figure 5). When an equivalent substrate stretch of 8 mm was applied in the simulation, the resulting tensile strain in the circular well along the loading direction was 30% with a lateral contraction of 14%. Thus the experimentally measured tensile strain (30% in response to 8 mm grip displacement) is in direct agreement with the results predicted by the simulation, however, the predicted value of the lateral contraction is 4% higher than observed experimentally. This deviation from experiment in the lateral contraction is expected to be a result of idealized clamping boundary conditions in the simulation in contrast to the experiment where clamping is achieved by a pair of aluminum plates held by bolts at the ends. In the experiment, after tightening the bolts, the aluminum clamps bend and the gap between the plates increases towards the center. This results in a complex state of stress in the substrate with a boundary condition that is pinching the substrate near the edges.

Biological Investigations

Our novel platform is capable of applying precise amounts of strain to cells and tissues including whole embryos while allowing in situ live imaging. To illustrate this advantage we investigated the mechanoresponse of single fibroblasts and whole Drosophila embryos.

4 Fibroblasts

Fibroblasts are a robust model system to study the basic response of the cytoskeleton to mechanical stimulus. They are the primary cells present in connective tissue and play a critical role in wound healing. Additionally they are easily cultured in vitro and have been extensively studied. Our system allows observation of real time subcellular dynamics in single cells to observe their mechanoresponse to applied strain.

Cell Culture and Transfection

Monkey kidney fibroblasts from ATCC were cultured in an incubator at 37 °C and 5% CO2 in growth medium consisting of Dulbecco’s Modified Eagle Medium (DMEM) (BioWhittaker Cat. No. 12–604F) with 10% Fetal Bovine Serum (FBS) and 1% Penicillin/Streptomycin (Pen/Strep) (Gibco). PDMS substrates were sterilized with 70% ethanol and washed with PBS. Cells were transfected with Cellular Lights Actin-GFP (Cat. No. C10126) using standard protocols from Invitrogen. After transfection, cells were trypsinized and sparsely plated on fibronectin functionalized PDMS substrates and allowed to attach for 24 hrs prior to the stretching experiment. Fibroblasts remained attached to the PDMS substrates for over 5 days indicating potential for long term stretching studies.

Microscopy and Image Analysis

To illustrate compatibility with high resolution imaging systems we observed the cytoskeletal dynamics in fibroblasts as a response to mechanical strain using a state of the art Zeiss LSM 710 NLO microscope capable of single photon and two photon laser excitation. Fluorescence and differential interference contrast images were collected simultaneously at 2 minute intervals for approximately 1 hr. The images were processed using 3-D blind deconvolution in Autoquant, and maximum intensity projection and data analysis was carried out in ImageJ [59] to measure actin fiber strain and angle change.

4.1 Dynamic rotation of intact stress fibers begins within minutes

Our novel platform is capable of applying both tensile and compressive strain to the cells. To apply tensile strain, the fibroblasts were seeded on unstretched substrates and allowed to attach overnight. Then the substrates were loaded into the stretching device and stretched. The strain rate is limited by the actuator speed, and in our case the maximum strain was applied over approximately 30 seconds. The resulting substrate strain is transferred to the cell as can be seen in the GFP actin transfected fibroblasts shown in Figure 8. To apply compressive strain, the fibroblasts were seeded on prestretched substrates and allowed to attach overnight. The substrates were then unloaded, transferring a compressive strain to the cells as shown in Figure 9.

Figure 8.

Images of fibroblasts under applied tensile strain. Cells were seeded on unstretched substrate and allowed to adhere overnight and then stretched. Due to the applied strain the actin fibers are stretched axially by (b) 16% and (c) 28%. (scale bar = 30 µm)

Figure 9.

Images of fibroblasts under applied compressive strain. Cells were seeded on a prestretched substrate overnight, and the substrate was unloaded. Due to applied strain the actin fibers are compressed axially by 7%. (scale bar = 30µm)

Real time high resolution imaging allowed observation of interesting cytoskeletal dynamics including change in actin fiber angle in response to applied strain. It is known that fibroblasts reorient themselves in response to stretching, and it has been reported that cell bodies begin to show alignment within 2–3 hrs [60]. We observed that subcellular reorganization begins much earlier where actin stress fiber reorientation occurs within minutes of the applied strain. An earlier study [61], found that actin fibers in the direction of applied tensile strain depolymerized, and new actin fibers formed at an oblique angle. Also, a recent mathematical model predicts reorientation of actin stress fibers as a function of turnover (i.e., polymerization and depolymerization processes) [62]. It seems to be widely believed that actin fiber reorganization occurs mainly due to new stress fiber formation.

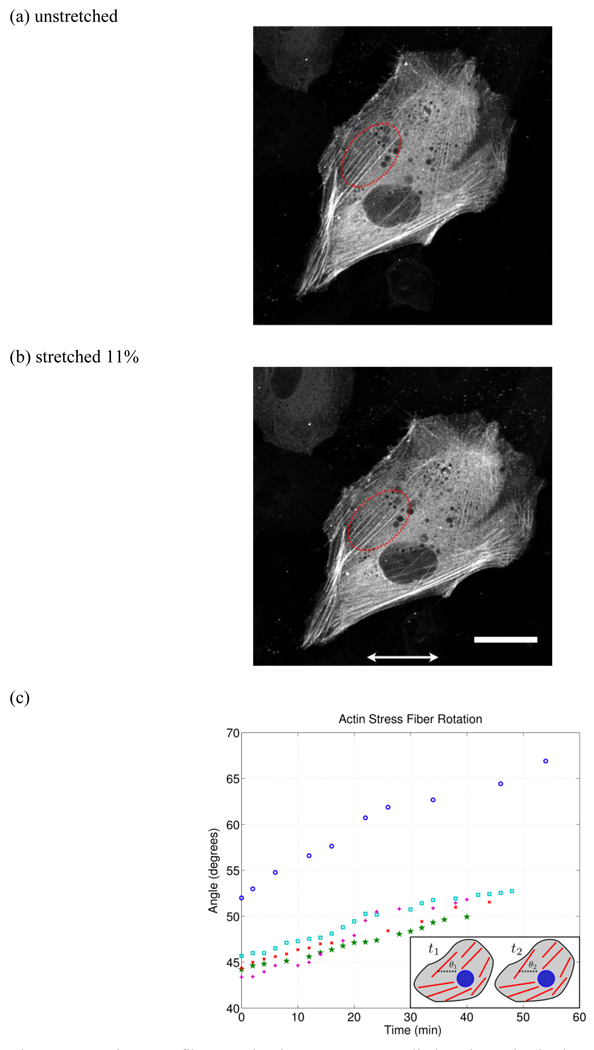
In contrast, we observed dynamic rotation of intact stable stress fibers (see supplementary video S1). In response to an applied axial strain of 11%, the actin stress fibers reoriented by rotating counter clockwise, away from the direction of applied strain (Figure 10 and Figure 11). Multiple stress fibers were measured and their rotation is plotted in Figure 10c. Thus actin fiber reorientation is not only due to fiber turnover, but intact and stable stress fibers also undergo dynamic rotation oblique to the direction of applied strain. Actin stress fibers are connected between focal adhesion complexes, which are anchored to the underlying substrate. Thus for an intact actin stress fiber to undergo dynamic rotation, it’s anchor points must move relative to each other. This observation suggests mobilization of focal adhesion complexes in response to applied strain. Interestingly, a recent study [63] found that focal adhesion sliding and actin fiber reorientation are key players in force-induced cellular reorganization independent of microtubules. This is in direct contrast to cellular reorganization during migration where microtubules are known to regulate focal adhesion dynamics [64]. These results [63] highlight the importance of in situ observation in uncovering the mechanisms of cellular mechanotransduction. It should be noted that the actin stress fibers, which underwent active dynamic rotation, extended through the center region of the cell whereas the stress fibers located at the cell periphery remained stable. This indicates that actin fiber reorganization varies spatially throughout the cell and it may be interesting to simultaneously visualize microtubules to investigate filament interaction.

Figure 10.

Actin stress fiber rotation in response to applied static strain (horizontal arrows indicate stretch direction). (a) and (b) are the original and stretched (11%) configuration respectively where the red dotted region indicates the stress fibers tracked. (c) Actin stress fiber rotation as a function of time (shown for 5 stress fibers). Here it is clear that the actin stress fiber reorientation occurs within minutes of applied strain. The small inset in the lower right schematically illustrates the stress fiber rotation where θ₁ is the initial angle and θ₂ is the final angle relative to the strain direction. (scale bar = 30 µm)

Figure 11.

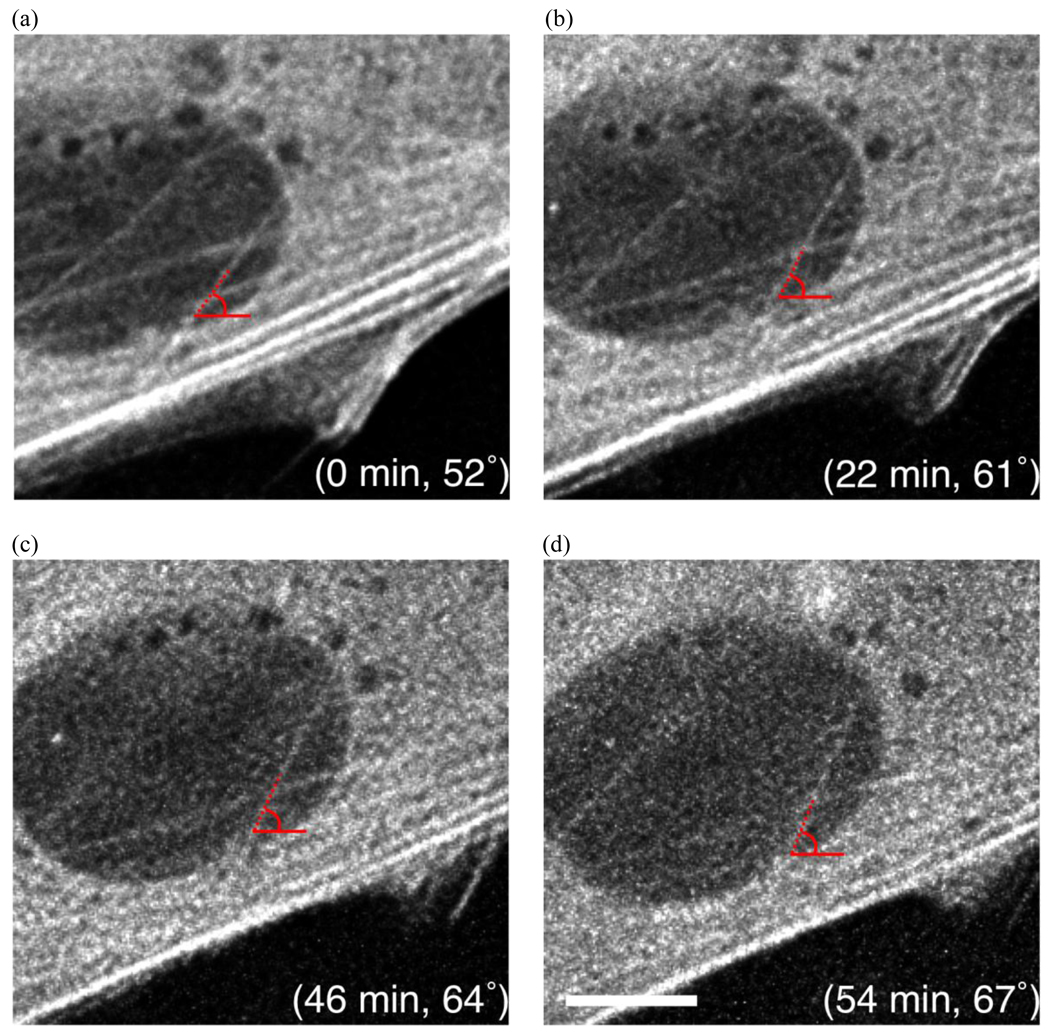
Images of actin stress fiber rotation in response to applied strain (horizontal direction). An actin stress fiber is shown with its angle and corresponding time after applied strain. The stress fiber rotates by approximately 15° within one hour. (scale bar = 10 µm)

It is also interesting to note that multiple stress fibers originally oriented around 45° rotated by approximately the same amount (7°) away from the applied strain to 52°, whereas a stress fiber originally at 52° rotated by nearly 15° to 67° over a similar period of time. This suggests that the amount and/or rate of rotation may be a function of the initial stress fiber configuration. The mechanism for this oblique orientation of actin stress fibers is unclear. If the driving force is minimization of axial strain [65, 66] then one would expect the fibers to align to approximately 60° which is the direction of minimal strain in our substrate, as calculated from the transformation equation for plane strain,

$${\epsilon }_x^{\text{'}}=\frac{{\epsilon }_x+{\epsilon }_y}{2}+\frac{{\epsilon }_x-{\epsilon }_y}{2}\text{cos}2\theta +\frac{{\gamma }_{xy}}{2}\text{sin}2\theta$$ (3)

where ε_x,ε_y are the normal strain in the x and y direction, γ_xy is the shear strain, and θ is the angle relative to the applied stretch. By setting equation (3) equal to zero and noting that γ_xy = 0, one can solve for θ which is the direction of zero axial strain. This may explain the rotation of stress fibers with an initial angle of approximately 45° as seen in Figure 10c. However, the stress fiber with an initial angle of 52° continues to rotate well beyond 60° and this cannot be explained by minimization of axial strain. A recent model predicts a more perpendicular orientation of the stress fiber if the cell senses stress rather than strain [67].

4.2 Lamellipodia activity and actin polymerization

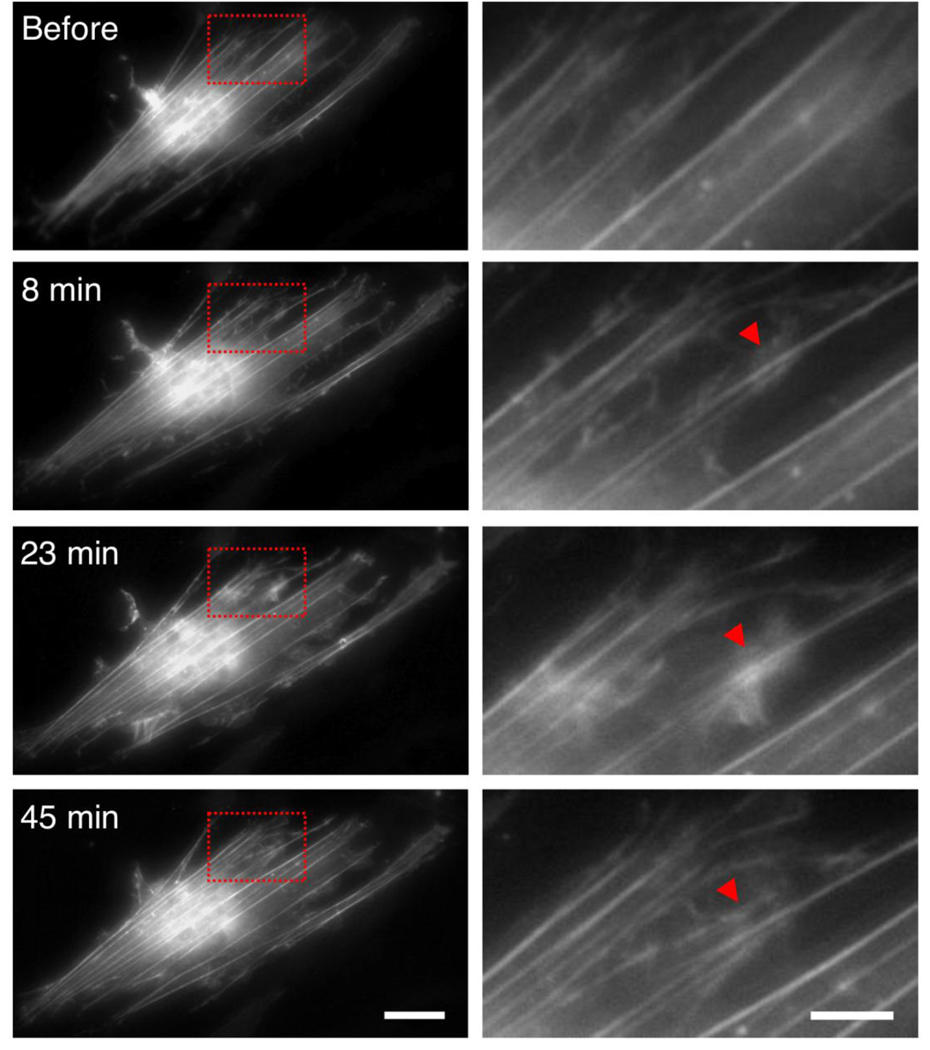
Fibroblasts were stretched inducing 10% axial strain in the actin stress fibers. After 8 minutes of applied tensile strain, we observed an abrupt onset of lamellipodia activity throughout the cell as shown in Figure 12. The lamellipodia exhibited wave-like motion emanating outward from the actin fibers. This continuing lamellipodia motion resulted in the formation of new actin stress fibers (see supplementary video S2). The propagation of actin waves may be a mechanism of cytoskeletal reorganization in response to mechanical stretching [68]. It has been shown that lamellipodial actin mechanically links myosin activity with adhesion-site formation [69]. Thus our observations of lamellipodial activity and actin polymerization in response to applied strain may suggest the formation of new adhesion sites, which is crucial to cellular motility. Assembly and disassembly of actin filaments drives cellular motility and has been shown to involve proteins such as Arp2/3, profilin, and ADF/cofilin [70, 71]. Arp2/3 complexes nucleate actin filaments, which grow from pre-existing filaments, and it has been shown to be distributed throughout actin waves [68]. Thus it is reasonable to hypothesize that Arp2/3 may be mechanically activated and is mobilized to these regions of lamellipodial activity resulting in nucleation of new actin fibers emanating from pre-existing filaments. Possible mechanisms for this mobilization are unclear and are a topic currently under investigation.

Figure 12.

Lamellipodia activity and actin polymerization induced by applied tensile strain (10% horizontal direction) was observed throughout the cell. The left column shows images of the entire fibroblast. The region within the red box is magnified and shown in the right column. The red triangle indicates an example of lamellipodia activity and actin polymerization. Lamellipodia activity begins after 8 minutes and results in new actin fiber formation by 45 minutes. (left scale bar = 30 µm)(right scale bar = 10 µm)

5 Drosophila embryos

Drosophila embryos are a convenient model system to study neurons in vivo. They have long been used to study synaptic development and neurotransmission and they are known to have structurally plastic neuromuscular junctions [72, 73]. It is believed that mechanical forces may play a role in neuronal sensing [74], and a recent in vivo study showed that mechanical tension leads to presynaptic clustering of neurotransmitters [75], although the underlying mechanisms are not well understood. Studying the role of mechanical forces in functional neurons is difficult due to experimental limitations. In vitro studies of neuronal mechanics [76, 77, 78, 79, 40, 80] use both primary and cultured cells, which lack the supporting glial cells present in in vivo systems. Our system allows mechanical stretch of the entire embryo to study the mechanoresponse of the functional neurons in their in vivo environment.

Drosophila Culture and Embryonic Dissection

Drosophila (elav’-gal4/UAS-gapGFP) embryos expressing green fluorescent protein (GFP) in all neurons were used for this investigation. Drosophila were cultured on standard grape agar plates under ambient light at 25 °C. Embryonic dissection was carried out on the silane functionalized PDMS substrates using techniques previously described by Budnik et al [81]. Briefly, the embryos were dechorionated using a 50/50 bleach and water solution for 1 minute. Embryos of the correct age (20 hrs after egg laying) were placed on double sided tape and then the PDMS reservoir was flooded with saline solution and the embryos were devitellinized. The embryos were oriented such that the ventral nerve cord was closest to the PDMS surface and the tape was removed. Upon contact with the functionalized APTES surface the embryos stick strongly and cannot be removed without damage. Glass micro-needles were created for dissection with a Sutter Instruments laser based micropippette/fiber puller. The micro-needle was used to create a dorsal incision in the embryo, remove the guts, and lay the body walls down flat on the PDMS surface resulting in a specimen that is approximately 25 µm thick (see [81] for detailed procedure). The motor neuron axons are attached to the cell body on one end and at the neuromuscular junction at the other, thus along its length the axons are not anchored.

Microscopy and Image Analysis

The mechanoresponse of Drosophila motor axons was observed using a Zeiss SteREO Luminar.V12 microscope. Fluorescence images were acquired for 30 minutes of applied strain and 30 minutes after unloading. ImageJ [59] was used to measure the strain in individual axons by two methods: (1) The change in straight line distance between the ends of the axon (P-P strain) and (2) the change in length of the axon itself (L-strain). To consistently measure the axon lengths, the image sequences were thresholded and skeletonized and NeuronJ [82] was used to trace the axon.

5.1 Drosophila motor neuron axons actively contract in response to applied strain

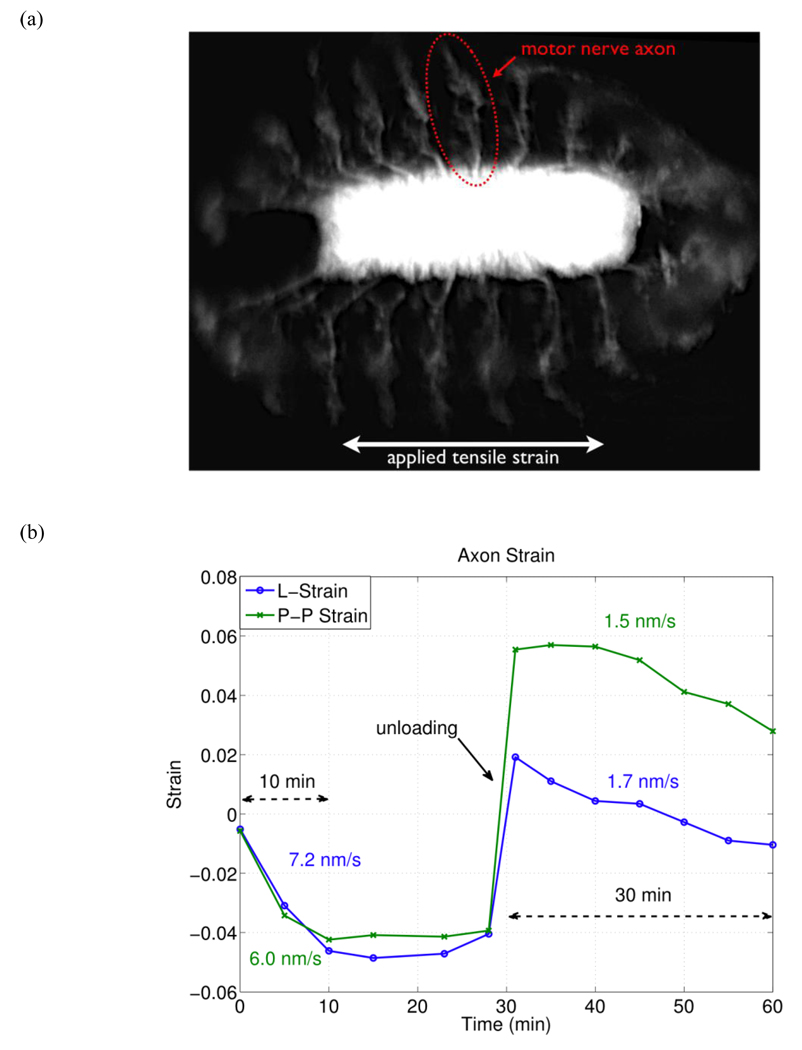
An image of a Drosophila embryo and a plot of active axonal contraction in response to the applied strain are shown in Figure 13. The embryo was oriented such that the central nervous system (CNS) is along the direction of tensile strain and the motor neuron axons of the peripheral nervous system (PNS) are along the direction of lateral Poisson’s contraction. A tensile strain of 30% was applied to the substrate resulting in a lateral compressive strain of 10%. This effectively moves the anchor points of the motor neuron axons closer together due to the Poisson’s effect in the substrate. This leaves the axons free of tension and additional shortening of axonal length over time implies an active process. Please note that compressive strains are denoted by negative numbers and tensile strains are positive numbers.

Figure 13.

Active axonal contraction was observed in response to applied strain. (a) A representative fluorescent image of the Drosophila embryo expressing GFP in all neurons. The arrow indicates a motor neuron axon. (b) Axon strain as a function of time. Here we observe axonal contraction twice, (1) after initial applied strain and (2) after substrate unloading. L-strain is the change in length of the axon, and P-P strain is the change in distance between the axon end points.

Immediately after the applied strain, the axon became more “zig-zagged” and exhibited compressive strain (decrease in length) of −5.9% relative to its original in vivo length. In this state it is assumed that the axon is in a stress free state since it is slack. Due to slight delay between applied stretch and the first image, this value was calculated by extrapolating the time-strain relation (one minute before the first image).

Over the next ten minutes the axon exhibited an active contraction to a strain of −4.6% relative to its stress free state at an average rate of 7.2 nm/s as seen in Figure 13b. After this period of active contraction, the axon’s length reached a steady state of approximately −4.9% strain. During this time the end-to-end axon strain (P-P strain) exhibited similar behavior. After a total duration of 30 minutes the substrate was unloaded (returned to zero strain) and the axons were effectively put under tension since they had contracted. As labeled by “unloading” in Figure 13b, the end points of the axon follow the substrate strain almost exactly. After unloading, the axon length was observed to have a tensile strain of 1.9%, relative to its stress free state, and it actively contracted to a compressive strain of −1.0% over the next 30 minutes at an average rate of 1.7 nm/s. It is worth noting that the average rate of axonal contraction is higher when measured along the length of the axon (L-strain) compared to measuring the distance between the end points of the axon (P-P strain). This suggests that during active contraction the axons may be building tension. (See supplementary videos S3 and S4)

We believe the active axonal contraction observed in the motor neurons of the Drosophila embryos is a response to the applied mechanical strain. Axonal contraction is observed twice: (1) after applied strain and (2) after the substrate is unloaded as shown in Figure 13b. One possible mechanism for the observed contraction could be explained by the maintenance of an internal tension within the axon, which may be involved in axonal development [83] or synaptic plasticity [75].

6 Conclusion

We have designed and characterized a novel platform to investigate the response of cells and tissues to applied strain. Our system is capable of applying prescribed uniform strain over a large substrate area for cell or tissue culture while allowing in situ observation by high resolution live imaging techniques. As a demonstration of our system we examined the mechanoresponse of single fibroblasts and whole Drosophila embryos under applied strain. In situ live imaging allowed three interesting observations: (1) Intact actin stress fibers in fibroblasts underwent dynamic rotation away from the direction of applied strain without depolymerizing. This may suggest mobilization of focal adhesion complexes in response to applied strain. (2) Lamellipodia activity and actin polymerization was induced by applied strain and resulted in new stress fiber formation in fibroblasts, suggesting mechanical mobilization of actin filament assembly proteins such as Arp2/3. (3) In Drosophila embryos, in vivo motor neuron axons exhibited active contraction in response to applied strain, possibly in an attempt to maintain a steady state internal tension necessary for neurotransmission. Our observations show the utility of our system and the importance of in situ observation during applied strain to investigate the mechanoresponse in biological systems.