Functional Brain Image Analysis Using Joint Function-Structure Priors

Abstract

We propose a new method for context-driven analysis of functional magnetic resonance images (fMRI) that incorporates spatial relationships between functional parameter clusters and anatomical structure directly for the first time. We design a parametric scheme that relates functional and structural spatially-compact regions in a single unified manner. Our method is motivated by the fact that the fMRI and anatomical MRI (aMRI) have consistent relations that provide configurations and context that aid in fMRI analysis. We develop a statistical decision-making strategy to estimate new fMRI parameter images (based on a General Linear Model-GLM) and spatially-clustered zones within these images. The analysis is based on the time-series data and contextual information related to appropriate spatial grouping of parameters in the functional data and the relationship of this grouping to relevant gray matter structure from the anatomical data. We introduce a representation for the joint prior of the functional and structural information, and define a joint probability distribution over the variations of functional clusters and the related structure contained in a set of training images. We estimate the Maximum A Posteriori (MAP) functional parameters, formulating the function-structure model in terms of level set functions. Results from 3D fMRI and aMRI show that this context-driven analysis potentially extracts more meaningful information than the standard GLM approach.

1 Introduction

Functional magnetic resonance images (fMRI) has revolutionized the study of normal and pathological brain function. Its ability to localize brain function has become crucial in neuroscience for characterizing and understanding brain function.

General Linear Model (GLM) [1] was introduced to functional imaging to generalize the simple t-test approach to activation detection and allow the incorporation of more specific modeling. These ideas can be written as an estimation problem, where one has a set of data at one voxel over time written as a column vector, v, a design matrix B made up of column vectors representing different temporal aspects of the modeling, including the functional paradigm, cardiac motion, etc., and a set of coefficients y also written as a column vector. One estimates an optimal set of coefficients by solving: ŷ = arg max_y ||v − By||. Then, for each component of y, one can observe the variation over many data sets or spatial voxels and test for differences under different conditions.

In order to improve the detection of activated areas, spatial smoothing is used. However, smoothing may produce a biased estimate by displacing activation peaks and underestimating their height. Spatial modeling has been proposed to begin to take the spatial activation pattern into consideration using, for example, Markov random field approaches [2] which model the activation with spatial smoothing priors. Others incorporate local spatial context with probabilistic models of the signal [3]. Woolrich et al. [4] use an autoregressive spatiotemporal model of the noise. Solo et al. [5] proposed incorporating spatial information without smoothing using spatio-temporal system identification. A spatiotemporal linear regression method for fMRI activation detection [6] has also been developed. Friston and Penny [7] use a hierarchical model with an expectation-maximization (EM) framework to estimate spatial covariances that will help determine statistical priors for a voxel-wise estimation of the GLM parameters. Other work formulates fMRI signal reconstruction using support vector regression [8].

Contextual information can be incorporated using clustering methods for fMRI data analysis. Statistical clustering offers a relatively unsupervised approach for partitioning data into self-similar groups without prior knowledge of the form of the fMRI response [9]. These techniques are primarily concerned with temporal features, although spatial context is sometimes considered. Salli et al. use clustering in conjunction with an MRF model [10]. The contextual information here is primarily limited to agreement with local neighborhoods. Kiebel et al. [11] have incorporated anatomic basis functions based on Gaussian-blurred flattened gray matter surfaces. However, the surface-based representation limits the expressiveness of the approach. Penny and Friston [12] use EM for a kind of spatio-temporal clustering based on a GLM model using mixtures of Gaussians.

It is our goal in this paper to develop a framework where coherent information in a single registered function/structure space can be reasoned about in a unified way to obtain more contextually-informed functional and structural quantitative parametric information about the human brain. We intend to incorporate context not simply in terms of local neighborhoods but in terms of anatomic regions. The study of normal and Autism Spectrum Disorders (ASD) subjects with fMRI using face/object recognition tasks designed based on the deficits associated with ASD, yielded significant functional activation differences between groups in the area of the fusiform gyrus and the amygdala. We endeavor to incorporate both function and structure in order to gain more sensitivity and apply them into ASD study.

2 Integration for Functional/Structural Analysis

2.1 MAP Framework with Function-Structure Joint Prior

Local spatial continuity of functional activation parameters (e.g. regularizing, or smoothing, assumptions on components of Y) as well as proper anatomical location (e.g. is the functional information in gray matter or not?) each are separately useful as constraints for more sensitively detecting activation. Here, we propose to combine these two ideas with GLM in order to find improved estimates of GLM-like parameters Y′ that: agree with the functional data V, are spatially-coherent over individual voxels at spatial position and are roughly constrained (accounting for image resolution) to lie within particular regions. Assume a level set [13] representation of the underlying gray matter structure of interest S and the activation clusters image that is related to this structure I_A, we can maximize p(I_A, Y′|V, S) using the following MAP equation (including simplification via multiple applications of Bayes rule and taking logarithms):

$${\widehat{\mathbf{I}}}_{\mathbf{A}},{\widehat{\mathbf{Y}}}^{\prime }=arg\underset{{\mathbf{I}}_{\mathbf{A}},{\mathbf{Y}}^{\prime }}{max}\left[lnp(\mathbf{V}\mid {\mathbf{I}}_{\mathbf{A}},{\mathbf{Y}}^{\prime },\mathbf{S}=\stackrel{\sim }{\mathbf{S}})+lnp({\mathbf{Y}}^{\prime }\mid {\mathbf{I}}_{\mathbf{A}},\mathbf{S}=\stackrel{\sim }{\mathbf{S}})+lnp({\mathbf{I}}_{\mathbf{A}},\mathbf{S}=\stackrel{\sim }{\mathbf{S}})\right]$$ (1)

While the joint prior p(I_A, S) will be found from training data, the segmented structure in each aMRI test image S̃ will limit the search space for each problem (i.e. S = S̃).

The first term requires that the new GLM-like parameter values Y′ agree with the fMRI data V. For our initial design, this term essentially reduces to GLM with design matrix B:

$$lnp(\mathbf{V}\mid {\mathbf{I}}_{\mathbf{A}},{\mathbf{Y}}^{\prime },\mathbf{S}=\stackrel{\sim }{\mathbf{S}})\propto -\left|\right|\mathbf{V}-B{\mathbf{Y}}^{\prime }\left|\right|$$ (2)

The second term relates to the gathering of similar-valued Y′ (x)’s over spatial voxels x in the fMRI image. This term will push the estimation towards functional clusters containing Y′ (x) values that are relatively homogeneous and separated in value from the Y′ (x) values that are just outside it, while at the same time requiring that the clusters be near an anatomical structure S. Since the most basic and common approach to activation detection from fMRI data is to separate different Y′ values for two different conditions(task vs. baseline or task vs. task), we can approximate the second term by:

$$lnp({\mathbf{Y}}^{\prime }\mid {\mathbf{I}}_{\mathbf{A}},\mathbf{S}=\stackrel{\sim }{\mathbf{S}})\propto -{\{T({\mathbf{Y}}^{\prime })·[H(T({\mathbf{Y}}^{\prime })-t_1)-H(T({\mathbf{Y}}^{\prime })-t_2)]-{\mathbf{I}}_{\mathbf{A}}\}}^2$$ (3)

T (Y′) gives the difference of the Y′ with respect to a reference Y_ref obtained from some reference task. H is the Heaviside function: H(z) = 1, if z ≥ 0; H(z) = 0, if z < 0. t₁ and t₂ are the low and high thresholds to suppress the noise. The computation T (Y′) is a key component of any statistical test that would be used to detect activations (e.g. t-test). Improvements in T (Y′) will directly result in more significant statistics. Construction of appropriate statistical significance tests for this methodology is in ongoing work.

The third term is the joint prior between I_A and S. It contains the functional prior information, the related structural prior information, as well as their relationship.

2.2 Function-Structure Joint Prior Model

We use level set [13] as our representation to build a model for the function-structure joint prior, and then define the joint probability density function used in Equation 1.

Consider a training set of 2n aligned structural and functional images from n subjects, with a shape of interest in each of the n structural images and the coherent activation regions in each of the n functional images I_A1, I_A2, …, I_An. The registration between structural and functional images was done with a rigid linear intensity based method [14]. The surfaces of each of the n shapes in the training set are embedded as the zero level set of n separate higher dimensional level sets {S₁, S₂, …, S_n} with negative distances inside and positive distances outside the object. Using techniques developed previously [15], each of the I_Ai and S_i is placed as a column vector with N³ elements, where N³ is the number of voxels of each functional image or number of samples of each level set function. We can use vector ${[I_{Ai}^T,S_i^T]}^T$ as the representation of the activation image and the anatomical structure. Thus, the corresponding training set is { ${[I_{A1}^T,S_1^T]}^T,{[I_{A2}^T,S_2^T]}^T,\dots ,{[I_{An}^T,S_n^T]}^T\}$. Our goal is to build a function-structure model over the distribution of the level set function and activation intensity pair.

The mean and variance of the function-structure pair can be analyzed using Principal Component Analysis(PCA) [15]. The mean function-structure pair, $\overline{{[I_A^T,S^T]}^T}=\frac{1}{n}{\sum }_{i=1}^n{[I_{Ai}^T,S_i^T]}^T$, is subtracted from each ${[I_{Ai}^T,S_i^T]}^T$ to create the deviation from the mean. Each such deviation is placed as a column vector in a 2N³ × n dimensional matrix Q. Using Singular Value Decomposition(SVD), Q = U ΣW^T. U is a matrix whose column vectors represent the set of orthogonal modes of function-structure variation and Σ is a diagonal matrix of corresponding singular values. An estimate of the function-structure pair ${[I_A^T,S^T]}^T$ can be represented by k principal components and a k dimensional vector of coefficients(where k < n), α[15] $\stackrel{\sim }{\left[\begin{array}{c}{I}_A\\ S\end{array}\right]}=\overline{\left[\begin{array}{c}{I}_A\\ S\end{array}\right]}+U_k\alpha$.

Under the assumption of a Gaussian distribution of function-structure pair represented by α, the joint probability of a certain shape S and the related activation image intensity I_A, p(I_A, S), can be represented by:

$$p(\alpha )=\frac{1}{\sqrt{{(2\pi )}^k\mid {\mathrm{\sum }}_k\mid }}exp[-\frac{1}{2}{\alpha }^T{\mathrm{\sum }}_k^{-1}\alpha ]$$ (4)

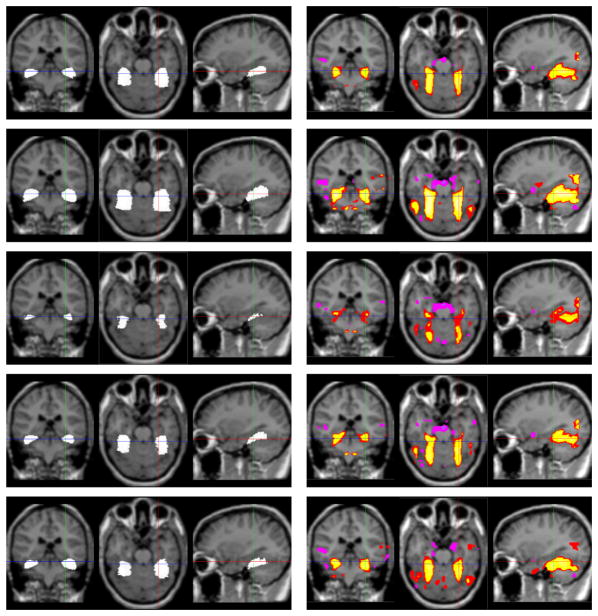
Figure 1 shows a training set of fusiform gyri(FG) in 2 out of 9 MR brain images in our sample and the coherent functional activation images generated by T (Ŷ_GLM) · [H (T (Ŷ_GLM) − t₁) − H (T (Ŷ_GLM) − t₂)] (where Ŷ_GLM is the GLM based estimation) for a face recognition task. Using PCA, we can build a model of the function-structure profile of the FG. Figure 2 illustrates zero level sets and the associated activation intensities corresponding to the mean and two primary modes of variance of the distribution of the profile of the FG. The mean function-structure pair and primary modes are representative of the shapes and activation regions being learned. The shape varies correspondingly as the associated functional intensities vary, and vice versa.

Fig. 1.

Training set:fusiform gyri (left) and functional activation clusters (right) from 2 out of 9 subjects overlaid on the anatomical MR brain images.

Fig. 2.

The two primary modes of variance of the fusiform gyrus (left) and the functional activation clusters (right) overlaid on the mean aMRI. 1^st row: The mean; 2^nd, 3^rd row: ±σ variance of the 1^st primary mode; 4^th, 5^th row: ±σ variance of the 2^nd primary mode.

2.3 Estimation of the Functional Activation Clusters

The MAP estimation of the functional parameters and the activation clusters in Equation 1 can be expressed by combining Equations 2, 3, and 4.

$$\begin{array}{l}{\widehat{\mathbf{I}}}_{\mathbf{A}},{\widehat{\mathbf{Y}}}^{\prime }=arg{min}_{{\mathbf{I}}_{\mathbf{A}},{\mathbf{Y}}^{\prime }}-ln\left[p({\mathbf{I}}_{\mathbf{A}},{\mathbf{Y}}^{\prime }\mid \mathbf{V},\mathbf{S})\right]=arg{min}_{{\mathbf{I}}_{\mathbf{A}},{\mathbf{Y}}^{\prime }}[\lambda \left|\right|\mathbf{V}-B{\mathbf{Y}}^{\prime }\left|\right|\\ +{\lambda }_1{\{T({\mathbf{Y}}^{\prime })·[H(T({\mathbf{Y}}^{\prime })-t_1)-H(T({\mathbf{Y}}^{\prime })-t_2)]-{\mathbf{I}}_{\mathbf{A}}\}}^2+{\lambda }_2{\alpha }^T{\mathrm{\sum }}_k^{-1}\alpha ]\end{array}$$ (5)

While we can pose the MAP estimation of both Ŷ′ and Î_A from the time-series data V and structural aMRI data I in this integrated framework, we Y are more intereted in the estimation of functional activation clusters. Assuming Ŷ′ ≈ Ŷ_GLM, we simplify the estimation of the activation Î_A:

$$\begin{array}{l}{\widehat{\mathbf{I}}}_{\mathbf{A}}=arg{min}_{{\mathbf{I}}_{\mathbf{A}}}-ln\left[p({\mathbf{I}}_{\mathbf{A}},{\mathbf{Y}}^{\prime }\approx {\widehat{\mathbf{Y}}}_{\mathbf{GLM}}\mid \mathbf{V},\mathbf{S})\right]\\ =arg{min}_{{\mathbf{I}}_{\mathbf{A}}}{\lambda }_1{\{T({\widehat{\mathbf{Y}}}_{\mathbf{GLM}})·[H_{\epsilon }(T({\widehat{\mathbf{Y}}}_{\mathbf{GLM}})-t_1)-H_{\epsilon }(T({\widehat{\mathbf{Y}}}_{\mathbf{GLM}})-t_2)]-{\mathbf{I}}_{\mathbf{A}}\}}^2\\ +{\lambda }_2{\left(\left[\begin{array}{c}G({\mathbf{I}}_{\mathbf{A}})\\ S\end{array}\right]-\overline{\left[\begin{array}{c}{I}_A\\ S\end{array}\right]}\right)}^T{U}_k{\mathrm{\sum }}_k^{-1}{U}_k^T\left(\left[\begin{array}{c}G({\mathbf{I}}_{\mathbf{A}})\\ S\end{array}\right]-\overline{\left[\begin{array}{c}{I}_A\\ S\end{array}\right]}\right)\end{array}$$ (6)

where G(·) is an operator to form a column vector from a matrix by column scanning. We use a regularized version of the Heaviside function H, denoted by $H_{\epsilon }(z)=\frac{1}{2}[1+\frac{2}{\pi }arctan(\frac{z}{\epsilon })]$ [15]. Thus, the MAP functional activation can be estimated at each evolving step using simple gradient descent on Equation 6.

The parameters λ₁ and λ₂ are used to balance the influence of the estimation from GLM and the function-structure joint prior model. The tradeoff between GLM estimation and function-structure information depends on how much faith one has in the function-structure joint prior model and the functional data for a given application. We set these parameters empirically for particular functional tasks, given the general fMRI quality and the relations between the activation clusters and the coherent anatomical structures from aMRI.

3 Experimental Results

We have implemented this new context-driven fMRI analysis strategy described in Equation 1 to demonstrate feasibility of the approach. In this implementation, a modified form as described in Equation 6 is employed. The first term essentially pushes the new Î_A values towards the values constrained by the pre-computed GLM-based values Ŷ_GLM.

An example result based on 3 run fMRI data for a face recognition task is shown in Figure 2.2, using n=9 normal controls to form the prior information (Figure 1 and 2) regarding the joint relationship between the underlying shape/size of the fusiform gyrus (FG) and the typical functional parameter variation in response to this task. Basically, the solution provides a tradeoff between pure GLM data-driven results and prior model-based information. As seen in Figure 2.2, for this test example, the new approach improves the expected homogeneity of object-related activation bilaterally in and around the FG, while suppressing unexpected activations outside these regions, in comparison to standard GLM. The improvement is more evident in the case of the left FG where activations are generally weaker (shown on the right in the images). The results are encouraging, and show that the context-driven analysis potentially extracts more meaningful information than the standard GLM approach.

Next, we test our estimation method comparing the analysis of a single run of data using our method with standard GLM using one and three runs (Using the same task and same subjects as above). As shown in Figure 4, our estimation greatly improves the homogeneity of the activations in the FG and suppresses activations outside these regions. The improvement is very evident for 1 run data, where activations are generally weaker. Furthermore, our 1 run data based estimation results in activation clusters close to the 3 run GLM results. Although a task or stimulus can be repeated over and over again, there are limits due to time constraints, habituation, etc. The results show that our method achieves greater similarity in the detection and characterization of functional activity.

Fig. 4.

Contextual fMRI result on 1 run fMRI data. Three orthogonal slices of functional clusters overlaid on the aMRI showing functional activation computed using our integrated estimation method (labeled as contextually clustered) compared with standard GLM on 1 run data and GLM on 3 run data. λ1 = 0.3, λ2 = 0.7.

4 Conclusions

The use of context in the analysis of fMRI data that incorporates spatial relationships between functional parameter clusters and anatomical structure has the potential to improve sensitivity. We present a Bayesian MAP formulation using joint prior information of function and anatomy, along with information derived from the input fMRI and aMRI. Our results show that this context-driven analysis potentially extracts information more sensitively and more coherently than the standard GLM approach.

Fig. 3.

Contextual fMRI result for two subjects (left and right). Three orthogonal slices of functional clusters overlaid on the aMRI showing functional activation computed using our integrated estimation method (bottom – labeled as contextually clustered) compared with standard GLM (row 2) and smoothed GLM (row 3). λ1 = λ2 = 0.5.