Resonant acoustic spectroscopy of soft tissues using embedded magnetomotive nanotransducers and optical coherence tomography

Abstract

We present a new method for performing dynamic elastography of soft tissue samples. By sensing nanoscale displacements with optical coherence tomography, a chirped, modulated force is applied to acquire the mechanical spectrum of a tissue sample within a few seconds. This modulated force is applied via magnetic nanoparticles, named ‘nanotransducers’, which are diffused into the tissue, and which contribute negligible inertia to the soft tissue mechanical system. Using this novel system, we observed that excised tissues exhibit mechanical resonance modes which are well described by a linear damped harmonic oscillator. Results are validated by using cylindrical tissue phantoms of agarose in which resonant frequencies (30–400 Hz) are consistent with longitudinal modes and the sample boundary conditions. We furthermore show that the Young’s modulus can be computed from their measured resonance frequencies, analogous to resonant ultrasound spectroscopy for stiff material analysis. Using this new technique, named magnetomotive resonant acoustic spectroscopy (MRAS), we monitored the relative stiffening of an excised rat liver during a chemical fixation process.

1. Introduction and background

The variety of palpation techniques employed by medical doctors suggest the strong diagnostic value of tissue mechanical properties for disease diagnosis. The emergence of biomedical elastography imaging techniques in ultrasound (Fatemi and Greenleaf 1998) and MR imaging (Muthupillai et al 1995) rely on tissue mechanical contrast between normal and diseased states. In order for elastography imaging to be successful, however, there is a need for stronger correlations between tissue viscoelastic properties and the developmental stage of human disease. These correlations are established by performing mechanical analysis of small tissue biopsies of a known disease state (Samani et al 2007).

Small tissue samples are particularly suitable for analysis by optical coherence elastography (OCE) (Schmitt 1998), a method by which the internal deformation of tissues is imaged using optical coherence tomography (OCT) (Huang et al 1991). OCE has previously been used to study arterial wall biomechanics by tracking endogenous arterial wall motion (Chan et al 2004) and for studying developing engineered tissues (Ko et al 2006). Phase-sensitive OCE enables the measurement of material deformation directly from the optical phase by employing spectral interferometry, which does not require moving parts, in comparison to temporal interferometry (Wang et al 2007, Crecea et al 2009). This has obviated the need for cumbersome speckle-tracking algorithms and has enabled sub-nanometer deformation resolution. The excellent displacement sensitivity afforded by OCE should allow for measurements to be obtained in the linear regime of the stress–strain response, avoiding nonlinearities which add ambiguity to the computation of the Young’s modulus. The high sampling rate afforded by spectral-domain OCT (>20 kHz), (Nassif et al 2004) also enables dynamic mechanical analysis at higher frequencies than typically afforded by commercial analyzers (~100 Hz).

Toward this end, we constructed a phase-resolved OCE system that provides <10 nm displacement sensitivity, corresponding to <10⁻⁵ strain sensitivity in >1 mm thick samples. In order to circumvent contact and inertial problems associated with external force transducers (Ogi et al 1999), we use magnetic nanoparticles diffused into the tissues to act as inertialess nanotransducers that apply a distributed body force on the tissue. In previous studies, we found that diffusion of 20 nm diameter magnetite nanoparticles into tissues was rapid (effective saturation after 1 h), and driven tissue displacements could be sensed using OCT with nanoparticle mass concentrations of <30 ppm (Oldenburg et al 2008). In this study, a temporally chirped (frequency-swept) magnetic field gradient is applied while simultaneously imaging with OCT, to deduce the mechanical spectral response of the tissue. These nanoparticles can function not only as nanotransducers, but also as biomedical imaging contrast agents for optical (Chan et al 2004) and magnetic resonance imaging studies (Sosnovik and Weissleder 2007).

Using this novel system, we observed that excised rat organs (including liver, kidney, and spleen) exhibited mechanical resonances with quality factors Q ≈ 3, which was sufficient to quantify the resonance frequencies. We expect this may also hold true for human breast tissues based on their reported attenuation rates (Sinkus et al 2000). Spatio-temporal in vivo breast imaging of propagating elastic shear waves has previously been reported in magnetic resonance (Sinkus et al 2005) and ultrasound elastographies (Bercoff et al 2003) using fixed frequency excitation. Similarly, OCT elastography was previously performed on ex vivo human breast samples at 20 Hz (Liang et al 2008). For the spectral method described here, conventional wisdom suggests resonances should be avoided for materials with large damping, due to the added complexity and model dependence of the analysis required (Lakes 2004). However, as we will show, a linear viscoelastic model can reveal the Young’s modulus of tissue phantoms with relative ease. This is partly mediated by the fact that the magnetic nanoparticles used to modulate the tissues contribute negligible inertia to the system and do not need to be modeled to accurately quantify the frequency response. This is extremely important because of the small stiffness and mass typical of soft tissue samples; previous experience with harmonically driven OCE using an external force transducer required extensive modeling of the coupled transducer-tissue system to extract meaningful Young’s moduli (Liang et al 2008).

In this system, the measured mechanical resonance spectra are inverted to provide the sample’s Young’s modulus using knowledge of the sample boundary conditions, similar to resonant ultrasound spectroscopy, a method for determining the elastic tensor of stiff materials (Maynard 1996) and stiff tissues (Kinney et al 2004). The primary differences in soft tissues are that damping is non-negligible and the resonant frequencies are smaller (1–1000 Hz) due to the smaller Young’s moduli (E = 0.1–1000 kPa). This ‘magnetomotive resonant acoustic spectroscopy’ (MRAS) technique can also quantify relative changes in E for a tissue sample with unknown boundaries.

In this paper, we first demonstrate that the observed resonances are consistent with longitudinal modes in an isotropic medium using tissue-mimicking phantoms. It is shown that the mode frequencies are predicted by the cylindrical boundary conditions and are consistent with the Young’s modulus E measured independently by a commercial texture analyzer. The computation is inverted to estimate E in a least-squares sense from a set of mode frequency data. We then validate this computational MRAS method by analyzing agarose tissue phantoms of varying concentration, revealing consistency over two decades of E values. Finally, MRAS is performed to monitor the evolution of resonance frequencies in a rat liver during application of formaldehyde, demonstrating that the relative value of E increases during the fixation process as expected.

2. Theory

To model the resonance modes, we realize that the tissues and tissue phantoms are effectively fixed at the bottom due to supporting the sample weight, and otherwise have open (zero stress) boundaries, as shown in figure 1. In this case, the longitudinal resonance condition is satisfied when the wavelength ${\lambda }_n=\frac{4L}{2n-1}$ for mode numbers n = 1, 2, 3, …. The associated resonance frequency ${\omega }_n=2\pi \frac{v}{{\lambda }_n}$, where v is the longitudinal wave velocity, which can be written generally as

Figure 1.

Diagram of the OCE system and longitudinal modes in tissues. A high axial magnetic field gradient below the electromagnet induces a force on embedded magnetic nanoparticles (TEM shown in the inset) that is parallel with the OCT imaging beam. The resulting tissue displacement is detected as an optical phase shift with OCT. Mechanical resonant frequencies observed in cylindrical tissue phantoms correspond to longitudinal modes where the bottom surface is fixed under its own weight and the top surface is free.

$$v=g\left(\frac{R}{{\lambda }_n},\sigma \right)\sqrt{\frac{E}{\rho }},$$ (1)

where σ is Poisson’s ratio, E is the Young’s modulus, ρ is the density of the medium and g is a geometrical factor depending only on n, σ, and the aspect ratio of the cylinder L/2R. In the limit of high aspect ratio where R ≪ λ_n, g ≈ 1.

For typical samples we must predict resonance modes in the intermediate regime where R ~ λ_n. In a homogeneous, isotropic, elastic cylinder with stress-free boundaries at the side walls (r = R), we can rewrite the longitudinal resonance condition (Love 1944) as

$$\left((2\mu k^2-\rho {\omega }^2)J_0(hR)+\frac{2\mu h}{R}{J}_1(hR)\right)((k^2-{\kappa }^2)J_1(\kappa R))+(4\mu k^{2}h{J}_1(hR))\times \left(\kappa J_0(\kappa R)-\frac{1}{R}{J}_1(\kappa R)\right)=0,$$ (2)

where the shear modulus $\mu =\frac{E}{2(1+\sigma )}$, wavenumber k = 2π/λ_n and parameters $h=\sqrt{\frac{{\omega }^2\rho }{M}-k^2}$ and $\kappa =\sqrt{\frac{{\omega }^2\rho }{\mu }-k^2}$. By computing the roots of (2), we can predict the resonant frequency ω_n given n, L, R, ρ, σ and E.

MRAS is then performed by finding the value of E that predicts the measured resonant frequency ω_n. For a single sample, this can be performed by realizing that ${\omega }_n/\sqrt{E}=c_n$, where c_n is a constant for a sample of fixed geometry according to equation (1), computing the theoretical ω_n for all n using an initial guess of E by solving equation (2), computing c_n, and then setting E = (ω_n/c_n)² using the experimental ω_n values. To fit ω_n data collected for an ensemble of samples of fixed E, we performed a weighted least-squares fit using the assumption that the variance of each ω_n is proportional to ${\gamma }_n^2$, the square of the damping coefficient γ_n, because the resonance spectral peak width is proportional to γ_n. The curve fitting to determine ω_n and γ_n is discussed below. Error bars were then estimated by the values of E where the goodness of fit was doubled.

3. Methods

3.1. Magnetomotive OCT methods

Nanotrandsucers consisted of magnetic nanoparticles (~20 nm diameter iron oxide, –COOH terminated, Ocean NanoTech, LLC) in an aqueous solution that are either diffused into the tissues or premixed into tissue phantoms before gelation. To mechanically drive the nanoparticles, a solenoid is placed 1–2 mm above the tissue to apply a temporally modulated magnetic field from B ≈ 0–600 G along its central axis (z), as described previously (Oldenburg et al 2005). The resulting gradient force on the nanoparticles F⃗ ∝ ∇ |B⃗|² is directed primarily toward the solenoid along +z, according to figure 1.

As previously described (Oldenburg et al 2008), a broadband Ti:Sapphire laser beam is directed through the center of the solenoid, and the homodyne spectral interferogram of the tissue backscattered light is sampled with a line camera (Dalsa Pirahna) capable of up to 33 kHz operation. Each spectral-domain OCT interferogram S(Ω), where Ω is the optical angular frequency, is associated with a column of scatterers along z sampled at a mechanical excitation time t (no transverse scanning). The complex analytic time-domain signal S̃(τ) = ℑ⁻¹[S(Ω) − S₀(Ω)], where S₀(Ω) is the reference spectrum, ℑ is the Fourier transform and τ is the relative delay associated with a scatterer at position z.

To measure the mechanical impulse response of the tissue, an apodized, chirped driving force F(t) is applied at 0–200 Hz, 0–400 Hz or 0–1000 Hz with 1 kHz, 2 kHz or 5 kHz sampling rates, respectively. When the resulting tissue displacement Δz is much less than the optical coherence length, the time-dependent signal can be approximated as (Choma et al 2005) S̃(τ, t) ≈ S̃(t, 0) exp(2ikΔz(τ, t)). The phase angle of S(τ, t) along t is unwrapped to compute Δz, which exhibited a typical rms noise of 6 nm. Assuming a linear, time-invariant system, the mechanical spectral response is then Ĩ(ω) = ℑ[Δz(t)]/ℑ[F(t)]. Ĩ(ω) is subsequently averaged over all τ having |S̃(τ)| greater than a threshold value. (The z-dependence of Δz under constant strain is negligible in this experiment, as the tissue samples were thick compared to the OCT imaging depth of ~1.5 mm.) The entire process is completed after a frequency sweep time of 2–4 s and a computation time of <10 s. The frequency sweep time is chosen to be sufficiently long to obtain good signal to noise in the mechanical spectrum.

3.2. Sample preparation and data collection

Cylindrical tissue phantoms were prepared to simulate the mechanical properties of tissues while controlling for the dimensions and stiffness. Varying concentrations C = 3–40 mg mL⁻¹ of agarose (low EEO, Sigma) were mixed with ~0.15 mg mL⁻¹ magnetic nanoparticles for mechanical force actuation, and with ~0.5–0.8 mg mL⁻¹ TiO₂ (micropowder, Sigma) to increase the optical scattering. We note that this concentration of magnetic nanoparticles corresponds to an ~0.08% increase in the average mass density of the agarose phantom, suggesting that the inertia contributed by the nanotransducers is negligible. Mixtures were gelled into cylindrical molds of radius R = 1 cm and varying heights L = 0.5–5 cm. After removing the gels from their molds, mechanical resonance spectra were collected along the cylinder’s central z axis while aligned with the magnetic excitation and optical imaging axes (figure 1). This geometry promoted excitation and detection of longitudinal vibrations only.

To study ex vivo tissues, a rat liver specimen was collected according to protocols approved by the University of Illinois Institutional Animal Care and Use Committee. The specimen was divided into two approximately equal volume samples (~1 cm³) but of somewhat irregular shape. A soak solution consisting of 0.9% NaCl and ~1 mg mL⁻¹ magnetic nanoparticles was prepared. Both samples were immersed in the soak solution for >12 h. Then, a mechanical spectrum was acquired of each sample at time zero. Subsequently, one sample was immersed in a fixing solution of buffered formalin and ~1 mg mL⁻¹ magnetic nanoparticles, while the control sample was re-immersed in the original soak solution. Multiple mechanical frequency sweeps (N = 3–5) were acquired at various time points (N = 7) for up to 6 h post-fixation.

4. Results and discussion

4.1. Lorentzian acoustic resonance spectra and linear viscoelastic modeling

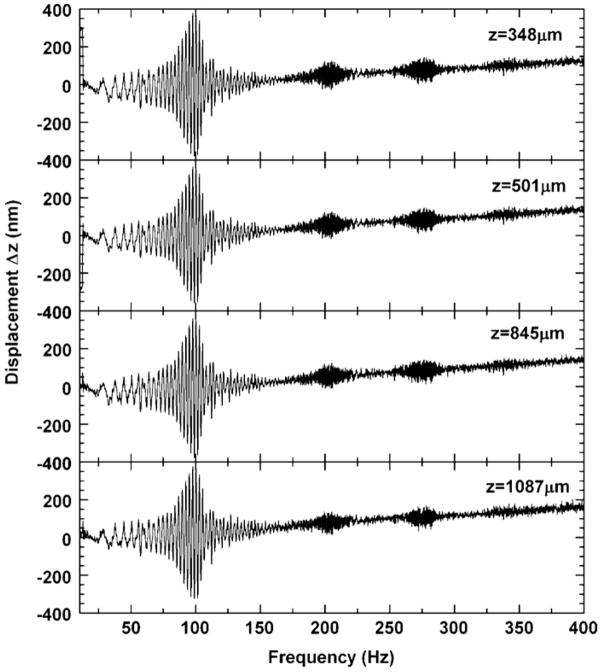
The displacement waveforms Δz(t) at varying relative depths z within an agarose cylinder of aspect ratio L/2R = 1 are plotted in figure 2. As the instantaneous driving frequency is swept from 0 to 400 Hz, the sample passes through several modulation peaks, with amplitudes ranging from tens to hundreds of nanometers. Importantly, we see that the phases and peak positions of the vibration are constant for varying depths, demonstrating that the observed vibration is global throughout the sample.

Figure 2.

Displacement waveform for an agarose cylinder at varying depths z inside the cylinder demonstrating global vibrations in response to a swept driving frequency. z positions were chosen within equally spaced intervals by selecting the position with the highest OCT signal amplitude, in order to minimize noise.

The computed mechanical spectral response Ĩ(ω) of the same agarose cylinder is plotted in figure 3. The amplitude of Ĩ(ω), computed by dividing the displacement spectrum by the chirped driving waveform spectrum, shows resonances (n = 1, …, 4) correlated with those of the displacement waveform, as expected. Furthermore, the associated phase of Ĩ(ω) is characteristically close to zero (stress and strain in phase) immediately below each resonance and equal to π (stress and strain opposed) immediately above each resonance.

Figure 3.

Resonance modes are observed in an agarose cylinder during swept-frequency excitation. Top: raw displacement data versus instantaneous driving frequency. Middle and bottom: computed amplitude and phase, respectively, of the mechanical spectral response Ĩ(ω). Four longitudinal resonance modes are indicated as n = 1, …, 4. As expected, the phase of Ĩ(ω) shifts from 0 (stress and strain in phase) below each resonance to π (stress and strain opposed) above each resonance.

This result can be understood by assuming that Love’s spatial solution described above is separable from the temporal solution, and that there is an added linear viscous damping term such that

$$F(t)\propto q{\text{e}}^{\text{i}\omega t}=\mathrm{\Delta }{z}^{″}(t)+{\gamma }_n\mathrm{\Delta }{z}^{\prime }(t)+{\omega }_n^2\mathrm{\Delta }z(t),$$

where q is proportional to the driving force, ω_n is the resonant frequency for mode n and γ_n is the damping coefficient. We note that this is different from other models that assume that viscoelastic rod vibrations are described by a Kelvin–Voigt relationship with the explicit addition of an inertial mass (Gurgoze and Zeren 2006) or by incorporating a complex elastic modulus directly into Love’s solution (Pritz 1981). Our model is appropriate for underdamped systems (γ_n < ω_n) which require the inertial term Δz″, and with perturbative displacements such that the temporal and spatial solutions are separable. Given a time-harmonic solution Δz(t) = Ãe^iωt, the amplitude à is then described by a complex Lorentzian function as follows:

$$\stackrel{\sim }{A}(\omega )=\frac{q}{{\omega }_n^2-{\omega }^2-\text{i}\omega {\gamma }_n}.$$ (3)

Then, Ĩ(ω) = ℑ[Δz(t)]/ℑ[F(t)] = Ã(ω)/q is inversely proportional to a complex elastic susceptibility, the longitudinal analog of G̃(ω) for shear. (For the purposes of discussion, experimental values of ω_n and γ_n will be reported in Hz which is understood to be their angular frequency values divided by 2π.) Based on observation we approximated γ(ω) ≈ γ_n because γ did not change appreciably over a single resonance peak (i.e. $\frac{\partial \gamma (\omega )}{\partial \omega }\ll 1$).

As shown in figure 4, the linear viscoelastic model well describes both the amplitude and phase of the experimental mechanical spectral data, as shown for modes n = 1 and 2. Because the phase of Ĩ(ω) swings from 0 to π over a resonance, phase is particularly helpful in discriminating a resonance against a noisy background.

Figure 4.

Complex resonance mode data from figure 3 are fit to Lorentzian curves (solid lines) according to equation (3) to determine the resonant frequencies ω_n and damping factors γ_n. Data are shown for n = 1 and 2 (left and right columns, respectively).

4.2. Comparison of elastic modulus using MRAS and a commercial device

We applied the MRAS method to extract Young’s modulus from these mechanical spectra. After fitting ω_n and γ_n to the data of figure 3 using equation (3), we least-squares estimated E = 44.2 ± 1.6 kPa for the agarose sample by iteration of equation (2), as described above. We assumed a Poisson’s ratio σ = 0.49, but found the predicted E varied by <5% for the range σ = 0.35–0.499. The same agarose sample was then analyzed by parallel plate compression (TA-XT plus, Stable Micro Systems), from which the quasi-static E = 30.0 ± 0.4 kPa for a single scan sampled (N = 123) over the range from 0.5 to 1% strain. The quasi-static modulus obtained from the texture analyzer is approximately two-thirds of the MRAS value, which is consistent with previous observations of the frequency-dependent modulus in agarose (Gu et al 2003), where the effect was attributed to fluid pressurization. Others have suggested that, in dynamic excitation, the fluid supports a significant fraction of the load, whereas during static measurements the pressure has time to dissipate (Soltz and Ateshian 1998).

4.3. Evidence for longitudinal tissue resonance modes

Next, we explored the effect of the dimensions of the tissue sample. In figure 5, we plot the measured resonances obtained from agarose cylinders of varying L that were prepared from a single batch mixture (C ≈ 10 mg mL⁻¹) against the predicted ω_n for the least-squares E = 57.1 ± 4.8 kPa. We found that the observed mode structure is not consistent with either flexural or torsional resonances, while it does fit the above model for longitudinal resonances with an average error of 3%. As expected, the resonance structure is highly dependent on the cylinder dimensions. For high aspect ratios and low n, the geometrical factor g ~ 1, and the resonance modes ω_n are spaced as odd harmonics (e.g. when L = 5 cm and n = 1–3). For higher aspect ratios, g decreases with increasing n, modifying the harmonic spacing. Also, the resonance modes shift to higher frequencies with decreasing aspect ratio because L and consequently λ_n decrease. We note that a single value of E is adequate to describe all resonance modes, suggesting that its frequency dependence is negligible in the 30–400 Hz range.

Figure 5.

Resonant frequencies in agarose cylinders as a function of their aspect ratio are consistent with the solution for longitudinal modes. Resonant frequency data for modes n = 1, …, 5 (where detectible) are plotted with theoretical curves by solving equation (2) using the best-fit Young’s modulus E = 57.1 kPa.

4.4. Dynamic range of Young’s modulus determination using MRAS

To determine the dynamic range over which this MRAS method is useful for extracting the Young’s modulus, we prepared agarose cylinders with a fixed aspect ratio (L/2R = 1) while varying the concentration C. The results are plotted in figure 6 and are fit to a phenomenological model E = αC^β, which can be related to the fractal dimension of the molecular chains comprising the agarose network (Jones and Marques 1990). The fit parameters are α = 390 ± 70 Pa mL mg⁻¹ and β = 2.07 ± 0.07 and are consistent with previous measurements of agarose (Benkherourou et al 1999). We note that the results of figures 3 and 5 should not be compared here because different batch mixtures were used.

Figure 6.

Young’s modulus is measured over 2 decades using MRAS in agarose cylinders of varying concentration. Moduli are plotted on a log–log plot and are fit to a phenomenological model (solid line, R² = 0.9965). Error bars are derived from the half maxima of the resonant frequencies.

4.5. Monitoring tissue stiffening in ex vivo tissue samples via acoustic resonances

Realizing that $E\propto {\omega }_n^2$ for a fixed sample geometry, according to (1), we expect that MRAS can monitor active processes that modify E, even in irregularly shaped samples. One such process is formaldehyde fixation of biological tissues. Formaldehyde fixatives cross-link proteins in tissue, increasing the modulus over time. This property has previously been used for elastography imaging studies by injecting formaldehyde into liver samples to create artificial lesions (Fahey et al 2004).

As described in the methods section, a rat liver specimen was divided in half and treated with magnetic nanoparticles. One portion was then treated with formalin while the control remained in the buffer solution. The mechanical frequency spectra of these samples were monitored for 6 h after formalin treatment. We found that mechanical resonances from the fixing liver became too weak to reliably detect after 67 min, while the control sample remained unchanged. Representative mechanical spectra of each half of the liver are plotted in figure 7 for time points up to 147 min. (For the control liver at 0 min, only a 0–100 Hz frequency sweep was acquired.)

Figure 7.

Mechanical resonances with Q ≈ 3 are observed in a rat liver, and are used to measure its relative stiffening during formaldehyde fixation. The mechanical spectra of control liver (top panel) and fixing liver (middle and bottom panels) are plotted from 0 to 147 min after exposure to formaldehyde. Results indicate increasing resonant frequency in the fixing liver only, consistent with an increasing Young’s modulus.

We found that the mechanical spectral response of the liver specimen exhibits a single resonance mode with greater γ than that observed in the agarose cylinders (figure 7). This dominant peak and associated phase shift are sufficiently distinctive to be tracked during the fixation process up to 67 min. Despite the difference in shape between the two samples, we found that their initial resonances ω₁ = 55 Hz were nearly identical, while their damping factors consistently differed, with γ₁ = 23 Hz and 12 Hz for the fixing liver and control, respectively. These correspond to quality factors Q ≈ 2–4. As expected, the control liver remained constant over time with ω₁ = 59.0 ± 2.6 Hz and γ₁ = 15 ± 2 Hz, while the fixing liver incrementally increased to ω₁ = 107 Hz and γ₁ = 36 Hz over 67 min.

Assuming that the liver samples were initially of the same viscosity and Young’s modulus, the initial discrepancy in γ suggests that γ is geometrically dependent. This may arise from small deviations from parallel of the top and bottom tissue boundaries, which would appear as line broadening. Despite the irregular and uncontrolled tissue shapes, the time-dependent change in ω_n during 0–67 min is as expected. The doubling of ω₁ suggests a quadrupling of E during fixation according to equation (1). Other reports of formaldehyde fixation in rabbit liver samples of similar size show that the half-maximal binding is reached at ~100 min (Helander 1994). At 147 min, the mechanical spectral amplitude of the fixing liver is small, even in the low-frequency part of the spectrum that is typically noisy for the less stiff liver specimens. For the phase of this spectrum (not shown), the rapid wrapping of the phase from 0 to 0 again between 50 and 100 Hz does not fit the profile of a Lorentzian. The phase shift near 180 Hz and associated amplitude peak may indicate a weak resonance.

5. Conclusion

In summary, an optical coherence elastography system was developed to monitor tissue displacements on a scale <10 nm induced by embedded magnetic ‘nanotransducers’. An inversion technique called MRAS was developed to extract Young’s moduli from the measured longitudinal resonance spectra of agarose cylinders, analogous to resonant ultrasound spectroscopy. The extracted Young’s moduli were consistent with independent analysis using a commercial mechanical analyzer. Concentration-dependent moduli were measured over two decades and were consistent with previously reported values in agarose. MRAS was then applied to ex vivo liver tissues with irregular boundaries. During a chemical fixation process of the liver sample, a twofold increase in the mechanical resonance frequency was attributed to a fourfold relative increase in Young’s modulus over a fixation period of 67 min.

To the best of our knowledge, while the effect of soft tissues resonating in response to mechanical stimuli has often been reported (Sinkus et al 2000), and while shear wave dynamic mechanical analysis is a staple of small sample elastography (Bercoff et al 2003), we have found no reports showing soft tissues that have discernable Q values and complex mechanical spectra similar to the Lorentzian longitudinal modes that we have observed. We attribute our unique observations to the high sensitivity and speed afforded by phase-sensitive optical coherence tomography, and to the low inertia of the magnetic nanotransducers. This setup allowed us to directly query the complex elastic susceptibility of the medium 1/Ĩ(ω), analogous to the complex shear modulus G̃(ω).

In future work, finite element analysis can provide quantitative, anisotropic E for irregularly shaped tissue samples (Samani et al 2003). While topical application of magnetic nanoparticles is possible for in vivo applications, a better understanding of how to control for irregular boundary conditions is needed before we can know the prospects of MRAS for in vivo assessment. Further study is needed to separate the contributions of tissue shape and viscous damping to the linewidth γ. Also, it may be possible to image the resonance mode structure inside millimeter-scale tissues using OCT to map heterogeneities of E, similar to one form of MR elastography (Sinkus et al 2000). The sensitivity afforded by coherence imaging combined with effectively inertialess nanoparticle transducers is a novel technique which has revealed tissue resonance spectra in an entirely new way. We expect that this MRAS technique will provide many new insights into tissue biomechanics, and help establish needed correlations between human disease and viscoelasticity.