Visualizing Chromosome Mosaicism and Detecting Ethnic Outliers by the Method of “Rare” Heterozygotes and Homozygotes (RHH)

Abstract

We describe a novel approach for evaluating SNP genotypes of a genome-wide association scan to identify “ethnic outlier” subjects whose ethnicity is different or admixed compared to most other subjects in the genotyped sample set. Each ethnic outlier is detected by counting a genomic excess of “rare” heterozygotes and/or homozygotes whose frequencies are low (<1%) within genotypes of the sample set being evaluated. This method also enables simple and striking visualization of non-Caucasian chromosomal DNA segments interspersed within the chromosomes of ethnically admixed individuals. We show that this visualization of the mosaic structure of admixed human chromosomes gives results similar to another visualization method (SABER) but with much less computational time and burden. We also show that other methods for detecting ethnic outliers are enhanced by evaluating only genomic regions of visualized admixture rather than diluting outlier ancestry by evaluating the entire genome considered in aggregate. We have validated our method in the Wellcome Trust Case Control Consortium (WTCCC) study of 17,000 subjects as well as in HapMap subjects and simulated outliers of known ethnicity and admixture. The method's ability to precisely delineate chromosomal segments of non-Caucasian ethnicity has enabled us to demonstrate previously unreported non-Caucasian admixture in two HapMap Caucasian parents and in a number of WTCCC subjects. Its sensitive detection of ethnic outliers and simple visual discrimination of discrete chromosomal segments of different ethnicity implies that this method of rare heterozygotes and homozygotes (RHH) is likely to have diverse and important applications in humans and other species.

INTRODUCTION

Genome-wide association (GWA) scans typically genotype at least 1000 subjects at hundreds of thousands of SNPs densely covering the human genome (1,2). Similar genome-wide SNP genotyping is also providing densely genotyped reference subjects (e.g. in HapMap) which are useful for investigating diverse genomic features (CNVs, gene expression, linkage disequilibrium, ethnic and forensic identification, population history, etc.) that can be specific to a chromosomal region or evaluated more globally (3–9). Whether used for GWA, reference, or other purposes, the ethnic ancestry of genotyped subjects is often pivotal since GWA scans can yield statistically inflated or false-positive results if cases and controls are ethnically mismatched or admixed (10); and conclusions from reference samples can be undermined by unknown ethnic differences or enhanced by accurate ethnic characterization (11). Since a subject's ethnic admixture or difference is often confined to a fraction of the genome, tools are now needed that use GWA genotypes to identify the chromosomal location(s) of admixed DNA and to detect subjects whose admixture may be relatively minor genome-wide while being substantial within specific chromosomal regions.

To avoid results confounded by ethnic differences or admixture, studies with GWA or reference samples often aim to include only subjects of a single ethnicity and to exclude “ethnic outliers” whose ancestry is admixed or different from the majority of genotyped subjects (10). One current approach for identifying ethnic outliers from their GWA genotypes uses principle components-multidimensional scaling (PC-MDS) to plot each subject along principle axes of genotypic variation, thereby mapping subjects into visually tight, ethnic clusters that identify outliers who fail to cluster with other subjects in the dataset (12). A second approach evaluates allele sharing between pairs of genotyped subjects at all GWA SNPs and identifies ethnic outliers by very low allele sharing with most other subjects as quantified by a Z-score statistic implemented in PLINK (13). As customarily applied, these approaches provide a global assessment of outlier status that contains no information about the chromosomal location of ethnic outlier DNA which may be confined to a fraction of the genome in ethnically admixed individuals. Furthermore, these approaches also customarily evaluate genotypes from the entire genome considered in aggregate which can dilute the fraction of a subject's genome that contains outlier DNA, resulting in failure to detect more modest ethnic admixture.

Here we describe a novel strategy for evaluating GWA genotypes that detects subjects whose ethnicity is different or admixed compared to most other subjects in the genotyped sample set. Furthermore, we demonstrate that this approach enables simple and striking visualization of non-Caucasian DNA segments interspersed within ethnically admixed chromosomes, thereby delineating a clearly defined chromosomal mosaicism analogous to the chromosomal mosaicism produced by intercrossing different strains of inbred mice (14,15). We demonstrate visualization of admixed chromosome mosaicism and detection of ethnic outliers by applying our method to self-reported European Caucasian subjects in 7 disease and 2 control sample sets genotyped for GWA scans by the Wellcome Trust Case Control Consortium (WTCCC) (see www.wtccc.org.uk). We also further validated the method in HapMap subjects and in simulated outliers of known ethnicity and admixture. Our method is shown to detect ethnic outliers not identified by WTCCC application of PC-MDS (12) or by the PLINK allele-sharing Z-score (13); and we also show that our visualization of mosaicism in ethnically admixed chromosomes gives results similar to those of a fundamentally different visualization method (SABER) but with much less computational time and burden.

Our method combines two techniques for detecting ethnic outliers that provide complementary information. One technique is based on evaluating homozygote genotypes of low frequency (which we call “rare homs”) while the other evaluates low-frequency heterozygotes (referred to as “rare hets”). We call the combined technique the method of rare heterozygotes and homozygotes or “RHH”. Software for performing RHH analyses will be made available at the time of publication via the internet (http://sourceforge.net/projects/rhh/ or http://www.sanger.ac.uk/resources/software/rhh/).

Although the RHH method evolved from initial investigations of genotype quality and detection of ethnic outliers, the method is enhanced by its subsequently discovered ability to visualize and precisely map ethnic outlier DNA to discrete chromosomal segments and to also delineate the portion of an outlier's genome which is not ethnically admixed (Fig. 1, 2). This simple visual discrimination of discrete chromosomal segments of different ethnicity provides a visual mosaic “fingerprint” of an admixed subject's genome which is likely to have a number of important applications. One such application is to greatly enhance detection of genomes containing ethnic admixture even when the amount of admixture is small. For example, to the best of our knowledge, we report for the first time that while most HapMap Caucasian (CEU) parents show no evidence of non-Caucasian admixture, two CEU parents (NA12872, NA11993) each carry a single large chromosomal segment of non-Caucasian DNA of probable African origin. These segments are 19 and 29 megabases (Mb) long making this outlier DNA too dilute to be detected by alternative outlier methods that evaluate genotypes from the entire human genome (∼3000 Mb) considered in aggregate. But RHH was able to visualize the location of each non-Caucasian segment and we then evaluated only genotypes from the region spanned by the segment using a PC-MDS algorithm that clearly demonstrated each segment's ethnic similarity to HapMap Africans (see DISCUSSION).

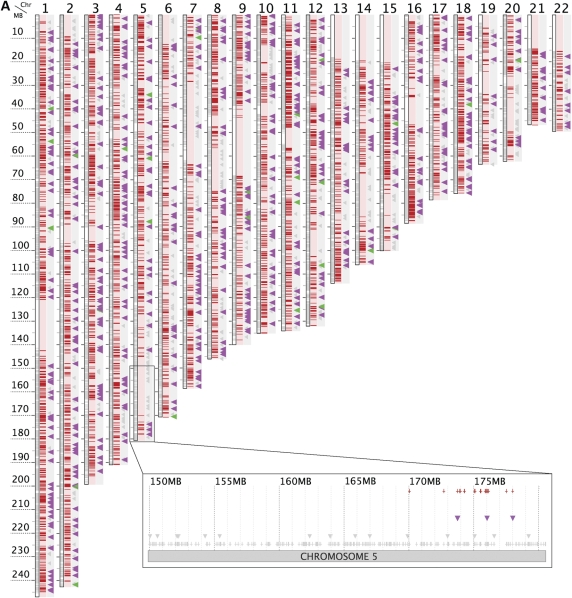
Figure 1.

Admixed chromosome mosaicism in subjects A1-1-1-1 and B5-4-12-2. The mosaicism is shown by the chromosomal positions of each subject's rare hets (red dashes beside chromosomes in whole genome view; red crosses above chromosome in fine-scale view). The positions of the red dashes and red crosses should be compared to all possible genomic locations of rare hets derived empirically by mapping all rare-het positions observed in the sample set (A or B) of the subject (gray crosses immediately above fine-scale chromosome; gray shading inside whole-genome chromosomes). (A) Subject A1-1-1-1 is the most extreme ethnic outlier in set A as judged by both RHH and PLINK but lacks rare hets in a number of chromosomal regions (see fine-scale view and Table 2) implying that these are regions of unadmixed Caucasian ancestry. (B) Mosaicism in subject B5-4-12-2 is more typical of outliers and is visually obvious with rare-hets densely packed into a few discrete segments that mark the chromosomal locations of non-Caucasian DNA. Tiny triangles in whole-genome and fine-scale views denote the positions of “ethnic” SNPs which are monomorphic in HapMap CEU subjects but have MAF ≥0.4 in HapMap YRI subjects (“YRI SNPs”) or in CHB subjects (“CHB SNPs”). Triangles are enlarged if the subject carries the “non-Caucasian” allele as a heterozygote or homozygote at a YRI SNP (purple triangle) or CHB SNP (green triangle) whereas homozygotes for the “Caucasian” allele are unenlarged gray triangles. The rarity of non-Caucasian alleles (purple/green triangles) outside rare-het segments and their far higher frequency inside the segments confirms the non-Caucasian origin of segments with dense rare hets and Caucasian ethnicity of regions in which rare hets are largely absent.

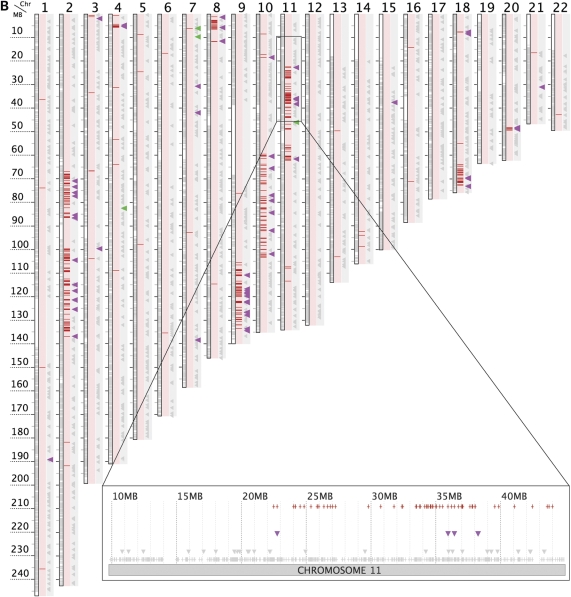
Figure 2.

Rare-het chromosomal mosaicism in four RHH-detected outliers, two of whom were also detected by PLINK. Subjects A8-9-13-7 (A) and B7-7-18-5 (B) exhibit dense rare hets on only a few chromosomes. They are not detected as outliers by PLINK when genotypes are evaluated for the whole genome but are strongly detected when PLINK considers only genotypes from the subject's longest rare-het segment (see Table 2). Subjects A2-6-2-5 (C) and B2-5-2-3 (D) exhibit dense rare hets on most chromosomes and are strongly detected as ethnic outliers when PLINK evaluates the whole genome; but PLINK provides no evidence that the two subjects are outliers when genotypes are only included from regions that lack rare hets (Table 2). These results imply that outlier DNA is largely confined to segments marked by dense rare hets. (See Fig. 1 for definitions of figure annotations.).

The RHH method was developed in several stages which is reflected in the RESULTS section. The first two sections describe observations that led to the discovery that ethnic outliers carry excess numbers of rare homs and/or rare hets. We also demonstrate the use of genotype quality scores to eliminate samples with excess rare hets or rare homs due to genotyping error rather than ethnicity. Then we describe our discovery that many ethnic outliers exhibit a chromosomal mosaicism in which discrete segments of “non-Caucasian” DNA are visualized by the presence of dense rare hets surrounded by segments of “Caucasian” DNA that lack rare hets. We also compare RHH with two other, fundamentally different algorithms for detecting ethnic outliers (PC-MDS, PLINK Z-score) in order to: (a) show the validity and sensitivity of the RHH method, and (b) illustrate how RHH visualization of chromosomal outlier segments can markedly increase detection of outlier DNA by other algorithms when these algorithms consider only the fraction of the genome marked by dense rare hets.

RESULTS

Discovery of the “Rare Homs” Method

The WTCCC conducted GWA scans of 7 disease and 2 control sample sets, each containing between one and two thousand subjects, the vast majority of whom self-reported as being of European Caucasian ancestry (12). In evaluating genotypes of the Affymetrix 500K SNP array (Affy500K) for departure from Hardy-Weinberg equilibrium (HWE) in individual WTCCC sample sets, we noticed a few SNPs with zero counts for the heterozygote and only one or a few counts for the rarer homozygote. We labeled these SNPs and their rare homozygotes as “rare homs” and initially attributed the heterozygote deficit at these SNPs to genotyping error since genotype-calling algorithms sometimes preferentially “drop” heterozygotes (16). However, a marked deficit of heterozygotes at a SNP can also arise if genotyped subjects originate from two non-interbreeding populations, a phenomenon sometimes called the Wahlund effect (17). This stimulated the idea that instances of rare-hom SNPs might be due to the inclusion of a few non-Caucasian subjects in the datasets being evaluated.

To test this possibility, we counted instances of rare hom genotypes found in individual subjects belonging to the same WTCCC case or control set. We reasoned that if total instances of rare homs in a sample set were approximately equally distributed among the subjects, then rare homs would be unlikely to be caused by non-Caucasian ethnicity since most WTCCC samples were selected for being unadmixed Caucasians. By contrast, if most rare hom genotypes were found to cluster in relatively few subjects, then these subjects might be non-Caucasians or admixed Caucasians. When we examined the distribution of rare-hom counts per subject for individual WTCCC sample sets, we found that some sets exhibited a small number of obvious outlier subjects carrying many (50 to 300) rare-hom genotypes whereas almost all other subjects carried only 0 or 1 rare homozygotes. As detailed below, the ethnic outlier status of the subjects with excess rare homs was subsequently confirmed by: (a) their excess of non-Caucasian genotypes at HapMap SNPs which are monomorphic in Caucasians and (b) statistical verification by other ethnic outlier detection methods.

Discovery of the “Rare Hets” Method

Having identified ethnic outliers based on within-subject clustering of rare homs, we examined WTCCC sample sets to determine if low-frequency heterozygotes (“rare hets”) might also cluster in ethnic outliers. We counted only heterozygotes for SNPs that had zero counts for the rarer homozygote and only a few counts for the heterozygote in the WTCCC sample set being considered, ultimately settling on 0.5% as the upper bound on heterozygote frequency (see METHODS for details). When we examined total rare-het counts in each individual from specific WTCCC sample sets, we found that the distribution for each set contained a number of individuals with high rare-het counts separated from the main body of the distribution. In these distributions, subjects with the highest rare-het counts included all subjects with high rare-hom counts; however, most individuals with high rare-het counts had few or no rare-hom genotypes. We subsequently inferred that excess rare homs occur only in the subset of ethnic outliers who have inherited outlier ethnicity from both their father and mother (see DISCUSSION). It should also be noted that unlike rare-hom SNPs, genotypes at rare-het SNPs do not depart from HWE and the RHH method is therefore not equivalent to or logically dependent on departure from HWE.

In seeking to understand the clustering of rare hets and rare homs within ethnic outliers, we hypothesized that these rare genotypes derive from SNPs which are monomorphic (or nearly so) in European Caucasians but which are polymorphic in non-Caucasians. The “non-Caucasian” allele at such SNPs would have very low frequency in large sample sets containing few non-Caucasians. We further hypothesized that the reason rare alleles at these SNPs cluster in an ethnic outlier is because they are very common in the outlier's native population and hence many such “non-Caucasian” alleles are carried by an individual outlier even though these alleles appear rare if their frequencies are calculated in a large dataset consisting mainly of Caucasians.

The next section of RESULTS shows the extreme tail of the rare-het and rare-hom count distributions of two WTCCC sample sets to illustrate typical results for the WTCCC data. Our analyses used all WTCCC Affy500K genotypes called by the Affymetrix BRLMM algorithm which excludes genotypes with BRLMM confidence scores above 0.5 (see METHODS). We also applied the WTCCC filter of excluding DNA samples with genotype call rates below 97% in order to remove poor quality DNA samples and genotype calls (12). In addition to describing formal analyses of the WTCCC genotype data (see METHODS for details), the next section clearly demonstrates that subjects with excess rare hets and/or rare homs are ethnic outliers.

However, before proceeding to the next section, we briefly highlight some other sections of the paper and other information that also confirm the validity and usefulness of the RHH method:

1. In the DISCUSSION (Table 3), RHH is applied to a simulated dataset and is shown to detect known outliers of non-Caucasian ethnicity (HapMap subjects, and simulated subjects with varying degrees of non-Caucasian admixture).

2. RHH analysis of excess counts of rare hets detected 151 of the 153 subjects which the WTCCC excluded from their case-control analyses for being of “non-Caucasian ancestry” (12) and RHH also detected many other ethnic outliers not identified by the WTCCC (e.g. the six RHH-detected outliers in the top rows of Table 2).

3. In the final section of RESULTS, ethnically admixed subjects are shown to exhibit a chromosomal mosaicism in which discrete segments of non-Caucasian and Caucasian DNA are visualized by the presence or absence of dense rare hets mapped to their chromosomal locations. This ability to visualize the genomic location of non-Caucasian DNA can markedly increase statistical detection of ethnic outliers by methods other than RHH (see Table 2; also see DISCUSSION for detection of non-Caucasian admixture in two HapMap CEU parents).

Table 3.

Extreme “tail” of RHH count distribution containing outliers from sample set B, HapMap, and simulated matings of HapMap individuals^a

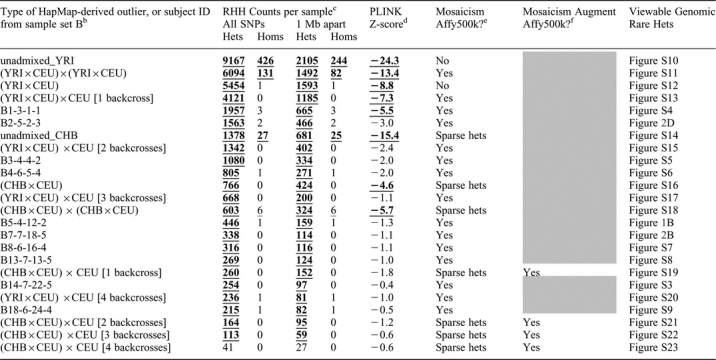^aRHH analysis of simulated HapMap ethnic outliers combined with sample set B; subjects are sorted from highest to lowest rare-het counts under “All SNPs” (column 2) with some set B subjects omitted to show all HapMap-derived outliers. “CEU”, “CHB”, “YRI” denote HapMap subjects of Caucasian, Chinese, and African Yoruban ancestry respectively.

^bEach “unadmixed” outlier is a HapMap YRI or CHB subject; other HapMap-derived outliers are progeny of simulated matings denoted by “×”; for example, “(YRI×CEU)×CEU [2 backcrosses]” denotes offspring from mating of a HapMap YRI and CEU subject followed by mating (“backcross”) in next two generations with a CEU subject; set B subjects have same ID used in Table 1

^cUnthinned counts under “All SNPs” and thinned counts under “1 Mb apart” are from 401,430 HapMap SNPs genotyped on Affy500K and having resolvable strand for HapMap versus Affy. Counts exceeding permutation-derived threshold are bold and underlined (signifying p<0.001) or only underlined (signifying p<0.05).

^dLowest PLINK Z-score from 1st thorough 10th nearest-neighbor distributions. Z-scores are bold and underlined if statistically significant (Z<−4.0).

^eMosaicism using Affy500K chip: “Yes” if rare-het mosaicism is visually obvious; “No” if dense rare hets cover entire genome; “Sparse hets” if rare het density is too sparse to clearly discern mosaicism (as in simulated subjects of CHB ancestry).

^f“Yes” if subject shows obvious rare-het mosaicism when Affy500K chip is augmented with ∼40,400 HapMap SNPs monomorphic in HapMap CEU but with minor allele frequency above 0.1 in CHB.

Table 2.

Recalculated ethnic-outlier Z-scores for chromosomal region(s) with or without dense rare-hets in subjects exhibiting rare-het mosaicism^a

Subject IDb	PLINK Z-scorec		Characteristics of Partial Genome
	Whole Genome	Partial Genome	Chromosome Region(s) Includedd	Putative Ethnicity of Included Region(s)	Viewable genomic rare-hets
A8-9-13-7	−1.2	−4.6	1(40–115 Mb)	Non-Caucasian	Figure 2A
A19-9-30-7	−0.4	−5.2	2(145–200 Mb)	Non-Caucasian	Figure S1
A14-10-25-8	−0.9	−4.1	1(180–230 Mb)	Non-Caucasian	Figure S2
B5-4-12-2	−1.4	−5.2	2(65–140 Mb)	Non-Caucasian	Figure 1B
B7-7-18-5	−1.1	−5.0	11(0–75 Mb)	Non-Caucasian	Figure 2B
B14-7-22-5	−0.8	−5.3	6(120–165 Mb)	Non-Caucasian	Figure S3
A1-1-1-1	−21.4	−0.7	2(0–6 Mb); 5(150–165 Mb); 6(0–10 Mb); 7(35–55 Mb); 8(60–70 Mb); 14(70–80 Mb)	Caucasian	Figure 1A
A2-6-2-5	−5.5	−1.2	2(0–140 Mb); 5(55–100 Mb); 7(50–70 Mb); 8(0–100 Mb); 9(25–70 Mb); 10(20–50 Mb); 11(0–95 Mb); 12(15–95 Mb); 13(0–65 Mb); 15(70–90 Mb); 18(0–50 Mb); 19(0–50 Mb); 20(10–50 Mb); 22(0–45 Mb)	Caucasian	Figure 2C
B1-3-1-1	−6.0	−2.6	1(60–175 Mb); 2(10–40, 140–150, 180–190 Mb); 6(105–120 Mb); 7(105–145 Mb); 8(65–85 Mb); 10(55–115 Mb); 11(25–70 Mb); 13(30–65 Mb); 14(30–55 Mb); 17(55–80 Mb)	Caucasian	Figure S4
B2-5-2-3	−4.2	−1.0	1(15–30 Mb); 2(40–220 Mb); 3(0–40,70–125,145–185 Mb); 4(0–20,115–165 Mb); 5(15–70,125–135,165–185 Mb); 7(0–140 Mb); 8(20–115 Mb); 10(75–115 Mb); 11(90–115 Mb); 12(75–135 Mb); 14(65–105 Mb); 15(65–90 Mb); 17(0–50 Mb); 18(15–80 Mb); 19(20–80 Mb); 21(30–50 Mb)	Caucasian	Figure 2D

^aPLINK Z-scores are based on all Affy500K SNPs in the “Whole Genome” or in a “Partial Genome” marked in subjects 1–6 by their largest rare-het segment and defined in subjects 7–10 by pooling all major regions not marked by dense rare-hets. Each subject shows a dramatic change in Z-score statistical significance for “Whole” versus “Partial” Genome, thus showing that non-Caucasian and Caucasian DNA are respectively marked by presence or absence of dense rare hets.

^bSame SubjectID as in Table 1

^cLowest PLINK Z-score from 1st thorough 10th nearest-neighbor distributions. Z-scores are bold and underlined if statistically significant (Z<−4.0).

^dChromosome number and boundaries of included region(s).

Extreme “tails” of rare-het and rare-hom distributions for two typical sample sets

All 9 WTCCC sample sets contain many ethnic outliers detectable by excess rare het counts; but only about half of the sets contain one or more outliers with very high rare hom counts. Table 1 shows subjects with the highest rare-het and hom counts in two typical sample sets (set A=UKBS controls, set B=58BC controls), one of which contains several outliers with high rare-hom counts (set A) and one of which does not (set B). The table shows per-subject rare-het and rare-hom counts totalled for all SNPs contributing to that subject (columns 2–3) and alternatively totalled only for SNPs contributing to that subject which are at least 1 Mb apart (columns 4–5). Spacing of 1 Mb is somewhat arbitrary but was chosen since pairwise linkage disequilibrium (LD) would usually be negligible for SNPs this far apart (5,18) and hence the “thinned” counts from these SNPs can be considered independent. Each table's rows (subjects) are ordered from highest-to-lowest rare-het counts for “All SNPs” (column 2). SubjectID (column 1) also gives subject rank in the four het and hom count distributions by concatenating set name (A or B) with the subject's count rank in columns 2, 3, 4 and 5, respectively. Both sample sets show statistical evidence of containing many ethnic outliers as indicated by high het or hom counts in bold and underlined (signifying p<0.001) or only underlined (signifying p<0.05) when counts exceed permutation-derived thresholds specifically calculated for hets or homs of each sample set (see SUPPLEMENTARY METHODS). Note that these p-values do not require a multiple-test or multiple-subject correction since the p-value is the entire sample set's probability of containing one or more non-outliers who, by chance, exceed the het or hom count threshold calculated for that sample set.

Table 1.

Subjects in the extreme “tail” of the rare-het and rare-hom count distributions of two typical sample sets

SubjectIDa	RHH Counts and p-valuesb				Genotype Confidencec		“Ethnic” Het Countsd		Other Ethnic Outlier methods
	All SNPs		1 Mb apart		All 500K	Rare Hets	YRI	CHB	WTCCC PC-MDSe	PLINK Z-scoref
	Hets	Homs	Hets	Homs
Sample set A (UKBS controls)
A1-1-1-1	9063	386	2003	229	0.06	0.04	356	19	YES	−21.4
A2-6-2-5	3040	6	787	6	0.04	0.04	164	14	YES	−5.5
A3-9-6-7	2090	1	617	1	0.04	0.04	111	5	YES	−3.2
A4-3-3-3	1528	48	678	32	0.04	0.04	40	66	YES	−14.5
A5-4-4-2	1315	46	659	38	0.03	0.03	50	64	YES	−13.4
A6-2-5-2	1314	51	634	38	0.03	0.02	50	65	YES	−13.8
A7-5-8-4	949	7	329	7	0.04	0.04	62	12	YES	−2.7
A8-9-13-7	810	1	223	1	0.03	0.03	30	6		−1.2
A9-10-9-8	704	0	257	0	0.03	0.04	40	6	YES	−2.0
A10-10-7-8	569	0	438	0	0.06	0.20	23	6		−1.4
A11-9-10-7	524	1	248	1	0.05	0.04	35	22	YES	−3.7
A12-8-12-6	446	2	236	2	0.03	0.02	33	17	YES	−7.2
A13-7-11-6	406	3	244	2	0.05	0.05	38	16	YES	−6.1
A14-10-25-8	394	0	117	0	0.04	0.04	26	3		−0.9
A15-9-15-7	361	1	175	1	0.03	0.04	21	19	YES	−4.2
A16-10-15-8	337	0	175	0	0.03	0.03	27	18	YES	−5.7
A17-9-18-7	311	1	154	1	0.04	0.06	30	4		−1.9
A18-10-20-8	306	0	151	0	0.05	0.04	25	8		−2.0
A19-9-30-7	276	1	85	1	0.04	0.05	23	0		−0.4
A20-9-24-7	262	1	118	1	0.04	0.05	16	2		−1.6
A20-10-26-8	262	0	111	0	0.03	0.04	26	1		−1.1
A21-10-22-8	259	0	120	0	0.04	0.05	21	3		−2.2
A22-10-21-8	258	0	138	0	0.04	0.06	22	7	YES	−4.7
A23-9-28-7	251	1	107	1	0.05	0.07	21	7		−0.6
A24-10-26-8	243	0	111	0	0.03	0.02	22	6		−1.0
Sample set B (58BC controls)
B1-3-1-1	2802	4	814	4	0.04	0.03	114	33	YES	−6.0
B2-5-2-3	2221	2	556	2	0.03	0.03	102	9	YES	−4.2
B3-4-4-2	1525	3	404	3	0.03	0.03	72	5	YES	−2.4
B4-6-5-4	1068	1	317	1	0.06	0.05	49	3	YES	−2.5
B5-4-12-2	600	3	180	3	0.04	0.05	33	2		−1.4
B6-7-3-5	507	0	411	0	0.07	0.22	24	7		−2.1
B7-7-18-5	488	0	137	0	0.03	0.03	35	1		−1.1
B8-6-16-4	451	1	141	1	0.04	0.04	25	2		−0.9
B9-7-11-5	442	0	185	0	0.07	0.07	22	9		−1.5
B10-5-8-3	432	2	224	2	0.06	0.06	39	17	YES	−2.5
B11-2-17-2	413	7	139	3	0.02	0.04	34	2		−4.1
B12-7-15-5	384	0	151	0	0.06	0.07	24	3		−0.5
B13-7-13-5	383	0	161	0	0.06	0.08	25	1		−1.1
B14-7-22-5	352	0	108	0	0.03	0.03	22	1		−0.8
B15-7-17-5	318	0	139	0	0.05	0.08	19	3		−1.4
B16-1-18-1	313	8	122	4	0.03	0.03	28	5		−3.7
B17-7-15-5	298	0	151	0	0.03	0.03	20	5		−2.7
B18-6-24-4	294	1	98	1	0.03	0.04	14	6		−0.3
B19-7-14-5	282	0	157	0	0.05	0.06	24	8		−2.3
B20-7-7-5	269	0	233	0	0.07	0.19	14	7		−0.7
B21-7-19-5	257	0	121	0	0.03	0.03	25	3		−2.1
B22-7-25-5	255	0	96	0	0.03	0.03	23	2		−1.2
B23-7-6-5	252	0	234	0	0.05	0.19	14	4		−1.2
B24-7-20-5	248	0	118	0	0.03	0.03	19	5		−2.3
B24-7-26-5	248	0	88	0	0.04	0.04	15	5	YES	−1.8

^aSubjects are sorted from highest to lowest rare-het counts for “All SNPs” (column 2); subjectID is sample set followed by count rank in columns 2, 3, 4 and 5.

^bCounts from all Affy500K SNPs or “thinned” to derive only from SNPs at least 1 Mb apart. Counts exceeding permutation-derived threshold are bold and underlined (signifying p<0.001) or only underlined (signifying p<0.05).

^cMean BRLMM confidence for subject genotypes at all Affy500K SNPs and at all rare hets. Mean rare-het confidence above 0.1 is in bold italics to indicate doubtful genotype accuracy and likely false-positive ethnic outlier.

^dCounts of heterozygotes at “ethnic” SNPs at least 1 Mb apart. Statistically excess counts (p<0.001 or p<0.05) denoted by bold and underline as in footnote b.

^eSubject identified by WTCCC as having “non-Caucasian ancestry” based on PC-MDS analysis (12).

^fLowest PLINK Z-score from 1st thorough 10th nearest-neighbor distributions. Z-scores are bold and underlined if statistically significant (Z<−4.0).

To further examine outlier status, the penultimate and final columns of Table 1 show the results of applying two other ethnic outlier detection methods that are fundamentally different from RHH. The penultimate column denotes whether a subject was detected as an ethnic outlier by the PC-MDS method used by the WTCCC to identify and exclude 153 WTCCC subjects with non-Caucasian ancestry (12). When applied to the 9 WTCCC sample sets, RHH detected 151 of these 153 WTCCC-detected outliers including all 14 subjects in sample set A and all 6 subjects in set B (see Table 1).

The second outlier method we compared with RHH is implemented by PLINK software (13) and generates a Z-statistic which is shown in the final column of Table 1. This method calculates genome-wide identity-by-state (IBS) allele sharing between each subject and its “nearest neighbor” in the data set (the subject with whom it shares the highest proportion of alleles); and this enables derivation of a Z-score distribution in which outliers are identified by an extremely negative Z-score produced by low allele sharing with their nearest neighbor. The final column of Table 1 therefore shows each subject's lowest Z-score from the 1st through 10th nearest-neighbor distributions with all Z-scores below -4.0 being underlined and in bold to indicate subjects who are ethnic outliers according to the threshold recommended by PLINK documentation. This bold highlighting indicates that PLINK-detected outliers are mainly subjects with the highest rare het counts in each data set; but many other subjects identified as outliers by RHH have minimum PLINK Z-scores well above the -4.0 threshold, suggesting that RHH is more sensitive in detecting some outliers. This difference in sensitivity is illustrated by six RHH-detected outliers in Table 1 (A8-9-13-7, A19-9-30-7, A14-10-25-8, B5-4-12-2, B7-7-18-5, B14-7-22-5) which were not detected by PLINK and are not among the 153 ethnic outliers excluded by the WTCCC, yet are confirmed as genuine ethnic outliers by additional evidence presented in the next section (see Table 2).

To further evaluate the ethnicity of RHH outliers, we counted their heterozygous Affy500K genotypes at HapMap SNPs spaced at least 1 Mb apart which are monomorphic in HapMap Caucasians (CEU) but have minor allele frequency (MAF) of at least 0.4 in Yorubans (YRI) or in Chinese (CHB) [see “Ethnic Het Counts” in columns 8–9 of Table 1, and “Ethnic SNPs …” in SUPPLEMENTARY METHODS]. These “YRI SNPs” or “CHB SNPs” would rarely be heterozygous in a non-admixed Caucasian, but we chose their near-maximal MAF (≥0.4) in YRI and/or CHB since the SNPs would be among those most likely to be heterozygous in DNA of non-Caucasian ancestry. The 1 Mb spacing of the SNPs implies that within-subject het counts can be considered independent (explained above) and evaluated by permutation to determine if a subject carries a statistically significant excess of counts from YRI or CHB SNPs (see SUPPLEMENTARY METHODS). Het counts in Table 1 that exceeded a permutation-derived threshold for YRI or CHB SNPs are shown in bold and underlined (signifying p<0.001) or only underlined (signifying p<0.05), providing confirmation of non-Caucasian ancestry for many RHH outliers. Note that outliers often exhibit far more het counts at YRI than CHB SNPs which might be expected since the YRI panel (838 SNPs) is much larger than the CHB (139 SNPs). However some outliers have relatively high ratios of CHB:YRI het counts (e.g. A4-3-3-3, B10-5-8-3) indicating that the source of non-Caucasian admixture in such subjects is Asian rather than African.

To avoid erroneously inferring non-Caucasian outlier status based on genotyping errors, we also examined each subject's mean BRLMM confidence score at all SNPs contributing to that subject's rare-het counts (column 7). A BRLMM genotype call becomes less certain as its confidence score increases and the Affymetrix BRLMM protocol drops genotypes with confidence scores of 0.5 or higher (http://www.affymetrix.com/support/technical/whitepapers/brlmm_whitepaper.pdf). We regard heterozygous genotypes as being of doubtful accuracy if the mean confidence for rare hets is considerably higher than the mean BRLMM confidence for all genotypes called in the same subject (under “All 500K”, column 6). In this connection, when mean BRLMM confidence is above 0.1 for rare hets, we usually observe much better confidence scores for all 500K SNPs genotyped in the same subject and often find that such subjects are not confirmed as ethnic outliers by exhibiting a statistically significant excess of YRI and/or CHB hets. Mean confidence scores above 0.1 are therefore highlighted in bold italics in Table 1, and subjects exhibiting such low quality het genotypes are considered to be likely false-positive outliers if detected by RHH.

Admixed Chromosome Mosaicism

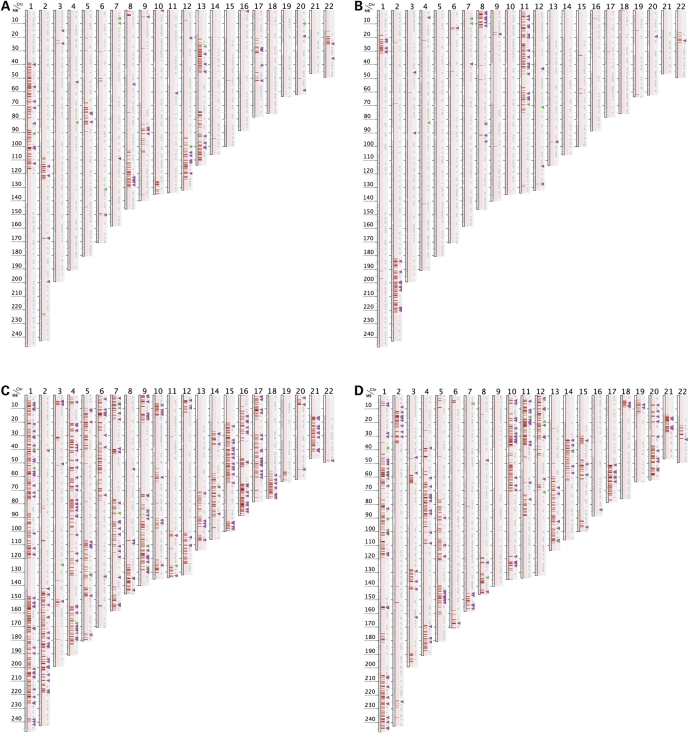
We noticed that het counts at SNPs “1 Mb apart” decreased from het counts at “All SNPs” more precipitously in some subjects (e.g. A8-9-13-7) than in others (e.g. A10-10-7-8) suggesting that some subjects' rare hets and homs might be concentrated in particular chromosomal regions rather than being evenly distributed across the genome. Therefore we generated chromosomal maps to visualize rare-het positions in individual outliers compared to all possible genomic positions of rare hets as determined by pooling rare hets from all subjects in the outlier's sample set (Fig. 1). In each set examined, pooled hets densely cover most of each chromosome (apart from centromeric and a few other small regions that lack Affy500K SNPs). However, as illustrated in Figure 1, many individual outliers exhibit an obvious mosaicism in which their rare hets are densely packed within discrete chromosomal segments surrounded by long tracts showing near-complete absence of rare hets in that outlier. Indeed, in many outliers, rare hets were found only within a few discrete segments located on a small number of chromosomes (Fig. 1B, 2A, 2B and Supplementary Fig. S1–S3, S7–S9). Other outliers exhibited discrete rare-het segments on a majority of their chromosomes while also exhibiting long chromosomal tracts lacking rare hets (Fig. 1A, 2C, 2D and Supplementary Fig. S4–S6). The large subset of outliers who exhibit visually obvious mosaicism generally have low ratios of CHB:YRI het counts indicating that they may be of African or non-Asian origin (discussed above). In these outliers, non-Caucasian admixture appears to be largely confined to the fraction of the genome which is delimited by rare-het segments.

To further assess the ethnicity of rare-het segments, our chromosomal maps also show tiny triangles denoting the positions of all SNPs genotyped on the Affy500K chip which were monomorphic in HapMap CEU but had MAF≥0.4 in YRI (“YRI SNPs”) or in CHB (“CHB SNPs”). The triangles are enlarged if a subject is heterozygous or homozygous for the “non-Caucasian” allele at a YRI SNP (purple triangle) or CHB SNP (green triangle) whereas homozygotes for the “Caucasian” allele are unenlarged gray triangles (Fig. 1, 2). The non-Caucasian allele at YRI or CHB SNPs should be relatively rare in a non-admixed Caucasian but might occasionally be observed due to genotyping error or genuine alleles with very low frequency in Caucasians. Consistent with this expectation, homozygotes for the Caucasian allele (gray triangles) were observed at almost all YRI or CHB SNPs located outside rare-het segments. However inside rare-het segments, the non-Caucasian allele was frequently observed at YRI or CHB SNPs (purple or green triangles, respectively) as is shown in Figures 1 and 2. This rarity of the non-Caucasian allele outside rare-het segments and its far higher frequency inside the segments confirms the non-Caucasian origin of segments with dense rare hets and Caucasian ethnicity of regions in which rare hets are largely absent. We therefore sometimes refer to rare-het segments as “outlier” or “non-Caucasian” segments.

To further illustrate the ability of RHH to distinguish chromosomal regions of Caucasian and non-Caucasian origin in subjects with RHH mosaicism, we recalculated PLINK Z-scores for specific RHH outliers by considering only genotypes from chromosomal regions that (a) contained dense rare hets or (b) lacked rare hets. For example, Table 2 lists six subjects (A8-9-13-7, A19-9-30-7, A14-10-25-8, B5-4-12-2, B7-7-18-5, and B14-7-22-5) who each show obvious RHH mosaicism (Fig. 1B, 2A, 2B and Supplementary Fig. S1, S2, S3) and give highly significant RHH p-values.These subjects are not among the 153 WTCCC-detected ethnic outliers and each gives a non-significant PLINK Z-score close to zero when PLINK evaluates the whole genome. Yet when we executed a PLINK run for each subject that only evaluated genotypes from that subject's largest rare-het segment, the recalculated PLINK distributions gave highly significant Z-scores (Z<−4.0) for all 6 subjects, clearly demonstrating the presence of ethnic outlier DNA within the subject's rare-het segment (Table 2). Conversely, we also recalculated PLINK Z-scores only for regions that lacked rare hets in the two most extreme outliers from Table 1 for set A (A1-1-1-1, A2-6-2-5) and set B (B1-3-1-1, B2-5-2-3). These four subjects were identified as ethnic outliers by WTCCC and by PLINK which gave highly significant Z-scores (−21.4 to −4.2) when genotypes were evaluated from the whole genome. But the PLINK Z-scores became non-significant and close to zero when we reran PLINK for each outlier considering only genotypes from all major chromosomal regions that lacked rare hets in that outlier (Table 2). Taken together, these recalculated PLINK analyses again imply that admixed non-Caucasian DNA is largely marked by and confined to rare-het segments. Note that the agreement of PLINK and RHH in this regard is based on evaluating completely separate sets of SNPs since RHH only considers SNPs whose MAF in the data is below 0.01 while PLINK omits such SNPs at its default MAF setting (http://pngu.mgh.harvard.edu/purcell/plink/). The PLINK and RHH analyses are therefore independent being based on different SNPs from the same chromosomal segment(s).

DISCUSSION

We have shown that the RHH method can sensitively detect ethnic outliers among samples mainly derived from a single ethnic group and have also shown the method's ability to visualize chromosomal mosaicism in many ethnically admixed individuals. A fundamental feature of RHH is that all outliers it detected among WTCCC samples exhibited a statistical excess of rare heterozygotes (rare hets), but only a small subset of RHH outliers exhibited an excess of rare homozygotes (rare homs). We believe that the presence of excess rare homs and of admixed chromosome mosaicism depends on the type of outlier – as can be inferred hypothetically or demonstrated empirically by applying RHH analysis to simulated admixed or unadmixed outliers of different types (see Table 3).

For example, one basic type of ethnic outlier shown in Table 3 is an unadmixed member of a non-Caucasian population such as HapMap YRI or CHB. Based on observed HapMap genotype frequencies (5,6), such individuals would be homozygous and heterozygous at many SNPs for “non-Caucasian” (nC) alleles frequently found in YRI and/or CHB subjects but never or rarely found in Caucasians such as CEU. These nC alleles and the SNPs from which they derive (“nC SNPs”) would, if genotyped, generate both rare homs and rare hets in an unadmixed YRI or CHB subject included in a large sample of Caucasians. Indeed, we empirically confirmed the presence of excess rare homs and hets in a typical pair of unadmixed YRI and CHB subjects by including their HapMap genotypes with those of WTCCC sample set B to form a test dataset for which RHH evaluated all HapMap SNPs genotyped on the Affy500K chip (see “Unadmixed” YRI and CHB subject in Table 3). For both subjects, RHH p-values for homs and hets are highly significant (p<0.001), but consistent with a recurring pattern in Table 3 for HapMap-derived outliers of the same type, excess counts are much higher in the YRI-derived outlier (homs=426, hets=9167) than in the CHB (homs=27, hets=1378).

Interspersed among subjects of WTCCC sample set B, Table 3 also shows RHH and PLINK results for admixed outliers of different types produced by different simulated matings between HapMap CEU and non-CEU (YRI or CHB) subjects or their simulated offspring (see SUPPLEMENTARY METHODS). These simulated outliers are named in Table 3 according to their parent's simulated mating (denoted by “×”) and we refer to matings involving HapMap populations (CEU, YRI, CHB) as if they were crosses between different mouse strains (for detailed terminology see Supplementary Material, Table S1 and www.informatics.jax.org/silverbook/ (19)). Inspection of Table 3 indicates several trends: Rare hom counts are near zero in F1 offspring from the two outcrosses (YRI×CEU, CHB×CEU) or in offspring from any subsequent CEU backcross [e.g. (YRI×CEU)×CEU×CEU]. This dramatic drop from the high hom counts observed in unadmixed YRI or CHB subjects is almost certainly due to CEU outcross offspring having only one non-CEU chromosome in each homologous chromosome pair, thus eliminating the possibility of being homozygous for nC alleles at nC SNPs. By contrast, rare het counts are very high in F1 offspring of both outcrosses (YRI×CEU, CHB×CEU) and, despite being steadily decreased by each successive CEU backcross, the statistical excess of rare hets persists in YRI-admixed offspring of the 4th CEU backcross and in CHB-admixes of the 3rd backcross (RHH p-values of 0.001 for rare hets “1 Mb apart”).

The final type of simulated outlier in Table 3 are the offspring of F1 hybrid intercrosses [(YRI×CEU)×(YRI×CEU) or (CHB×CEU)×(CHB×CEU)]. Though F1 hybrid parents lack rare homs, each carries nC alleles at many rare hets and hence Table 3 shows the reappearance of excess rare homs in F1 intercross offspring (RHH p<0.001 to 0.01), apparently because nC alleles are inherited from both parents at many of the same SNPs. Based on HapMap-derived outliers of various types, we therefore conclude that excess rare homs imply that the carrier is (a) an unadmixed member of an outlier population or (b) an admixed individual who has inherited ethnic outlier DNA from both father and mother. Outliers with excess rare hets but few or no rare homs may be individuals with admixture from only one parent or, alternatively, might have admixture from both parents which has been sufficiently diluted in prior generations that nC alleles are almost never inherited at the same SNP. A simplified overview and summary of conclusions from Table 3 is provided in Supplementary Material, Table S1.

Mosaicism is visually obvious for African admixture and can be made obvious for Asian admixture

Table 3 also denotes whether admixed chromosome mosaicism is observed in each subject and lists a figure where the subject's genomic distribution of rare hets can be viewed. The unadmixed YRI and CHB outliers as well as F1 hybrid offspring of each outcross (YRI×CEU, CHB×CEU) have very high numbers of rare hets which are approximately evenly distributed across the genome and hence do not exhibit a mosaic pattern. By contrast, mosaicism is visually obvious in offspring from YRI×CEU F1 hybrids that are (a) intercrossed to each other or (b) backcrossed to CEU for 1 to 4 generations (Supplementary Fig. S11, S13, S15, S17, S20). Though mosaicism is not evident in the counterpart offspring of CHB×CEU F1 hybrids, we discovered that it can be made visually obvious by augmenting the 500,000 SNPs on the Affy500K chip with ∼40,400 additional HapMap SNPs that are monomorphic in HapMap CEU subjects but have MAF above 0.1 in HapMap CHB. The visual enhancement of including the 40,400 HapMap SNPs is shown in each CHB picture where a short red dash next to a chromosome denotes a rare het position for a SNP on the Affy500K chip whereas a blue dash in the adjacent gray track denotes a rare het at one of the additional 40,400 SNPs (Supplementary Fig. S19, S21–S23). These figures demonstrate that, in principle, rare-het mosaicism can be clearly visualized in subjects whose admixed Caucasian ancestry is CHB-like as well as YRI-like.

Admixed chromosome mosaicism demonstrates non-Caucasian admixture in two HapMap CEU parents

The WTCCC previously used the PC-MDS method to identify 153 outliers of “non-Caucasian” ancestry by their failure to visually cluster with HapMap Caucasians (CEU) in principle component (PC) plots of genotype distances between subjects produced by multi-dimensional scaling (MDS) (12). We now illustrate a similar method in which only a fraction of the genome is evaluated by PC-MDS to demonstrate non-Caucasian admixture in two HapMap CEU parents who each carry a single large rare-het segment visualized by RHH analysis as shown in Supplementary Figures S24 and S25 (NA11993: chrm. 6 from 65443059 to 94743101 Mb; NA12872: chrm. 3 from 172300870 to 191048899 Mb). Using MDS of pairwise IBS genotype distances provided by PLINK (13), we plotted the first two principle components of distance for all HapMap subjects (CEU, YRI, CHB/JPT) by including only genotypes from the rare-het segment observed in NA11993 or, for a separate analysis, only from the segment in NA12872. For the specific analysis corresponding to its rare-het segment, NA11993 and NA12872 were observed halfway between the CEU and YRI clusters (Supplementary Material, Fig. S26) whereas all other HapMap subjects tightly clustered within their own ethnic group. By contrast, when PC-MDS analysis was performed for all other genomic windows of the same size, NA11993 and NA12872 clustered within the CEU ethnic group, implying that none of the other genomic windows contained appreciable non-Caucasian DNA in NA11993 or NA12872. Taken together, these results are strong evidence that the single, large rare-het segment in each CEU parent is of probable African origin and illustrates a type of PC-MDS analysis that could be routinely performed on individual rare-het segments. It should be noted that NA11993 and NA12872 fell halfway between the CEU and YRI clusters in the PC-MDS analysis of their rare-het segments because the YRI-like DNA in each rare-het segment is carried on only one of the two homologous chromosomes.

RHH visualization compared to SABER and extended to the Illumina 550K array

To further characterize the applicability of RHH for visualizing the mosaicism of admixed chromosomes, we now briefly discuss: (a) comparing RHH with SABER, an alternate visualization method (20), and (b) RHH visualization based on the Illumina 550K array (abbreviated “Illm550K”). Visualizations from RHH based on Illm550K genotypes and from SABER using either the Affy500K or Illm550K chip are shown in Supplementary Figures S27–S29 for individual subjects whose mosaicism is also shown for RHH-Affy500K in Figures 1B, 2B, and 2D, respectively. Although minor differences exist for some tiny regions of admixture (see SUPPLEMENTARY DISCUSSION), the main conclusion from comparing these visualizations is that SABER and RHH based on either the Affy500K or Illm550K array show an almost identical pattern of genome mosaicism for each subject. In executing SABER and RHH software, we found that RHH analysis of 1500 58BC subjects required ∼1 hour on a 2.4 GHz UNIX processor with 8 GB of RAM or ∼110 minutes on a 1.4 GHz Windows laptop with 512 Mb of RAM (in order to produce RHH counts as in Table 1 and 1500 RHH genome visualizations as in Figs 1 and 2). By contrast, a SABER run required at least 20 minutes on the UNIX processor to analyze a single subject (by comparing to known ethnicities of 60 CEU and 60 YRI HapMap parents) and hence SABER analysis of 1500 subjects would require ∼21 days for one UNIX processor or more than 100 parallel UNIX processors to achieve the same speed as RHH.

Mathematical Model of RHH performance

The RHH method was derived from a series of empirical observations rather than from an a priori statistical or population genetic model and thus we have not presented a population genetic model from which the method was inferred. However in this section we provide a mathematical model which explores the method's performance under variation in key parameters; but we also emphasize that the RHH method is not based on or circumscribed by the presented model or its assumptions. Like the field of GWA scans which grew out of empirical observation (i.e. that association tests possess greater power than linkage tests [e.g. see Table 7 in (21)]) followed by subsequent mathematical modeling that provided important additional insight (22), it may be that further modeling of the empirical results of the RHH approach will also prove valuable.

Results from the model we present are summarized in Supplementary Figures S30–S33 and Supplementary Tables S2–S5 which examine RHH detection of ethnic outliers as a function of several key parameters including: (a) percentage of the outlier's genome which is admixed, (b) continental origin (African or Asian) of the admixed non-Caucasian DNA, (c) genotype frequency cutpoint (C_het) chosen to define rare hets and (d) GWA genotyping array (Affy500K or Illm550K). Since most WTCCC ethnic outliers exhibited excessive rare hets but very few rare homs, our mathematical model assumes a hypothetical data set in which all outliers have inherited non-Caucasian DNA from only one parent, and thus admixed outliers would carry excess rare hets but few rare homs (see Table 3 and related discussion above). Under the further assumption that all admixture derives from a single non-Caucasian population, the expected genotype frequency (F_het) of heterozygotes at any SNP is shown in METHODS to be:

1

where Y is the proportion of dataset subjects which are admixed at the SNP's genomic position, p is the MAF of the SNP in the Caucasian population, and q is the frequency of the same allele in the non-Caucasian outlier population.

As explained in METHODS, eqn. (1) enables adjudication of whether each GWA SNP qualifies as a rare-het SNP (because F_het≤C_het based on substituting HapMap and 58BC allele frequencies into eqn. (1) for q and p). Counts contributed by each rare-het SNP can then be calculated as well as total counts expected in an individual with a specific percentage of genome admixture. To accurately model our data, we assumed a hypothetical sample size of 1500 subjects and used RHH (see METHODS) to estimate the mean value of Y for each WTCCC data set which we found to vary from Y×100=0.11% and 0.16% (Hypertension cases and 58BBC controls) to Y×100=0.67% (Crohn's cases). Thus, a series of curves corresponding to Y values of 0.1%–1.0% summarize the performance of RHH under various parameter combinations of the mathematical model as shown in Supplementary Figures S30–S33 and Supplementary Tables S2–S5.

Each figure and table corresponds to one combination of commercial SNP array (Affy500K or Illm550K) with outlier ethnicity (African or Asian) and is based on “1 Mb apart” RHH results like those in Tables 1 and 3 in which rare-het counts are “thinned” for each subject so that the SNPs contributing counts to that subject are at least 1 Mb apart and unlikely to be in LD. Figures show the smallest percent of genome admixture detectable in an outlier for different values of Y and C_het while each table shows total rare-het counts at selected Y-C_het combinations.

Several patterns emerge from examining these figures and tables: (1) The Affy500K and Illm550K arrays perform similarly at each parameter combination, but when the admixture is African, the Affy chip detects slightly lower percentages of genome admixture. (2) For both arrays, African DNA generates ∼2 to 5 times more rare-het counts than Asian DNA at the same parameter combination, and thus RHH can detect much lower amounts of African admixture (∼1%–3% of genome) than minimum detectable Asian admixture (∼4%–7% of genome). (3) Higher mean Y-values (i.e. data sets with a higher proportion of subjects with admixture at each genome position) steadily decrease RHH sensitivity as shown by higher minimum detectable genome admixture; for example, when Y=0.1%, minimum detectable African admixture is ∼1% of the genome, but this increases to ∼3% when Y=1.0% (see Supplementary Material, Figs S30 and S32). (4) In each figure, the curves for Y≤0.3% are relatively flat and show detection of the smallest admixture percents over a wide range of rare-het frequency cutpoints (C_het=0.1%–1.0%); but as Y increases above 0.3%, the curves are progressively more “U-shaped” with the smallest admixture consistently detected for C_het=0.45%–1.0%. This supports our observationally derived use of C_het=0.5% as a generally applicable rare-het frequency cutpoint for statistical detection of ethnic outliers. Furthermore, Supplementary Figures S34 and S35 also provide complementary evidence that C_het=0.5% provides near-optimal visualization of mosaicism in admixed chromosomes by illustrating the type of less optimal visualization that occurs at C_het values above and below 0.5%.

In concluding this section, we point the reader to the SUPPLEMENTARY DISCUSSION for detailed treatment of additional important results related to the mathematical model including: (1) We show that RHH can perform very effectively using small datasets of only 50-200 subjects (see also Supplementary Figs S36–S39). (2) We discuss mathematical model results for unthinned rare-het counts (see Supplementary Figs S40–S43) and show that 1 Mb-thinning of counts does not substantially increase the minimum admixture detectable by RHH. (3) We discuss applying RHH to a single “test” subject added to a large panel of unadmixed individuals and show that this strategy enhances RHH sensitivity, enabling detection of African admixture covering as little as 0.25% of the genome (or approximately 7 Mb). (4) We explore the important question of how much disease association statistics (i.e. p-values) are altered by failure to exclude cases or controls with modest admixture detected by RHH but not by less sensitive outlier methods like PC-MDS or PLINK nearest neighbor Z-score.

Conclusion

We have shown that RHH can survey 1500–2000 GWA subjects in 1–2 hours on a single PC or UNIX processor to visualize genome mosaicism in admixed Caucasians and statistically detect small amounts of genome admixture (∼1%–3% African, ∼4%–7% Asian). RHH is convenient to execute (e.g. in not requiring phased chromosomes or allele frequencies from ethnic panels) and RHH numerical and visual output is also easily understood by the non-specialist since it is transparent (i.e. counts and chromosomal locations of rare genotypes whose highest dataset frequencies are user-specified). In Table 3, we illustrated targeted RHH analysis of 14 simulated ethnic outliers merged with the 58BC dataset, and our mathematical model also showed enhanced RHH sensitivity in detecting and visualizing small percentages of genome admixture when one or a few targeted subjects are added to a large, unadmixed reference panel (see SUPPLEMENTARY DISCUSSION).

Thus, in addition to scanning GWA or other large datasets, targeted RHH analysis could be applied to preselected subjects for a variety purposes. For example, when accurate results depend on the ethnicity of analyzed DNA such as in studies of gene expression (11) or sequencing projects aimed at discovering rare alleles (23), RHH could identify subjects with undetected segments of admixture and thereby avoid confounded or false-positive results. RHH visualization of the number and chromosomal lengths of outlier DNA segments in a population sample could also be used to estimate population genetic parameters like migration rate or time (generations) since an original admixture event (24). Furthermore, RHH mosaic visualizations might also complement or enhance admixture mapping studies of disease (25,26) and forensic analyses (27,28).

In conclusion, we expect that RHH will provide an excellent, practical tool for screening small or large numbers of DNA samples to detect ethnic outliers and visualize the chromosomal locations of outlier DNA. The technique's simplicity and speed in revealing fine-structure mosaicism of admixed human chromosomes implies that the RHH method is likely to have diverse and important applications in humans and in other species.

MATERIALS AND METHODS

Samples

Our data were genotypes from 7 disease and 2 control sample sets, each of which totalled ∼1500–2000 subjects and were genotyped for GWA scans by the WTCCC (12). The vast majority of subjects in each sample set were self-reported as of European Caucasian ancestry (12). Results in the two control sample sets were similar to the disease sets and provide the primary data presented in the tables and figures. We refer to the control set from the UK Blood Service (UKBS) as “sample set A” and to controls from the 1958 British Birth Cohort (58BC) as “sample set B”.

Genotyping and Sample QC

We used genotypes from the Affymetrix GeneChip 500K array (Affy500K) available through the WTCCC (12) and its website. To show RHH performance and mosaic visualization with the Illumina HumanHap550 array (Illm550K), we also used Illm550K genotypes assayed by the Sanger Institute on the 58BC controls (sample set B). Further details on genotyping and sample QC can be found in SUPPLEMENTARY METHODS.

Tabulation of rare-het and rare-hom counts

Our method identifies ethnic outliers as subjects with a high total number of rare heterozygote and/or rare homozygote genotypes compared to other subjects in the same dataset. Rare-het counts included all heterozygous genotypes for any SNP that: (a) had zero counts for the rarer homozygote and (b) a heterozygote genotype frequency in the data set of 0.005 or below. The cutpoint or “C_het” of 0.5% specifying the highest allowable frequency of rare-hets was settled upon through empirical observation and is supported by Supplementary Figures S30–S35 (see DISCUSSION and SUPPLEMENTARY METHODS for more details).

In initially conceiving and applying the method, rarer homozygote genotypes of a SNP were included among the “rare hom” counts only if no subjects in the dataset were heterozygous at that SNP (i.e. the SNP had zero heterozygote counts and non-zero but typically very few counts for the rarer homozygote). However, for analyses described here, we relaxed the initial criterion so that rare-hom counts were included for any SNP if: (a) the genotype frequency of its rarer homozygote exceeded the genotype frequency of its heterozygote, and (b) the heterozygote genotype frequency in the dataset was 0.002 or lower. If two SNPs are in LD, rare-het or rare-hom counts may not be independent. Therefore, to better assess statistical significance, we tabulated rare-het and –hom counts which were individually “thinned” for each subject to include only counts from SNPs at least “1 Mb apart” as well as tabulating unthinned counts from “All SNPs”. SUPPLEMENTARY METHODS gives more details explaining: (a) genotype frequency cutpoints chosen to define rare hets and rare homs, and (b) the rationale for “thinning” rare-het or rare-hom counts. RHH software is flexible in allowing users to specify other rare-het and -hom frequency definitions as well as a thinning distance other than 1 Mb.

Mathematical Model of RHH Performance

Hypothetical dataset and proportion of genome admixture in individual subjects (F_i) and in the entire dataset (Y)

RHH performance was modeled in a hypothetical dataset of 1500 unrelated subjects conceived as consisting mainly of unadmixed Caucasians assumed to derive from the same random mating population. All ethnic outlier subjects were assumed to have one unadmixed Caucasian parent and one parent with non-Caucasian ancestry from the same outlier population (in Asia or Africa). Thus, at any genomic base-pair position, an ethnic outlier could carry non-Caucasian DNA on only one of the two homologous chromosomes and this “single-stranded” non-Caucasian DNA would cover a specific fraction (F_i) of the ith subject's genome. F_i is also the probability that a random SNP falls in the admixed portion of the ith subject's genome, and if Y is the fraction of dataset subjects who carry non-Caucasian DNA at the SNP's genomic position then the expected value of Y would equal the mean F_i of all 1500 subjects 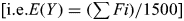. Note that in this calculation, F_i would be 0 in unadmixed Caucasians and would equal 1 in outliers with an unadmixed African or Asian parent, and also note that when 0<F_i<1, the pattern of mosaicism in different subjects is assumed to be independent as would usually be true in unrelated individuals. For modeling purposes, we estimated E(Y) for each WTCCC data set by estimating each subject's F_i value (based on clustering of rare hets) and found E(Y) varied from lows of Y×100=0.11% and 0.16% (in Hypertension cases and 58BBC controls) to highs of Y×100=0.52% and 0.67% (in Arthritis and Crohn's cases). Thus Supplementary Figures S30–S33 and Tables S2–S5 show values of Y that vary from Y×100=0.1%–1.0%.

Derivation of eqn. (1) for expected SNP heterozygote frequency (F_het) in the dataset

Equation (1) in the DISCUSSION shows any SNP's heterozygote genotype frequency (F_het) expected in the hypothetical dataset. To derive eqn. (1), let the minor allele of the SNP have frequency p in Caucasians, and let q be the frequency of the same allele in the non-Caucasian outlier population. In the fraction Y of subjects with non-Caucasian DNA at the genomic location of the SNP, note that heterozygotes could be formed in two ways: the Caucasian minor allele is randomly inherited with probability p from the Caucasian population and the Caucasian major allele is randomly inherited with probability (1 − q) from the non-Caucasian population yielding a heterozygote genotype probability of p(1 − q); or alternatively, the two alleles are inherited from the opposite populations yielding a heterozygote probability of q(1 − p). Adding these two probabilities [i.e. p(1 − q) + q(1 − p)] gives the conditional probability of a heterozygote within the Y fraction of dataset subjects; and within the (1 − Y) subjects who are unadmixed Caucasian at the SNP's genomic location, the conditional heterozygote probability would simply be the Hardy-Weinberg proportion 2p(1 − p). Weighting each conditional probability by Y or (1 − Y) gives eqn. (1) for the expected frequency of heterozygotes (F_het) at the SNP:

1

RHH performance for the Affymetrix500K and Illumina550K SNP arrays

Given specific values of Y, p and q, eqn. (1) can determine if a SNP's F_het value falls at or below the rare-het frequency cutpoint (C_het) which qualifies the SNP to contribute rare-het counts to individual subjects and the entire dataset. By thus identifying rare-het SNPs among the larger pool on a commercial SNP array, RHH performance can be modeled under various combinations of Y, C_het, outlier ethnicity and Affymetrix or Illumina array since each of these parameters determines the SNP subset which qualifies as rare-het SNPs. For more details, see Hodges and Lehmann (29), and the expanded version of this section in SUPPLEMENTARY METHODS which describes the empirically derived allele frequencies and calculations used to model RHH performance as presented in Supplementary Figures S30–S33 and S40–S43 and Supplementary Tables S2–S9.

RHH Software

Downloadable at: http://sourceforge.net/projects/rhh/ or http://www.sanger.ac.uk/resources/software/rhh/ Email enquiries: rhh.software@gmail.com