Backside Calibration Potentiometry: Ion Activity Measurements with Selective Supported Liquid Membranes by Calibrating from the Inner Side of the Membrane

Abstract

In direct potentiometry, the magnitude of the measured potentials is used to determine the composition of the sample. While this places rather formidable demands on the required reproducibility of the associated potential measurements, typically on the order of microvolts, in vitro clinical analyses of blood samples are today successfully performed with direct potentiometry using ion-selective electrodes (ISEs). Unfortunately, most other analytical situations do not permit the sensor to be recalibrated every few minutes, as in environmental monitoring or in vivo measurements, and direct potentiometry is often bound to fail as an accurate method in these circumstances. This paper introduces a novel direction for potentiometric sensing, termed backside calibration potentiometry. Chemical asymmetries across thin supported liquid ISE membranes are assessed by determining the direction of potential drift upon changing the stirring rate on either side of the membrane. Disappearance of this drift indicates the disappearance of concentration gradients across the membrane and is used to determine the sample composition if the solution composition at the backside of the membrane and the interfering ion concentration in the sample are known. For practical determinations, the concentration of either the primary or the interfering ion is varied in the reference solution until the stirring effect disappears. The procedure is demonstrated with a Ca²⁺-selective membrane using Ba²⁺ as the dominant interfering ion. Another example includes the determination of Pb²⁺ in environmental samples where the pH is adjusted to a known level. At pH 4.0, H⁺ turns out to be the dominant interfering ion. The practical applicability of the method is shown with different environmental water samples, for which the results obtained with the novel method are compared with those got by traditional calibration using standard additions. The limitations of the novel method in terms of accuracy and applicable concentration ranges are discussed.

The response of conventional polymeric membrane-based ion-selective electrodes (ISEs)^1–3 is usually dominated by the phase-boundary potential at the membrane/sample interface.^4,5 Other potential contributions, including that at the interface between membrane and inner solution are typically kept constant or their changes are minimized as much as possible. The membrane potential is also dominated by the phase-boundary potentials when ion fluxes through the membrane lead to significant deviations from the Nernstian response because considerable differences between the concentrations in the sample bulk and at the membrane surface arise.⁶ The recent success of potentiometric trace analysis relies on the control of such ion fluxes.^7,8

Occasionally, significant changes in the inner phase-boundary potential also occur when the composition of the membrane in contact with the inner solution is significantly altered during the measurement. This is the case, e.g., if the membrane is put in contact, first, with a discriminated interfering ion and, only later, with the preferred primary ion.⁹ If the volume of the internal solution is very small, as a water film between the sensing membrane and the inner metal electrode, its composition can alter when the sample is changed.¹⁰ Also, such effects have been successfully accounted for by variations in the inner phase-boundary potential.¹⁰ Due to the slow diffusion through conventional PVC-based membranes, such changes on the inner membrane side are always slow, typically within a time frame of hours.^9,10

Recently, the response of thin (ca. 25 μm) supported liquid membranes has been investigated.¹¹ It was shown that steady-state concentration profiles reproducibly build up across such membranes within ca. 1 min after a change in the contacting solutions. At primary ion concentrations below ca. 10⁻⁵ M, a change in the solution on one side of the ISE membrane brings about significant emf changes at both phase boundaries of the membrane. The steady-state emf response of such membranes in stirred or unstirred solutions has been successfully described as the sum of the two phase-boundary potentials taking into account ion fluxes in the three diffusion phases, i.e., in the membrane and in both contacting aqueous layers.¹¹

Because the change in the phase-boundary potential on the back side of the ISE membrane depends on the composition of the solutions on both sides, the above-mentioned thin supported liquid membranes allow, in principle, to determine the composition of an unknown sample on one side by varying the concentrations of the primary and interfering ions in the reference solution on the other side of the membrane. In this work, we further evaluate this system and show that quantitative determinations using this backside calibration are indeed possible.

Except for primary analytical methods, such as for example coulometry and gravimetry where the signal intensity is proportional to the amount of analyte, quantitative analysis always requires calibration, which means that the sample must be altered. This might be problematic in case of process control, continuous environmental monitoring, or in vivo measurements. For such applications, the backside calibration introduced here may be useful.

THEORY

The effect of stirring, i.e., a substantial change in the membrane potential as a function of a symmetrical change in the stirring speed on both sides of the ISE membrane, is used here on thin supported membranes to determine ion activities in the sample solution. The membrane internal composition is brought into symmetry by altering the composition of the inner solution. The disappearance of the stirring effect indicates that symmetry is achieved. The ion activity of the sample solution can then be calculated if the activity of the interfering ion in the sample and the composition of the calibration solution are known.

This theoretical section outlines the general limits and possibilities of the approach and calculates expected relationships between interfering and primary ion activities to yield symmetrical membrane compositions.

Neglecting membrane internal diffusion potentials, the membrane potential, E_M, is written as a function of the two phase-boundary potentials of the membrane to give:^1,5

$$E_M=\frac{RT}{zF}ln\frac{c_{if}}{{[{IL}_n^{z+}]}_f}\frac{{[{IL}_n^{z+}]}_b}{c_{ib}}$$ (1)

where c_if and c_ib are the boundary concentrations (strictly, activities) of the primary ion I^z+ in the aqueous phases at the front (f) and back (b) sides of the membrane, respectively (see Figure 1). The two membrane phase-boundary concentrations of the primary ion complex are denoted by square brackets. Equation 1 assumes that the concentration of the primary ion complex is proportional to that of the uncomplexed ion,¹² which is normally valid when the complex formation constants are sufficiently high¹³ and an excess ionophore is present in the membrane. As previously described,¹² the primary ion concentration at the organic phase boundary is a function of the primary and interfering ion concentrations on the aqueous side of the interface. For solutions containing only one type of interfering ion with the same charge, z, as the primary ion, and for membranes containing an excess of ionophore, this relationship is written as:¹²

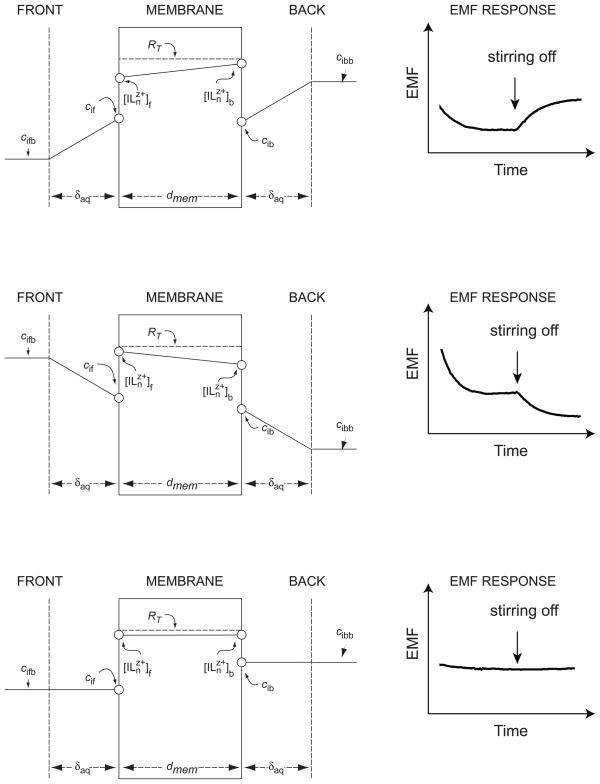
Figure 1.

Schematic representation of the system under study. Top and center: The concentration of the primary ion, c_i, in the aqueous phases is polarized at both sides of the membrane (c_ifb ≠ c_if and c_ibb ≠ c_ib), whereas that of the complex, [IL_n^z+], is polarized in the membrane phase. Right panels: The stirring effect on the emf response depends on the sign of the concentration gradient. Symmetrical situation in the membrane causes the stirring effect to disappear. Note that, if the interfering ions (not shown) have different concentrations, the concentration of the primary ion does not need to be the same in the aqueous solutions on both sides of the membrane in order to eliminate the concentration gradient in the membrane.

$$\frac{c_i}{[{IL}_n^{z+}]}=\frac{z}{R_T}(c_i+K_{ij}^{\mathit{pot}}{c}_j)$$ (2)

where $K_{ij}^{\mathit{pot}}$ is the potentiometric selectivity coefficient and R_T, the concentration of the lipophilic ion-exchanger in the membrane.

From eq 2 follows that the primary ion concentration at the organic phase boundary is a function of the concentration ratio of primary and interfering ion at the aqueous phase boundary:

$$[{IL}_n^{z+}]=\frac{R_T}{z}{\left\{1+K_{ij}^{\mathit{pot}}\frac{c_j}{c_i}\right\}}^{-1}$$ (3)

A change in the stirring rate in both contacting solutions has a direct bearing on the aqueous diffusion layer thickness, δ_aq, which here is assumed to be equal in both solutions because of symmetrical stirring conditions. The supported liquid membrane studied here assume steady-state concentration profiles establishing in a short time.¹¹ The steady-state concentrations in the membrane are related to the concentration profile in the aqueous Nernst diffusion layer as follows:

$$q=\frac{{\delta }_{aq}{D}_{\mathit{mem}}}{{\delta }_{\mathit{mem}}{D}_{aq}}=\frac{c_{if}-c_{\mathit{ifb}}}{{[{IL}_n^{z+}]}_b-{[{IL}_n^{z+}]}_f}=\frac{c_{ib}-c_{\mathit{ibb}}}{{[{IL}_n^{z+}]}_f-{[{IL}_n^{z+}]}_b}$$ (4)

where c_ifb and c_ibb are the bulk concentrations of I^z+ in the solution at the front and back of the membrane, respectively (cf. Figure 1). In contrast to traditional membrane electrodes, where the composition of the inner solution is kept as independent of the sample as possible, conditions are chosen here such that the primary ion concentration at the inner membrane side is similar to that on the outer side. From eq 4 follows that the primary ion concentration gradients at either side of the membrane must be equal:

$$c_{if}-c_{\mathit{ifb}}=c_{\mathit{ibb}}-c_{ib}$$ (5)

Under asymmetrical conditions, the transmembrane concentration gradient leads to a change in the concentration polarization on the aqueous side upon changing the stirring speed in the sample (eq 4). The change in c_if and c_ib is nonsymmetrical and causes the membrane potential to change. This stirring effect disappears when the transmembrane concentration gradient is zero ( ${[{IL}_n^{z+}]}_b={[{IL}_n^{z+}]}_f$). According to eq 3, this condition is achieved when:

$$\frac{c_{if}}{c_{ib}}=\frac{c_{jf}}{c_{jb}}$$ (6)

Under this condition, concentration gradients in the aqueous diffusion layer also disappear and the primary ion concentrations at the interfaces assume their bulk solution values.

For a monovalent primary ion, I⁺, and a dominating divalent interfering ion, J²⁺, eq 3 can be rewritten as:^12,14,15

$$[{IL}_n^{z+}]=R_T{\left\{\frac{1}{2}+\sqrt{\frac{1}{4}+{(K_{ij}^{\mathit{pot}})}^2\frac{c_j}{c_i^2}}\right\}}^{-1}$$ (7)

Similarly, for a divalent primary ion, I²⁺, and a dominating monovalent interfering ion, J⁺, eq 3 can be rewritten as:^12,14,15

$$[{IL}_n^{z+}]=\frac{R_T}{2}{\left\{\frac{1}{2}\sqrt{K_{ij}^{\mathit{pot}}\frac{c_j^2}{c_i}}+\sqrt{\frac{1}{4}{K}_{ij}^{\mathit{pot}}\frac{c_j^2}{c_i}+1}\right\}}^{-2}$$ (8)

From eqs 7 and 8, we may formulate the following generalized relationship with z_i and z_j as the charges of the corresponding ions:

$$\frac{c_{if}}{c_{ib}}={\left(\frac{c_{jf}}{c_{jb}}\right)}^{z_i/z_j}$$ (9)

Obviously, therefore, the established thermodynamic rule that single-ion activities cannot be independently determined without some extrathermodynamic assumptions, still holds. Primary ion activities can be obtained by assuming that the interfering ion activity is known or equal on both sides of the membrane. If this is not possible, additional experiments are required to determine the magnitude of the membrane potential (with the associated assumptions about the potential at the reference electrode).

EXPERIMENTAL SECTION

Reagents

Celgard 2500 microporous flat sheet polypropylene membranes of 0.057 × 0.22 μm² pore size, 25 μm thickness, and 55% porosity were purchased from Celgard Inc. (Charlotte, NC). High-molecular-weight poly(vinyl chloride) (PVC), the Pb²⁺ ionophore 4-tert-butylcalix[4]arenetetrakis(thioacetic acid dimethylamide) (lead ionophore IV), the lipophilic salt tetradodecylammonium tetrakis(4-chlorophenyl)borate (ETH 500), sodium tetrakis[3,5-bis (trifluoromethyl)phenyl]borate (NaTFPB), bis(2-ethylhexyl) sebacate (DOS), and tetrahydrofuran (THF) were Selectophore from Fluka AG (CH-8071 Buchs, Switzerland). Aqueous solutions were prepared with deionized water (specific resistance, >18 MΩ cm) from a NANOpure reagent-grade water system (Barnstead, CH-4009 Basel, Switzerland). HNO₃, NaOH, Ca(NO₃)₂, CaCl₂, MgCl₂, KCl, and NaCl were Suprapure from Merck (Darmstadt, Germany). Nitrilotriacetic acid (NTA) of Microselect purity and the aqueous Pb²⁺ standard solution (1.000 g Pb(NO₃)₂/L in 10⁻³ M HNO₃) were obtained from Fluka.

Membranes and Electrodes

The Pb²⁺-selective Celgard-based membranes contained the lead ionophore IV (1.68 wt %, 15.96 mmol kg⁻¹), NaTFPB (0.44 wt %, 5.0 mmol kg⁻¹), and DOS (97.9 wt %). These components (totalling 145.22 mg) are dissolved in THF (1 mL). After stirring for 1 h, a Celgard membrane disk of 1.6 cm diameter was impregnated with this solution (3.8 μL) and the solvent was let to evaporate. The resulting membrane was immediately mounted in a plexiglass membrane holder and placed in a symmetrical Teflon cell allowing an exposed area of 0.79 cm² and with compartments of 20 mL on either side. Before starting the measurements, the membrane was symmetrically conditioned in the solution as indicated.

The Pb²⁺-selective PVC-based membranes contained the lead ionophore IV (0.07 wt %, 0.67 mmol kg⁻¹), Na-TFPB (0.03 wt %, 0.32 mmol kg⁻¹), ETH 500 (1.31 wt %, 22.13 mmol kg⁻¹), PVC (36.3 wt %), DOS (62.3 wt %), and Pb(NO₃)₂ (0.15 mmol kg⁻¹). The membrane was prepared by dissolving these components (416.89 mg, except Pb(NO₃)₂) in THF (5 mL). Then, 10⁻³ M aqueous Pb(NO₃)₂ (62 μL) was slowly added and this membrane solution shaken for ca. 1 h. After casting it into a glass ring (4.6 cm i.d.) fixed on a glass plate, overnight evaporation of the solvent yielded a membrane of ca. 200 μm thickness.

A disk of 5 mm diameter was punched from the Pb²⁺-selective PVC-based membrane and glued to a plasticized PVC tubing with a THF/PVC slurry. The internal filling solution was 10⁻³ M NTA, 2.1 × 10⁻³ M NaOH, and 10⁻⁴ M Pb(NO3)₂, adjusted to pH 7.0 with 0.1 M NaOH. The calculated activity of the uncomplexed Pb²⁺ was 1.3 × 10⁻⁹ M.⁶ A diaphragm separated the internal filling solution from the reference half-cell (Ag/AgCl in 2 × 10⁻³ M NaCl). The conditioning solution was always 4.8 × 10⁻⁹ M Pb(NO₃)₂, 10⁻³ M CaCl₂, and 10⁻⁴ M HNO₃. The ISEs were conditioned for at least 24 h and used for not more than one week. Each measurement was done with six ISEs having the same membrane composition.

Emf Measurements

Measurements were performed with a 16-channel electrode monitor (Lawson Labs Inc., Malvern, PA) at ambient temperature (21–23 °C). Activity coefficients were obtained from the Debye-Hückel approximation, and emf values were corrected for liquid-junction potentials with the Henderson equation.

During measurements with Celgard-based membranes in the symmetrical Teflon cell, the solutions in both compartments were magnetically stirred or unstirred, as indicated. Calibration solutions that were changed on the front side of the membrane contained Pb(NO₃)₂ with an ion background typical of drinking water (5 × 10⁻⁴ M NaCl, 5 × 10⁻⁵ M KCl, 10⁻⁴ M HNO₃, 10⁻³ M CaCl₂, 5 × 10⁻⁴ M MgCl₂). The two reference electrodes were double-junction Ag/AgCl reference electrodes (No. 6.0729.100, one with 3 M KCl, the other with 1 M KCl as reference electrolyte, the bridge electrolyte being 1 M NH₄NO₃; Metrohm AG, CH-9101 Herisau, Switzerland).

The experiments with PVC-based membranes were performed at pH 4.0 in polyethylene beakers cleaned with 0.1 M HNO₃ overnight. The samples were collected in polyethylene bottles, and the pH values were adjusted to 4.0 immediately after sampling by adding the required amount of 1 M HNO₃ (1.50–2.35 mL to a 500-mL sample in the case of natural water). The specific measurements protocol was as follows:⁶ The ISEs were equilibrated in a 500-mL beaker containing the target sample and the potential was monitored until its drift was < 1 mV/10 min. Subsequently, the ISEs were immersed into the same sample (50 mL), but adding the above Pb²⁺ standard solution (80 μL), and the potential was acquired during 5 min. Four more Pb²⁺ additions were performed on the same sample (80, 150, 250, and 500 μL of standard solution), and the potential was recorded for 1 min each. The double-junction Ag/AgCl reference electrode (Metrohm No. 6.0729.100) had 3 M KCl as reference and 1 M NH₄NO₃ as bridge electrolyte.

RESULTS AND DISCUSSION

Backside calibration potentiometry, the novel method introduced here, allows one to obtain information on the composition of an unknown sample on one side of the ISE membrane by iteratively altering the composition of the calibration solution on the other side of the sensing membrane. For this method to work, concentration gradients of the analyte ion in the Nernst diffusion layer of both contacting aqueous solutions must be relevant when the two solutions are asymmetrical. Such gradients occur under dilute conditions in a defined concentration range, as described in recent work. [old reference ¹¹ Tompa] After every change, the emf of the cell is, first, measured when the solutions on both sides of the membrane are stirred and, again, after stirring is stopped. The symmetrical situation in the membrane is reached when stirring is shown to have no effect on the observed emf. This is the case when the concentration gradient of primary ions in the membrane disappears, but does not necessarily mean that the concentrations of primary and interfering ions in the solutions on either side of the membrane are equal. As shown by eq 9, the symmetrical situation can be achieved with an infinite number of compositions of the two solutions. However, when the concentration of the dominant interfering ion in the sample is known, the concentration of the primary ion can easily be calculated according to this equation.

With trace analyses of heavy metal ions in environmental samples the sample pH must often be controlled. At the rather low pH values required to avoid complex formation of the investigated metal ions, H⁺ is often the dominant interfering ion. This is the case, e.g., with a Pb²⁺-selective membrane used earlier for trace analyses of environmental samples.⁶ It was shown that at pH > ca. 4.0, carbonate formation significantly reduces the measured activity of free Pb²⁺.⁶ The extent of interference by various cations can be estimated from the Nicolsky equation as $K_{\text{Pbj}}^{\text{pot}}\times {c_{\text{j}}}^{{\text{z}}_{\text{i}}/{\text{z}}_{\text{j}}}$. The selectivity coefficients, log $K_{\text{Pbj}}^{\text{pot}}$, for the relevant interfering ions using PVC membranes,⁶ which are good approximations also with Celgard membranes,¹¹ are −3.5 (j: H⁺), −6.3 (Na⁺), and −12.3 (Ca²⁺). Thus, at pH 4.0 and the typical concentrations of the other ions in environmental samples,⁶ the log $K_{\text{Pbj}}^{\text{pot}}\times {c_{\text{j}}}^{{\text{z}}_{\text{i}}/{\text{z}}_{\text{j}}}$ values are −11.5 (j: H⁺), −13.2 (Na⁺), and −14.9 (Ca²⁺) so that H⁺ is, indeed, the dominant interfering ion.

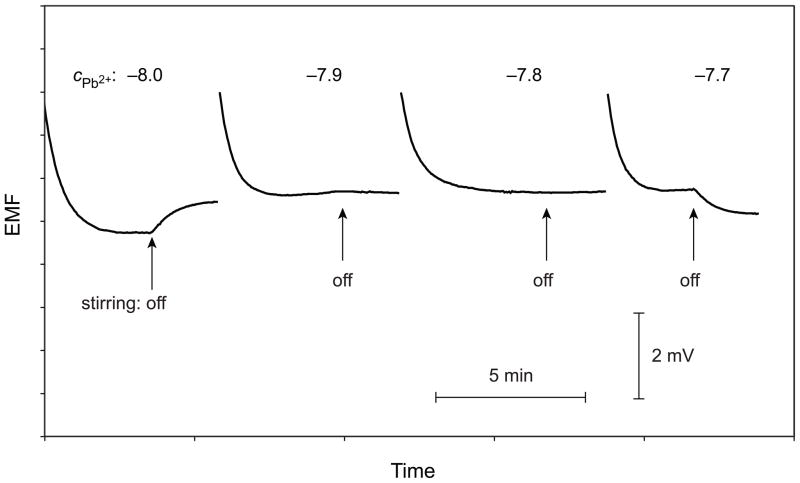
To demonstrate the feasibility of backside calibration, a series of environmental samples were analyzed by this procedure (cf. Table 1). For each sample, the Pb²⁺ activities were also determined using the traditional calibration with multiple standard addition, a method that has earlier proved to give results in good agreement with ICPMS.⁶ Time curves of the potential response are shown in Figure 2 for one example. Upon switching off the stirrers in both solutions, a positive drift is observed with 10⁻⁸ M Pb(NO₃)₂ of pH 4.0 in the calibration solution on the front side of the membrane. This concentration is lower than in the sample because a flux of Pb²⁺ toward the calibration solution occurs. A potential drift in the opposite direction is observed with 10^−7.7 M Pb(NO₃)₂, while no stirring effect is seen with 10^−7.8 and 10^−7.9 M Pb(NO₃)₂. The experiment shown in Figure 2 also indicates that the precision of backside calibration under the applied conditions is around ± 0.1 logarithmic activity units. The results obtained with both calibration methods are close to each other for all investigated samples shown in Table 1.

Table 1.

Determination of Pb²⁺ in environmental water samples

water source	backside calibration	standard addition
Budapest tap	(1.3–1.6) × 10−8 M	(2.00 ± 0.20) × 10−8 M
Warsaw tap	(1.3–1.6) × 10−8 M	(1.86 ± 0.04) × 10−8 M
Zurich tap	(1.6–2.0) × 10−8 M	(1.70 ± 0.08) × 10−8 M
Zurich, Sihl river	(3.2–4.0) × 10−9 M	(4.30 ± 0.50) × 10−9 M

Figure 2.

Time curves of the emf response for measuring Pb²⁺ activities at a constant level of the dominant interfering ion H⁺ (pH adjusted to 4.0) in a sample of Warsaw tap water. Labels show the logarithmic Pb²⁺ concentrations in the calibration solution on the front side of the Pb²⁺-selective Celgard membrane. Arrows mark the time instances when stirring was switched off.

The above example is rather straightforward because the activity of the dominant interfering ion was known. Backside calibration is not limited to such cases, however, some more experiments are required after finding the symmetrical situation if the concentration of the dominant interfering ion is unknown. The absence of ion fluxes only indicates that the transmembrane concentration gradient of primary ions is zero but not that the activities of the relevant ions are the same on either side of the membrane (eq 9). The latter condition is met if, in addition to the absence of stirring effects, the transmembrane potential is zero as well. Since, in practice, reference electrodes are never perfectly symmetrical first, the emf of the cell is measured under fully symmetrical conditions, e.g., by using the sample solution on both sides of the membrane. Then, the composition of the calibration solution is varied until the effect of stirring disappears. Finally, the concentrations of the primary and the dominant interfering ion are varied simultaneously until the point zero transmembrane difference is found.

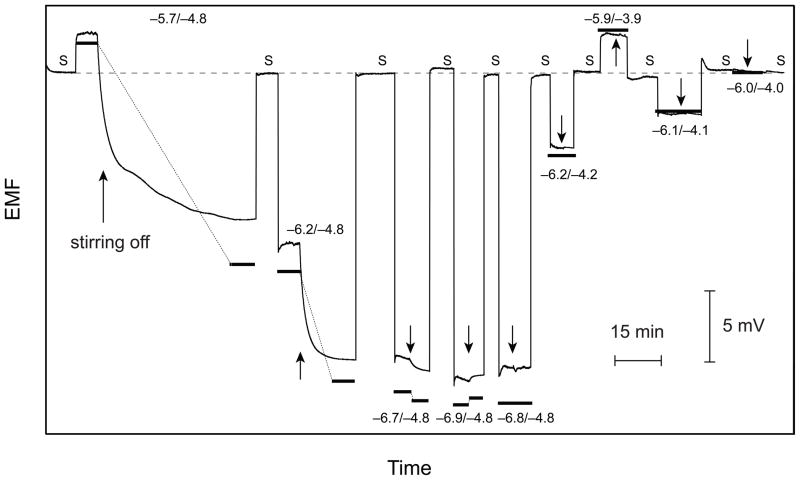
Experiments illustrating this strategy are shown in Figures 3 and 4 with a Ca²⁺-selective membrane and using Ba²⁺ as the dominant interfering ion, a system that was characterized previously.¹¹ For the experiments shown in Figure 3, first, the concentration of Ca²⁺ was varied at a constant background of 10^−4.8 M Ba²⁺. Between each replacement of the calibration solution, the emf was recorded for a short time in the symmetrical situation (S) by placing the “unknown” sample on both sides of the membrane. The negative potential drifts observed after the first three measurements (10^−5.7, 10^−6.2, and 10^−6.7 M Ca²⁺, cf. Figure 3) indicate that the Ca²⁺ concentration is higher in the calibration solution than in the sample on the back side of the membrane. On the other hand, the positive drift with 10^−6.9 M Ca²⁺ shows that this concentration is too low. Indeed, the effect of stirring disappears with 10^−6.8 M Ca²⁺, which proves that the symmetrical situation is found. In the subsequent experiments, the concentrations of both Ca²⁺ and Ba²⁺ are varied by keeping their ratio constant, until the transmembrane potential becomes equal to that observed for the symmetrical situation (S, cf. Figure 3). The bold lines in Figures 3 and 4 are the potential values calculated by eqs 1 and 11 of ref. 11 and the parameters used there. As in the previous study,¹¹ the calculated values are in good agreement with the observed ones.

Figure 3.

Time responses for a series of measurements with backside calibration using a Pb²⁺-selective Celgard membrane. Numbers designate the logarithmic concentrations of the primary (Ca²⁺) and interfering ions (Ba²⁺) in the calibration solution (front side), S denotes the symmetrical case (sample on both sides). For each concentration of the calibration solution, the stirrer was switched off after ca. 5 min (indicted by an arrow). First, the concentration of the primary ion was varied until the stirring effect disappeared (−6.8/−4.8) and then, the concentration of both ions was varied simultaneously until the symmetrical situation was reached (−6.0/−4.0). Bold lines connected with thin dotted lines for each concentration of the calibration solution represent calculated steady-state responses.¹¹

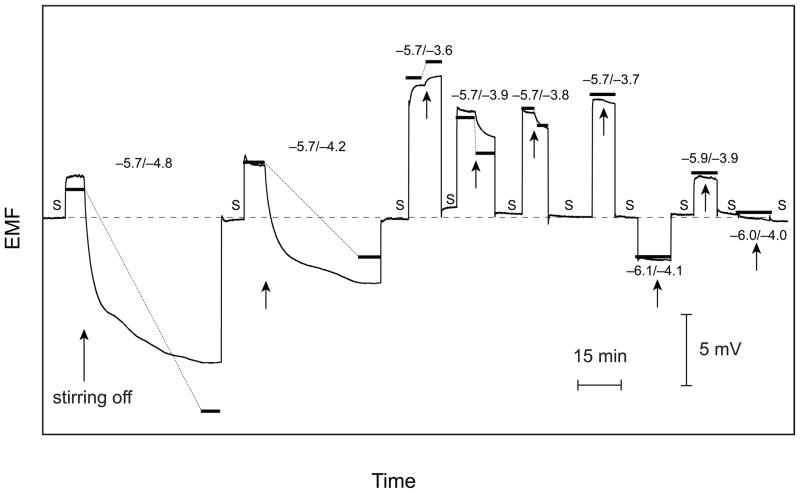
Figure 4.

Time responses for a series of measurements with backside calibration using a Pb²⁺-selective Celgard membrane. The numbers designate the logarithmic concentrations of the primary (Ca²⁺) and interfering ions (Ba²⁺) in the calibration solution (front side), S signifies the symmetrical case (sample on both sides). For each concentration of the calibration solution, the stirrer was switched off after ca. 5 min (indicted by an arrow). First, the concentration of the interfering ion was varied until the stirring effect disappeared (−5.7/−3.7) and then, the concentration of both ions was varied simultaneously until the symmetrical situation was reached (−6.0/−4.0). Bold lines connected with thin dotted lines for each concentration of the calibration solution represent calculated steady-state responses.¹¹

It is not relevant whether the symmetrical situation is found by varying the concentration of the primary or the interfering ion (or both). This is demonstrated by Figure 4 where, first, the concentration of the interfering ion was varied until the symmetrical situation is reached (10^−5.7 M Ca²⁺ and 10^−3.7 M Ba²⁺). Note that the sign of the drift upon stopping the stirrers is opposite to that given in Figure 3. A negative drift is caused by a lower concentration of the interfering ion, as explained in detail earlier.¹¹ As shown by Figure 4, also this strategy leads to the correct final result. The feasibility of both procedures was further confirmed by analyzing a series of solutions whose composition was not known to the experimenter.

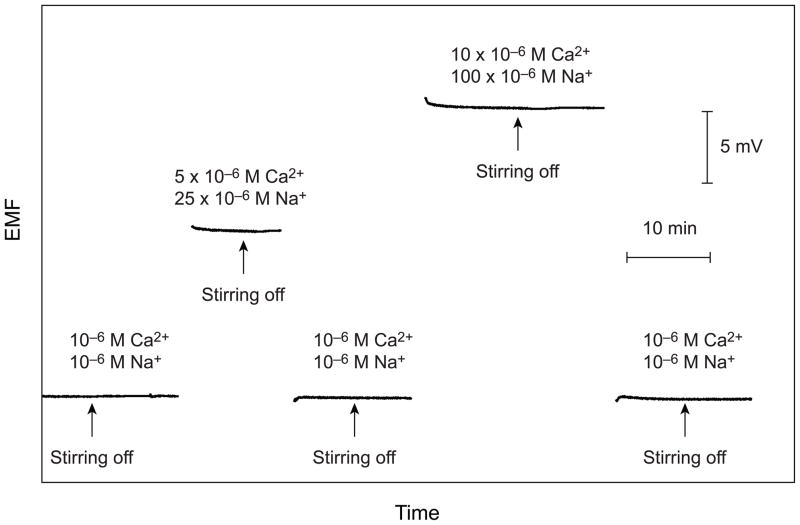
In the above experiments, after reaching the condition at which the effect of stirring disappears, the concentrations of Ca²⁺ and Ba²⁺ are varied by keeping their ratio constant. This relationship, expressed in eq 6, is based on eq 3, a direct consequence of the Nicolsky equation and is not valid if the charges of the primary and interfering ions are different.^14,15 If the primary ion is monovalent and the dominant interfering ion is divalent, eq 7 must be applied and in the reverse case, eq 8. Interestingly, the relationship of the concentrations of the two ions for equal exchange (eq 9) derived from eqs 7 and 8 is the same as from the Nicolsky equation. The validity of this result was experimentally confirmed using a Ca²⁺-selective membrane with Na⁺ as the interfering ion. As shown in Figure 5, there is no stirring effect in the case of the completely symmetrical situation (10⁻⁶ M Ca²⁺ with 10⁻⁶ M Na⁺ on both sides of the membrane) and when the factor of increase in the concentration of Na⁺ is equal to the square of the increase in Ca²⁺, i.e., when a_i/a_j² is constant.

Figure 5.

Emf time curves observed for the symmetrical situation and upon a 5-fold and 10-fold increase in the concentration of the primary ion (Ca²⁺) and a 25-fold and 100-fold increase in the concentration of the interfering ion (Na⁺). Between measurements, the Pb²⁺-selective Celgard membrane is symmetrically conditioned in the original solution (10⁻⁶ M for both cations). After ca. 5 min after each sample change, the stirrer is stopped.

The primary ion concentrations determined in this study were between 10⁻⁶ M (for Ca²⁺) and 10⁻⁸–10⁻⁹ M (for Pb²⁺). This seems to cover the typical concentration range in which backside calibration is applicable with the setup described here. At significantly higher concentrations, stirring effects will decline because the transmembrane ion fluxes are not pronounced enough to significantly alter the concentrations in the surface layers at the ISE membrane.¹¹ The lower the concentrations of the contacting solutions, the smaller are the ion fluxes required to generate a significant emf difference between stirred and unstirred solutions. This means that the level of interference, i.e., $K_{\text{Pbj}}^{\text{pot}}\times {c_{\text{j}}}^{{\text{z}}_{\text{i}}/{\text{z}}_{\text{j}}}$ must be much smaller than the concentration of the primary ion. The situation is analogous to direct potentiometry at trace levels where ion fluxes may bias the results.¹² In both cases, the level of interference must be reduced by about two orders of magnitude in order to improve the detection limit by one order of magnitude. For example, calculations based on eqs 1 and 4 indicate that for monovalent primary and interfering ions the optimal signal is observed if the primary ion concentration is 10^−5.8 M for $K_{\text{ij}}^{\text{pot}}\times c_{\text{j}}={10}^{-7}$, and 10^−8.8 M for $K_{\text{ij}}^{\text{pot}}\times c_{\text{j}}={10}^{-13}$. Even with today’s highly selective sensor membranes, the latter value can be achieved only with very low activities of the interfering ions.

The influence of stirring on the emf, i.e., the intensity of the signal change at the optimal level of interference is about half the value when using direct potentiometry. For example, for a concentration difference of 0.1 logarithmic units of a monovalent primary ion between the two sides of the ISE membrane, it amounts to 2.8 mV as compared with 5.9 mV obtained by direct potentiometry. The intensity of signal change rapidly decreases if the level of interference is not optimal (cf. Figure 5 in ref. 11) and is about half if the concentration of the primary ion deviates by ± 0.5 log units from the optimum value.

In view of a practical application of backside calibration, the above limitations of concentration range and sensitivity must be taken into account. If the concentration ranges are appropriate, this new technique may enlarge the field of practical applications of potentiometry. Furthermore, one may envision the use of controlled current coulometry [ref Vish: Selective Coulometric Release of Ions from Ion Selective Polymeric Membranes for Calibration-Free Titrations, V. Bhakthavatsalam, A. Shvarev, E. Bakker, Analyst, 131 (2006) 895–900] as a fully automated approach to alter the composition of the inner solution in order to make this an even more practical sensing approach.

CONCLUSIONS

We demonstrate that one can obtain relevant potentiometric information on the composition of a sample without the need of measuring absolute emf values and without having to replace the sample with calibration solutions. Instead, only the composition of the reference solution is varied. If the activity of the dominant interfering ion in the sample is known, it is sufficient to find a composition of a reference solution with which stirring has no effect on the emf. If this activity is not known, one must, additionally, find a composition at which the transmembrane potential difference is zero. The method is applicable in difficult cases in which calibration is not feasible in a simple manner (e.g., process control and in vivo measurements) and when the use of highly stable reference electrodes is not possible (e.g., continuous monitoring).