A comparison of blindpulling and blindwalking as measures of perceived absolute distance

Abstract

Blindwalking has become a common measure of perceived absolute distance and location, but it requires a relatively large testing space and cannot be used with people for whom walking is difficult or impossible. In the present article, we describe an alternative response type that is closely matched to blindwalking in several important respects but is less resource intensive. In the blindpulling technique, participants view a target, then close their eyes and pull a length of tape or rope between the hands to indicate the remembered target distance. As with blindwalking, this response requires integration of cyclical, bilateral limb movements over time. Blindpulling and blindwalking responses are tightly linked across a range of viewing conditions, and blindpulling is accurate when prior exposure to visually guided pulling is provided. Thus, blindpulling shows promise as a measure of perceived distance that may be used in nonambulatory populations and when the space available for testing is limited.

Absolute (or egocentric) distance is the distance from an observer to an object. Perceived absolute distance has been measured in a variety of ways, including verbal report, dart throwing, and ball tossing (e.g., Morrison & Whiteside, 1984; Pagano, Grutzmacher, & Jenkins, 2001; Sahm, Creem-Regehr, Thompson, & Willemsen, 2005; for reviews, see Da Silva, 1985; Loomis & Philbeck, 2008). A particularly common method of measuring the perceived distance or the location of targets is blindwalking, in which observers view a target for several seconds, then cover their eyes and attempt to walk without vision to the remembered target location (e.g., Allen, Kirasic, Rashotte, & Haun, 2004; Creem-Regehr, Willemsen, Gooch, & Thompson, 2005; Philbeck, Loomis, & Beall, 1997; Rieser, Ashmead, Talor, & Youngquist, 1990; Thomson, 1983; Wu, Ooi, & He, 2004; and a host of others). Performance in this task shows very little average systematic error for targets initially seen at distances of up to 20 m or more (Corlett, 1992; Rieser et al., 1990; see also Andre & Rogers, 2006). The good accuracy has been interpreted as evidence that the initial target position has been accurately localized and that the walking response is well calibrated with respect to the physical target location (Loomis, Da Silva, Philbeck, & Fukusima, 1996).¹

Blindwalking is subject to several practical limitations, however. First and foremost, it requires space. Outdoor environments can provide sufficient space, but they can introduce other logistical challenges (e.g., dealing with inclement weather). Indoor hallways can provide acceptable distances, but their narrowness can increase the risk that participants might bump into the walls. If blindwalking is used to measure space perception in virtual environments, there may be additional equipment-related constraints that limit the range of distances that may be studied. Also, walking responses are relatively time consuming and effortful—this can significantly reduce the amount of data that may be collected in one session when studying space perception in elderly or brain-injured participants (Allen et al., 2004; Philbeck, Behrmann, Levy, Potolicchio, & Caputy, 2004; Worsley et al., 2001). Many of these practical limitations may be avoided by asking participants to provide verbal reports of perceived distance. Verbal reports have been used as a perceived distance measure for many years (Da Silva, 1985), and they are tightly linked with blindwalking responses in many viewing conditions (Philbeck & Loomis, 1997).

Verbal reports may not be suitable in some research contexts, however. They require manipulation of numbers, and researchers may wish to avoid this in certain populations (e.g., children or aphasic patients). Researchers may prefer an action-based response, because controlling action is one of the primary functions of vision; responses involving body movement may engage the visual system in a way in which it is optimized to perform. If they are specifically interested in how body motions are sensed and integrated, researchers may also require some sort of action-based response. Finally, some research contexts may require a response that is closely matched to blindwalking along as many dimensions as possible. Blindwalking involves not only visually perceiving and remembering the initial target location, but also updating one's self-motion through the environment (Loomis et al., 1996). Each of these subcomponents may recruit distinct neural mechanisms. This means that, in order to interpret the patterns of impairment in brain-injured patients, one may wish to contrast conditions in which a participant moves (or imagines moving) through the environment when indicating a target location against conditions in which participants do not move through the environment. A response that is otherwise similar to blindwalking, but that does not entail movement through the environment, would be beneficial in this regard.

Here we describe a response type that shows promise for solving many of the practical limitations of blindwalking, although being closely matched to it in other respects. The response, blindpulling, involves pulling a length of tape or rope between the hands to match a previously seen target distance. Because the participant does not locomote into the testing environment, many of the space limitations mentioned above are reduced dramatically. The time required to execute a blindpulling response is similar to that required for blindwalking, meaning that the retention interval for remembering the target location is approximately matched between the two responses. However, the blindpulling response is somewhat faster in practice, because there is no need to return the participant to the starting location. Because blindpulling is less effortful than blindwalking is, it therefore may be better tolerated in elderly and medical patient populations. Both blindpulling and blindwalking involve active control of cyclical body movements and integration of movements between functionally paired limbs. Several studies have used tape pulling or rope pulling, but these have involved either passively feeling a rope pass through the hands with little or no arm motion (Epstein, 1965; Mershon, Kennedy, & Falacara, 1977) or pulling out a retractable tape measure with one hand under visual control (Hagen & Teghtsoonian, 1981). These methods can yield good performance under optimal viewing conditions and may be perfectly acceptable in their own right. However, they are less well matched to blindwalking in terms of the motor-control requirements and the information available for perceiving and integrating motion of the rope or tape.

How well calibrated is blindpulling with respect to the physical absolute distances of nearby objects, and what factors affect this calibration? To what extent does blindpulling behave similarly to the well-studied blindwalking response? Is blindpulling responsive to perceived absolute distance? The goal of this article is to explore these issues, thereby assessing the potential applicability of this response as an alternative to blindwalking when walking is disadvantageous but an action-based response is nevertheless preferred. Experiment 1 investigated the effects of pulling at different speeds and of pulling different amounts of tape in each draw on blindpulling accuracy. Experiment 2 examined the importance of providing exposure to visually guided pulling before engaging in blindpulling. Experiments 3 and 4 directly compared blindpulling with blindwalking in a variety of viewing conditions. Taken together, these experiments establish several methodological features that are crucial for maximizing performance in blindpulling tasks and suggest that blindpulling is indeed a viable measure of perceived distance.

EXPERIMENT 1

In Experiment 1, we investigated the possible dependence of the overall amount of tape pulled for a given target on pulling speed and on draw length. We define a draw as a single arm motion to pull the tape toward the body. We imposed three categorical levels of pulling speed (slow, medium, and fast) and three categorical levels of draw length (short, medium, and long). We made no attempt to ensure that all participants used the same pulling speed or draw length within each of these levels; boundary conditions for both variables were modeled for participants, but otherwise, participants were allowed to choose their actual pulling speed and draw length within each level according to their own standards (see Mittelstaedt & Mittelstaedt, 2001, for a similar methodology in the domain of walking). A fully factorial design involving these variables would entail nine combinations of pull speed and draw length. We elected to use a nested design involving five of the nine possible combinations (see below) to minimize the number of trials.

Method

Participants

Fourteen individuals (7 males, 7 females) consented to participate in exchange for course credit. Their ages ranged from 18 to 20 years (M 19.1 years). All were naive as to the purposes of the study and had normal or corrected-to-normal vision, and all but one were right-handed. The data from 1 additional participant were excluded. This individual pulled much faster than instructed, often missing the measuring tape entirely in fast pull trials. This made the number of pulls difficult to count.

Design and Apparatus

The experiment was conducted in a well-lit indoor hallway, 1.8 × 10.0 m. The four possible target distances were 2.5, 3.5, 5.0, and 7.0 m. When pulling the measuring tape to indicate target distance on each trial, participants were asked to use one of five different couplings of pull speed and draw length: (1) normal pull speed–normal draw length, (2) slow speed–normal length, (3) fast speed–normal length, (4) normal speed–short length, or (5) normal speed–long length. This choice of five conditions yielded three levels of pull speed using a normal draw length and three levels of draw length using a normal pull speed. (The manipulations of pull speed and draw length shared a common normal speed–normal length condition.) Each possible combination of the four distances and five pull-speed–draw-length couplings was measured three times, for a total of 60 experimental trials per participant. The presentation order was fully randomized.

We recorded not only the length of measuring tape pulled on each trial, but also the total duration of each response and the total number of draws for each completed response. We used these values to calculate the average speed of tape pulling (meters per second) and the average draw length (meters per draw) for each response. Note that these derived measures are insensitive to the variations in speed and draw length that no doubt existed within each trial. Instead, they provide an estimate of the mean speed and draw length within each trial.

Procedure

Participants were instructed that they would see the experimenter standing a certain distance away and that they would then put on a blindfold and attempt to pull a length of measuring tape between their hands to match the distance to the experimenter. They were instructed to use a hand-over-hand pulling technique, rather than using one hand for pulling and the other hand for holding accumulated tape. This may not match every individual's preferred pulling technique, but, in this series of studies, our goal was to evaluate bimanual pulling methods because of their similarity to (bipedal) walking. Participants were instructed that they would be asked to use slow, normal, and fast rates of pulling and short, normal, and long draws. Excessively slow and fast rates of pulling were demonstrated. We did not measure the demonstrated rates, but the excessive slow rate was modeled as being about 15 cm/sec and the excessive fast rate was modeled as about 1 m/second. The excessively short draw length was modeled as about one hand width per draw, and the excessively long draw length was modeled as swinging the pulling hand from directly in front of the body to directly behind on each draw. Participants were instructed to not use excessive pull rates or draw lengths. Participants were allowed to select their own normal pull speed and draw length, and they were instructed to make their pull rate a bit slower or faster relative to this self-selected rate if slow or fast pulling was required and to make their draw length a bit shorter or longer than their self-selected normal length if short or long pulls were required. Thus, all pulling parameters were ultimately self-selected, within the bounds created by the instruction to not use excessive rates or draw lengths.

Five practice trials were conducted before the experiment to provide participants some experience with seeing how fast the tape advanced as they pulled on it. (Experiment 2 addresses the effect of visually guided practice.) On each practice trial, participants stood while holding the “zero” end of a measuring tape at waist level. The experimenter stood at one of five possible locations (2, 3, 4, 6, or 8 m, presented in random order), holding the other end of the tape at waist level, such that the tape was suspended between experimenter and participant and a loose coil of excess tape lay on the floor behind the experimenter. A pipe cleaner was wrapped around the tape immediately in front of the experimenter. With eyes open, participants pulled the tape and viewed the pipe cleaner as it advanced. The experimenter let the tape slip freely through her fingers as participants pulled, drawing from the loose coil on the floor; friction against the experimenter's fingers thus provided some resistance on the tape. Participants used a self-selected normal pull speed and draw length and stopped when the pipe cleaner reached them. The numbers were visible on both sides of the measuring tape, graduated in centimeters on one side and inches on the other. When participants pulled, the tape typically underwent a considerable amount of twisting and oscillating motion that tended to make the numbers and measurement units difficult to read. No data were collected on such trials.

On each experimental trial, the experimenter served as the target, holding one end of the tape at waist level, while the participant held the other end. After viewing the experimenter for several seconds, participants donned a blindfold and the experimenter announced the tape-pulling parameters to be used on that trial (i.e., slow, fast, normal, less tape, more tape). Participants then began pulling the tape, using the specified parameter. The experimenter again let the tape pass freely through her fingers. A research assistant started a stopwatch when the participant began pulling and stopped it at the termination of the response. Participants were instructed to hold up the tape measure between their thumb and forefinger to signal the end of their response. The assistant counted the number of draws for each response and recorded the amount of pulled tape by noting the value on the tape measure next to the participant's thumb. No error feedback was given. The experimenter then moved to the next target location and pulled the tape taut to begin the next trial. After every 10 trials, participants were exposed to 1 refresher trial, in which they saw the target stimulus at a distance of 2, 3, 4, 6, or 8 m (one distance for each refresher trial, in random order). The method in these refresher trials was the same as in the initial 5 practice trials. These refresher trials were intended to maintain participants’ calibration at a relatively constant level. No data were recorded in these trials.

Data Analysis

We calculated average pulling speed and average draw length on each trial by dividing the amount of tape pulled by the response time and number of draws, respectively. For the amount of tape pulled, we analyzed the data in terms of signed errors to assess the degree to which responses tended to systematically overshoot or undershoot the target distance. Signed error was calculated by subtracting the physical target distance from the total amount of tape pulled on each trial. The signed error data, as well as the average pulling speed and average draw length, were averaged over the within-subjects repetitions prior to analysis.

The primary analysis of interest was a repeated measures ANOVA conducted on the signed errors. In this ANOVA, target distance, requested pull speed, and requested draw length were manipulated as within-subjects factors. The pull speed and draw length manipulations were nested, rather than fully factorial, so we analyzed for main effects of pull speed and draw length, but not their interaction. The pull-speed and draw-length analyses were performed in a similar way and served to characterize the degree to which participants were able to follow our instructions to alter their pull speed and draw length. For all ANOVAs reported in this article, we used the Greenhouse–Geisser correction to obtain corrected p value whenever appropriate.

Results

The mean data are shown in Figure 1, separated according to the three levels of the pulling-speed manipulation (panel A) and the three levels of the draw-length manipulation (panel B). In general, blindpulling responses were well calibrated. The accuracy of responses was not reliably affected by pulling speed, but there was some evidence that shorter draw lengths were associated with less tape pulled.

Figure 1.

Mean blindpulling responses in Experiment 1 as a function of pulling speed (A) and draw length (B). Error bars denote ±1 SEM. The dashed diagonal lines show the level of accurate responding.

Amount of Tape Pulled, Signed Error

The grand mean signed error across all conditions was −0.06 m, indicating virtually no systematic error in overall performance across participants. A repeated measures ANOVA showed a main effect of requested draw length [F(2,259) = 5.08, MS_e = 9.57, p < .01, ${\eta }_{\mathrm{p}}^2=.02$], with signed errors tending to be progressively less negative as draw length increased (see Table 1). The low ${\eta }_{\mathrm{p}}^2$ value suggests that the effect of draw length, although highly significant, is relatively small. There was no main effect of either target distance [F(3,259) = 0.40, p = .754] or requested pull speed [F(2,259) = 1.20, p = .302]. Similarly, neither the draw length × distance interaction nor the speed × distance interaction were statistically reliable [F(6,259) = 0.91 and 0.09, respectively; p = .486 and .997, respectively].

Table 1.

Experiment 1 Results

	Mean Signed Error (m)		Mean Speed (m/sec)		Mean Draw Length (m)
	M	SE	M	SE	M	SE
Instructed pull speed (draw length = medium)
Slow	–0.25	0.24	0.36	0.03	0.35	0.02
Medium	–0.14	0.27	0.52	0.04	0.37	0.01
Fast	0.14	0.38	0.77	0.05	0.36	0.01
Instructed draw length (pull speed = medium)
Short	–0.42	0.33	0.34	0.03	0.19	0.01
Medium	–0.14	0.27	0.52	0.04	0.37	0.01
Long	0.39	0.37	0.71	0.06	0.67	0.04

Note—Values in the medium rows of requested pull speed and requested draw length are identical, because they come from the same condition (medium speed–medium draw length). N = 14.

Average Pulling Speed

Descriptive statistics for the average speed of tape pulling in the various conditions are given in Table 1. A repeated measures ANOVA on the requested pull speed data showed main effects of both speed and requested draw length [F(2,259) = 96.17 and 73.04, MS_e = 2.40 and 1.82, respectively; both ps < .0001; ${\eta }_{\mathrm{p}}^2=.43$ and .36, respectively]. There was no effect of target distance and no interaction of distance with speed or draw length (all Fs < 0.57, all ps > .633). The main effect of speed confirms that participants were successful in varying their pulling velocity, as instructed. However, the main effect of requested draw length reflects a tendency to pull the tape faster when the requested draw length was longer, despite instructions to hold pulling velocity constant at the normal speed while varying draw length.

Average Draw Length

Descriptive statistics for the average amount of tape pulled in the various conditions are given in Table 1. A repeated measures ANOVA on the average draw length data showed only a main effect of requested draw length [F(2,259) = 385.12, MS_e = 3.28, p < .0001, ${\eta }_{\mathrm{p}}^2=.75$]. This effect confirms that participants successfully increased their average draw length when instructed to do so. However, there was no main effect of target distance or of requested pull speed, and there were no distance speed or distance × draw length interactions (all Fs > 0.71, all ps > .491). When there are no instructions to hold the amplitude of arm motions constant, people tend to make smaller amplitude motions with increased speed (Kay, Kelso, Saltzman, & Schöner, 1987). The lack of a speed main effect in the draw length data of Experiment 1 confirms that, when instructed to hold draw length constant as they vary speed, participants are able to do so.

Discussion

Blindpulling responses were accurate with respect to the physical target distances. Across all tested pulling methods, there was only a small amount of overall undershooting. However, when participants pulled fairly quickly at a medium draw length, there was virtually no systematic error across participants (see Table 1). Longer requested draw lengths were associated with increases in the amount of tape pulled for a given target distance. Medium and longer requested draw lengths resulted in fairly accurate pulling, whereas short requested draws resulted in significant undershooting. Note that draw length was manipulated under the instruction to keep pulling speed constant across variations in draw length. Participants generally did not follow this instruction, however. They tended to pull faster when using larger draw lengths (cf. main effect of draw length in the pulling speed data). Previous studies have found that participants haptically judge lines as shorter when the arm moves faster, at least for velocities up to 50 cm/sec (Armstrong & Marks, 1999; Hollins & Goble, 1988; Wapner, Weinberg, Glick, & Rand, 1967; see also Mittelstaedt & Mittelstaedt, 2001). As it turns out, however, we found no effect of the pulling speed manipulation on the amount of tape pulled, even though the mean pulling speed in the fast condition was twice that of the slow condition. To the extent that these large variations in pulling speed did not systematically affect pulling errors, the unrequested changes in pulling speed across the draw length manipulation may have no practical consequence.

COMMON METHODS IN EXPERIMENTS 2–4

Experiments 2–4 involve the blindpulling response, and Experiments 3 and 4 additionally involve a blindwalking response. As such, these experiments share many methodological features. Before describing each experiment in detail, we will outline the methods that these studies share.

Instructions and Procedure

As in Experiment 1, the instructions in Experiments 2–4 stipulated that the tape should be pulled hand over hand, using a medium draw length and pulling speed. An experimenter demonstrated examples of too fast, too slow, too short, and too long draws, as well as an example of an ideal draw length and draw speed. Participants were instructed not to count their draws (or paces, in Experiments 3 and 4). Before beginning, participants donned foam earplugs and tight-fitting over-ear hearing protectors to minimize auditory cues that might otherwise provide information about the target location.

In Experiments 2–4, the experimenter announced a five-digit number just before participants viewed the target and asked them to repeat the number back immediately after completing their pulling or walking response. This was intended to interfere with subvocal draw- counting (or pace-counting) strategies that might otherwise be used to produce a relatively accurate response without any integration of body motion. By discouraging counting strategies, the task thus focused more directly on the participant's ability to keep track of the amount pulled or distance walked by integrating their body motion over time. The mean percent correct in recalling the five-digit memory numbers was approximately 90% in Experiments 2–4; individual percentages ranged from 50% to 100%. Although we only recorded whether or not the entire five-digit number was recalled correctly, we noticed that participants often recalled three or four of the numbers when they did not remember all five. This result suggests that participants at least attempted the memory task. To this extent, we assume that there was some deterrent against counting draws on the vast majority of trials. We therefore did not discard data from trials in which the number was recalled incorrectly.

Data Analysis

We calculated signed (constant) errors by subtracting the physical target distance from the response value on each trial. Before the analysis, the resulting signed errors were averaged across repetition (within subjects) in each condition.

EXPERIMENT 2

Tape pulling and rope pulling differ dramatically from walking in terms of the amount of experience most people have with these behaviors. In a research setting, participants typically arrive for testing with a vast amount of experience with visually guided walking (i.e., gained in the course of their normal locomotion), extending right up to the time the experiment begins. By contrast, they undoubtedly have much less experience with tape pulling. In Experiment 1, we exposed participants to visually guided pulling before testing, to ensure that they had at least some experience performing this action with eyes open. The behavioral outcome of this previous exposure to visually guided pulling is unknown, however. On one hand, people reach to hundreds of objects every day under visual control, and the effect of this experience may be sufficiently general that providing exposure to visually guided pulling has little consequence for blindpulling responses. On the other hand, obtaining experience with visually guided pulling may be crucial for maximizing performance in blindpulling tasks. In Experiment 2, we investigated this issue and took the opportunity to investigate the generality of the results in Experiment 1 by using a target object more typical of blindwalking studies—namely, a small object resting on the floor (here, a cone)—rather than the human target of Experiment 1.

This study involved two phases (familiarization phase, followed by a test phase) and two groups. The groups were distinguished by whether or not participants were exposed to visually guided tape pulling experience during the familiarization phase.

Method

Participants

Two groups of George Washington University students (n = 14 per group) consented to take part in this experiment. Four students participated in exchange for $10; the rest participated in exchange for research credit in an undergraduate psychology class. Each group contained 9 females and 5 males. Participants were randomly assigned to the two familiarization groups (with vision and without vision), subject to the constraint that an equal female/male ratio was obtained in each group. The mean age of the without-vision group was 19.1 years (range, 18–22 years); the mean age of the with-vision group was 21.2 years (range, 18–38 years). (The demographics of 1 female participant in the with-vision group were lost, but we have no reason to expect them to be unusual.) Participants in both groups were naive as to the purposes of the study and reported normal or corrected-to-normal vision. All participants in the with-vision group were right-handed; all but one were right-handed in the without-vision group.

Design and Apparatus

The experiment took place in a well-lit hallway (1.4 × 12.4 m) and used four possible target distances (2.5, 3.5, 5.0, and 7.0 m). Each distance was presented five times apiece in random order. The target was an orange cone (29 cm high) placed on the floor. The experiment was divided into a familiarization phase and a test phase. Both groups were exposed to blindpulling during the familiarization phase. For the without-vision familiarization group, these blindpulling trials were the only exposure to tape pulling provided prior to the test phase. The with-vision group was exposed to both visually guided pulling and blindpulling during the familiarization phase.

Procedure

Familiarization phase (without-vision group)

Five tape-pulling trials without vision were conducted before the test phase. Feedback about draw length or pull speed was provided if the participant's pulling method appeared to deviate dramatically from the requested parameters. No data were collected and no feedback was given concerning the accuracy of pulled distance. These blindpulling familiarization trials used the same methods as were used in the test phase trials, described below.

Familiarization phase (with-vision group)

First, five visually guided pulling trials were conducted, in which the experimenter stood at one of five locations, holding one end of the tape. A pipe cleaner was wrapped around the tape immediately in front of the experimenter. With eyes open, participants pulled the tape and viewed the pipe cleaner as it advanced, using a self-selected normal pull speed and draw length, and stopping when the pipe cleaner reached them. No data were collected. Following these visually guided trials, five blindpulling familiarization trials were conducted (i.e., eyes closed during pulling), using the same methodology as was used in the without-vision familiarization group. Again, no data were collected. Finally, the blindpulling test phase was conducted as described below. For the with-vision group only, after every eight trials involving the blindpulling response (starting with the blindpulling familiarization trials), a visually guided refresher pulling trial was administered, with the experimenter holding one end of the tape and a pipe cleaner wrapped around the tape at 3 or 6 m serving as the target.

Test phase (same procedure for both groups)

Participants began each trial wearing a blindfold and hearing protectors. The experimenter verbally signaled the participant to raise the blindfold. After several seconds, the experimenter cued the participant to lower the blindfold. At this point, the experimenter put one end of a tape measure into the participant's right hand. The tape ran from the participant's hand to a loose coil on the ground. To execute a response, the participant pulled from the coil an amount of tape that he or she felt matched the previously seen target distance. Note that, in this method, the experimenter did not hold the tape and the primary source of tension was the weight of the tape itself. At the end of the response, the participant held up the tape between thumb and forefinger to indicate the exact termination point on the tape. The experimenter recorded the value at the indicated location on the tape. No error feedback was given.

Results

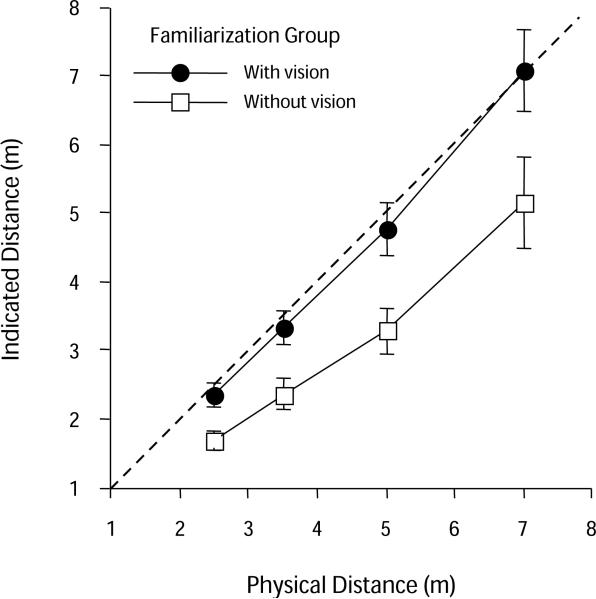
The mean blindpulling data from the test phase for the two groups are shown in Figure 2. We conducted a repeated measures ANOVA on these data, with target distance as a within-subjects factor and familiarization group (with vision, without vision) as a between-groups factor. There was a clear benefit in terms of accuracy for being exposed to visually guided pulling before the test phase. There was a main effect of familiarization group [F(1,26) = 6.87, MS_e = 42.02, p = .015, ${\eta }_{\mathrm{p}}^2=.21$]. The mean signed errors in the test phase for the with- and without-vision familiarization groups were −0.15 and −1.38 m, respectively, averaged across target distance. There was no effect of target distance and no target distance × familiarization group interaction [F(3,78) = 1.96 and 2.28, respectively; both ps > .138]. A two-tailed paired-sample t test showed that the familiarization groups did not differ in terms of the within-subjects standard deviations (SDs), averaged over target distance (p = .150; M = 0.64 and 0.48 m for with-vision and without-vision groups, respectively; between- subjects SE = 0.07 and 0.09 m, respectively). As might be expected, Figure 2 indicates that a similar t test on the absolute errors showed that errors for the with-vision familiarization group were lower than those for the without-vision group (p = .013, d = 1.04; Ms = 1.16 and 1.75 m, respectively; between-subjects SE = 0.160 m for both groups).

Figure 2.

Mean blindpulling responses in Experiment 2 for the with-vision and without-vision familiarization groups. Note that the data shown are for the blindpulling test phase, not for the familiarization phase. Error bars denote ±1 SEM. The dashed diagonal lines show the level of accurate responding.

Discussion

Experiment 2 replicated the results of Experiment 1 in showing that, when participants were exposed to a small amount of visually guided tape pulling just prior to engaging in a blindpulling task, their responses were accurate. This held true when a smaller, more localized target object was used and despite methodological differences that altered the amount of tension on the tape. More importantly, however, Experiment 2 clearly showed that, when participants were exposed to visually guided pulling prior to engaging in blindpulling, their responses were significantly more accurate than if no such exposure was given. This recalibration may have an explicit cognitive component—for example, participants may become aware of seeing the tape move less than they intended and consciously plan to subsequently pull more. In our introspective experience, visually guided pulling entails little or no such awareness, but additional research would be required to confirm this.

EXPERIMENT 3

An overarching goal of this study was to evaluate blindpulling as an alternative to blindwalking as a measure of absolute distance perception. How closely do blindpulling responses correspond with blindwalking responses? Pulling and walking differ along a number of dimensions, and some of these dimensions ultimately may yield differences in the underlying spatial representations that are used to control the two response types. For example, pulling and walking might differ in terms of whether they are responsive to perceived target distance versus perceived target location (e.g., Corlett & Patla, 1987; Loomis et al., 1996; Vishton, Rea, Cutting, & Nuñez, 1999); they might differ in their responsiveness to definite versus relative target distance (e.g., Bingham, 1993; Bingham & Pagano, 1998) or to perceived target distance versus a more abstract representation that is a combination of both perceptual and cognitive factors (e.g., Gogel & Da Silva, 1987). They might differ in terms of whether they are controlled by dorsal versus ventral cortical streams of visual processing (Milner & Goodale, 1995). There may also be important differences arising from what kind of spatial updating the responses entail (e.g., self-motion updating versus object-motion updating). The goal for Experiment 3 was to evaluate whether the two response types are controlled by functionally distinct representations (regardless of how these separate representations might be generated).

It is important to note at the outset that two spatial representations could be processed in anatomically distinct neural pathways, yet both might independently construct a representation corresponding to the same location in space. In this case, the representations may be anatomically distinct, but functionally similar, in terms of their role in controlling behavior. From the perspective of evaluating the acceptability of blindpulling as a substitute for blindwalking, the question of whether the two response types are controlled by the same underlying representation (e.g., the same neural substrate) is less important than whether they are responsive to the same locations in space (i.e., functionally similar representations). Accordingly, our goal in Experiment 3 was to compare the two response types in a variety of viewing conditions and to look for evidence that they are being controlled by functionally distinct representations. If the two responses behave similarly across a range of viewing conditions, it will be taken as evidence that they are controlled by functionally similar representations under the tested conditions.

A main effect of response type in this analysis would indicate that there is an overall difference in the two responses—one response type may tend to yield smaller values than the other, for example. However, such a main effect by itself would not be definitive evidence that the two response types are controlled by functionally distinct representations; the effect could be due either to differences at the representational stage (i.e., control by functionally distinct representations) or to control by functionally similar representations with differences arising at the output stage (e.g., differences in response calibration). A more informative comparison in this regard involves the response × type viewing condition interaction. If the two response types behave similarly across all tested viewing conditions (no interaction), it would suggest that both response types are controlled by functionally similar representations under the tested conditions. If changing the viewing conditions has a larger effect on one response type than on the other (i.e., response type × viewing condition interaction), it would be evidence of a behavioral dissociation and would suggest that the processes controlling the two response types use the available cues differently and construct functionally distinct underlying representations. For example, if a person always pulls 2.5 m under circumstances that cause her to walk 3 m, no matter what viewing condition or configuration of stimuli causes her to walk 3 m, there would be no evidence to suggest that the two responses are controlled by functionally separate underlying representations—the numerical difference could arise because the responses are calibrated differently. By contrast, if she walks 3 m and pulls 2.5 m in one viewing condition, but walks 3 m and pulls 4 m in another, it would be evidence of a behavioral dissociation—a single underlying representation (or functionally similar representations) would not be able to explain such a pattern. In our design, it would be manifested as a response type × viewing condition interaction.

The logic of comparing response types under different viewing conditions is described in more detail elsewhere (Foley, 1977; Philbeck & Loomis, 1997; see also Gogel, Loomis, Newman, & Sharkey, 1985). The analysis assumes that there is an ordinal relation between each method of responding and the spatial representation used to control them and that the mapping from the underlying representation and the overt response for both response types remains the same as the stimulus cues are varied. To enhance the probability that the output mappings remain the same across viewing conditions, we randomized the combinations of viewing condition and response type for each participant, on the assumption that the output mappings would be unlikely to exhibit systematic changes on a trial-by-trial basis.

Method

Participants

Nine females and 5 males consented to participate. Their ages ranged from 20 to 29 years (M = 21.3 years). Four participated in exchange for $20; the rest participated in exchange for $10 plus research credit in an undergraduate psychology class. All were naive as to the purposes of the study and had normal or corrected-to-normal vision. All but one were right-handed.

Design and Apparatus

Laboratory

The experiment took place in an indoor classroom, 3.4 × 10.0 m.

Target distances and target

There were four possible absolute distances: 1.25, 2.11, 3.57, and 6.00 m. The target holder was a wooden box mounted on a tripod at eye level. The box contained an electroluminescent panel, 4.5 × 5.2 cm, marketed as a night-light (EI Products, Inc., Maxwell, TX; Model 11100). The panel was oriented normal to the line of sight. Cards with square apertures of varying sizes could be slid immediately in front of the panel, so that, when the overhead lights were extinguished, participants saw a glowing square that subtended a constant visual angle of 0.42°, regardless of its absolute distance. When the overhead lights were illuminated, participants could see the classroom environment with the tripod resting on the floor. The light box was visible at eye level on the tripod in the lights-on condition (see below) and no aperture cards were used, exposing the unmasked panel.

Viewing conditions

There were three viewing conditions: (1) lights on, in which the target was the tripod light box apparatus, seen binocularly in a well-lit room; (2) dark with reflections, in which the target was a glowing square subtending 0.42° of visual angle, seen binocularly at eye level, and in which, although the overhead lights were extinguished, the target created visible reflections off the lacquered brick floor and white walls; and (3) dark without reflections, in which the target was the same glowing square from the dark-with-reflections condition (seen binocularly), but with all reflections masked from the participant's view by a reduction tube. This 7-cm-diameter tube was lined with black velvet and extended 45 cm from the surface of the light box toward the observer's eyes.

Each combination of response mode (blindwalking, blindpulling), target distance, and viewing condition was performed four times per participant, for a total of 96 trials. The presentation order was fully randomized.

Procedure

Before testing began, the light box was centered at the participant's eye level. In addition to the pulling instructions described in the Common Methods in Experiments 2–4 section above, participants were instructed to walk at a medium speed on walking trials, neither very slow nor very fast; the experimenter demonstrated an example of the ideal walking speed. They were also informed that target size, target distance, or both might appear to change from trial to trial but that they were to ignore perceived changes in size and to base their responses only on distance.

Six visually guided pulling trials were conducted, using a similar method as was used in Experiment 1. Distances of 1.6, 3.0, and 6.9 m were presented twice apiece in random order; no data were collected on these trials. Then, after every eight trials of the experimental phase, a visually guided refresher pulling trial was administered at a distance of 1.6, 3.0, or 6.9 m (three times apiece in random order). Next, six practice trials (without vision and without error feedback) were conducted to familiarize participants with the procedure. During these practice trials, feedback about the draw length or pull speed was provided if the participant's pulling method appeared to deviate dramatically from the requested parameters. Three possible target distances were presented during the practice trials: 1.6, 3.0, and 6.9 m, presented twice apiece (once using a pulling response and once using walking) in random order. All practice trials involved the lights-on viewing condition, and no data were collected.

Participants began each practice trial and each experimental trial wearing a blindfold and hearing protectors. The experimenters prepared the stimulus by placing the tripod at the appropriate location (all trials), plus sliding an appropriate aperture card in front of the electroluminescent panel and turning off the overhead lights (dark trials only). In dark trials, the stimulus appeared as a glowing rectangle at eye level. When ready, the experimenter signaled the participant to raise the blindfold. After several seconds, the experimenter cued the participant to lower the blindfold. At that point, the response type was specified (walking or tape pulling), the overhead lights were illuminated, and the tripod was removed from the participant's path.

On blindwalking trials, the participant walked without vision and attempted to stop at the previously viewed target location. The walked distance was recorded, and the blindfolded participant was guided back to the starting location without error feedback. Blindpulling trials were conducted as they were in Experiment 2.

Results

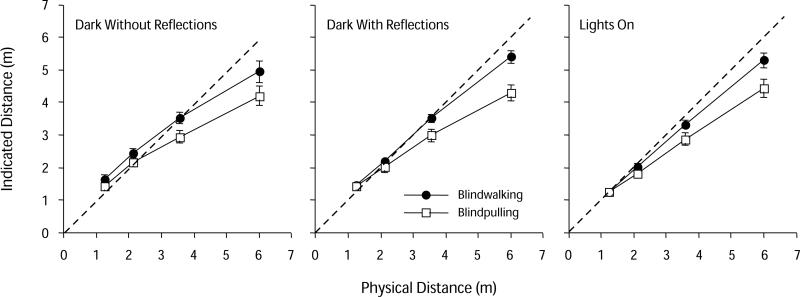
The mean data are shown in Figure 3. In general, with both response types, participants undershot the physical target distance, with pulling responses tending to undershoot somewhat more than walking responses did.

Figure 3.

Mean blindpulling and blindwalking responses in Experiment 3 for three viewing conditions. In the lights-on condition, the overhead lights were illuminated and the target and its supporting tripod were viewed binocularly. In the dark-with-reflections condition, the overhead lights were extinguished and the target was a glowing square of constant visual angle, viewed binocularly; reflections of the glowing target off the floor and walls were visible. In the dark-without-reflections condition, only a glowing square of constant visual angle was visible binocularly. Error bars denote ±1 SEM (N = 14). The dashed diagonal lines show the level of accurate responding.

Signed Errors

A repeated measures ANOVA performed on the signed error data showed a main effect of response type [F(1,13) = 9.50, MS_e = 16.09, p = .009, ${\eta }_{\mathrm{p}}^2=.42$; signed errors averaged −0.58 m for blindpulling vs. −0.15 m for blindwalking]. There was also a main effect of target distance [F(3,39) = 57.52, MS_e = 32.70, p = .0001, ${\eta }_{\mathrm{p}}^2=.82$] but no main effect of viewing condition [F(2,26) = 1.55, p = .236]. The response type main effect depended on target distance [F(3,39) = 13.01, MS_e = 2.72, p = .0002, ${\eta }_{\mathrm{p}}^2=.50$], with the overall difference between response types tending to become larger as target distance increased.

For our purposes, the most important comparison is the response type × viewing condition interaction, which was not reliable [F(2,26) = 1.16, MS_e = 0.07, p = .328]. The three-way interaction of viewing condition × response type × target distance was also not reliable [F(6,78) = 1.32, p = .284]. This indicates that the two response types were not affected differentially across the viewing condition manipulation. There was, however, a marginal target distance × viewing condition interaction [F(6,78) = 3.12, MS_e = 0.65, p = .051], which reflects a general decrement in performance as distance cues were removed. To characterize this interaction more fully, we calculated the best-fitting straight lines through each participant's data, relating their walking and pulling responses to the physical target distances (least squares criterion). Table 2 gives the mean slopes and intercepts of these lines, calculated across participants. These data show a tendency toward decreasing slopes and increasing intercepts as distance cues were removed.

Table 2.

Mean Response Function Parameters in Experiment 3

	Blindpulling						Blindwalking
	Dark Without Reflections		Dark With Reflections		Lights On		Dark Without Reflections		Dark With Reflections		Lights On
	M	SE	M	SE	M	SE	M	SE	M	SE	M	SE
Slope	0.57	0.06	0.60	0.05	0.67	0.06	0.68	0.06	0.83	0.04	0.85	0.05
Intercept	0.84	0.15	0.73	0.15	0.41	0.14	0.93	0.15	0.47	0.10	0.22	0.12

Note—Straight lines were fit to each participant's data relating the indicated distance to physical target distance, for each of two response types and three viewing conditions. N = 14.

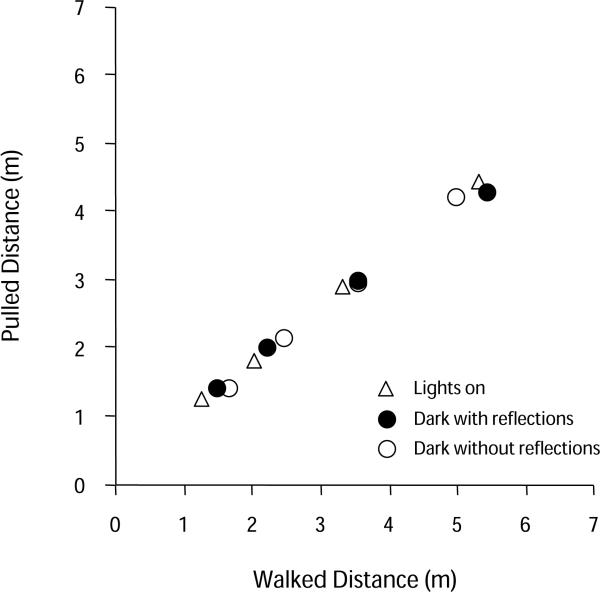
Figure 4 illustrates the relation between response types more directly, by plotting the mean pulling responses as a function of the mean walking responses (calculated across participants) for the three viewing conditions. Using the least squares criterion, we calculated the best-fitting straight lines through each participant's pulling and walking responses in each viewing condition. The relation between pulling and walking responses was well fit by a straight line; most crucially for our purposes, the mapping was very similar in all three conditions. This is reflected in the degree of overlap in Figure 4 across the three conditions. The mean slopes (across participants) for the lights-on, dark-with-reflections, and dark-without-reflections trials were 0.78, 0.74, and 0.80, respectively, and the corresponding mean intercepts were 0.27, 0.37, and 0.18 m. The corresponding mean squared correlation coefficients were 0.96, 0.97, and 0.90, showing that straight lines provided excellent fits to the data in each condition.

Figure 4.

Mean blindpulling responses in Experiment 3 plotted as a function of mean blindwalking responses. Data for three viewing conditions are shown.

Absolute Errors and Within-Subjects SDs

Although, in principle, the absolute errors and within-subjects SDs could be analyzed using the same three-way repeated measures ANOVA design as the signed errors did, we had no specific predictions for many of the tested comparisons in the case of absolute errors and SDs. Our primary interest was in an overall comparison of the absolute and variable errors for the two response types. We calculated an absolute error score for each trial by subtracting the physical target distance from the response value and then took the absolute value of the resulting error score. We then averaged over repetition, target distance, and viewing condition, obtaining two absolute error scores (one for each response type) per participant. A two-tailed paired-sample t test showed that the two response types differed significantly in terms of overall error (pulling, M = 0.90 m, SE = 0.07; walking, M = 0.60 m, SE = 0.04, p = .001, d = 1.46). To assess the pattern of variable errors between the two response types, we calculated the within-subjects SDs across the three measurements per condition and then averaged across target distance and viewing condition for each response type. A two-tailed paired-sample t test showed there to be no difference between the two response types (pulling, M = 0.49 m, SE = 0.04; walking, M = 0.41 m, SE = 0.04, p = .05).

Discussion

Experiment 3 shows that blindwalking and blindpulling responses were tightly linked under viewing conditions in which the available cues differed dramatically, from well-lit, multicue conditions to more restricted viewing conditions in a nearly dark environment. We found no evidence that blindpulling and blindwalking are controlled by functionally distinct underlying representations. Thus, in a variety of settings, these two response types appear to be responsive to functionally similar underlying spatial representations. Performance was somewhat more accurate in the dark-without-reflections condition than it was under similar viewing conditions in our previous work, particularly for the shorter distances (Philbeck & Loomis, 1997). Experiment 3 differed in several methodological details from our previous work, including the specific range of target distances, the types of viewing conditions participants encountered from trial to trial, and the visual angle of the stimuli (targets here were nearly half the size of those in Philbeck & Loomis, 1997). These differences may be behaviorally relevant in some way that is currently unclear. Nevertheless, the marginally significant (p = .051) distance × condition interaction reflects a strong trend toward less accurate performance as absolute distance cues were removed; the lack of interaction with response type shows that both response types showed a similar decline in performance. Furthermore, the general flattening of the response slope and increase in intercept associated with the more reduced viewing conditions (see Table 2) is a pattern often associated with perceptual errors (Gogel et al., 1985; Sedgwick, 1986). Thus, blindpulling shows promise as a substitute for blindwalking in a variety of viewing contexts, and there is evidence that both response types may be used to measure perceived distance.

Figure 3 shows that the slopes of the blindpulling responses are generally flatter than for those of blindwalking. As mentioned earlier, this kind of response type main effect is not diagnostic for determining whether or not the two responses are controlled by functionally similar representations. The more diagnostic test is to determine whether the relationship between the two responses remains constant across changes in viewing conditions. Figure 4 shows that, under our tested conditions, this mapping indeed remains remarkably constant, and this was confirmed by the lack of a significant response type × viewing condition interaction. Importantly, this evidence of functionally similar representations controlling blindwalking and blindpulling does not rule out the existence of anatomically distinct cortical pathways that carry independent spatial representations. On the assumption that there are multiple visual cortical pathways, it is possible that both responses might be controlled by the same pathway (e.g., the ventral stream; Milner & Goodale, 1995) under the tested conditions. Alternatively, the two response types might be controlled by separate pathways, with the target location represented in each pathway corresponding to the same location in space. In either case, both response types are controlled by representations that specify the same location in space, with the overall difference between the responses being determined by differences in calibration that arise as the responses are planned and executed.

Both blindpulling and blindwalking responses showed some undershooting, even under well-lit, binocular viewing conditions. Although this further underscores the linkage between these two response types, blindwalking is often more accurate under similar conditions (e.g., Loomis, Da Silva, Fujita, & Fukusima, 1992; Rieser et al., 1990), and Experiments 1 and 2 showed that blindpulling can also be accurate. Experiment 4 explored a possible explanation for the general pattern of undershooting in the lights-on conditions of Experiment 3.

EXPERIMENT 4

As has been shown, both blindpulling and blindwalking responses exhibited some undershooting in Experiment 3, even under well-lit, binocular viewing conditions. Experiment 3's design was fairly complex, with two response types being randomly paired with three viewing conditions that varied widely in the availability of distance information. In the case of blindwalking, there is some precedence for undershooting in the face of complex designs (Loomis, Klatzky, Philbeck, & Golledge, 1998). The source of this effect is poorly understood and may well require extensive experimentation to unravel. Rather than attempting to isolate the causes of undershooting in Experiment 3, in Experiment 4, we followed the approach of comparing blindpulling and blindwalking by using a relatively simple design, which more nearly replicates the testing contexts that have yielded accurate performance in past work (e.g., Rieser et al., 1990; our Experiment 2) and thereby permits a more equitable evaluation of the accuracy of the two response modes under well-lit, binocular viewing conditions.

Method

Participants

Seven females and 7 males consented to participate in exchange for research credit in an undergraduate psychology class. Their ages ranged from 18 to 21 years (M = 19.1 years). All were naive as to the purposes of the study and had normal or corrected-to-normal vision. All were right-handed.

Design and Apparatus

Laboratory, target distances, and target

The experiment took place in the same indoor hallway as did Experiment 2 and used the same target and target distances. Each participant took part in two blocks of trials—one using the blindwalking response and one using the blindpulling response. The block order was counterbalanced, with 7 individuals pulling first and the rest walking first. A two-tailed t test (p = .05) showed that there was no difference in the standing heights of these two block-order groups. Within each block, each target distance was presented five times apiece in random order.

Procedure

Blindwalking block

Before beginning the blindwalking test phase, five trials were conducted to familiarize participants with the blindwalking response. On each of these trials, the target cone was placed on the floor at a distance of 2, 3, 4, 6, or 7.5 m (presented in random order). Blindwalking was conducted as in Experiment 2. Other than using a different set of stimulus distances, these trials were conducted in the same way as the test phase trials that were conducted immediately thereafter; no error feedback was given.

Blindpulling block

. The procedure in this block exactly duplicated the procedure used for the with-vision familiarization group in Experiment 2. There were five visually guided pulling trials, then five practice blindpulling trials, and finally the test phase trials.

Results

Figure 5 shows the data for the two response types. Both methods of indicating the target distance yielded well-scaled responses under the tested conditions. We conducted a repeated measures ANOVA on these data, with target distance and response mode being within-subjects factors and block order being a between-groups factor.

Figure 5.

Mean blindwalking and blindpulling responses for Experiment 4. Error bars denote ±1 SEM (N = 14). The dashed diagonal line shows the level of accurate responding.

Signed Errors

Although blindpulling responses were slightly smaller than were blindwalking responses (overall mean signed error of −0.38 vs. 0.13 m for pulling vs. walking responses, respectively), this difference was not statistically significant [F(1,12) = 2.83, p = .118]. There was no main effect of the between-group block-order manipulation [F(1,12) = 0.64, p = .439] and no effect of the within-subjects distance manipulation [F(3,36) = 0.78, p = .458]. None of the interaction terms reached statistical significance (all Fs < 1.19, all ps > .320).

Absolute Errors and Within-Subjects SDs

We calculated absolute errors as in Experiment 3, averaging over repetition and target distance to obtain two error scores (one for each response type) per participant. A two-tailed paired-sample t test showed that the two response types did not differ significantly in terms of overall error (pulling, M = 0.75 m, SE = 0.14; walking, M = 0.47 m, SE = 0.09, p = .092). To assess the pattern of variable errors, we calculated the within-subjects SDs across the five measurements per condition and then averaged across target distance for each response type. A two-tailed paired-sample t test showed that there was a reliable difference between the two response types in terms of this measure of response precision (pulling, M = 0.58 m, SE = 0.06; walking, M = 0.43 m, SE = 0.02, p = .026, d = 0.93).

Discussion

Despite slight differences between blindpulling and blindwalking responses, the response types did not differ reliably in terms of either signed or absolute errors; pulling responses exhibited somewhat greater within-subjects variable error. This experiment shows that, when a relatively simple experimental design is used, participants’ walking and pulling responses were equally accurate under well-lit, binocular viewing conditions. One interpretation of the greater accuracy of responses in Experiments 1, 2, and 4 relative to Experiment 3 is that complex procedural requirements in an experimental setting may negatively affect the calibration of these response types. This possibility remains an interesting topic for future work. In sum, however, this experiment reinforces the strong linkage between blindpulling and blindwalking responses as indicators of perceived distance.

GENERAL DISCUSSION

Our results show that blindpulling responses are tightly linked with blindwalking responses across a range of viewing conditions. Blindpulling, like blindwalking, can be remarkably accurate. Providing exposure to visually guided pulling prior to testing appears to play an especially important role in improving the calibration of blindpulling responses. These results held true under multicue viewing conditions with targets up to 7 m distant; whether these results continue to hold true for larger distances remains to be seen. In general, however, blindpulling shows great promise as a measure of target localization. Like blindwalking, it is a nonverbal, action-based response, involving integration of cyclical limb motions over time. The time required to execute the response is approximately matched with blindwalking, as well. However, blindpulling does not involve motion of the entire body through space. This is convenient in applications in which the size of the physical testing environment is limited and when nonambulatory participants are to be tested. Naturally, good mobility in both arms remains an important requirement in using this method, so this may preclude its use in individuals who, for example, are hemiparetic as a result of stroke or of some other brain injury.

Can blindpulling responses be interpreted as a relatively untransformed measure of perceived target distance? This complex issue may require additional research to resolve. The magnitude of individual blindpulling responses is determined by several factors. At a minimum, blindpulling responses are based on (1) the initial, visually encoded target location, which in many research contexts is the quantity of interest; (2) perception and integration of limb movements over time; and (3) motor-control and response-selection processes (Loomis et al., 1996). For blindpulling responses to be interpreted at face value as a relatively untransformed measure of perceived distance, one would need to know that there are no systematic errors in factors 2 and 3. As yet, this question remains unanswered. Regarding factor 2, to our knowledge, no past investigations have studied arm motions under the conditions involved in our pulling response. Our studies allowed participants to move their arms with few spatial constraints and required them to make multiple draws with both arms; previous studies have generally constrained the movement locations by having participants move a manipulandum along a fixed track or run a finger over a fixed line (Armstrong & Marks, 1999; Hollins & Goble, 1988; Kelso, 1977; Marteniuk & Roy, 1972; Summers, Levey, & Wrigley, 1981). The applicability of these previous studies for understanding the perception of arm movements in the blindpulling paradigm remains to be seen. In any case, both factors 2 and 3 presumably operate at the output stage (i.e., after an internal representation of the target distance has been constructed), and they collectively determine the calibration of the overt blindpulling response. Therefore, these two factors may be difficult to differentiate, behaviorally.

In some research contexts, one may have reason to believe that the target is localized accurately—for example, when there is a rich variety of distance cues and other response types suggest that the target distance is perceived accurately. If there are no systematic errors in blindpulling under such circumstances, one may be justified in concluding that systematic errors in factors 2 and 3 are minimal. In Experiment 4, for example, blindpulling responses were equally as accurate as blindwalking responses were under well-lit, multicue conditions. We interpret this as indicating that the targets were localized without sizeable systematic errors and that errors in sensing, integrating, and controlling arm motions were likewise minimal. In that experiment, participants were exposed to visually guided pulling prior to beginning the blindpulling trials, and the experimental design was fairly simple. If these conditions produce responses that are relatively free from systematic error in sensing, integrating, and controlling arm movements, it is reasonable to interpret inaccurate blindpulling performance under other viewing conditions as evidence of errors in target localization. Note that in some research contexts, one may have reason to believe that the underlying representation of the target location is accurate (e.g., spatial information is plentiful and other response types yield relatively accurate performance), and yet there are systematic errors in blindpulling. In such cases, it is plausible that systematic errors in factors 2 and/or 3 are responsible. Of course, the strength of this reasoning depends on the strength of the evidence that the representations that control responses are accurate.