Spatial Memory During Progressive Disorientation

Abstract

Human spatial representations of object locations in a room-sized environment were probed for evidence that the object locations were encoded relative not just to the observer (egocentrically) but also to each other (allocentrically). Participants learned the locations of 4 objects and then were blindfolded and either (a) underwent a succession of 70° and 200° whole-body rotations or (b) were fully disoriented and then underwent a similar sequence of 70° and 200° rotations. After each rotation, participants pointed to the objects without vision. Analyses of the pointing errors suggest that as participants lost orientation, represented object directions generally “drifted” off of their true directions as an ensemble, not in random, unrelated directions. This is interpreted as evidence that object-to-object (allocentric) relationships play a large part in the human spatial updating system. However, there was also some evidence that represented object directions occasionally drifted off of their true directions independently of one another, suggesting a lack of allocentric influence. Implications regarding the interplay of egocentric and allocentric information are considered.

A variety of animal species, including humans, are able to demonstrate that they maintain stored spatial information about the location of objects in their environment (e.g., Loomis et al., 1993; O'Keefe & Nadel, 1978; Wehner & Srinivasan, 1981). More remarkably, many species, including humans, are able to demonstrate knowledge of object locations even while locomoting along novel paths without visual perception of the objects (e.g., Esch & Burns, 1996; Loomis, Da Silva, Fujita, & Fukusima, 1992; Mittelstaedt & Mittelstaedt, 1982; Wehner & Wehner, 1986). This indicates that the represented object locations are updated during body motion. In addition to blind navigation, this ability supports foraging, food caching and exploration of novel territory in nonhumann animals (Allen, 1999; Gallistel, 1990; Jacobs & Liman, 1991), and analogous behaviors in humans.

A central issue for characterizing the representations that are updated during self-motion concerns the frame of reference within which objects are encoded. The two primary candidates are egocentric and allocentric frames of reference; these reference frames are not necessarily mutually exclusive, but objects may be encoded preferentially within one or the other frame, and this possibility is the subject of current debate. Egocentric accounts posit that the dominant human spatial reference system is one in which the locations of significant objects are encoded relative to oneself (Wang et al., 2006; Wang & Spelke, 2000; Wang & Spelke, 2002). Allocentric accounts, by contrast, suggest that the locations of significant objects (oneself included) are encoded relative to each other and to other external, environmental referents (Gallistel, 1990; O'Keefe & Burgess, 1996).

In one particularly clear formulation of the egocentric account, Wang and Spelke (2000) suggested that representations of object locations, which may be thought of as position vectors encoding information about an object's distance and direction relative to the body, are independent of one another and so are updated independently over self-motion. As one moves without vision, each object's displacement relative to oneself (in vector form) is added to the previous position vector for that object. Thus, updating multiple object locations requires multiple, discrete vector additions. So while individual object displacement vectors are presumably based on a common set of self-motion cues, no individual object position vector is thought to influence or be used in the updating of any other object position vector. In this sense, updating within an egocentric framework is done in piecemeal fashion. In the allocentric view, one's position, and all other object positions, are coded within the same environmental representation. Over self-motion, only one's position within this representation is updated, and thus all subject–object relationships change simultaneously according to this single updating process. In this sense, updating within an allocentric framework is done in a more global fashion. The current study directly addresses this piecemeal–global aspect of the egocentric–allocentric debate.

Previous studies have generated results consistent with both egocentric and allocentric representational systems (e.g., Burgess, Spiers, & Paleologou, 2004; Easton & Sholl, 1995; Mou, McNamara, Valiquette, & Rump, 2004; Presson & Montello, 1994; Rieser, 1989; Woodin & Allport, 1998). However, many of these studies required participants to manipulate spatial representations in ways that may not be common in everyday, online spatial processing (e.g., “Imagine you are at object x, facing object y, point to object z”). Using a paradigm that directly probed participants’ current sense of their surroundings, Wang and Spelke (2000) reported results suggesting that updating in this case involves egocentrically encoded object representations. In Wang and Spelke's basic paradigm (Experiments 1 and 2) participants first learned the locations of six objects, distributed throughout an experimental room. Then, from a position amid the object array, blindfolded participants pointed to all the objects before and after disorientation (induced by a minute of self-rotation while blindfolded). Error in pointing to the objects was calculated separately for the pre- and postdisorientation conditions. For each participant, the standard deviation of the error scores for the six objects in a given condition was calculated to measure how accurately the object locations were remembered and updated relative to each other. Wang and Spelke found that this standard deviation, which they labeled configuration error was greater in the postdisorientation condition than in the predisorientation condition.

According to Wang and Spelke (2000), increases in configuration error should not be observed under an allocentric representation system. After choosing a heading, presumably at random, disoriented participants would have been able to “look up” object locations from the undisturbed representation. The increase in configuration error was taken as evidence that the location of each object was represented in an egocentric reference frame and individually updated over rotation. By this account, the egocentric updating process broke down over disorientation; disoriented participants lost track of the individual objects and an increase in configuration error occurred as a consequence. Wang and Spelke did not observe a similar pattern of elevated configuration error when participants were asked to remember the locations of the corners of the experimental chamber. Wang and Spelke concluded that, whereas the geometry of an environment is updated on the basis of allocentric information, objects within an environment are updated on the basis of egocentric information.

Replication of Wang and Spelke's (2000) basic results (disorientation associated increase in configuration error) has proven difficult (Brou & Doane, 2003; Holmes & Sholl, 2005; Mou, McNamara, Rump, & Xiao, 2006; but see Waller & Hodgson, 2006). For example, Holmes and Sholl (2005) were unable to reproduce the disorientation related increase in configuration error (configuration error effect) in either very familiar or novel environments. Holmes and Sholl interpreted their results as evidence of allocentric coding of both novel and overlearned environments. Mou et al. (2006) were able to replicate Wang and Spelke's configuration error effect only when participants learned the locations of objects from a viewpoint amid the array and only when that array was irregularly configured (e.g., not in rows). Like Holmes and Sholl, Mou et al. (2006) interpreted their results according to the logic that egocentric representations are used when the configuration error effect is observed and that allocentric representations are used when it is not. They concluded that, without vision, an egocentric system may be used when reliable allocentric representations cannot be formed or are of low fidelity, as is the case when an array of objects is irregular and no integrative, external viewpoint of the array is allowed beforehand.

While the results of Holmes and Sholl (2005) and Mou et al. (2006) may cast doubt on Wang and Spelke's claim that updating is performed primarily on egocentric object representations, the current study uses Wang and Spelke's paradigm to search for more concrete evidence of allocentric representations. Rather than taking the absence of a disorientation associated increase in configuration error as evidence for allocentric encoding, we conducted distinct analyses seeking evidence of both egocentric and allocentric encoding. Thus, the current study is the first, using this paradigm, that includes analyses capable of finding evidence for both egocentric and allocentric object location encoding in the same context. As described below, Analysis 1 tests an egocentric prediction, Analysis 2 tests an allocentric prediction, and Analysis 3 tests both ego- and allocentric predictions. Results show some evidence for both types of representation.

Most previous studies, including that of Wang and Spelke, have subjected the observer to relatively small amounts of real or imagined motion or else have taken pains to completely disorient the observer. The experiments described below take advantage of unique opportunities that arise when the spatial representations of observers are probed as the observers are progressively disoriented. Waller and Hodgson (2006) employed a similar paradigm (in Experiment 4), but the analyses used in the current study are novel.

Experiment 1

This experiment probed participants’ spatial representations of objects in a room for evidence of encoding within egocentric and allocentric frames of reference. Participants were first trained to point accurately to targets at various eccentricities using a manual pointing device (pointer training phase). Participants then learned the locations of four target objects around them in a room (learning phase). Finally, participants were blindfolded and underwent various magnitudes of passive whole-body rotation (test phase). Each test trial consisted of five successive 70° or 200° rotations.¹ After each rotation, we recorded pointing responses to the objects. We examined the pointing errors to determine whether, under progressive disorientation, the represented object locations tended to “drift” off of their physical locations independently of one another, or as an ensemble.

Method

Participants

Twelve George Washington University undergraduates (4 women, 8 men) participated in this study in exchange for course credit. Their mean age was 19.8 years (range: 18–21). Three participants reported being left-handed.

Apparatus

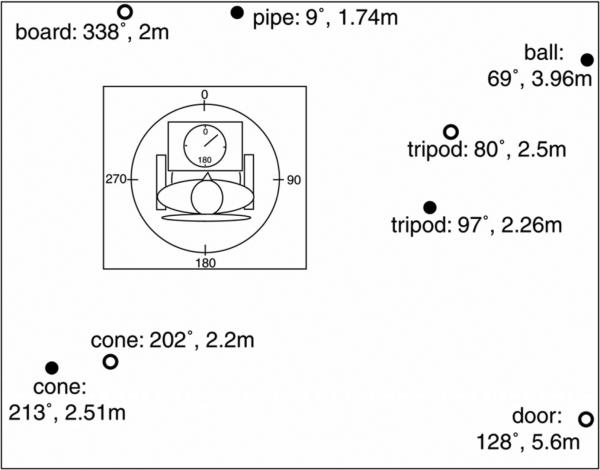
The experiment took place in a 5 × 7-m room. The room was lit by overhead fluorescent lights during the pointer training and learning phases. During the Test phase, the room was lit by a string of dim Christmas lights mounted in a circle above the participant. This served to minimize directional illumination cues that might otherwise be visible underneath the blindfold. Participants were seated in a swivel chair, which protruded through a circular aperture in a square table (1.52 m square × 76 cm tall). A pointing device was mounted horizontally on the chair in the observer's median sagittal plane, at about the level of the abdomen (see Figure 1). The pointer's axis of rotation was offset 23 cm from that of the chair. While this offset may require slight transformations of self-to-object directional responses, use of such an offset is common in the literature (e.g., Easton & Sholl, 1995; Holmes & Sholl, 2005) and there is evidence that people perform small translational transformations well (Easton & Sholl 1995; Presson & Montello 1994; Rieser, 1989). At any rate, participants in the current study underwent extensive pointer training so that they would become familiar with the offset. The pointer itself was a thin rod extending 16 cm from its axis of rotation. A pointer scale graduated to the nearest degree lay just under the rod. An experimenter recorded pointing responses by noting the scale value under the rod. Four objects—a tripod, a door, a cone and a board—were arranged in the room, at varying distances from the chair, in an irregular configuration such that none was located directly in a corner or at the center of a wall (see Figure 1).

Figure 1.

Overhead diagram of the experimental room (not to scale). Objects are represented by open circles for Experiment 1 and filled circles for Experiments 2 and 3. Clockwise angular distance from “home” direction (0°) and the linear distance from the pivot axis of the chair are given for each object.

Procedure

Participants completed two sessions lasting 1 hr each, separated, on average, by about 2 days (never more than 1 week or less than 1 day). Prior to testing, participants were alerted to the fact that the pointer's center of rotation was offset from that of the chair and were instructed to use their preferred hand to set the pointer so that an imaginary line passing through the pointer would connect directly with the physical target location. Participants were allowed to turn their head and torso to look at locations behind them.

Session 1: Main pointer training phase

These trials trained participants to point accurately to specified locations with vision. Participants viewed a small bottle of correction fluid on the perimeter of the table at 1 of 15 locations (45°, 70°, 90°, 115°, 140°, 160°, 170° left and right of straight ahead, and 180°) and aimed the pointer at the bottle (with vision). A response was scored as correct if the pointer was aimed within ±3° of the bottle. The correct pointing direction was demonstrated to the participant after each incorrect response. Once a location had elicited three correct responses without an intervening incorrect response, it was considered “passed” and tested no more. Locations were tested in random order until all were passed.

Session 1: Main learning phase

In these trials, participants learned the locations of the four objects and practiced pointing to them without vision. Participants first spent several minutes studying the locations of the objects and practicing pointing to each. They then donned a blindfold, and a set of hearing protectors (overall noise reduction rating, 20dB) to minimize auditory orientation cues, and attempted to point to each object. A response was scored as correct if the pointer was within ±5° of the object. After each incorrect response, participants raised the blindfold to observe the location of the object and the correct direction of the pointer. Once an object had elicited three correct responses without an intervening incorrect response, it was considered passed and tested no more. Objects were tested in random order until all were passed.

Session 2: Refresher pointer training phase

These trials gave participants an abbreviated refresher training on pointing accurately to specified locations with vision, using methods similar to those used in the main pointer training phase.

Session 2: Refresher learning phase

These trials gave participants an abbreviated refresher training on pointing accurately to the target objects without vision, using methods similar to those used in the main learning phase.

Session 2: Test phase

For each of the 13 trials in this phase blindfolded participants began facing 0° on the table (“home”) and were then rotated through five clockwise turns. After each turn, participants pointed (without vision) once to each object in an individually randomized order as called out by an experimenter, without error feedback. Four different trial types were presented. In the shorter turn experimental trials (S) all turns were 70°, and in the longer turn experimental trials (L) all turns were 200°. Two sequences of turns were used on filler trials. One sequence (F1) consisted of consecutive turns of 70°, 200°, 70°, 110°, and 40°, and the other sequence (F2) consisted of consecutive turns of 40°, 110°, 200°, 200°, and 70°. The order in which the 13 trials were administered was as follows: F1, F1, F2, S, L, L, F1, S, S, L, F2, L, S. This is one of many possible arrangements that result in neither experimental trial type (S or L) having a disproportionately greater chance of occurring earlier or later in the testing session. Participants completed the first two filler trials with unrestricted vision and hearing and then wore the blindfold and hearing protectors for the rest of the trials. Between trials, participants removed the blindfold and hearing protectors and rested briefly. The experimenter who called out the order of the objects moved constantly so as not to provide an auditory azimuthal reference, while another experimenter recorded the pointing responses. A third experimenter executed the rotations, attempting to impose a bell-shaped velocity profile, with rapid, monotonic accelerating and decelerating phases and a minimum of jerky starts and stops. The magnitude of accidental over and underrotations was recorded, and the pointing data were adjusted to reflect the body rotation that was actually administered. For half of the participants, only one of the first two eyes-open filler trials was administered in order to shorten the running time. Eight participants completed all 13 trials; because of time constraints, 2 completed 10 trials, and another 2 completed 8 trials. Thus, all participants completed at least two replications of the S and L experimental trials.

Data Analysis

All statistical tests were conducted against a significance criterion of .05. For each pointing response on an experimental trial, a raw error score was calculated by subtracting the correct response value from the observed response value. Notice that raw error scores are circular (e.g., a score of 350° does not represent a greater degree of error than a score of 10°). In order to use linear statistics on such error scores, the circular data must be treated as linear data. Adjusting raw error so that the inherent discontinuity is moved from 0/360 to –180/180 allows us to more reasonably treat the data as linear (350° would become –10°). Thus, we refer to this adjustment as linearization. It should be noted, however, that such adjustment requires certain assumptions about the directionality of errors and what value to use, in bounding error by –180/180, as the zero point. These assumptions will be explained below in the context of the specific analyses (2 and 3) for which they are necessary. For Analysis 1, which does not require directional classification of error scores, circular statistics were used in order to avoid making the assumptions necessary to use linear statistics. Refer to Table 1 for a description of the various error measures used and how they were derived from raw error.

Table 1.

Error Measures Used

Error name	Error calculation	Error description
Raw error	eRij = dIij – dAij	Response error for object i, turn j, relative to actual target direction (dA) on a circular scale (dI = indicated target direction)
Linear error	eLij = eRij ± 360°	Raw error (eR) adjusted to be within 180° of a particular reference direction (e.g., 0°, eLij – 1)
Heading error	$e_{{\mathrm{H}}_j}=\text{arc tan}\frac{\left({\sum }_i\text{sin}{e}_{{\mathrm{R}}_j}\right)∕4}{\left({\sum }_i\text{cos}{e}_{{\mathrm{R}}_j}\right)∕4}$ a	Mean (using circular statistics) raw error (eR) for all 4 objects for a particular turn (j)
Deviation error	eDij = eRij – eHj	Raw error (eR), for object i adjusted by mean eR for all 4 objects on corresponding turn (j)
Adjusted linear error	eALij = eLij – eLij–1	Linear error (eL) for object i on turn j adjusted by eL for object i on turn j – 1
Adjusted linear deviation error	$e_{{\mathrm{ALD}}_{ij}}=e_{{\mathrm{AL}}_{ij}}-\frac{{\sum }_i{e}_{{\mathrm{AL}}_j}}{4}$	Adjusted linear error (eAL) for object i adjusted by mean eAL for all objects on corresponding turn
Angular separation error	$e_{{\mathrm{AS}}_{i_1,i_{2j}}}=\mid e_{{\mathrm{AL}}_{i_{1j}}}-e_{{\mathrm{AL}}_{i_{2j}}}\mid$	Absoluteb error in angular separation between a given pair of objects (i1, i2) on a given turn (j)
Position error	$e_{{\mathrm{P}}_{i_1,i_{2j}}}=\mid e_{{\mathrm{AL}}_{i_{1j}}}+e_{{\mathrm{AL}}_{i_{2j}}}\mid$	Absolute sum of adjusted linear error for a given pair of objects (i1, i2) on a given turn (j)

^aIf $({\sum }_i\text{cos}{e}_{{\mathrm{R}}_j}∕4)<0$, then e_Hj = e_Hj + 180.

^bAbsolute differences and sums were used so that the error scores could be aggregated within and across participants without positive and negative errors canceling each other out. Transforming the differences and sums in this way also rendered irrelevant the issue concerning which way around the circle angular separation was measured.

Results

Analysis 1—Correlations Across Successive Turns

Implementation

This analysis examined relationships between the error scores that were observed on successive turns of the experiment. Specifically, the analysis asked whether the error for a given object was better predicted by the error for the same object on the previous turn than by the error for other objects on the previous turn. If, as suggested by Wang and Spelke (2000), participants maintain egocentric, individually updated representations of each object, then the best predictor of error for a given object on a given turn should be the error for that same object on the previous turn. In their view, during a body rotation, each object's displacement vector should be added to the previous egocentric position vector for that particular object. If, on the other hand, participants maintain allocentric representations of the objects, then error for a given object should be equally well predicted by the error for any of the objects on the previous turn. While objects may exhibit random perturbation about their correct locations relative to each other, they will tend toward these locations on average.

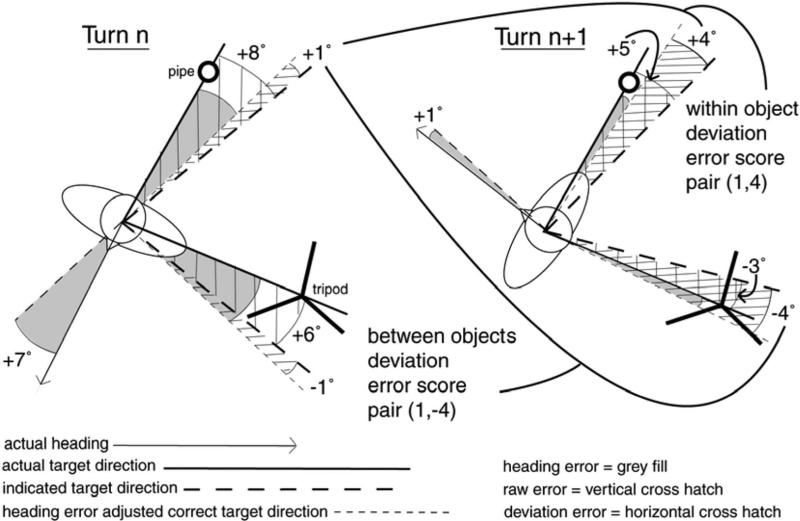
To isolate error for the individual objects from error common to all the objects, we calculated deviation error scores from the raw error scores (see Table 1 for details of this calculation). A circular–circular rank correlation (Batschelet, 1981) was used. A parametric circular correlation was inappropriate as the assumption that the errors were randomly distributed around the circle was not tenable. Because there were four objects, each pair of adjacent turns produced four possible within-object error correlations and 12 possible between-objects error correlations (see Figure 2). For each adjacent turn pair, the mean of the 4 within-object error correlations and the mean of the 12 between-objects error correlations were computed, yielding 16 mean within-object error correlations and 16 mean between-objects error correlations each, for both S and L trials (4 adjacent turn pairs per each of the 4 trials). Because of participant attrition, the correlations from the later experimental trials were based on fewer participants than those from the earlier trials (12 participants completed Trials 1 and 2, 10 completed Trial 3, and 8 completed Trial 4).

Figure 2.

Illustration of 1 participant over two turns showing the origin of within- and between-objects error pairs used in Analysis 1. For simplicity, only two of the four objects are shown, and the figure is not to scale. Note that heading error is calculated as the mean of the raw error scores for all objects.

Results

Paired sample, one-tailed t tests treating each of the 16 turn pair–trial combinations as an independent case failed to show significantly larger within-object than between-objects error correlations for either the S trials, t(15) = 0.36, SE = .017, p = .36, or the L trials, t(15) = 0.59, SE= .015, p = .28. Thus, the pattern expected under an egocentric encoding scheme failed to materialize. Because this is a null result, it is important to consider the statistical power of this analysis to detect the egocentric pattern if it indeed exists. To maximize this power, we analyzed results from the S and L trials together (providing 32 cases) so that the resulting paired sample t test achieved power to detect a medium effect size (d = .5, Cohen, 1988) of .89. This higher powered test again failed to show greater within-object error correlations, t(31) = 0.68, SE = .011, p = .25 (see Table 2).

Table 2.

Mean Within- and Between-Objects Error Correlations (With Standard Deviations in Parentheses)

Experiment	Turn size	Within-object error correlation	Between-objects error correlation	Powera
1 (n = 16)	70°	.375 (.066)	.369 (.035)	.50
1 (n = 16)	200°	.395 (.076)	.386 (.069)	.75
1 (n = 32)	70° and 200°	.385 (.071)	.378 (.055)	.89
2 and 3 (n = 12)	70° and 200°b	.430 (.117)	.413 (.093)	.42
All (n = 44)	70° and 200°c	.398 (.087)	.387 (.068)	.94

Note. None of the comparisons showed significant differences. The n values refer to the number of correlation pairs used to calculate the means, and in the paired t tests, not the number of participants. Notice that these correlations are low by the standards of circular statistics, in which both positive and negative correlations are calculated, expressed on the scale 0 to 1, and the lower of the two is discarded (Batschelet, 1981).

^aCalculated as ability of one-tailed paired t test to detect medium effect sizes (Cohen's d = .5) at α = .05.

^bPost-disorientation turns only.

^cCombined data from pre- and post-disorientation turns.

Simulation

To further address concerns about power, we conducted a simulation to confirm that this analysis would be able to detect the egocentric pattern (i.e., significantly larger within-object than between-objects error correlations), if it in fact exists. Deviation error, which was used in the preceding analysis, may be considered an observable proxy for the theoretical error component that is of interest in our present simulation: error that an individual makes in updating the direction of a particular target relative to the other targets over whole-body rotation, or updating error.

For the present simulation, how updating error might accrue over successive turns within an egocentric-referenced framework was conceptualized as follows. During body rotations, each egocentric object representation would accrue some amount of updating error, and this error would be added to whatever updating error may have been associated with that object before the rotation. In the simulation, the updating error accruing on a given turn was selected at random from a normal distribution with a mean of zero and a standard deviation equivalent to that observed for the deviation error scores in the actual data (approximately 18°, across both S and L trials). Because power is an important issue in this analysis, simulations were run using the same number of subjects (12) and turn pairs (32, for the S and L trials combined) used in Experiment 1 in order to simulate the power achieved in the analysis of the actual data. Ten sets of simulated data generated in this way were analyzed exactly as was the real data from experiment 1. Each of the 10 iterations showed significantly larger within-object than between-objects error correlations (in no case did the p value exceed .05). This confirms that the statistical power of Analysis 1 is sufficient to detect the egocentric pattern if it exists. Thus, our failure to find evidence of the egocentric pattern is not simply due to insufficient statistical power.

Analysis 2—Position Error–Angular Separation Error

Implementation

This analysis focused on pairs of objects and asked whether the errors that participants made in locating the individual objects in a pair (a) produced error in the angular separation between the objects (angular separation error) or (b) preserved the correct angular separation and produced error in the aggregate position of the objects ( position error). If, as suggested by Wang and Spelke (2000), participants maintain egocentric representations of the objects, then over successive turns the indicated object positions should drift off of previously indicated object positions independently of one another, in random directions. As described below and in the Appendix, this would result, on average, in equivalent angular separation error and position error scores. If, on the other hand, participants maintain allocentric representations of the objects, then over successive turns the indicated object positions should drift off of previously indicated object positions in the same direction for all objects, with the result that position error should be larger than angular separation error. Thus, this analysis allows a statistical test of an allocentric prediction, to complement Analysis 1, which tests an egocentric prediction.

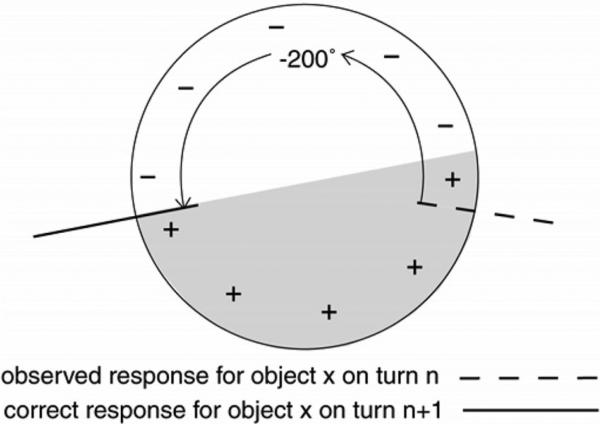
To make possible the directional classification of errors, linear error scores were derived from the raw error scores: The raw error scores for the first turn of each trial were adjusted so that they were neither greater than 180° nor less than –180°. The raw error scores for the subsequent turns of each trial were then adjusted so that each score was within ±180° of the linear error score for the corresponding object on the previous turn of the trial (see Figure 3.) This makes it possible to classify errors as being in a clockwise (positive) or a counterclockwise (negative) direction relative to the actual (or previously indicated) object locations. As the ensuing discussion makes clear, this directional classification was essential to these analyses, and circular statistics are therefore inappropriate. This linearization method favors an egocentric account in assuming that the best indicator of where a participant believes an object to be is the location in which he or she placed that object on the previous turn, regardless of where the other objects were placed.

Figure 3.

Schematic illustration of how error scores were adjusted and linearized. This example assumes a turn size of 200°. Shaded region represents response range for which adjusted linear error scores associated with object x on turn n + 1 would be positive. Notice that the correct response for object x on turn n + 1 is adjusted for any error that may have been associated with the response for object x on turn n.

To allow the treatment of error scores as independent measures over successive turns, the linear error score for each object on Turns 2–5 (for a given participant on a given trial) was adjusted against the linear error score for that object on the previous turn of the trial to get adjusted linear error scores (see Figure 3). (Notice that we did not, as in Analysis 1, perform adjustments to isolate error for the individual objects from error common to all the objects. Position error is essentially a measure of error that is common to all the objects and to subtract that error out would be inconsistent with the logic of the present analysis. This issue is addressed in the Discussion and in Experiments 2 and 3.)

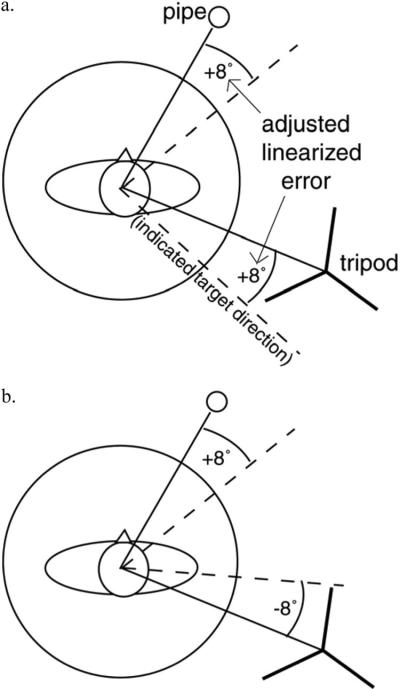
For each combination of trial and turn, within-subject angular separation error scores and position error scores were calculated for the six possible object pairs: four adjacent-object pairs and two pairs of objects separated from one another by a third object. (Actual calculations are described in Table 1.) To the extent that objects drift in the same direction, angular separation error scores will remain low while position error scores increase (see Figures 4A and 4B). However, to the extent that objects drift in random directions, independently of one another, position error scores will not differ from angular separation error scores. (See the Appendix for mathematical proof showing that the absolute sum of two normal random deviates [m = 0], is equal to their absolute difference.) Thus, position error provides an index of error in the position of the configuration as a whole (similar to heading error in the Wang and Spelke, 2000, study) against which we may gauge the size of the error in the position of objects relative to each other, measured here by angular separation error (similar to configuration error in the Wang and Spelke, 2000, study).

Figure 4.

A: Example of condition in which the objects are drifting in the same direction and Analysis 2 would show larger position error than angular separation error. Participant is off by 8° in a clockwise direction for both the pipe and the tripod. The adjusted linear error scores for the objects are + 8 and + 8. The angular separation error score for the two objects will be 0 (8 – 8), and the position error score will be 16 (8 + 8). (For clarity, the adjusted linear error scores in the figure represent error accruing over Turn 1. For subsequent turns, each object's linear error score was adjusted: calculated against indicated location for that object on the previous turn, not against actual object location.) B: Example of condition in which the objects are drifting in opposite directions and Analysis 2 would show larger angular separation error than position error. Participant is off by 8° in a clockwise direction for the pipe and 8° in a counterclockwise direction for the tripod. The adjusted linear error scores for the objects are + 8 and –8, respectively. The angular separation error score for the two objects will be 16 [8 – (–8)], and the position error score will be 0 [(8 + (–8)].

Results

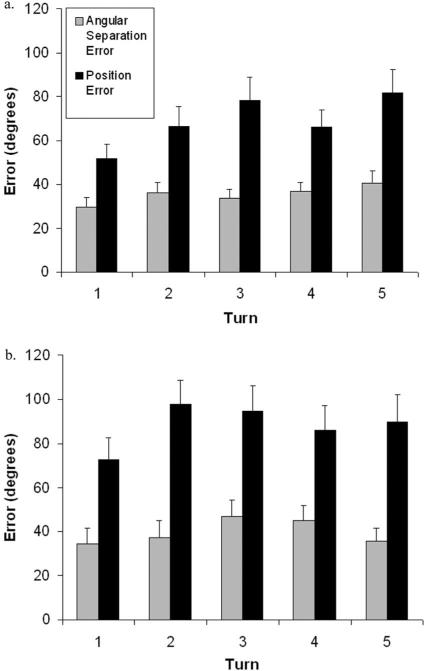
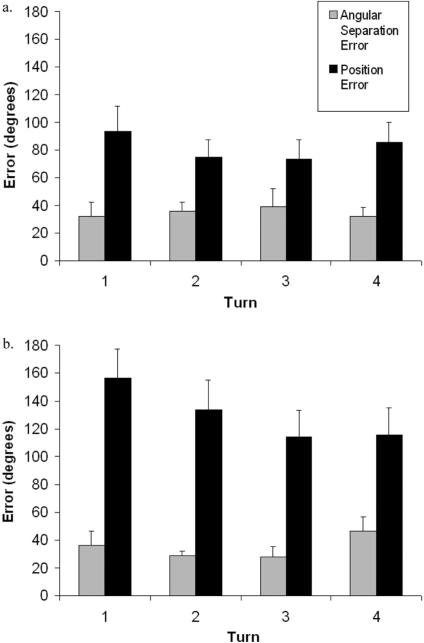
For each participant, on a given trial and a given turn, a within-subject mean was computed across the six error scores of each type (angular separation–position). Because no effect of trial was observed, and so that participants who did not complete all trials could be included in the analyses, the data were collapsed across trials. Because none of the results differed for S (70°) and L (200°) turns, data were collapsed across turn size as well (but see Figures 5A and 5B for separate visual representations of S and L data). A two-way analysis of variance was conducted treating participants as cases and turn and error type (angular separation–position) as independent variables. Results showed a significant main effect of error type: greater mean position error than angular separation error, F(1, 11) = 26.01, MSE = 1,825.8, p < .001. No significant interaction between turn and error type was observed, F(4, 44) = 0.75, MSE = 505.57, p = .56. This is the pattern predicted by an allocentric encoding scheme, rather than an egocentric scheme.

Figure 5.

Mean angular separation and position error scores collapsed across 70° trials (A) and across 200° trials (B) in Experiment 1. Error bars are the standard errors of the mean.

Analysis 3—Error Pattern Distribution

Implementation and results

This analysis focused on the patterns of directional errors that participants produced in locating the four objects and compared the distribution of error patterns to what would be expected given egocentric and allocentric representations. Each case in the analysis comprised the errors in pointing to the four objects made by a participant, on a given trial, on a given turn. Each case was put into one of three possible outcome categories: (a) all four error scores of the same sign (where clockwise errors were positive and counterclockwise errors were negative), (b) three error scores of the same sign, and (c) two error scores of the same sign. If, as suggested by Wang and Spelke (2000), participants maintain egocentric representations of the objects, then the direction in which each object drifts off of its previous location (whether the error score is positive or negative) should be unaffected by the direction in which any of the other objects drift. Thus, each individual object's error score should have an equal chance of being positive or negative. The egocentric view, then, would predict that the resulting proportions of cases falling into the three categories would be .125, .50, and .375, respectively. If, on the other hand, participants maintain allocentric representations of the objects, then (once the influence of random perturbation is removed) all objects should drift in the same direction and all cases should fall into Category a. This analysis allows statistical tests of predictions consistent with both the egocentric and the allocentric views.

Because directional classification of errors was necessary, and in order to allow the treatment of error scores as independent measures over successive turns, this analysis was carried out in terms of adjusted linear error scores (see Table 1). For each participant, the proportion of cases falling into each of the three possible outcome categories described above was calculated across both S and L trials. In testing the egocentric prediction, three separate single sample t tests (here treating subjects as cases) showed the proportions observed for each outcome category (.46, .34, and .20, respectively) differed significantly from the proportions predicted under the assumption that each object's error sign is independent of the others (.125, .50, and .375, respectively): Category a, t(11) = 6.88, SE = .049, p < .001; Category b, t(11) = 5.03, SE = .032, p < .001; Category c, t(11) = 5.66, SE = .031, p < .001. This result argues against a fully egocentric encoding scheme.

The allocentric conception predicts that the error scores for the four objects will have the same sign in all cases. However, as was noted earlier, a realistic allocentric conception should allow the position of each object to exhibit random perturbation around a fixed position within a configural representation and should thus include some random error across objects. Given such a conception, cases may exist in which the configuration of objects drifted in the same direction, but, because the random perturbation for one or more objects exceeded this common drift, one or more objects have an error sign that differs from the others. The criteria described below were applied to minimize the inclusion of such cases in testing the allocentric prediction. First, to estimate random perturbation, adjusted linear deviation error scores were calculated (see Table 1). Then, only those cases were included in which all four absolute adjusted linear error scores were more than two standard deviations from the mean absolute adjusted linear deviation error score.² It would be highly unlikely, given this criterion, that a discrepant error score would reflect random perturbation and thus such discrepancies are difficult to explain within an allocentric model. In testing the allocentric prediction a single sample, one-tailed t test showed the proportion of this subset of cases (.64) falling into Category a (all four error scores of the same sign) differed significantly from 1, the proportion predicted by an allocentric model, t(9) = –3.06, SE = .118, p = .01.³ This argues against a fully allocentric encoding scheme.

Simulation

The prediction for this analysis given an egocentric model, wherein each object's error has an equal chance of being positive or negative, is determined according to probability theory. However, a simulation was conducted to confirm that an allocentric model would predict that all cases meeting the criterion used above would have four adjusted linear error scores of the same sign. The theoretical error component of interest here may be thought of as random perturbation + heading error, and the observable measure of the two combined is adjusted linear error. Note that in testing an allocentric prediction the clear theoretical distinction between random perturbation and heading error dictates that the simulated values of the two error types be sampled separately.

Ten new sets of simulated allocentric data, each of the same size as the actual data set (418 cases), were generated by first assigning each object in each case a random perturbation score selected at random from a normal distribution with a mean of zero. The standard deviation of this distribution was based on the standard deviation of the observed adjusted linear deviation error scores (28°) as calculated in the above analysis. Then, for each case, a heading error score was selected at random from a normal distribution with a mean of zero and standard deviation of 51°, based on the standard deviation of heading errors observed across all cases in the actual data (both S and L trials). Recall that a case comprises the four object adjusted linear error scores corresponding to a given participant, trial and turn, and that heading error for a case is calculated as the average of those error scores. Finally, the heading error score for a given case was added to each of the four object random perturbation scores in that case, resulting in simulated, allocentric adjusted linear error scores. Across 10 simulations, 100% of the 496 cases meeting the criterion outlined above comprised four error scores of the same sign.

Admittedly, actual data may be expected to be noisier than simulated data. Participants may have occasionally completely forgotten where one of the objects was and guessed. In order to examine this possibility, additional simulations of Analysis 3 were run exactly as described above, except that a varying proportion of the simulated, allocentric adjusted linear error scores were replaced with values drawn at random from a uniform distribution between –180 and + 180. Each simulated error score that was replaced in this way represented a pointing response on which the participant guessed randomly. Not until 20% of the simulated pointing responses were replaced with “guesses” did Analysis 3 produce a pattern of results similar to that observed in the real data (25% of the cases meeting criteria violated the allocentric prediction). This suggests that in order for the observed pattern of results to reflect the use of purely allocentric, configural representations, about every fifth pointing response, on average, would have to have been a random guess.

Discussion

The results are not consistent with the view that the updating system is primarily egocentric. In fact, the weight of the evidence indicates reliance on allocentric representations.⁴ However, there is also evidence that this system is not purely allocentric. None of the analyses produced results consistent with the predictions of a pure egocentric account, two of the three analyses produced results consistent with the predictions of a pure allocentric account, and a third analysis produced results consistent with neither a pure allocentric nor a pure egocentric account. The results suggest, then, that the updating system is at least partly allocentric in character and in fact employs both types of encoding in this situation.

An alternative interpretation of the results from Analyses 2 and 3 is possible, however. It is possible that the updating system is primarily egocentric in character but that the proprioceptive and vestibular cues experienced during nonvisual, whole-body rotation in Experiment 1 provided erroneous information about the extent of the turn that was utilized in updating the egocentric representation of each object individually. If participants were misperceiving the turns and applying the same misperception to the egocentric updating of each object location separately, it would give the impression that the objects were drifting off of their true locations as an ensemble. This alternative interpretation is not a concern for Analysis 1. Because the raw error scores for a given participant on a given turn were adjusted to have a mean of zero, any misperception of the turn was removed from the data. In arguing against the egocentric position, then, the results of Analysis 1 suggest that the results of the other analyses were not caused merely by turn misperception. Experiments 2 and 3 further addressed the issue of turn misperception by including a disorientation condition. In this condition, presumably, no quantifiable perception of the “turn” existed that could be applied to the egocentric updating of each object location separately.

Experiments 2 and 3

Experiments 2 and 3 followed Experiment 1 in most respects but included additional conditions and manipulations that made it possible to extend the analyses of Experiment 1 to the situation of complete disorientation such as was explored by Wang and Spelke (2000). The trials of interest involved a series of four successive turns, each of which was followed by pointing responses as in Experiment 1. However, the first turn of each of these series consisted of a long, random back and forth rotation meant to cause disorientation. Subsequent turns were of a specified size (70° in Experiment 2 and 200° in Experiment 3) and always in the same direction (clockwise). This allowed the analyses described in Experiment 1 to be performed on postdisorientation data. Several other minor, procedural changes were also made with an eye toward attempting to replicate the analyses (and results) of Wang and Spelke (2000). Although we failed to replicate Wang and Spelke's primary result (disorientation associated increase in configuration error), this was not considered particularly informative because of a number of remaining procedural differences between the two studies, any of which may have explained the failure to replicate. Therefore, the Wang and Spelke analysis is not reported here. However, in order to make the attempted replication possible, two trials (roughly corresponding to Wang and Spelke's eyes-open and eyes-closed conditions) were conducted in addition to those reported here. Also, whereas in Experiment 1 participants were required to point only once to each object after each turn, in Experiments 2 and 3 four responses were required to each object after each turn (following Wang and Spelke). Thus, 16 total pointing responses were required at each heading. Experiments 2 and 3 were identical to each other except that Experiment 2 used successive turns of 70° and Experiment 3 used successive turns of 200°.

Method

Participants

George Washington University undergraduates participated in this study in exchange for course credit. Twelve students (6 women, 6 men) participated in Experiment 2. Three of the participants in Experiment 2 reported being left-handed. The mean age for Experiment 2 was 19.3 years (range: 18–21). Fifteen students (9 women, 6 men) participated in Experiment 3. None of the participants in Experiment 3 reported being left-handed. The mean age for Experiment 3 was 18.6 years (range: 18–20).

Apparatus and Procedure

The apparatus was the same as in Experiment 1 except that two of the four objects (the door and the board) were replaced with new objects (a pipe and a ball) and all of the objects were rearranged (see Figure 1). All pointer and object training procedures were the same as for Experiment 1.

Experiments 2 and 3 each included three experimental trials of interest. Filler trials were excluded in order to allow more time for participants to complete the experimental trials. Trials 1–3 were procedurally identical to one another. In these trials, the first turns of which represent the disorientation condition, participants donned the blindfold and hearing protectors and were then turned slowly clockwise and counterclockwise for approximately 60 s so that they would become disoriented. At the end of the disorientation procedure participants were returned to the home position (presumably unbeknownst to them) and asked to point to each object four times apiece in individually randomized order as called out by an experimenter. As before, each pointing response was recorded from the polar scale directly under the pointer. Then participants underwent a series of three clockwise turns (Turns 2, 3, and 4; 70° in Experiment 2, 200° in Experiment 3) after each of which pointing responses (again, four times to each object) were recorded. All 12 participants in Experiment 2 completed Trial 1. Seven participants completed Trial 2 and only 3 completed trial 3. In Experiment 3, 9 of the 15 participants completed Trial 1, 5 completed Trial 2, and again only 3 completed Trial 3. In all cases, noncompletion was consequent to time constraints.

Results

The three analyses from Experiment 1 were conducted again, here on postdisorientation data. The four pointing responses that were required for each object in Experiments 2 and 3 were averaged together, using circular statistics, to produce a single response value for each object on each turn.

Analysis 1—Correlation Across Successive Turns

To increase statistical power (by including more cases), and because the results of this analysis did not differ for the 70° and 200° turn data in Experiment 1, the data from Experiments 2 and 3 were analyzed together. A paired sample, one-tailed t test failed to show significantly larger within-object than between-objects error correlations, t(11) = 0.49, SE = .036, p = .32. However, the power of this test remains low (see Table 2). This issue is addressed further in the Discussion.

Analysis 2—Position Error–Angular Separation Error

The analysis was done exactly as in Experiment 1 except that here data for 70° and 200° turns came from different participants, could not be collapsed within participant, and so were analyzed separately. A two-way analysis of variance, treating turn and error type (position error or angular separation error) as independent variables, showed a significant main effect of error type (greater mean position error than angular separation error) for Experiment 2, F(1, 11) = 29.95, MSE = 1,767.45, p < .001, and Experiment 3, F(1, 8) = 66.27, MSE = 1,779.6, p < .001. No other significant effects were observed (see Figures 6A and 6B).

Figure 6.

A: Mean angular separation and position error scores collapsed across postdisorientation 70° trials in Experiment 2. (Turn 1 was the disorientation procedure; Turns 2–4 were 70°.) B: Mean angular separation and position error scores collapsed across postdisorientation 200° trials in Experiment 3. (Turn 1 was the disorientation procedure; Turns 2–4 were 200°.) Error bars are the standard errors of the mean.

Analysis 3—Error Pattern Distribution

Again, this analysis was done exactly as in Experiment 1. Recall that if each object error is independent of the others and has an equal chance of being positive or negative (the egocentric prediction), then the probabilities that a set of four adjusted linear error scores for a given participant on a given turn and a given trial (treated as an independent case in this analysis) will fall into categories (a) all four scores of the same sign, (b) three scores of the same sign, or (c) two scores of the same sign are .125, .50, and .375, respectively. Replicating results from Experiment 1, three separate single sample t tests showed the proportions observed across (Experiment 2 and 3) subjects for each outcome category (.64, .28, and .08, respectively) differed significantly from the proportions predicted by an egocentric model: Category a, t(26) = 12.57, SE = .04, p < .001; Category b, t(26) = –5.55, SE = .04, p < .001; Category c, t(26) = –16.18, SE = .019, p < .001.

In comparing observed results against the allocentric prediction (all four adjusted linear error scores being of the same sign in 100% of cases), as in Experiment 1, only cases meeting the criteria described there were analyzed. A single sample, one-tailed t test showed the proportion of this subset of cases (.76) falling into Category a (all four error scores of the same sign) differed significantly from 1, the proportion predicted by an allocentric model, t(17) = –3.28, SE = .073, p = .003. It should be noted that many cases in which one or more adjusted linear error score (calculated as described in the test of the allocentric prediction in Experiment 1) differed from the others in sign had means near 180°. This presents the problem described in Footnote 4. However, the more conservative approach described there that solves this problem is not possible here because, as in the L trials of Experiment 1, the more conservative inclusion criteria exclude all cases from the analysis. Therefore, some caution is warranted in interpreting these results.

Discussion

Experiments 2 and 3 extended the analyses of Experiment 1 to the situation of complete and relatively abrupt disorientation such as was explored by Wang and Spelke (2000). The results of the experiment bolster the conclusion that allocentric as well as egocentric information is used in object updating.

Analysis 1 again showed that a participant's error in locating a given object on a given turn was no better predicted by the participant's error in locating that object on the previous turn than by the participant's error in locating any of the other objects on the previous turn. As before, these results suggest that participants maintained allocentric rather than egocentric representations of the objects. However, even combining the data from Experiments 2 and 3, the sample size (12) is still small and power remains unacceptably low. (Remember that cases in this analysis were correlations across successive turn pairs, not participants.) Therefore, results from all three experiments were analyzed together. The resulting one-tailed paired sample t test achieved power to detect a “medium” effect size (d = .5) of .94 at α = .05. This higher powered test again failed to show greater within-object error correlations, t(43) = 0.82, SE = .012, p = .21. Analysis 2 again showed that position error was greater than angular separation error. Furthermore, Analysis 3 again showed that the distribution of error patterns was not what would be expected given either a purely egocentric representation or a purely allocentric representation.

As before, these results argue that the updating system has an allocentric as well as an egocentric component. The possibility remains, however, that the system is egocentric in character and that the results failed to match egocentric predictions because participants applied the same turn misperception to the individual updating of each object. In response to this concern, we again note that the turn misperception argument is not a problem for Analysis 1. To further address this concern, we redid Analyses 2 and 3 using only data from turns on which our analyses indicated that the disorientation procedure had been successful⁵ (Experiment 2: Turn 1 of Trials 3 and 5; Experiment 3: Turn 1 of Trials 3, 4, and 5). Presumably, immediately following the disorientation procedure no quantifiable perception of the “turn” existed that could be applied to the egocentric updating of each object location separately. How then did participants perform the task on these trials? Although other possibilities (discussed below) are mentioned, Wang and Spelke's (2000) primary account seems to be that participants were forced to reset their sense of orientation on some arbitrary basis. Under the rationale of the Wang and Spelke (2000) study, this resetting process would have taken on a different character depending on the nature of the underlying object representation. If that representation was allocentric in character, then participants would have selected a heading at random and inferred the orientations of the objects on the basis of this heading. If that representation was egocentric in character, then participants would have independently selected new directions for each of the objects in the stimulus set. Notice that if participants selected new object directions in the latter fashion, then once the first object direction was selected, participants could not have subsequently placed other objects in the correct locations relative to the first object unless they had access to object–object information.

Analysis of the disorientation subsample showed that position error was again greater than angular separation error in both Experiments 2, t(11) = 2.58, SE = 24.02, p < .05, and 3, t(14) = 4.25, SE = 28.31, p < .001. For both experiments, the observed proportions of cases from the disorientation subsample falling into each of the three possible outcome categories (a, b, and c, as identified above) differed from the proportions predicted under the assumption that each object's error was independent of the others: Category a, t(26) = 7.82, SE = .068, p < .001; Category b, t(26) = –3.76, SE = .058, p < .001; Category c, t(26) = –10.55, SE = .03, p < .001. These analyses provide further evidence for the role of an allocentric component in the updating system that is not vulnerable to the turn misperception argument.

It should be noted that Wang and Spelke (2000) also observed results consistent with the influence of an allocentric component in the updating system. They noted that among disoriented participants “configuration error was relatively small and localization was not by chance” (p. 245). This point has been reiterated by several other researchers using this paradigm as well (e.g., Mou et al., 2006; Waller & Hodgson, 2006). Wang and Spelke offered several explanations of these results that discounted the contribution of allocentric spatial representations. For example, perhaps dynamic egocentric representations are maintained throughout the disorientation procedure, and while increased random errors in the disturbed updating process lead to increased configuration error, updating is sufficiently accurate to maintain some configural integrity. This explanation is not supported by the current data. If random error is constantly accumulating in this way then angular separation error should increase steadily over successive turns, but it does not. Another possibility suggested by Wang and Spelke is that disoriented participants respond on the basis of remembered egocentric images formed from and corresponding to the learning heading. Brou and Doane (2003), Mou et al. (2006), and others have shown that certain individuals do use this strategy in this paradigm. However, the number of these individuals included in the current analyses appears to be relatively small as indicated by the random distribution of heading errors observed in the disorientation conditions (as discussed in Footnote 5). Wang and Spelke also suggested that egocentric images formed from other headings might play a role in reorientation. While this possibility is beyond the scope of the current data, the authors believe the role of egocentric images and their possible contribution to and interaction with allocentric representations are fertile grounds for future research. Finally, Wang and Spelke offered that a crude allocentric representation, such as simple ordinal information, may guide disoriented participants. In response to this, we note that current results consistently showed the same degree of angular separation error accruing over relatively small, “oriented” turns and disorientation alike. It seems unlikely that over turns as small as 70° participants abandoned richer representations in favor of simple ordinal lists of objects.

General Discussion

The current study examined data gathered over successive blind rotations, or progressive disorientation, to search for evidence of egocentric and allocentric coding in the human updating system. Results showed that, in keeping track of the locations of objects, the updating system makes use of information about the locations of objects relative to each other. As such, the current results, in disagreement with the conclusions of Wang and Spelke (2000), suggest that allocentric information plays an important role in the updating of object locations. However, evidence was also found that object representations demonstrate some degree of independence. In sum, current results suggest that independent (egocentric) and yoked (allocentric) object representations coexist and may be utilized simultaneously.

Over the course of the study, Analyses 1 and 2 consistently confirmed the prediction of the allocentric view and failed to confirm the prediction of the egocentric view. Analysis 3 showed results differing from what would be predicted by either purely egocentric or purely allocentric views. This suggests some independence of the individual object representations, which raises a question. Why does one of our analyses (3) show such object independence while the others do not? We believe this is because Analysis 3 (the error pattern distribution analysis) is more sensitive than the others in that it makes specific numerical predictions for both the egocentric and allocentric models, while the others predict either no differences or ordinal relations among measures.

The proposition that spatial representations, as they support the updating system, do not comprise purely egocentric representations of distances and directions relative to the self is in alignment with most extant models (e.g., Byrne, Becker, & Burgess, 2007; Mou et al., 2006; Sholl, 2001), which posit that both egocentric and allocentric encoding of objects occurs. For example, Mou et al. (2006) proposed a model in which people rely on a transient egocentric system in some cases and an enduring, allocentric system in others. When the egocentric system is unavailable because perceptual input has ceased, the allocentric system may be used if the representation it delivers is sufficiently high in fidelity. While several candidates have been identified (e.g., learning viewpoint, array geometry, number of objects), what causes an allocentric representation to achieve high fidelity is still being explored. It is possible that certain aspects of the current experiments (e.g., salient room geometry, extended study time) resulted in the early formation of high-fidelity allocentric representations that were used to guide pointing after 70° turns and disorientation alike. This would explain current evidence of allocentric coding.

However, current evidence of egocentric coding may not be consistent with this model. The results of Analysis 3 suggest the influence of egocentric coding long after perceptual support has ceased and in situations in which enduring, allocentric representations should be well formed. Simulations showed that were pointing responses guided by an allocentric representation, excluding cases where random perturbation about the correct configural object locations is likely to be a factor, all four object errors should always be of the same sign. If we assume that violations of this allocentric prediction were merely the result of occasional forgetting or guessing, such guessing would have to occur on 20% of pointing responses in order to produce the observed pattern of results. This seems unlikely, given the relatively rigorous training participants went through to learn the object locations and the small number of objects involved (four). We propose, instead, that this result provides evidence of egocentric representation. This is inconsistent with the proposition by Mou et al. (2006) that in the absence of perceptual support, people rely on well-formed allocentric representations.

While current results may fit within other models in which control shifts recurrently between the egocentric and the allocentric modes (e.g., Sholl, 2001), they are also congruent with the alternative possibility that the updating system makes use of egocentric and allocentric information simultaneously (Burgess, 2006, and Byrne et al., 2007, have made similar suggestions). The key point is that egocentric and allocentric representations were not differentially in evidence across different updating conditions. Rather, while the influence of allocentric information was observed throughout progressive, blind rotation, results did not accord with the predictions of a purely allocentric account. One way of conceptualizing the simultaneous usage of egocentric and allocentric information is to allow for the binding together of representations for separate objects so that the objects are updated as a unit. For example, it makes sense that spatial representations of the corners of a room might bind together according to the law of Prägnanz (they are connected by walls, etc.). Wang and Spelke (2000) showed that the corners of a room may, in fact, be updated as a unit. Easton and Sholl (1995) showed evidence that participants had some direct access to object–object information provided the objects were regularly configured (at the corners and midpoints of each side of a square).

The unified representation emerging from such a binding process might be updated egocentrically, as a single, independent vector encoding information about the distance and direction of a reference point on the object group (e.g., the middle, a forward edge, a particularly salient object, etc.). Then as task demands direct attention to particular points within the bound representation, the egocentric vector conception of the representation might give way to a richer conception in which objects are encoded relative to each other. This richer representation may reside offline during updating as suggested by Amorim, Glasauer, Corpinot, and Berthoz (1997) and Hodgson and Waller (2006), and it may be supported partly or wholly by egocentric imagery, but it undoubtedly contains a wealth of spatial information about the relative location of its component parts, independent of the location of one's body. It is in this sense that the bound representations may be considered allocentric. Previous studies (McNamara, 1986; McNamara, Hardy, & Hirtle, 1989) showing evidence that spatial memories are organized hierarchically provide a framework for conceptualizing how some of the objects in a given environment might be bound in this way. This idea provides a possible explanation of how egocentric and allocentric information coexist within the updating system. Such a conception provides a perspective on the relationship between the systems that represent space and objects, at least at a theoretical level, that may provide an impetus for future research. More immediately, whether the type of binding proposed here occurs in spatial representations needs to be investigated. Notice that if such binding occurs, then egocentric and allocentric information interact somewhat more closely than in most current models that propose that egocentric and allocentric information is handled by two different systems or subsystems (Easton & Sholl, 1995; Mou et al., 2004; Sholl, 2001; Wang & Brockmole, 2003; Wang & Spelke, 2000; for review, see Allen & Haun, 2004).

Finally, we have assumed, following Wang and Spelke (2000), that egocentrically encoded object representations are updated independently of one another. However, other conceptions of egocentric representation are possible (besides that of Wang and Spelke) wherein updating may occur in a global fashion. Further study of the updating system is needed to determine the extent to which egocentric representations may or may not exhibit global characteristics.

Appendix

Proof of Egocentric Prediction for Analysis 2

If random variable x has a normal distribution, with mean zero and variance σ², then it has probability distribution function (written as x ≈ N(0, σ²))

$$f\left(\mathrm{x}\right)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-{\mathrm{x}}^2∕2{\sigma }^2},-\infty <\mathrm{x}<\infty .$$

The distribution function of random variable Y = |x| is

$$g\left(\mathrm{y}\right)=\frac{2}{\sigma \sqrt{2\pi }}{e}^{-{\mathrm{y}}^2∕2{\sigma }^2},\mathrm{y}\ge 0.$$

In our case, we have two independent random normals, x₁ and x₂. We want to show z₁ = |x₁ + x₂| and z₂ = |x₁ – x₂| have the same distribution.

Proof: Let w₁ = x₁ + x₂ ≈ N(0, σ₁² + σ₂²) w₂ = x₁ – x₂ ≈ N(0, σ₁² + σ₂²)

Hence, z₁ = |w₁| and z₂ = |w₂| have probability distribution functions

$$h\left({\mathrm{z}}_{\mathrm{i}}\right)=\frac{2}{\sqrt{{\sigma }_1^2+{\sigma }_2^2}\sqrt{2\pi }}{e}^{-{\mathrm{z}}_i^2∕2({\sigma }_1^2+{\sigma }_2^2)}\text{for}{\mathrm{z}}_i\ge 0,i=1,2.$$

And, the absolute sum of two independent normal deviates has the same probability distribution as their absolute difference (Leone, Nelson, & Nottingham, 1961).