ECM-Aware Cell-Graph Mining for Bone Tissue Modeling and Classification

Abstract

Pathological examination of a biopsy is the most reliable and widely used technique to diagnose bone cancer. However, it suffers from both inter- and intra- observer subjectivity. Techniques for automated tissue modeling and classification can reduce this subjectivity and increases the accuracy of bone cancer diagnosis. This paper presents a graph theoretical method, called extracellular matrix (ECM)-aware cell-graph mining, that combines the ECM formation with the distribution of cells in hematoxylin and eosin (H&E) stained histopathological images of bone tissues samples. This method can identify different types of cells that coexist in the same tissue as a result of its functional state. Thus, it models the structure-function relationships more precisely and classifies bone tissue samples accurately for cancer diagnosis. The tissue images are segmented, using the eigenvalues of the Hessian matrix, to compute spatial coordinates of cell nuclei as the nodes of corresponding cell-graph. Upon segmentation a color code is assigned to each node based on the composition of its surrounding ECM. An edge is hypothesized (and established) between a pair of nodes if the corresponding cell membranes are in physical contact and if they share the same color. Hence, multiple colored-cell-graphs coexist in a tissue each modeling a different cell-type organization. Both topological and spectral features of ECM-aware cell-graphs are computed to quantify the structural properties of tissue samples and classify their different functional states as healthy, fractured, or cancerous using support vector machines. Classification accuracy comparison to related work shows that ECM-aware cell-graph approach yields 90.0% whereas Delaunay triangulation and simple cell-graph approach achieves 75.0% and 81.1% accuracy, respectively.

1 Introduction

Osteosarcoma is the most common type of bone sarcoma, accounting for approximately 35% of bone tumors. Osteosarcoma develops in new tissue of growing bones and occurs most commonly in children or adolescents. Among children under age 15, it is the 6^th most frequently diagnosed cancer. Osteogenic sarcoma affects 400 children under age 20 and 500 adults who are mostly between the ages of 15–30 every year in the USA. Long term survival of osteosarcoma is 66%, leading to 300 deaths each year.

Pathological examination of a biopsy is the most reliable and widely used technique to diagnose bone cancer in the current practice of medicine. Successful biopsy requires knowledge of sarcomas and their treatment, and is best performed by a surgical specialist, followed by examination of the sample by an experienced pathologist. Biopsies can be performed as an open (surgical) procedure or a closed (percutaneous) procedure (using a large needle to remove the tissue). The biopsy must be performed properly such that enough tissue is collected to obtain a diagnosis, while still allowing surgical treatment of the tumor. In general, the preferred method is the least invasive technique that still allows the pathologist to give a definitive diagnosis. The pathologist examination of biopsy suffers from both inter- and intraobserver subjectivity and thus techniques to reduce this subjectivity with quantitative measures for cancer diagnosis are in great demand.

Several automated cancer diagnosis tools have been reported in the literature. Depending on the feature set these tools use, they can be divided into five categories; morphological, textural, fractal, intensity based and topological. Morphological features such as area, perimeter, and roundness of nuclei are used in [12,19,20,25,28,32, 33,36,40,42]. Textural features such as the angular second moment, inverse difference moment, dissimilarity, and entropy derived from the co-occurrence matrix are used for diagnosis in [12,38,20,24,34,36,40].

Complimentary to the morphological and textural features, colorimetric features such as intensity, saturation, red, green, and blue components of pixels [19,42] and densitometric features such as the number of low optical density pixels [38,24,34] have been reported. Fractals that describe the similarity levels of different structures found in a tissue image over a range of scales are proposed in [11,13]. Fractal dimensions are used as the feature set in these studies.

Orientational features extracted by making use of Gabor filters that respond to contrast edges and line-like features of a specific orientation are used in [37]. Other mathematical diagnosis tools rely on gene expression [4,18,21,23] and mass spectroscopy [41] to detect a cancer tumor.

Using these features, automated cancer diagnosis tools build classifiers to distinguish the healthy and cancerous tissues. Artificial neural networks [34,36,42], k-nearest neighborhood algorithm [38,13,19], support vector machines [20], linear programming [32], logistic regression [11,40], and fuzzy [28] and genetic [33] algorithms have been used for cancer diagnosis.

These techniques do not capture the structure-function relationship that is encoded by the spatial distribution of the cells and organization of the ECM in a tissue sample. Initial approach in this direction is the construction of Voronoi graphs which aim to model spatial distribution of cell where each nucleus represents a vertex in the graph [39,31,29]. Graph properties such as minimum spanning trees computed over voronoi graphs to capture the structural organization of tissue samples [10]. However, there are several limitations of Delaunay triangulation that colored cell-graphs successfully remedy. First, Delaunay triangulations are restricted to planar graphs which are very limited in their structure and do not allow crossing of edges. There is no evidence to justify such a limitation in a tissue’s structural organization. Second, a Delaunay triangulation is a single connected component (i.e., the tissue is represented by a connected graph) which may not be a valid assumption for sparse tissues. Third, the girth, defined as the length of the shortest path in the graph, of a Delaunay graph is always three, independent from how cells are spatially distributed. These restrictions bring many problems in tissue representation, ie for a connected planar graph G, the number of edges is bounded by E ≤ 3n − 6 where E is the number of edges and n is the number of nodes.

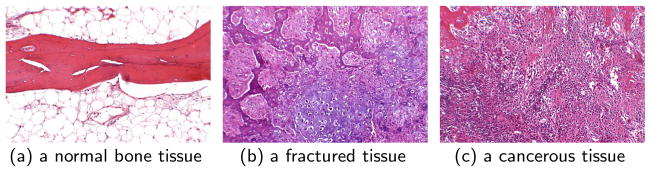
Recently, we proposed the cell-graph approach which remedies the shortcomings of Voronoi graphs and permits a more general and hypothesis-driven edge definition between a pair of vertices. We successfully analyzed brain [22] and breast tissues [5] using cell-graphs and demonstrated its advantages by comparing this method to related techniques. In this work we present a paradigm shift in cell-graph mining by incorporating the ECM information and allowing multiple colored cell-graphs, each modeling a different cell-type organization, coexist on the same tissue sample. We demonstrate this method on bone tissue samples that represent three different functional state: healthy, fracture, and cancerous. Figures 1(a), 1(b) and 1(c) illustrate H&E stained images of normal bone tissue, fractured bone tissue and cancerous bone tissue. The distinction between the healthy versus fractured and cancerous tissues is obvious but the cancerous versus fractured tissue is not easily distinguishable.

Fig. 1.

Microscopic images of tissue samples surgically removed from human bone tissues and stained with hematoxylin and eosin.

Contributions

This paper presents a new computational method (ECM-aware cell-graphs) that can model the organization of different cell types co-existing in the same tissue by considering the ECM niche surrounding each cell. We demonstrate the effectiveness of this method on histopathological bone tissue samples (provided by the pathology department of Hospital for Special Surgery in NYC) for automated cancer diagnosis.

In ECM-aware cell-graph technique multiple graphs, each with a different color, are constructed and their both graph theoretical and spectral features are computed for the classification problem by using an SVM with a radial kernel function. We compare the accuracy of our new method to previous cell-graph approaches and to the voronoi diagrams for automated cancer diagnosis. The results demonstrate the importance of capturing the information encoded by the ECM niche since ECM-aware cell-graphs outperform the related work significantly. Furthermore, we perform a feature selection procedure to determine the discriminative power of each feature.

Organization

The rest of the paper is organized as follows. In section 2 we explain our methodology for nuclei segmentation, graph generation, metric extraction from the graphs, and our learning algorithm. Section 2.3 explains in detail the graph metrics and spectral metrics extracted from cell-graphs. We present our experiments and results in section 3, and conclude our discussion in section 4.

2 Methodology

We propose to use ECM-aware cell-graphs that can capture the topological structures as well as the extracellular structures for bone tissue modeling and classification. Our general methodology consists of segmenting nuclei in tissue samples using the eigenvalues of the Hessian matrix, building cell-graphs that capture both the structural and extracellular properties, extracting graph theoretical features from these graphs and use them to learn different states of the tissues.

Multiple cell types can coexist in bone tissue samples i.e. mature bone forming cells (osteocytes), their precursors (osteoblasts), as well as osteoclasts, adipocytes, etc. These cells are enclosed in an extracellular matrix (ECM) that varies in composition and color when stained with typical histological dyes such as hematoxylin and eosin. To differentiate between different cell types in our graphs, we encode color information to each nucleus, thus assign color labels to each node. Depending on the predominant R, G, B values of neighboring pixels, we cluster nuclei in 4 groups; red, green, blue and white. We hypothesize a relationship between two nodes if they have the same color and if the distance between them is smaller than a threshold. In this setting, nuclei correspond to the vertices of our graph and the relationship between the nuclei corresponds to the edges of our graph. After forming ECM-aware colored cell-graphs we extract a rich graph theoretical feature set including spectral features. These features are then input to kernel machines for learning purposes. We use cross validation to report our results and other machine learning techniques to select the most important and distinguishing features.

We implemented ECM-aware cell graphs using the ITK library [27] for segmentation, Boost Graph Library(BGL) [35] for graph construction and libSVM library [7] for machine learning. We further discuss our methodology in the following sections.

2.1 Image Segmentation

ECM-aware cell-graph mining technique uses nuclei as the vertex set when generating graphs. Therefore, we start with nuclei detection in hematoxylin and eosin stained images.

Let f be the intensity function of an image. A common approach to analyzing the local behaviour of image f is to consider the second order approximation of f(x) around x₀ given by the Taylor expansion in equation (1).

$$f(\text{x})=f(x_0)+{(\text{x}-x_0)}^T\nabla f_0+\frac{1}{2}{(\text{x}-x_0)}^T{\nabla }^2{f}_0(\text{x}-x_0).$$ (1)

In this expansion ∇f₀ and ∇²f₀ denote the gradient vector and the Hessian matrix at x₀ respectively. The gradient vector, given by ∇f = (f_x, f_y), is a 2D vector composed of the partial derivatives in x and y directions. The partial derivatives of the image are defined as $f_x=\frac{\partial f}{\partial x}$ and $f_y=\frac{\partial f}{\partial y}$.

At any point the gradient vector points in the largest possible intensity increase. The gradient magnitude, given by $\mid \nabla f\mid =\sqrt{(f_x^2+f_y^2)}$, measures the magnitude of this change. The gradient and the magnitude have been used as edge detectors in the literature. Using the gradient information second partial deviates are calculated and the Hessian matrix is built as in (2).

$${\nabla }^{2}f=\left[\begin{array}{cc}\frac{{\partial }^{2}f}{\partial x^2}& \frac{{\partial }^{2}f}{\partial x\partial y}\\ \frac{{\partial }^{2}f}{\partial y\partial x}& \frac{{\partial }^{2}f}{\partial y^2}.\end{array}\right]$$ (2)

The eigenvalues of the Hessian matrix are of particular interest as they encode shape information. Depending on the values of the eigenvalues ridge-like membranes and blob-like nuclei can be segmented. Let λ₁ and λ₂ be the eigenvalues of the Hessian matrix and e₁ and e₂ be the corresponding eigenvectors for pixel x₀. These eigenvalues, λ_1,2 of the hessian matrix can be numerically calculated as in (3).

$${\lambda }_{1,2}=\frac{1}{2}\left\{\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}\pm \sqrt{{\left(\frac{{\partial }^{2}f}{\partial x^2}-\frac{{\partial }^{2}f}{\partial y^2}\right)}^2+4\frac{{\partial }^{2}f}{\partial x^2}}\right\}.$$ (3)

For 2D images, these eigenvalues can be used to detect ridge-like and blob-like structures. The blob-like structures are given by negative eigenvalues with high absolute values. More specifically, bright blob structures are given by λ₁ ≈ λ₂ ≪ 0 and likewise dark blob structures are given by λ₁ ≈ λ₂ ≫ 0. Table 1 summarizes how the eigenvalues and the structures in a tissue are related to each other. Note that we are only interested in blob-like structures as they represent nuclei in our tissue samples.

Table 1.

Local structures and their relations to eigenvalues are presented. High absolute values of the eigenvalues represent blob-like structures.

λ1	λ2	Structure
Low	High−	bright tubular
Low	High+	dark tubular
High−	High−	bright blob
High+	High+	dark blob

Frangi et al. introduced using a vesselness measure function for 2D images in [14]. This vesselness measure takes into account the $R_B=\frac{{\lambda }_1}{{\lambda }_2}$ ratio and $S={\left|\right|{\nabla }^{2}f\left|\right|}_F=\sqrt{{\sum }_{j\le D}{\lambda }_j^2}$. S is the Frobenius matrix norm and used to differentiate objects of interest from the background, whereas R_B is a measure to differentiate between blob-like structures and ridge-like structures. S will be low in background pixels as the eigenvalues for pixels lacking contrast will be small. In high contrast regions however, at least one of the eigenvalues will be high and S will be large.

As proposed in [15] a simple way of concluding the segmentation using these two measures is to use them together to decide whether a pixel is background or foreground as in equation (4).

$$I_{\mathit{seg}}[p]=\{\begin{array}{ll}1,\hfill & \text{if}{R}_B[p]\ge T_1\text{and}S[p]\ge T_2\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$ (4)

Often times these threshold values T₁ and T₂ are dependent on dataset and will not work on a new set of images. Furthermore, even with the same dataset, scaling the intensity values of the same image will change the corresponding thresholds. There have been studies in the image processing community on the automatic detection of these thresholds. One such study uses half the value of the standard deviation of the first eigenvalues [17]. In [16], using the Frangi’s vesselness enhancement filter, defined as in equation (5) the tubular structures are enhanced and then the image is thresholded with adaptive thresholding to segment the nuclei borders. It should be noted that a perfect segmentation is not our main concern. Considering the deficiencies of hematoxylin and eosin staining and the resolution of the images we are using, a rough segmentation of the tissue is all we need.

$$v_o(s)=\{\begin{array}{ll}0,\hfill & \text{if}{\lambda }_2>0\hfill \\ exp\left(-\frac{R_B^2}{2{\beta }^2}\right)exp\left(1-exp\left(\frac{S^2}{2c^2}\right)\right)\hfill & \text{otherwise}\hfill \end{array}$$ (5)

2.2 Cell-Graph Generation

In image segmentation, we identified the cells using eigenvalues of the Hessian matrix. In the cell-graph generation step, we build our cell-graphs on these cells.

Formally a graph is represented by G = (V, E) where V is the vertex set and E is the edge set of the graph. Each cell constitutes a vertex in our cell-graphs. We define two different ways to construct cell-graphs capturing the pairwise distance relationship between the vertices, namely simple cell-graphs and ECM-aware cell-graphs. We also compare these two models to Delaunay triangulations method.

Simple cell-graphs and Delaunay triangulations are built without considering the ECM niche. That is, they capture only the structural properties of the tissue, whereas ECM-aware cell graphs encode ECM into graph formation and therefore capture both the structural and extracellular properties of tissues. The following subsections explain these models in detail.

2.2.1 Simple Cell-Graphs

Simple cell-graphs hypothesize that a relationship between two nodes exists if these two nodes are touching or close to each other. Biologically, this might mean that these cells are communicating with each other.

We find the center of mass for each cell and store their x-y coordinates. We hypothesize a communication by setting a link between two nodes if the euclidean distance between them is less than a threshold that ensures a physical contact between the corresponding cell membranes. The Euclidean distance between two cells is simply given by equation (6)

$$d(u,v)=\sqrt{{(u_x-v_x)}^2+{(u_y-v_y)}^2},$$ (6)

where u_x and u_y are x and y coordinates of node u respectively. The threshold for communication is chosen by a 10-fold cross validation process.

2.2.2 ECM-Aware Cell-Graphs

Both simple cell-graph approach and Delaunay triangulations are limited to modeling the spatial distribution of cells over a tissue sample. Both of these approaches segment the tissue samples and use graph theoretical approaches to link the cells and address the problems of diagnosis, classification, etc. However, these graphs ignore the composition (i.e., color) and distribution of the extracellular matrix(ECM) surrounding the cells.

The ECM is composed of a complex network of proteins and oligosaccharides that play important roles in cellular activities such as division, motility, adhesion, and differentiation [3] and therefore plays an important role in the functional state of the tissue. ECM-aware cell-graphs try to embed this information as well as the structural properties between cells for bone tissue modeling and classification.

ECM-aware colored cell-graphs are built in three phases:

1. Image processing and segmentation: we segment the digital images of histopathological tissue samples as explained in section 2.1 to identify the cells.

2. Cell-based filtering: we assign a color to each cell, based on the RGB values of its surrounding ECM. We find the center of mass for each cell and store the x-y coordinates of each nucleus. To incorporate the ECM composition information, for each nucleus center, we examine the δ neighboring pixels in each direction, giving a square of 2δ + 1 by 2δ + 1 pixels including the center of the mass for that nucleus. More specifically, we consider all the pixels in a 2δ + 1 pixels by 2δ + 1 square where the center of the square is the center of the nucleus. We calculate the mean R, G, B values in this square and assign each cell a color depending on R, G, B values of these (2δ + 1)² neighboring pixels¹. Note that this step can be perceived as a new filtering technique applied to each nucleus (instead of a pixel).

3. Construction of colored cell-graphs: we cluster the cells into four color groups (i.e., red, green, blue and white) based on the predominant color of the ECM pixels. We then build four separate cell-graphs for each color group. Having generated the ECM-aware cell-graphs, we calculate a set of global metrics from these graphs and use them as the feature set for machine learning. In these graphs, the assignment of a link between two nodes is determined by both the distance between the nodes and the color of the ECM surrounding each node. A link between two nodes is possible only if the distance between these nodes is smaller than the threshold, and the color of the ECM surrounding these nodes fall into the same color group i.e. red, green, blue, white.

2.2.3 Voronoi Graphs and Delaunay Triangulation

We compare our ECM-aware cell-graph technique to simple cell-graph technique and to the other well-known Voronoi diagram method. Voronoi diagrams and their Delaunay triangulations are proposed in [29,31,39]. On a tissue image, the Voronoi diagram partitions the image into convex polygons such that each polygon contains exactly one cell (generating point) and every point in a given polygon is closer to its generating point than to any another generating point in the tissue. Each such polygon constitutes a Voronoi cell. The dual of Voronoi graphs are built by linking the generating points of neighboring Voronoi cells. The Voronoi diagram of a sample tissue image and its Delaunay triangulation is illustrated in figure 2(c) and 2(d). We build Delaunay triangulations on cells that are identified in the segmentation step. After triangulation we follow the same steps as in other cell-graph learning techniques. We calculate the metric explained in section 2.3 and then use these metrics as the feature set for our classifier.

Fig. 2.

A fractured bone tissue example is shown in 2(a). Note the fracture cells in the middle of the original image. The simple-cell-graph representation, the Voronoi diagram and the Delaunay triangulation for this sample tissue are depicted in 2(b), 2(c) and 2(d) respectively. The corresponding ECM-aware cell-graph is drawn in 2(e). The interactions between fracture cells are drawn with blue and the red cells with red color. Delaunay triangulation represents the tissue as a single connected component and does not allow crossing of edges. Simple-cell-graphs relaxes these restrictions and allows the tissue to be non-planar and disconnected. Likewise, ECM-aware cell-graphs do not put such restrictions on the tissue and moreover it can also capture the structural organization of different cells in a tissue. Furthermore, ECM-aware cell-graphs can be adjusted with different linking thresholds whereas Delaunay triangulations are fixed representations.

2.3 Metrics

After identifying the cells and forming cell-graphs on them, we extract a set of topological and spectral features from these graphs. These features quantify the different types of tissues and serve as the feature set for our learning algorithm.

We start with the metrics we have used in simple cell-graphs [22] and hierarchical cell-graphs [5]. These metrics proved to be useful for brain cancer diagnosis and breast cancer diagnosis. In addition to these metrics, we also included metrics derived from spectral properties of the cell-graph. Table 2 gives a summary of these metrics.

Table 2.

Graph metrics, their definitions and interpretations

Simple Metrics: Density of the tissue sample. Healthy tissues contain fewer cells and yield to sparse graphs. Both fracture and cancerous (dis)functional state presents a dense cell population.
Number of Nodes	Number of cells in the tissue.
Number of Edges	Number of hypothesized interactions
Distance Based Metrics: These metrics measure how far away the nodes are from each other. Since uncontrolled cell divisions occur in cancer tissues, the nodes will be closer to each other and as a result distance based metrics will be smaller than that of the normal tissue samples.
Eccentricity of a Node	Maximum value of the shortest path from a given node to any other node.
Closeness of a Node	Average value of the shortest path from a given node to any other node.
Diameter	Maximum eccentricity.
Radius	Minimum eccentricity.
Number of Central Points	Number of nodes that have eccentricity equal to radius.
Hop-plot Value	For hop h, number of node pairs such that the path length between these node pairs is ≤ h hops.
Hop-plot Exponent	Slope of the hop-plot values as a function of h in log-log scale.
Connectedness and Cliquishness Measures: Typically a normal bone tissue example is less connected than a cancerous tissue example.
Average Degree	Average value of number of neighbors a node has.
Clustering Coefficient of a Node	The ratio of the links a node’s neighbors have in between to the total number that can possibly exist.
Giant Connected Component Ratio	Ratio of the size of the largest set of the nodes that are reachable from each other to the number of nodes.
Percentage of Isolated Points	The ratio of number of nodes with degree equal to zero, to the total number of nodes.
Percentage of End Points	The ratio of number of nodes with degree equal to one, to the total number of nodes.
Spectral Metrics: both adjacency matrix and its Laplacian provide features about the structural organization. For example the number of eigenvalues with value 0 correspond to connected components.
Number of 0,1,2 eigenvalues	Number of eigenvalues that have a value 0, 1 and 2 respectively.
Lower slope	The slope of the line segment corresponding to eigenvalues between 0 and 1.
Upper slope	The slope of the line segment corresponding to eigenvalues between 1 and 2.
Trace	Sum of the eigenvalues
Energy	Squared sum of the eigenvalues

Our metrics can be grouped in four categories, simple metrics, distance based metrics, connectedness metrics and spectral metrics. The simplest metrics are the number of nodes and number of edges existing in the graph. The ratio of the number of edges to the number of nodes is called the average degree. Although in some cases higher values of these metrics is an indication of abnormality in the tissue, it is not always the case that the higher these values the more likely that the tissue is cancerous.

In the next category we use various metrics that quantify how far the nodes are apart from each other. The shortest path between two nodes is defined as the minimum number of hops between them. Using the definition of the shortest path distance, the eccentricity of a node u is given as the maximum shortest path distance from node u to any of the nodes in the graph. After the calculation of the eccentricities of each node, the diameter of the graph is simply given by the maximum eccentricity. The minimum eccentricity is defined as the radius, and the nodes that have eccentricity values equal to the radius are defined as central points in the graph.

In the connectedness measures, the clustering coefficient of a node u is the ratio of the number of edges u’s neighbors have in between, and the number of possible edges that could have existed between node u’s neighbors. This metrics quantifies how well a node’s neighbors are connected to each other. The average value of the clustering coefficients of a graph shows how close the graph is to be a clique and whether a node’s neighbors are also neighbors of each other. The giant connected component of a graph is defined as the largest set of the nodes that are reachable from each other. The ratio of the size of the giant connected component to the number of nodes in the graph is called as giant connected component ratio. Other connectivity measures, such as isolated points, nodes that have degree 0 and end points, nodes that have degree 1 are also included in this category.

2.3.1 Spectral Graph Analysis

Apart from the graph metrics defined above, we also performed spectral graph analysis on our cell-graphs. The spectral analysis of graphs [9] deal with the eigenvalues of the adjacency matrix or other matrices derived from the adjacency matrix.

The adjacency matrix A of a graph G(V, E) where V is the vertex set and E is the edge set is defined as in (7).

$$A(u,v)=\{\begin{array}{ll}1,\hfill & \text{if}(u,v)\in E\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}.$$ (7)

The degree matrix D is constructed by D(u, u) = Σ_v∈V A(u, v). More specifically, the degree matrix is a diagonal matrix that holds the degree of node i at (i, i) entry. The Laplacian matrix L is then given by the difference between the degree matrix and the adjacency matrix, L = D − A. Laplacian matrix is strongly connected to the gradient of the graph, nevertheless we use the normalized version of the Laplacian matrix given as (8).

$$\mathcal{L}(G)=\{\begin{array}{ll}1,\hfill & \text{if}i=j\text{and}{d}_i\ne 0\hfill \\ -\frac{1}{\sqrt{d_i{d}_j}},\hfill & \text{if}i\text{and}j\text{are}\text{adjacent}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (8)

The spectral decomposition of the normalized Laplacian matrix is given by ℒ = ΦΛΦ^T where Λ = diag(λ₁, λ₁ … λ_|V|) with the eigenvalues as its elements and Φ with the eigenvectors as columns. The normalized Laplacian matrix and its spectral decomposition provide insight to the structural properties of the graph. Since ℒ is a symmetric positive semi-definite matrix the eigenvalues of normalized Laplacian matrix are all between 0 and 2.

For normalized Laplacian matrices the number of zero eigenvalues gives the number of connected components in the graph. We include the number of zero eigenvalues, the number of eigenvalues equal to one, and the number of eigenvalues equal to two in our feature set. We sort and plot the eigenvalues of the normalized Laplacian matrix in an increasing order. We fit a line to this plot in a least squares manner and calculate the slope of the line for the eigenvalues that are between 0 and 1. We call this slope lower slope. Likewise, we also calculate the upper slope that corresponds to the slope of the eigenvalues between 1 and 2. The last two normalized Laplacian matrix features we include in our feature set are the trace of the normalized Laplacian and energy of the normalized Laplacian defined as Σ_iλ_i and ${\sum }_i{\lambda }_i^2$. It has been reported that the eigenvalues of the normalized Laplacian graph are more distinguishing than that of the Laplacian or the adjacency matrices [9]. Nevertheless we also included the same set of measurements for the adjacency matrix and leave it to the feature selection method to decide which metrics are more valuable to distinguish the tissues. For a tissue sample we calculate all these features for the red graph, blue graph, white graph, green graph and represent the tissue with all these features.

2.4 Cell-Graph Mining

To learn the structural differences between the different types of bone tissues, we compute the graph metrics for each tissue sample as explained in section 2.3 and build a classifier using these metrics. The range of these metrics are different from each other, i.e. the average clustering coefficient of a graph is a number between 0 and 1, whereas the number of edges in a graph is around a thousand. We uniformly scale each metric to the range [−1, 1] to improve learning.

Support vector machines (SVMs) have been used successfully for classification purposes [6]. The basic idea of SVM is to map the data into a higher dimension and then to create an optimal separating hyperplane between data points such that the data points of different classes fall on the opposite sides of this hyperplane. If there is no hyperplane that separates the classes (i.e., if the data is not linearly separable in this higher dimension), this algorithm creates a hyperplane that leads to the least error.

Let x₁, x₂, … x_n be the training samples and y₁, y₂, … y_n be the corresponding class labels. The decision boundary of a linear classifier is given by w.x + b = 0 where w and b are parameters of the model.

In the case of a non-separable data set, slack variables, ξ_i, are introduced to minimize the error. Parameters of the optimal separating hyperplane are derived by solving the quadratic programming optimization problem, given in equation (9), with linear equality and inequality constraints. This optimization problem maximizes the margins.

$$\begin{array}{c}\text{minimize}:g(\mathbf{w},\xi )=\frac{1}{2}{\left|\right|\mathbf{w}\left|\right|}^2+C\sum _{i=1}^N{\xi }_i\\ \text{subject}\text{to}:y_i(<w,\phi (x_i)>+b)\ge 1-{\xi }_i,\\ {\xi }_i\ge 0,i=1,2\dots m.\end{array}$$ (9)

Equation (9) can be rewritten as (10),

$$\begin{array}{l}min:W(\alpha )=-\sum _{i=1}^N{\alpha }_i+\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{y}_i{y}_j{\alpha }_i{\alpha }_{j}k(x_i,x_j)\\ \text{s}.\text{t}.:\sum _{i=1}^N{y}_i{\alpha }_i=0,\forall i:0\le {\alpha }_i\le C\end{array}$$ (10)

where α_i a Lagrange multiplier that corresponds to the sample x_i. In this dual representation k(., .) is a kernel function that maps the input space to a higher and more suitable feature space by (11)

$$k(x_i,x_j)=<\phi (x_i),\phi (x_j)>.$$ (11)

An important feature of support vector machines is the use of kernel functions. The kernel function transforms the input space to a new space and allows the algorithm to find the optimal separating hyperplane in this new space. The use of nonlinear kernel functions allows using non-linearity without explicitly requiring a non-linear algorithm. We have used the radial basis kernel, also called Gaussian kernel, defined as in (12),

$$k(x_i,y_i)=e^{\gamma {\left|\right|x_i-y_i\left|\right|}^2}.$$ (12)

With a careful choice of γ and C, a Gaussian kernel can indeed model a linear kernel [30]. That is, linear kernels can be thought of as a subset of Gaussian kernels. This is why Gaussian kernel is often times considered to be more useful than the linear kernel. However, Gaussian kernel introduces another parameter γ that effects the accuracy of the SVM significantly. For Gaussian kernels, γ along with C has to be decided carefully for a successful classification.

The parameter selection step for Gaussian kernels is more time consuming as a result of the newly introduced γ parameter. We take the same approach as in [26] to search the best parameters. The best parameter pair (C^*, γ^*) is searched within the grid C ∈ 2⁻⁵, 2⁻³ … 2¹⁵ and γ ∈ 2⁻¹⁵, 2⁻¹³, …, 2³. Since there are only two parameters, the computational time by this grid-search is not much more than that by other advanced methods for parameter selection. After finding best values for these parameters, a finer search is performed within that neighborhood to fine-tune the parameters even further.

It should be noted that the original SVM is capable of binary classification, where there are only two classes. In our case we have three classes, healthy, fractured, and cancerous, that is we need multi-class SVMs. Two different types of methods have been introduced for multi-class SVMs, combining binary classifiers to construct a multi-class SVM or considering all classes at once and solving multi-class SVM in one step. We take the first approach and use the one-against-one method. In this approach for c classes, $\frac{c(c-1)}{2}$ binary classification problems are defined for each pair of these classes. These SVMs are then merged using majority voting.

2.5 Cross Validation and Feature Selection

We use K-fold cross validation to report our results. K-fold cross validation partitions the dataset into K disjoint subsets called folds. Of these K folds, K − 1 are used to train the model, and the remaining fold is used to test the model. This constitutes one iteration of the K-fold cross validation. This process is repeated K times, each time leaving out one fold for validation and using the other folds as the training set. The accuracy of each run is then averaged and reported as the cross validation accuracy. The advantage of this method over repeated random sub-sampling is that all observations are used for both training and validation, and each observation is used for validation exactly once. A common choice for K value is 10 and we used 10-fold validation.

Since there are more cancerous instances than fracture and healthy instances in our dataset, there is a chance that a given fold may not contain any fracture and even more probably no healthy tissue samples at all. To ensure that this does not occur, we used stratified K-fold cross-validation where each fold contains roughly the same proportion of class labels as in the original set of samples.

For a tissue, each of the four different ECM-aware cell-graphs (red, blue, green and white) has 34 features, including both the graph metrics and spectral metrics, making a total of 136 features to represent a tissue. Not all features have the same importance and some can be neglected. Indeed, using too many features can degrade the accuracy of the classifier due to the curse of the dimensionality. We perform feature selection to find the most important features for classification. We used the F-score metric [8] to rank the importance of features. The F-score for feature i is calculated as in (13),

$$F(i)=\frac{{({\overline{\mathbf{x}}}_i^{(+)}-{\overline{\mathbf{x}}}_i)}^2+{({\overline{\mathbf{x}}}_i^{(-)}-{\overline{\mathbf{x}}}_i)}^2}{\frac{1}{n_{+}-1}{\displaystyle \sum _{j=1}^{n_{+}}}{(x_{j,i}^{(+)}-{\overline{\mathbf{x}}}_i^{(+)})}^2+\frac{1}{n_{-}-1}{\displaystyle \sum _{j=1}^{n_{-}}}{(x_{j,i}^{(-)}-{\overline{\mathbf{x}}}_i^{(-)})}^2}$$ (13)

where x_i is the average of feature i in the whole data set and likewise $x_i^{(+)},x_i^{(-)}$ are the averages of the i^th feature, positive and negative instances in the datasets respectively. $x_{j,i}^{(+)},x_{j,i}^{(-)}$ are the i^th feature of the j^th positive and negative instances respectively. F-score gives the discriminative capability of each feature, when feature f is more discriminative, the associated F-score F_d is larger.

3 Experiments

3.1 Data Set Preparation

Histopathology slides of bone tissues, stained with hematoxylin and eosin, are randomly collected from the Hospital for Special Surgery in NY under the direct supervision of Dr. Peter Bullough who is the head of the pathology department. These slides are numerically coded, the patient identifiers are removed and the coded tally of individual cases are secured in the pathologists office. Digital photomicrographs are obtained in a standardized fashion with regards to magnification and illumination by Dr. Bullough.

In addition to healthy bone samples, two diagnostic groups of bone tissues were collected for analysis by Dr. Bullough. The first group was obtained from patients with both simple and comminuted fractures requiring open reduction. The second group was from patients diagnosed as having malignant bone forming tumors (osteoscarcoma, osteogenic sarcomas). Tissue from both of these conditions may be cellular and produce varying types of ECM including mineralized and unmineralized woven bone, hyaline cartilage and disorganized collagen bundles. Generally, the damaged tissue (i.e. fracture callus) will have a more homogeneous cell population than the sarcomatous tissue; the former will on occasion have marked atypicality and mitotic activity whereas the sarcomatous tissues may appear rather bland. Nevertheless, an experienced pathologist is generally able to distinguish these two conditions based upon certain patterns of organization which we hypothesize using graph theory.

The final data set contained 20 images of healthy bone tissues, 39 fractured tissues, and 75 diseased bone tissues.

3.2 Results and Interpretation

There are three parameters to be set and fine-tuned for the ECM-aware cell-graph construction. The first parameter is the number of pixels to use to decide on the color of the node, that is the δ value. For example, choosing a value of 5 for δ will define a grid entry of 11 pixels × 11 pixels and place the center of the nuclei to the center of this grid entry. After this placement the color assignment can be carried on in this grid as explained in the methodology. To decide on the δ value, we keep the link threshold values (red link threshold, blue link threshold) constant and experiment with different values of δ. The results of this search are given in table 3. Clearly, choosing a very small value for δ will not define the surrounding ECM fully and choosing a large value for δ will lead to considering other nuclei’s ECM. We see that δ = 10 gives the best prediction accuracy for all values of link threshold except 4. We therefore use δ = 10 in our calculations.

Table 3.

Cell-Graph prediction results with varying threshold values and δ values. A choice of 10 for grid size yields the best accuracy values.

Link Threshold	Grid Size
	5	10	15
2	87.03	88.69	87.28
3	86.61	88.26	86.91
4	87.66	85.64	85.95
5	87.00	88.17	86.78
6	86.50	88.30	87.73

ECM-aware cell-graphs set a link between two nodes when the color code for those nodes are same and the distance between them is less than a threshold. For each tissue, there are four different ECM-aware colored cell-graphs, red, green, blue, and white and therefore four different thresholds to be decided. However, in almost all tissue samples, the number of white cells and number of green cells are far less than that of the red and blue cells. That is, red cell-graphs and blue cell-graphs are more important than the others. Nonetheless, we include the white and the green cell-graphs for the sake of completeness. However, to reduce the parameter search space we only tune the parameters that are going to affect the results, which in this case is the red threshold and blue threshold.

The result of edge threshold search is given in table 4. We see that ECM-aware cell-graphs obtain the best accuracy of 90% with a blue link threshold of 4 and red link threshold of 2. During this search, the green threshold and the white threshold are set to 4. Note again that the number of green and white vertices are far less than that of the blue and red vertices and therefore changing the threshold value for green and white will not change the overall graph structure and therefore the results will not be effected significantly. This limits the number of parameters to be searched to three, namely, neighborhood parameter δ, blue edge threshold T_blue and the red edge threshold T_red.

Table 4.

ECM-Aware Cell-Graph results with varying red and blue link thresholds is given. A blue threshold of 4 and a red threshold of 2 yields the best accuracy values.

Blue Threshold	Red Threshold
	2	3	4	5	6
2	88.33±1.69	84.33±3.91	83.67±8.53	82.67±2.93	83.67±2.58
3	89.67±6.84	83.67±4.48	84.67±6.84	84.00±6.10	87.33±3.52
4	90.00±4.64	86.00±4.48	84.67±3.52	83.00±2.59	82.67±4.25
5	87.00±0.02	88.33±4.77	86.67±4.57	83.33±4.11	84.67±4.52
6	86.33±3.82	88.33±3.93	87.67±1.65	82.67±2.67	83.00±3.84

Using these fine-tuned parameters δ, T_red, T_blue for ECM-aware cell-graphs, we give a comparison of the prediction accuracies of the Delaunay-based approach, simple cell-graph approach, and ECM-aware cell-graph method in table 5. In this table Hea. Fra. Can. and Act. stands for healthy, fracture, cancerous and actual class respectively. This table shows the ratios of the predicted classes to the actual classes. Simple cell-graphs obtain an overall accuracy of 81.5% and yet obtain better learning ratios for each tissue type than the Delaunay triangulation technique. With the ECM-aware cell-graphs the learning ratio increases further to 90%. We see that the ECM-aware cell-graph approach not only gives the best overall performance, but also for each of the individual tissue classes gives comparable classification ratios, if not better than the rest of the methods.

Table 5.

Detailed Comparison of Simple cell-graphs, ECM-aware cell-graphs and Delaunay triangulation is given. ECM-aware cell-graphs have better accuracy in each individual class.

	Simple Prediction			Delaunay Prediction			ECM-aware Prediction
Act	Hea	Frac	Can	Hea	Frac	Can	Hea	Frac	Can
Hea	98.8	0	1.2	100	0	0	100	0	0
Fra	0	79.3	20.7	9.1	69.7	21.21	0	87.1	12.9
Can	1.8	22.4	75.7	2.5	28.33	69.17	0	6.5	93.5

Due to the sparseness of healthy bone tissues, it is not surprising that all of the methods are nearly 100% accurate. Since healthy bone samples are easy to classify, the real problem is how well a method can differentiate between fractured and cancerous tissues. With this in mind we see that ECM-aware cell-graphs are better than both simple cell-graph and the Delaunay triangulation methods. The Delaunay triangulation especially proves unreliable for the fractured versus cancerous tissue classification as it obtains the lowest accuracy.

There are several reasons why ECM-aware cell-graphs perform better on bone tissue modeling and classification than the simple cell-graphs and Delaunay triangulation. Delaunay triangulations result in planar graphs, which can be embedded in a plane. More specially, the edges of the Delaunay triangulation do not cross each other and intersect only at the end points. There is no evidence to justify such a limitation in tissue organization. Second, in Delaunay triangulations all the nodes are reachable from each other, meaning that the giant connected component ratio is one. This assumption might hold for some of the cancerous tissue samples but is especially not valid for healthy tissue samples, as the healthy graphs are sparse in nature. Third, the shortest cycle of a Delaunay graph, called the girth, is 3 which may not hold for sparse tissue representations.

Simple cell-graphs on the other hand overcomes the limitations of the Delaunay triangulations, but still is restricted compared to ECM-aware cell graphs since they do not distinguish different cell-types that co-exist. ECM-aware cell-graphs model relationships between the same type of cells rather than blindly assuming a relationship exists between two nodes if the distance is smaller than a threshold. For each node, the intensity properties of the ECM around that node are incorporated into the modeling step which results in higher accuracies for classification.

3.2.1 ROC Analysis

We also give the sensitivity vs specificity analysis, also known as receiver operator characteristics (ROC) curves, for comparing ECM-aware cell-graph to Delaunay triangulation approach. A ROC curve is simply the plot of sensitivity versus 1-specificity for a binary classification problem. After obtaining the ROC curves, the area under the curve (AUC) is used as goodness measure for the classifier. The conventional ROC analysis is introduced for binary classification problems. Our dataset has three classes, healthy, fractured, and cancerous tissues and thus we compared fracture vs cancer, healthy vs fracture and healthy vs cancer classification problems separately for ROC analysis. Second, we need a probabilistic SVM so that a cut-off value can be introduced enabling the observation of sensitivity vs specificity by varying that cut-off value. We used the probabilistic SVM idea proposed in [1] and the implementation in Lin et al [2].

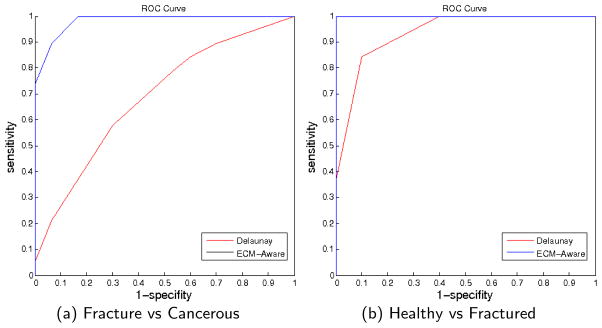
From the confusion matrix in table 5 we see that there is almost no confusion between normal vs cancerous tissue types in both Delaunay graph method and the ECM-aware cell-graph method. The ROC curves for these two cases are the best case scenario and area under the curve is very close to 1. However, as noted before, fracture vs cancer and healthy vs fracture classification problems are more difficult and biologically more challenging. We give comparisons of ROC curves of Delaunay triangulation and ECM-aware techniques in figure 3(a) and 3(b) respectively. The AUC for ECM-aware cell-graph technique is 0.9781 while Delaunay triangulation achieves 0.6667 for fractured versus cancerous tissue classification. For healthy vs fractured classification problem, our ECM-aware technique achieves a AUC value of 1 whereas Delaunay triangulation method gives 0.9237.

Fig. 3.

Receiver operator characteristics curves are given for the fracture vs cancerous and healthy vs fracture in 3(a) and 3(b) respectively. The area under curve (AUC) for ECM-aware colored cell-graphs is 0.97 and 1 whereas for Delaunay this value is 0.66 and 0.92 respectively. Thus, ECM-aware cell-graphs perform better than Delaunay graphs.

3.2.2 Feature Selection

In our experiments, we calculate a rich set of features to be used in the classification. These features are possibly correlated to each other and moreover some of these features might be better suited for bone tissue structure representation. Since using too many features can degrade the accuracy due to the curse of the dimensionality, we perform feature selection on our dataset. Table 6 gives the f-scores of the most important features. We only used these features to report our cross validation results.

Table 6.

F-scores for the features that yielded the best prediction results are given. Out of 84 graph metrics, connectivity measures such as giant connected component ratio, clustering coefficient, isolated points and normalized Laplacian metrics are the most discriminative features.

Green Giant Connected Ratio	1.43
White Clustering Coefficient	1.11
White Giant Connected Ratio	1.07
White Percentage of Isolated Points	1.07
Red Clustering Coefficient	0.98
Number of 2s in Red Normalized Laplacian	0.93
Blue Clustering Coefficient	0.89
Number of 1s in Red Normalized Laplacian	0.89
Red Normalized Laplacian Energy	0.87
Red Percentage of Isolated Points	0.82
Blue Percentage of Isolated Points	0.81

Table 7 gives the f-score values of the most distinguishing metrics for fractured versus cancerous classification. From red cell-graphs, average clustering coefficient, normalized Laplacian energy, normalized Laplacian trace, percentage of isolated points, average eccentricity 90, average degree are the most distinguishing features and the list continues with giant connected component ratio, average clustering coefficient, and percentage of central point of blue graphs. It is not surprising to see that the most discriminative features are from the red and the blue graphs as these graphs are the most dominant structures in our fractured and cancerous tissue examples.

Table 7.

F-scores for the features that yielded the best prediction results for cancerous vs fractured. As well as the connectivity measures and the Laplacian features the shortest path related measures such average eccentricity and number of central points are important.

Red Clustering Coefficient	1.07
Red Normalized Laplacian Energy	0.94
Red Percentage of Isolated Points	0.81
Red Normalize Laplacian Trace	0.77
Red Average Eccentricity 90	0.76
Red Average Degree	0.71
Blue Giant Connected Ratio	0.67
Blue Clustering Coefficient	0.66
Blue Percentage of Isolated Points	0.61
Blue Percentage of Central Points	0.61

4 Conclusion

Bone tissue usually contains multiple cell types, i.e., mature bone forming cells (osteocytes) and their precursors (osteoblasts), as well as osteoclasts, adipocytes, etc. These cells are surrounded by an extracellular matrix (ECM) that varies in composition and color. It is often difficult to identify meaningful (i.e., diagnostic) relationships between cells and their surrounding ECM in histopathological sections. In this paper we present ECM-aware cell-graphs that distinguish between different types of cells by incorporating the ECM niche into the topological organization of the cells. We show that ECM-aware cell-graph approach can model and classify bone tissue samples in different (dis)functional states such as healthy, fractured and cancerous.

ECM-aware cell-graph approach is a paradigm shift in our previous work on cell-graph mining method used to model and classify brain tissue samples and breast tissue samples. Cancerous brain tissue samples have a diffusive structure and best represented by simple cell-graphs [22] whereas breast have lobular structures and therefore best represented by hierarchical cell-graphs [5]. Although these techniques achieved comparatively good results, they consider the cells in perfect isolation from the surrounding ECM. In this work we extended our previous results on brain and breast tissue samples to bone tissue modeling by incorporating the ECM information. Our technique achieved 90.0% prediction rate whereas Delaunay triangulation achieved 75.8 and our simple cell-graph technique achieves 81.4%.

ECM-aware cell-graph approach has several components: image segmentation for identification of nodes, ECM-aware labeling of each node, establishing edges between labeled nodes, graph theoretical feature extraction, and finally supervised learning with SVM over feature sets. Our image processing is based on the eigenvalues of the hessian matrix to capture the shape information. For 2D images, these eigenvalues can be used to detect ridge-like and blob-like structures to segment the cells in a given tissue. To incorporate the ECM information to each cell, we considered the k neighborhood of every cell and encode a color code to it depending on the predominant color around that cell. We hypothesize a relationship between two cells when the color code for those cells are same and the distance between them is smaller than a threshold to ensure that there is a physical contact between the membranes. Considering the cells as the vertex set and the relations between the cells as the edge set, we model a given tissue with ECM-aware cell-graphs. We calculate a rich set of features for these graphs. We also include spectral graph analysis in our calculations. These quantitative features represent a tissue. We used support vector machines for healthy, cancerous and fracture tissues classification. We report our results using 10-fold cross validation and conclude with finding the most important features for bone tissue modeling and classification. We included the sensitivity vs specificity analysis to better assess the accuracy of our representation. A computational comparison of our approach to the related work in the literature shows that ECM-aware cell-graphs are more discriminative of the functional states of bone tissues. However, we believe that accuracy can be improved further by increasing our limited data size and a more accurate segmentation of nuclei and ECM.