Combining information across frequency regions in fundamental frequency discrimination

Abstract

Sensitivity to fundamental frequency (F0) differences was measured for two complex tones, A and B, which had the same F0 but were filtered into two different frequency regions. Tones were presented either alone or together. A signal-detection analysis was used to predict effects of combining F0 information across frequency regions. For 400-ms tones containing only unresolved harmonics, the first experiment showed that performance (in terms of d′) for the combined presentation was better than for the isolated tones but was not optimal (assuming independent channels and noises) and was independent of the relative timing of pulses in the envelopes of tones A and B (varied by changing the starting phase of components of tone B relative to those of tone A). The nonoptimal performance was shown not to be due to peripheral masking (experiment II), or to listeners paying attention mainly to one frequency region (experiment III), nor was it specific to conditions where all harmonics were unresolved (experiment IV). In contrast, optimal performance in F0 discrimination for combined presentation was observed for 50-ms tones (experiment V). The results may reflect the limited ability of the human auditory system to integrate information simultaneously in the time and the frequency domains.

I. INTRODUCTION

In many everyday situations, listeners are required to estimate the fundamental frequency (F0) of periodic sounds, such as the voiced portions of speech. Such sounds are often broadband and sometimes contain several fairly discrete spectral peaks, indicating that the majority of information comes from fairly discrete spectral regions. Thus, it is important to understand the extent to which the auditory system can combine F0 information across spectral regions and the dependence of this ability on the physical parameters of the stimulus.

In recent years, several studies have reported an impairment in discrimination of F0 for two sequentially presented complex target tones due to the presence of another complex tone (the interferer) which was filtered into a spectral region remote from that of the target tones (Gockel et al., 2004, 2005, 2009a, 2009b; Micheyl and Oxenham, 2007). This “pitch discrimination interference (PDI)” is strongest when target and interferer tones have similar F0s, but can be observed even for large F0 separations between the target and interferer (Gockel et al., 2004). Its existence indicates that listeners are not able to optimally weight information across spectrally separated regions for the purpose of deriving the residue pitch of a target tone. It may impair the ability of the listener to process pitch when more than one sound is present.

A somewhat simpler paradigm concerns the ability of listeners to combine information on a single pitch. If across-frequency integration is the “default” mode of operation, especially when the complex tones in the two regions have similar F0s, then listeners might do well in this situation. For example, Kaernbach and Bering (2001) measured F0 discrimination for high-pass filtered harmonic complexes, and showed that performance improved as the high-pass cutoff frequency was lowered. However, in their experiment, it was not possible to determine whether this improvement was the result of across-frequency combination of information or simply due to the introduction of frequency regions where sensitivity was relatively high. The present study investigated the combination of information across frequency regions, using a paradigm that controlled for sensitivity in each individual spectral region.

The main objective of the present study was to investigate how well pitch information is combined across spectral regions when combination of information is advantageous for the task. Two complex tones, A and B, were filtered into two separate spectral regions. With one exception, which will be discussed later, tones A and B had identical F0s. F0 discrimination performance was measured for each of the tones presented alone and for the two presented together. The exact spectral (and other) parameters of tones A and B were chosen so as to give approximately equal d′ values for discrimination of each of the tones when presented alone. This reduced the risk of performance in the combined case being dominated by performance for either A or B, and thus increased the chance of observing any effect of combination of information across spectral regions. The combination of F0 information across regions was measured in five experiments under various conditions.

Signal detection theory (Green and Swets, 1966) predicts that, if performance is mainly limited by independent internal peripheral noises¹ for each of the two complexes, and if information is combined optimally across the two regions, i.e., there is no central noise at the decision stage, then the d′ value observed in the combined case, d′_c, should correspond to

$${d\prime }_c={({{d\prime }_A}^2+{{d\prime }_B}^2)}^{0.5},$$ (1)

where d′_A and d′_B are the d′ values for discrimination of tones A and B, respectively, when presented alone.

If the internal peripheral noises that mainly limit performance were partly correlated across the two complexes, due to, for example, respiratory or circulatory processes, and if information is combined optimally across the two regions, then d′_c is given by

$${d\prime }_c={[({{d\prime }_A}^2+{{d\prime }_B}^2-2\cdot r\cdot {d\prime }_A\cdot {d\prime }_B)∕(1-r^2)]}^{0.5},$$ (2)

where r corresponds to the correlation between the two internal noises across the two complexes (with r< 1). Thus, by assuming a partial correlation between the peripheral noises affecting F0 discrimination for the two complexes, the predicted value for d′_c will be smaller than under the assumption of independent noises. Solving Eq. (2) for r gives

$$r={d\prime }_A\cdot {d\prime }_B∕{{d\prime }_c}^2-{\left[({d\prime }_A\cdot {d\prime }_B∕{{d\prime }_c}^2){}^2-({{d\prime }_A}^2+{{d\prime }_B}^2-{{d\prime }_c}^2)∕{{d\prime }_c}^2\right]}^{0.5}.$$ (3)

The derivation for Eq. (2) and the resulting solution for r are given in the Appendix. Here and throughout, the terms central and peripheral noises do not refer to anatomical structures but are used in the context of decision theory where peripheral noise refers to noise added before (rather than after) information has been combined across spectral regions.

If performance is mainly limited by a central noise that is common to A and B, occurring after information from A and B has been combined, and if information is combined optimally, then the d′ value observed in the combined case should correspond to

$${d\prime }_c={d\prime }_A+{d\prime }_B.$$ (4)

It is conceivable that a large central noise limits performance for frequency discrimination. For example, Siebert (1970) argued that, in the case of frequency discrimination of pure tones, the information that is available in the auditory nerve is not used optimally at a later stage. This argument was based on his optimal observer calculations, which predicted much lower thresholds than observed. A study by Hafter et al. (1990) provides an example of additivity of d′ values in auditory perception due to the combined presentation of two signals. Hafter et al. (1990) investigated how information arising from interaural level differences (ILDs) and interaural time differences (ITDs) is combined. Stimuli were bandpass filtered clicks (centered at 4 kHz) with various combinations of ILD and ITD. Performance was measured using a two-interval two-alternative forced choice (2I-2AFC) task, where in one randomly chosen interval, the interaural differences favored the left side, while in the other, they favored the right side; when both ILD and ITD were present, they always favored the same side. Subjects listened for the lateral movement of the images between the two intervals. The results showed that the d′ values for the combined conditions (when an ILD and an ITD were present) were the sum of the individual d′ values observed when only ILD or only ITD was present.

The second objective of the present study was to investigate whether, when tones A and B contained only harmonics which were unresolved by the peripheral auditory system, there was an effect of the relative timing of peaks (sometimes called pitch pulses) in the envelopes of tones A and B. Human listeners have been shown to be sensitive to asynchronies of pitch pulses [pitch pulse asynchrony (PPA)] in different frequency regions (Patterson, 1987; Summerfield and Assmann, 1991; Carlyon, 1994; Carlyon and Shackleton, 1994). Thus, it is conceivable that the size of the PPA affects performance for F0 discrimination in the combined condition. For example, envelope modulation which is in-phase across auditory filters (synchronization in time of envelope peaks in different auditory filters) might lead to a more salient temporal pitch than out-of-phase modulation. This assumption has been made e.g., by Laneau et al. (2006) in their development of a sound processing scheme that was designed to optimize pitch perception in cochlear implant (CI) listeners (see also Vandali et al., 2005). As in most processing schemes, F0 information was conveyed by the envelope repetition rate applied to pulse trains on a number of electrodes, and Laneau et al. (2006) investigated the effects of enhancing the envelope modulation depth and of synchronizing the envelopes across electrodes. Although a modest improvement was observed, it is not clear whether this was due to the envelope enhancement or to the synchronization. The present study, using acoustic stimuli and normal-hearing listeners, provides a more direct measure of the effect of relative envelope phase on the integration of F0 information by keeping constant the envelope modulation depth within auditory channels tuned to the passband of the stimuli.

II. GENERAL METHOD AND PROCEDURE

In all experiments, a 2I-2AFC task was used. Subjects had to indicate which of the two intervals contained the sound with the higher F0 (“higher pitch”). Visual feedback was provided on whether their answer was right or wrong, except in experiment III. The method of constant stimuli was used, and performance was expressed in terms of d′ (Macmillan and Creelman, 1991). For each subject, the exact characteristics of the tones were determined in preliminary experiments such that the d′ values for F0 discrimination of tones A and B when presented alone were approximately equal and ranged from 1.0 to 1.2. The details are described below for each experiment.

In experiments I–III and V, the overall root-mean-square (rms) level of tones A and B was 52 dB sound pressure level (SPL), irrespective of bandwidth. In experiment IV, the rms level of the tone in the low-frequency region was increased to 55 dB SPL, to make it approximately as loud as the tone in the midfrequency region. A continuous background of pink noise with a spectrum level of 15 dB (re 20 μPa) at 1 kHz was presented in all experiments. Its purpose was to mask possible distortion products and to prevent subjects from relying on possible within-channel cues arising from the interaction of components at the outputs of auditory filters having center frequencies midway between the two spectral regions, specifically in experiments I and V, where complex tones were separated in spectral region by one octave and consisted of unresolved harmonics (see below). Calculation of excitation patterns (following Moore et al., 1997) for the pink noise and for the two complexes together (as used in experiments I and V) showed that the excitation level of the pink noise at the output of an auditory filter midway between the two regions was at least 5 dB above the excitation level of the primary components. While Gockel et al. (2002) showed that masked thresholds for complex tones in noise could be as low as −9.5 dB when the components were added in cosine phase and the F0 was low (62.5 Hz), the contribution from auditory filters with such a low signal to noise ratio toward F0 discrimination was expected to be negligible relative to the contribution of auditory filters centered on the passbands of the two regions. Furthermore, due to the presence of the pink noise, the sensation levels of the complex tones would be far below that required (about 50 dB SL) to produce an audible distortion product at the F0 (see Plomp, 1965).

In experiments I–IV, the duration of the stimuli was 400 ms, and in experiment V the duration was 50 ms. All durations included 20-ms raised-cosine onset and offset ramps. The silent interval between the two intervals within a trial was 500 ms.

Tones were generated and (in experiments I–III and V) bandpass filtered digitally in MATLAB (The MathWorks, Inc., Natick, MA). Bandpass filtering was achieved with a linear-phase finite impulse response (FIR) filter (order 16000) implemented in MATLAB with a flat passband and linear slopes on a logarithmic frequency scale of 48 dB/octave. Stimuli were played out using a 16-bit digital-to-analog converter (CED 1401 plus), with a mean sample rate of 40 kHz. The actual sample rate was varied between trials over the range ±10% (this produced a slight variation in F0, duration, and the filter cutoff frequencies). This was done to encourage subjects to compare the F0s of the stimuli across the two intervals within a trial and to discourage them from using a long-term memory representation of the pitches. Stimuli were passed through an antialiasing filter (Kemo 21C30) with a cutoff frequency of 14 kHz (slope of 96 dB/oct) and were presented using Sennheiser HD250 headphones.

Conditions were fixed in blocks of 105 trials. The first five trials were considered as “warm-up” trials and results from those were discarded. Conditions were run in counter-balanced order. The duration of each session was about 2 h, including rest times. Before data collection proper, subjects were trained until performance seemed stable. Including the preliminary experiments, aimed at finding stimulus parameters resulting in approximately equal d′ values for tones A and B, typically about four to ten sessions were run for each subject in each experiment. Usually, the final d′ value for each subject and condition was based on at least 500 trials.

Overall, eight subjects participated, one of whom was the first author. They ranged in age from 19–47 years, and their absolute thresholds at octave frequencies between 250 and 8000 Hz were within 15 dB of the ISO 389-8 (2004) standard. Six of them had some musical training.

III. EXPERIMENT I: MONAURAL UNRESOLVED TONE COMPLEXES

A. Rationale

It is generally believed that components in a harmonic complex tone are resolved up to about the eighth harmonic (Plomp, 1964; Plomp and Mimpen, 1968; Moore and Ohgushi, 1993; Shackleton and Carlyon, 1994; Bernstein and Oxenham, 2003). For harmonic complex tones containing only unresolved harmonics, pitch information is carried in the repetition rate of the envelope fluctuations and possibly, for intermediate harmonics (8th–13th), in the temporal fine structure (Moore et al., 2006, but see Oxenham et al., 2009). The main objective of the first experiment was to determine whether and how well F0 information is combined across frequency regions when the complex tones in both regions contain only unresolved harmonics (above the 13th), i.e., pitch information is only carried in the repetition rate of the envelope fluctuations, and are presented to the same ear. The second objective was to investigate whether the relative timing of the envelope peaks in the two frequency regions has an effect on F0 discrimination in the combined condition. It has previously been shown that listeners (i) can discriminate a stimulus with a PPA from a stimulus without a PPA (Carlyon, 1994), (ii) are moderately sensitive to the direction of the PPA across frequency regions (Gockel et al., 2005), and (iii) can use PPA to discriminate the F0 of one tone complex in the presence of another tone complex with fixed F0 (Miyazono and Moore, 2009). Thus, it is conceivable that the relative timing of the pitch pulses of the two complex tones affects F0 discrimination performance. For example, the tones might sound more fused if the pitch pulses occur simultaneously in the two regions.

B. Stimuli and subjects

The 400-ms complex tones were presented monaurally to the left ear of each of six subjects. For three subjects, tone A was filtered from 1350–1650 Hz (mid region) and tone B was filtered from 3300–4200 Hz (high region). The nominal F0, which was identical for the two tones, was 75 Hz, and for both complexes components were added in sine phase. The difference in F0, ΔF0, between the complex tones in the two intervals of the 2AFC task was fixed at 3%, 4%, and 5% for subjects 1, 2, and 3, respectively. Preliminary experiments showed that for these three subjects equal performance for the two tones, with d′ values around 1.1, could be achieved with those parameters. For the other subjects, with the same parameters, sensitivity was greater for tone A than for tone B. For subjects 4, 5, and 6, the components in both complexes were added in alternating phase. This doubled the repetition rate in the stimulus envelope, thereby increasing the pitch by one octave (Shackleton and Carlyon, 1994), and increased sensitivity to F0 differences in the high frequency region relative to that in the mid region. For subjects 4 and 5, performance was about equal for the two tones, with nominal F0 and filter regions identical to those used for subjects 1–3. For these two subjects, ΔF0 was fixed at 1.5% and 4%. For the sixth subject, in order to obtain equal sensitivity for the two tones, the nominal F0 was increased to 90 Hz and the filter regions were adjusted to 1375–1875 Hz and 3900–5400 Hz. For this subject, ΔF0 was fixed at 3%.

In the combined condition, where tones A and B were presented simultaneously, to introduce a PPA, the envelope (but not the onset) of tone B was advanced relative to that of tone A by various amounts. To achieve this, the starting phase of the nth harmonic in tone B was shifted by n·Δϕ. The values of Δϕ were 0°, 90°, 180°, and 270°.

To prevent subjects from using differences in the shape of the waveform at onset between the two stimuli to be discriminated, the time point within each period at which the waveform was turned on was chosen at random for each presentation. Note that this did not affect the difference between the starting phases of components in the two frequency regions, i.e., ongoing differences between the peaks in the envelopes in the two regions were unaffected.

C. Results and discussion

In the combined condition, the mean d′ values [and standard errors (SEs) across subjects] observed for the four values of Δϕ were 1.27 (0.07), 1.24 (0.06), 1.27 (0.7), and 1.22 (0.05) for Δϕ equal to 0°, 90°, 180°, and 270°, respectively. There was no significant difference between these d′ values, as shown by the results of a repeated-measures one-way analysis of variance (ANOVA) performed on the individual d′ values [F(3,15)=0.86, p=0.47].² Thus, the relative timing of the pulses in the two frequency regions did not significantly affect F0 discrimination when both tones were presented simultaneously, at least not for the values of Δϕ chosen here. Therefore, in what follows, the d′ value shown for the combined condition is based on the percent correct values averaged across the four Δϕ conditions.

Figure 1 shows the mean d′ values and the corresponding SEs across subjects for the conditions where tones A and B were presented individually (conditions “Mid” and “High,” white bars), and simultaneously (condition “Combined,” black bar), and the predicted d′ value for the combined condition, assuming optimal combination of information across frequency regions and independent noises [Eq. (1), hatched bar]. In the rest of the paper, we focus on the predictions for d′ derived from Eq. (1) [and correlation values derived from Eq. (3)], because the differences between predicted and observed d′ values in the combined condition would be even larger for predictions based on Eq. (4). The predicted d′ value was calculated first for each subject individually. The mean and the SE across subjects’ individual predictions are shown.

FIG. 1.

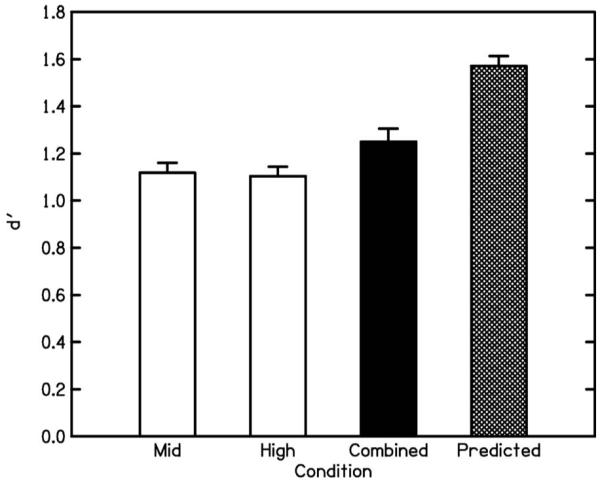
Means and SEs of obtained d′ values for experiment I, plus prediction, for F0-discrimination task. Stimuli were 400-ms complex tones filtered either into a mid spectral region (tone A) or a high spectral region (tone B) (white bars) or tones A and B combined (black bar). The prediction for the combined condition, assuming optimal combination of F0 information across the two frequency regions, is shown by the hatched bar. See text for details.

As intended, mean d′ values for the individually presented tones were about 1.1 and were very similar for the two frequency regions. In the combined condition, the mean d′ value was 1.25, which indicates a small improvement over individual presentation. A paired-sample t-test showed that the d′ value in the combined condition was significantly larger than the higher of the two d′ values observed for individual presentation [t(5)=2.08, p<0.05; one-tailed]. The predicted mean for the combined condition, assuming optimal combination of information and independent noises, was 1.57. The observed sensitivity in the combined condition was clearly below the prediction (by a factor of 0.79). A paired-sample t-test showed this difference to be highly significant [t(5)=8.15, p<0.001; two-tailed]. Assuming partial correlation between the two noises, the mean of the estimated r values was 0.64, with a SE (across subjects) of 0.09.

Overall, the results showed a small but significant improvement in F0 discrimination when tones A and B were presented simultaneously compared to when they were presented in isolation. This indicates that information can be combined across frequency regions. This effect was not dependent on the relative timing of the pitch pulses in the two regions and was markedly less than predicted assuming optimal combination of information and independent noises.

IV. EXPERIMENT II: MONAURAL AND DICHOTIC UNRESOLVED SPECTRALLY ADJACENT TONE COMPLEXES

A. Rationale

The objective of the second experiment was to investigate whether the nonoptimal combination of information across frequency regions (assuming independent noises) that was observed in the first experiment could have been partly due to partial masking between the two stimuli, in spite of them being filtered into frequency regions separated by one octave and being presented at a low level in a pink background noise. The calculated excitation patterns for the stimuli in experiment I (see Sec. II) showed that the signal to noise ratio at auditory filters centered halfway between the two regions was below about −5 dB. Thus, the effect of partial masking on F0 discrimination for the combined condition was expected to be negligible. To investigate any remaining role of peripheral masking, here the frequency separation between the two spectral regions was reduced relative to that in experiment I. Tones A and B were presented either to opposite ears or to the same ear. If peripheral masking had a negative effect, performance would be expected to be better for dichotic than for monaural presentation of the two tones.

B. Stimuli and subjects

The same six subjects as in experiment I participated. Tone A, filtered into the mid region, had exactly the same parameters as in the first experiment. Tone B was filtered into a high region which was now adjacent to the mid region, rather than separated by an octave. Thus, the lower cut-off frequency (3-dB down point) of the high region was 1650 Hz for subjects 1–5 and 1875 Hz for subject 6. Following preliminary experiments, the upper cut-off frequency of the high region was fixed at 2250 Hz for subject 1, at 1950 Hz for subjects 2–4, at 2600 Hz for subject 5, and at 2100 Hz for subject 6. This was done to achieve approximately equal d′ values for F0 discrimination of the two tones, for each subject. The values of ΔF0 used were the same as in experiment I, except for subject 3, for whom it was decreased from 5% to 4%, and for subject 6, for whom it was increased from 3% to 3.4%.

As experiment I showed no effect of PPA, here the value of Δϕ was fixed at 0°. In the monaural condition, both tones were presented to the left ear. In the dichotic condition, tones A and B were delivered to the left and to the right ears, respectively. Note that, in the dichotic condition, subjects reported perceiving a single sound source which was located at the center of the head, i.e., the two complex tones were fused, consistent with previous evidence (Broadbent and Ladefoged, 1957).

C. Results and discussion

Figure 2 shows the results of experiment II. As intended, the mean d′ values for the individually presented complex tones were quite similar at 1.09 and about 1.17 for the mid- and the high regions, respectively (three white bars on the left-hand side). In the combined conditions (black bars), the mean d′ values were 1.32 and 1.36 for monaural and dichotic presentations, respectively. Thus, as in the first experiment, F0 discrimination was somewhat better for combined than for individual presentation of the two tones. Paired-sample t-tests showed that, for both monaural and dichotic presentation, the d′ values in the combined conditions were significantly larger than the higher of the two d′ values observed for the corresponding individual presentations [monaural: t(5)=2.47, p<0.05; one-tailed; dichotic: t(5)=2.19, p<0.05; one-tailed]. In the combined conditions, performance was unaffected by whether the tones were presented monaurally or dichotically, and was clearly below the level(s) predicted, assuming independent noises and optimal combination of information across regions (by factors of 0.83 and 0.84 in the monaural and the binaural conditions, respectively). This was supported by the results of a repeated-measures two-way ANOVA, which used the obtained and the predicted d′ values for monaural and dichotic presentations as input. There was a significant main effect of the factor observed vs predicted [F(1,5)=15.08, p<0.05], but no significant main effect of mode of presentation (monaural vs dichotic) nor interaction. Furthermore, an additional paired-sample t-test, calculated on the data for the dichotic condition only, showed that the d′ values obtained in the combined condition were significantly smaller than the predicted d′ values [following Eq. (1)] [t(5)=3.2, p<0.05; two-tailed]. Assuming partial correlation between the two noises, the mean of the estimated r values was 0.53, with a standard error of 0.13 [following Eq. (3)].

FIG. 2.

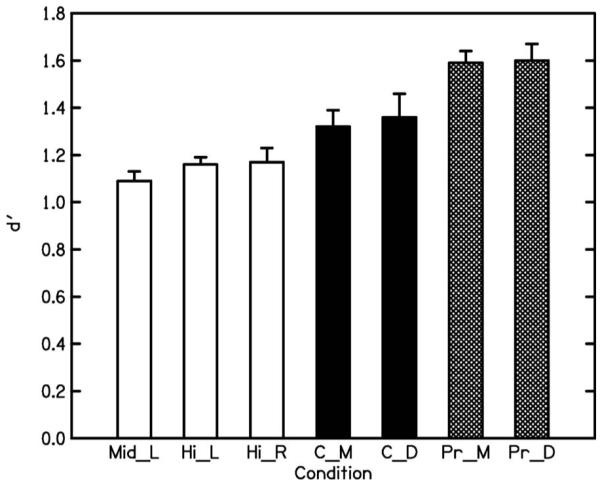
Results and predictions for F0-discrimination task (experiment II). The mean obtained d′ values and the corresponding SEs across subjects are shown by the five bars to the left and the predictions are shown by the two hatched bars to the right. The three white bars show performance in the conditions where each tone was presented individually: outer left—tone A, filtered into the mid region and presented to the left ear (Mid_L); second from the left—tone B, filtered into the high region and presented to the left ear (Hi_L); third from the left—tone B, filtered into the high region and presented to the right ear (Hi_R). The two black bars show performance in the conditions where the tones were combined: left—combined, monaural presentation (C_M); right—combined, dichotic presentation (C_D). The two hatched bars on the right-hand side show the predictions derived for the monaural combined condition (Pr_M) and for the dichotic combined condition (Pr_D), assuming optimal combination of information across frequency regions and independent noises. See text for details.

Overall, the results were quite similar to those observed for experiment I, where the two complexes were more spectrally separated. Furthermore, there was no effect of monaural vs dichotic presentation, and, for dichotic presentation, obtained performance in the combined condition was below optimal performance (assuming independent noises), similar to what has been observed for monaural presentation. The results indicate that the nonoptimal combination of information [following Eq. (1)] was not caused by partial masking in the auditory periphery.

V. EXPERIMENT III: RELATIVE DOMINANCE

A. Rationale

The objective of the third experiment was to investigate whether the nonoptimal combination of F0 information across frequency regions (assuming independent noises) observed in experiments I and II could have been due to subjects mostly ignoring F0 information coming from one frequency region. For example, it could be that, in spite of equal performance for the individually presented tones, when both were presented together, the tone in the lower frequency region was dominant because it was closer to the usual dominance region (Ritsma, 1967; Moore et al., 1985a; Dai, 2000).

To address this question, tones A and B were presented simultaneously, in both intervals of the 2AFC task. In each interval, tones A and B now had different F0s, rather than the same F0 as in the previous experiments. In one randomly chosen interval, the F0 of tone A (mid region) was increased above the nominal F0, while that of tone B (high region) was decreased below the nominal F0; this is called the interval with the “compressed signal.” In contrast, the other interval contained the “stretched signal;” the F0 of the tone in the lower frequency region was decreased below the nominal F0, while that of the tone in the higher frequency region was increased above the nominal F0. Subjects still had to indicate which of the two intervals had the complex with the higher pitch. The idea was that if subjects attended to both regions, then the stretched and the compressed signal should be chosen about equally often. In contrast, if subjects listened mainly to a specific frequency region, then their pitch judgments should follow the change in F0 of the tone in that region, and thus, scores should markedly differ from 50%.

B. Stimuli and subjects

The same six subjects as in the first two experiments participated in experiment III. For each subject, tones A and B were filtered as in experiments I and II. Specifically, there were two filter conditions: the “far regions” condition, where the tones were filtered into two spectral regions separated by one octave (with filter parameters as in experiment I), and the “adjacent regions” condition, where the tones were filtered into two spectrally adjacent regions (with filter parameters as in experiment II). The nominal F0 and the phase relationship between components within each region were identical to those in the previous experiments, for each subject. In one randomly chosen interval, the F0 of tone A was lowered by ΔF0/2 from the nominal F0, while the F0 of tone B was increased by ΔF0/2, and in the other interval it was the other way round. The difference between the F0s of tones A and B within each interval could take two values for each subject: one was identical to the value of ΔF0 with which this subject had been tested in experiment II (which resulted in a d′ value of about 1.1 when this F0 difference occurred between the two intervals of a trial for each of tones A and B; condition “small ΔF0”) and the other was twice that size (condition “large ΔF0”). Both tones were always presented monaurally and simultaneously. They were perceived as one sound source in the small ΔF0 condition, but were perhaps somewhat less fused in the large ΔF0 condition. In each of the four conditions, at least 1400 trials were collected for each subject.

C. Results and discussion

Figure 3 shows the percentage of trials in which subjects judged the stretched signal to be higher in pitch than the compressed signal, i.e., where their judgments followed the change in F0 of the complex filtered into the high region. The empty symbols show the individual results for each of the six subjects. The solid squares and error bars show the mean and SEs across subjects. For all conditions, the mean scores were around 50%, although scores in the far-region condition with the large ΔF0 (far right) seem to be somewhat lower. The individual scores within conditions clearly do not follow a bimodal distribution. This is important because it indicates that the mean scores around 50% are not the result of half of the subjects only listening to one frequency region and the other half only listening to the other region.

FIG. 3.

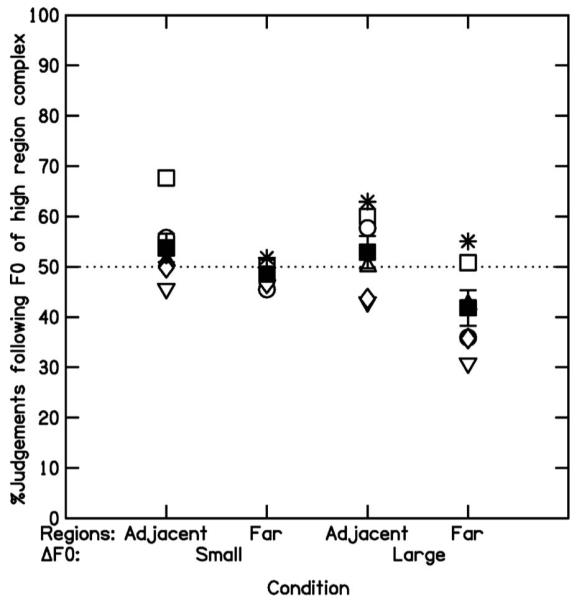
Results for experiment III, showing the percentage of trials in which subjects judged the stretched signal (F0 of complex in high region increased; F0 of complex in mid region decreased) to be higher in pitch than the compressed signal (F0 of complex in high region decreased; F0 of complex in mid region increased). Empty symbols show the scores for six subjects. The solid squares (and error bars) show the mean score (and SEs) across subjects. See text for details.

A repeated-measures two-way ANOVA, with factors filter condition and ΔF0, was calculated. The results showed a significant main effect of filter condition [F(1,5)=14.72, p<0.05]. Neither the main effect of size of ΔF0 nor the interaction was significant. Therefore, within each filter condition, the mean was determined across the two ΔF0 conditions. Two separate one-sample t-tests (one for each filter condition) showed that the mean percentages were both not significantly different from 50% [adjacent region: t(5)=1.09, p>0.05; far region: t(5)=2.07, p>0.05; two-tailed for both filter conditions].

In an additional analysis, it was checked whether, across subjects, a somewhat larger deviation from a 50% score in the present experiment might be correlated with less optimal combination of information across frequency regions in experiment I or II. Spearman’s rank correlation coefficients were calculated between the ratios of observed to predicted d′ values obtained in experiments I and II, on the one hand, and the unsigned deviations from 50% scores observed in conditions with large ΔF0s and corresponding frequency region in the present experiment, on the other hand. A negative correlation between these two measures would indicate that the nonoptimal combination of information could have been due to subjects consistently listening more to (or giving more weight to) pitch information coming from one frequency region than from the other. The values of the correlation coefficients were (i) 0.086, for the correlation between the ratios of observed to predicted d′ values obtained in experiment I and the unsigned deviations from 50% scores in the far-region large-ΔF0 condition; (ii) 0.886, for the correlation between the ratios of observed to predicted d′ values obtained in experiment II in the monaural condition and the unsigned deviations from 50% scores in the adjacent-region large-ΔF0 condition; and (iii) 0.314, for the correlation between the ratios of observed to predicted d′ values obtained in experiment II in the dichotic condition and the unsigned deviations from 50% scores in the adjacent-region large-ΔF0 condition. Only the second of these coefficients was (just) significant (p<0.05; two-tailed), but it actually had the opposite sign to that predicted, i.e., a somewhat larger deviation from the 50% score was correlated with somewhat more optimal combination of information across frequency regions.

In summary, the results indicate that subjects did not selectively and consistently listen to one specific frequency region. Thus, the nonoptimal combination of information across frequency regions [following Eq. (1)] observed in experiments I and II cannot be explained by the existence of a “dominant region” which leads subjects to ignore information from the other region. Note, however, that the data of the third experiment do not necessarily imply that the pitch of the stretched and compressed signals was perceived as equal and that, therefore, subjects responded randomly. This is because a similar pattern of results might be observed if subjects sometimes listened to one region and sometimes to the other.

VI. EXPERIMENT IV: RESOLVED TONE COMPLEXES

A. Rationale

The objective of the fourth experiment was to investigate whether the nonoptimal combination of F0 information across frequency regions (assuming independent noises) was specific to complex tones containing only unresolved harmonics. It could be that nonoptimal combination occurs only for pitches encoded solely by envelope information. To test this idea, complex tones containing at least some resolved harmonics were used as stimuli.

B. Stimuli and subjects

Four subjects participated, three of whom also took part in the previous three experiments. Tone A consisted of harmonics 1–3 of a 400-ms harmonic complex tone with an F0 of 200 Hz, added in sine phase (condition “Low Harmonics”), for all subjects. Tone B contained higher harmonics of a 200-Hz F0 complex, also added in sine phase (condition “Mid Harmonics”). Which harmonics were present in tone B and the size of ΔF0 between the two intervals in the 2AFC F0-discrimination task were determined in a preliminary experiment individually for each subject, such that performance for tones A and B was approximately equal and that d′ values were around 1.1–1.2. For two subjects, tone B consisted of harmonics 6–8 and ΔF0 was set to 0.4% and 0.32%, respectively. For the third and fourth subjects, tone B contained harmonics 7–9 and 6–9, and ΔF0 was fixed at 0.2% and 0.6%, respectively. The rms level of tone A was increased from 52 to 55 dB SPL, so that it was approximately as loud as tone B.

C. Results and discussion

Figure 4 shows the mean d′ values and the corresponding SEs across subjects for the conditions where tones A and B were presented individually (conditions Low Harmonics and Mid Harmonics, white bars), and simultaneously (condition “Combined,” black bar), and the predicted d′ value for the combined condition, assuming optimal combination of information across frequency regions (hatched bar), following Eq. (1).

FIG. 4.

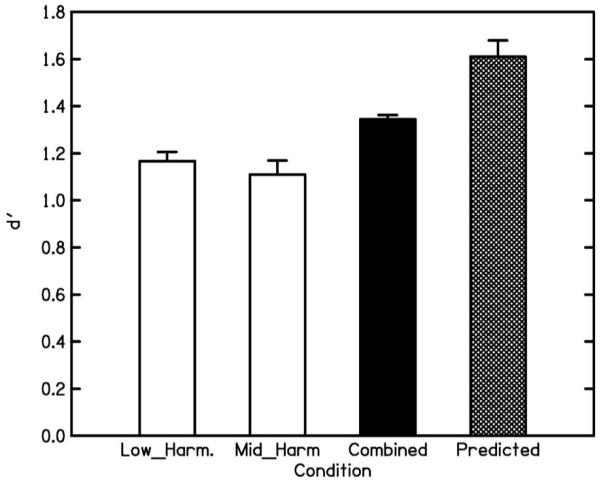
Results for experiment IV. As Fig. 1, but for complex tones containing resolved harmonics.

Mean d′ values for the individually presented tones were quite similar at about 1.17 and 1.11 for the Low Harmonics and Mid Harmonics conditions, respectively. In the combined condition, the mean d′ value was 1.34, again indicating a small improvement over individual presentation. A paired-sample t-test showed that the d′ value for the combined condition was significantly larger than the higher of the two d′ values observed for individual presentation [t(3)=5.5, p<0.01; one-tailed]. The predicted mean for the combined condition, assuming optimal combination of information [following Eq. (1)], was 1.61. As in the previous experiments, the observed sensitivity in the combined condition was clearly below the prediction (by a factor of 0.84). A paired-sample t-test showed that this difference was significant [t(3)=4.17, p<0.05; two-tailed]. Assuming partial correlation between the two noises [following Eq. (2)], the mean of the estimated r values was 0.44, with a SE of 0.1. To assess whether performance in the combined condition was closer to optimal performance when the tone complexes contained resolved (experiment IV) rather than only unresolved harmonics (experiment I), an independent-sample t-test was calculated on the factors by which the observed combined performance was smaller than the predicted optimal performance for the six subjects in experiment I and the four subjects here. This t-test showed that the observed shortfalls from optimal performance (mean ratios of 0.79 and 0.84 in experiments I and IV, respectively) were not significantly different [t(8)=1.15, p>0.05; two-tailed].

To summarize, the results showed a significant improvement in F0 discrimination when the tones in the two frequency regions were presented simultaneously compared to when they were presented in isolation. However, this improvement was significantly smaller than predicted assuming optimal combination of information [following Eq. (1)], and was not significantly closer to optimal performance than observed in the previous experiments with tones containing only unresolved harmonics. This indicates that nonoptimal combination of information across frequency regions occurs for tones with both resolved and unresolved harmonics.

VII. EXPERIMENT V: SHORT DURATION

A. Rationale

In the previous experiments, the stimulus duration was always 400 ms. This duration was chosen so that the current results could be compared with previous findings on PDI, where F0 information seemed to be combined across regions, in spite of it being disadvantageous, and where the stimulus duration was also 400 ms.

The objective of experiment V was to investigate whether combination of F0 information across frequency regions would improve for shorter stimuli. One reason to suspect that signal duration might affect combination of F0 information across frequency comes from a study on signal detection by Houtgast (1987). He presented listeners with a compound stimulus that consisted of nine individual Gaussian-shaped tone pulses. Each tone pulse covered a well-defined and restricted region in time and frequency. All nine individual tone pulses had the same masked threshold when present in pink noise. Houtgast (1987) measured the masked threshold for the compound stimulus for various placements of the nine pulses in spectral region and time. He found that concentrating the signal energy in either time or frequency led to lower masked thresholds than spreading pulses over 100 ms and several critical bands. For short tone pulses, optimal combination of (energy) information across critical bands was observed when the peaks of all Gaussian envelopes coincided in time. Later studies confirmed the importance of very short signal duration (less than about 30 ms) for (near) optimal integration of energy across frequency regions for signal detection in a background noise (see van den Brink and Houtgast, 1988, 1990a, 1990b). While the current study is not concerned with signal detection in the sense of energy detection and integration, it is conceivable that pitch discrimination and integration of pitch relevant information from sounds that are clearly audible are limited in a similar way, i.e., subjects can either integrate over time or over frequency, but not both.

B. Stimuli and subjects

Four subjects participated. Of those four, two also took part in experiments I–III, one had participated in experiment IV and one was recruited new. Apart from the duration being shortened from 400 to 50 ms, the main stimulus parameters were identical to those for experiment I, i.e., tones A and B contained only unresolved harmonics, they were filtered into regions separated by one octave, and the starting phase of the nth harmonic in tone B was shifted by n·Δϕ, with values of Δϕ at 0°, 90°, 180°, and 270°. As in experiment I, the time point within each period at which the waveform was turned on was chosen at random for each presentation. This discouraged subjects from relying on onset differences and on differences in the duration between the first and last pulses in each interval. Different PPAs between the envelope peaks in the two frequency regions were tested again, just to check whether the absence of an effect would also be observed for the short stimulus duration.

For three subjects, tones A and B were filtered from 1350–1650 Hz (mid region) and 3300–4200 Hz (high region), respectively, and the nominal F0 was 75 Hz. For two of the three subjects, components in both complexes were added in sine phase and for the third one they were added in alternating phase. The values of ΔF0 were fixed at 12%, 14%, and 5.5% for subjects 1, 2, 3, respectively. Preliminary experiments showed that, for these three subjects, similar performance levels for tones A and B could be achieved with these parameters, with d′ values around 1.1–1.2. For the fourth subject, in order to obtain equal sensitivity for the two tones, the nominal F0 was increased to 90 Hz, the filter regions were adjusted to 1375–1875 and 3900–5400 Hz, and components within each tone were added in alternating phase. For this subject, ΔF0 was fixed at 14%. This subject was not the same as the sixth subject in experiment I, who also was tested with a 90 Hz F0. Note that the values of ΔF0 required to achieve d′ values around 1.1–1.2 are markedly larger than those in experiment I, where the duration of the stimulus was 400 rather than 50 ms. All tones were presented monaurally to the left ear of each subject.

C. Results and discussion

In the combined condition, the mean d′ values (and SEs across subjects) observed for the four values of Δϕ were 1.63 (0.09), 1.58 (0.09), 1.57 (0.11), and 1.51 (0.11) for Δϕ equal to 0°, 90°, 180°, and 270°, respectively. There was no significant difference between these d′ values, as shown by the results of a repeated-measures one-way ANOVA performed on the individual d′ values [F(3,9)=1.11, p=0.38]. Thus, as in experiment I for the longer stimulus duration, the relative timing of the pulses in the two frequency regions did not affect F0 discrimination significantly when both tones were presented simultaneously. Therefore, in what follows, the d′ value for the combined condition is based on the percent correct values averaged across the four Δϕ values.

Figure 5 shows the results of experiment V. Mean d′ values for the individually presented tones were quite similar at about 1.23 and 1.13 for the mid- and high region conditions, respectively (two white bars to the left). For the combined condition (black bar), the mean d′ value was 1.57, indicating a clear improvement over individual presentation. A paired-sample t-test showed that the d′ value for the combined condition was significantly larger than the higher of the two d′ values for individual presentation [t(3)=5.03, p<0.01; one-tailed]. The predicted mean d′ for the combined condition, assuming optimal combination of information and independent noises, was 1.68 (hatched bar on the right-hand side). The observed sensitivity in the combined condition was somewhat below the predicted value, but only by a factor of 0.93. This factor is clearly larger than those observed in the previous experiments (experiment I: 0.79; experiment II: 0.83, monaural and 0.84, binaural; experiment IV: 0.84). An independent-sample t-test was calculated on the factors by which the observed combined performance was smaller than the predicted optimal performance for the six subjects in experiment I and the four subjects here. The results showed that the ratio of observed to predicted d′ values was significantly larger [t(8)=3.88, p<0.01; two-tailed] for the 50-ms than for the 400-ms stimuli. Furthermore, a paired-sample t-test showed that, for the short duration, the observed and the predicted d′ values for the combined condition were not significantly different from each other [t(3)=3.06, p>0.05; two-tailed]. Assuming partial correlation between the two noises, the mean of the estimated r values was 0.16, with a standard error of 0.05.

FIG. 5.

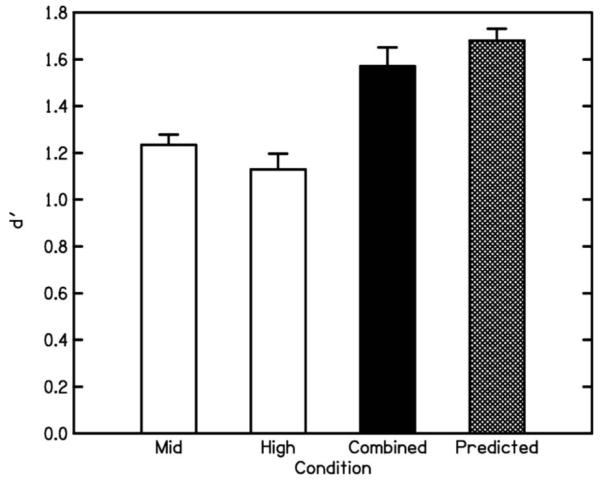
Results for experiment V. As Fig. 1, but for tones with a duration of 50 ms.

To summarize, the results showed a clear improvement in F0 discrimination when the short tones A and B were presented simultaneously, compared to when they were presented in isolation. This improvement was significantly larger than that observed in experiment I, where similar but longer tone complexes were used. As for the longer duration tones, performance did not depend on PPA. Performance observed for the 50-ms duration was not significantly different from that predicted assuming (1) optimal combination of information across frequency regions and (2) independent internal noises for each of the two complexes as the main factor limiting performance. The difference in results for the long and short tones may indicate that, when subjects discriminate between the F0s of two clearly audible complex tones, they cannot simultaneously and optimally integrate pitch information over frequency and time. This limitation resembles that previously observed in signal-detection tasks (Houtgast, 1987; van den Brink and Houtgast, 1988, 1990a, 1990b).

VIII. GENERAL DISCUSSION

In the Introduction, we described a phenomenon—PDI—in which listeners are unable to selectively process F0 information in a specific frequency region (Gockel et al., 2004; 2005, 2009a, 2009b; Micheyl and Oxenham, 2007). The present results showed that nonoptimal combination of F0 information [following Eq. (1)] occurs even in a paradigm where combination is advantageous, for the same stimulus duration as used in the PDI studies (400 ms). Thus, the nonoptimal performance previously reported in PDI studies is not restricted to situations that require assigning a zero weight to a particular frequency region.

Somewhat in contrast to the present results, Moore et al. (1984) observed optimal combination of information across frequency for long duration (420 ms) stimuli. In a 2I-2AFC task, they measured frequency difference limens (DLs) for individual harmonics within complex tones (in the presence of the remainder of the complex) and F0DLs for the periodicity (the residue pitch) of the whole complex. They found that the F0DLs were always smaller than the smallest of the DLs for the individual harmonics and that the former could be predicted from the latter, using a modified version of Goldstein’s (1973) model in which no “central” noise was assumed. This indicated optimal combination of information about the frequencies of the harmonics within the complex for the purpose of deriving the residue pitch.

More recently, Gockel et al. (2007) investigated whether this also held for shorter stimulus durations. They used the same paradigm as Moore et al. (1984), and complex tones of 200-, 50-, and 16-ms durations. For the 200-ms duration, the pattern of results found by Gockel et al. (2007) was consistent with that observed by Moore et al. (1984). However, for the 50-ms duration, the predicted F0DLs were consistently larger than the obtained values. This was assumed to be due to difficulties in hearing out individual harmonics when the duration of the sound was short, leading to increased DLs for the individual harmonics within the complex and resulting in an underestimate of the precision with which the frequencies of the individual harmonics were represented at the input to the central pitch processor. For the 16-ms duration, the F0DLs predicted from the DLs for the individual harmonics were not significantly different from the observed F0DLs. While this seemed to indicate optimal combination of information across frequencies, this interpretation was questioned by the results of a supplementary pitch-matching experiment. The pitch-matching experiment showed that the contribution of the upper-edge harmonic to the residue pitch of the complex was markedly smaller than would be predicted from its especially small FDL (relative to the FDLs observed for the other harmonics).

In summary, the studies by Moore et al. (1984) and Gockel et al. (2007) indicated that, for the purpose of deriving the residue of a complex tone, information about the frequencies of the individual harmonics seemed to be combined optimally for long tone durations, with “supra-optimal” combination for the 50-ms tones. This differs from the present study for combination of F0 information across frequency regions, which showed optimal combination for short complex tones but sub-optimal combination for long complex tones (assuming independent noises). We can think of two possible reasons for this. The first reason is related to the differences in the paradigms used in the initial stage of the experiment where the amount or the precision of information on the individual components, which are presented simultaneously in the second stage of the experiment, was determined. In the studies by Moore et al. (1984) and Gockel et al. (2007), the individual components (harmonics), whose FDLs were to be determined, were presented within the remainder of the complex tone. Especially for short durations, this method might lead to an underestimate of the precision with which component frequency is represented in the auditory system because it might rely on subjects hearing out the individual component, whose FDL is measured, from the remainder of the complex. In contrast in the present study, the individual parts of the combined sound, tones A and B, were presented alone when performance for F0 discrimination for the parts was determined. If, in the present study, F0 discrimination performance had been determined for each of the two tones in the presence of the other tone—that is, in the PDI paradigm, corresponding to the measurement used in the initial stage by Moore et al. (1984) and Gockel et al. (2007)—then predictions for the combined stimulus would have been lower, and maybe similar to the observed performance levels, at least for the 400-ms duration. For the short duration, the predictions probably would be below the observed performance in the combined condition.

The second reason for the different pattern of results observed in the present study and those by Moore et al. (1984) and Gockel et al. (2007) could be related to the differences in what exactly was estimated in the initial stage of the experiment. In the present study, the prediction for performance in F0 discrimination of the combined stimulus was derived from performance in F0 discrimination of complex tones, i.e., perception of the same attribute—F0—was measured in the combined case and in the initial stage of the experiment. In contrast, in the previous studies, the attributes measured in the initial stage and in the combined case were not identical. The initial stage measured FDLs of tones, while in the combined case, perception of F0 was measured. The latter could be a higher stage process, using information from the initial stage. Combination of information at the same level (present study) might follow different rules/restrictions from combination of information for a higher stage process (previous studies).

Optimal combination of information across frequency regions, following Eq. (1), has also been reported by Buell and Hafter (1991). They measured sensitivity to ITDs of low-frequency stimuli. Stimuli consisted of either one, two, or three sine tones. They found that the observed d′ values in the combined conditions, where two or three sine tones with identical ITDs were presented simultaneously, were predicted well assuming optimal combination of ITD information across frequency. This was true irrespective of whether the frequencies in the combined conditions were harmonically or inharmonically related to each other. Buell and Hafter (1991) did not specifically investigate the effect of stimulus duration; they used a short stimulus with a 50 ms raised-cosine envelope. It is important to point out that the combination of binaural information across frequency observed by them was optimal assuming independent internal noises, rather than a common noise as the main factor limiting performance.

In a second experiment, Buell and Hafter (1991) presented two-frequency complexes, in which one component, the target, contained the ITD which had to be detected, while the other component, the interferer, was presented diotically. This paradigm is analogous to that used in the PDI studies (Gockel et al., 2004, 2005, 2009a, 2009b; Micheyl and Oxenham, 2007) mentioned above. In this paradigm, optimal combination of information requires assigning zero weight to the (non-relevant) information arising from the interferer. Buell and Hafter (1991) found that, for inharmonically related components, performance in the “combined” conditions was equal to that observed for targets presented alone, while for harmonically related components, performance was impaired. The finding of unimpaired performance with inharmonically related components suggested segregation of the target and interferer into separate auditory objects based on (in)harmonicity (Moore et al., 1985b; Hill and Darwin, 1996). In contrast, with the harmonically related components, harmonics seemed to be grouped together and ITD information from the target and the interferer was combined, thus lowering performance.

The results of the present study on combination of pitch information across frequency largely conform with those of Buell and Hafter (1991) on combination of ITD information across frequency. When combination of information across frequency was advantageous, both studies showed optimal combination across frequency for short stimuli. Longer duration tones were not tested by Buell and Hafter (1991), so it is unclear whether ITD information is combined optimally across frequency for long tones as well. In addition, when combination of information across frequency was disadvantageous, Buell and Hafter’s (1991) second experiment showed impaired performance when the tones were harmonically related, but optimal combination of information across frequency when the two tones were clearly segregated due to inharmonicity. Similarly for PDI, Gockel et al. (2004; 2009b) reported that the impairment was markedly reduced when the difference between the F0s of target and interferer was increased, leading to clearer segregation of the two complex tones. While one would expect larger PDI for shorter stimuli, future studies may show the exact effects of stimulus duration in the PDI paradigm.

So far in the discussion we have concentrated on predictions for the combined condition that were derived from Eq. (1), based on the assumption that the noises that affected F0 discrimination of the complexes in the two frequency regions were statistically independent. However, as described in the results sections (III C, IV C, VI C, VII C), by assuming partial correlation between the noises and optimal combination of information otherwise, it is possible to estimate correlation coefficients such that the predicted d′ values for the combined condition equal the observed values. The correlation coefficients estimated for experiment V (mean of 0.16) were markedly smaller than those estimated for the experiments using longer stimulus durations (mean of 0.54 across experiments I, II, and IV). While this is a consequence of performance in the combined condition being closer to optimal (assuming independent noises) for the short than for the long duration, it means that the assumed component of the noise that is common to both “channels” decreases relative to the independent component with decreasing duration.

According to Durlach et al. (1986), partial correlation between peripheral internal noises might be caused, for example, by respiratory or circulatory processes. It is not obvious why such a common noise component would decrease with decreasing duration. On the contrary, one might expect the relative contribution of a circulatory noise component to increase with decreasing duration. On the other hand, it could be that the component of the noise that is independent across channels decreases with increasing duration, due, for example, to temporal integration, while the part of the noise that is common across channels does not decrease. This could happen if the source of the common noise was located at a stage of processing after temporal integration. Although this is possible, it is not obvious what the source of this “semi-peripheral” noise would be. Alternatively, one could assume independent peripheral noises and a central noise at the decision stage that decreases with decreasing duration due, for example, to memory limitations in the time-frequency space. The latter description is just another way of saying that combination of information was more optimal (assuming independent noises) for the short than for the long duration. The present data do not allow one to distinguish between these two descriptions (or combinations thereof), but the latter seems more parsimonious.

IX. SUMMARY AND CONCLUSIONS

The combination of F0 information across spectral regions was investigated in five experiments using a 2AFC task in which subjects had to indicate the stimulus with the higher pitch. Stimuli were two complex tones, A and B, in separate frequency regions. Tones A and B were either presented alone or simultaneously. Performance in the combined condition was compared to predicted performance, assuming optimal combination of F0 information across spectral regions. Following signal-detection theory, predictions were derived based on the performance observed when tones A and B were presented alone, assuming independent peripheral noises for A and B as the limiting factor. The results showed the following.

1. When 400-ms tones A and B contained only unresolved harmonics, were separated in spectral region by one octave, and were presented monaurally, performance in the combined condition was poorer than predicted assuming optimal combination of information (experiment I). The relative timing of envelope peaks in tones A and B had no significant effect on performance in the combined condition.

2. When 400-ms tones A and B contained only unresolved harmonics and were filtered into two contiguous spectral regions, performance in the combined condition was unaffected by whether A and B were presented monaurally or dichotically (experiment II), and was very similar to that observed for experiment I, indicating that peripheral masking was probably not the reason for the observed sub-optimal performance.

3. When tones A and B were presented simultaneously but differed in F0 in both intervals of the 2AFC task (in one randomly chosen interval the F0 of tone A was increased, while that of tone B was decreased, and in the other interval it was the other way around), subjects’ pitch judgments were equally determined by the F0 change in the two spectral regions (experiment III). Thus, the nonoptimal combination of information observed in experiments I and II cannot be explained by subjects “listening” consistently to one specific frequency region.

4. When 400-ms tones A and B contained at least some resolved harmonics, performance in the combined condition was poorer than predicted, assuming optimal combination of F0 information across spectral regions (experiment IV). The ratio of observed to predicted performance in the combined condition was similar to that observed in experiments I and II for complex tones containing only unresolved harmonics, indicating that the limitation in combination of F0 information across spectral regions was not limited to unresolved harmonic complexes.

5. When the duration of the tones was shortened to 50 ms, keeping other stimulus parameters similar to those used in experiment I, observed performance in the combined condition was not significantly different from that predicted, assuming optimal combination of information and independent noises (experiment V). As for the longer duration, the relative timing of envelope peaks in tones A and B had no significant effect on performance in the combined condition.

Overall, the results indicate that F0 information can be combined across spectral regions in a optimal way, when the stimulus duration is short. They may give another example of the difficulty human listeners have with integrating information simultaneously across frequency and time.

APPENDIX

In this appendix the method for predicting d′_c is derived, assuming partly correlated internal peripheral noises and optimal combination of information. Following van Trees (1968, pp. 96–99) assuming optimal combination of information across n Gaussian-distributed random variables (RVs) leads to the following prediction for d′ in the combined condition:

$${{d\prime }_c}^2=D^T{K}^{-1}D,$$ (A1)

where d′_c is the value of the d′ for the combined condition, and D^T is the transpose of D, with D^T=(Δ₁ Δ₂ Δ₃ ⋯ Δ_n). The value of each Δ_i specifies the difference between the expected values of the ith RV, x_i, for the signal distribution and for the noise distribution, and K⁻¹ is the inverse of the variance-covariance matrix K.

If one assumes that the individual RVs are all statistically independent, except for the addition of a common noise variable, R, to each, where R has expected value zero and variance ${\sigma }_R^2$, then

$$K=\left(\begin{array}{ccccc}\hfill {\sigma }_1^2+{\sigma }_R^2\hfill & \hfill {\sigma }_R^2\hfill & \hfill \cdots \hfill & \hfill {\sigma }_R^2\hfill & \hfill {\sigma }_R^2\hfill \\ \hfill {\sigma }_R^2\hfill & \hfill {\sigma }_2^2+{\sigma }_R^2\hfill & \hfill {\sigma }_R^2\hfill & \hfill \cdots \hfill & \hfill {\sigma }_R^2\hfill \\ \hfill {\sigma }_R^2\hfill & \hfill {\sigma }_R^2\hfill & \hfill \ddots \hfill & \hfill {\sigma }_R^2\hfill & \hfill {\sigma }_R^2\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill {\sigma }_{n-1}^2+{\sigma }_R^2\hfill & \hfill ⋮\hfill \\ \hfill {\sigma }_R^2\hfill & \hfill {\sigma }_R^2\hfill & \hfill \cdots \hfill & \hfill {\sigma }_R^2\hfill & \hfill {\sigma }_n^2+{\sigma }_R^2\hfill \end{array}\right),$$ (A2)

where σ_i is the standard deviation of the ith RV before the addition of the common noise. For the current case of n=2, the inverse of K is especially simple with

$$K^{-1}=\frac{1}{({\sigma }_1^2+{\sigma }_R^2)({\sigma }_2^2+{\sigma }_R^2)-{\sigma }_R^4}\left(\begin{array}{cc}\hfill {\sigma }_2^2+{\sigma }_R^2\hfill & \hfill -{\sigma }_R^2\hfill \\ \hfill -{\sigma }_R^2\hfill & \hfill {\sigma }_1^2+{\sigma }_R^2\hfill \end{array}\right).$$ (A3)

Substituting into Eq. (A1), this gives

$${{d\prime }_c}^2=\frac{1}{({\sigma }_1^2+{\sigma }_R^2)({\sigma }_2^2+{\sigma }_R^2)-{\sigma }_R^4}[{\Delta }_1^2({\sigma }_2^2+{\sigma }_R^2)+{\Delta }_2^2({\sigma }_1^2+{\sigma }_R^2)-2{\Delta }_1{\Delta }_2{\sigma }_R^2].$$ (A4)

Substituting ${d\prime }_A={\Delta }_1∕\sqrt{({\sigma }_1^2+{\sigma }_R^2)}$ and ${d\prime }_B={\Delta }_2∕\sqrt{({\sigma }_2^2+{\sigma }_R^2)}$ into Eq. (A4) gives

$${{d\prime }_c}^2=\frac{1}{({\sigma }_1^2+{\sigma }_R^2)({\sigma }_2^2+{\sigma }_R^2)-{\sigma }_R^4}\cdot [{{d\prime }_A}^2({\sigma }_1^2+{\sigma }_R^2)({\sigma }_2^2+{\sigma }_R^2)+{{d\prime }_B}^2({\sigma }_2^2+{\sigma }_R^2)({\sigma }_1^2+{\sigma }_R^2)-2{d\prime }_A{d\prime }_B\sqrt{({\sigma }_1^2+{\sigma }_R^2)}\sqrt{({\sigma }_2^2+{\sigma }_R^2)}{\sigma }_R^2],$$ (A5)

which simplifies to

$${{d\prime }_c}^2=\frac{1}{1-\frac{{\sigma }_R^4}{({\sigma }_1^2+{\sigma }_R^2)({\sigma }_2^2+{\sigma }_R^2)}}\cdot \left({{d\prime }_A}^2+{{d\prime }_B}^2-2{d\prime }_A{d\prime }_B\frac{{\sigma }_R^2}{\sqrt{({\sigma }_1^2+{\sigma }_R^2)({\sigma }_2^2+{\sigma }_R^2)}}\right).$$ (A6)

The correlation coefficient r between two random variables z₁ and z₂ is defined as the covariance of z₁ and z₂, divided by the product of the standard deviations of z₁ and z₂, so here we can replace the term ${\sigma }_R^2∕\sqrt{({\sigma }_1^2+{\sigma }_R^2)({\sigma }_2^2+{\sigma }_R^2)}$ by r which gives the final result,

$${{d\prime }_c}^2=\frac{1}{1-r^2}({{d\prime }_A}^2+{{d\prime }_B}^2-2{d\prime }_A{d\prime }_{B}r).$$ (A7)

Equation (A7) can be rewritten as

$$r^2-r\frac{2{d\prime }_A{d\prime }_B}{{{d\prime }_c}^2}+\frac{{{d\prime }_A}^2+{{d\prime }_B}^2-{{d\prime }_c}^2}{{{d\prime }_c}^2}=0.$$ (A8)

There exist two solutions for r:

$$r_{1∕2}=\frac{{d\prime }_A{d\prime }_B}{{{d\prime }_c}^2}\pm {\left[{\left(\frac{{d\prime }_A{d\prime }_B}{{{d\prime }_c}^2}\right)}^2-\frac{{{d\prime }_A}^2+{{d\prime }_B}^2-{{d\prime }_c}^2}{{{d\prime }_c}^2}\right]}^{0.5}.$$ (A9)

In the present study, only the smaller of the two solutions for r was used because the objective was to assume the smallest value of the common noise variable possible that would predict the d′ values in the combined condition.