Efficient Calculation of P-value and Power for Quadratic Form Statistics in Multilocus Association Testing

SUMMARY

We address the asymptotic and approximate distributions of a large class of test statistics with quadratic forms used in association studies. The statistics of interest take the general form D = X^T AX, where A is a general similarity matrix which may or may not be positive semi-definite, and X follows the multivariate normal distribution with mean μ and variance matrix Σ, where Σ may or may not be singular. We show that D can be written as a linear combination of independent chi-square random variables with a shift. Furthermore, its distribution can be approximated by a chi-square or the difference of two chi-square distributions. In the setting of association testing, our methods are especially useful in two situations. First, when the required significance level is much smaller than 0.05 such as in a genome scan the estimation of p-values using permutation procedures can be challenging. Second, when an EM algorithm is required to infer haplotype frequencies from un-phased genotype data the computation can be intensive for a permutation procedure. In either situation, an efficient and accurate estimation procedure would be useful. Our method can be applied to any quadratic form statistic and therefore should be of general interest.

INTRODUCTION

The multilocus association test is an important tool for use in the genetic dissection of complex disease. Emerging evidence demonstrates that multiple mutations within a single gene often interact to create a ‘super allele’ which is the basis of the multilocus association between the trait and the genetic locus [Schaid et al. 2002]. For the case-control design, a variety of test statistics have been applied, such as the likelihood ratio test, the logistic regression model, the χ² goodness-of-fit test, the score test, and the similarity- or distance-based test, etc. Many of these statistics have the quadratic form X^T AX or are functions of quadratic forms, where X is a vector of functions of the phenotype and A is a matrix accounting for the inner relatedness of haplotype or genotype categories. Some of these test statistics follow the chi-square distribution under the null hypothesis. For those that do not follow the chi-square distribution, the permutation procedure is often performed to estimate the p-value and power [Sha et al., 2007, Lin et al. 2009].

Previous attempts to find the asymptotic or approximate distribution of this class of statistics have been limited or case-specific. Tzeng et al. [2003] advanced our understanding of this area when they proposed a similarity-based statistic T and demonstrated that it approximately followed a normal distribution. The normal approximation works well under the null hypothesis provided that the sample sizes in the case and control populations are similar. However, the normal approximation can be inaccurate when the sample sizes differ, when there are rare haplotypes or when the alternative hypothesis is true instead, as we describe later. Schaid [2002] proposed the score test statistic to access the association between haplotypes and a wide variety of traits. Assuming normality of the response variables, this score test statistic can be written as a quadratic form of normal random variables and follows a non-central chi-square distribution under the alternative hypothesis. To calculate power, Schaid [2005] discussed systematically how to find the non-central parameters. However, their result cannot be applied to the general case when a quadratic form statistic does not follow a non-central chi-square distribution, such as the test statistic T [Tzeng et al. 2003] or S [Sha et al. 2007].

In the power comparisons made by Lin and Schaid [2009], power and p-values were all estimated using permutation procedures. However, a permutation procedure is usually not appropriate when the goal is to estimate a probability close to 0 or 1. For example, if the true probability p is about 0.01, 1,600 permutations are needed to derive an estimate that is between p/2 and 3p/2 with 95% confidence. The number of permutations increases to 1.6 million if p is only 10^–5. Consequently, permutation tests are not suitable when a high level of significance is being sought.

Additional complications arise with permutations since most of the data in the current generation of association studies are un-phased genotypes. To explore the haplotype-trait association, the haplotype frequencies are estimated respectively in cases and controls using methods such as the EM-algorithm [Excoffier and Slatkin, 1995; Hawley and Kidd, 1995] or Bayesian procedures [Stephens and Donnelly, 2003]. This process is again computationally intensive because in each permutation, the label of case or control to each individual is randomly assigned and therefore the haplotype frequencies need to be re-estimated every time. Sha et al. [2007] proposed a strategy to reduce the number of rare haplotypes, which leaded to a computationally efficient algorithm for the permutation procedure. This method is considerably faster than the standard EM algorithm. However, since the testing method is still based on permutations it is not a satisfactory solution to the computational problem.

The permutation procedure can also be very computationally intensive when estimating power. In a typical power analysis, for example, the significance level is 0.05 and power is 0.8. Under these assumptions the p-value could be based on 1,000 permutations. Subsequently if the power of the test is estimated with 1,000 simulations, the statistic must be calculated 1 million times. Though one can argue that the time required using a permutation procedure can be reduced dramatically by using a two stage method: on the first stage, one use a small number of permutations to assess whether the p-value is likely to be small, if not, one could establish that and save time, a large number of permutations is still needed for the replicates that have small p-values. In practice, to apply the multilocus association test method to genome-wide studies, the required significance level would be many orders of magnitude below 0.05 to account for multiple comparisons and even 1,000 minimal permutations will often be completely inadequate.

Based on these considerations, it is apparent that a fast and accurate way to estimate the corresponding p-value and associated power would be an important methodological step forward and make it possible to generalize the applications of the current quadratic form statistics. In this paper, we explore the asymptotic and approximate distribution of those statistics. Based on the results of these analyses, p-values and power can be estimated directly, eliminating the need for permutations. We assess the robustness of our methods using extensive simulation studies.

To simplify the notation, we use the statistic S proposed by Sha et al. [2007] as an illustrative way to display our methods. We first assume that the similarity matrix A is positive definite. We then extend this analysis to the case when A is positive semi-definite and the more general case assuming symmetry of A only. This is important because A is often not positive definite in practice. In the simulation studies, we use qq-plots and distances between distributions to explore the performance of our approximate distributions. In addition, we examine the accuracy of our approximations at the tails. As an additional example, we apply our method to the statistic T proposed by Tzeng et al. [2003] and compare the result with their normal approximation. Finally, we use our method to find the sample size needed for a candidate gene association study when linkage phase is unknown.

METHODS

Notations

Assume that there are k distinct haplotypes (h₁, · · · , h_k) with frequencies p = (p₁, · · · , p_k)^T in population 1 and q = (q₁, · · · , q_k)^T in population 2. In addition, we assume Hardy-Weinberg Equilibrium and observed haplotype phases. We also assume that sample 1 and sample 2 are collected randomly and independently from population 1 and population 2 respectively. Let n_j and m_j, j = 1, · · · , k, represent the observed count of haplotype h_j in sample 1 and sample 2 respectively. Let $n={\sum }_{i=1}^k$ n_i = size of sample 1, $m={\sum }_{i=1}^k$ m_i = size of sample 2, p̂ = (p̂₁, · · · , p̂_k)^T =(n₁, · · · , n_k)^T/n, q̂ = (q̂₁, · · · , q̂_k)^T = (m₁, · · · , m_k)^T/m, a_ij = S(h_i, h_j) = the similarity score of haplotypes h_i and h_j, and A = (a_ij) = the k × k similarity matrix. Let s = p − q and ŝ = p̂ − q̂. Then Sha et al.'s statistic is defined as $S=\left({\widehat{s}}^{T}A\widehat{s}\right)∕{\widehat{\sigma }}_0$, where ${\widehat{\sigma }}_0^2$ is an estimate of the variance of ŝ^T Aŝ under the null hypothesis. In this paper, we focus on the distribution of D_s = ŝ^T Aŝ since asymptotically, ${\widehat{\sigma }}_0$ can be treated as a constant.

The Asymptotic Distribution

In short, D_s asymptotically can be written as a linear combination of chi-square distributions with a constant shift for a general nonsingular similarity matrix A. To state this conclusion in detail, we define the necessary notation below (see Appendix I for proofs).

It is easy to see that E(ŝ) = s and Var(ŝ) = Σ_s = Σ_p + Σ_q, where Σ_p = Var(p̂) = (P – pp^T)/n with P = diag(p₁, · · · , p_k) being a k × k diagonal matrix. Likewise, Σ_q = (Q – qq^T)/m is the variance matrix of q̂. Let r_σ denote the rank of Σ_s. Then r_σ ≤ k – 1 since ŝ = (ŝ₁, · · · ,ŝ_k)^T only has k - 1 free components due to the restriction ${\sum }_{i=1}^k{\widehat{s}}_i=0$. If we assume p_i + q_i > 0 for all i = 1, · · · , k, then r_σ = k – 1. Since Σ_s is symmetric and positive semi-definite, there exists a k × k orthogonal matrix U = (u₁, · · · , u_k), and a diagonal matrix Λ = diag(λ₁, · · · , λ_rσ, 0), such that Σ_s = UΛU^T and λ₁ ≥ · · · ≥ λ_rσ > 0. Define matrices U_σ = (u₁, · · · , u_rσ) which is k × r_σ, Λ_σ = diag(λ₁, ··· , λ_rσ) which is r_σ × r_σ, and $B=U_{\sigma }{\left({\Lambda }_{\sigma }\right)}^{\frac{1}{2}}$ which is k × r_σ of rank r_σ.

Let $W=B^{T}AB={\left({\Lambda }_{\sigma }\right)}^{\frac{1}{2}}{U}_{\sigma }^{T}A{U}_{\sigma }{\left({\Lambda }_{\sigma }\right)}^{\frac{1}{2}}$. Define V to be a r_σ × r_σ orthogonal matrix such as W = VΩV^T, where Ω = diag(ω₁, ··· , ω_rσ) is a diagonal matrix. Then W is nonsingular when A is Nonsingular. Therefore, Ω^–1 = diag(1/ω₁, ···, 1/ω_rσ) is well-defined. Let $b={(b_1,\cdots ,b_{r_{\sigma }})}^T={\Omega }^{-1}{V}^T{\left({\Lambda }_{\sigma }\right)}^{\frac{1}{2}}{U}_{\sigma }^T$ As and c = s^T As – b^T Ωb. Then D_s can be written as

$$D_s\approx {(Y+b)}^T\Omega (Y+b)+c=\sum _{i=1}^{r_{\sigma }}{\omega }_i{(Y_i+b_i)}^2+c$$ (1)

where Y = (Y₁, · · · , Y_rσ) follows the multivariate standard normal distribution.

Provided that the similarity matrix A is positive definite, then W will also be positive definite. We may assume that ω₁ ≥ · · · ≥ ω_rσ > 0. In this case, a non-central shifted chi-square distribution can be used for approximation, which is discussed in detail in the next two subsections. Note that equation (1) is true for any general variance matrix Σ_s. In the special case when Σ_s is non-singular, it is easy to verify that the shift c = s^T As – b^TΩb is always 0.

The Approximate Distribution

The probability calculation for quadratic form D = X^T AX is usually not straightforward except in some special cases. The approximations based on numerical inversion of the characteristic function can be very accurate [Imhof, 1961; Davies, 1980], however, they are not easy to implement and require a lot of computation. The alternative majority of approximation approaches are based on the moments of D [Solomon and Stephens 1977, 1978]. Those approaches compare the cumulants of D and a chi-square random variable. Since the chi-square distribution function is available in nearly all statistical packages, it is much easier to implement. Liu et al. [2009] proposed a non-central shifted chi-square approximation by fitting the first four cumulants of D which is better than the current widely-used Pearson's three-moment central chi-square approximation approach [Imhof, 1961]. Unfortunately, Liu et al. [2009] assume X has a nonsingular variance matrix while in our case the rank of Σ_s is at most k − 1. In addition, they assume A is positive semi-definite which is not necessarily true in our situation. We extend Liu's approximation for a general similarity matrix A, which might be positive definite or not, singular or not; and for a general variance matrix Σ_s, which might be singular or not.

Following the idea of Liu et al. [2009], we first derive the corresponding formula for singular variance matrix Σ_s with positive definite A (see Appendix II for details). Define κ_ν = 2^ν–1(ν – 1)!(tr((AΣ_s)^ν) + νs^T (AΣ_s)^ν–1As), ν = 1, 2, 3, 4. Let $s_1={\kappa }_3^2∕\left(8{\kappa }_2^3\right)$ and $s_2={\kappa }_4∕\left(12{\kappa }_2^2\right)$. If s₁ ≤ s₂, let δ = 0 and df_a = 1/s₁. Otherwise, define $\xi =1∕({\sqrt{s}}_1-\sqrt{s_1-s_2})$, and let $\delta ={\xi }^2(\xi \sqrt{s_1}-1)$ and $d{f}_a={\xi }^2(3-2\xi \sqrt{s_1})$. Now let ${\beta }_1=\sqrt{2(d{f}_a+2\delta )∕{\kappa }_2}$, and β₂ = df_a + δ – β₁κ₁. Then we have the following 4-cum approximation:

$${\beta }_1{D}_s+{\beta }_2\stackrel{\cdot }{~}{\chi }_{d{f}_a}^2\left(\delta \right)$$ (2)

Note that if s = 0, we have b = c = 0 and $D_s=\sum w_i{Y}_i^2$. According to Satorra and Bentler [1994], the distribution of the adjusted statistic βD_s can be approximated by a central chi-square with degrees of freedom df₀, where β is the scaling parameter based on the idea of Satterthwaite et al. [1941]. Denote the trace of a matrix as tr(·). Then β = tr(W)/tr(W²) and df₀ = (tr(W))²/tr(W²), where tr(W) = tr(AΣ_s) and tr(W²) = tr(AΣ_sAΣ_s). This method is referred to in this paper as the 2-cum approximation.

Calculation of P-value, Critical Value and Power

The p-value is calculated under the null hypothesis H₀ : p = q. In this case, the true haplotype frequencies p and q are usually unknown, although the difference s = p − q is assumed to be zero. Therefore, both the 4-cum and 2-cum approximations can be used to find the p-value. We show only the results for the 4-cum approximation; the 2-cum approximation under the null hypothesis can be applied likewise. To find the corresponding β₁ and β₂ in the 4-cum approximation, we can use 0 to replace s and ${\widehat{\Sigma }}_s$ to replace Σ_s. Here ${\widehat{\Sigma }}_s=(\widehat{R}-\widehat{\rho }{\widehat{\rho }}^T)(1∕n+1∕m)$ is a consistent estimate of Σ_s with $\widehat{R}=\mathrm{diag}({\widehat{\rho }}_1,\cdots ,{\widehat{\rho }}_k)$, $\widehat{\rho }={({\widehat{\rho }}_1,\cdots ,{\widehat{\rho }}_k)}^T$, and ${\widehat{\rho }}_i=(n{\widehat{p}}_i+m{\widehat{q}}_i)∕(n+m)$ for i = 1, . . . , k. Note that the center parameter δ is always 0 under the null hypothesis. To prove this, it is sufficient to show s₁ ≤ s₂, which is equivalent to [tr((AΣ_s)³)]² ≤ [tr((AΣ_s)²)][tr((AΣ_s)⁴)], itself a direct conclusion from Yang et al. [2001]. Then the p-value is estimated as

$$\mathrm{p}\text{-value}=P_{H_0}(D_s\ge {\widehat{d}}_s)\approx P\left({\chi }_{d{f}_a}^2\ge {\beta }_1{\widehat{d}}_s+{\beta }_2\right)$$ (3)

Equivalently, let $c_{\alpha }^{\ast }$ be the quantile such that $P({\chi }_{d{f}_a}^2\ge c_{\alpha }^{\ast })=\alpha$. Then the critical value $d_{\alpha }^{\ast }$ for rejection at significance level α is

$$d_{\alpha }^{\ast }\approx (c_{\alpha }^{\ast }-{\beta }_2)∕{\beta }_1$$ (4)

Power is usually calculated when p and q are known but not equal. In this case, the values of s = p – q and Σ_s = Σ_p + Σ_q = (P – pp^T)/n + (Q – qq^T)/m are both known. Let $d_{\alpha }^{\ast }$ be the critical value as defined in equation (4). The power to reject H₀ at significance level α is

$$\text{power}=P_{H_a}(D_s\ge d_{\alpha }^{\ast })\approx P({\chi }_{d{f}_a}^2\left(\delta \right)\ge {\beta }_1{d}_{\alpha }^{\ast }+{\beta }_2)$$ (5)

Extension for General Similarity Matrix

We assume that the similarity matrix A is positive definite in formulas (1) to (5). However, in practice, A can be singular or have negative eigenvalues.

If A is singular, that is, rank(A) = r_a < k, there exists an orthogonal matrix G = (g₁, · · · , g_k) and a diagonal matrix Γ = diag(γ₁, · · · , γ_ra, 0, · · · , 0), where γ₁ ≠ 0, · · · , γ_ra ≠ 0, such that A = GΓG^T . Let G_a = (g₁, · · · , g_ra) and Γ_a = diag(γ₁, · · · , γ_ra). Then A can be written as $A=G_a{\Gamma }_a{G}_a^T$. Now define ${\widehat{s}}_a=G_a^T\widehat{s}$. We have $D_s={\widehat{s}}^{T}A\widehat{s}={\widehat{s}}_a^T{\Gamma }_a{\widehat{s}}_a$, where Γ_a is nonsingular and ŝ_a asymptotically follows a normal distribution with mean ${\mu }_a=G_a^{T}s$ and variance ${\Sigma }_a=G_a^T{\Sigma }_s{G}_a$. Therefore, even if A is singular, we can perform the above calculation to reduce its dimensionality and convert it into a non-singular matrix Γ_a. Then by replacing s with μ_a, Σ_s with Σ_a, and A with Γ_a, all the above formulas can be applied as long as A does not have negative eigenvalues. We apply this method in the example of HapMap 3 data, where the similarity matrices are often singular or nearly singular.

If A is nonsingular but has negative eigenvalues, equation (1) is still true although formulas (2) to (5) are not. In this case, we need to find the actual matrix W according to its definition. Next, we separate the eigenvalues of W into positive and negative groups. Assume that W has r_p positive and r_n negative eigenvalues, where r_p + r_n = r_σ. Without loss of generality, let ω₁ > 0, · · · , ω_rp > 0 and ω_rp+1 < 0, · · · , ω_rp+rn < 0. Now define ŝ₁ = (Y₁ + b₁, · · · , Y_rp + b_rp)^T and A₁ = diag(ω₁, · · · , ω_rp). We get quadratic form $D_1={\widehat{s}}_1^T{A}_1{\widehat{s}}_1$, where A₁ is positive definite. Therefore, its distribution can be approximated using formula (2). Similarly, define ŝ₂ = (Y_rp+1 + b_rp+1, · · · , Y_rp+rn + b_rp+rn) and A₂ = diag(–ω_rp+1, · · · , –ω_rp+rn). Then $D_2={\widehat{s}}_2^T{A}_2{\widehat{s}}_2$. Likewise, we can get the approximate distribution of D₂. Since D_s = D₁ –D₂ + c, the corresponding probability of D_s can be calculated by the technique described in Appendix IV. We apply this method in the simulation study when using length measure for Gene I, where the similarity matrix has both positive and negative eigenvalues. This method is also applied to find the approximate distribution of D_t [Tzeng et al. 2003].

Software Availability

We have integrated our approaches in an R source file named quadrtic.approx.R. Given the mean μ_x and variance Σ_x of X, this R file contains subroutines to estimate: (i) the probability p = P{X^T AX ≤ d} for a specific d, which is useful in approximating p-values or power; (ii) the quantile d* such that α = P{X^T AX ≤ d*} for a specific α; and (iii) the required sample size for a specific level of significance α and power 1 – β. This R file, as well as the readme and example files, can be downloaded from http://webpages.math.luc.edu/ltong/software/.

Simulation Study

In the simulation studies, we use the same four data sets as in Sha et. al. [2007]: Gene I, Gene II, Data I and Data II. Genes I and II represent two typical haplotype structures [Knapp and Becker, 2004]. There are 5 typed SNPs and 15 distinct haplotypes in Gene I and 10 typed SNPs and 21 distinct haplotypes in Gene II. Data I come from the study of association between DRD2 locus and alcoholism [Zhao et. al., 2000]. There are 3 typed SNPs and 8 distinct haplotypes in Data I. Data II come from the Finland-United States Investigation of Non-Insulin-Dependent Diabetes Mellitus Genetic Study [Epstein and Satten, 2003]. There are 5 typed SNPs and 17 distinct haplotypes in Data II (some of the haplotypes show up in normal group only and some in disease group only). We also consider three similarity measures: (i) matching measure - 1 for complete match and 0 otherwise; (ii) length measure - length spanned by the longest continuous interval of matching alleles; and (iii) counting measure - the proportion of alleles in common. We explore the performance of our approximations to the statistics D_s = (p̂ – q̂)^T A(p̂ – q̂) [Sha et al. 2007] and D_t = p̂^T Ap̂ – q̂^T Ap̂ [Tzeng et al. 2003] using sample sizes: n = m = 20, 50, 100, 500, 1000, 5000, and 10000.

Application to HapMap 3 data

For given values of significance level and power, we calculate sample size required to claim a significant difference in haplotype distributions around the LCT gene (23 SNPs) between two distinct populations: HapMap3 CHB (n = 160) and HapMap3 JPT (m = 164) using the statistic D_s. Since the linkage phase information is unknown, an EM algorithm was used to estimate the frequency of each distinct haplotype category.

RESULTS

Simulation Study

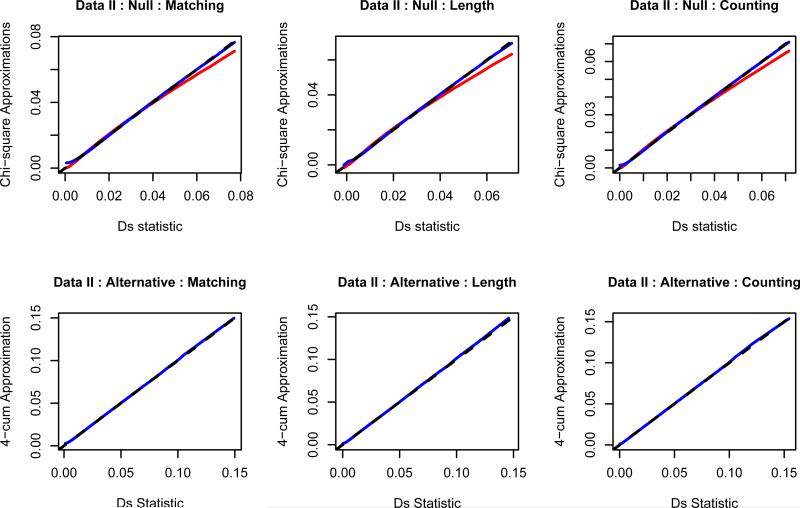
Figure 1 shows the qq-plot of the 2-cum and 4-cum approximations versus the empirical distributions of D_s for Data II under the null and alternative hypotheses with sample size n = m = 100. The x-axes are the quantiles of D_s, which are estimated based on 1.6 million independent simulations according to the true parameter values. The y-axes are the theoretical quantiles of our approximations based on the true parameter values. The range of the quantiles is from 0.00001 to 0.99999. From Figure 1, we observe that most of the points are around the straight line y = x, which leads to the conclusion that our approximations are good in general even when there are rare haplotypes such as in this example. At the right tails of the plots under the null hypothesis, the 2-cum approximations are all below the straight line, which indicates that the 2-cum approximation tends to underestimate the p-values. This is further verified in Table 2 below. The 4-cum approximation appears to perform better than the 2-cum one under the null hypothesis. We also examined the qq-plots as the sample size increased. As expected, our approximations are more accurate with larger sample sizes (results not shown here). The plots on the second row indicate that the 4-cum approximation is fairly accurate under the alternative hypothesis. The patterns for the other data sets are similar.

Figure 1.

The qq-plots of the 2-cum (red line) and 4-cum (blue line) approximations to the distribution of D_s under the null (first row) and alternative (second row) hypotheses using Data II. The black dashed line is y = x. We use the true values of p and q here. The left, middle, and right columns are for matching, length, and counting measures respectively. The sample sizes are m = n = 100.

TABLE 2.

Kolmogorov and Cramer-von Mises distances under the null hypothesis when sample sizes n = m = 100

		K-dist			CM-dist
Data	Method	Matching	Length	Counting	Matching	Length	Counting
Gene I	2-cum	4.71	7.89	5.52	2.05	3.73	2.78
	4-cum	4.54	9.25	10.50	1.24	3.29	2.84
Gene II	2-cum	3.84	2.57	2.19	2.07	1.55	1.26
	4-cum	2.85	1.74	1.45	1.21	0.68	0.61
Data I	2-cum	3.12	4.02	1.59	1.59	2.09	0.69
	4-cum	4.15	3.97	2.16	1.62	1.48	0.66
Data II	2-cum	3.80	6.43	6.28	1.71	3.17	2.96
	4-cum	3.92	8.12	10.99	1.08	2.46	2.73

Table 1 compares the Kolmogorov distance (K-dist) and the Craimer-von Mises distance (CM-dist) [Kohl and Ruckdeschel, 2009] between the 4-cum approximation and the empirical distribution of D_s and those distances between the permutation procedures and the empirical one for different sample sizes. The Kolmogorov distance measures the maximum differences between two distribution functions, while the Craimer-von Mises distance measures the average differences throughout the support of x (See Appendix III for more details). The empirical distribution is based on 10K simulations under the null hypothesis. To get Table 1, we first use the true parameter values p(= q) in the approximations (Table 1, rows ‘true’). Then we simulate 20 independent samples and replace p(= q) and Σ_s with $\widehat{\rho }$ and ${\widehat{\Sigma }}_s$ respectively. The distribution based on 1000 permutations is also calculated for each of the 20 samples. We did not perform permutations when n = m ≥ 1000 because those procedures are very slow when n and m are large. For each method, the mean and standard deviation of distances based on these 20 samples are displayed in Table 1, rows ‘mean’ and ‘s.d.’. To simplify the output, we show only the results for Gene I using the matching measure.

TABLE 1.

Kolmogorov and Cramer-von Mises distances (%) under the null hypothesis for Gene I using matching measure

			sample size (n = m)
Distance	Method		20	50	100	500	1000	5000	10000
		true	6.30	4.82	4.54	4.65	4.70	4.51	4.75
K-dist	4-cum	mean	8.76	6.81	4.80	4.57	4.61	4.52	4.77
		s.d.	3.43	3.37	1.11	0.48	0.34	0.14	0.09
	perm.	mean	10.39	6.74	4.16	3.00	NA	NA	NA
		s.d.	3.16	2.89	1.15	1.18	NA	NA	NA
		true	1.98	1.47	1.24	1.20	1.38	1.52	1.31
CM-dist	4-cum	mean	4.15	3.38	2.10	1.35	1.54	1.53	1.32
		s.d.	2.23	2.24	1.03	0.26	0.23	0.10	0.05
	perm.	mean	4.32	3.21	1.96	1.29	NA	NA	NA
		s.d.	2.27	1.91	0.71	0.70	NA	NA	NA

From Table 1, we observe that for the 4-cum approximation, the mean distances using estimated parameter values converge to the distance using the true parameter values when sample sizes n and m increase. This is because both the asymptotic and the approximate components contribute to the distance. When sample sizes increase, the discrepancy due to the asymptotic component decreases eventually to zero, however, the discrepancy due to the approximate component does not. For example, the K-dist for the 4-cum method based on true parameter values decreases from 6.30% to 4.82% when the sample size increases from 20 to 50. But when the sample size increases from 50 to 10,000, this distance stays constant around 4.6%. Compared with the permutation procedure, the 4-cum approximations show better performance for n as small as 20, and comparable performance when n is reasonably large. As for computational intensity, the permutation procedure in this case costs about 6 hours using a standard computer with Intel(R) Core(TM) CPU @ 2.66 GHz and 3.00 GB of RAM, while only two seconds are needed using our approximations. Moreover, when the sample size increases, the computational time increases rapidly for a permutation procedure, while it stays the same for our approximations.

Table 2 compares the distances from the 2-cum and 4-cum approximations using true parameter values for all the data sets and similarity measures when n = m = 100. When sample sizes are as large as 100, the distances are mainly due to the approximation, not the asymptotic part (conclusion from Table 1). Since the Cramer-von Mises distances from the 4-cum approximations are smaller in general, we conclude that the 4-cum approximation performs better than the 2-cum approximation on average. However, there are some situations when the 2-cum approximation is preferred, such as those in the column ‘Counting’ under ‘K-dist’ in Table 2. To determine how much of the distance is due to the discrete empirical distribution of D_s, we also examined the distance between the approximate distributions with their own empirical distributions based on 10K independent observations. The average Kolmogorov distance is around 0.87% and the average Cramer-von Mises distance is around 0.38%, which are about 20% of the average distances in Table 2. Therefore, for the 2-cum and 4-cum approximation, the average Kolmogorov distances due to approximation are around (3.46%, 5.20%) and (4.43%, 6.17%) respectively; the average Cramer-von Mises distances are around (1.75%, 2.51%) and (1.28%, 2.04%) respectively.

Table 3 explores the performance of the 4-cum approximation and the permutation procedure to estimate probabilities at the right tails for Data II using a matching measure. Notice that the 4-cum approximation is accurate in estimation of a p-value of 0.1%. For probabilities around 0.01%, the 4-cum approximation tends to slightly underestimate the true value. For probabilities around 0.001%, we list results in the last column of Table 3. However, since the number of simulations is limited, we can have only modest confidence in these approximations, although it is evident that those approximations will provide underestimated probabilities. Note that this also indicates that the type I error rates could be slightly higher than expected when using a small significant level, such as 0.01% or 0.001%. The permutation procedure gives good estimates for a p-value as small as 0.01% if the number of permutations is large enough (160K here). However, in the last column of Table 3, we note that the standard deviation of estimated p-values is 0.001%, which is about the same as the mean (0.0012%) of these estimates. This is because 160K permutations are far too few to give accurate estimate of a p-value of 0.001%. The conclusions based on the other data sets are similar (results not shown).

TABLE 3.

Probabilities at the right tail for Data II using matching measure when sample sizes n = m = 100

		p = %
Method		5	1	0.1	0.01	0.001
	true	5.1828	1.0273	0.0929	0.0076	0.0008
4-cum	mean	5.2266	1.0297	0.0926	0.0076	0.0008
	s.d.	0.1331	0.0753	0.0161	0.0022	0.0003
perm.	mean	5.0482	0.9976	0.1011	0.0104	0.0012
	s.d.	0.1602	0.0771	0.0238	0.0033	0.0010

Table 4 summarizes the results for approximate distributions of D_s under the alternative hypothesis when n = m = 20, 100, or 1000, which is useful in a power analysis. In this situation, we assume that the parameter values are known. The quantiles at (0.50, 0.60, 0.70, 0.80, 0.90, 0.95) are estimated through 160K simulations. Table 4 shows the corresponding probabilities that are greater than or equal to these quantiles under the alternative hypothesis using the 4-cum approximation. Since most of the estimated powers are close to the empirical value, we conclude that the power estimation is fairly accurate with moderate sample size (n = m = 100) and moderate true power (less than 95%).

TABLE 4.

Probabilities at the left tail (4-cum approximation only)

		Sample	Power (%)
Data	Measure	Size	50	60	70	80	90	95
		20	48.59	56.45	65.41	80.95	92.40	98.01
	Matching	100	50.10	59.63	69.71	79.27	89.64	95.62
		1000	50.17	60.10	70.17	79.89	90.00	95.00
		20	48.17	57.12	67.11	78.42	96.29	99.63
Data II	Length	100	50.00	59.73	69.26	78.91	89.48	96.80
		1000	50.13	60.22	70.13	80.01	89.97	95.01
		20	48.41	58.54	67.59	79.45	96.01	100.00
	Counting	100	49.92	59.79	69.54	79.19	90.00	97.12
		1000	49.92	59.92	69.92	79.95	90.05	94.99

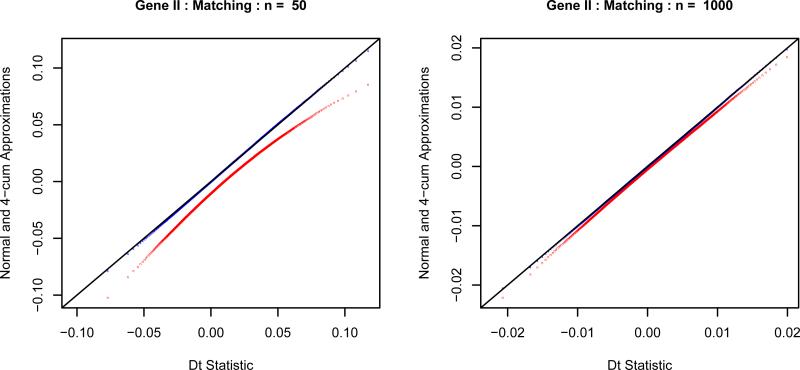
Figure 2 shows the qq-plot of the 4-cum approximation and the normal approximation versus the empirical distributions of D_t [Tzeng et al. 2003]. From this figure, we can see that our 4-cum approximation can approximate the distribution of D_t very well even when the smaller sample size is as small as 50. If the smaller sample size increases to 1000, the normal approximation also becomes acceptable.

Figure 2.

The qq-plots of the 4-cum chi-square approximation (blue “4”) and the normal approximation (red “n”) to the distribution of D_t under the null hypothesis using Gene II and the matching measure. We use the true values of p and q here. The left plot has a smaller sample size n = 50 and m = 150. The right plot has a larger sample size n = 1000 and m = 3000.

Application to HapMap 3 Data

Table 5 lists the required sample size for given values of significance level and power using a counting measure. Using the approximations described in our METHODS section, we can easily calculate the required sample size. The quantities needed here are haplotype lists, frequencies and variance estimates for each population separately and jointly, which can be estimated using the EM algorithm. We first use the package haplo.stat [Sinnwell and Schaid, 2008] in R to find the starting value. Then we use a stochastic EM to refine the estimated haplotype frequency and its variance. Note that all these calculations take only minutes on a standard computer with Intell(R) Core(TM) CPU @ 2.66 GHz and 3.00 GB of RAM. However, it requires at least several days to finish a single calculation using a permutation procedure.

TABLE 5.

Sample sizes required given significance level and power

	Power (%)
	70		80		90
Significance (%)	CHB	JPT	CHB	JPT	CHB	JPT
1	181	186	203	208	234	240
0.1	275	282	302	309	339	348
0.01	366	375	395	405	438	449
0.001	435	446	467	479	513	526

DISCUSSION

In summary, the major contribution of the analytic approach presented in this paper is the description of the asymptotic and approximate distributions of a large class of quadratic form statistics used in multilocus association tests, as well as efficient ways to calculate the p-value and power of a test. Specifically, we have shown that the asymptotic distribution of the quadratic form ŝ^T Aŝ is a linear combination of chi-square distributions with a shift. In this situation, ŝ asymptotically follows a multivariate normal distribution which may be degenerate.

To efficiently calculate the p-value under the null hypothesis s = E(ŝ) = 0, we propose the 2-cum and 4-cum chi-square approximations to the distribution of ŝ^T Aŝ. We extended the 4-cum approximation in Liu et al. [2009] to allow singular variance matrix of ŝ and general symmetric matrix A which may not be positive semi-definite. Generally speaking, the 4-cum is better than the 2-cum approximation when dealing with probabilities less than 0.01. Nevertheless, the latter may perform better for moderate probabilities, say 0.05. On the other hand, the 2-cum method only involves the products of up to two k × k matrices, while the 4-cum approach relies on a product of four k × k matrices. When the number of haplotypes k is large, the 2-cum approach is computationally much less intensive. To estimate the power of a test, however, only the 4-cum approximation is valid.

The similarity matrix A can be singular or nearly singular due to missing values. In this case, we decompose A and perform dimension reduction to get a smaller but nonsingular similarity matrix. The most attractive feature of our method is that we do not need to decompose matrices Σ_s or W when A is positive semi-definite because the decompositions do not appear in the final formula. This not only simplifies the formula, but also results in better computational properties since it is often hard to estimate Σ_s accurately.

In this paper we do not consider the effect of latent population structure. It has been widely recognized that the presence of undetected population structure can lead to a higher false positive error rate or to decreased power of association testing [Marchini et al. 2004]. Several statistical methods have been developed to adjust for population structure [Devlin and Roeder 1999, Prichard and Rosenberg 1999, Pritchard et al. 2000, Reich and Goldstein 2001, Bacanu et al. 2002, Price et al. 2006]. These methods mainly focus on the effect of population stratification on the Cochran-Armitage chi-square test statistic. It would be interesting to know how these methods can be applied to the similarity or distance-based statistic to conduct association studies in the presence of population structure.

Our methods can potentially be applied to the genome-wide association studies because the computations are fast and small probabilities can be estimated with acceptable variation. To perform a genome screen one must define the regions of interest manually, which will be exceedingly tedious. However, due to limitation in length, we do not discuss the problem of how to define haplotype regions automatically. Clearly before this approach can be applied in practice, such methods and software will have to be developed. We also propose to explore this issue in the future.

Appendix

I: Proof that D_s can be written as a linear combination of independent chi-square random variables under the alternative hypothesis

According to multivariate central limit theorem, ŝ is asymptotically normally distributed with the mean vector s = p − q and variance matrix Σ_s. Note that $U_{\sigma }^T{U}_{\sigma }=I_{r_{\sigma }}$ while $U_{\sigma }{U}_{\sigma }^T$ = who knows what. Then ${\Sigma }_s=U_{\sigma }{\Lambda }_{\sigma }{U}_{\sigma }^T=B{B}^T$ and there exist r_σ independent standard normal random variables Z = (Z₁, · · · , Z_rσ) such that ŝ ≈ BZ + s for sufficiently large n and m. Then we have

$$D_s={\widehat{s}}^{T}A\widehat{s}\approx {(BZ+s)}^{T}A(BZ+s)=Z^T{B}^{T}ABZ+2s^{T}ABZ+s^{T}As$$

Since W = B^T AB = VΩV^T, then Z^T B^T ABZ = Z^TWZ = Z^TV · Ω · V^TZ = Y^TΩY, and s^T ABZ = s^T ABVΩ^–1 · Ω · V^TZ = b^TΩY, where Y = V^TZ ~ N(0, I_rσ). Let c = s^T As – b^TΩb. We have

$$\begin{array}{cc}\hfill D_s& \approx Z^T{B}^{T}ABZ+2s^{T}ABZ+s^{T}As\hfill \\ \hfill & =Y^T\Omega Y+2b^T\Omega Y+s^{T}As\hfill \\ \hfill & ={(Y+b)}^T\Omega (Y+b)+s^{T}As-b^T\Omega b\hfill \\ \hfill & =\sum _{i=1}^{r_{\sigma }}{\omega }_i{(Y_i+b_i)}^2+c\hfill \end{array}$$

II: Four-cumulant non-central chi-square approximation

Rewrite the original statistic D = ŝ^T Aŝ into its asymptotic form (Y + b)^TΩ(Y + b) + c (see Appendix I). We only need to consider the shifted quadratic form

$$Q\left(Y_b\right)=Y_b^T\Omega Y_b+c,$$

where Y_b = Y + b ~ N(b, I_rσ), and Ω = diag(ω₁, . . . , ω_rσ) with ω₁ ≥ ω₂ ≥ · · · ω_rσ > 0.

According to Liu et al. [2009], the th cumulant of Q(Y_b) is

$${\kappa }_{\nu }=2^{\nu -1}(\nu -1)!({\kappa }_{\nu ,1}+\nu {\kappa }_{\nu ,2})$$

In our case, for ν = 1, 2, 3, 4,

$${\kappa }_{\nu ,1}=\text{tr}\left({\Omega }^{\nu }\right)=\text{tr}\left({\left(V^{T}WV\right)}^{\nu }\right)=\text{tr}\left(W^{\nu }\right)=\text{tr}\left({\left(B^{T}AB\right)}^{\nu }\right)=\text{tr}\left({\left(A{\Sigma }_s\right)}^{\nu }\right)$$

And for ν = 1,

$${\kappa }_{\nu ,2}=b^T\Omega b+c=b^T\Omega b+s^{T}As-b^T\Omega b=s^{T}As$$

For ν = 2, 3, 4,

$$\begin{array}{cc}\hfill {\kappa }_{\nu ,2}& =b^T{\Omega }^{\nu }b\hfill \\ \hfill & =s^{T}A{U}_{\sigma }{\left({\Lambda }_{\sigma }\right)}^{\frac{1}{2}}V{\Omega }^{-1}\cdot {\Omega }^{\nu }\cdot {\Omega }^{-1}{V}^T{\left({\Lambda }_{\sigma }\right)}^{\frac{1}{2}}{U}_{\sigma }^{T}As\hfill \\ \hfill & =s^{T}A{U}_{\sigma }{\left({\Lambda }_{\sigma }\right)}^{\frac{1}{2}}V{\Omega }^{\nu -2}{V}^T{\left({\Lambda }_{\sigma }\right)}^{\frac{1}{2}}{U}_{\sigma }^{T}As\hfill \\ \hfill & =s^{T}AB{\left(V\Omega V^T\right)}^{\nu -2}{B}^{T}As\hfill \\ \hfill & =s^{T}AB{\left(B^{T}AB\right)}^{\nu -2}{B}^{T}As\hfill \\ \hfill & =s^T{\left(A{\Sigma }_s\right)}^{\nu -1}As\hfill \end{array}$$

Therefore,

$${\kappa }_{\nu }=2^{\nu -1}(\nu -1)!(\text{tr}\left({\left(A{\Sigma }_s\right)}^{\nu }\right)+\nu s^T{\left(A{\Sigma }_s\right)}^{\nu -1}As),\nu =1,2,3,4$$

which actually takes the same form as in Liu et al. [2009]. So the discussion here extends Liu et Al. [2009]'s formulas to more general quadratic form which allows degenerate multivariate normal distribution.

III: Distance between a continuous distribution and an empirical distribution

To compare one continuous cumulative distribution function F₁ and one empirical distribution F₂ (or discrete distribution), two natural distances are the Kolmogorov distance

$$d_K(F_1,F_2)=\underset{x}{\text{sup}}\mid F_1\left(x\right)-F_2\left(x\right)\mid$$

and the Cramer-von Mises distance with measure μ = F₁

$$d_{cv}(F_1,F_2)={\left(\int {[F_1\left(x\right)-F_2\left(x\right)]}^{2}d{F}_1\left(x\right)\right)}^{\frac{1}{2}}$$

Note that F₂ is piecewise constant. Let x₁, x₂, . . . , x_n be all distinct discontinuous points of F₂. We keep them in an increasing order. If F₂ is an empirical distribution, x₁, x₂, . . . , x_n are distinct values of the random sample which generates F₂. Write x₀ = –∞.

For Kolmogorov distance, the maximum can be obtained by checking all the discontinuous points of F₂. Therefore,

$$d_K(F_1,F_2)=\underset{i}{\text{max}}\left\{\mid F_1\left(x_i\right)-F_2\left(x_i\right)\mid \right\}\bigvee \underset{i}{\text{max}}\left\{\mid F_1\left(x_i\right)-F_2\left(x_{i-1}\right)\mid \right\}$$

For Cramer-von Mises distance,

$$\begin{array}{cc}\hfill d_{cv}^2(F_1,F_2)& ={\int }_{-\infty }^{x_1}{F}_1{\left(x\right)}^{2}d{F}_1\left(x\right)+{\int }_{x_n}^{\infty }{[1-F_1\left(x\right)]}^{2}d{F}_1\left(x\right)+\sum _{i=1}^{n-1}{\int }_{x_i}^{x_{i+1}}{[F_1\left(x\right)-F_2\left(x_i\right)]}^{2}d{F}_1\left(x\right)\hfill \\ \hfill & =\frac{1}{3}{F}_1^3\left(x_1\right)+\frac{1}{3}{[1-F_1\left(x_n\right)]}^3+\frac{1}{3}\sum _{i=1}^{n-1}\{{[F_1\left(x_{i+1}\right)-F_2\left(x_i\right)]}^3-{[F_1\left(x_i\right)-F_2\left(x_i\right)]}^3\}\hfill \end{array}$$

Note that the formulas above work better than the corresponding R functions in the package ‘distrEx’ (downloadable via http://cran.r-project.org/). Those R functions have difficulties with large sample sizes (say n ≥ 2000), because their calculation replies on the grids on the real line.

IV: Calculating the difference between two non-central chi-squares

Let Y₁ and Y₂ be two independent non-central chi-square random variables with probability density function f₁(y) and f₂(y) respectively. Write Z = Y₁ –Y₂. Then the probability density function f(z) of Z can be calculated through

$$\begin{array}{cc}\hfill f\left(z\right)& ={\int }_{-\infty }^{\infty }{f}_1(z+y)f_2\left(y\right)dy\hfill \\ \hfill & ={\int }_0^1{f}_1\left(z+\text{log}\frac{x}{1-x}\right)f_2\left(\text{log}\frac{x}{1-x}\right)\cdot \frac{1}{x(1-x)}dx\hfill \end{array}$$

The cumulative distribution function F (z) of Z can be calculated through

$$\begin{array}{cc}\hfill F\left(z\right)& ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^z{f}_1(y_1+y_2)f_2\left(y_2\right)d{y}_{1}d{y}_2\hfill \\ \hfill & ={\int }_0^1{\int }_0^{\frac{e^z}{1+e^z}}{f}_1\left(\text{log}\frac{x_1{x}_2}{(1-x_1)(1-x_2)}\right)f_2\left(\text{log}\frac{x_2}{1-x_2}\right)\cdot \frac{1}{x_1{x}_2(1-x_1)(1-x_2)}d{x}_{1}d{x}_2\hfill \end{array}$$

Note that we perform the transformation y = log (x/(1 – x)) in both formulas to convert the integrating interval from (–∞, ∞) into (0, 1) for numerical integration purpose.