Down-State Model of the Voltage-Sensing Domain of a Potassium Channel

Abstract

Voltage-sensing domains (VSDs) of voltage-gated potassium (Kv) channels undergo a series of conformational changes upon membrane depolarization, from a down state when the channel is at rest to an up state, all of which lead to the opening of the channel pore. The crystal structures reported to date reveal the pore in an open state and the VSDs in an up state. To gain insights into the structure of the down state, we used a set of experiment-based restraints to generate a model of the down state of the KvAP VSD using molecular-dynamics simulations of the VSD in a lipid bilayer in excess water. The equilibrated VSD configuration is consistent with the biotin-avidin accessibility and internal salt-bridge data used to generate it, and with additional biotin-avidin accessibility data. In the model, both the S3b and S4 segments are displaced ∼10 Å toward the intracellular side with respect to the up-state configuration, but they do not move as a rigid body. Arginine side chains that carry the majority of the gating charge also make large excursions between the up and down states. In both states, arginines interact with water and participate in salt bridges with acidic residues and lipid phosphate groups. An important feature that emerges from the down-state model is that the N-terminal half of the S4 segment adopts a 3₁₀-helical conformation, which appears to be necessary to satisfy a complex salt-bridge network.

Introduction

Electrical signals traveling along nerve cells are propagated via action potentials generated by sodium and potassium ions that cross the plasma membrane through voltage-gated ion channels. These channels open and close in response to changes in the transmembrane (TM) potential (1). Voltage-dependent gating events are collective in nature and present complex kinetics with multiple closed states and, in some cases, several open states (1). Voltage-gated potassium (Kv) channels of known structure are homotetramers, with each monomer contributing one voltage-sensing domain (VSD) comprised of four TM segments (S1–S4) and two TM segments (S5 and S6) to the pore domain (2,3). The S4 helix contains several basic residues that render the VSDs sensitive to changes in TM potential. In the resting state of the channel, these positive-charged side chains are expected to be closer to the intracellular side of the membrane with the VSDs in a down state. Upon depolarization, effective charge motion within the membrane electric field toward the membrane extracellular side is accomplished through a series of conformational changes in the VSDs that lead to opening of the channel (4–6). All available crystal structures of Kv channels reveal the pore domain in the ion-conducting open state and the VSDs in an up state (3,7–9). However, despite the availability of these structures, comprehensive kinetic modeling (reviewed in 1,4), and a wide variety of spectroscopic, biochemical, and functional data (reviewed in 5,6), the molecular mechanism of voltage gating remains uncertain. In particular, the molecular configuration of VSDs in their down state is unknown. As a result, the extent of VSD movements and their mechanical coupling to the pore-domain activation gate are uncertain. Although no direct structural data exist for the down state, Ruta et al. (10) were able to examine the movement of the KvAP VSD by measuring avidin accessibility to tethered biotin reagents. Their measurements yielded estimates of the positions of VSD amino acids, along the TM direction, relative to the membrane interface during electrical stimulation. We used these estimates, complemented by two salt-bridge configurations, as restraints to produce an atomistic model of the down state using molecular-dynamics (MD) simulations.

The structures of Kv channels (3,7–9) show that their modular architecture is conserved from Archaea to mammals. The four peripheral VSDs of the intact channels are only loosely attached to the pore domain and exhibit very few interactions with it in the extracellular half of the assembly, suggesting that each VSD is an independent structural unit. Several lines of evidence support this conclusion. First, the isolated VSD from Aeropyrum pernix (KvAP) used in our simulations has been expressed in bacteria, crystallized (3), and reconstituted into membrane environments (11,12). Second, Kv VSDs engineered into non-voltage-gated K⁺ channels confer strong voltage dependence (13,14). Third, two recently discovered proteins, the Ciona intestinalis voltage-sensitive phosphatase (Ci-VSP) (15) and the Hv1 voltage-sensitive proton channel (16,17), have VSDs but no pore domains (18–21). Fourth, VSD modularity is consistent with electrophysiological kinetic models of Kv channel gating (22,23), which assume that each VSD moves independently between the resting state and a preopen activated state, followed by a concerted opening transition that opens the pore domain gate. Taken together, these results suggest that the voltage-sensitive movements of the S1-S4 segments in VSDs are not strongly influenced by the presence or motions of the pore domain in Kv channels. Consequently, we simplified modeling of the down state by considering an isolated VSD from KvAP.

Two structural features are characteristic of VSDs: 1), the highly conserved positions of charged residues in VSD sequences (see Fig. S1 in the Supporting Material); and 2), the helical hairpin motif of S3b-S4. S4 exhibits four to eight conserved triplet repeats composed of one basic residue (mostly arginine) followed by two hydrophobic residues. Four acidic residue positions are conserved in S1–S3 (one at the extracellular end of S1, two in S2, and one at the intracellular end of S3). Salt bridges between these conserved basic and acidic side chains are critical for VSD folding and stability (24–26). The capacitive currents (gating currents) that precede ion channel conduction demonstrate the movement of VSD charged residues with respect to the membrane electric field during activation (27). In the case of the Shaker channel, gating current measurements have shown that, during activation, each VSD displaces between 3 and 3.6 elementary charges within the membrane electric field, and that the first four extracellular arginines in S4 contribute most of the gating charge (28–30).

The conserved helical hairpin motif called the voltage-sensor paddle is formed by the C-terminal half of S3 (S3b) and S4, and appears to be highly mobile (10,31,32). The paddle can be transplanted between different proteins containing VSDs without loss of function (33,34) and is the target of spider toxins that inhibit the voltage-sensing function (35,36), suggesting that the functional role of this motif is conserved among VSDs.

Molecular models of voltage-dependent VSD conformational changes have a long and still-evolving history (reviewed in 5,37). These models have engendered controversy at times, because different lines of experimental evidence seemed to point toward divergent models. In the last few years, however, as old and new experimental data are interpreted in the light of the most recent crystal structures (8,9), it has been possible to distill the main features of VSD motions that are consistent with a broad range of experimental evidence (6). It is well established that during activation, S4 moves outward along the TM direction with a consensus magnitude of ∼10 Å (5,6). This motion has been modeled as a rigid-body, translation-rotation motion (38–40) or as a translation accompanied by a change in secondary structure (8). In both models, the conformational change fulfills the requirement of charge displacement with respect to the membrane electric field while maintaining the stability of the VSD through salt-bridge interactions between S4 and S1–S3. Although S4 is part of a conserved structural and functional motif with S3b, it is not clear how these two segments move relative to one another during activation.

Here we describe an atomistic model of the resting state of the KvAP VSD in an explicit membrane environment generated by MD simulations and experiment-based restraints. Our methodology is similar to the one used for structural refinement by NMR, whereby experimental restraints are complemented by molecular-mechanics constraints to obtain a final set of configurations. We find that the S3b and S4 paddle segments are displaced ∼10 Å toward the intracellular side, with respect to the up-state configuration, but they do not move as a rigid body. Arginine side chains that carry the majority of the gating charge also make large excursions between the up and down states. In both states, the arginines interact with water and participate in salt bridges with acidic residues and lipid phosphate groups. An important feature that emerges from the down-state model is that the N-terminal half of the S4 segment adopts a 3₁₀-helical conformation, which appears to be necessary to satisfy a complex salt-bridge network.

Materials and Methods

The model of the KvAP VSD down state was generated by means of a restrained all-atom MD simulation in a palmitoyl oleoyl phosphatidyl choline (POPC) bilayer in excess water, followed by a 75 ns unrestrained simulation, as described in the Supporting Material. The MD runs were performed with NAMD 2.6 (41). The CHARMM22 and CHARMM27 force fields (42,43) were used for the protein and lipids, respectively, and the TIP3P model was used for water (44). The smooth particle mesh Ewald method (45,46) was used to calculate electrostatic interactions, and the short-range, real-space interactions were cut off at 11 Å via a switching function. A reversible, multiple time-step algorithm (47) was employed to integrate the equations of motion with a time step of 4 fs for electrostatic forces; 2 fs for short-range, nonbonded forces; and 1 fs for bonded forces. All bond lengths involving hydrogen atoms were held fixed using the SHAKE (48) and SETTLE (49) algorithms. Molecular graphics and simulation analyses were performed using VMD 1.8.6 (50). The system was run at a constant temperature of 300 K and constant pressure of 1 atm. A Langevin dynamics scheme was used for temperature control, and a Nosé-Hoover-Langevin piston was used for pressure control (51,52). The simulation system was composed of one KvAP VSD (residues 24–147), 246 POPC molecules (123 per leaflet) waters, and two chloride counterions, for a total of 66,428 atoms.

Results

The atomistic model for the KvAP VSD, based on experimental data, was obtained in two steps (see Fig. 1 and Supporting Material). First, starting from the end configuration of an MD simulation of the up-state KvAP VSD in a POPC bilayer in excess water (53) (Fig. S2 A), we performed a restrained MD simulation using as restraints the 36 C_α atom positions in the VSD, along the TM direction, deduced from biotin-avidin accessibility data (10) and two interatomic distances, consistent with salt-bridge configurations, between S2 and S4. Second, once these restraints were satisfied (Fig. S2 B), we performed an unrestrained 75 ns MD simulation (Fig. S2 C) to generate a set of configurations in which both the protein chain stereochemistry and protein-environment interactions were optimized. The down-state VSD model was taken from the last 34 ns of the unrestrained trajectory. The up-state model was taken from the last 16.5 ns of the up-state trajectory of Freites et al. (53).

Figure 1.

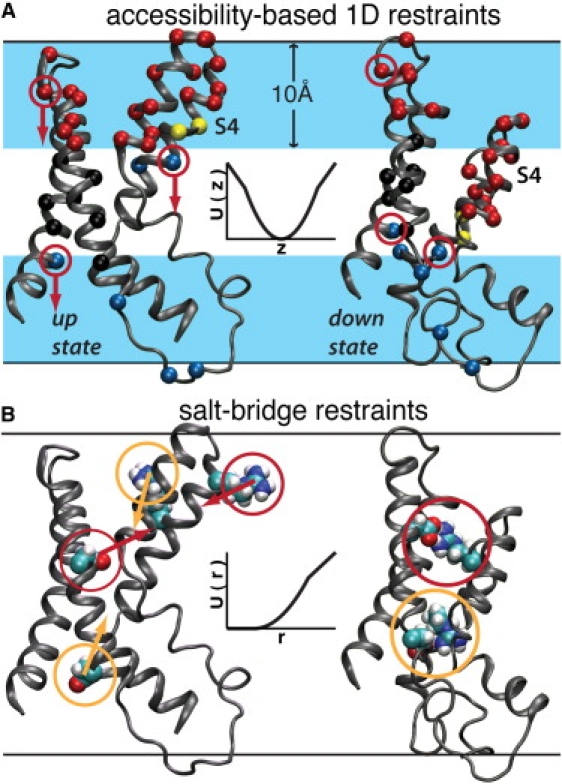
MD restraint definitions used to generate the down-state model. In both panels, the pairs of VSD structures correspond to a configuration from the end of a simulation of the isolated voltage sensor (53) based on the structural model reported by Lee et al. (7) and to the down-state configuration taken from the end of the unrestrained trajectory reported here. The pair of black horizontal lines represents the location of the lipid bilayer interface. (A) Ruta et al. (10) used biotinylated cysteine substitutions throughout the VSD to measure the accessibility of avidin to biotin tethers of three different lengths to map the TM depths of the labeled residues. We used these data as one-dimensional position restraints on the corresponding 36 C_α atoms (shown here as spheres). The atom coloring scheme corresponds to the reported biotin-avdin accessibility for a tether length of 10 Å. Red indicates accessibility to extracellular avidin, blue is intracellular, yellow is both intra- and extracellular, and black indicates inaccessibility to avidin. The light-blue band represents a depth of 10 Å into the hydrocarbon core. (B) Three-dimensional distance restraints were applied to form salt bridges between R117-D62 and R123-D72, based on experimental evidence discussed in detail in the Supporting Material. The insets in A and B illustrate the form of the corresponding restraint potentials. The arrows represent the directions of the restraint forces.

Our simulation trajectories for both the up and down states are, overall, consistent with the biotin-avidin accessibility data of MacKinnon and coworkers (10,54) when the mean positions of the lipid carbonyl distributions (−18 and 16 Å from the system center; see Fig. S3) are used to define the lipid bilayer interface (see section entitled Comparison to biotin-avidin accessibility data and Fig. S4 and Fig. S5 in the Supporting Material for details). The overall C_α root mean-square deviation of the down-state simulation from the end of the constrained configuration (Fig. S6 A) is ∼3 Å, a value similar to the typical C_α root mean-square deviation of MD simulations of membrane proteins in lipid bilayers from their crystal structures. In Fig. 2 we compare the C_α TM displacements of the end configuration of the constrained simulation (red dots) with the C_α TM displacements of the equilibrated down-state simulation (blue line). Absolute differences are within the width of the carbonyl distributions (full width at half-maximum of ∼6 Å; see Fig. S3).

Figure 2.

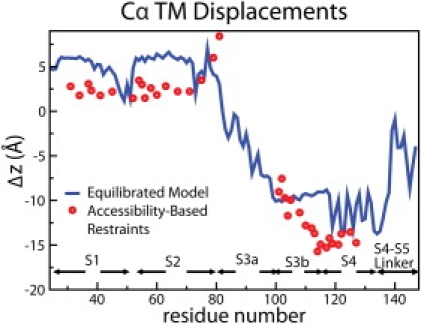
Quantitative comparison of the biotin-avidin accessibility constraints to the down-state unrestrained simulation. The blue line indicates the difference between the mean position of the C_α atoms in our equilibrated up- and down-state trajectories (last 16 and 35 ns, respectively). The red dots indicate the difference between the mean position of the C_α atoms in our equilibrated up state and the locations assigned by Ruta et al. (10) for the VSD in the down state, i.e., the initial constraints used to generate the model.

For S1 and S2, the C_α TM effective displacements between the up- and down-state simulations (Fig. 2, blue line) are ∼5 Å, which is within the width of the carbonyl distributions. It can be considered, therefore, as concluded by Ruta et al. (10), that there is no significant motion of S1-S2 along the TM direction. In contrast, for S3b and S4, the C_α TM displacements between the up- and down-state simulations are 10–15 Å, which may be considered to be in reasonable agreement with the 15–20 Å inferred by Ruta et al. (10) after taking into account the dynamic structure of the lipid bilayer.

VSD conformation in the down state

Both S3b and S4 translate ∼10 Å toward the intracellular side of the membrane in our down-state model relative to the up-state model (Fig. S7 A). However, the voltage-sensor paddle did not move as a rigid body. Rather, the two helices, which are approximately antiparallel in the up-state configuration, have a relative angle of ∼56° in the down state (Fig. S7 B), corresponding to a tilting of S3b with respect to the TM direction (Fig. S7 C).

In contrast to the up-state simulation, where only R3, R4, and R6 (see Fig. S1 for identification of arginines in the S4 segment) participate in salt bridges with acidic residues (53) (Fig. 3 A), in the down-state model all of the S4 arginines form salt-bridge interactions (Fig. 3 B). This reconfiguration of the VSD salt-bridge network, which requires all of the arginine side chains to face the interior of the protein, is not accomplished by a rigid-body rotation of S4, but rather by a change in secondary structure (Fig. 4 and Fig. S8 B). The S4 segment in the up-state simulation is α-helical between R1 and R6 (Fig. S8 A), whereas in the down-state simulation, the turn in the voltage-sensing paddle extends up to the second hydrophobic position after R1 (V119), and S4 exhibits a 3₁₀-helical conformation between R2 and the first hydrophobic position after R4 (I127). The 3₁₀-helical region is followed by two α-helical turns ending at R6.

Figure 3.

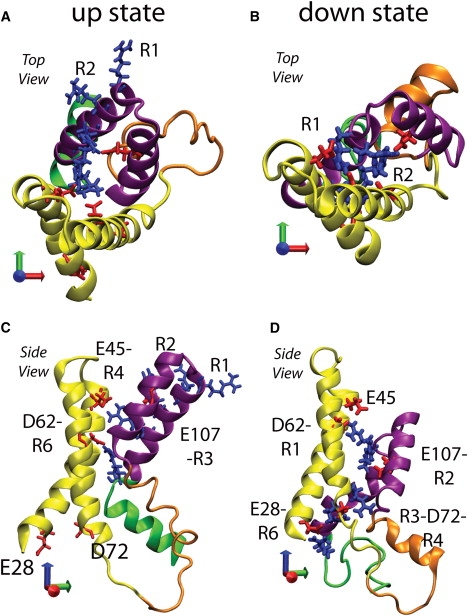
Structural comparison of the VSD up- and down-state configurations. S1 and S2 are yellow, S3a is orange, S3b and S4 are purple, and the S4-S5 linker is green. The S4 arginines (blue) and key acidic residues (red) are shown in licorice representation, and salt bridges between them are labeled. The blue axis indicates the TM direction. (A and C) Top and side views of the starting up state. (B and D) Top and side views of the down-state model. S3b and S4 are displaced ∼10 Å in the down state relative to the up state. In the up-state configuration, S3b–S4 are projected away from the rest of the helices, and R1 and R2 face away from the VSD interior. In the down-state configuration, S4 has changed secondary structure, and all of the S4 arginines face inward and are forming salt bridges with acidic residues.

Figure 4.

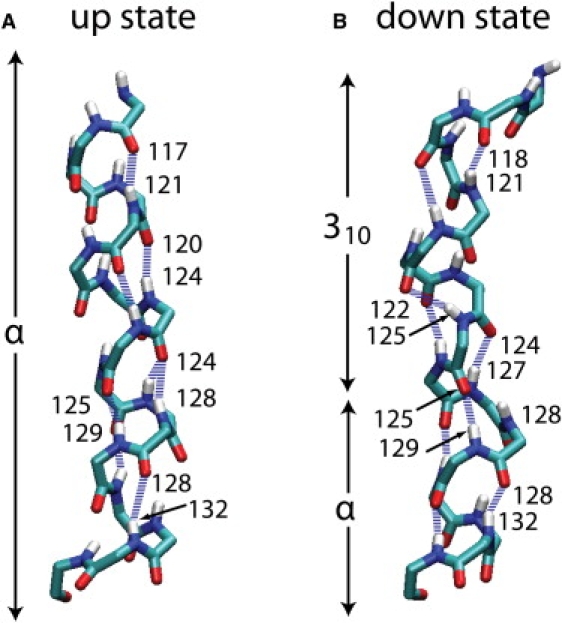
Backbone hydrogen-bond configuration of the S4 segment in the up and down states. (A) Up-state configuration showing that S4 is α-helical from R117 to G134. (B) Down-state configuration showing that the S3b–S4 turn extends to L118, and that S4 is a 3₁₀-helix from V119 to I127, and α-helical from L128 to R133. An N-O distance ≤ 4 Å and an N-H-O angle ≥ 150° were used as backbone hydrogen-bonding criteria.

The conformation of the VSD in the down-state model makes for more compact helix packing than in the up-state conformation, which is reflected in the salt-bridge network organization. R1 has a persistent salt-bridge interaction with D62 and another with E45 that alternates between direct and water-mediated salt bridge. R2 forms a persistent salt bridge with E107. In the intracellular cavity, five side chains (R3-D72-R4-E28-R6) form a persistent cluster, with each acidic chain interacting simultaneously with two arginines. The changes in helix packing and salt-bridge network configuration render the down-state conformation more rigid than the up-state, as is evident in the C_α root mean-square fluctuations (Fig. S6 B).

VSD interactions with the membrane environment

The hourglass-like architecture of the VSD revealed by the Kv crystal structures exhibits two cavities that house the charged side chains (3,8,9). When modeled in the lipid bilayer, this configuration allows for the solvation of the S4 arginines by water molecules and lipid phosphates (Fig. 5 A). Similar results have been reported in other atomistic simulations of the isolated KvAP VSD (55,56) and Kv full channels (57–60) in a lipid bilayer. More recently, a combination of experimental techniques confirmed that the VSD causes reshaping of the bilayer, and that water molecules interact with the protein within the membrane (12).

Figure 5.

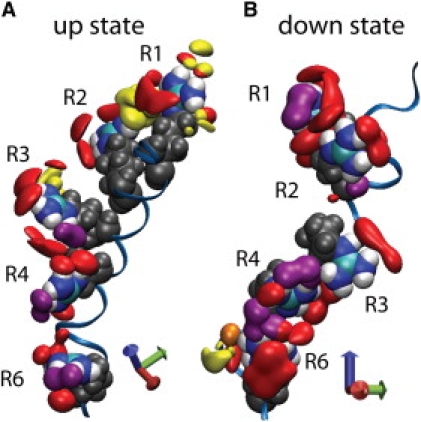
VSD solvation in the up (A) and down (B) states. Solvation of arginine residues in the S4 segment is described by isodensity surfaces of oxygen atoms forming the first coordination shell of the guanidinium moieties. Solvation by water oxygens is shown in red, lipid phosphate oxygens in yellow, and acidic chain carboxyl oxygens in purple. The blue axis indicates the TM direction.

In both simulations, a local distortion of the lipid bilayer around the VSD allows water and lipid headgroups to penetrate to the membrane midplane from both sides (Fig. S3). However, the nature of these interactions is quite different in the up and down states (Fig. 5). In contrast to the up state, in which only R1–R4 have interactions with extracellular water, in the down state only R1 and R2 interact with extracellular water. R3 and R4 are solvated by internal pockets of only a few waters that have penetrated the bilayer, but are not connected via hydrogen bonds to the water-filled cavities. R6 is in contact with intracellular water in both states. In the up state, R1 and R2 form direct salt bridges with lipid phosphate groups at the extracellular interface, whereas in the down state, extracellular lipid phosphate groups are only present in the R1 second coordination shell, and only R6 interacts directly with lipid phosphates at the intracellular interface. Experiments have shown that KvAP channels expressed in lipids lacking phosphate groups are nonfunctional (61). Our results suggest that interactions between S4 and lipid phosphates play an important role in stabilizing the up state, but that those interactions may be less important in the down state, likely because the down-state configuration is stabilized by the S4 salt bridges.

Electrostatics and gating charge

Although our simulations were performed without an applied electrostatic potential, we can estimate the effect of the presence of the VSD on the membrane electric field using linearized Poisson-Boltzmann theory (62,63) (Fig. 6, A and B). In this approximation, we assumed that all of the system components are linear, uniform, isotropic dielectrics (see Supporting Material for details). Under a constant electrostatic potential difference across the membrane, planar dielectric boundaries would generate a uniform membrane electric field that would translate into a set of uniformly distributed isopotential surfaces parallel to the membrane plane. In contrast, the dielectric boundaries defined by the MD atomistic configurations distort the isopotential surfaces in such a way that the membrane electric field becomes concentrated in a region that is 65–75% of the membrane thickness (as defined by the carbonyl distributions) around the VSD. This result is consistent with several lines of experimental evidence (reviewed in 64), indicating that VSD charges move within the membrane electric field over a length substantially smaller than the thickness of the membrane hydrophobic core.

Figure 6.

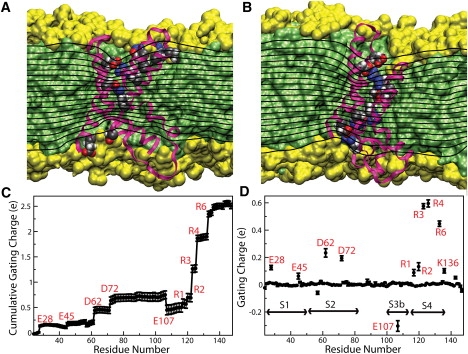
Electrostatic properties of the VSD in the up and down states. Panels A and B show equipotential surfaces for the up and down states, respectively, by means of a slice through the center of the VSD. See the Supporting Material for details of the calculation of the equipotential surfaces. In both states, the electrostatic potential exhibits focusing features in the VSD cavities that suggest that charges could be displaced across the membrane electric field over a region that is 65–75% of the membrane thickness. Contributions to the molecular surface by aliphatic chains and polar groups are shown in green and yellow, respectively. The corresponding cutaway views are shown as background. The S4 arginines and their corresponding acidic partners are shown in space-filling representation using van der Waals radii and colored by atom name. (C) Cumulative gating charge. The total charge displaced between the up- and down-state configurations is 2.51 ± 0.05 e. (D) Gating charge as a function of residue position. The S4 arginines account for 73% of the total gating charge. The electrostatic potential was averaged over 340 configurations of the down-state simulation and 160 configurations of the up-state simulation, taken every 100 ps. Error bars in the gating charge calculation correspond to one standard deviation.

Our calculations indicate a total charge displacement of 2.51 ± 0.05 e for the single VSD between the up- and down-state configurations (Fig. 6 C). The S4 arginines (R1–R4 and R6) account for 73% of the total gating charge (Fig. 6 D). Their contributions, as expected, do not depend on the absolute magnitude of the side-chain charge and the overall translation of the TM segment, but rather on the extent of the displacement of each individual charge within the membrane electric field (i.e., the magnitude of the so-called electrical travel distance) (1,65). Comparing their locations in Fig. 6, A and B, it can be seen that R3 and R4 cross the entire membrane electric field, whereas R1 and R2 remain roughly within the outermost isopotential surfaces as a consequence of the adaptation of the fluid lipid bilayer in the neighborhood of the VSD.

Similarly, although S1 and S2 do not exhibit an effective translation along the TM direction between the up- and down-state configurations, the reconfiguration of the VSD salt-bridge network translates into non-negligible displacements, within the membrane electric field, of the acidic side chains engaged in salt bridges with the S4 arginines, particularly D62 and D72 in S2. Interestingly, the acidic side-chain contributions to the gating charge can be considered to partially cancel each other due to the contribution by E107 in the S3b segment.

Discussion

The biotin-avidin accessibility data reported by Ruta et al. (10) provide sufficient one-dimensional constraints to reveal which parts of the VSD are unambiguously mobile within the span of the lipid bilayer along the TM direction. However, the accuracy of these data is limited by the uncertainty about the location of the bound biotin-avidin pair in the polar region of the lipid bilayer, so that the VSD mobile regions can be identified within an uncertainty corresponding to the width of the interface between the hydrocarbon core and the headgroup region of the lipid bilayer. In our spatial constraints-based atomistic model, specific salt-bridge interactions between S4 and S2 provide the necessary three-dimensional complement to the biotin-avidin accessibility data. Voltage-dependent cation currents elicited in Shaker VSD mutants (66) and accessibility data (67,68) identify a salt bridge between the outermost arginine in S4 and the conserved N-terminal acidic side chain in S2 as a structural signature of the VSD resting state. In addition, we considered a pairing of the conserved C-terminal acidic side chain in S2 likely, based on the reported effect that neutralization of this residue has on the total gating charge in Shaker (29) and the distribution of the conserved acidic side chains observed in the crystal structure of the Kv1.2 paddle-chimera channel (8,10).

The conformational state produced by combining these constraints is preserved within the timescale of an equilibrium atomistic MD simulation in a lipid bilayer. Although the stability of the unrestrained trajectory does not bear directly on the quality of the model, the model can be judged by how well it conforms to the available experimental evidence, and whether it provides new insight to generate testable predictions. The state-dependent motions predicted by the biotin-avidin accessibility data (10,54) are quantitatively consistent with our two simulation trajectories within the accuracy of the experimental data. The combination of these two kinds of constraints leads to two emergent features that characterize the conformational changes between the VSD activated and resting states in our model: 1), motion of both S3b and S4 with relative motion between them along the TM direction; and 2), a change in the S4 segment secondary structure.

Substantive motion of S3b during activation in conjunction with S4 can be inferred from the comprehensive voltage-clamp fluorescence in the Shaker channel reported by Pathak et al. (39), as well as from the biotin-avidin accessibility data (10). In agreement with these reports, translation of S3b along the TM direction in our model is limited to the extracellular half of the membrane, which, as pointed out by those authors, explains why previous reports did not exhibit loss of extracellular accessibility for S3b in the resting state (69–71). MacKinnon and collaborators (3,10,31) put forward the parsimonious notion that the voltage-sensing paddle would translate as a rigid body along the TM direction. Here we find that such a rigid-body motion is not necessary to produce a stable resting-state configuration of the VSD that is consistent with the biotin-avidin accessibility data (8,10). The de novo atomistic models for the resting and open states of the Kv1.2 channel reported by Pathak et al. (39), based primarily upon their voltage-clamp fluoresence data and the studies of the omega current pathway in Shaker (66,72), also imply motions of S3b and S4 that are consistent with the KvAP biotin-avidin accessibility data with relative displacements between them.

Recently, Broomand and Elinder (73) reported state-dependent disulfide bond formation between S3b and S4 in double-cysteine Shaker mutants, suggesting that S4 moves relative to S3b during activation. Their inferred range of translation length is consistent with our simulations; however, a more detailed comparison is precluded because the corresponding interresidue distances in our simulations, as well as in the available Kv crystal structures, are not consistent with disulfide bond formation. Nevertheless, we emphasize that relative motion between S4 and S3b is not inconsistent with identification of the voltage-sensing paddle as a conserved motif, as this is based on two sequence-dictated kinks in secondary structure at the N-terminal end of S3b (P99 in KvAP) and the C-terminal end of S4 (G134 in KvAP), and on the resulting mobility of S3b and S4 within the VSD architecture.

In addition to translational motion along the TM direction, cysteine and histidine scanning mutagenesis and resonance energy transfer measurements suggest that, during activation, the basic side chains in the S4 segment are alternatively exposed to the interior of the VSD (4,74). A widespread interpretation in terms of VSD conformational changes is that the S4 segment undergoes a large rotation (∼180°) about its axis. Considered in isolation, such a motion would be sufficient to account for the gating current and proton currents observed in Shaker channel mutants in a manner consistent with the VSD architecture (4,75–77). However, this model cannot account for a substantial translation along the TM direction. Motion of S4 as a rigid body involving both translation and rotation is the basis of the longstanding helical-screw model (74,78), in which S4 executes a ratchet-like motion along the TM that allows each S4 basic side chain, in turn, to form a salt bridge with one of the conserved acidic side chains in S1–S3. Shrivastava et al. (79) reported an updated version of the helical-screw model based on the isolated VSD of KvAP and the full-channel crystal structures. However, an adaptation of the pure helical-screw model to the architecture of the VSD and its relation to the pore domain requires that S4 project out of the region spanned by the hydrocarbon core of the lipid bilayer in one of the end states, the energetic implications of which are not clear. A simpler, more appealing alternative proposed by Tombola et al. (72) and Pathak et al. (39) posits that the rigid-body motions implied in the helical-screw model can be made consistent with extensive experimental data if a tilt about the TM normal is added to the set of S4 rigid-body motions.

A helical-screw motion of S4 presumes that S4 remains α-helical during activation, and thus the periodic pattern in the S4 sequence follows a helical path. When S4 is modeled as a 3₁₀-helix, as presented here, the basic side chains in the three-residue periodic pattern are on a single face of the helix, and a large rotation is not required to satisfy the stability and packing constraints imposed on the VSD architecture by experimental evidence. The recently reported (80) closed-state structure of MlotiK, a six-TM cyclic nucleotide-gated K⁺ channel, reveals an S4 segment with 3₁₀-helical secondary structure in the equivalent region found in our model of the KvAP VSD resting state. Because the MlotiK S4 segment contains only two basic charges at its intracellular end, and S1 and S2 lack acidic side chains, the S1–S4 region does not form a VSD, implying that the presence of 3₁₀-helical secondary structure is most likely due entirely to the overall S1–S4 helix packing. Contrasting the S1–S4 region in the crystal structures of MlotiK and Kv channels, Clayton et al. (80) point to a more compact assembly of S1–S4 in the closed state of MlotiK than in the open state of Kv channels, an observation that is consistent with our modeling of the KvAP VSD.

The open-state Kv1.2 paddle chimera crystal structure exhibits a stretch of 3₁₀-helical secondary structure at the C-terminal end of the S4 segment. This led Long et al. (8) to suggest that an α-to-3₁₀ helix transition could propagate along S4 during activation. In other words, the N-terminal region of S4, containing the complement of charges that contribute to the gating current, would exhibit a 3₁₀-helical secondary structure in the resting state, as our model predicts. The notion of secondary structure changes in S4 has been contemplated since the early insights into molecular mechanism of VSD function as an alternative to a set of rigid-body motions (28,65). The conceptual model proposed by Long et al. (8) and supported by our simulations suggests a compromise between these two seemingly inconsistent alternatives. This view was also recently adopted by Guy and coworkers (81), who performed open- and closed-state homology modeling of the NaChBac channel (using the Kv1.2 paddle chimera and MlotiK structures as templates, respectively), and proposed that the voltage-dependent movements of S4 may include both helical-screw motions and α-to-3₁₀ helix transitions.

Based on histidine scanning mutagenesis in Shaker and voltage-clamped fluorescence measurements in Ci-VSP, Villalba-Galea et al. (82) recently proposed an alternative scenario to a secondary structure transformation along S4 during activation. In their interpretation, S4 remains a 3₁₀-helix from the resting to the activated state of the VSD, and the transition to an α-helix occurs due to the transient nature of the activated state. The implication is that any long-time structural assay under depolarized conditions, including x-ray crystallography, will probe the VSD in this relaxed state where S4 is entirely α-helical. This scenario is not inconsistent with our results, provided that we consider that our up-state model represents their putative relaxed state.

Our model is also consistent with the notion that the S4 charges move through a focused membrane electric field, which, as suggested before, may be intrinsic to the VSD architecture of the Kv crystal structures (6,12,64). As expected, the major contributions to the gating charge come from those charged side chains that traverse the longest portion of the region over which the electric field is changing rapidly, i.e., have longest electrical travel distance. This is consistent with the notion (83) that gating current arises strictly from the extent of motion of protein charges in the membrane electric field, and not their absolute magnitude or translation in configuration space. As far as we can establish, no measurements of total gating charge have been reported for the KvAP channel; however, our estimate of the total gating charge is similar to that reported by Pathak et al. (39) for the Kv1.2 VSD region (calculated using the same continuum electrostatics model), and it is comparable to experimental measurements obtained in Drosophila and mammalian Kv channels (23,28–30,83). Assuming that the nature of the VSD motions in the membrane electric field are similar in the Shaker and KvAP channels, the small discrepancy in total gating charge may be entirely attributable to the lack of a pore domain in our simulations, because the cooperative component of VSD motion that opens the pore in Shaker has been shown to contribute ∼2 e to the total gating charge (22,23). However, this kind of comparison may not be justified because, as clearly demonstrated by Islas and Sigworth (83), the gating charges in Kv2.1 and the Shab channel differ by ∼5 e despite the very high sequence identity.

Supporting Material

Additional methods, discussion, eight figures, and two PDB coordinate files are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00364-4.