Force Transmission in the Organ of Corti Micromachine

Abstract

Auditory discrimination is limited by the performance of the cochlea whose acute sensitivity and frequency tuning are underpinned by electromechanical feedback from the outer hair cells. Two processes may underlie this feedback: voltage-driven contractility of the outer hair cell body and active motion of the hair bundle. Either process must exert its mechanical effect via deformation of the organ of Corti, a complex assembly of sensory and supporting cells riding on the basilar membrane. Using finite element analysis, we present a three-dimensional model to illustrate deformation of the organ of Corti by the two active processes. The model used available measurements of the properties of structural components in low-frequency and high-frequency regions of the rodent cochlea. The simulations agreed well with measurements of the cochlear partition stiffness, the longitudinal space constant for point deflection, and the deformation of the organ of Corti for current injection, as well as displaying a 20-fold increase in passive resonant frequency from apex to base. The radial stiffness of the tectorial membrane attachment was found to be a crucial element in the mechanical feedback. Despite a substantial difference in the maximum force generated by hair bundle and somatic motility, the two mechanisms induced comparable amplitudes of motion of the basilar membrane but differed in the polarity of their feedback on hair bundle position. Compared to the hair bundle motor, the somatic motor was more effective in deforming the organ of Corti than in displacing the basilar membrane.

Introduction

With the evolution of the mammalian cochlea, several new features emerged including a second category of hair cell, the outer hair cell (OHC), and a distinctive assembly of supporting cells that define the organ of Corti (Fig. 1 A). Two prominent constituents are the pillar cells lining the tunnel of Corti and the Deiters' cells that buttress the OHCs and bridge their attachment to the reticular lamina. Particularly striking are the Deiters' cell phalangeal processes originating at the base of one OHC and tilted to insert into the reticular lamina several OHCs that are more apical (Fig. 1 B; (1–3)). Both types of supporting cell are reinforced with parallel columns of microtubules, implying a structural role, but their complex geometry hints at a deeper function. Much work has shown that the acute sensitivity and frequency selectivity of the cochlea depend on the OHCs acting as motors to amplify the sound-evoked vibrations of the basilar membrane (4). Two mechanisms for force generation by the OHCs have been proposed: contractions of the cell soma contingent on the membrane protein prestin and intrinsic motion of the hair bundles driven by gating of the mechanoelectrical transducer (MET) channels (5–7).

Figure 1.

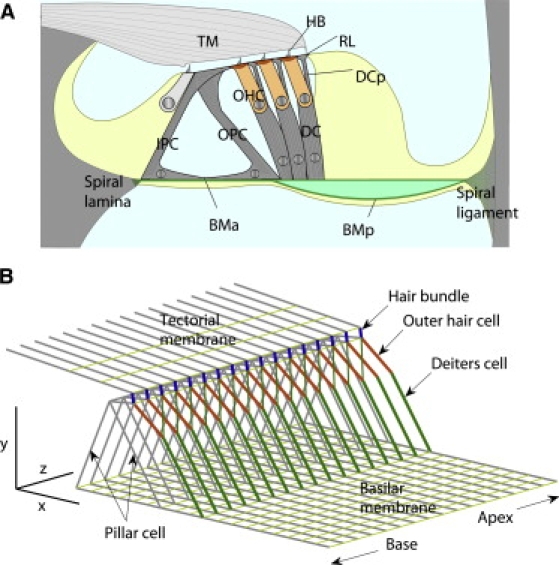
Finite element model of cochlear partition. (A) Radial section of cochlear partition. Organ of Corti sits on basilar membrane (BM), which is divided into arcuate (BM_A) and pectinate (BM_P) zones. BM_A supports inner and outer pillar cells (IPC and OPC) and BM_P supports Deiters' cell (DC) and outer hair cell (OHC). Reticular lamina (RL) comprises tops of pillar cells, OHC cuticular plates, and tops of DC phalangeal processes (DC_P). (B) Structural components of cochlear partition represented by beam elements allowing elongation and bending. The medial and lateral ends of the basilar membrane were hinged at the spiral lamina and spiral ligament and the tectorial membrane (TM) was fixed. Both elements were composed of beam elements aligned in radial and longitudinal directions. Three rows of OHCs and DCs merged into one with Young's modulus and force generation three-times that of single cell. Deiters' cell phalangeal process (DC_P) and OHC form two arms of a Y-shape, surmounting the basal part of the DC. Scale bars 40 μm.

The micromechanics of the organ of Corti have been studied experimentally in several rodent preparations, but many unanswered questions remain. For example:

• Do the basilar membrane and reticular lamina move in opposite directions with OHC somatic motility (8,9)?

• Does the radial section of the basilar membrane vibrate as a first-order mode or a higher-order mode (10,11)?

• Can hair bundle motility generate sufficient force to deform the basilar membrane (12,13)?

Most early models assumed a rigid organ of Corti (14), although a few did not (e.g., (15)). More realistic representations of the organ of Corti employed a finite element method to derive precise information on its mechanics (16–19), yet those models were simplified to a two-dimensional or a rectangular grid system, which might be insufficient to define the pattern of deformation of the organ of Corti. The aim of this work was to produce a three-dimensional finite element model of the organ of Corti incorporating data on the mechanical compliance of the cellular components and the basilar and tectorial membranes. Where mechanical parameters were unknown, values were chosen to reproduce the stiffness and longitudinal space constants measured in the gerbil cochlea (20–22). The resulting simulations demonstrate the efficacy of either hair bundle or somatic motor to displace the basilar membrane and augment bundle motion. Our work does not try to answer whether either active force generator can amplify at sound threshold but instead defines force transmission in the organ of Corti because this may be ultimately crucial for understanding the action of the amplifier.

Methods

Reduction of organ of Corti structure into beam elements

Sections at 10 mm and 2 mm from the basal end of the gerbil cochlea, which has a total length of 13 mm, were chosen for the modeling. Most structurally significant cells in the organ of Corti, such as pillar cells, OHCs, and Deiters' cells, have long thin morphology whose primary direction can be easily defined (Fig. 1 A). Acellular structures such as the basilar membrane and the tectorial membrane are obviously anisotropic because of the unidirectional collagen fibers running in a radial direction. The organ of Corti structures were therefore represented by beam elements allowing axial and bending deformation (Fig. 1 B). The basilar and tectorial membranes were also represented by a meshwork of beam elements arranged in radial and longitudinal direction. Because of their orthogonal microstructure, the radial and longitudinal elements were given different elastic moduli. The OHC hair bundle was represented by a hinged link between the reticular lamina and the tectorial membrane. A rotational spring at the hair bundle rootlet had the equivalent shear stiffness of the bundle. The reticular laminar was also represented by radial and longitudinal beams. OHCs were also tilted radially at a point between 40° (base) and 50° (apex) to the vertical y axis. Hensen's and Claudius' cells were omitted in the mechanical model, as they have no organized cytoskeletal fibers. In each radial section, triads of OHCs and of Deiters' cells were each replaced by single elements with three-times the elastic moduli of individual OHCs or Deiters' cells situated at the radial position of the middle OHC.

Longitudinal coupling

Along the longitudinal direction, radial sections were repeated every 10 μm, corresponding to the approximate spacing of the OHCs. This stack of radial sections was coupled in the longitudinal direction by four different structures. Three of the longitudinal coupling structures are continuous: longitudinal beams of basilar membrane, reticular lamina, and tectorial membrane, whereas the coupling by the OHC and Deiters' cell phalangeal process complex is discrete like the truss structure of a bridge. To match anatomical data (1–3), the OHCs and Deiters' cells were tilted in opposite directions, toward the base and apex, respectively. The top endolymphatic ends of the OHC and Deiters' cell phalangeal processes were separated by two radial-section distances (20 μm). Tilting of the Deiters' cells has been exploited in some cochlear models as a feed-forward mechanism affecting amplification (e.g., (23)).

Force and displacement boundary conditions

Simulated longitudinal lengths of 400 and 600 μm at the base and apex were sufficiently long to observe isolated local responses. For some simulations, a longer span of 1200 μm was simulated. Because the simulated lengths were much shorter than entire basilar membrane (13 mm in gerbil cochlea), the geometric and mechanical properties were assumed constant within the simulated piece and curvature along the longitudinal direction was ignored. The medial and lateral ends of the basilar membrane were assumed to be hinged at both the spiral lamina and spiral ligament. The medial end of the tectorial membrane was fixed. Additionally the z displacements of the longitudinal ends were constrained; i.e., there were no longitudinal displacements at the two ends of the section. To simulate the glass probe stimulation to the basilar membrane, the force was distributed over a 30-μm span. Active forces were normally distributed longitudinally with standard deviation of σ_z = 60 (apex) and 25 μm (base). This distribution was chosen to match the longitudinal space constant of the cochlear partition at each location and might be irrelevant to the activated span in vivo. When the force distribution was narrower than the space constant, the pattern of deformation was dependent on σ_z, but when it was wider the deformation pattern was unaffected by σ_z. Therefore, we chose the minimal distribution of active forces to remove the dependence of the deforming pattern on the active force span and to reduce model size. The activated span in vivo is reported to be several hundred microns at the base, wider than our stimulated span of active forces. When we simulated broader longitudinal distribution of active force, the deforming pattern of cochlear partition remained the same but the absolute displacement increased in proportion to σ_z. The program was written in MATLAB (The MathWorks, Natick, MA) and executed on an IBM PC.

Choice of parameter values

The mechanical properties of the basilar membrane were determined as follows. The width and thickness were first established (24–26), the thickness referring to that of fiber layer(s) running in a radial direction (25). Longitudinally continuous structures such as the basilar membrane, reticular lamina, and tectorial membrane in the base were given approximately one order-of-magnitude greater Young's moduli than those in the apex. The Young's modulus for basilar membrane radial elements was half that of bundled collagen fibers (1 GPa). Young's moduli of basilar membrane longitudinal elements were chosen to obtain a longitudinal space constant comparable to the value measured for the basilar membrane alone (21). Other material properties were selected such that the cochlear partition had a stiffness gradient of ∼4.4 dB/mm (22) and a longitudinal space constant close to that measured for the whole structure (21).

Motor forces

The magnitudes of the OHC somatic and hair bundle active forces, f_OHC and f_MET, respectively, were determined as follows. f_OHC = 2 nN independent of location, calculated from a voltage-dependence of 0.1 nNmV⁻¹ (27) driven by a depolarizing receptor potential of 20 mV. The maximum force generated by the hair bundle motor was estimated from the number of MET channels per bundle, N (twice the number of tip links; (28)), and the single-channel gating force, z_F, which depends on geometrical gain. The geometrical gain is defined as the ratio of the displacement at the tip of the bundle to that produced at the MET channel, and it varies inversely with hair bundle height. At the base of the cochlea, the hair bundles are approximately fivefold shorter than those at the apex. At the apex, N = 100 and z_F = 0.5 pN so f_MET = 0.05 nN, within the range of that estimated for nonmammalian bundles of similar height (29,30). For the base, the OHC bundles were assumed to have 70 tip links compared 50 at the apex and a hair bundle geometrical gain of 0.5 compared to 0.1 at the apex, so f_MET = 0.35 nN. Similar hair bundle forces were measured for rat OHCs (12). f_OHC was applied at the apex and base of the OHC as a coupled axial force and f_MET at the tip and root of the hair bundle as a coupled shear force. (See Table 1.)

Table 1.

Properties of organ of Corti components at cochlear apex and base

Structure	Parameter	Apex	Base	References
Basilar membrane∗	Width (BMA+BMP)	280	160	(24–26)
	Thickness	0.7	3
	YMx, YMz	1000, 0.15	1000, 0.6
OHC soma	Diameter	8	8	(27,49)
	Length	50	20
	YM	0.015	0.015
OHC hair bundle	Height	5	1	(30,50–52)
	Stiffness	2	50
Inner and outer pillar cells	Diameter	4	8	‡
	YM	10	10
Deiters cell (base, phalangeal process)	Diameter	10, 1	10, 1.5	‡
	YM	0.3, 0.3	0.3, 0.3
Reticular lamina (tunnel of Corti, OHC)	Thickness	5, 2	5, 2
	YMx, YMz	1.0, 0.5	1.0, 0.5
Tectorial membrane (root, body)†	Total width	210	80	(25,26,53–55)
	Thickness	25, 50	15, 30
	YMx	0.04, 0.01	0.8, 0.2
	YMz	0.005	0.01
Tectorial membrane Organ of Corti and basilar membrane	Cross-sectionalarea	7875	1800	(26,56)
		27,045	9225
	Total	34,920	11,025

All dimensions in μm, areas in μm², Young's moduli, Y_M, in MPa, and stiffness in mN/m.

^∗The basilar membrane is divided into two parts, the arcuate zone (BM_A) beneath the tunnel of Corti and the pectinate zone (BM_P), BM_A being one-third of the total width. The thickness is that of the fiber layer(s) running radially (25).

^†A radial section of the tectorial membrane is divided into two parts, the root attached to the spiral limbus and the body overlying the OHC stereocilia, the root being the same length and half the thickness of the body. Further justification is given in Methods.

^‡Geometry of supporting cells taken from Angelborg and Engström (1) and Slepecky (3). Pillar cell stiffness is assumed to be larger than the experimental measurement (57), which, if used, caused buckling of the triangle.

Dynamic simulations

The masses of the tectorial membrane, organ of Corti, and basilar membrane were calculated from the cross-sectional areas of these structures extrapolated from measurements in gerbil (26) assuming a density of 1.0 kg·L⁻¹. Viscous forces were assumed to consist of two components: the damping within the cleft between the tectorial membrane and reticular lamina, and the viscous resistance acting on other parts of the organ of Corti. The first component was calculated as the viscous force between two parallel plates of separation d immersed in a Newtonian fluid of viscosity 0.72 mN m⁻² s. This yields frictional coefficients per unit cochlear length of 0.01 and 0.03 Ns/m² at apex and base, respectively, the differences chiefly reflecting a smaller d at the base. Radial lengths of the reticular lamina plates were 71 μm (apex) and 41 μm (base). This friction between two layers was lumped with that of the hair bundles, acting against their shear direction. The damping of other structures was considered proportional to their stiffness and was adjusted to match the simulated step responses with experimental results and required structural damping per unit length of 0.03 and 0.07 Ns m⁻² for apex and base, respectively.

Results

The stiffness and space constant of the cochlear partition

Several hundred-micron lengths were simulated centered on distances from the cochlear base of 10 mm (apical) and 2 mm (basal), which in the gerbil have characteristic frequencies of 0.4 and 25 kHz, respectively (31). Deflection of the basilar membrane with a point load (Fig. 2) yielded stiffness values for the cochlear partition of 25 mN m⁻¹ at the apical location and 1690 mN m⁻¹ at the base, within the range of those measured experimentally (20,22). Parameter values, especially those underlying longitudinal coupling, were chosen to achieve reasonable accord between model and experimental values for the longitudinal spread of deformation. Thus the model space constant, λ, for deflection during a point load was 48 μm (apex) and 18 μm (base), matching the experimental values of 46 μm and 16 μm, respectively (21). After removal of the organ of Corti, both stiffness and length constants were reduced in the model as in the experiments (Fig. 2). Stiffness values and length constant for the model basilar membrane alone were 5 mN m⁻¹ and 27 μm at the apex and 770 mN m⁻¹ and 11 μm at the base. These changes show that the organ of Corti made a larger contribution to the overall stiffness of the cochlear partition at the apex (∼80%) compared to the base (∼50%).

Figure 2.

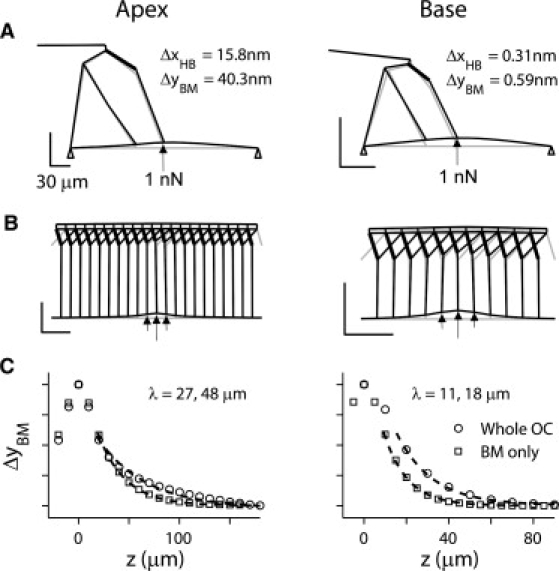
Deformation due to point load at cochlear apex and base. (A) Radial section of organ of Corti showing deformation by 1 nN of force applied to basilar membrane beneath Deiters'cell. Scale bars 30 μm. Deformation exaggerated for illustration. (B) Longitudinal section showing force is distributed over 30 μm, OHCs 10 μm separation. Note Y-shaped structure of OHC (thick line) and Deiters cell. (C) Plots of basilar membrane displacement, Δy_BM, normalized to maximum value, Δy_BM-MAX, along the longitudinal direction for entire cochlear partition (circles) and basilar membrane alone without the organ of Corti (squares). Stiffness of the partition and the longitudinal space constant, λ, for the apex were 0.025 N/m and 48 μm, which were reduced to 0.005 N/m and 27 μm when only basilar membrane was simulated. Stiffness and λ for base were 1.69 N/m and 18 μm, which were reduced to 0.77 N/m and 11 μm with basilar membrane alone.

Motion evoked by the somatic motor depends on the tectorial membrane and Deiters cell

A common technique for examining the efficacy of the OHC somatic motor is to evoke motion by current injection through a coarse extracellular electrode (e.g., (8)), thus depolarizing the OHCs over a length of the cochlea. This approach was simulated by imposing an OHC contraction with Gaussian standard deviation (σ_z) of 200 μm to mimic current spread from the electrode. With the standard parameter set, the basilar membrane and reticular lamina moved in opposite directions, the displacement amplitude of the reticular lamina being ∼50% larger than that of the basilar membrane at the apical location (Fig. 3 A). At the basal location (not shown) the evoked displacement of the reticular lamina was >10-fold that of the basilar membrane, reflecting the larger contribution of the basilar membrane to the stiffness of the cochlear partition in the base. Experimental observations (8) also indicate motion of the two structures in opposite directions with relative amplitudes of 5–10, between the values obtained in the simulation.

Figure 3.

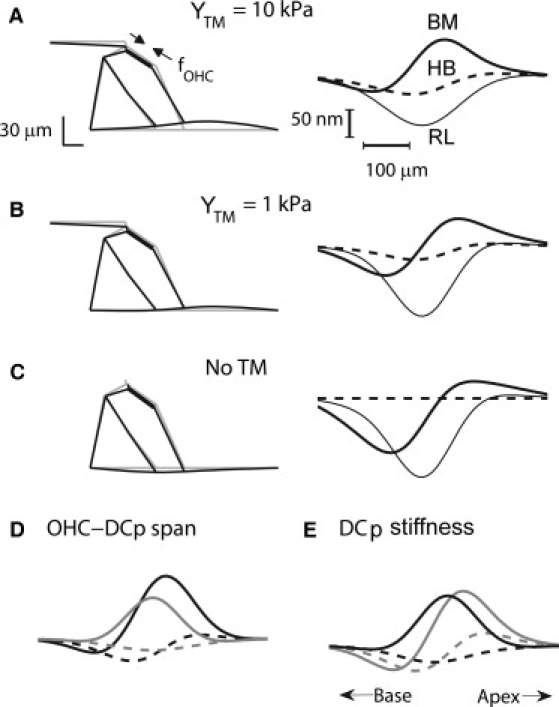
Deformation of the organ of Corti by OHC somatic motor depends on mechanical properties. Effects of variations in tectorial membrane stiffness (A–C) and tilt and stiffness of Deiters' cell phalangeal process (DC_P) (D and E). OHCs stimulated to produce an axial contractile force (f_OHC) of 2 nN per OHC distributed longitudinally with standard deviation σ_z = 60 μm. The cochlear apex was simulated for three different values of tectorial membrane body radial stiffness with Young's modulus, Y_TM, of 10 kPa (A), 1 kPa (B), and 0 kPa (C). (Left) Radial sections; (right) longitudinal profile of the displacements of the basilar membrane (BM; thick line), hair bundle (HB, dashed line), and reticular lamina (RL, thin line), each at a radial position beneath the base of the DC. Scale bars 30 μm. The radial profile in panel B resembles that measured in Karavitaki and Mountain (37). (D) Effects on longitudinal profile of displacement of the basilar membrane (thick line) and hair bundle (dashed line) for changes in OHC-DC longitudinal span, 40 μm (four OHC diameters; black), and 0 μm (no separation; gray) where default in panel A is 20 μm (two OHC diameters). (E) Change in DC-phalangeal process stiffness, 0.05 MPa (black), 5 MPa (gray) where default is 5 MPa. In panels A–C, the OHC-DC span was 20 μm with OHCs tilted 5 μm toward the base. In panels D and E, Young's modulus of the tectorial membrane body was 10 kPa.

For the OHC contractions to function efficiently, they require a frame of reference against which to react (32), a frame thought to be supplied by the rigidity of the tectorial membrane, a hypothesis supported by the effects of mutating α-tectorin, one of the tectorial membrane structural proteins (33). This notion was examined in the model by reducing the radial stiffness of the tectorial membrane. A 10-fold reduction diminished the ability of the somatic motor to move the basilar membrane or the hair bundle (Fig. 3, A and B), whereas abolition of the stiffness, equivalent to removing the tectorial membrane, reversed the polarity of the basilar membrane motion (Fig. 3 C). As a consequence, both reticular lamina and basilar membrane showed the same polarity of predominant motion and the deflection of the hair bundle disappeared. Comparison of the three conditions also revealed a change in the radial pattern of basilar membrane deformation, with the peak displacement shifting toward the spiral lamina as the radial stiffness of the tectorial membrane was diminished. This reflects an increased tendency of the OHC contraction to rotate the pillar cell triangle in the absence of a tectorial membrane stiffness to pull against.

A feature of the simulations was the bimodal longitudinal deformation of the basilar membrane elicited by the somatic motor, a property less obvious in the motion of the reticular lamina. The extent of such bimodal behavior depends on the tectorial membrane radial stiffness (Fig. 3 C). It was also influenced by the properties of the Deiters' cell phalangeal processes that are tilted apically with respect to the OHCs. The bimodal behavior was exacerbated by increasing the longitudinal span between the top of the OHC and the insertion of the corresponding phalangeal process into the reticular lamina (Fig. 3 D); in the standard case, the separation at the endolymphatic surface was two OHC diameters. The contribution of the phalangeal process was confirmed by altering its stiffness. A 10-fold increase in its Young's modulus augmented the bimodal motion, similar to removing the tectorial membrane, whereas a 10-fold reduction in the Young's modulus produced an almost unimodal deformation (Fig. 3 E). This aspect of the model has not yet been reported experimentally and would disappear with a smaller elastic modulus for the Deiters' cell. However, the one experimental measurement (34) gave an even greater modulus than our default value. The value for the stiffness of the Deiters' cell phalangeal process was chosen to make it similar to the axial stiffness of OHC, resulting in a smaller value than reported experimentally (34). Matching the stiffnesses of the OHC and DC phalangeal process minimized longitudinal displacement of the OHC base during operation of the somatic motor. The advantage of this geometrical arrangement, where the OHC body and the DC phalangeal process form two arms of a Y of similar stiffness supported on a rigid DC base, is that it prevents buckling of the cells, a feature exploited in architectural structures. The simulations strongly support the notion that the organ of Corti cannot be regarded as a rigid structure and they demonstrate that deformations produced by OHC contractions are complex. These depend upon the mechanical properties of the tectorial membrane and the Deiters' cells and their contribution to the overall stiffness of the cochlear partition.

Altering the stimulation conditions to excite a single OHC with maximum force provided an opportunity for comparison with experimental results. In the absence of the tectorial membrane, the stimulus in the model generated a radial displacement of the reticular lamina of 35 nm. Such conditions have been met during depolarization of one OHC in an isolated coil while measuring the displacement of the hair bundle in both gerbils (35) and rats (36). In the former case, large, ∼800 nm, radial motion of the reticular lamina was measured whereas in the latter experimental preparation, the mean displacements attributable to the somatic motor were only 48 nm, similar to that found in our simulations. The major difference between the two types of experiment was that the rat measurements were effectively static, employing an extended depolarization, and thus directly comparable with the simulation but the gerbil measurements were implemented with a sinusoidal stimulus at 100 Hz. The reason for the discrepancy is unclear but the rat results support the modeling whereas the gerbil measurements suggest that using a periodic stimulus evokes much larger reticular lamina motion (35,37).

Static displacements produced by the somatic or stereociliary motors

The relative efficacies of the two motors to deflect the basilar membrane and hair bundle were examined by comparing displacement due to either somatic- or stereocilia-based motor. The active forces applied (see Methods) were 0.05 nN and 0.35 nN for the stereociliary motor at apex and base, respectively, and 2 nN for the somatic motor at both cochlear locations. The forces were distributed longitudinally with standard deviations of 60 μm (apex) and 25 μm (base) to produce longitudinal waveforms matching the passive space constants at the two cochlear locations. Because of the substantial difference in stiffness between the two cochlear locations, the displacement amplitudes of the basilar membrane were much larger, tens of nanometers, at the apex than at the base where they were a few nanometers at most. The resulting displacements of the basilar membrane and hair bundle are shown in response to the active forcing (Fig. 4) and demonstrate that both types of motor are capable of deforming the basilar membrane by physiologically significant amounts.

Figure 4.

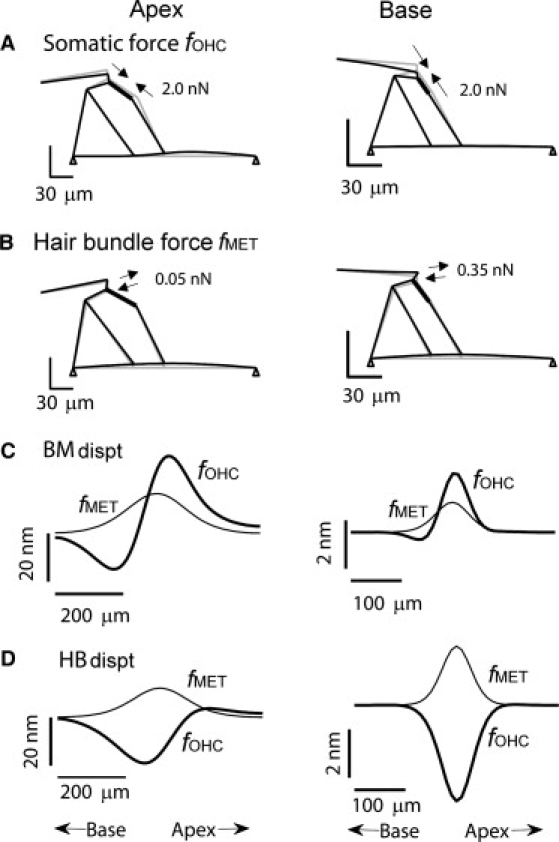
Static displacements induced by OHC active forces. Radial sections of the organ of Corti showing motion produced by (A) an OHC somatic (contractile) force (f_OHC) or (B) a hair bundle force (f_MET). Forces distributed longitudinally with σ_z = 60 μm (apex) and 25 μm (base) with peak values of f_OHC = 2.0 nN (base and apex) and f_MET = 0.05 nN (apex) or 0.35 nN (base). Longitudinal profiles of the basilar membrane (BM) displacement (C) and hair bundle (HB) displacement (D) for application of the active forces f_OHC (thick lines) and f_MET (thin lines). Displacement determined at a radial position beneath the base of the DC. (Left column) Apex. (Right column) Base.

In the model, the somatic motor supplied 40-fold more force at the apex and sixfold more at the base than did the hair bundle motor. Despite the large difference in applied force, both active processes deformed the basilar membrane by similar amounts. The simulations in Fig. 4 suggest that, other things being equal, either type of motor could participate in cochlear amplification. However, the processes differ in one respect—the polarity of the feedback on hair bundle deflection, which is positive for the hair bundle motor but negative for the somatic motor (see Movie S1 in the Supporting Material). The somatic motor provides opposite feedback to the basilar membrane and to the hair bundle. OHC contraction deformed the basilar membrane further in the positive direction (positive feedback), while it moved the hair bundle in the negative direction (negative feedback). Compared to this complicated mode of action by the OHC somatic force, the effect of the hair-bundle generated force was straightforward, providing positive feedback to both basilar membrane and hair bundle.

The efficacies of the two motors were little affected by assigning distinct properties to the arcuate zone (BM_A) and the pectinate zones (BM_P) of the basilar membrane. The two parts appear different in cochlear sections (Fig. 1 A) but no quantitative information is available about the fiber structure in the arcuate zone. A fourfold reduction in BM_A thickness altered negligibly the response to a somatic motor force, f_OHC, (Fig. S1 in the Supporting Material) but the response to the hair bundle force, f_MET, nearly doubled at the base. Introducing a pivot in the basilar membrane beneath the outer pillar cell (38) also had only minor consequences for actively driven motion at the cochlear apex (Fig. S2). However, as with changes in BM_A thickness, the effects were more pronounced in the base. These changes are reasonable because at the base, the basilar membrane dominates the stiffness of the cochlear partition, whereas at the apex the basilar membrane and organ of Corti contribute equally to overall stiffness. In all simulations, there was considerable deformation within the organ of Corti. One manifestation of this internal deformation was the dependence on the forcing sites of the shear gain, Δx_HB/Δy_BM, defined as the ratio of the hair bundle shear displacement to the basilar membrane transverse displacement. If the organ of Corti were a rigid body, the shear gain should be invariant with the mode of stimulation. For a passive force applied to the basilar membrane, the shear gain was 1:2.6 and 1:1.9 at the apex and base, respectively—values similar to experimental observations (39,40). When the hair bundle force was applied, the shear gain increased to 1:1.1 and 1:0.5 for apex and base, respectively, and with the somatic force, the shear gain was ∼−1; these larger values were not seen in the experimental preparation (40) where active forces were probably not operational.

The magnitudes and distribution of the active forces used in Fig. 4 were somewhat arbitrary, even though their relative sizes and location dependence reasonably reflect those expected to occur in situ. Moreover, their interpretation is complicated by the bimodal deformation of the basilar membrane, especially with the OHC somatic force. A method of comparing the efficacies of the somatic and hair bundle motors to displace the basilar membrane is to compute the volume compliance induced by passive or active forces. This measure is independent of the force magnitude. The volume compliance is the volume of basilar membrane displaced by unit pressure. The volume compliance for an evenly distributed passive force applied to the basilar membrane was 121 and 0.31 mm⁴ N⁻¹ at the apex and base, respectively, with the difference reflecting the larger stiffness at the base. The volume compliances during application of a unit active pressure (force per unit area of basilar membrane) by the somatic motor were 7.0 and 0.18 mm⁴ N⁻¹ at the apex and base, respectively. The corresponding volume compliances attributable to the hair bundle motor were 253 and 0.77 mm⁴ N⁻¹ at the apex and base. These results reveal the differences between the two active motors. Firstly, the hair bundle force is so effective that the active volume compliance is greater than the passive volume compliance. Thus, the hair bundle force is more effective at displacing the basilar membrane than is a passive force applied directly to the membrane. Secondly, the OHC somatic force is associated with an order-of-magnitude smaller volume compliance than the hair bundle force. Thirdly, the somatic force was more effective, especially at the base, in deforming the organ of Corti than in displacing the basilar membrane. The overall difference between the different forces was maintained even when the tectorial membrane stiffness was diminished—a procedure that accentuates the bimodal behavior (Table S1 in the Supporting Material).

Dynamic response of the organ of Corti

Dynamic analysis was used to extend the results in Fig. 3 and reproduce measurements of reverse transduction to electrical stimulation (8). To represent step current injection, coupled axial forces were applied to the OHCs distributed along the cochlea with σ_z = 60 μm and f_OHC = 1 nN in the middle of simulated segment. This force would be produced by 10 mV depolarization of the OHCs. The damping, assumed to be the sum of friction in the subtectorial space plus damping from the remainder of the organ of Corti (see Methods), was determined by comparing simulations with experimentally measured step response of the basilar membrane (8,41). With this damping, in response to the step force, the basilar membrane displayed two (apex) to five (base) cycles of oscillation at frequencies of 0.7 kHz and 16kHz at apex and base, respectively. These frequencies were reasonably similar to the natural frequencies of the system obtained from modal analysis, 0.76 kHz and 14.5 kHz. According to the frequency map, the characteristic frequencies of the two chosen locations are 0.4 and 25 kHz so the measured passive properties account for part (20) but not all (22) of the frequency range. For the reticular lamina, the displacement was measured at the root of the OHC bundle for the reticular lamina and for the basilar membrane at its center and at these points, the steady displacement of the reticular lamina was similar to that of the basilar membrane at the apex and approximately eightfold larger at the base (Fig. 5, A and B). When compared with the experimental measurements, these ratios would be two-to-three times larger, because the interferometric measurements were focused on beads placed on the more radially distant Hensen's cells (8) that would augment the reticular lamina displacement. Thus the simulations are in reasonable agreement with the experiments. They showed a small frequency difference between the reticular lamina and basilar membrane at the apex but not as large as the twofold difference seen in the experiments. That difference in resonant frequency was interpreted (8) as reflecting two oscillators within the cochlear partition, but this was not apparent in our model. In particular, the rigid attachment of the tectorial membrane to the spiral limbus reduces the ability of this element to act as a second resonator, comprising tectorial membrane mass and hair bundle stiffness. A 10-fold reduction in the attachment stiffness of the tectorial membrane at the apex only slightly altered the oscillations frequencies to 660 Hz (BM) and 590 Hz (RL) whereas a more drastic 1000-fold reduction in the attachment stiffness changed the oscillations frequencies to 440 Hz (BM) and 400 Hz (RL) (Fig. 5 C). However, the latter condition effectively converted the tectorial membrane to a floating mass, and consequently the hair bundle displayed damped resonance at a frequency of 1.4 kHz, near that predicted from the combination of tectorial membrane mass (7.9 mg·m⁻¹) and hair bundle stiffness (0.6 kN·m⁻²). Thus, the tectorial membrane can contribute a second resonance, as implied in some experiments (42) and modeling (43), but only when it has a loose attachment to the spiral limbus.

Figure 5.

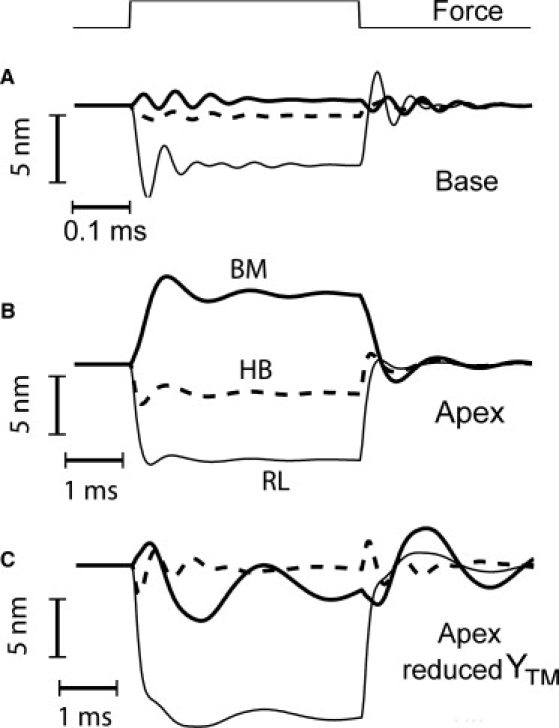
Dynamic responses of the organ of Corti to current injection. OHCs stimulated to produce an axial contractile force (f_OHC) of 1 nN peak value distributed longitudinally with standard deviation σ_z = 60 μm at the base (A) and apex (B and C). (A) Base: time course of dynamic displacements of the basilar membrane (BM, thick line), hair bundle (HB, dashed line), and reticular lamina (RL, thin line) for a force-step timing that is shown in the top trace. (B) Apex: time courses of displacements for the same force step. (C) Apex: effects of a 1000-fold reduction in tectorial membrane attachment stiffness. In panel C, the hair bundle shows damped oscillations at a frequency (1.4 kHz) higher than the basilar membrane, determined by tectorial membrane mass and hair bundle stiffness. In the standard conditions, the basilar membrane displays damped oscillations at 0.7 kHz (apex) and 16 kHz (base).

Discussion

We have implemented a three-dimensional finite element analysis of the organ of Corti to define the displacements during loading of the basilar membrane and with addition of OHC forces generated by somatic or hair bundle motors. Our model is not a kinematic one that uses rigid sticks linked to one another (44). It is also differs from finite element models that use area or volume elements to represent organ of Corti structures (16–19). These may suffer from aspect-ratio problems (when one dimension of a finite element is much smaller than the others) that can result in a decline in accuracy. To regain accuracy, a finer mesh is required that increases computational cost. Therefore, when a structure is long and thin, like the basilar membrane or cells in the organ of Corti, it is better to use a one-dimensional element (link or beam) to avoid aspect ratio problems, instead of inaccurate or costly two- or three-dimensional elements. Our work extends previous analyses by providing more detailed information about the radial and longitudinal deformations and their dependence on the properties of the component structures in the rodent cochlea. A strength of the approach is that it allows incorporation of experimental data on all the important structural elements and dissection of their relative contributions to organ of Corti stiffness, longitudinal space constant, and responses to current injection (8,20–22). The analysis emphasized the importance of the tectorial membrane stiffness and the Deiters' cell phalangeal processes in the operation of the somatic motor. Most significantly, the results indicate that both active OHC forces can modify basilar membrane and hair bundle motion, the hair bundle motor inducing comparable displacements to the somatic force even though the applied force was much less (Fig. 4). The greater efficacy of the hair bundle motor to induce static displacements of the basilar membrane was underscored by analysis of the volume compliance. Because of gradients in stiffness of the cochlear partition, the overall motion was more than an order-of-magnitude larger in the low-frequency apical region than in the high-frequency base for the same force stimuli. Comparison of the response at the apex and base also demonstrated that the behavior depended on the relative contribution of the basilar membrane and organ of Corti to the overall stiffness of the cochlear partition. This was manifested, for example, by the displacement of the reticular lamina relative to that of the basilar membrane being greater at the base than at the apex (Fig. 5).This difference arose because the tonotopic gradient in the stiffness of the basilar membrane was larger than the gradient in cellular constituents of the organ of Corti. Consequently the properties of the organ of Corti were more significant for the stiffness at the apex than the base. It is important to verify the conclusion that basilar membrane dominates the stiffness at the base but not at the apex by making point stiffness measurements of the cochlear partition in the presence and absence of the organ of Corti (21).

At both cochlear locations, the OHC somatic motor, driven by voltage-dependent conformation changes in the motor molecule prestin (4,7,45), displaced the basilar membrane slightly more than the hair bundle motor. No account was taken of the potential reduction in efficacy of the somatic motor at the base due to filtering of the OHC receptor potential by the membrane time constant (reviewed in (4)). If this were to occur, the somatic motor would be less effective than the hair bundle at the base. Furthermore, the results indicate that the polarity of the static feedback on hair bundle position is negative. Thus, in the absence of any phase shifts in the feedback loop, basilar membrane movement toward scala vestibuli would excite the OHCs and generate a depolarizing receptor potential causing OHC contraction and displacement of the hair bundle in the negative direction, thus behaving like transducer adaptation (Fig. 4). The negative feedback action of the somatic motor on hair bundle position has been recognized in previous cochlear modeling and has been countered by introducing an arbitrary phase shift between hair bundle displacement and OHC force generation to elicit amplification (15,23,43,46). These models differed from the present one in using high-frequency dynamic simulations. Another recent model using somatic forces (47) successfully produced OHC amplification without an arbitrary phase shift but, in that model, hair bundle displacement is unrealistically independent of displacement of the OHC apex (Eq. 15 in (47)). Although there is overwhelming evidence that the somatic prestin-based motor is essential for cochlear amplification (45), its exact mode of operation to deform the organ of Corti and influence transduction or participate in amplification remains unclear. It should be emphasized that the present model does not incorporate the nonlinear OHC feedback loop involving linked forward and reverse transduction. There are likely to be phase shifts in this loop, including a phase lead attributable to adaptation in the MET channels (48) and in the hair bundle motor (12) and a lag due to the OHC membrane capacitance (4).

How these processes perform, especially at high frequencies, is contentious. Nevertheless, our model, with its extensive representation of the main electro-mechanical elements of the cochlear partition, is well poised to incorporate future experimental observations.

Supporting Material

Two figures, one table, and one movie are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00418-2.