Abstract
Vorticella convallaria is one of a class of fast-moving organisms that can traverse its body size in less than a millisecond by rapidly coiling a slender stalk anchoring it to a nearby surface. The stalk houses a fiber called the spasmoneme, which winds helically within the stalk and rapidly contracts in response to calcium signaling. We have developed a coupled mechanical-chemical model of the coiling process, accounting for the coiling of the elastic stalk and the binding of calcium to the protein spasmin. Simulations of the model describe the contraction and recovery processes quantitatively. The stalk-spasmoneme system is shown to satisfy geometric constraints, which explains why the cell body sometimes rotates during contraction. The shape of the collapsing and recovering stalk bounds its effective bending stiffness. Simulations suggest that recovery from the contracted state is driven by the stalk at a rate controlled by dissociation of calcium from spasmin.
Introduction
Relative to its size, Vorticella convallaria is one of the fastest moving organisms on the planet (1). Its cell body is tethered to a substrate by a slender stalk which coils up into a helix to move the body (Fig. 1, a and b). A thin, elastic structure called the spasmoneme, enclosed within the cell membrane, winds helically inside the stalk close to its outer sheath (2,3). The spasmoneme generates an ATP-independent (4,5) tensile force in response to calcium signaling, which drives the coiling of the stalk (6). The cell body contains calcium storage sites in the endoplasmic reticulum (7), which release Ca2+ ions spontaneously or in response to an external stimulus (8). The signal is propagated down the spasmoneme by calcium-induced-calcium-release (CICR) from calcium storing membranous tubules within the spasmoneme (3,7,9,10). In this mechanism, tubules release the stored calcium upon permeabilization by a small external calcium concentration. In vivo experiments (9) show that a Ca2+ concentration as small as 10−7 M is sufficient to trigger the release of stored calcium. A permeabilized tubule provides a sharp increase in the local Ca2+ concentration, which triggers further calcium release from the surrounding tubules. Thus, an initial calcium signal generated in the cell body can propagate through the stalk by successive permeabilization of the preexisting calcium tubules in the spasmoneme—a diffusion cascade similar to what is observed in muscle cells (11).
Figure 1.
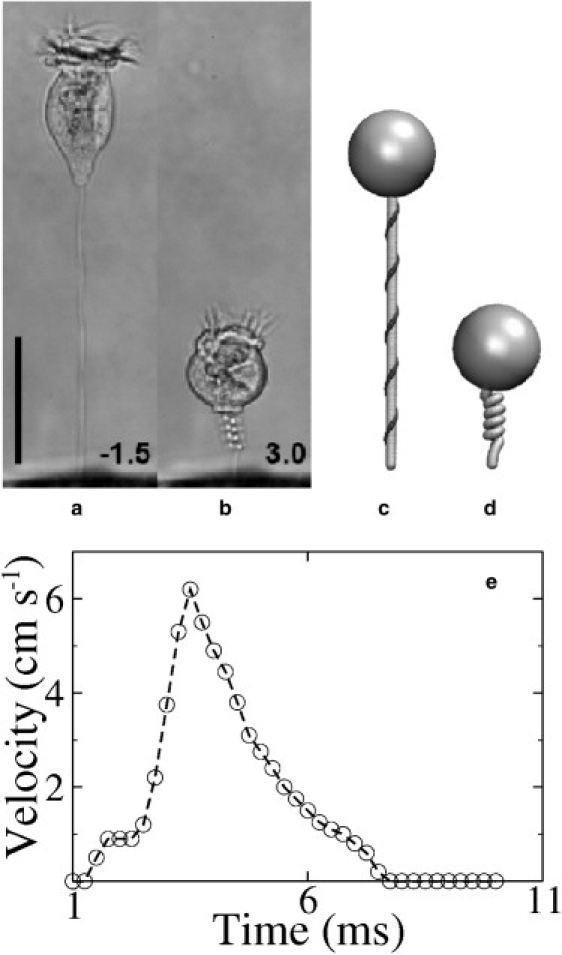
(a and b) Images of V. convallaria in extended and contracted states (22), reproduced with permission. (c and d) The model in extended and contracted states. The head is modeled by an incompressible sphere, the stalk by an elastic rod (in gray), and the spasmoneme by a thin fiber (in black) winding helically around the stalk. (e) A typical velocity profile of the cell body is shown from the time when the motion starts; the graph was redrawn from Fig. 2 of Upadhyaya et al. (25). The scale bar in panels a–d is 50 μm.
The released Ca2+ ions bind to a 20-kDa calcium-binding protein called spasmin, which constitutes 40–60% of the spasmoneme dry mass (12,13). As a result, a state of tension is induced in the spasmoneme which drives its contraction with a maximum speed of ∼6 cm s−1 (Fig. 1 e) and a tensile force up to 500 nN (S. Ryu, MIT, personal communication, 2009). Because the spasmoneme winds helically inside the stalk, the contraction collapses the straight stalk into a helix, which is similar to the mechanics of some coiling bacteria (14). The reverse process (recovery) is powered by dissociation of Ca2+ ions from spasmin and active sequestration back into the calcium storage sites.
Although the general causes of contraction and recovery are known, the mechanics of the coiling process and its rate limitations are not well understood. In this work, we have coupled a computational model for the mechanical aspects of Vorticella contraction and recovery with a kinetic model for calcium binding. Simulations capture several features of the experimental observations, including the velocity profile (Fig. 1 e), the scaling of the peak velocity with viscosity, and the shape of the fully contracted stalk. Furthermore, the experimentally observed shapes of the collapsing and recovering stalk can only be reproduced if the Young's modulus of the stalk lies in a narrow range around 1 kPa. Our simulations suggest that the recovery process of the organism is driven by the bending energy of the coiled stalk, at a rate controlled by the dissociation of the calcium-spasmin complex. By identifying geometric constraints applicable to the stalk-spasmoneme system, we can explain the connection between the final configuration of the stalk and the rotation of the cell body. We have determined that the rate of contraction of the stalk is controlled by calcium-spasmin binding kinetics, as well as by the speed of the calcium signal.
Model and Simulations
Mechanical model
Our mechanical model for Vorticella, Fig. 1 c, contains three components:
-
1.
The cell body (also referred to as the “head”).
-
2.
The stalk.
-
3.
The spasmoneme.
The head acts as a source of inertia and viscous drag, and its shape is approximated by a rigid sphere. The translational drag acting on a sphere at time t is given by (15)
| (1) |
where ρ and η are the mass density and dynamic viscosity of the fluid, R and u are the radius and velocity of the sphere, and t is the time. The first term in Eq. 1 accounts for the added mass from the rapidly propagating pressure waves, the second term is the Stokes drag, and the last term is due to the diffusion of vorticity in the fluid. The rotational drag on a sphere relaxes faster than the translational drag (15), so we take only the Stokes contribution to the rotational friction, 8πR3η.
The stalk is a pliable slender structure, which bends into a helical shape during contraction of Vorticella and recovers its original shape after the removal of calcium. It is modeled as a homogenous elastic rod with six degrees of freedom—two shears; an extension; two bends; and a twist. The equations of motion for an overdamped elastic rod are
| (2) |
| (3) |
where F and M are the elastic force and moment acting on the rod, u and ω are the translational and rotational velocities, t is the tangent to the centerline of the rod, and ξT and ξR are the translational and rotational friction per unit length. In a frame aligned with the tangent vector, the friction matrices are diagonal and in the slender-body approximation (16,17),
| (4) |
| (5) |
where d is the diameter and A is the aspect ratio of the rod. The precise values of the friction coefficients are not important because the drag on the stalk is small in comparison with the drag on the head. Simulations confirm that the dynamics remain unaffected if ξT and ξR are varied by a factor of four. Further details of the model can be found in Ladd and Misra (18).
The spasmoneme contracts in the presence of free calcium ions, and exerts forces and couples on the stalk that bend it into a helix. We assume that the spasmoneme does not offer any bending resistance but only generates a tension along its length. Hence, it is modeled by an elastic fiber attached helically around the stalk.
What happens at the molecular level when calcium binds to spasmoneme is not known. However, from a mechanistic point of view, it is sufficient to assume that the rest length of spasmoneme decreases significantly upon calcium binding. As the calcium signal traverses successive parts of the spasmoneme, the local rest length decreases, resulting in contractile force generation. We define the rest length of a spasmoneme segment in its calcium-free state as le, and its rest length in the calcium-bound state as lc; its time-dependent length, l, varies between le and lc as illustrated in Fig. 2.
Figure 2.
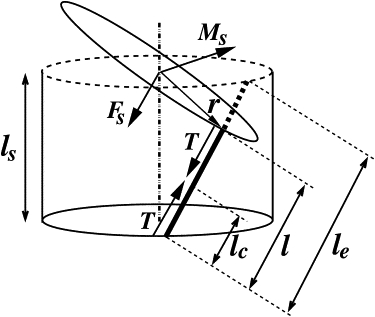
A segment of the rod-fiber assembly showing the tension (T) in the fiber and its position relative to the centerline of the rod. The segment length in the discretized model is given by ls = L/Ns where L is the length of the rod and Ns is the number of segments. The force acting on the centerline (Fs) is parallel to T and exerts shear and compression forces. The moment (Ms) of the tension is perpendicular to r and Fs, and generates bend and twist couples. The rest length of the spasmoneme segment in its calcium-free state is le and its rest length in the calcium-bound state is lc; its time-dependent length, l, varies between le and lc. The force and couple acting on the bottom plane are not shown.
The force-extension relationship of the Zoothamnium spasmoneme has been reported to be nonlinear (19), and it may be nonlinear for the Vorticella spasmoneme as well. However, in the absence of experimental data, we assume a linear relationship between the tensile force and the extension of the spasmoneme. The local tension vector in a spasmoneme segment (Fig. 2) is given by
| (6) |
where γ = l/le is the tensile strain and γc = lc/le is the strain in the reference configuration; κ is the extensional stiffness and is a unit vector in the direction of the fiber. Before calcium binding γc = γ = 1, but γc decreases in response to an increase in the local concentration of calcium-bound spasmin. This generates a force that drives l from le to lc. The force and couple exerted by the fiber on the axis of the rod are given by
| (7) |
| (8) |
where r is the vector from the rod axis to the fiber (Fig. 2). The force, Fs, and the couple, Ms, are added to the elastic forces and moments of the rod, ∂sF and ∂sM (Eqs. 2 and 3).
Chemical model
Spasmin has been shown to carry two functional calcium-binding (EF-hand) domains (20), which occur in several calcium-binding proteins (21). The association of free calcium ions to a binding site, S, on a spasmin protein is modeled by second-order kinetics,
| (9) |
where C represents the Ca2+-EF-hand complex. The rate equation for the reaction,
| (10) |
is subject to constraints on the total number of binding sites, [ST], and calcium ions, [Ca2+T],
| (11) |
| (12) |
and the initial condition
| (13) |
The local reference strain of the spasmoneme in the calcium-bound state, γc, is assumed to be linearly related to the local concentration of the complex, [C],
| (14) |
where the parameter γc∞ is defined as the strain of the calcium-saturated spasmoneme. Initially [C] = 0 and γc = 1 when the binding sites are saturated [C] = [ST] and γc = γc∞.
Propagation of the calcium signal is modeled by a constant velocity front that travels down the spasmoneme, triggering the onset of the calcium binding reaction at successive segments.
Geometric constraints
If we assume that the stalk and spasmoneme are attached, then there are geometric constraints relating the initial straight configuration and the final helical configuration. The length of the stalk in the helical configuration is
| (15) |
where Nf is the number of turns in the helix, D is its diameter, and P is the pitch. The helix formed by the spasmoneme has the same pitch and number of turns as the stalk, but its diameter is D − 2r, where r is the distance of the fiber from the rod's axis (Fig. 2); its length is given by
| (16) |
The equations can be simplified because the pitch, P ∼3.5 μm (Fig. 1 b), is small in comparison to the perimeters, πD ∼17 μm and π(D − 2r) ∼10 μm; by omitting the terms in P2 from Eqs. 15 and 16, we have
| (17) |
| (18) |
It is significant, and somewhat counterintuitive, that the number of turns in the final contracted helix is independent of the initial number of turns the spasmoneme makes around the stalk. Instead, Nf depends primarily on the extent of contraction, Lc, which we have confirmed with simulations.
High-resolution images of Vorticella (22) have been used to estimate the lengths of the fully extended and contracted spasmoneme, Le and Lc. The images in Fig. 1 were used to measure the dimensions of the extended stalk, L and d, and the geometry of the contracted spasmoneme, Nf, D − 2r, and P. We then calculated Lc from Eq. 16 and Le from the equivalent relation for the helical spasmoneme in the fully extended stalk,
| (19) |
where Ni is the initial number of turns of the spasmoneme around the straight stalk and r ≈ d/2. On comparing Lc with Le, we conclude that the spasmoneme has shrunk to approximately a quarter of its length, which is consistent with estimates based on the configuration of the helical stalk (Eqs. 17 and 18). The spasmoneme of Carchesium, a relative of Vorticella, has been reported to contract to approximately a third of its length (2), so shrinkage of Vorticella spasmoneme to a quarter of its length is not unreasonable. We assume the contraction ratio, Lc/Le = 0.25, to be an intrinsic property of Vorticella spasmoneme, valid locally as well as globally. Therefore, the reference strain in the calcium saturated state, γc∞ (Eq. 14), is taken to be 0.25.
The predictions of the constraints (Eqs. 17 and 18) can be compared with the images in Fig. 1, a and b. The length of the contracting part of the stalk, L, is ∼100 μm, the average stalk-spasmoneme distance, r, is ∼2 μm, the initial length of the spasmoneme, Le, is ∼112 μm (Eq. 19), and its contracted length, Lc, is 28 μm (= Le/4). Using Eqs. 17 and 18, we get Nf = 5.7 turns and D = 5.6 μm while the observation is Nf ∼4.5 and D ∼5.9 μm.
A further consistency check on the geometry of the final helix can be obtained from Eqs. 15 and 16, including the contribution from the pitch. There are three unknowns (P, D, and Nf) and only two equations, but real values of P require
| (20) |
The experimentally observed diameter, D = 5.9 μm, lies outside this range when r = d/2 = 2 μm. However, it is evident from the higher magnification images of the helical stalk (Fig. 1 b) that it has been squeezed into an oval shape by the spasmoneme and, as a result, the distance between the stalk axis and the spasmoneme, r, has increased. Hence, the geometric constraints correctly imply a squeezing of the stalk as well.
Parameter estimation
Geometric and mechanical parameters
There are several geometric parameters required to describe the Vorticella model; these can be estimated from published images and are listed in Table 1. The stalk diameter and length vary from source to source but the aspect ratio (L/d) remains close to 30. The strain at saturation is obtained from the fully contracted and the fully extended lengths as γc∞ = Lc/Le; Lc and Le are the macroscopic equivalents of the segment lengths lc and le shown in Fig. 2.
Table 1.
Geometric parameters from images of Vorticella
| Parameter | Symbol | Range | Value |
|---|---|---|---|
| Stalk diameter | d | 3–6 μm | 5 μm |
| Head diameter | dh | 8–11d | 50 μm |
| Stalk length | L | 25–30d | 150 μm |
| Initial turns of spasmoneme | Ni | ∼1 per 25 μm | 6 |
| Stalk-spasmoneme distance | r | ∼d/2 | 2.5 μm |
| Uncontracted spasmoneme length | Le | ((2πrNi)2 + L2)1/2 | 177 μm |
| Contracted spasmoneme length | Lc | ∼Le/4 | 44 μm |
| Strain at saturation | γc∞ | Lc/Le | 0.25 |
The range of parameters encompasses the data in the literature (2,3,22,25,33,34), including the images in Fig. 1, a and b. The values used in the simulation were taken from Upadhyaya et al. (25), where velocity data for the contraction was reported.
The parameters describing the mechanical properties of the stalk, the spasmoneme, and the surrounding medium are listed in Table 2. The tension in the spasmoneme was deduced by fitting a linear force-extension relation (Eq. 6) to the available data on the maximum force, Fmax, generated by a fully extended spasmoneme. The force will be maximum when the length of the spasmoneme is at its maximum, γ = 1, while its rest length is at its minimum, γc = γc∞. The maximum force for in vivo measurements,
| (21) |
ranges from 200 nN (23) to 500 nN (S. Ryu, MIT, personal communication, 2009). We take Fmax = 300 nN and γc∞ = 0.25, which gives κ = 400 nN. The extensional modulus of spasmoneme estimated from κ is ∼100 kPa, which is two orders-of-magnitude larger than the Young's modulus of the stalk (estimated later). Simulations show that if the spasmoneme is significantly stiffer than the stalk, small variations in κ (up to 25%) do not alter the dynamics significantly.
Table 2.
Mechanical parameters
| Parameter | Symbol | Value | Source |
|---|---|---|---|
| Spasmoneme stiffness | κ | ∼400 nN | Maximum force (23) |
| Stalk extensional modulus | Ye | ∼1 MPa | Incompressibility |
| Stalk Young's modulus | Y | ∼1 kPa | Simulations |
| Stalk shear modulus | G | ∼0.33 kPa | Elasticity relations |
| Medium viscosity | η | 1 cP | Viscosity of water |
These parameters are material properties and are independent of the size of the organism.
Micrographs of contracted Vorticella indicate no apparent shrinkage in the stalk length under maximum contraction, suggesting that the extensional modulus, Ye, of the fluid-filled stalk is significantly larger than the maximum compressive stress exerted by the spasmoneme. Simulations confirm that any value of Ye > 25κ/d2 ≈ 400 kPa yields the same contraction dynamics. We have used Ye = 1 MPa for the results shown here. The extensional modulus of a Carchesium stalk is similar, at ∼400 kPa (24). We have found that the extensional modulus, Ye, is a few orders-of-magnitude larger than the Young's modulus that appears in the bending stiffness, YI. We think this is because the fluid-filled gel inside the sheath resists change in volume but has little shear resistance.
The bending stiffness of the stalk determines the elastic resistance of the contracting stalk relative to the viscous drag from the head, which sets the viscosity range where power-limited contraction is observed (25). Furthermore, the bending energy stored in the coiled stalk, ∼YIL/D2, is responsible for recovery of the organism from the contracted state. Thus, the range of values for Y can be bounded by comparison with experimental observations of contraction and recovery. Here we have assumed that the moment of inertia of the stalk is I = πd4/64.
The shear modulus of the stalk, G, is related to the Young's modulus,
| (22) |
where σ is Poisson's ratio, which we take to be 0.5. The dynamics of collapse and recovery are insensitive to changes (twofold) in the value of G and its exact value is immaterial for our purposes. A viscosity of 1 cP is assumed for the medium (water), except when glycerine is added to increase the viscosity.
It is evident from Fig. 1 b that the stalk is squeezed into an oval shape by the contraction, leading to an increase in the distance between the stalk axis and the spasmoneme, r. As suggested by the geometric relations, our simulations confirm that this slight increase in r is important to explain the observed configuration of the collapsed stalk. We increased r in proportion to the local calcium-EF-hand complex concentration, [C], from an initial value of 0.45d to a final value of 0.65d to capture the squeezing of the stalk.
A small part of the stalk shown in Fig. 1 b remains uncoiled for reasons unknown to us. Simulations show that, keeping the spasmoneme uncontracted in a small length (∼10 μm) next to the tethered end, leaves the corresponding length of the stalk uncoiled (Fig. 1 d).
Chemical parameters
The parameters for the chemical model are listed in Table 3. The dissociation constant, Kd, of the calcium-EF-hand complex, C, has been independently estimated to be ∼10−6.5 M (26). The forward rate constant, k, was obtained by fitting the simulated velocity profile (discussed later) to experimental observations; it is the only directly fitted parameter in our model. The backward rate constant, k−1, is given by kKd ≈ 0.15 s−1. The calcium-binding-site concentration, [ST], is not known for Vorticella; we estimate a value of 8 mM from in vitro experiments with Zoothamnium, which show that ∼0.34 gram of calcium per kg of wet spasmoneme saturates all binding sites (27). Assuming a density of 1.1 kg/L for wet spasmoneme yields a value of ∼8 mM for [ST]. No direct measurement of in vivo calcium concentration, [Ca2+T], is available. However, [Ca2+T] cannot be significantly less than [ST] because the maximum force measured in calcium saturation experiments (26) is less than what is observed in the in vivo experiments (23), which suggests that the spasmin is saturated by calcium. [Ca2+T] is not likely to be significantly larger than [ST] because Vorticella has to work to sequester the released Ca2+ ions back into the calcium storing tubules. Hence, we assume [Ca2+T] ≈ [ST]. The speed of the calcium signal, VCa = 10 cm s−1, is taken from experimental observations (25).
Table 3.
Chemical parameters
| Parameter | Symbol | Value | Source |
|---|---|---|---|
| Dissociation constant | Kd | ∼10−6.5 M | (26,35) |
| Binding rate constant | k | ∼5.105 M−1 s−1 | Simulations |
| Dissociation rate constant | k−1 | ∼0.15 s−1 | Thermodynamics (= kKd) |
| Total binding sites concentration | [ST] | ∼8 mM | (12) |
| Total calcium concentration | [Ca2+T] | ∼8 mM | Binding site concentration |
| Ca2+ signal speed | VCa | ∼10 cm s−1 | (25) |
Results
Fast binding
We will first treat the case where the calcium binding reaction is not rate-limiting, resulting in an instantaneous force (γc = γc∞) in those parts of the spasmoneme where the signal has propagated. We will later show that a finite binding rate must be assumed to capture the experimentally observed dynamics.
The stalk-substrate attachment is modeled by a clamped boundary condition (no translation or rotation) at one end of the stalk. The other end bears the head and is free to translate and rotate. Initially the stalk is straight with the spasmoneme winding helically around it. A signal travels down the spasmoneme from the head bearing end, with a constant speed of 10 cm s−1. The spasmoneme experiences an instantaneous decrease in the local reference strain (γc = γc∞) as the signal traverses each segment, generating a tensile force (Eq. 6), as illustrated in Fig. 2. The head gets pulled downwards and the lower part of the stalk, where the signal has not yet reached, is pulled upwards. Snapshots of the simulations for two Young's moduli are shown in Fig. 3. For Y = 1 kPa, we can see that the lower part of the stalk undergoes significant deformation while the signal is still in the upper part (t ∼1 ms), which is contrary to experimental observations. On the other hand, for a stiffer stalk, Y = 4 kPa, the lower part remains essentially at rest until the signal reaches it.
Figure 3.
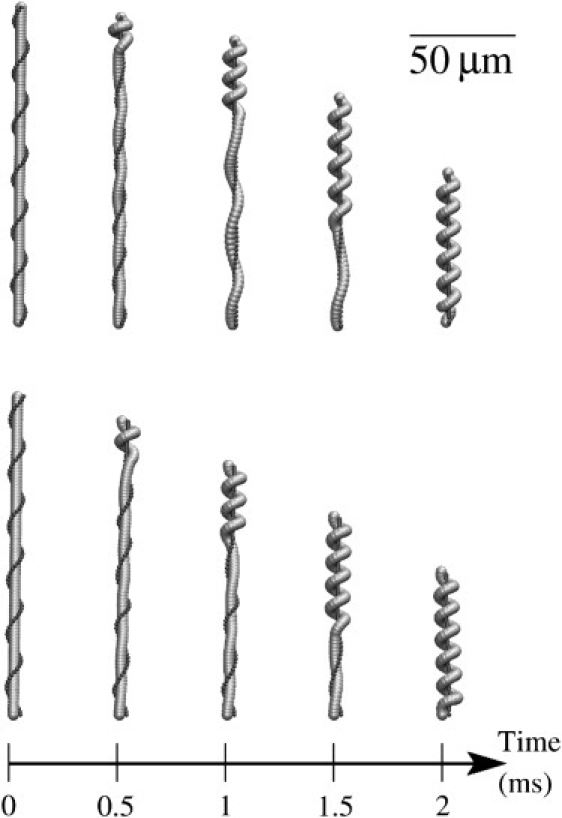
Time-lapse images of the initial phase of contraction driven by a propagating calcium signal (for clarity, the head is not shown). (Top) Young's modulus Y = 1 kPa. (Bottom) Y = 4 kPa.
It has been observed that the maximum velocity of the head scales with viscosity as η−0.5, which implies that most of the energy from spasmoneme contraction is spent in overcoming the viscous drag (25) rather than bending the stalk. Fig. 4 a shows the peak velocity plotted against viscosity for Y = 1 and 4 kPa. At lower viscosities (∼1 cP), the peak velocity follows experimental scaling if Y ≤ 1 kPa, but for Y = 4 kPa there is a significant deviation. Hence the upper bound on the bending rigidity of the stalk is between 1 and 4 kPa.
Figure 4.
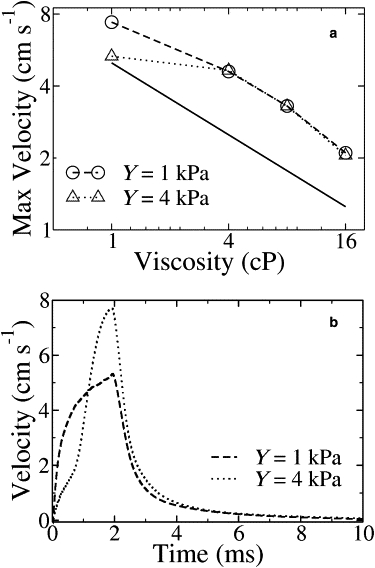
Simulation results for contraction driven by a propagating calcium signal. (a) Peak velocity versus viscosity. The solid line indicates a slope of –0.5. (b) Velocity profiles. The peak velocity decays more rapidly than the experimental data shown in Fig. 1e. For the stiffer stalk (Y = 4 kPa), the velocity increases much too rapidly as well.
Velocity profiles of the simulations shown in Fig. 3 are plotted in Fig. 4 b. For Y = 1 kPa, the velocity peaks at 8 cm s−1 and then drops to 1 cm s−1 within a millisecond. For Y = 4 kPa, the velocity peaks at 5 cm s−1 but with a very different profile. Neither of these profiles captures the delayed buildup and slow decay of the velocity shown in Fig. 1 e. We propose that the additional timescale indicates delayed calcium-spasmin binding kinetics.
Delayed binding
Velocity profiles for different values of the binding rate constant, k, are shown in Fig. 5 a. Simulations with k = 5 × 105 M−1 s−1 quantitatively reproduce the experimental data (Fig. 1 e) including the overall shape, peak velocity (6 cm s−1), and peak position (2 ms). The time-dependent position of the tip of the stalk, shown in Fig. 5 b, is also in good agreement with the experiment. The shape of the velocity profile is sensitive to the calcium-binding rate constant; other values of k do not fit the observations (Fig. 5).
Figure 5.
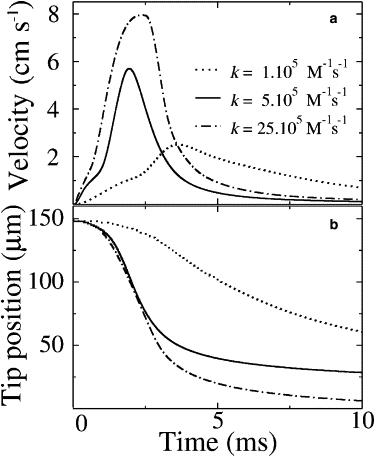
Results for Young's modulus Y = 1 kPa and different values of the rate constant, k. (a) Velocity of the head versus time. (b) Position of the head versus time.
Snapshots of a simulation with k = 5 × 105 M−1 s−1 and Y = 1 kPa are shown in Fig. 6 (see Movie S1 in the Supporting Material). Owing to the delayed binding, the stalk remains straight until the calcium signal passes by and the collapse is more uniformly distributed over the stalk. This is closer to the observed shapes of the contracting stalk than the simulations assuming instantaneous binding (compare to Fig. 3).
Figure 6.

Time-lapse images of contraction with Young's modulus Y = 1 kPa and rate constant k = 5 × 105 M−1 s−1.
The velocity profiles for different fluid viscosities are shown in Fig. 7 a. The peak position is relatively insensitive to the viscosity and the peak velocity scales asymptotically as η−0.5 (Fig. 7 b); both findings are consistent with experimental data (25). Moreover, simulations and experiments find similar deviations from η−0.5 scaling at low viscosity.
Figure 7.
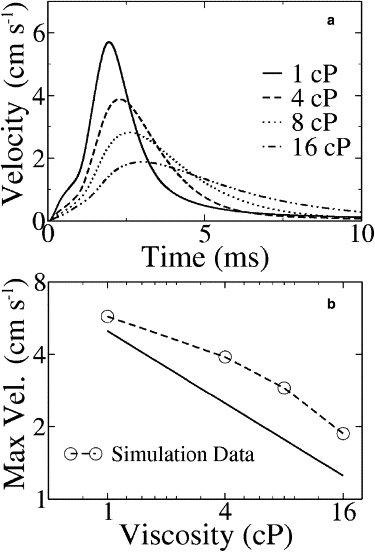
Velocity data for Young's modulus Y = 1 kPa and rate constant k = 5 × 105 M−1 s−1. (a) Velocity profile for different viscosities. (b) Peak velocity versus viscosity. The solid line depicts the slope of –0.5.
Recovery
The recovery of Vorticella is ATP-driven and takes place on a much longer timescale than contraction. Calcium ions are thought to be sequestered back into the calcium storing tubules in the spasmoneme using ATP hydrolysis as the energy source. Several questions regarding recovery have been left unanswered in the current literature. Is the recovery rate limited by Ca2+ ion sequestration, by Ca2+ ion dissociation from spasmin, by the drag on the head, or by a combination of these? What is the role of the spasmoneme in recovery: is it under compression against the drag forces or under tension against the stalk's bending strain? Our simulations address the mechanics aspects of these questions.
Recovery simulations start with the stalk at rest in the fully contracted helical shape; its elastic restoring forces are balanced by the tension in the spasmoneme. To start recovery, the tension in the spasmoneme is reduced uniformly along its length, at a rate similar to the rate of recovery observed in the living organism (∼0.2 s−1). Simulations with different bending stiffnesses of the stalk are shown in Fig. 8. For a small Young's modulus, Y ≤ 0.25 kPa, the stalk uncoils without moving the head significantly (Fig. 8, a1 and a2), which is contrary to experimental observations. However, for stiffer stalks, Y ≥ 1 kPa, the head is pushed up in the observed fashion (Fig. 8, b1 and b2). Hence the lower bound on the Young's modulus of the stalk is between 0.25 and 1 kPa.
Figure 8.
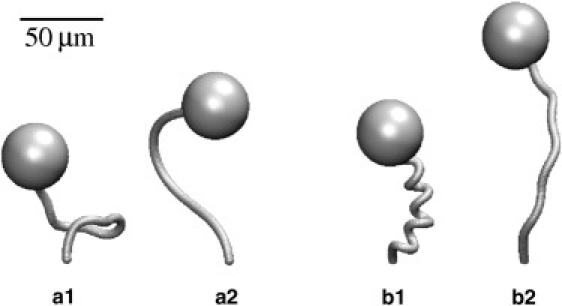
Recovery simulations with Young's modulus Y = 0.25 kPa (a1 and a2) and Y = 1 kPa (b1 and b2). Early stalk shapes are shown in a1 and b1, while a2 and b2 show the shapes at a later time.
We simulated recovery with an enhanced rate of reduction of the tension in the spasmoneme, to show what would happen if the Ca2+ dissociation and sequestration was faster by an order of magnitude. Simulations show that even a stiffer stalk, Y = 2 kPa, uncoils without moving the head, and exhibits shapes similar to those shown in Fig. 8 a. Hence, chemistry must control the rate of recovery rather than viscous drag.
The molecular mechanism for force generation by calcium-spasmin binding is not known and what happens upon calcium unbinding is also unclear. There has been speculation in the literature that the recovery is driven by the stalk (26) or by the spasmoneme (5), but no one has demonstrated either case to be true. It is possible that upon calcium unbinding, the rest length of the spasmoneme increases so rapidly that it starts exerting an extensional force on the stalk. In this case, the recovery will be driven by the spasmoneme rather than the stalk. We simulated this mechanism of recovery and found that for a realistic rate of recovery, the spasmoneme never develops a compressive force, because the stalk always uncoils fast enough to keep the spasmoneme under tension. Hence, our simulations indicate that recovery is driven by the elastic energy stored in the coiled stalk.
Discussion
Our model of Vorticella contraction yields a number of insights that are not obvious from the experiments. The geometric analysis shows that the final number of turns in the helical stalk is independent of the initial number of turns of the spasmoneme around the stalk. The difference between the initial and final number of turns is made up for by rotation of the head, because the other end is fixed. Most images of Vorticella show that the initial number of turns of the spasmoneme is quite close to the final number of turns of the helical stalk, and that the rotation of the head is small (22,25,28). Because the number of turns in the contracted state is independent of the initial number of turns of the spasmoneme, it is interesting that the two end up being so close. Perhaps nature has evolved the organism in such a way that the initial and final number of turns is similar and the stalk-body junction does not have to bear large torsional strains.
The effective Young's modulus of the stalk must be close to 1 kPa; otherwise the experimentally observed contraction and recovery cannot be explained. The Vorticella stalk has fine slender structures on its surface (called “bâtonnets”) that wind around the stalk with the same pitch as the spasmoneme, but with opposite handedness (2). Because they always lie on the outer side of the helix, oriented parallel to the local centerline, their supposed function is to provide extra bending stiffness to the stalk. A simple deflection experiment may therefore underpredict the effective bending stiffness during collapse and recovery. Simulations predict that when the organism recovers from its contracted state in a high viscosity fluid (∼20 cP), the stalk will uncoil without significant motion of the head; later the bent stalk will gradually straighten, as seen in Fig. 8, a1 and a2. This prediction could be used to test our estimate of Y = 1 kPa.
The collapse of the stalk (sixfold) is larger than the reduction in length of the spasmoneme (fourfold). Simulations show that the collapsing stalk forces the spasmoneme into a helical coil, thereby increasing the tension in the spasmoneme and generating additional force for contraction.
It has been suggested that an action-potential induces calcium release in the Vorticella spasmoneme (25). However, the observation that membrane depolarization occurs after cellular contraction (29) argues against an action-potential driven signal. The observed signal speed (10 cm s−1) can in fact be explained by the CICR mechanism, as shown in the Appendix, contrary to what has been suggested previously (25). However, a CICR signal cannot entirely explain the dynamics of the collapsing stalk; there must be an additional delay which we propose comes from the calcium-spasmin binding kinetics.
Simulations show that recovery is driven by the bending energy stored in the coiled stalk, at a rate limited by calcium dissociation and sequestration. A dissociation time of 7 s, as calculated from (k−1)−1, is consistent with experimentally observed recovery.
The simulations offer some unexpected insights into the contraction mechanics. While the signal is still in the upper part of the stalk, tension in the spasmoneme pulls the head downwards and the lower part of the stalk upwards, thereby storing strain energy in the stalk-spasmoneme segments that have not yet been triggered by calcium. The effect, the extent of which depends on the head size, is magnified by the inertia of the initially stationary fluid around the cell body (Eq. 1). When the signal reaches the lower region, stored strain energy is quickly converted into kinetic energy of the head, which brings about a sudden rise in the velocity. The model predicts that for long stalks (L ≳ 150 μm), there will be a plateau in the velocity profile before the maximum velocity is reached (as in Fig. 1 e), which will be missing for short stalks (L ≲ 75 μm). The rise to the peak velocity will be steeper for long stalks than for short ones.
It is evident that the spasmoneme exerts a local tension along the whole length of the stalk. Nevertheless, the assumption that the spasmoneme is rigidly bound to the stalk along its entire length may not be entirely correct. The micrographs (2,3) and spasmoneme extraction experiments (19,26) suggest that it simply occupies a helical cavity inside the stalk's fibrillar matrix. Thus, it might be able to acquire some twist without twisting the stalk, an effect we have neglected in our geometric analysis. The spasmoneme also has a significant cross section in comparison to the stalk, unlike the thin fiber modeled here. Hence, it might contribute asymmetrically to the bending stiffness of the stalk. We have not considered cooperative binding of calcium and spasmin (26,30) in our kinetic model, for lack of experimentally measured rate constants. However, we have been able to explain the observed velocity profile reasonably well, which suggests that cooperative binding does not play a critical role in the dynamics of the organism.
The main conclusions drawn from this model are as follows. The contraction of Vorticella is rate-limited by calcium-spasmin binding kinetics as well as by the signal propagation speed. Recovery is driven by the elastic energy stored in the coiled stalk, at a rate controlled by calcium dissociation and sequestration. The effective Young's modulus of the stalk is estimated to be ∼1 kPa. Vorticella contraction is subject to geometric constraints, which determine the number of turns in the helical stalk and the rotation of the head. Finally, the number of turns in the coiled stalk is geometrically independent of the number of turns the spasmoneme makes around the straight stalk.
Appendix
Here we show that the CICR mechanism can explain the signal speed observed in V. convallaria.
The only calcium-binding proteins in the spasmoneme are the spasmins (12,13), which are integral to the spasmonemal structure (20). Hence, there are practically no calcium-binding proteins in the aqueous phase inside the spasmoneme. Upon release from the tubules, free Ca2+ ions would have a diffusivity of ∼230 μm2 s−1 (31), unlike muscle cells where the apparent diffusivity is only 30 μm2 s−1 (31). Calcium channels in Vorticella spasmoneme are supposedly gated by ryanodine receptors (9). The average density of these receptors on the sarcoplasmic reticulum of rat cardiac cells is ∼370 per μm2 (32). The membranous tubules in spasmoneme are ∼0.07 μm in diameter and ∼0.5 μm in length (3) and hence carry a surface area of ∼0.11 μm2, or ∼40 receptors per tubule. The distance between successive receptors is then ∼0.06 μm, which is comparable to the average distance between the tubules ∼0.1 μm (3).
In a one-dimensional diffusion model, the calcium concentration, [Ca], at a distance x from an active calcium channel at a time t is given by
| (23) |
where d is the distance between successive channels (the characteristic length in the problem), D is the diffusivity of free calcium (230 μm2 s−1), and [Ca]0 is the calcium concentration released by an active channel, which we assume to be ∼0.01 M (Table 3). The threshold calcium concentration required to activate a channel is 2 × 10−7 M (9). The time taken by an active calcium channel to activate the nearby channels can be estimated from Eq. 23 by using [Ca] = 2 × 10−7 M and x = d = 0.06 μm, which yields t ∼0.2 μs. In a 150-μm-long spasmoneme, there will be ∼2500 successive activation events, yielding a maximum speed of ∼30 cm s−1, which is consistent with the observed signal speed of 10 cm s−1 (25).
We have assumed that diffusion of Ca2+ ions is unaffected by ion depletion due to binding with spasmin. This is justified because the diffusion time of Ca2+ ions between the channels (0.2 μs) is negligible in comparison to the binding time, (k[Ca2+T])−1 ∼0.5 ms.
Supporting Material
One movie is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00355-3.
Supporting Material
Acknowledgments
We thank Sangjin Ryu of the Massachusetts Institute of Technology for providing us with the high-resolution images of V. convallaria.
This work was supported by the National Science Foundation (grant No. CTS-0505929).
References
- 1.Mahadevan L., Matsudaira P. Motility powered by supramolecular springs and ratchets. Science. 2000;288:95–99. doi: 10.1126/science.288.5463.95. [DOI] [PubMed] [Google Scholar]
- 2.Amos W.B. Structure and coiling of the stalk in the peritrich ciliates Vorticella and Carchesium. J. Cell Sci. 1972;10:95–122. doi: 10.1242/jcs.10.1.95. [DOI] [PubMed] [Google Scholar]
- 3.Allen R.D. Structures linking the myonemes, endoplasmic reticulum, and surface membranes in the contractile ciliate Vorticella. J. Cell Biol. 1973;56:559–579. doi: 10.1083/jcb.56.2.559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hoffmannberling H. The mechanism of a novel contraction cycle that differs from the muscle contraction. [Der mechanismus eines neuen, von der muskelkontraktion verschiedenen kontraktionszyklus] Biochim. Biophys. Acta. 1958;27:247–255. doi: 10.1016/0006-3002(58)90331-7. [DOI] [PubMed] [Google Scholar]
- 5.Amos W.B. Reversible mechanochemical cycle in the contraction of Vorticella. Nature. 1971;229:127–128. doi: 10.1038/229127a0. [DOI] [PubMed] [Google Scholar]
- 6.Weis-Fogh T., Amos W.B. Evidence for a new mechanism of cell motility. Nature. 1972;236:301–304. doi: 10.1038/236301a0. [DOI] [PubMed] [Google Scholar]
- 7.Carasso N., Favard P. Obtaining evidence of calcium in the stem myonemes of peritrichous ciliates. [Mise en evidence du calcium dans les myonemes pedonculaires de cilies peritriches] J. Microsc. Oxford. 1966;5:759–770. [Google Scholar]
- 8.Katoh K., Kikuyama M. An all-or-nothing rise in cytosolic [Ca2+] in Vorticella sp. J. Exp. Biol. 1997;200:35–40. doi: 10.1242/jeb.200.1.35. [DOI] [PubMed] [Google Scholar]
- 9.Katoh K., Naitoh Y. Control of cellular contraction by calcium in Vorticella. J. Exp. Biol. 1994;189:163–177. doi: 10.1242/jeb.189.1.163. [DOI] [PubMed] [Google Scholar]
- 10.Katoh K., Naitoh Y. A mechanosensory mechanism for evoking cellular contraction in Vorticella. J. Exp. Biol. 1992;168:253–267. [Google Scholar]
- 11.Keizer J., Smith G.D., Pearson J.E. Saltatory propagation of Ca2+ waves by Ca2+ sparks. Biophys. J. 1998;75:595–600. doi: 10.1016/S0006-3495(98)77550-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Amos W.B., Routledge L.M., Yew F.F. Calcium-binding proteins in a vorticellid contractile organelle. J. Cell Sci. 1975;19:203–213. doi: 10.1242/jcs.19.1.203. [DOI] [PubMed] [Google Scholar]
- 13.Routledge L.M. Calcium-binding proteins in the vorticellid spasmoneme. J. Cell Biol. 1978;77:358–370. doi: 10.1083/jcb.77.2.358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wolgemuth C.W., Inclan Y.F., Koehl M.A. How to make a spiral bacterium. Phys. Biol. 2005;2:189–199. doi: 10.1088/1478-3975/2/3/006. [DOI] [PubMed] [Google Scholar]
- 15.Landau L.D., Lifshitz E.M. Pergamon Press; London: 1959. Fluid Mechanics. [Google Scholar]
- 16.Cox R.G. The motion of long slender bodies in a viscous fluid. Part l. General theory. J. Fluid Mech. 1970;44:791–810. [Google Scholar]
- 17.Cox R.G. The motion of long slender bodies in a viscous fluid. Part 2. Shear flow. J. Fluid Mech. 1971;45:625–657. [Google Scholar]
- 18.Ladd A.J.C., Misra G. A symplectic integration method for elastic filaments. J. Chem. Phys. 2009;130:124909. doi: 10.1063/1.3077863. [DOI] [PubMed] [Google Scholar]
- 19.Moriyama Y., Okamoto H., Asai H. Rubber-like elasticity and volume changes in the isolated spasmoneme of giant Zoothamnium sp. under Ca2+-induced contraction. Biophys. J. 1999;76:993–1000. doi: 10.1016/S0006-3495(99)77263-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Maciejewski J.J., Vacchiano E.J., Buhse H.E. Cloning and expression of a cDNA encoding a Vorticella convallaria spasmin: an EF-hand calcium-binding protein. J. Eukaryot. Microbiol. 1999;46:165–173. doi: 10.1111/j.1550-7408.1999.tb04601.x. [DOI] [PubMed] [Google Scholar]
- 21.Kretsinger R.H. Calcium-binding proteins. Annu. Rev. Biochem. 1976;45:239–266. doi: 10.1146/annurev.bi.45.070176.001323. [DOI] [PubMed] [Google Scholar]
- 22.Ryu S., Matsudaira P. Unsteady motion, finite Reynolds number and wall effects on Vorticella convallaria contribute contraction force greater than the stokes drag. Biophys. J. 2010;98:2574–2581. doi: 10.1016/j.bpj.2010.02.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.France, D. C. 2007. Structure and mechanics of the spasmoneme, a biological spring within the protozoan Vorticella convallaria. PhD thesis. Massachusetts Institute of Technology, Cambridge, MA.
- 24.Rahat M., Parnas I., Nevo A.C. Extensibility and tensile strength of the stalk “muscle” of Carchesium sp. Exp. Cell Res. 1969;54:69–76. doi: 10.1016/0014-4827(69)90294-8. [DOI] [PubMed] [Google Scholar]
- 25.Upadhyaya A., Baraban M., Mahadevan L. Power-limited contraction dynamics of Vorticella convallaria: an ultrafast biological spring. Biophys. J. 2008;94:265–272. doi: 10.1529/biophysj.107.108852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Moriyama Y., Yasuda K., Asai H. Ca2+-induced tension development in the stalks of glycerinated Vorticella convallaria. Cell Motil. Cytoskeleton. 1996;34:271–278. doi: 10.1002/(SICI)1097-0169(1996)34:4<271::AID-CM2>3.0.CO;2-B. [DOI] [PubMed] [Google Scholar]
- 27.Routledge L.M., Amos W.B., Weis-Fogh T. Microprobe measurements of calcium binding in the contractile spasmoneme of a vorticellid. J. Cell Sci. 1975;19:195–201. doi: 10.1242/jcs.19.1.195. [DOI] [PubMed] [Google Scholar]
- 28.Jones A.R., Jahn T.L., Fonseca J.R. Contraction of protoplasm. IV. Cinematographic analysis of the contraction of some peritrichs. J. Cell. Physiol. 1970;75:9–19. doi: 10.1002/jcp.1040750103. [DOI] [PubMed] [Google Scholar]
- 29.Shiono H., Naitoh Y. Cellular contraction precedes membrane depolarization in Vorticella convallaria. J. Exp. Biol. 1997;200:2249–2261. doi: 10.1242/jeb.200.16.2249. [DOI] [PubMed] [Google Scholar]
- 30.Asai H., Ochiai T., Kano F. Improved preparation and cooperative calcium contraction of glycerinated Vorticella. J. Biochem. 1978;83:795–798. doi: 10.1093/oxfordjournals.jbchem.a131974. [DOI] [PubMed] [Google Scholar]
- 31.Allbritton N.L., Meyer T., Stryer L. Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science. 1992;258:1812–1815. doi: 10.1126/science.1465619. [DOI] [PubMed] [Google Scholar]
- 32.Naudin V., Oliviero P., Charlemagne D. The density of ryanodine receptors decreases with pressure overload-induced rat cardiac hypertrophy. FEBS Lett. 1991;285:135–138. doi: 10.1016/0014-5793(91)80743-m. [DOI] [PubMed] [Google Scholar]
- 33.Sun P., Song W.B., Al-Rasheid K.A. Taxonomic characterization of Vorticella fusca Precht, 1935 and Vorticella parapulchella n. sp., two marine peritrichs (Ciliophora, Oligohymenophorea) from China. J. Eukaryot. Microbiol. 2006;53:348–357. doi: 10.1111/j.1550-7408.2006.00112.x. [DOI] [PubMed] [Google Scholar]
- 34.Ji D.D., Song W.B., Clamp J. Pseudovorticella zhengae n. sp., P. difficilis (Kahl, 1933) Jankowski, 1976, and P. punctata (Dons, 1918) Warren, 1987, three marine peritrichous ciliates from north China. Eur. J. Protistol. 2006;42:269–279. doi: 10.1016/j.ejop.2006.09.002. [DOI] [PubMed] [Google Scholar]
- 35.Ochiai T., Asai H., Fukui K. Hysteresis of contraction-extension cycle of glycerinated Vorticella. J. Protozool. 1979;26:420–425. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


