Multiscale Morphology of Organic Semiconductor Thin Films Controls the Adhesion and Viability of Human Neural Cells

Abstract

We investigate how multiscale morphology of functional thin films affects the in vitro behavior of human neural astrocytoma 1321N1 cells. Pentacene thin film morphology is precisely controlled by means of the film thickness, Θ (here expressed in monolayers (ML)). Fluorescence and atomic force microscopy allow us to correlate the shape, adhesion, and proliferation of cells to the morphological properties of pentacene films controlled by saturated roughness, σ, correlation length, ξ, and fractal dimension, d_f. At early incubation times, cell adhesion exhibits a transition from higher to lower values at Θ ≈ 10 ML. This is explained using a model of conformal adhesion of the cell membrane onto the growing pentacene islands. From the model fitting of the data, we show that the cell explores the surface with a deformation of the membrane whose minimum curvature radius is 90 (± 45) nm. The transition in the adhesion at ∼10 ML arises from the saturation of ξ accompanied by the monotonic increase of σ, which leads to a progressive decrease of the pentacene local radius of curvature and hence to the surface area accessible to the cell. Cell proliferation is also enhanced for Θ < 10 ML, and the optimum morphology parameter ranges for cell deployment and growth are σ ≤ 6 nm, ξ > 500 nm, and d_f > 2.45. The characteristic time of cell proliferation is τ ≈ 10 ± 2 h.

Introduction

Cell-substrate interactions determine cell adhesion, motility, growth, proliferation, and fate. They can influence cell differentiation and commitment, as well as intracellular signaling. Their technological impact concerns transducers, sensors, cell carriers, and scaffolds for tissue growth. Besides surface tension and chemical and mechanical composition (1), it is recognized that surface topography significantly influences cell-material interaction and cell behavior (2–4): surface pattern and periodicity (5,6); shape and symmetry (7); height of features (8); and roughness (9–11). It has been demonstrated that the three-dimensional topography of polymers (12), oxides (13), carbon nanofibers (9), and metals (14) is related to biocompatibility. Cell-substrate interactions occur at different lengthscales: micrometers for shear forces at the cell-substrate interface; nanometer lengthscales for protein clustering in focal adhesion; ∼10–15 nm as the diameter of the adhesion protein integrin in the cell membrane (15).

To our knowledge, a systematic investigation of the substrate lengthscales relevant to cell behavior has not been reported. Fractal morphologies exhibit scaling features across a few orders of magnitude of the spatial lengthscales; simply put, they retain a similar morphology upon a change in lengthscale. For this reason, they can be useful model surfaces for studying how cells explore the surface space, what are the relevant lengthscales for cell-substrate interactions, and for identifying the mechanisms of interaction beyond simple phenomenological correlations. These studies can provide input toward the technological control of cell culture and tissue growth, because many surfaces and interfaces in nature possess fractal character.

The aim of this work is to quantitatively assess how scaling morphology from micrometers to nanometers affects adhesion, proliferation, and viability of human central nervous system (CNS) astrocytoma cells. We focus on an important class of surfaces, termed self-affine surfaces, which are often encountered in nature and in technology (16,17). In self-affine surfaces, the roughness scales as a power law of the lengthscale (18). The roughness exponent is related to the fractal dimension, and the scaling range is limited at the upper bound by the correlation length.

As a model substrate, we choose pentacene thin films on a silicon wafer. The self-affine morphology (19,20) of this surface arises from the statistical stacking of monolayer terraces with well-defined molecular orientation (molecules standing), height (1.5 nm), and packing (21,22). In this context, the desirable feature of pentacene thin films is the accurate and systematic control of the lateral size, shape, and distribution of terraces through the growth parameters (21,23,24). Pentacene is the most studied organic semiconductor because of its applicability in organic electronics devices. It is highly insoluble in any type of solvent and is structurally/morphologically stable in water and buffer (25). Ultrathin film pentacene field effect transistors have been used as biosensors (26,27). In this context, pentacene embodies several attractive features; 1), Thin films are grown by high vacuum sublimation, which is an environment- and solvent-clean technology that can be easily adapted to sterility requirements. 2), Pentacene hydrophobicity is similar to that of lipid bilayer membranes (28). We have demonstrated the possibility of growing murine stem cells on pentacene ultrathin films and differentiating them in neural networks (25). 3) Pentacene electronic devices could be used to transduce signals and stimulate cells, similar to other functional materials such as carbon nanotubes (29).

We investigated the adhesion and growth of human brain astrocytoma 1321N1 cells (astroglial cells) on pentacene thin films in a thickness range from 1 to 65 monolayers (MLs). Astroglial cells are the most abundant cells in the CNS, and their ratio to neurons increases with the complexity of the CNS (30). Astroglial cells are involved in the most integrated brain functions under pathophysiological conditions, including neuronal support-development, synaptic activity, and homeostatic control of the extracellular environment (31,32). Therefore, 1321N1 represents a relevant line of prototype neural cells.

Methods

Growth and characterization of pentacene thin films

Pentacene thin films were grown by sublimation from a Knudsen cell in high vacuum (10⁻⁶ mbar) on native silicon oxide substrates (20) at room temperature (25°C) with a deposition rate of 0.8 ML/min (21). Film thickness, h, was systematically varied from 1 to 65 ML. In total, 120 pentacene thin film samples have been used as substrates for cell cultures. Thin films were imaged by atomic force microscopy (AFM) (Smena, NT-MDT, Moscow, Russia) in air in semicontact mode, with NSG10 cantilevers (NT-MDT). The images were processed using the Gwyddion program (GNU, Free Software Foundation, Boston, MA). Three morphological parameters were analyzed from the power spectrum density (18): the saturated root mean-square (rms) roughness, σ, the correlation length, ξ, and the fractal dimension, d_f. The saturated rms roughness, σ (18,33), is a lengthscale invariant measure of the topographical fluctuations on lengthscales larger than the correlation length, ξ (18,33). The latter is the characteristic lateral distance between domains, and it scales as the island size as the film becomes compact. The fractal dimension, d_f, expresses the scaling of the topographical fluctuations on lengthscales smaller than ξ (16,17,34). The maximum variation of σ, measured on AFM images with different sizes (1–40 μm) across all samples, ranged from 0.9 to 12.4 nm. AFM topography power spectrum analysis (35) and water contact angle measurements (Digidrop, GBX, Romans, France) with analysis software (Windrop²⁺, GBX) have been used to assess the reproducibility of growth for each sample. The contact angle did not change significantly for pentacene thin films of different thickness.

Cell culture

Human brain astrocytoma 1321N1 cells (ECACC 86030402, Sigma Aldrich, St. Louis, MO) were cultured in Dulbecco's modified Eagle's medium (DMEM F-12) supplemented with 2 mM L-glutamine, 100 IU/ml penicillin, 100 μg/ml streptomycin and 10% fetal bovine serum. Cells were maintained in standard conditions at 37°C in humidified atmosphere (95% humidity, 5% CO₂) and split regularly (rate 1:4) by trypsinization. Cells (7th–27th passage) were cultured in Petri dishes until subconfluence and then were harvested for cell functional tests. Cell culture products and Trypsin were purchased from Cambrex Bio-Science (Verviers, Belgium).

Cell adhesion and viability assays

The 1321N1 cells were seeded (5 × 10⁴ cells/ml, 0.5 ml/cm²) and cultured on pentacene thin film samples in 24-well plates, for 12–72 h under standard cell culture conditions. For adhesion experiments, 1321N1 cells were incubated for 3 h in serum-free conditions. In all experiments, glass coverslips were used as control culture surfaces and characterized by AFM and contact-angle measurements. Experiments were carried out in cell seeding conditions leading to confluence culture within 48–72 h in standard culture surfaces.

AFM imaging was performed on cell samples fixed with 4% paraformaldehyde solution in PBS (pH 7.4) for 15 min at room temperature, then washed two times with PBS and one time with bidistilled H₂O and dried by N₂ gas.

Cell viability, adhesion, and morphology assays were carried out with fluorescein diacetate (FDA) (Sigma Aldrich). FDA staining (36) was performed by incubating 1321N1 cells with the dye (75 μg/ml) in culture medium for 5 min at 37°C. Samples were subsequently washed with PBS and observed under fluorescence microscopy. FDA is passively loaded into cells and converted by nonspecific intracellular esterases into fluorescein (fluorescent at excitation wavelengths of 490 nm), which is retained by viable cells whose plasma membrane is intact, whereas the unhydrolyzed substrate rapidly leaks out from dead or damaged cells. An inverted epifluorescence microscope attached to the optical stereomicroscope Olympus IX71 with SPM Biosolver (NTM-DT) was used to monitor the density and shape of the cells, which were analyzed with the software NIS Elements F 2.20 Nikon (Nikon, Tokyo, Japan). Cell number and cytoplasmatic spreading area were measured on the inverted epifluorescent images by means of a threshold-watershed algorithm (Program R, The R Foundation for Statistical Computing, Vienna, Austria); at least six images at a time were taken and analyzed for each sample. Cell proliferation was quantified by means of Trypan Blue (Sigma Aldrich) exclusion test, performed by counting the number of viable (transparent) and nonviable (blue) cells using a Burker chamber under an inverted microscope (37).

Statistical analysis

All data from cell experiments are reported as the mean's average ± SE, where SE is the standard error of the mean, i.e., the standard deviation/√n, where n is the number of statistical sets. Cell experiments on all substrates were replicated at least three times (n = 3). Data sets were statistically analyzed by one-way analysis of variance (ANOVA) (Bonferroni's multiple comparison test) or by Student's t-test (two-tail, unpaired) with the GraphPad PRISM Version 4.00 program (GraphPad Software, San Diego, CA); statistical significance refers to results where P < 0.05 was obtained. Curve fits are carried out on data weighted by their respective SE using IgorPro Carbon (Wavemetrics, Lake Oswego OR).

Results

The evolution of morphology of pentacene thin films imaged by AFM is shown in Fig. 1 as a function of thickness, Θ, expressed as a number of pentacene monolayers (ML; 1 ML = 1.5 nm). At the early stages, corresponding to one to two monolayers, pentacene film grows layer-by-layer with nucleation of two-dimensional islands. At the sublimation rate used here, two-dimensional monolayer islands nucleate and grow on the second layer. The stable nucleus size and the nucleation density depend on the deposition rate and the surface tension of the substrate, whereas the distribution of the fractional coverage of each layer is a function of Θ (19). This film morphology is retained after exposure to water and cell culture medium, and there is no evidence for extensive molecular dissolution or reorganization (25).

Figure 1.

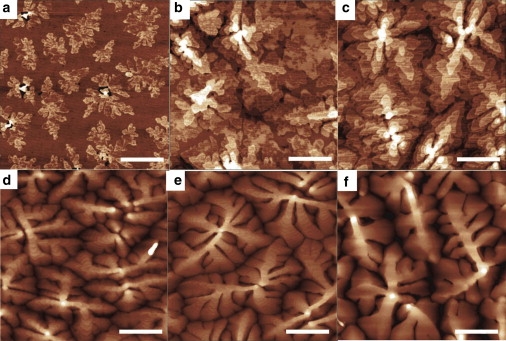
AFM images of pentacene thin films of varying thickness in monolayers (1 ML = 1.5 nm), (a) 1.5 ML, (b) 3 ML, (c) 6 ML, (d) 13 ML, (e) 26 ML, and (f) 65 ML. Scale bar: 1 μm.

Fig. 2 shows the trend of the rms roughness, σ, the correlation length, ξ, and the fractal dimension, d_f, versus Θ (for details, see Methods). Fig. 2 a shows σ from a large pentacene sample set, and its fit by a model obtained by numerical solution of the coupled growth equations of the stacking layers (not detailed here) (19). In a regime of layer-by-layer growth for Θ ≤ 2 ML, the model yields σ (nm) = 1.5 Θ^0.5 (1 − Θ)^0.5; for Θ > 2 ML, it predicts a power law scaling:

$$\sigma \left(\text{nm}\right)=-1.61\left(\pm 0.01\right)+2.00\left(\pm 0.01\right)\times {\mathrm{\Theta }}^{0.437\left(\pm 0.001\right)}\text{.}$$ (1)

Figure 2.

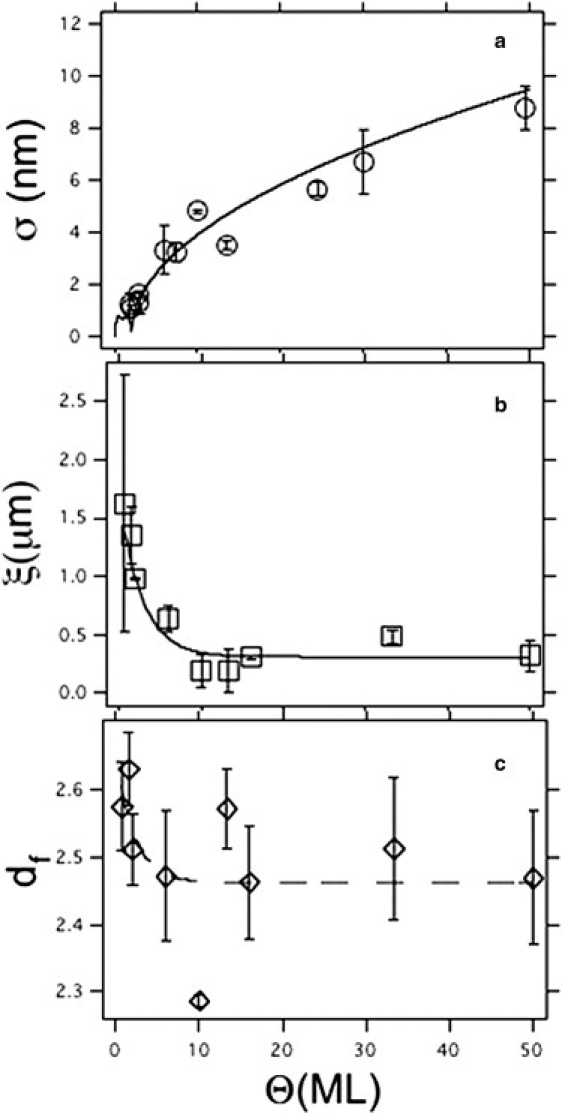
Surface morphological properties of pentacene thin films versus thickness Θ (in monolayers): (a) Roughness σ (circles); (b) correlation length ξ (squares); continuous lines are fitting curves with Eqs. 1 and 2 respectively. (c) fractal dimension d_f (diamonds). Dashed line is a guide to the eye. Error bars are rms fluctuations of the corresponding property measured from AFM images.

The correlation length, ξ, in Fig. 2 b decreases for Θ > 1 ML and saturates to a plateau when Θ ∼ 10 ML. This trend is fitted to the phenomenological equation

$$\xi \left(\text{nm}\right)=316\left(\pm 18\right)+1373\left(\pm 40\right)\times \exp \left(-\mathrm{\Theta }/2.8\left(\pm 1.4\right)\right)\text{.}$$ (2)

This behavior deviates from the simple power law scaling expected for self-affine behavior. Forcing a power law in the range where ξ decays yields ξ (nm) = 1444 (± 28) × Θ^{−0.55(±0.02)}. The fractal dimension, d_f, in Fig. 2 b decreases from 2.7 to 2.4. Although a precise trend is barely hinted at (see dashed line as guide to the eye), these values can be compared to the fractal dimension D, extracted from the perimeter versus area relationship (34) by d_f − 1 = D. The combined evidence indicates that a stationary morphological scaling is achieved for Θ > 10 ML. The decreasing value of the fractal dimension indicates that the topography is becoming more jagged, i.e., the higher frequency fluctuations increase in amplitude as three-dimensional stacking of monolayer terraces is enhanced (38). This 10 ML characteristic thickness may incidentally be related to the onset of a different growth mode and possibly to the transition from a thin film phase (39) to a bulk phase (22,40).

Cell viability, adhesion, and size assays were performed to investigate the influence of the pentacene surface morphology on the cell features. Fig. 3, a–c, shows typical images of 1321N1 astrocytoma cells cultured at different times on a bare pentacene organic thin film. The cells are viable and proliferate, as is apparent from their typical shape (Fig. 3, a–c, insets). The AFM image in Fig. 3 d shows that the morphology of the pentacene thin film near a cell is not damaged by interactions with the cell. As also observed with murine stem cells (25), the forces exerted by the astroglial cells are not sufficient to rupture the film or detach molecules from it.

Figure 3.

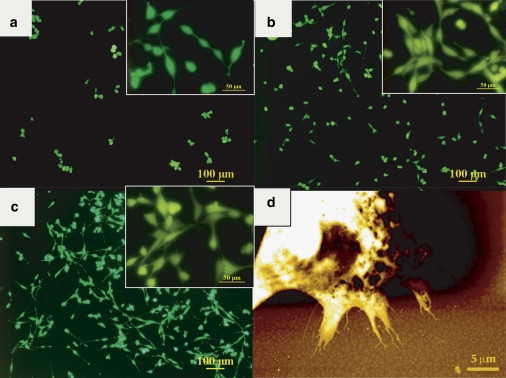
(a–c) Typical images of 1321N1 human astroglial cells grown on pentacene thin films with incubation times of 12 h (a), 24 h (b), and 48 h (c), stained with FDA vital dye and observed with an epifluorescence microscope (ruler 100 μm). Insets show details of the cell morphologies (ruler 50 μm). (d) AFM image of astroglial cell grown on pentacene thin film (6 ML thick) for 48 h upon standard conditions and fixed in 4% paraformaldehyde.

The cell adhesion on pentacene thin films was estimated as the fraction of cells attached 3 h after the seeding in serum-free conditions. The initial density of seeded cells was always 250 cells/mm². The results are shown in Fig. 4 for a large set of independent samples. The mean values (± SE as error bars) decrease from ∼24 ± 4 at <10 ML to 13 ± 3 at >30 ML. Although one-way ANOVA yields no significant difference among the data sets at different thickness for a level of confidence <0.2, the transition from higher adhesion at Θ < 10 ML to lower adhesion for Θ < 10 ML emerges clearly. The continuous line is the best fit of the data with a model of elastic deformation of the cell membrane, as detailed in the Discussion section. This model takes Eqs. 1 and 2 as input. As a comparison, control experiments were run on glass coverslips and silicon dioxide (SiOx) surfaces. The AFM (glass coverslips, σ = 2 ± 0.5 nm; SiOx/Si wafers, σ = 0.5 ± 0.2 nm) and contact-angle measurements (glass coverslips, 23 ± 2°; SiOx/Si wafers, 35.4 ± 7.6°). In relation to the results shown in Fig. 4, the cell adhesion was 81.2 ± 11.7% on glass coverslips, and 89.3 ± 9.5% on SiOx/Si wafers compared to the highest value, 24%, on pentacene (P < 0.01 for glass and silicon dioxide versus pentacene samples; one-way ANOVA, Bonferroni's multiple comparison test). Adhering 1321N1 cells on pentacene thin films exhibit a morphology similar to that on control culture surfaces. The average cytoplasmatic spreading areas of an astroglial cell on pentacene and glass do not differ significantly (323 ± 38 and 273 ± 24 μm², respectively; Student's t-test). The enhanced adhesion of SiOx with respect to pentacene can be ascribed to the different surface chemistry, indicating a preference of the cell for hydrophilic substrates.

Figure 4.

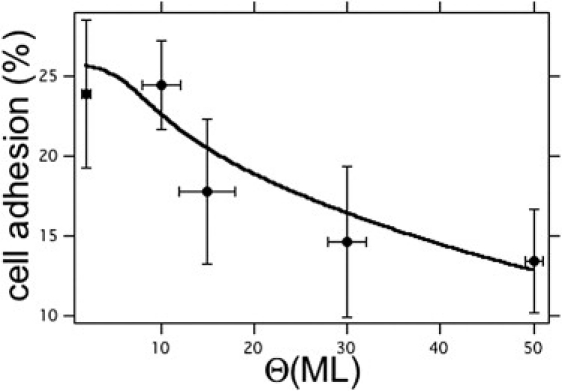
Astroglial 1321N1 cell adhesion versus pentacene film thickness. Circles are the mean's average percentage fraction of attached cells 3 h after the initial seeding of 250 cells/mm² in serum-free conditions. Vertical error bars are the standard error of the mean (SE), horizontal error bars represent the coarsegraining on thickness. The continuous line is the weighted best fit using Eq. 9.

To investigate cell proliferation, the cells were seeded on pentacene thin films of different thickness and allowed to proliferate up to 48 h in standard cell culture conditions. The evolution of the number of viable cells versus time and thickness is represented as a three-dimensional plot in Fig. 5 a. There, we have added as a reference the adhesion data from Fig. 4 at 3 h incubation in serum-free conditions. On the timescale, there is an initial lag in areal density of cells on pentacene, which is then recovered within 12 h. At fixed times, and varying the thickness, we observe an increased proliferation in the region of Θ < 10 ML, with the maximum around 4 ML. The highest proliferation rate (local slope) is observed in the same range. A rapid decrease of viable cells occurs as the pentacene film thickness increases to >10 ML. The samples of >30 ML thickness exhibit the slowest proliferation rate. The statistical test confirms that the data are significantly different in the high-density region (<10 ML) with respect to 65 ML (Student's t-test yields: at 12 h, P = 0.006 and 0.035 for 1.5 ML and 4 ML, respectively, versus 65 ML; at 24 h, P = 0.033 and 0.047 for 1.5 ML and 4 ML, respectively, versus 65 ML; at 48 h P = 0.049 and 0.032 for 1.5 ML and 4 ML, respectively, versus 65 ML). In Fig. 5 b, we show section profiles (normalized to the number of seeded cells at time t = 0) of Fig. 5 a versus time, for different thicknesses. The data at 3 h are taken from Fig. 4, and again we underline that these cells were incubated in a serum-free medium. For each thickness, there is a smooth trend of the time evolution, which can be represented with an exponential growth equation: viable cell %(t)= viable cell %(∞) − A exp(−t/τ). The characteristic timescale, τ, estimated for each thickness data set for cell proliferation is shown in the inset. The values of τ fluctuate around a mean value of 10 ± 2 h (Fig. 5 b, inset, dashed line), without exhibiting a clear trend versus Θ.

Figure 5.

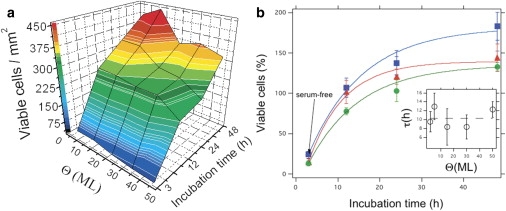
Viability and proliferation characteristics of Human 1321N1 astroglial cells on pentacene thin films. Cells were incubated for up to 48 h on pentacene films of varied thickness and tested by the Trypan blue exclusion test. (a) The three-dimensional graph showing density of viable cells/mm², versus thickness Θ (in ML) and incubation time (h). Maximum is for thicknesses <10 ML (respectively at 12 h, P = 0.006 and 0.035, 1.5 ML and 4 ML vs. 65 ML; at 24 h, P = 0.033 and 0.047 for 1.5 ML and 4 ML vs. 65 ML; at 48 h, P = 0.049 and 0.032 for 1.5 ML and 4 ML vs. 65 ML; Student's t-test, two-tailed, unpaired). The adhesion data at 3 h incubation in a serum-free medium has also been added. (b) Cell proliferation reported as the % of viable attached cells (with respect to seeded cells) versus time, for different Θ values: 4 ML (squares), 27 ML (triangles), and 65 ML (circles) The data at 3 h have been included. The solid line is the exponential fit using the equation: Viable cell %(t) = viable cell %(∞) − A exp(−t/τ). Inset: characteristic timescale, τ, versus Θ.

The viability of astroglial cell is correlated with the evolution of the cell death level, which is estimated by the Trypan Blue test (results not shown) as the percentage of necrotic cells over the total cell number. The cell death level was similar in pentacene thin films with respect to the control culture substrates, within 24 h (P > 0.05, one-way ANOVA, Bonferroni's multiple comparison test; n = 3). At 48 h, the cell death level doubles for pentacene films thicker than 30 ML. The cell death level on 65 ML pentacene film was significantly higher than that on thin films with thickness <15 ML (P = 0.031, one-way ANOVA, Bonferroni's multiple comparison test; n = 3). This is also significantly higher than the cell death level on the glass control surface (19 ± 3% pentacene 65 ML versus 10 ± 2% glass; P = 0.039). These results show that pentacene thin-film morphology for thickness <10 ML does not alter the death pattern of astroglial cells, whereas for the thicker films it does.

Discussion

Our results show that cell adhesion, viability, and proliferation are significantly influenced by the morphological parameters of the pentacene thin film, which we have explored systematically by controlling the film thickness across a wide range. Although it was recognized that the surface nanoscale topography affects cell-substrate interactions, most of the investigations dealt with micrometer-scale topography and saturated surface roughness (10,11). Our work shows that surface roughness is not the only relevant parameter. Nanoscale features and correlation of the topographical fluctuations, which are embodied in the self-affine morphology, are important in determining cell behavior.

The data set in Fig. 4 and Fig. 5 a, in combination with the morphology evolution in Fig. 2, clearly show that there is a crossover thickness, ∼10 ML, which on one hand separates the scaling from the saturated behavior of the correlation length and the fractal dimension and on the other represents the upper bound to the region of optimum adhesion and viability of cells. This strongly suggests that the cells are not sensitive exclusively to the saturated roughness (whose thickness dependence is monotonic above two MLs, as depicted in Fig. 2 a). The cells tend to adhere to substrates with large islands (>500 nm), modest roughness, and small fluctuations on the local scale, as higher fractal dimension reflects surface smoothness on the smaller lengthscales (38). For the deposition rate chosen, the thinner pentacene films have quasi-two-dimensional morphology, with a few monomolecular terraces piled up on top of large basal islands that form the first monolayers. Above the crossover thickness (10 ML), the pentacene film becomes jagged as the result of an extensive proliferation of terraces that enhances the three-dimensional growth. These figures suggest that the mechanism by which the cell senses the substrate features is manifold, involving not only the mechanical response to the shear forces exerted (41), but also the local interactions on lengthscales comparable to the monolayer terrace width, i.e., from a few tens to hundreds of nanometers.

An intriguing question concerns the mechanism by which the cells explore and sense nanometer surface topography. The first event, occurring at the early stages (e.g., 3 h), at the cell-material interface is the deformation of the cell membrane to conformationally adapt to the pentacene surface. The occurrence of this physical-chemical mechanism is indirectly supported by the large difference in cell adhesion between SiOx and pentacene, with the former mechanism known to be governed by the formation of focal contacts (43). On pentacene, the cell adapts its local curvature to the curvature of the pentacene layer to maximize the contact area. This elastic deformation has an energy cost that increases with the curvature of pentacene islands. Fig. 6 a depicts our simple approximation of pentacene islands as a closely packed ensemble of hemispherical caps whose width is approximated by the correlation length, ξ. The height, h, is measured above ν(Θ) fully occupied layers (the first two are shown in the schematics), and includes the uppermost fully occupied monolayer. We estimate h from the same model used for deriving the curve in Fig. 2 a, since it provides the occupancy of each layer Θ_n, and allows us to extract the exact stacking profile. It turns out that h is strictly correlated to σ, and we approximate it using the smoothly varying function

$$h\left(\mathrm{\Theta }\right)=1.5\left(\text{A}\mathrm{\Theta }+1\right)+\text{B}\sigma \left(\mathrm{\Theta }\right)\text{nm},$$ (3)

with the latter term given by Eq. 2. Best fit of the numerical h versus Θ yields A = 0.07 (± 0.09) and B = 4.8 (± 0.5). The radius of curvature, R, of the hemispherical cap is estimated from the chord theorem as

$$R=\left[h+\xi /\left(4\gamma \right)\right]/2,$$ (4)

where γ = h/ξ is the aspect ratio of the pentacene islands. An equivalent expression is given in terms of the contact angle, θ, formed by the tangent to the hemispherical cap at the crossing with the basal plane:

$$\theta =2\text{arctg}\left(\frac{\xi }{2h}\right)\text{.}$$ (5)

Figure 6.

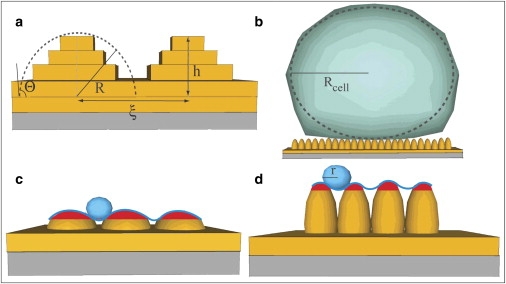
Schematic drawings of (a) pentacene islands growing on a complete pentacene bilayer. Lowest slab represents the substrate where the film grows. The island formed by terrace stacking is approximated as a hemispherical cap. The quantities are described in the text; (b) a cell sitting on a rough pentacene surface; The size reflects the ratio of the cell and pentacene length scales; (c) and (d) the effective contact area between the cell membrane and pentacene film for small (c) and large (d) pentacene film thicknesses is represented as a continuous line. The sphere of radius r represents the minimum curvature formed by deformation of the cell membrane.

It reads

$$R=\frac{\xi }{2\sin \theta }\text{.}$$ (6)

In Fig. 6 b, we schematically represent a cell sitting on a rough pentacene model surface. The cell membrane progressively relaxes and conformationally adapts to the rough surface. The effective surface accessible to the cell membrane is limited by the minimum radius of curvature, r, which the cell membrane can form by deforming itself locally and penetrating into the recesses between the islands. The effective surface is the envelope traced by a sphere of radius r rolling across the pentacene topography landscape. Fig. 6, c and d, depicts cross sections of the effective surface as continuous blue lines in the case of two different pentacene surfaces with a small and a large radius of curvature, R, respectively. The red area is the effective surface that can be accessed by the rolling sphere. The contact area between the cell and the pentacene surface is easily derived as

$$S_{\text{contact}}=2\pi R^2\left[1-\sqrt{1-{\xi }^2/4{\left(R+r\right)}^2}\right],$$ (7)

and the surface area of the whole hemispherical cap is

$$S_{\text{cap}}=2\pi R^2\left(1+\cos \theta \right)\text{.}$$ (8)

The areal density of adherent cells, N_cell, normalized to the initially seeded cells, N₀, will be proportional to the accessible areal fraction, which is given by the ratio between Eqs. 7 and 8:

$$\frac{N_{\text{cell}}}{N_0}=k\frac{1-\sqrt{1-{\xi }^2/4{\left(R+r\right)}^2}}{\left(1+\cos \theta \right)}\text{.}$$ (9)

We fit the data in Fig. 4 with Eq. 7, using the scaling constant, k, and the minimum radius, r, as fitting parameters. The best-fit continuous line in Fig. 4 corresponds to k = 27 (± 4), and r = 90 (± 44) nm. The curve suggests the crossover between the two different regimes at low thickness (smooth surface) and large (rough) surface. The minimum local feature that can adapt the cell curvature to the surface curvature is between 45 and 135 nm, i.e., 5–10 times smaller than the cell radius of curvature. This r value is within the range of cell membrane features and fusing vesicles on the membrane (∼30–40 nm) (42,44). Our model reproduces the experimental data quite satisfactorily, despite the large error bars. This suggests that at the early stage, the elastic deformation of the membrane, rather than the anchoring by means of surface-binding proteins expressed by the cell, is the dominant mechanism of interaction with the substrate, and that it may be driven by hydrophobic interactions.

To understand the occurrence of the transition in Fig. 4, we analyzed the radius of curvature, R, versus Θ (Fig. 7). R decreases with the film thickness from tens of micrometers at low Θ to a few hundred nanometers for Θ > 10 ML. The radius of curvature of the unperturbed cell, R_cell, is ∼5 μm (Fig. 7, horizontal dashed line). The decay of R undergoes three regimes: the first for R > R_cell up to Θ ≤ 4 ML; the second for R ≤ R_cell in the range 4 ML < Θ < 10 ML; and the third for R << R_cell at Θ > 10 ML. The first regime corresponds to optimum adhesion, as the cell feels a smooth surface; the second represents a transition regime; and the third represents lower adhesion, with the cell sensing a rough pin-bed surface. It is interesting to note that the onset of the third regime corresponds to the saturation of ξ. Since σ continues to increase, the radius of curvature will scale according to the roughness alone in this regime. It is also interesting to observe the contact angle, θ, of the pentacene island, reported on the right axis, which also exhibits three regimes in the same range: one with a very small angle, which implies complete conformity between the membrane and pentacene; an intermediate region in the range 5° < θ < 15°; and a faster rise at Θ >10 ML. Thus, both contact angle and radius of curvature hint at changes in the growth mode, an observation that is substantiated by the trend of the correlation length but not by the trend of the rms roughness. The evolutionary trends of R and θ support the schematic drawings in Fig. 6, c and d.

Figure 7.

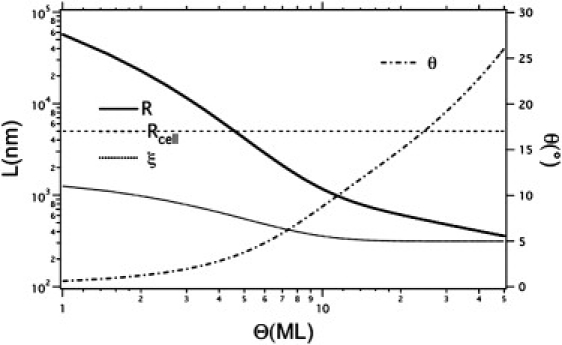
The left vertical axis indicates the lengthscale (L) versus thickness, Θ, where L represents either the radius of curvature, R, of the pentacene island as derived from Eq. 4 (solid line), the typical 5 μm radius of a cell (dashed line), or the correlation length, ξ (dotted line). The right vertical axis indicates the contact angle (θ) of the pentacene island (dot-dashed line), derived from Eq. 5, versus Θ.

It is interesting to note the resemblance of the cell adhesion dependence versus Θ to the Wenzel-Cassie transition described in the study of wetting/dewetting transitions occurring in roughening surfaces (45). There, the driving force is surface tension, whereas here it is the decrease of accessible area or, equivalently, the increase of elastic energy required. A link between the two phenomena could still be provided in terms of the increase of the surface energy, considering the cell membrane as hydrophobic: the less hydrophobic surface area increases due to proliferation of the terrace edges the hydrophobic basal plane remains geometrically invariant and becomes progressively less accessible as the terraces stack. Therefore, we expect the effect of surface and elastic energy to be correlated, since both depend on film thickness.

At later times, the cell expresses the adhesion proteins and forms focal adhesion contacts. Protein deposition will initiate at the conformational interface between the cell and pentacene. The proteins can probe the smaller lengthscales (46–49) of the pentacene surface, e.g., the terrace edges whose height is on the order of a few nanometers. In this case, the substrate structure determines the type and conformation of surface-binding proteins (46,47) and sets the timescale for proteins to diffuse across the cell membrane and adsorb onto pentacene to form the focal contacts. A quantitative discussion on the interplay between morphology of the pentacene thin film and protein diffusion across the conformationally attached cell membrane requires a detailed description of the model of growth and goes beyond the scope of this work. However, it is interesting that the data points in Fig. 5 exhibit a trend resembling that in Fig. 4, and that the characteristic timescale does not differ substantially from one pentacene surface to another.

Our work also demonstrates that pentacene ultrathin films behave as biocompatible substrates for cells for thicknesses <10 ML. A recent work (50) reported the cytotoxicity of pentacene toward mouse fibroblast cells, for films 60 nm thick (∼40 ML). These results do not conflict with the finding in this work of increased necrosis at large thicknesses. From this and our previous work (25), we infer that pentacene ultrathin films make cells viable for several days, allowing the cell culture to achieve confluence culture conditions. This strongly suggests that the toxicity of pentacene depends not only on the chemical nature but subtly on its organization across lengthscales. Factors related to the three-dimensional pentacene structure that may cause toxicity are, for instance, the ease of detachment of molecules from the edges of small terraces and their incorporation by the cell, or the increased production of singlet oxygen, a known cytotoxic agent, by exposure of pentacene to light.

One advantage of using pentacene as a model substrate is the accurate control of the morphological lengthscales by means of the growth parameters. The fine tuning of the growth process can be used to modulate cellular responses and to control cell viability and proliferation. The optimum range for building a functional pentacene layer for human astroglial 1321N1 cell growth in vitro is <10 ML. This allows minimization of the amount of functional material needed for fabricating the substrate, also reducing the toxicological risks.

Conclusions

We have investigated how the surface morphological properties of pentacene affect cellular behavior by comparing human 1321N1 astroglial cell adhesion and proliferation on pentacene thin films while systematically varying the film thickness. We show that cells adhere and proliferate on bare pentacene thin films, and exhibit higher adhesion and optimum viability for pentacene films with thickness <10 ML, which correlates to a marked preference for larger correlation lengths and larger fractal dimensions, rather than for a specific surface roughness.

Our observation regarding adhesion is explained by means of a conformational adaptation of the cell membrane to the pentacene surface. As this implies an elastic deformation of the cell membrane, the energy cost will depend on the local curvature of the pentacene surface. The radius of curvature of pentacene islands will decrease for Θ > 10 ML due to the saturation of the correlation length and the increase in the rms roughness. In this case, a change of a few nanometers in the surface roughness can lead also to substantial changes in the pentacene radius of curvature and hence to a substantially decreased area accessible to the cell. The trend for cell viability mimics that just described for cell adhesion, though the mechanism may be entirely different. Here, we highlight the observation that optimum viability is achieved for ultrathin films. This finding hints that a technology capable of controlling the multiscale morphology of ultrathin films is attractive also for engineering substrates for cell research, sensing interfaces, and tissue engineering.