Electrostatics of Deformable Lipid Membranes

Abstract

It was recently demonstrated that significant local deformations of biological membranes take place due to the fields of charged peptides and ions, challenging the standard model of membrane electrostatics. The ability of ions to retain their immediate hydration environment, combined with the lack of sensitivity of permeability to ion type or even ion pairs, led us to question the extent to which hydration energetics and electrostatics control membrane ion permeation. Using the arginine analog methyl-guanidinium as a test case, we find that although hydrocarbon electronic polarizability causes dramatic changes in ion solvation free energy, as well as a significant change (∼0.4 V) in the membrane dipole potential, little change in membrane permeation energetics occurs. We attribute this to compensation of solvation terms from polar and polarizable nonpolar components within the membrane, and explain why the dipole potential is not fully sensed in terms of the locally deformed bilayer interface. Our descriptions provide a deeper understanding of the translocation process and allow predictions for poly-ions, ion pairs, charged lipids, and lipid flip-flop. We also report simulations of large hydrophobic-ion-like membrane defects and the ionophore valinomycin, which exhibit little membrane deformation, as well as hydrophilic defects and the ion channel gramicidin A, to provide parallels to membranes deformed by unassisted ion permeation.

Introduction

Ion permeation across biological membranes is vital for electrical and chemical activity in all organisms, as well as for maintaining ionic gradients and osmotic flow of solvent (1). Although rapid and selective permeation is catalyzed by specific channel proteins (2,3), unassisted ion permeation across lipid membranes is also of substantial biological significance (4). The interaction of charged protein groups with the membrane is also characteristic of many important processes, including the actions of cell-penetrating (5), antimicrobial (6), and viral peptides (7); toxins (8); and voltage-gated ion channels (9). The ability of charges to associate with or translocate membranes is therefore a fundamental biological phenomenon that needs to be understood at the microscopic level.

Biological membranes are complex dynamical structures (10), with hundreds of different species of lipids, proteins, and other amphiphilic molecules undergoing fluctuations over a wide range of timescales and length scales (11) and exhibiting various phase states and microdomain behaviors (12,13). Although the microscopic structure of membranes is well understood, traditional arguments about permeation phenomena have pictured the membrane as a simplified slab-like structure that consists of a purely hydrophobic core segregated away from the aqueous phase. This “standard model” of membrane permeation, which was pioneered by Parsegian in the 1960s (14), assumes that the energy required to move an ion across the membrane is that due to the Born solvation energy associated with moving from a high-dielectric aqueous environment (ɛ ≈ 80) to low-dielectric lipid hydrocarbon (ɛ ≈ 2). In addition, the membrane presents interfaces between distinct solvents and an alignment of phospholipid headgroups and interfacial water, giving rise to the membrane dipole potential (a positive potential of ∼200–500 mV (15,16) inside the membrane). If this were the case, the membrane would exhibit a significant intrinsic selectivity for anions over cations (17–19) that would be inconsistent with recent observations (I. Vorobyov, T. W. Allen, O. S. Andersen, and R. Koeppe, III, unpublished results).

It has long been predicted (14) and recently shown via all-atom molecular dynamics (MD) simulations that membranes deform substantially due to the presence of an ion (4,21–25), such that the ion may remain at least partially hydrated, even at the center of the membrane (e.g., see Fig. 1 A for the arginine (Arg) side-chain analog, MGuanH⁺, where at least one to two lipid phosphate and four to six water oxygen atoms coordinate the ion (24)). The potential of mean force (PMF) of MGuanH⁺ across a lipid bilayer, from fully atomistic simulations (26), exhibits a distinct “Λ” shape and climbs to ∼21 kcal/mol (Fig. 1 B, black curve). Although the energetic cost is still very large, as a result of local membrane deformation it is considerably lower than continuum rigid-slab estimates (see Fig. S1 A of the Supporting Material). In fact, removal of the free-energy contributions from polar components (lipid headgroups, water, and ions) inside the membrane (Fig. S3 C) leads to an estimate of what the PMF might look like for an unperturbed bilayer (21,24). This estimate is similar to continuum predictions for a slab-like geometry and reveals that the barrier has been reduced by up to 40 kcal/mol due to local membrane deformations.

Figure 1.

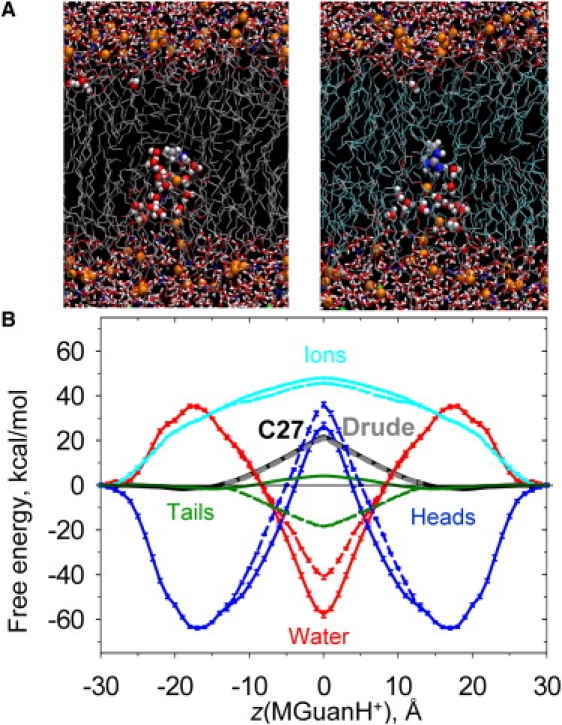
(A) Snapshots of MGuanH⁺ inside a DPPC bilayer (at z ≈ 0 Å) from nonpolarizable C27 (left) and Drude polarizable C27+pol1 (right) simulations. (B) PMFs (solid black curve: C27; dashed gray: Drude; taken from Vorobyov et al. (26)) and corresponding free-energy components from mean force decomposition (solid curves: C27; dashed curves: Drude). Error bars represent standard errors of means from block averaging.

In previous work (26), we also explored the role of explicit treatment of electronic polarizability in water/hydrocarbon partitioning and lipid permeation energetics. This effect is expected to be the most profound for lipid hydrocarbon tails, which in the nonpolarizable CHARMM (C27) model has ɛ∼1 instead of ∼2, and to be less important for polar moieties such as lipid headgroups and aqueous solution, as well as for the ion itself (26). We demonstrated that the different dielectric responses of polarizable and nonpolarizable hydrocarbon models would lead to a sizeable change in the MGuanH⁺ solvation free energy (∼20 kcal/mol more negative for the polarizable model) in nonpolar solvents such as cyclohexane (cHex) (26). Given that the benefit of deforming a membrane is of similar magnitude (although larger), we questioned whether an ion could enter a bilayer without deformation if that bilayer was described with a polarizable model. However, very similar bilayer perturbations occurred (Fig. 1 A), though with slightly less deformation (see Fig. S2 B and Fig. S3 A). Surprisingly, the PMF was almost unaffected (Fig. 1 B, gray curve) (26), contrary to previous suggestions that the barrier may even be halved (4). This outcome intuitively suggests that dehydration (and subsequent solvation by hydrocarbon) must not be a significant factor for permeation. Moreover, the energetics of K⁺, Na⁺, and even Cl⁻ are similar to that of MguanH⁺ translocation, despite widely differing hydration free energies (I. Vorobyov, T. W. Allen, O. S. Andersen, and R. Koeppe, III, unpublished results) (4,27,28). It is fascinating that the free energies of lipid flip-flop are similar to that of ion translocation, which intuitively suggests that permeation must be dominated by the energetic costs of deforming the membrane (29). However, this explanation appears oversimplified given the observed rapid changes in ion-membrane interactions (24), and thus warrants further investigation.

Differences in membrane permeability of large, hydrophobic ions such as tetraphenyl-borate (TPB⁻) and tetraphenyl-arsonium (TPA⁺) have been used for the experimental measurement of dipole potentials (30,31), in addition to techniques such as cryo-electron microscopy (16) and electrochromic dyes (32,33). The dipole potential can also be calculated from fully atomistic MD simulation, yielding ∼910 mV for the nonpolarizable C27 force field (34) (being roughly twice the experimental estimates, e.g., 510 mV from cryo-electron microscopy (16)), but it varies widely with the force field (16,35,36). We have shown that the inclusion of explicit polarizability for lipid hydrocarbon tails in the C27 model provides a lower dipole potential (∼500 mV), in agreement with experiment (34). The dipole potentials obtained with nonpolarizable and polarizable models are different in both shape and magnitude (see Fig. 5, solid and dashed green lines, to be discussed below). We found that the change in magnitude (and shape) is predominantly due to different lipid tail contributions (by ∼1 V) (34), with a result similar to that predicted by a recent monolayer study using explicit water and lipid headgroup polarizability as well (37). Although previous studies incorporated the dipole potential into continuum membrane models (38,39), it has been suggested that it may not play a significant role in ion permeation energetics, as a result of shielding by the partial hydration environment maintained around the ion (17). However, we will show that, due to disruption of the membrane interface alone, this potential is not fully sensed by an ion. Remarkably, although the decreased dipole potential for the polarizable membrane (by ∼400 mV) should have led to a ∼9 kcal/mol drop in the barrier faced by a cation, this was not seen in the PMF.

Figure 5.

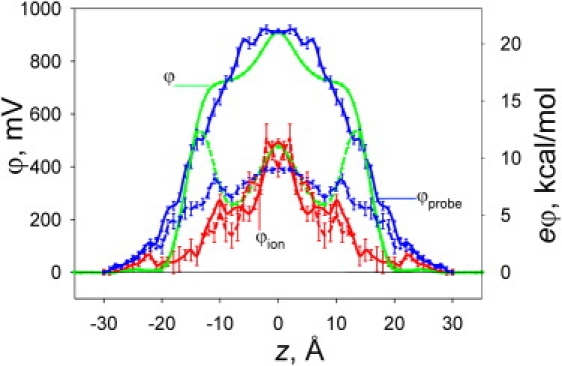
Electrostatic potential, ϕ, and corresponding energy, eϕ, across a DPPC bilayer (with z = 0 Å at its center) from C27 (solid lines) and C27+pol1 (dashed lines) simulations sampled by a test point charge (ϕ; taken from Vorobyov and Allen (34)), a discharged MGuanH⁺ probe (ϕ_probe; taken from Vorobyov and Allen (34)), or MGuanH⁺ ion across the bilayer (ϕ_ion). Error bars represent standard errors of means from block averaging.

Since large hydrophobic ions are actually used to measure the dipole potential, this implies that they may not deform the membrane to the same extent, and that traditional models of membrane permeability (14) may still hold. We carried out simulations of lipid bilayers containing model hydrophobic defects or the ionophore valinomycin (VM) (40) as analogs of large hydrophobic ions with less membrane deformation (30). To gain a basic understanding of the effects of membrane deformations on electrostatics, we also explored bilayers perturbed by model hydrophilic defects that bear a resemblance to the case of unassisted ion permeation, as well as transient pores and ion channels. We also investigated the dipole potential felt by an ion translocating through the ion channel, gramicidin A (gA) (41), to provide an interesting comparison with deformed bilayer electrostatics.

Materials and Methods

For this study, we used the CHARMM program (42) with the C27 force field (43,44), which provides accurate bilayer structure (35,43), hydration free energies, and ion-lipid interactions (26). A classical Drude oscillator model (45) was employed to investigate the role of electronic polarizability, which was introduced by adding auxiliary charged particles to nonhydrogen atoms via harmonic springs. Drude polarizable alkane partial atomic charges and polarizabilities (46) were applied to lipid hydrocarbon tails in the C27+pol1 model, whereas C27 charges (43) were used for the C27+pol2 model to isolate the effect of polarizability (Table S1). These polarizable models provide the correct dielectric response for liquid hydrocarbons (46) and an accurate solvation energy for MGuanH⁺ in cHex (26), thus eliminating a major shortcoming of the C27 force field. Previous calculations of bilayer structural properties using this polarizable model revealed no significant changes (34). The VMD program (47) was used for visualization, and further simulation details are provided in the Supporting Material.

Membranes of 48 dipalmitoylphophatidylcholine (DPPC) lipids, using hexagonal periodic boundary conditions (PBC) and hydrated by ∼45 waters/lipid and 0.5 M KCl, were simulated. Although ion translocation is influenced by other components that can change the structure and mechanical properties of a membrane (12), we first aimed to understand the process of crossing a pure lipid bilayer. Simulations of MGuanH⁺ translocation (24) were analyzed for structure, interactions, electrostatics, and free-energy contributions. Simulations were also carried out using a discharged MGuanH⁺ solute to probe electrostatics without bilayer perturbations due to the charge, at 1 Å increments across the membrane using ∼3 ns of simulation for each position (sufficient for a neutral solute). The bilayer was also perturbed by placing hydrophobic defects (spherical voids modeled by 10 kcal/mol/Ų flat-bottom constraints) of different radius (1–10 Å) at the bilayer center and simulated for ∼5 ns. Lipid bilayers were also perturbed by water-filled spherical cavities (hydrophilic defects) with radius 2–10 Å, by constraining a number of water molecules (1 to 140, corresponding to bulk density) by 10 kcal/mol/Ų flat-bottom constraints, simulated for 20 ns each.

To study the effect of an ionophore on the dipole potential, VM was held at the bilayer center (z = 0 Å) and in bulk solvent (z = 40 Å, and other positions not shown) by a 5 kcal/mol/Ų planar constraint, with a similar cylindrical constraint used to prevent drift in the xy plane. Lipid bilayers consisting of 78 or 80 DPPC molecules (for VM at z = 0 or 40 Å, respectively), 5278 or 5216 waters, and 98 or 97 K⁺Cl⁻ ion pairs were simulated. The crystal structure for a bound configuration in nonpolar solvent VM (48) was used as the initial geometry and maintained in the absence of a K⁺ ion using a 10 kcal/mol/Ų root mean-square deviation constraint. Each system was simulated for ∼10 ns using tetragonal PBC at 330 K and 1 atm normal pressure, with 5–7 ns of equilibration. The gA channel peptide (PDB: 1JNO (49)) was embedded in a bilayer of 20 dimyristoylphosphatidylcholine (DMPC) molecules, 1080 water molecules, and 19 K⁺Cl^- pairs for direct comparisons with published results (50). The K⁺ ion PMF through the gA channel using a polarizable lipid hydrocarbon (C27+pol2, to isolate lipid tail polarizability) was calculated as described previously (50), using 81 simulations of 2–2.5 ns.

The electrostatic potential, ϕ, is expected to be uniform in the xy plane for unperturbed bilayers and was calculated by double integration of the electron density from charge distributions (34,51). Otherwise, 3D ϕ maps were obtained using the PMEPOT (52) module of VMD (47) with a ∼1 Å grid. Charge densities were smeared using Gaussian distributions with the smearing factor, κ, varied from 0.25 to 1.25 Å⁻¹ in ∼0.10 Å^-1 increments (explored in Fig. S4). The 1D and 2D profiles were extracted by means of trilinear interpolation and, where specified, axial symmetry was imposed. To estimate peptide dielectric shielding of the dipole potential, calculations using the dielectric constant ɛ_p were performed for VM and gA with the use of the Poisson-Boltzmann (PB) solver, PBEQ, of CHARMM. For VM and gA (with its pore water molecules), an approximate value of ɛ_p was determined (see Supporting Material).

Results and discussion

Membranes deformed by hydrophobic and hydrophilic defects

We begin by systematically exploring the effects of various model defects on the membrane's structure and electrostatics to help explain the results for unassisted and assisted ion permeation discussed further below. Hydrophobic defects were created by simulating vacuum-filled cavities of different radii (Fig. 2). These defects are likely relevant to hydrophobic ion and ionophore permeation (30,40), where we anticipate limited bilayer deformation. Hydrophilic defects, which maintain water molecules inside the membrane core (Fig. 3), may teach us much about unassisted ion permeation, transient pores, and possibly ion channels.

Figure 2.

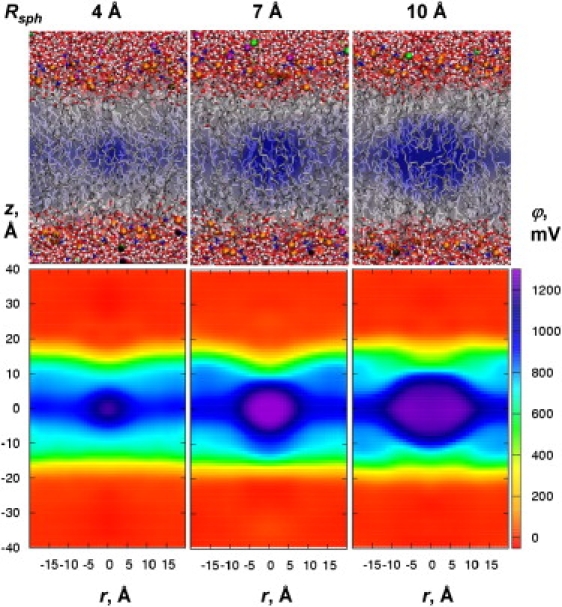
Electrostatic potentials for DPPC bilayers with hydrophobic defects of radii R_sph at the bilayer center from C27 simulations. Final snapshots superimposed with average potential map slices in the xz plane are shown in the upper panels. 2D maps as a function of z and distance r from the z axis are shown in the bottom panels (obtained using PMEPOT with smearing parameter 0.34 Å⁻¹). For a complete set of results, see Fig. S5.

Figure 3.

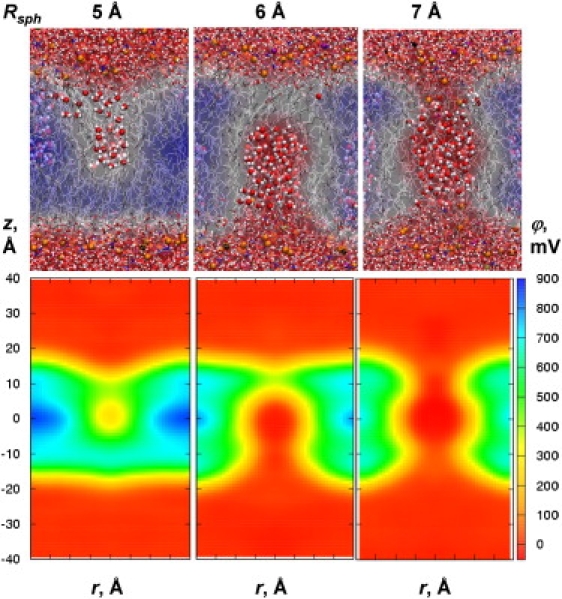
Electrostatic potentials for DPPC bilayers perturbed by hydrophilic defects of radii R_sph from C27 simulations. Snapshots and average potential slices are superimposed in the upper panels, and axially averaged maps are shown in the bottom panels. For a complete set of results, see Fig. S8.

The electrostatic potential maps for hydrophobic cavities of radius 1–10 Å (e.g., Fig. 2) reveal little membrane deformation and no protrusion of polar groups into the membrane core. The potentials are larger than the dipole potential, by up to 400 mV (reaching ∼1300 mV), and do not vary substantially with defect size for R > 4 Å (for smaller R there is some dependence, depending on the smearing; Fig. S6). Such an increase is due to the formation of an interface with lipid hydrocarbon, approximately equal to a hexane-air boundary (34). This does not mean, however, that an ion would necessarily feel such an additional potential, because it would be canceled by a similar air-water boundary that exists when the defect is in aqueous solution (for the C27 force field, water-air and hexane-air potentials differ by only ∼90 mV (34)). This cancellation of water-air and hydrocarbon-air interfacial potentials occurs because of the dominance of similar quadrupolar contributions to these solvent-air potentials (34,51,53).

Based on these calculations, we can predict that the dipole potential seen by a large hydrophobic ion or ionophore might be ∼820 mV for nonpolarizable C27 and ∼350 mV for C27+pol1 polarizable models, respectively. Then, allowing for dielectric shielding by the ion itself (likely with ɛ_ion∼2 for TPB⁻, TPA⁺ ions or VM; see “Membranes deformed by ionophores or ion channels” below), the potential actually felt by the central charge (using either the C27 or C27+pol1 model) would be consistent with the experimental estimates of ∼230-350 mV (15). We remark that the experimental value contains some uncertainty because of assumptions made for the solvation free energies of the hydrophobic ions (15).

Although these changes due to hydrophobic defects may tell us about the situation in which the membrane is largely unperturbed, this situation may have little in common with the case of small ions, transient pores, or channels. For the hydrophilic defects shown in Fig. 3, a number of water molecules were confined at the membrane center while other water molecules, ions, and lipids were free to move in and out of those spheres. For radii 2–4 Å, there were no substantial changes in lipid bilayer structure (Table S2). For the 5 Å sphere, a connection to the membrane interface began to form, as evidenced by the protrusion of 16 additional water molecules and ∼0.5 headgroups into the bilayer core (Table S3). Lipid phosphates penetrated as deep as 4 Å from the bilayer center (Table S4). Once water defects occurred, lipid headgroups spontaneously entered the bilayer (i.e., the work to deform the bilayer was already done). Greater bilayer perturbation took place for the 6 Å sphere, encompassing 30 constrained waters. On average, an additional 35 waters and 1.7 phosphates moved to the core in that case. For hydrophilic defects of radius ≥7 Å, a complete water pore across the bilayer was formed, with many additional water molecules (53–97 for radii 7–10 Å) moving into the core. On average, 2.2–3.5 lipid phosphate groups, 0.2–0.8 K⁺, and up to 0.15 Cl⁻ ions penetrated into the core. K⁺ and Cl⁻ ions could move freely to the membrane center, which was not seen for membranes with a connection to only one interface (Table S4). Membranes with continuous pores may reasonably reflect the case of transient pores or ion channels.

The 2D potential maps in the lower panels of Fig. 3 (and 1D profiles in Fig. S7 B) indicate that the perturbations due to hydrophilic defects have a profound effect on the membrane electrostatics. The formation of an interfacial connection for the defect of 5 Å leads to a drop in potential to <300 mV due to high dielectric shielding (and a small water-hydrocarbon interfacial contribution (34)). For the larger defect of 6 Å, the potential drops to nearly 0 mV and is completely eliminated for radius ≥7 Å, where a continuous pore is formed. Therefore, these pores are expected to be largely nonselective, as evidenced by the penetration of both K⁺ and Cl⁻ ions into the membrane center, with a slight preference for cation permeation (17). An ion traveling through a wide water-filled pore likely would not experience the dipole potential, as suggested by continuum models (38) and in marked contrast to the case of a hydrophobic ion or ionophore.

Membranes deformed by small ions

When a small ion, such as MGuanH⁺, is located in the membrane core, it is still coordinated by water molecules and lipid headgroups, and forms an interfacial connection similar to that observed for hydrophilic defects (compare Figs. 1 A and 3, upper left panels). We now present an analysis of the solvation and perturbed membrane electrostatics that may help explain the remarkable insensitivity to ion type and membrane electronic polarizability.

Free energy (mean force) decompositions (54) can reveal how different membrane components contribute to translocation energetics. The contributions from only those polar components that are drawn into the bilayer core (Fig. S3 C) reveal the remarkable ability of a limited number of water molecules to stabilize charges away from the aqueous phase, and suggest that it is costly to pull lipid headgroups deep inside the membrane (21). The effect of polarizability is a reduced stabilization by core-located water and a larger destabilization by core-located headgroups, which presumably is compensated for by an increased lipid hydrocarbon dielectric stabilization.

We can better resolve the contributions from membrane components by computing the free-energy contributions from all molecules (not just those groups that entered the membrane core), as shown in Fig. 1 B. Now evident are the trade-offs in different regions of the bilayer. In the interfacial region, the water contribution is smaller than bulk (by up to ∼35 kcal/mol), which, combined with reduced interactions with ions, leads to a significant destabilization. This is annulled by a large attractive contribution from lipid headgroups, resulting in slightly favorable binding at the interface. The contributions of water and headgroups are reversed near the bilayer center, with the lack of ionic contribution in the membrane also playing a significant role. However, lipid tails have little influence in the nonpolarizable simulations.

As a result of incorporating electronic polarizability (dashed curves), the water contributions become less stabilizing by ∼16, while the lipid headgroup contributions become more destabilizing by 10 kcal/mol, at the bilayer center. The contribution from lipid tails is ∼4 kcal/mol using C27, and −19 kcal/mol for the polarizable model. This ∼23 kcal/mol stabilization is remarkably similar to that predicted by continuum and water-cHex partitioning energetics (26), and, to within the errors, provides a canceling contribution for the reduced interactions with polar groups. As a result of this trade-off, there is little net change due to electronic polarizability.

Included in these free-energy terms are contributions from long-range electrostatics due to the deformable membrane, as we now explore. The potential maps in Fig. 4 are somewhat reminiscent of those in Fig. 3, i.e., the membrane deformation causes a substantial disruption of the dipole potential. As the ion moves deeper into the membrane core, causing greater perturbations, there is a reduction in the potential experienced by the ion, relative to the unperturbed membrane occurs. We observe that as the ion (indicated by the asterisk in the lower panels of Fig. 4) perturbs the membrane, it is always located at the interface between the low-potential aqueous region and the high-potential bilayer core region. Because the ion remains hydrated and does not completely cross this interface (it just reshapes it), it does not experience the full dipole potential (see Movie S1 and 1D plots in Fig. S10).

Figure 4.

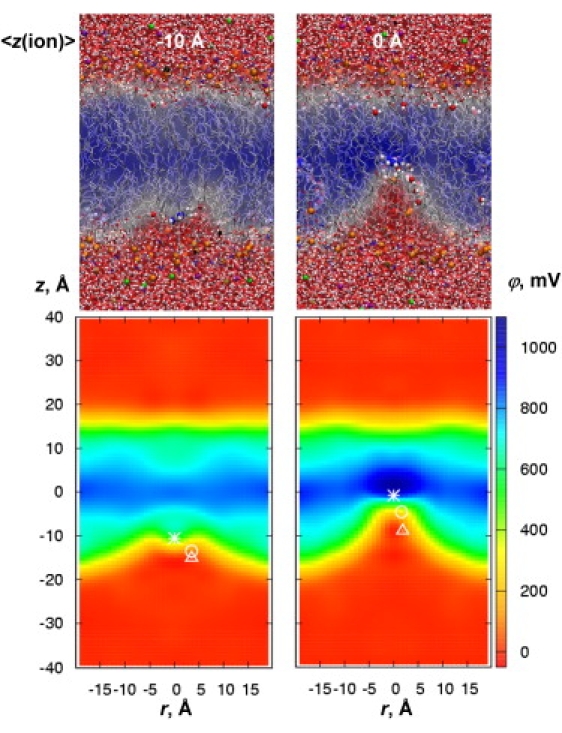
Snapshots and 2D electrostatic potential maps for MGuanH⁺ constrained around z = −10 or 0 Å in a DPPC bilayer using the C27 model. The average positions of the MGuanH⁺ guanidine C atom and its closest DPPC P and N atoms are shown as an asterisk, circle, and triangle, respectively. See Fig. S9 for C27+pol1 polarizable model results and additional C27 maps.

Additional evidence that the full dipole potential is not felt can be found by calculating ϕ_ion at the position of the MGuanH⁺ ion across the membrane (Fig. 5, red curves). We compare ϕ_ion to the dipole potential ϕ (as seen by a point charge (34)), as well as ϕ_probe for a neutral MguanH⁺-sized probe in Fig. 5. When the ion has entered the interfacial region (i.e., for |z| ∼15 Å), ϕ_ion is drastically reduced compared to that in the absence of the charge (from ∼500 down to <100 mV; compare blue and red curves in Fig. 5). Even at the center of the membrane, ϕ_ion for C27 remains as low as 500 mV (just over half of the C27 dipole potential). Intriguingly, a similar profile was obtained for the polarizable model (Fig. 5, dashed red curve). Whereas there were dramatic changes in the dipole potential for the unperturbed membrane, the effect of polarizability for the perturbed membrane is almost nonexistent. This, combined with compensation between the polar and hydrocarbon solvation contributions, explains the lack of effect of lipid tail polarizability on the PMF.

Our observation that the ion does not really cross the membrane interface, because as it enters the membrane it is continually forming a new interface, has significant implications. The first is that the ion never experiences the drastic change in potential across the interface. The second is that the ion is always located in a place of greatest electric field. It is the work done against this nearly constant electric field that maps out the unusual Λ-shape of the PMF for permeation (see Fig. 1 B, black curve). This observation leads us to further deductions. We note that as MGuanH⁺ moves into the membrane core, it leaves a region of low potential, and almost zero electric field in its wake (e.g., see Fig. 4 and 1D plots in Fig. S10). Therefore, if a second ion were to trail behind MGuanH⁺, it would experience little electric field pushing it back into the bulk solvent, resulting in little additional penalty for membrane translocation. We notice that the lipid phosphates that coordinate the ion (shown as circles in the lower panels of Fig. 4 and Fig. S9) almost always reside in the wake of the penetrating ion. Fig. S10 shows that although the phosphate resides in a region of lower field, it still experiences some force and the associated energy cost. However, the choline on the headgroup (triangles) is located farther behind in a region of almost zero electric field. It is this second positive charge that would enter the membrane, behind the leading charge, with essentially no additional energetic cost. We predict that the binding of the ion to a lipid with no choline group (e.g., an anionic lipid such as phosphatidic acid, phosphatidylserine, or phosphatidyglycerol), in place of a zwitterionic lipid, would lead to essentially no change in the free-energy profile for ion permeation, which we have now confirmed (I. Vorobyov and T. W. Allen, unpublished results). Similarly, if one were to move two cations (di-arginine or even a poly-cationic peptide (7)), one might anticipate an energy cost not much different from that of a single ion (55), where we predict that only the leading charge would experience a significant force expelling it from the membrane. This “leading-charge” picture of membrane translocation may also explain the similar energetics of zwitterionic lipid flip-flop (29).

Membranes deformed by ionophores or ion channels

Ionophores and ion channel proteins are thought to help reduce the barrier for an ion to cross a lipid membrane by shielding it from lipid hydrocarbon by a protein and/or aqueous pore. Not only would this diminish the dehydration costs, it might also reduce the dipole potential seen by an ion.

First, we examine the ionophore VM, which to some degree mimics a large hydrophobic ion. The VM molecule was simulated in bulk water and the bilayer center (see Fig. 6 for snapshots and potential maps). For the purpose of this illustration, we constrained VM in the conformation corresponding to its ion-bound crystal structure (48). This may not correspond to the actual permeation process (currently under investigation), but provides a suitable model that mimics a large hydrophobic ion. We observe little bilayer deformation around the ionophore. Our results indicate that the potential at the VM center (asterisks in Fig. 6) is very similar in bulk water and the bilayer center, and is ∼300 mV relative to bulk solvent (Fig. 6, central panels). This indicates that a K⁺ ion inside VM (constrained in this hypothetical bound configuration) would not feel a change in potential across the membrane. However, this appears to be due to water polarization around VM, as revealed by the ∼1500 mV potential in the absence of a peptide contribution (Fig. 6, top right panel), which is much greater than that for a typical water-air interface (∼500 mV (34)).

Figure 6.

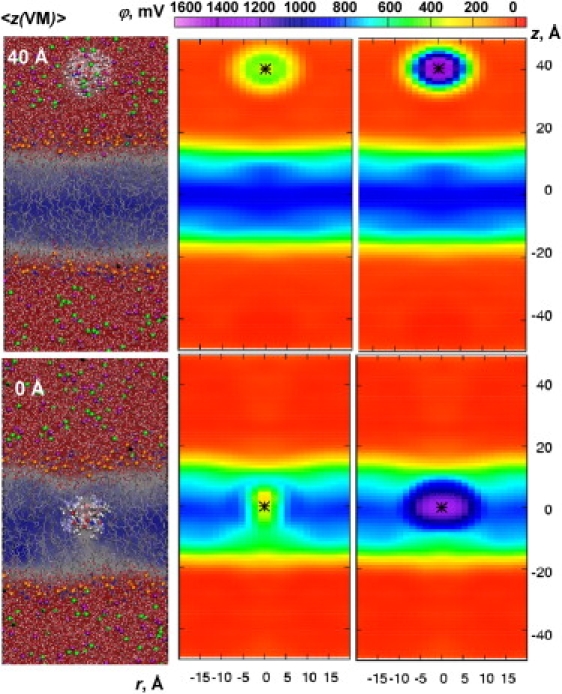
Snapshots and 2D potential maps from C27 simulations of VM constrained in bulk solvent (z = 40 Å) or membrane center (0 Å). The VM contribution is excluded in the right panels. The average position of VM center (defined as center of geometry of six ester carbonyl oxygen atoms) is shown as a black asterisk.

Excluding the peptide contribution, to remove stabilization from its own charge distribution, creates an artificial vacuum-lipid boundary at the bilayer center and elevates the potential to ∼1250 mV (Fig. 6, bottom right panel), which is similar to the dipole potential plus a hydrocarbon-air interface seen by hydrophobic defects (Fig. 2). By assigning a dielectric constant to the peptide, we can estimate the extent to which the dipole potential would be shielded. In the Supporting Material we estimate a VM dielectric constant of ∼2 using the C27 model (likely underestimated due to lacking electronic polarizability), which suggests that dielectric shielding will be small for this fairly rigid molecule. The ∼900 mV dipole potential of the C27 model will likely be reduced by a factor of ∼2 due to peptide shielding. MD-averaged potentials with different assignments of ɛ_p, shown in Fig. S11 B, reveal a drop from 1250 to ∼800 mV for ɛ _p = 2 (subject to the method used to assign ɛ on the grid). Thus, the dipole potential that is actually “seen” by this “large hydrophobic ion” is still significant and likely is similar to that estimated from experimental measurements (∼350 mV) (15), after accounting for the presence of an air-lipid interface (∼−420 mV (34)).

Now we turn to the case of the prototypical ion channel, gA. The channel was simulated in a DMPC bilayer using both nonpolarizable C27 and Drude polarizable (C27+pol2) models (see snapshots in Fig. 7 B and Fig. S12). The K⁺ ion PMF through the channel (Fig. 7 A, cyan) has been shown to exhibit a barrier of ∼11 kcal/mol with respect to the binding site at 11.3 Å, which is too high for agreement with flux measurements (56). However, the model suffers from artifacts owing to the finite size of the periodic membrane patch (∼1.6 kcal/mol (50)) and the inadequate description of hydrocarbon polarizability (56). The effect of lipid polarizability is 2.1 kcal/mol, which is found by solving PB using a slab model with dielectric constants of 1 and 2 (i.e., with dielectric shielding but no dipole potential changes), and 3.6 kcal/mol through postsimulation minimization of Drude particles on hydrocarbon tails (57). The postsimulation Drude-correction approach should capture some of the change in dipole potential due to polarizability (34). The C27 PMFs (corrected for both finite membrane patch size and lipid hydrocarbon dielectric constant) obtained using the PB or postsimulation Drude methods are shown as solid or dashed blue curves, respectively, and lead to fairly good agreement with experiment in terms of maximum conductance and dissociation constant (50).

Figure 7.

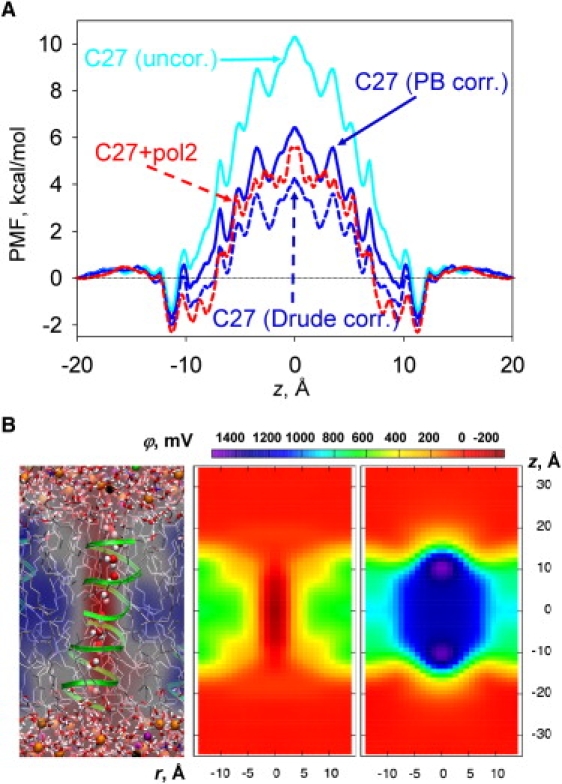
(A) PMFs of K⁺ crossing the gA channel with different models. (B) With a snapshot and 2D potential maps for the C27 model. The potential due to gA and channel water is excluded in the right-hand map. See Fig. S12 for polarizable C27+pol2 results, and Fig. S13 for the effect of charge smearing. The average errors are 0.3 kcal/mol for the C27 PMF and 0.4 kcal/mol for the C27+pol2 PMF (determined from block analysis as described previously (50)).

We performed new simulations using the C27+pol2 polarizable lipid model to capture the dielectric and changed dipole potential effects on permeation. Surprisingly, the PMF (dashed red curve in Fig. 7 A, corrected for membrane size as described in the Supporting Material) is similar to the PMF obtained using either PB or a posteriori Drude corrections (with similar agreement with experimental flux and binding). This tells us that no significant reorientation of protein or lipid groups occurred due to polarizability during the dynamics. A comparison of the PB-corrected and polarizable PMFs reveals a ∼1 kcal/mol difference, similar to the error margin. This demonstrates that a significant change in the dipole potential is not seen by the ion. We previously observed that the dipole potentials for C27 and C27+pol2 (based on DPPC) differ by ∼300 mV (34), yet that “seen” by gA must be ≤50 mV.

The electrostatic potential map across gA in Fig. 7 B (central panel) reveals that the potential has vanished inside the channel and actually becomes negative due to interaction with protein charges, explaining the known cationic selectivity of this channel (57). Remarkably, the potential along the z axis is nearly the same for the C27 and C27+pol2 models (see Fig. S13 A). Removing the peptide contribution creates artificial solvent-air and lipid hydrocarbon-air boundaries, leading to ∼1260 mV for C27 and ∼990 mV for C27+pol2 (Fig. 7 B, right panel, and Fig. S13 B). Thus, despite the interruption of the bilayer interface by gA, this number is essentially the sum of the dipole potential of an unperturbed bilayer and a hydrocarbon-air interfacial term (34). In the Supporting Material we show that the dielectric constant of a water-filled gA channel is ∼4–5, in agreement with previous estimates (58), leading to a potential drop of 800–900 mV (Fig. S13 C; noting, however, some ambiguities in the definition of the dielectric constant (59)). After the air-hydrocarbon interfacial contribution is accounted for, the dipole potential inside the channel will indeed be small. This is consistent with experimental measures of changes in flux due to a changed dipole potential (e.g., ether-ester lipid differences of up to 250 mV (16)) that correspond to just a few tens of millivolts seen by the ion (60), and resembles the situation presented by hydrophilic defects or pores or unassisted ion permeation.

Conclusions

We have demonstrated that perturbations of the bilayer structure can have a dramatic influence on the energetics of charged peptides or ions interacting with membranes. The net effect is a lowering of the free-energy barrier (although it is still prohibitively large) that leads to very different outcomes for flux across the membrane (20) and the protonation states of ionizable amino acids (24). Such an effect could be essential to explain the activities of many membrane-active peptides.

Intuitively, one would expect the ion type or the polarizability of a lipid hydrocarbon to lead to a change by tens of kcal/mol in the free energy for traversing a membrane, but this does not occur. Clearly, a larger, hydrated ion will exhibit reduced Born solvation energies; however, the overall lack of sensitivity can be attributed to the fact that, in the deformed membrane, the ion never partitions from water to hydrocarbon. Remarkably, the dramatic dependence on polarizability seen for ion solvation and dipole potential terms for an unperturbed membrane (34) disappears. This is due to compensation between solvation by polar water/lipid headgroups and polarizable lipid tails, as well as the fact that the dipole potential of the deformed membrane is not fully sensed.

We have observed that an ion never crosses the membrane interface to feel the full dipole potential, because it continually changes the interface as it enters, i.e., the ion is always located at the “interface”. This can explain why the change in the dipole potential (by ∼400 mV) by addition of electronic polarizability to the hydrocarbon tails did not noticeably influence the PMF. Also, the ion always resides where the electric field is large and fairly constant, which explains the Λ-shape of the PMF. Our observation allows for the prediction that a second ion trailing behind the first, bilayer-deforming ion would experience a reduced field and face little additional penalty for permeating the bilayer. This has implications for the mechanisms of multiple ion or charged protein movement into or across membranes, lipid flip-flop, and the roles of charged lipid components.

These observations, however, appear unique to the situation faced by a small ion. For larger hydrophobic ions (modeled here by spherical defects or the ionophore, VM), we found that the potential experienced is approximately a sum of the dipole potential for an unperturbed membrane sampled by a test point charge (the Galvani potential (53)), plus the difference in macroscopic air-water and air-hydrocarbon interfacial potentials. We predict that, after accounting for the electronic polarizability of the defect/solute, the dipole potential seen by a large hydrophobic ion would be consistent with experimentally measured dipole potentials obtained using such ions (30,31). An ion bound to VM would also see this dipole potential due to little dielectric shielding or membrane deformations.

The hydrophobic ion situation is distinct from that of small ions, transient pores, or ion channels that cause significant disruption of membrane electrostatics. We observed that for water defects of radius 5 or 6 Å, an interfacial connection similar to that formed by an ion occurred. Larger defects led to the formation of a continuous water pore across the membrane. Such bilayer perturbations can lead to a reduction or even complete elimination of the dipole potential similar to that seen for an ion channel. We found that lipid polarizability had a small effect (a few kcal/mol) on ion permeation through the gA channel, but the effect was mainly due to the membrane dielectric response and could be captured by continuum electrostatics. In this case, only a small fraction of the dipole potential was seen, due to dielectric shielding.

Our studies explain how local membrane deformations resulting from the presence of a charged peptide or small ion can make the permeation energetics insensitive to changes in solvation free energies and the membrane dipole potential, which constitute the standard model of charge-membrane interactions. However, although this standard model correctly yields large energetic barriers for small ion permeation, it does so via a mechanism that is inconsistent with the natural deformability of lipid membranes. These calculations illustrate the utility of all-atom MD simulations to model the flexible nature of membranes and to reveal the electrostatic determinants of charge-membrane interaction energetics.

Supporting Material

One movie, one scheme, four tables, and 14 figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(10)00412-1.