Two-Dimensional Nanoscale Structural and Functional Imaging in Individual Collagen Type I Fibrils

Abstract

The piezoelectric properties of single collagen type I fibrils in fascia were imaged with sub-20 nm spatial resolution using piezoresponse force microscopy. A detailed analysis of the piezoresponse force microscopy signal in controlled tip-fibril geometry revealed shear piezoelectricity parallel to the fibril axis. The direction of the displacement is preserved along the whole fiber length and is independent of the fiber conformation. It is shown that individual fibrils within bundles in skeletal muscle fascia can have opposite polar orientations and are organized into domains, i.e., groups of several fibers having the same polar orientation. We were also able to detect piezoelectric activity of collagen fibrils in the high-frequency range up to 200 kHz, suggesting that the mechanical response time of biomolecules to electrical stimuli can be ∼5 μs.

Introduction

Collagen type I is the most abundant structural protein and plays an important role in a number of hard calcified and connective tissues, such as bone, cartilage, and tendon. The physicochemical properties of collagen critically depend on its hierarchical structure spanning length scales from nanometers to millimeters. It is commonly accepted that collagen fibrils are formed by individual protocollagen molecules assembled into a triple helical structure. However, this model fails to explain several structural and functional problems, such as the directional growth of collagen fibrils and the fact that the D-band period is independent of the fibril diameter (1). To elucidate the complex mechanisms associated with the functional behavior of collagen tissues, the fibrils must be characterized with the highest possible resolution. Previous studies have characterized the topology of collagen fibrils in detail using electron microscopy (2,3) and atomic force microscopy (4,5), and revealed a characteristic D-banding pattern with a ∼67 nm periodicity. An examination of their mechanical properties provided additional insights into collagen structure (6). Direct measurements of the polar orientations and organization of collagen fibrils within microdomains are essential for ultimately understanding the functionality of the processes by which cells assemble collagen fibrils in response to directional tissue stress. In this regard, muscle fascia serves as a model for investigating these processes in tissues such as perineural sheaths, cornea, sclera, periodontal ligament, bones, and skin, as well as obtaining information about its functionality in muscle.

A new imaging approach based on monitoring electromechanical behavior by means of piezoresponse force microscopy (PFM) was recently developed (7,8). PFM allows evaluation of the electromechanical properties of collagen fibers within connective tissues (including calcified tissues) with nanoscale resolution (9,10). Previous work involving PFM of biomaterials focused on the proof of principle; in this study, however, we show that PFM really presents an invaluable opportunity to combine nanoscale structural and functional characterizations of biological systems. We performed high-resolution PFM of a collagen type I structure at the level of an individual collagen fibril. By analyzing the orientational dependence of the electromechanical response in the controlled PFM probe-fibril geometry, we were able to observe the anisotropy of structural properties along the fibril axis. Also, by measuring the frequency-dependent PFM signal of individual fibrils, we found that the functional response to electric stimulus in biological systems can occur at quite high frequencies (>200 kHz), allowing the development of bioelectromechanical systems and sensors with high-speed signal transmission. Our results provide a basis for experimental methods that will further our understanding of the physical-physiological functionality of collagen and promote the development of synthetic biomaterials. Such an understanding is essential for applications such as engineering highly functional cell-seeded polymer scaffolds for surgical tissue repair in patients with genetic disorders involving connective tissues, traumatic tissue damage, or postoperative tissue deficiency.

Materials and Methods

The fascia is a type I, collagen-rich sheath surrounding internal organs and muscle. Fascia tissue was harvested in situ, under a Nikon dissecting microscope, from the anterior tibialis muscle of C57/B6 mice after they were euthanized. The fascia tissue was fixed for 1–2 h in 4% paraformaldehyde at 4°C. Three fascia pieces (3 × 3 mm²) were then transferred to electrically conductive substrates (platinized silicon wafers). For optimal adhesion of the tissue, the substrates were treated with a gelatin-chromium potassium sulfate solution (gelatin type A and chromium potassium sulfate; Sigma-Aldrich, St. Louis, MO) before tissue deposition transfer was performed. Fascia tissue is naturally ∼10 μm thick. This harvesting procedure preserved the relative orientation of individual collagen fibrils in the tissue.

The basic units of collagen fibrils—tropocollagen molecules—are arranged in a crystallographic superlattice with quasihexangonal symmetry (11,12). Because of its nonsymmetric structure, collagen is characterized by linear electromechanical coupling, which can be examined by PFM. The PFM technique is an extension of contact mode atomic force microscopy, in which a conductive tip is used to scan the sample surface. A periodic bias voltage is applied to the tip and the induced surface vibration, representing the local piezoelectric response (PR), is transmitted to the cantilever via the same tip. The cantilever vibration is then extracted from the global deflection by means of a lock-in detection scheme. When a system of axes is chosen with the z axis parallel to the tip axis (perpendicular to the sample surface), and the y axis parallel to the cantilever, the signal extracted from the z cantilever deflection (also called vertical or out-of-plane) represents the PR along the z direction. It is also assumed that the signal extracted from the lateral deflection originates in a surface displacement parallel to the surface and perpendicular to the cantilever axis (i.e., along our x axis); this signal is denoted as the lateral or in-plane signal. Hereafter, we refer to the cantilever signals as VPR and LPR (for vertical and lateral PR, respectively), and the sample PRs are denoted as xPR, yPR, and zPR.

By performing vertical and lateral PFM measurements simultaneously on a collagen type I single fibril, we show that the application of an electric field across its diameter induces tip displacements that depend on the relative orientation of the fibril and the cantilever axis. We find that the resultant displacement of the surface is always along the fibril axis. We also show that the vertical PR signal in this configuration is induced primarily by the in-plane sample displacements parallel to the cantilever axis, via the cantilever buckling, thus allowing correct interpretation of the electromechanical data and providing a valuable insight into the anisotropic fibril properties.

We carried out local piezoelectric measurements using a previously described setup (13). The atomic force microscope (Enviroscope, Veeco Instruments, Santa Barbara, CA) was equipped with soft CSC38 (Mikromasch, Talinn, Estonia) cantilevers (k_z = 0.1–0.2 N/m) coated with Cr/Au and operated in contact mode, with a typical contact force in the range of 10–50 nN. A small AC voltage of 0.5–5 V (typically 1 V) with a frequency in the range of 10–250 kHz (typically 29 kHz) was applied between the conductive tip and the platinum-coated substrate. We then detected the cantilever vibrations induced by the (out-of-plane and in-plane) surface displacements in the contact region using two lock-in amplifiers from Signal Recovery (model 7265, AMETEK Advanced Measurement Technology, Wokingham, UK). We were able to superimpose an additional bias voltage on the AC voltage using a DC source (Keithley 2400 Sourcemeter, Keithley Instruments, Cleveland, OH). All of the PFM images presented consist of a mixed PR signal, i.e., PR = Amplitude × cos (Φ − Φ₀), where Φ and Φ₀ are respectively the phase of the signal and the phase offset with respect to the driving excitation voltage. This one-image data representation contains information about both the amplitude and phase of the PR signal. The amplitude and phase of the signal are associated with the magnitude and sign of the piezoelectric coefficient, respectively. The phase offset Φ₀ of the lock-in amplifier is adjusted such that a bright contrast corresponds to a surface vibration in phase with the AC excitation, a black contrast corresponds to an out-of-phase vibration, and an intermediate gray contrast corresponds to no vibration (14).

Results and Discussion

Fig. 1 shows AFM images of the fascia on a platinized substrate. As shown in Fig. 1 a, skeletal muscle fascia is composed of two layers, one of which consists of parallel, separate collagen fiber bundles 2–10 μm wide. No fibril within a bundle can be seen to end sharply. Higher-magnification images (Fig. 1, d and e) reveal that each collagen fibril exhibits the well-known 67 nm periodicity. This characteristic arises from the structural assembly of the collagen molecules (1 nm in diameter, 300 nm long) composing the fibril; adjacent molecules are displaced from one another by 67 nm, which is about one-quarter of their length. The second layer of fascia, seen over the background of parallel bundles in Fig. 1 a, is composed of a web of fibers and fiber bundles of connective tissue that are more randomly oriented. This layer of fascia is facing the muscle side and contains a relatively high content of loose connective tissue, such as reticular and elastin fibers (partially removed in our samples). The function of this partially elastic layer is to allow small changes of volume or length while reducing the interfacial stress between muscle and fascia.

Figure 1.

AFM topography images (a and d) and the corresponding PR images of the fascia: VPR (b and e) and LPR (c). The inset in a shows the cantilever orientation during the measurement. The scale bar in a is 2 μm (valid for images a–c). Higher-magnification images (d and e) clearly show the 67 nm periodicity and the organization of fibrils into domains (the domain boundaries are marked with dashed lines). The scale bar in d is 250 nm (valid for images d and e).

Fig. 1, b and c, show the PR of the same region shown in Fig. 1 a. The obtained data can be summarized as follows: First, the collagen fibrils exhibit a clear PR, which we will analyze later. Therefore, piezoelectricity in collagen type I-rich tissue indeed originates in the nanoscale-sized fibrils. Second, fibril contrast, either white or dark, is constant over large distances along the fibrils. This suggests that the fibrils possess an intrinsic property related to the piezoelectric properties observed. For the layer with parallel fibrils, this property can take only two values (corresponding to white and dark contrast). Since the fibrils possess a quasi-hexagonal symmetry, this suggests the presence of a polar direction along the fibril axis. The piezoelectric tensor of the fibrils should thus exhibit the same axial symmetry parallel to the fibril axis. A remarkable fact that can be observed in Fig. 1, d and e, is that the fibrils are organized in groups, or domains, that have the same polar orientation. Indeed, a careful comparison of the two images (topographic and PR) as viewed from the top surface shows that, on average, two to three fibrils form such a group. Given the fact that the PFM technique is sensitive mainly to the surface, it is also possible that the fascia is composed of alternate thin sheets within which collagen fibers have the same orientation. This organization may have a significant role in the biological functions of fascia, and will be further studied in a future work. Another feature that is revealed by comparing the two images is that the PR amplitude appears to be strongly correlated with the fibril topography, showing a 67 nm modulation along each fibril. The PR originating from the overlap regions along the fibril seems to be stronger than that of the gap regions. A similar observation was recently made in collagen type I from bovine tendon (15) and was attributed to a difference in symmetry in the two regions. In the overlap region, the fibril has a C₆ symmetry and thus exhibits a shear PR, whereas in the gap regions, less or no uniform symmetry reduces the electromechanical activity. However, although this explanation appears to be viable, we should not forget that there could be at least two other reasons for the observed contrast modulation. First, the gap region of fibril is not in contact with the substrate, and thus it is not able to transmit its deformation further to the tip. Second, it has been shown that the elastic properties of the material play a crucial role in PR contrast formation (16), proving that the elastic properties in the gap region are significantly different from those in the overlap region (17).

The fact that the collagen fibrils exhibit a nonzero VPR signal is, however, completely in disagreement with the presumed C₆ symmetry of collagen (18,1). Fig. 2 shows the piezoelectric d_zz surface calculated as described previously (19) using known values (18). Because in this symmetry class d₁₁ = d₂₂ = 0, there should be no PR along the direction z when the electric field is perpendicular to z₀ (θ = 90°), the fibril longitudinal symmetry axis. In contrast, the longitudinal response is maximum for θ ∼54°. To clarify this behavior, we investigated isolated individual fibrils. Fig. 3 a shows a survey topographic image of such a region, where several fibrils with various diameters running straight across the image can be seen. It is interesting to note here that fibrils ∼50 nm in diameter can be seen to divide into even thinner fibrils with a smaller diameter (arrow in Fig. 3 a).

Figure 2.

The longitudinal piezoelectric coefficient d_zz along different directions (the region [x₀ > 0, y₀ < 0] is removed). The coefficient nullifies for θ = 90° (d_zz = d₁₁ = d₂₂ = 0).

Figure 3.

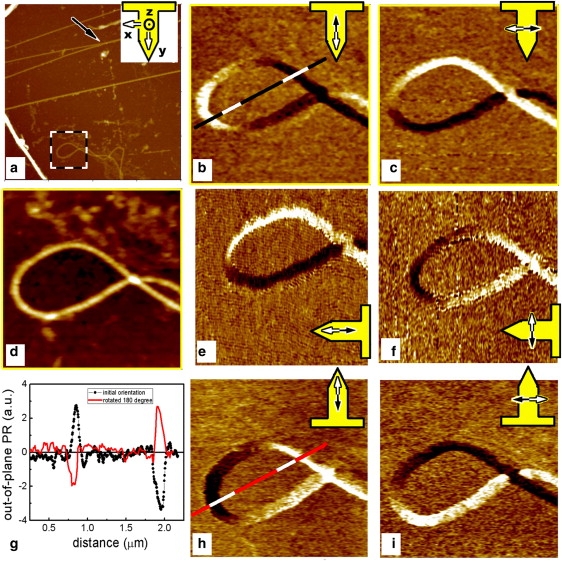
PR of an isolated collagen fiber at three cantilever orientations with respect to the sample: at an initial, arbitrary orientation (b and c); after a 90° clockwise rotation (e and f); and at 180° orientation (h and i). Images b, e, and h are constructed from the out-of-plane deflection signal, and c, f, and i represent the LPR. The topography of the area is shown in a (10 μm scan) and d (2 μm zoom of a). The plot in g shows the change in VPR along the same line of the sample (b and h) before and after the sample has been rotated by 180°. The cantilever orientation and the detection direction are overlaid on the PFM images.

To clarify the origin of the PR contrast in collagen, we focus our investigation on the fibril in the square region delimited in Fig. 3 a. We estimate that this single collagen fibril is ∼25 nm in diameter (assuming a tip radius of 30 nm, and consistent with the fibril height, 23 nm). We chose this region (Fig. 3 b) because the angle between the longitudinal axis of the fibril and the cantilever axis varies within a large range of ∼270°, depending on the exact location along the fibril. To perform a complete analysis of the collagen PR, we then physically rotated the sample with respect to the cantilever. Fig. 3, b, c, e, f, h, and i, show out-of-plane and in-plane PR images of the same collagen fibril loop recorded for three different angles. Fig. 3, b and c, are obtained at an initial (arbitrary) orientation, which we shall refer to as the 0° orientation. Next, we rotated the sample by 90° counterclockwise, resulting in the out-of-plane and in-plane PR images shown in Fig. 3, e and f, respectively. Finally, to avoid any misinterpretation, we acquired the images shown in Fig. 3, h and i, after the sample was again rotated counterclockwise by 90°, representing a 180° orientation. To facilitate comparison of the PR, the images are rotated as if the AFM cantilever and not the collagen fibril had been rotated. The relative orientation of the cantilever, together with the direction of detection during the measurement, is schematically shown superimposed on the images.

When we compare the images, we observe a direct dependence of both the VPR and LPR signals on the angle between the cantilever and the fibril axis. For the in-plane PR signal, this is expected, as we explain further below. However, the dependence of the VPR on the angle between the cantilever axis and the fibril is a striking and unexpected result. Indeed, according to the well-established interpretation, the signal extracted from the vertical deflection of the cantilever is attributed to the vertical piezoelectric displacement of the sample's surface, possibly superimposed on the electrostatic interaction (20–23). The vertical displacement is definitely expected to be independent of the relative orientation of the cantilever with respect to the sample.

To the contrary, however, the LPR signal depends on this relative orientation of the cantilever with respect to the sample, since the detection is sensitive to surface displacements perpendicular to the cantilever axis only. Since the sample displacement is a vector, one must detect all three of its components (xPR, yPR, and zPR) to completely describe it. This means that one must physically rotate the sample by 90° around the z axis (out-of-plane direction) to determine the two perpendicular in-plane components of the PR (24,25). However, few authors have noted that in-plane surface displacements parallel to the cantilever axis can induce, via friction forces, a buckling vibration resulting in an out-of-plane PR signal. This is because the detected out-of-plane signal is proportional to the cantilever deflection angle at its free end, and not to the absolute z position of the tip. It follows that when a buckling of the cantilever is present, the observed VPR is the superposition of two contributions: the first describing the real z displacement of the tip, and the other related to the cantilever buckling (23,26). One can separate the two contributions only by physically rotating the sample around the tip axis, and hence modifying the relative orientation of the sample with respect to the cantilever. By comparing the VPR images before and after the sample has been rotated by 90°, one can differentiate between the two contributions since the actual z displacement remains unchanged; the difference originates from a change in the induced buckling vibration.

In our experiment on an individual collagen fibril, the VPR of collagen changed its sign when the sample was rotated by 180°, as demonstrated in Fig. 3 g, which shows the signals across the same line marked in the images Fig. 3, b and h. This means that the only contribution to the cantilever vibration is the cantilever buckling induced via friction, i.e., zPR = 0 and thus VPR = yPR. Indeed, as seen in Fig. 3, b, e, and h, the signal is maximal where the collagen fibril is parallel to the cantilever axis. Similarly, in images Fig. 3, c, f, and i, the LPR signal is maximal where the fibril is perpendicular to the cantilever axis.

To describe the direction of the PR of collagen, we take the two signals that, when normalized to the same value, are considered as the x and y components of the PR vector (25). We then calculate the angle between this vector (demonstrated above to be in-plane) and the cantilever as α = arctan (xPR/yPR). In Fig. 4 a we compare the resulting angle with the geometric angle ψ between the cantilever axis and the direction tangent to the fiber at a given location (assumed to be identical to the fiber symmetry axis at that specific point). As shown in the plot (Fig. 4 b), the two angles are related by ψ = −α within 20°, which is within the experimental errors caused by noise in the images.

Figure 4.

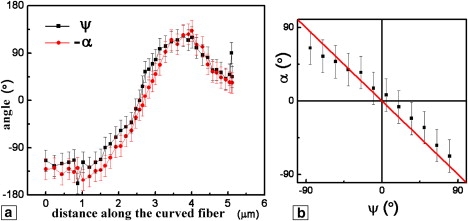
Comparison of the orientation of the fiber and the in-plane PR vector with respect to the cantilever axis. (a) Angles calculated from Fig. 2, b–d. (b) Independent measurement obtained on a long, straight fiber by rotating the sample in increments of 15°; calculated angle between the PR vector and the cantilever axis versus the angle between the straight fiber and the cantilever.

In doing so, we assumed that the fibril response is uniform along its length. This is justified by two experimental observations: 1), measurements on straight, long fibrils showed constant PR signals; and 2), the calculated magnitude of the resultant PR vector is indeed constant along the fiber (not shown). To further validate our results, we performed another experiment consisting of a series of measurements of the in-plane and out-of-plane PR signals from a single, straight fiber, by physically rotating the sample in steps of 15° using a rotating sample stage. We obtained these measurements above the same region of the fiber by averaging the signal over 5 μm of fiber length. The result, shown in Fig. 4 b, shows that the slope of the α(ψ) dependence is −1, confirming the previous measurement on the curved fiber, as well as two important conclusions:

• 1.The cantilever vibration detected from the z-deflection signal originates in the cantilever buckling induced by in-plane vibrations and transmitted to the cantilever via friction.
• 2.The PR of collagen under an electric field applied perpendicular to its longitudinal axis is parallel to the fiber's axis. Given the geometry of the experiment and the axial symmetry of collagen fibrils (using the standard convention for piezoelectric coefficients, with axis 3 being parallel to the fiber's axis; z₀ in Fig. 2), this implies that the coefficients d₁₁ = d₂₂ are indeed zero, and at least one of the shear coefficients (d₁₄, d₁₅, d₂₄, or d₂₅) is nonzero.

Indeed, Fukada (18) found that the symmetry of collagen is C₆, with the only nonzero coefficients being d₁₄ = −d₂₅, d₁₅ = d₂₄, and d₃₁ = d₃₂ and d₃₃. To check the consistency of our results, we compared the orientation of the PFM vector with theory by calculating the orientation dependence of the in-plane piezoelectric coefficients d₃₅^lab (or d_zxz, representing the in-plane PR signal, perpendicular to cantilever) and d₃₄^lab (or d_zyz, associated with the in-plane PR signal parallel to cantilever and proven to be the sole origin of the out-of-plane signal in our case). We therefore express the piezoelectric tensor (17,23) in the laboratory coordinate system using the Euler angles (ϕ, θ, ψ) to describe the fiber orientation, using the Z-Y-Z convention (23). The expressions for the coefficients of interest are found to be:

$$d_{zz}=d_{33}^{lab}=\cos \theta \left[\left(d_{31}+d_{15}\right)\left(1-{\cos }^2\theta \right)+d_{33}{\cos }^2\theta \right]$$

$$d_{zyz}=d_{34}^{lab}=\sin \theta \left[2\left(d_{33}-d_{31}-d_{15}\right){\cos }^2\theta \sin \psi +d_{14}\cos \theta \cos \psi +d_{15}\sin \psi \right]$$

$$d_{zxz}=d_{35}^{lab}=\sin \theta \left[-2\left(d_{33}-d_{31}-d_{15}\right){\cos }^2\theta \cos \psi +d_{14}\cos \theta \sin \psi -d_{15}\cos \psi \right]$$

As one can easily observe, none of the coefficients depends on the rotation angle ϕ (rotation about the longitudinal axis of symmetry of the collagen fiber), which means that a twisting of the fiber does not affect the PFM signal. For our specific geometry with the fiber lying on the substrate and with the electric field applied perpendicular to it, the angle θ = 90°, and we find that

$${\text{d}}_{\text{zz}}=0;{\text{d}}_{\text{zyz}}={\text{d}}_{15}\sin \psi ,{\text{d}}_{\text{zxz}}=-{\text{d}}_{15}\cos \psi$$

Therefore, the angle ψ between the cantilever axis and the fiber relates directly to the angle α between the PR vector (lying in the plane of the substrate) and the cantilever axis. In fact, α = −ψ, and this is exactly what we observe in Fig. 4, a and b. In the latter figure part, the slight difference between the two angles can be attributed to a crosstalk between the LPR and VPR signals possibly originating in an asymmetry of the tip, or a crosstalk in the electronics.

Having established that the PR of collagen lies in the direction of the fiber's longitudinal axis, we now estimate the shear piezoelectric coefficient d₁₅ responsible for the contrast observed in our experiments. To do this, we first calculate S_z = Δz/ΔV, the vertical sensitivity of the system, using the usual force spectroscopy measurements against the hard substrate, with Δz and ΔV being the vertical tip displacement and the detector output voltage, respectively. Next, we calculate the longitudinal sensitivity to buckling assuming that the deflection angle δ is not caused by a real vertical displacement, but entirely by the buckling caused by the tip displacement along the y axis, as illustrated in Fig. 5 a: ∼ tan δ = (3/2) Δz/L = Δy/h, where L and h are the cantilever length and tip height, and Δy and Δz are the longitudinal and vertical tip displacements, respectively. Therefore, S_y = (2h/3L) S_z. Assuming a uniform distribution of the field below the tip, Δy = d_zyz V_∼ (where V_∼ is the amplitude of the AC voltage applied), and therefore for regions where ψ = 0, we have d₁₅ = (2h/3L) × S_z × yPR/V_∼. Finally, after replacing the numerical values in our experiment (d = 30 nm, h = 20 μm, L = 350 μm, S_z =122 nm/V, yPR/V_∼ = 24 × 10⁻⁶), we obtain d₁₅ = 0.13 pm/V. This value is one order of magnitude lower than the known piezoelectric coefficients obtained in macroscopic measurements, and ∼1/5 the value obtained from bovine tendon single collagen fibrils (7). The low value obtained can be explained as follows:

Figure 5.

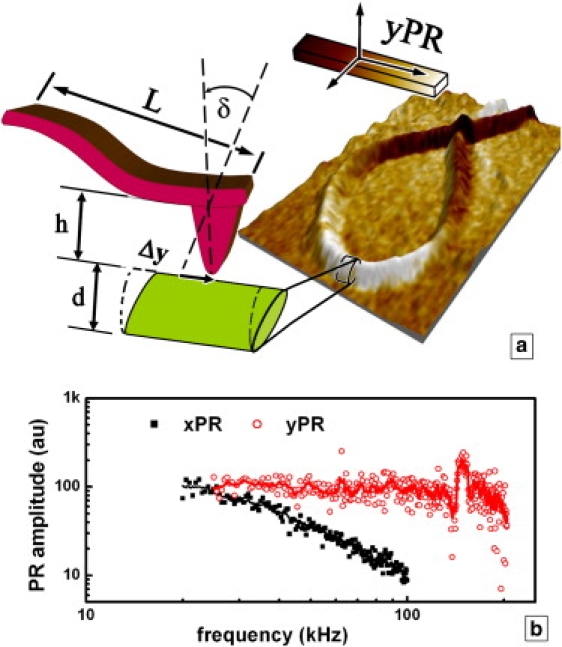
(a) Schematic representation of the VPR detection in PFM using the cantilever buckling. The fiber in Fig 2 is shown in a three-dimensional view, with the color scale being its yPR (Fig. 2b). Main physical quantities involved: L, cantilever length; h, tip height; δ, cantilever deflection angle; Δy, sample in-plane displacement; and d, sample thickness. (b) Frequency dependence of the amplitude of the VPR and LPR signals normalized to the same low-frequency value.

First, the shear piezoelectric deformation is clamped by the AFM tip. Indeed, the longitudinal force opposing the piezoelectric deformation is F_l = k_l Δy, where k_l is the longitudinal spring constant effective at the end of the tip (27) k_l = (2L/3h) × k_z ∼1.1 N/m, resulting in an elastic force F_l = F_y ∼0.14 pN. The shear stress associated with this force is S_yz = F_y/A_c ∼1.4 kPa, where A_c ∼100 nm² is the contact area. In addition to this shear stress opposing the deformation, the fibril is also exposed to a high compressive stress due to the contact force (F_z = 40 nN) S_zz = F_z/A_c ∼0.4 GPa. Indeed, preliminary independent measurements showed that decreasing any of F_y or F_z led to a significant increase of the piezoelectric coefficient. For example, decreasing F_z threefold (down to 13 nN) resulted in an almost fourfold increase of d₁₅ (0.54 pm/V).

Second, given the friction transduction mechanism, sliding of the tip across the surface may occur, leading to a measured displacement smaller than the actual in-plane displacement of the surface (i.e., VPR < yPR, LPR < xPR). It has been suggested that the transition from static to sliding friction may be identified from the frequency dependence of the PR (23,24,28). In Fig. 5 b, we show the frequency dependence of both LPR and VPR recorded from a single collagen fibril. The LPR signal gradually decreases above 20 kHz, and at 100 kHz vanishes below the noise level, in similarity to results reported by Bdikin et al. (28). We attribute this decrease to a limited bandwidth of the lateral detector in our atomic force microscope. In contrast, the VPR signal is relatively constant up to 170 kHz, with a maximum at the contact resonance (20) (∼150 kHz). Above 170 kHz the signal decreases, suggesting either the occurrence of sliding friction or a true decrease of the PR of collagen. To distinguish between these two scenarios, further experiments are needed, particularly with various cantilevers. Nevertheless, the data suggest that the tip is following the surface underneath at least up to 170 kHz, and thus our value for the piezoelectric coefficient is not affected by sliding friction.

It is important to emphasize that the presence of a PR at 200 kHz clearly demonstrates that single collagen fibrils have a response time to electrical stimuli below 5 μs. This is a surprising result, considering that biological processes are generally slow, with the shortest response time on the order of 1 ms (29). Such a short response time may find novel biotechnological applications, e.g., for sensors, actuators, or piezoelectric generators that could be implemented inside a living organism without interfering with it.

Conclusions

Two-dimensional nanoscale mapping of the electromechanical behavior of individual collagen fibrils resulted in several important findings. First, a detailed analysis of the PFM signal in a controlled tip-fibril geometry revealed clear shear piezoelectric activity associated with piezoelectric deformation along the fibril axis. The observed behavior was uniform over a large length scale (>80 μm). We found that fibrils within parallel bundles in fascia tissues can have opposite polar axis orientation and are generally organized in small groups (domains) having the same polar orientation (180° domains). Those findings allow a better understanding of the contrast in second harmonic generation (SHG) images of collagen type I arrays (12,30,31). Although both PFM and SHG microscopy techniques are sensitive to a structural organization lacking a center of inversion, the spatial resolution of PFM (20 nm in our case) is much better than that of SHG (∼1 μm) and allows piezoelectricity to be resolved in individual fibrils. Second, detection of shear PR in the high-frequency range (200 kHz) suggests that the electromechanical response time of biological molecules can be as fast as 5 μs. This is a remarkable result that creates new possibilities for biotechnological applications, including bio-microelectromechanical systems and sensors with high-frequency detection. Further PFM studies of collagen at different structural levels will provide a better understanding of the mechanism behind the physical-physiological functionality of collagenous tissues.