An Intuitive Safety Factor for Cardiac Propagation

Abstract

Safety factor is a useful concept for analyzing the propagation of impulses through cardiac tissue, which may have compromised ion channel function or electrical connectivity. Several formulations for its calculation have been proposed and have proved useful in one dimension; however, as we demonstrate, recent attempts to use the same formulation in multiple dimensions have led to questionable conclusions. In this study, we mathematically analyze the latest formulation of safety factor and explain its puzzling behavior. We propose a new formulation that is suitable for any dimension and can be estimated from experimental measurements. Its applicability is verified in two-dimensional simulations.

Cardiac safety factor (SF) is a putative quantifier of the robustness of propagation in heart tissue (1). It quantifies the surplus of current delivered to a cell relative to the amount required to depolarize the membrane to threshold. Leon and Roberge (2) put forth a version based on local cellular excitation. To address several shortcomings, Shaw and Rudy (3) developed a version that was later tweaked (4). This most recent formulation shall be referred to as SF_R.

A recent study by Aslanidi et al. (5) developed an excellent new ionic model for Purkinje cells, which was sorely needed as it replaces a pioneering-but-decades-old model (6). It also used SF_R to investigate propagation through Purkinje-ventricular (PVJs), which led to several counterintuitive observations:

• 1.SF_R was maximal surrounding the PVJ, even though propagation was most likely to fail in that region.
• 2.Tissue boundaries had a low SF_R, even though cells in that region lost no current to downstream cells.
• 3.SF_R decreased with distance from the PVJ, even though the radius of curvature of the propagation wavefront increased, requiring cells to excite fewer downstream cells.
• 4.For Purkinje strand widths above a certain threshold, SF_R decreased.

Similarly, in other studies SF_R did not change at points where wavefronts collided or changed in size (4).

Because SF_R was only verified for one dimension (3,7), the question of whether SF_R properly captures the dynamics of successful propagation in higher dimensions remains unanswered. Although the concept of SF is simple enough, its definition may not be so straightforward.

Derivation of Safety Factor

The equation describing cellular currents is derived from Kirchoff's current law, and is expressed in the monodomain formulation as

$$▿\cdot {\overline{\sigma }}_m▿V_{\text{m}}=\beta I_{\text{m}}-I_{\text{s}},$$ (1)

where ${\overline{\sigma }}_m$ is the harmonic mean of the intracellular and extracellular conductivities, V_m is the transmembrane voltage, β is the cell-surface-area/volume ratio, I_m is the total membrane current (outward positive), and I_s is an intracellular stimulus. Integrating over the volume of a cell, this becomes

$$I_{\text{in}}-I_{\text{out}}=C_{\text{m}}\frac{\partial V_{\text{m}}}{\partial t}+I_{\text{ion}}-I_{\text{s}},$$ (2)

where C_m is the membrane capacitance, I_in and I_out are the currents entering and leaving a cell through gap junctions, C_m is the membrane capacitance, and I_ion is the current passing through membrane channel proteins. Currents are expressed as whole cell quantities.

The expression for SF used by Romero et al. (4) and Aslanidi et al. (5) is given by

$$S{F}_{\text{R}}=\frac{C_{\text{m}}\Delta V_{\text{m}}+Q_{\text{out}}}{Q_{\text{in}}},$$ (3)

where the charge is computed over the time of rise of the membrane voltage (ΔV_m). Equation 2 can be integrated over the rise time, and terms rearranged to obtain

$$\frac{C_{\text{m}}\Delta V_{\text{m}}+Q_{\text{out}}+Q_{\text{ion}}}{Q_{\text{in}}}=1,$$ (4)

which, combined with Eq. 3, yields

$$S{F}_{\text{R}}=1-\frac{Q_{\text{ion}}}{Q_{\text{in}}}\text{.}$$ (5)

Thus, SF_R is >1 if total ionic charge, which is the active component, is inward. For this condition to occur, the cell must open enough Na⁺ or Ca² channels to counteract outward K⁺ channels, thereby initiating a positive feedback loop, causing an action potential to fire. Thus, as has been demonstrated (4,7), SF_R must be less than unity when propagation fails, but the question remains whether it relates correctly to the surplus or deficit of charge relative to a threshold value. The relationship is not readily apparent.

Analyzing Eq. 3, the paradoxical behavior of SF_R at the PVJ in Eq. 5 can be explained. Because the input wavefront width at the PVJ is much smaller than the output wavefront width, Q_in will be relatively small, increasing the SF_R. Similar reasoning explains the counterintuitive SF_R reductions with increasing wavefront curvature and PVJ width. At the boundaries, a lack of downstream cells to excite means that Q_out is zero in the numerator, reducing the SF_R.

New Formulation for Safety Factor

An intuitive expression for SF must explicitly consider the concept of the surplus of charge delivered relative to the minimum required to trigger an AP. Thus, we propose

$$S{F}_{\text{VB}}=\frac{\frac{1}{\beta }\underset{\text{A}}{\int }▿·{\overline{\sigma }}_m▿V_{\text{m}}dt}{Q_{\text{thr}}\left(t_{\text{A}}\right)};A\in \left[t_{1\%},t_{I_{\text{m}}0}\right],$$ (6)

$$=\frac{C_{\text{m}}\Delta V_{\text{m}}+Q_{\text{ion}}-Q_{\text{s}}}{Q_{\text{thr}}\left(t_{\text{A}}\right)};t_{\text{A}}=t_{I_{\text{m}}0}-t_{1\%},$$ (7)

where A is the interval from 1% take off (t_1%) to zero I_m $\left(t_{I_{\text{m}}0}\right)$, during which I_m is positive, Q_s is the intracellular stimulus charge, and Q_thr is the minimum charge required to elicit an action potential in a single cell, which is dependent on the stimulus duration (t_A). This is the period during which depolarizing ionic channels have just begun to open; thus, it approximates the duration of the depolarizing stimulus brought about through spatial interaction.

Unique Q_thr functions must be determined for each preexcitation tissue state. These can be determined from computationally inexpensive single-cell simulations, as shown for several ionic models in Fig. 1. These relationships are nearly linear with respect to t_A because the passive membrane acts like a lossy RC circuit; thus, linear continuous functions were fit to several measured values for each scenario. In addition to ionic model dependence, Q_thr is sensitive to changes in refractoriness and excitability, as shown for impaired sodium conductance (g_Na) and increased pacing. Although this does increase the amount of computation required to calculate SF_VB, it is a necessary component because the history of a cell strongly affects its response.

Figure 1.

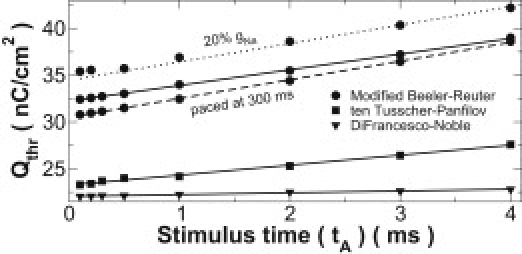
Threshold charge as a function of stimulus time for several preexcitation scenarios. Models were paced at 1000 ms with normal excitability except where otherwise indicated. Linear functions (lines) were fit to measured values (points).

SF_VB was tested using a similar experimental design to the Aslanidi et al. (5) study: a 2-mm-long strand of Purkinje cells was attached to a 2 × 4-mm piece of myocardial tissue (see Fig. 2). A monodomain finite element formulation was used, details of which can be found in Vigmond et al. (8). An edge length of 5 μm was used for all elements. Ion dynamics were described by the modified Beeler-Reuter model in the myocardium (9) and the DiFrancesco-Noble model (6) in the Purkinje strand. As in Aslanidi et al. (5), the complex architecture known to exist at PVJs (10) was ignored. In Aslanidi et al. (5), strand width was varied from 500 μm to 3.5 mm based on fiber bundle diameters (11); here, the range was reduced to 5–1000 μm to encompass the finer-scale PVJ diameters shown in microscopic analysis (12).

Figure 2.

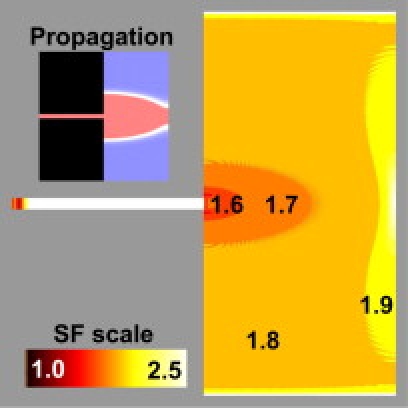
Distribution of SF_VB. Current was injected in the strand (width: 120 μm) and excitation spread to the myocardium through a PVJ. (Inset) V_m pattern 6 ms after stimulation. Blue, at rest; red, depolarized; white, wavefront.

The distribution of SF_VB during Purkinje-to-myocardium propagation with a 120-μm strand is shown in Fig. 2. As expected, SF_VB was minimal near the PVJ, where the preparation was most vulnerable to propagation failure, and increased as the wavefront curvature became larger. At the tissue boundary, there was a sharp increase in SF_VB due to the lack of downstream cells to be excited.

Detailed numerical values for two points along the myocardial slab are shown in Table 1. SF_VB increases with distance from the junction and decreases with impaired g_Na.

Table 1.

SF_VB under normal and impaired conduction

	Control		20% gNa
x (mm)	2.5	3.5	2.5	3.5
CmΔVm + Qion	56.72	59.65	45.35	50.98
tA (ms)	1.12	0.86	2.26	3.82
Qthr	34.11	33.67	38.90	41.98
SFVB	1.66	1.77	1.17	1.21

Numerical examples from two points along horizontal axis in the myocardial region, where Q_s = 0, for 120-μm strand with normal and impaired g_Na. In both cases, SF_VB increases with distance along preparation (x). SF_VB decreases with impaired g_Na due to reduced Q_ion and increased Q_thr. Units for C_mΔV_m + Q_ion and Q_thr are nC/cm².

Results for several other strand widths are presented in Fig. 3, which shows SF_VB from strand to myocardium, including the center of the PVJ. In cases where propagation was unsuccessful, SF_VB dropped below unity at the PVJ and the failed stimulus decayed exponentially into the surrounding tissue. For the critical strand width of 20 μm, SF_VB dipped similarly at the PVJ but never crossed below unity; as expected, for wider strands, junctional SF_VB increased monotonically.

Figure 3.

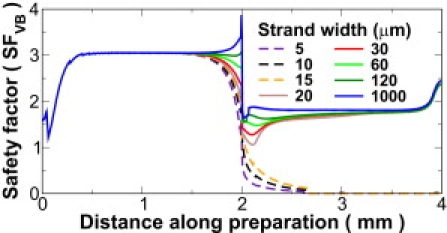
SF_VB along the horizontal axis, from stimulation site (0 mm) through PVJ (2 mm) to myocardial boundary (4 mm), for several strand widths. In failed propagation (dashed lines), SF_VB dropped below unity near the PVJ. Junctional SF_VB increased monotonically with strand width.

In summary, SF_VB has the following features:

• 1.It describes the surplus of charge delivered to single cells.
• 2.It avoids the decomposition of current into inward and outward components, which is particularly troublesome in three-dimensional continuum approaches with unstructured grids.
• 3.With reduced excitability due to compromised inward membrane current, it will decrease due to increased Q_thr.
• 4.In tissue monolayers or in planar propagation where there is no depth component, it can be estimated experimentally with Laplacian electrode measurements (see Eq. 6).

SF_VB behaved similarly when the more complex ten Tusscher and Panfilov (13) model was used for myocardial cells.

Discussion

This study highlights how care must be taken when a metric developed in one dimension is applied to higher-order dimensions. Unexpected results may occur, leading to erroneous conclusions. Such is the case for SF_R, which had shown proper behavior in a strand where wavefront curvature effects are not present. An alternative expression, SF_VB, is derived here to address shortcomings of previous formulations. It is simple to compute with unstructured grids, and captures the essential features of SF under conditions known to affect propagation. Two-dimensional simulations verified its applicability, although it is suitable for any dimension.

SF_VB is a ratio of the surplus or deficit between the charge available to a given node and the charge required for that node to achieve the depolarization threshold. Thus, if it has a value <1, propagation will fail because the cell will not undergo any active response.

The results presented here differ markedly from those of Aslanidi et al. (5), but agree with intuitive expectations; namely, increasing PVJ width provides more current, leading to faster, more robust propagation, which is reflected by higher SF_VB. The PVJ is the most critical point in the propagation path, so it makes sense that SF in that region is nearest to unity.

Other discrepancies between the two studies may be due to differences in numerical methods. The finite element method used herein preserves no-flux boundary conditions regardless of shape, whereas the finite difference approach used in Aslanidi et al. (5) cannot satisfy no-flux conditions properly at corners, which is where the PVJ is located. Also, this study used a finer discretization, which may be important for computing propagation accurately with narrow Purkinje strands.