Summary
We performed density functional calculations of backbone 15N chemical shielding tensors in selected helical residues of protein G. Here we describe a computationally efficient methodology to include most of the important effects in the calculation of chemical shieldings of backbone 15N. We analyzed the role of long-range intra-protein electrostatic interactions by comparing models with different complexity in vacuum and in charge field. Our results show that the dipole moment of the α-helix can cause significant deshielding of 15N; therefore, it needs to be considered when calculating 15N chemical shielding. We found that it is important to include interactions with the side chains that are close in space when the charged form for ionizable side chains is adopted in the calculation. We also illustrate how the ionization state of these side chains can affect the chemical shielding tensor elements. Chemical shielding calculations using a 8-residue fragment model in vacuum and adopting the charged form of ionizable side chains yield a generally good agreement with experimental data.
Keywords: chemical shielding tensor, chemical shielding calculation, ab initio, nitrogen-15, density-functional calculation, protein G
Introduction
Chemical shielding is determined by the local electronic environment of a nucleus of interest. In complex molecular systems, like proteins, the chemical shift tensors contain a wealth of potentially useful structural and dynamical information. There has been significant progress in using chemical shift information for characterization of protein structure (Cornilescu et al. 1999; Lipsitz and Tjandra 2003; Shen and Bax 2007; Shen et al. 2008; Shen et al. 2009) and dynamics (Hall and Fushman 2006). First-principles quantum chemical calculations have played an important role in understanding the relative importance of various effects, such as backbone and side chain conformation, hydrogen bonding, solvation, and protein electrostatics, on the chemical shielding of nuclei in proteins. These calculations have also provided parameters and conceptual ideas for the development of phenomenological models (Xu and Case 2001; Xu and Case 2002). Despite their contributions to our understanding of the chemical shielding phenomena and to model-building efforts, first-principles quantum chemical calculations have not become a routine practice in predicting chemical shifts in proteins because of several difficulties. First, chemical shifts could be influenced by a multitude of factors. In general, the backbone torsion angles, the side chain orientation, the hydrogen bonding and direct interactions with nearby side chains, the long-range intra-protein electrostatics, and solvent effect can all contribute. It is challenging to include all foreseeable effects and still be computationally efficient. Second, any experimental protein structure we use for calculating chemical shifts might require some geometry optimization in order to get an accurate prediction. This is particularly true for α-carbons because their calculated chemical shielding is very sensitive to bond lengths and bond angles (de Dios et al. 1993a). Third, proteins rapidly sample the available conformational space, hence no single snapshot (X-ray) or even a finite bundle of NMR structures of a given protein can fully represent the conformational ensemble (and dynamic ensemble averaging) for which the experimental chemical shifts are measured. Moreover, when using a solution structure for calculations, one has to consider not only the structural ensemble but also at what conditions (pH, temperature, etc) the structure was obtained. There can be fluctuations which may not only affect some structural parameters but also alter the ionization form of the side chains of Asp, Glu, Arg, and Lys (Vila and Scheraga 2007). Fourth, there are systematic errors associated with the level of theory used and the basis set chosen for calculating the electronic structure. In practice, an offset may exist that will need to be corrected if an absolute isotropic chemical shift prediction is the aim (Cai et al. 2008). An additional complication here is that this correction should differ between various residue types (Xu and Case 2001).
Despite these difficulties, theoretical chemical shift tensors are valuable in peptide and protein structure validation and refinement (Wylie et al. 2009) and therefore worth exploring. In this paper, we chose to focus on amide 15N chemical shielding tensor for several reasons: (i) it is influenced by numerous factors and, therefore, is arguably the most difficult case for computational prediction (de Dios et al. 1993b); (ii) perturbations in amide chemical shifts are often used for mapping protein-ligand interactions (Zuiderweg 2002); and (iii) amide 15N chemical shift tensor contributes to 15N spin relaxation rates that are widely used for analysis of protein dynamics (Fushman and Cowburn 2001; Hall and Fushman 2006). Thus, first-principles calculations may shed light onto the relationship between structural changes in proteins upon ligand binding and the accompanying changes in their chemical shifts. The quantum chemical calculations can also provide an understanding of the structural basis for site-to-site variability in 15N chemical shift tensors (Fushman et al. 1998; Hall and Fushman 2006).
Previous theoretical works (de Dios et al. 1993b; Le and Oldfield 1996; Xu and Case 2002; Cai et al. 2008) have established that 15N chemical shielding depends on the following factors with none seemingly dominating: ϕ, ψ, χ1, preceding side chain’s identity and conformation, hydrogen bonding partners, electrostatic interactions, and solvent effect. Whereas the short-range interaction with hydrogen-bonding partners can be included explicitly and exactly, model treatment has been required for long-range electrostatic interactions. Point charge representation can be an option here. For example, in addition to the main fragment, charges can be incorporated for the remaining atoms in the protein using some charge set. Thus, it was found that if the charge field perturbation (CFP) effects are included in the calculation of carbon chemical shielding in amino acids, the correlation between the theory and experiment is slightly improved (de Dios et al. 1994). The improvement is mainly for the sp2 carbonyl carbon, which is more sensitive to electrostatic field effects. The sp2-hybridized amide nitrogen shares this kind of sensitivity (Bader 2009) and showed some prediction improvement with inclusion of charge field perturbation in a dipeptide model (de Dios et al. 1993b). However, a later application to helical residues (Le and Oldfield 1996) indicated that a static charge field is inadequate to account for the long-range electrostatic field contribution to 15N shielding in an α-helix. There are probably two reasons for this: (i) each type of residue has a fixed set of approximated charges, which may not be accurate enough for the purpose of calculating 15N chemical shifts because the multiple-bond character of the peptide group makes the peptide nitrogen highly polarizable and hence very sensitive to the electric field that the charges generate; and (ii) the ionization state of Asp, Glu, Arg, and Lys is not well determined and can vary depending on the protein ensemble, temperature, and pH; this renders representation of the side chains of these residues as either neutral or charged somewhat arbitrary.
To address these issues we performed density functional calculations of backbone 15N chemical shielding for helical residues in protein G (GB3) and compared the results with experimental data from solid-state and solution NMR measurements. To assess the contributions from intra-protein electrostatic interactions, the density functional calculations were combined with charge field perturbations.
Computational methods
All calculations reported in this paper were performed using the GAUSSIAN03 suite of programs (Frisch et al. 2004). We used density-functional theory (DFT) with three-parameter Becke-Lee-Yang-Parr (B3LYP) exchange-correlation functional (Becke 1988; Lee et al. 1988; Becke 1993). The atom coordinates were taken from the best representative conformer (PDB code: 2OED) of the ensemble of GB3 solution NMR structures (Ulmer et al. 2003). The bond lengths and angles were taken directly from the experimental structure without geometry optimization.
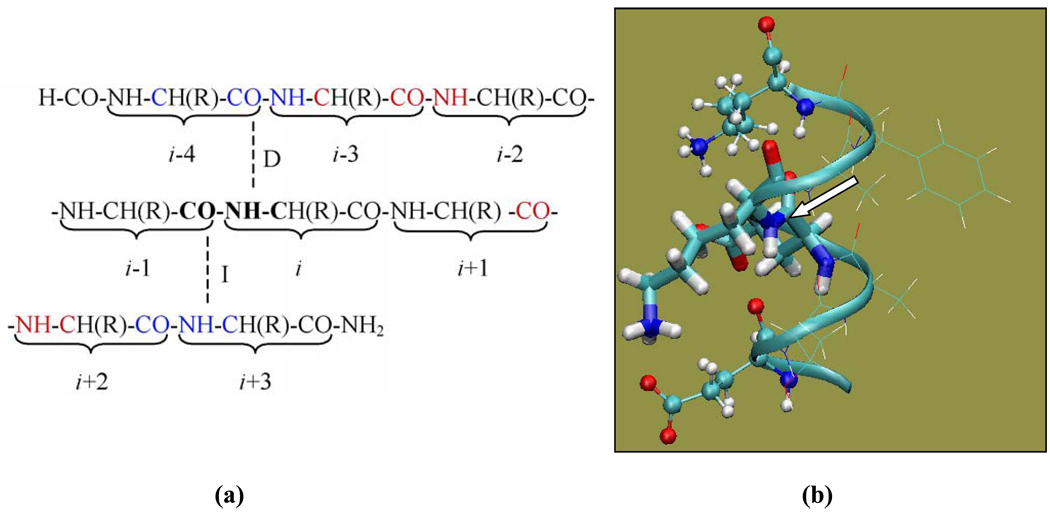
Only ‘classical’ helical residues, A26 through Y33, of the GB3’s α-helix (that spans residues D22-N37) are examined in this paper. According to the definition used here, a classical helical residue i is hydrogen bonded through its NH group to residue i−4 and through the CO group to residue i+4. Thus the backbone nitrogen of residue i has a direct hydrogen bonding partner i−4 and an indirect hydrogen bonding partner i+3 (Fig. 1). To avoid terminal artifacts, four residues at either end of the α-helix were not examined here because they are missing either a direct or an indirect hydrogen-bonding partner.
Fig. 1.
(a) Illustration of the basis set assignment. The dashed lines represent the direct (D) and indirect (I) hydrogen bonds for the peptide plane containing the amide group of residue i. (b) Illustration of various peptide fragment models used in the calculations. In the case of amide nitrogen of K28 shown here, Model A (a dipeptide model) includes E27 and K28 (thick sticks); Model B includes residues from Model A (thick sticks) and the two hydrogen bonding partners (ball-and-stick); Model C includes all residues from E24 to K31 (ribbon). Residues shown in thin-line representation are included in Model C but not in Model B. The molecular image was generated using VMD (Humphrey et al., 1996). The arrow points to the amide nitrogen whose chemical shielding is being calculated
Several models of different levels of complexity are investigated here (illustrated in Fig. 1b for the case of amide nitrogen of K28):
Model A: a simple dipeptide model containing only residues i and i−1. If not indicated directly, the ionizable side chains are assumed to be in their charged state. In some cases, as indicated in the text, the ionizable side chains were altered to be neutral.
Model B: a main fragment containing residues i and i−1 (as in Model A) and two additional fragments of the hydrogen bonding partners, both direct and indirect. This results in a “three-fragment” model. In some cases, as specified in the text, the side chains of the hydrogen bonding partners were altered to be neutral or modified to be −CH3.
Model C: a “long-chain” model containing a stretch of residues from the direct hydrogen bonding partner to the indirect hydrogen bonding partner as one main fragment. That is, for classical helical residues the “long chain” includes residues from i−4 to i+3. In some cases, as specified in the text, some side chains of the “long chain” were altered to be neutral or changed to −CH3, or the “long chain” was extended to include an additional residue at one end.
In our calculations, the main fragments in various models had the N-terminus capped by a formyl group (−COH) and the C-terminus capped by an amino group (−NH2), and the hydrogen bonding partners in Model B were modified to be CH3-CO-(NH-CH(R)-CO)-NH-CH3. When the charges from the atoms of the rest of the protein are included in the calculation, we refer to it as Charge Field Perturbation (CFP) calculation. If the charges are not included, we call it “vacuum” calculation. In CFP calculations, the point charges were all taken from AMBER charge set (Cornell et al. 1995) with the overall non-zero charge for ionizable residues. The calculations were performed using local dense basis sets (Chesnut et al. 1993). For the residue of interest (i), we applied a 6–311+G(2d,p) basis set for the Ni, Hi,Cαi, Ci−1, and Oi-1 atoms (shown in bold in Fig.1a). Where applicable, the 6–311+G(2d,p) basis set was also applied to similar atoms of its direct and indirect hydrogen bonding partners (shown in blue in Fig.1a), as well as the “second pair” (Xu and Case 2002) of hydrogen bonding partners (shown in red in Fig.1a). A 4-21G basis set was applied to the remaining atoms in the model. The charge field perturbation gauge-including atomic orbital method (Ditchfield 1974; Wolinski et al. 1990; de Dios and Oldfield 1993) was used.
Results and Discussion
Model building
Fragment Size
It was suggested (Xu and Case 2002) that a 7–9 residue sequence should be used for chemical shift calculations in the α-helix conformation in order to eliminate the terminal artifacts. The terminal effects may be due to (i) the lack of hydrogen bonding partners for the residues at either end; or (ii) the underestimation of the interaction with the dipole moment of the helix.
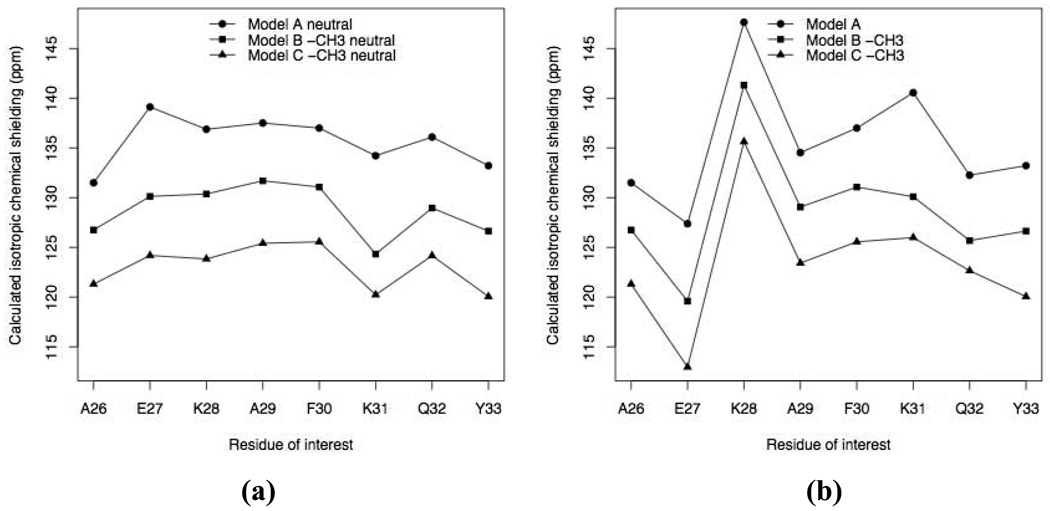
In order to analyze the magnitude of the hydrogen bonding and helical dipole effects without side chains complicating the picture, all non-alanine residues other than residues i and i−1 were altered to be alanines (see Table 1), and we compared isotropic chemical shieldings from Model A to Model C vacuum calculations. As shown in Fig. 2a, the first pair of hydrogen bonding partners deshields 15N. The deshielding ranges from 4.75 ppm to 9.89 ppm depending on the strength of hydrogen bonding. The effect is the strongest for K31 because the peptide plane containing the amide group of K31 makes the strongest hydrogen bonds. In fact, the distance between K31’s amide proton and E27’s carbonyl oxygen is 1.83 Å, compared to the 1.89 to 2.86 Å range for the rest of the hydrogen bonds in the GB3 helix. In addition, the O-H distance for the corresponding indirect hydrogen bond is 1.89 Å. Model C deshields 15N further from Model B, by the amount ranging from 4.10 ppm to 6.59 ppm (Fig. 2a). This is due to the inclusion of atoms from residues i−3, i−2, and i+2 in Model C, which introduced new aligned NH and CO groups, namely NH groups from residues i−2 and i+2, and CO groups from residues i−3 and i+1 (see Fig. 1). These groups contribute to the helical dipole moment and bring about electrostatic field contribution to 15N chemical shielding, in agreement with previous findings (Le and Oldfield 1996; Xu and Case 2002). Our calculation showed an increase by 18.5 Debye on average in the dipole moment from “Model A neutral” to “Model B neutral −CH3”; and on average an additional increase by 10.2 Debye from “Model B neutral −CH3” to “Model C neutral −CH3” (Table S1). Since the “long-chain” model further deshields the 15N compared to the “three-fragment” model and this deshielding differs for different residues (Table 1), we conclude that the “long-chain” model includes some new nontrivial contributions, which are not present in the simpler models.
Table 1.
Calculated isotropic 15N chemical shieldings (in ppm) for selected helical residues in GB3 using various models
| Residue | Model A neutrala |
Model B | Model C | Direct HB partner |
Indirect HB partner |
||
|---|---|---|---|---|---|---|---|
| neutrala −CH3b | neutrala | neutrala −CH3b | neutrala | ||||
| A26 | 131.50 | 126.75 | 128.46 | 121.31 | 122.21 | D22 | A29 |
| E27 | 139.12 | 130.13 | 130.65 | 124.19 | 125.17 | A23 | F30 |
| K28 | 136.88 | 130.37 | 131.31 | 123.84 | 125.06 | E24 | K31 |
| A29 | 137.51 | 131.70 | 131.98 | 125.41 | 125.74 | T25 | Q32 |
| F30 | 137.00 | 131.07 | 130.23 | 125.56 | 126.55 | A26 | Y33 |
| K31 | 134.22 | 124.33 | 123.80 | 120.23 | 119.27 | E27 | A34 |
| Q32 | 136.10 | 128.96 | 130.39 | 124.17 | 125.53 | K28 | N35 |
| Y33 | 133.22 | 126.64 | 126.47 | 120.05 | 120.96 | A29 | D36 |
| Residue | Model A | Model B | Model C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| * | CFP c | −CH3b | * | partial CFP d | CFP c | −CH3b | * | CFP c | |
| A26 | 131.50 | 126.52 | 126.75 | 128.28 | 120.33 | 121.58 | 121.31 | 120.07 | 120.57 |
| E27 | 127.38 | 120.64 | 119.59 | 120.12 | 113.06 | 110.49 | 112.96 | 113.98 | 112.65 |
| K28 | 147.65 | 136.05 | 141.32 | 134.65 | 127.07 | 127.86 | 135.63 | 128.42 | 127.58 |
| A29 | 134.53 | 130.89 | 129.06 | 129.45 | 122.01 | 125.63 | 123.42 | 122.20 | 124.26 |
| F30 | 137.00 | 130.40 | 131.07 | 130.23 | 122.80 | 123.34 | 125.56 | 125.01 | 124.27 |
| K31 | 140.56 | 127.09 | 130.10 | 125.80 | 120.89 | 117.52 | 125.99 | 123.17 | 118.08 |
| Q32 | 132.26 | 129.49 | 125.69 | 127.96 | 121.33 | 121.86 | 122.65 | 122.70 | 122.23 |
| Y33 | 133.22 | 132.59 | 126.64 | 132.02 | 123.70 | 125.18 | 120.05 | 124.78 | 125.96 |
neutral: all ionizable side chains were made neutral.
−CH3: All nonalanine residues other than residues i and i−1 had their side chains modified to be −CH3.
CFP: The calculation was performed in the presence of AMBER charges representing GB3 atoms that were not included in the model.
“Model B partial CFP”: This calculation was performed in the presence of AMBER charges representing atoms that were not included in Model B but were included in Model C.
generic model (A, B, or C) with no additional modifications.
Fig. 2.
Isotropic 15N chemical shieldings for selected helical residues calculated using various models. Where applicable, the ionizable side chains of residues i and i−1 are neutral in (a) but charged in (b)
We note here that in the calculations with charged ionizable side chains (Fig. 2b), the contributions from the first pair of hydrogen bonds and from the additional helical dipole are similar to those in the calculations with neutral ionizable side chains (Fig. 2a). This indicates that the side chain charges do not interfere with hydrogen bonding effects and helical dipole effects.
Charged or neutral side chain?
Previously, when building the database for SHIFTS (Xu and Case 2002), all ionizable amino acids took neutral forms because it appeared that in gas-phase calculations, neutral side chain provided a better model for solution chemical shifts than the charged side chains did. More recently, it was suggested (Vila and Scheraga 2007) that the whole protein and its chemical environment should be taken into account when considering the proton binding/release equilibria and then the chemical shifts should be calculated as a weighted average. That study also found that for Cα the results obtained for Asp and Glu are almost systematically worse when using charged rather than neutral side chains, presumably because these two amino acids have much shorter side chains compared to Arg and Lys. When charged, these side chains may have a bigger influence on the Cα chemical shielding. Here we explore how the 15N chemical shift can be affected by the ionization form of the side chains.
As shown in Table 1, the side chain charge on the residue of interest has an apparent effect on its 15N chemical shielding (compare the results from “Model A” and “Model A neutral” calculations for E27 and K31). Deprotonation of the side chains introduces deshielding while protonation introduces shielding, similarly to what was observed for Cα (Vila and Scheraga 2007). For example, the negative charge on the side chain of E27 deshields its 15N by 11.74 ppm while the positive charge on the side chain of K31 shields its 15N by 6.34 ppm in Model A.
Unlike Cα, surrounding side chain charges on other residues can influence amide nitrogen chemical shielding. Take K31 as an example. Its “Model B −CH3” calculation (130.10 ppm) yields a more shielded value than its “Model B neutral −CH3” calculation (124.33 ppm) for 15N. This shielding effect of 5.77 ppm is due to the charge on K31. In the Model B calculation where K31’s hydrogen bonding partner E27 is also charged, the amide nitrogen of K31 has a chemical shielding of 125.80 ppm. This 4.3 ppm deshielding from the “Model B −CH3” calculation is mainly due to the charge on E27. This example illustrates that the charges on other side chains can make 15N chemical shielding calculation more interesting but also more challenging because it introduces another source of variation. In the case of neutral side chains, on the contrary, their identity does not play a significant role, such that they can be safely replaced by a −CH3 group. This is supported by the close resemblance of the results from “Model B neutral” and “Model B neutral −CH3” calculations and, likewise, of the results from “Model C neutral” and “Model C neutral −CH3” calculations.
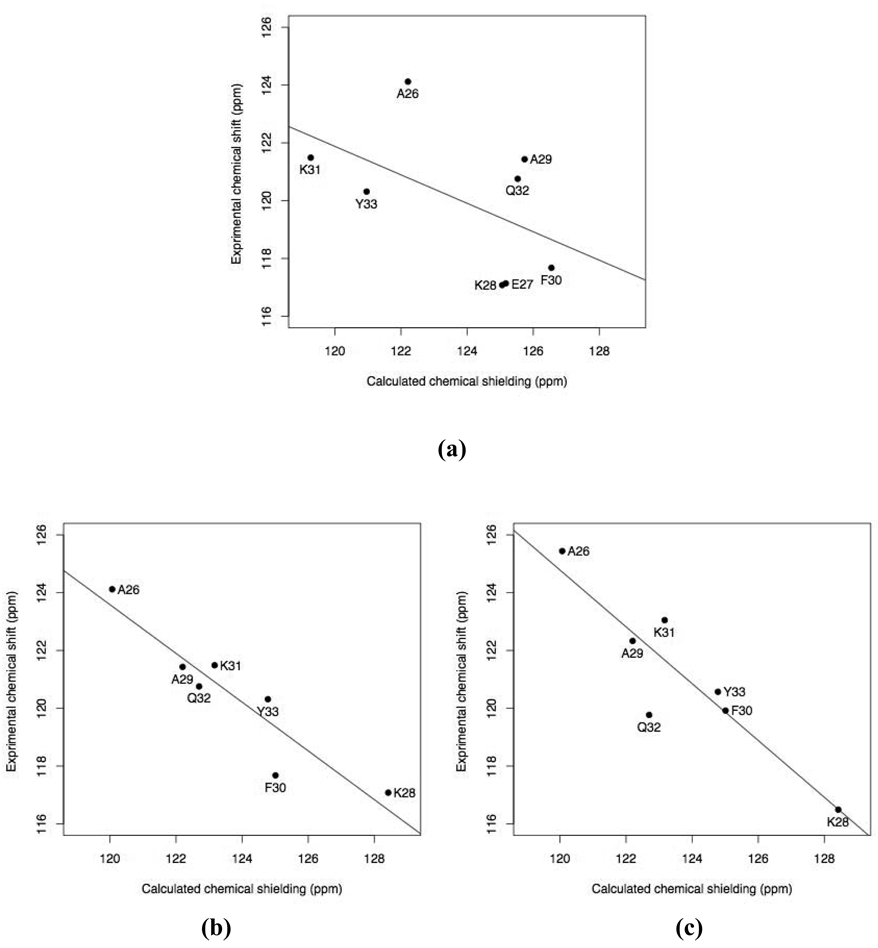
We used two approaches when calculating 15N chemical shielding with Model C. The first approach makes all ionizable side chains neutral in the Model C vacuum calculation. The comparison between experimental solid-state chemical shifts and the calculated chemical shieldings is shown in Fig. 3a. The correlation is poor (|r|=0.52), and the regression line has an intercept of 181.00 ± 41.00 ppm and a slope of −0.49 ± 0.33. The slope is far from the ideal value of −1. No obvious outlier can be identified. The second approach represents all ionizable side chains in their charged states. This yields an obvious outlier, E27 (see Fig.4a). By excluding E27, a better correlation is achieved (|r|=0.93) and the linear regression yields a slope of −0.84 ± 0.15 and an intercept of 224.91 ± 18.83 ppm (Fig. 3b). A comparison with solution NMR data yields similar results: |r| = 0.91, slope = −0.98 ± 0.20, and intercept = 242.87 ± 24.70 ppm (Fig. 3c). In this approach it is important to include all charges that are close to the 15N site of interest (Bader 2009). Consider E27 as an example. In the Model C vacuum calculation that includes residues from A23 to F30, we obtained an isotropic chemical shielding of 113.98 ppm for the amide nitrogen. This calculation did not include K31, which makes a salt bridge with the side chain of E27. However, extending the long chain to include K31 in the Model C vacuum calculation yielded a more shielded value of 117.94 ppm, bringing it closer to the experimental value (Fig. 4a). This shielding effect of 3.96 ppm is due to the charge on K31’s side chain. In comparison, a proton unit charge placed on the ε-amine of K31 produced a 4.77 ppm shielding effect in the Model A vacuum calculation (Table S3). Interestingly, having E27 in its neutral form can significantly deshield its amide nitrogen, as suggested by the difference (11.74 ppm) between its Model A and “Model A neutral” calculations (Table 1). Indeed, making E27 neutral while keeping other ionizable side chains charged (in Model C) yields an isotropic chemical shielding of 124.25 ppm. Thus, protonation of the side chain can make E27 not an outlier.
Fig. 3.
Comparison of the calculated isotropic 15N chemical shieldings with experimental data for GB3. (a) “Model C neutral” and (b) Model C versus solid-state NMR data (BioMagResBank accession number 15283 (Nadaud et al. 2007)). (c) Model C versus solution NMR data (Gronenborn et al. 1991). Residue E27 is not shown in b and c because its calculated chemical shielding (Model C) lies beyond the range shown here (see Fig.4).
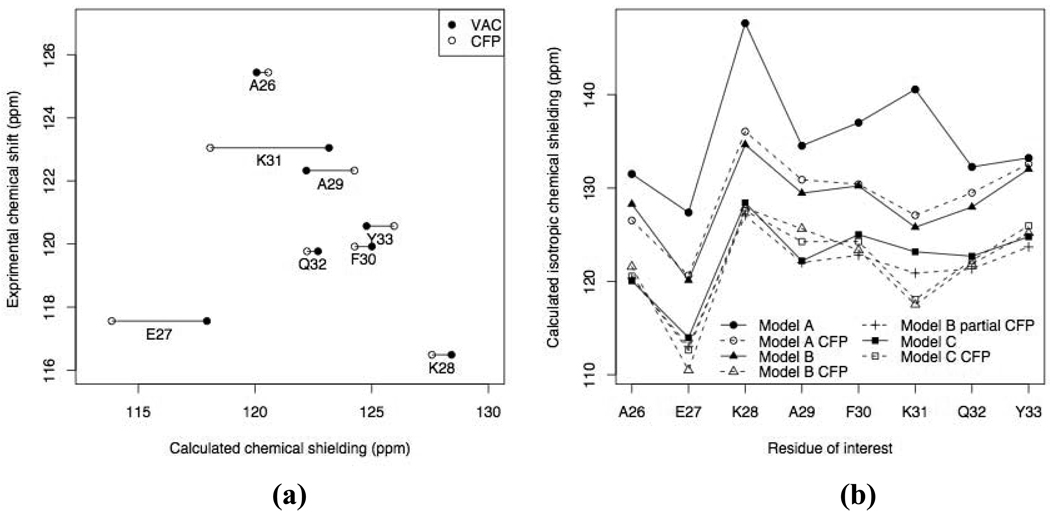
Fig. 4.
(a) Comparison of the isotropic 15N chemical shielding from Model C vacuum (solid circles) and Model C CFP (open circles) calculations with experimental (solution NMR) data. Note that the E27 data in this plot represent the results from Model C extended to include K31. (b) Comparison of the isotropic 15N chemical shieldings for selected helical residues calculated using various models considered in this study
In principle, there can be other possible combinations of ionization states of D22, D24, D27, K28, K31, and D36 that are involved here (Table 1). The two approaches shown here emphasize the complexity of calculating backbone 15N chemical shielding when dealing with uncertainties of the charge states of ionizable side chains. On the other hand, a detailed comparison with experimental NMR data might provide useful information on the ionization state of these residues.
Counterions were not explicitly included in our calculations, primarily because the amino acid composition and the structure of GB3’s α-helix are such that every charged side chain (except for D22 at the very N-terminus and D36 at the very C-terminus) has a salt-bridge partner (E27–K31, E24–K28), which could naturally balance its charge effect. Of the long-chain fragments used in Model C calculations, the one for K28 was neutral (as was the extended fragment for E27, see above), while the rest of the fragments had one or two unbalanced charges. Including the extra residues necessary for charge balancing would have further increased the size of the fragment. However, the effect of those unbalanced charges is generally small, as can be inferred from Table 1 (compare, for example, Model C with Model C −CH3), perhaps because of the rather long distances from most of these charged groups to the amide nitrogen of interest. To explore this effect further, we performed a dipeptide-model calculation in which we included point charges mimicking the side chains that could serve as “counterions” but were not present in the corresponding Model C fragments. The results (Table S3) show that the effect of these additional charges on 15N chemical shielding is generally small, except for E27, where including the side chain charge of K31 introduces a significant shift in the shielding, as discussed above.
The Tensor
Comparing the shielding tensor’s principal values between the calculations with “Model C neutral” and “Model C” (Table S2), the variation mainly exits in the least and most shielded components, σ11 and σ33, while the intermediate component, σ22, appears less susceptible to model selection. Residue E27 showed the biggest difference in all three principal components between these two calculations, with a 20 ppm difference in σ11. There is a generally good agreement between these two models in the orientation of the principal components of the chemical shielding tensor (Table S2).
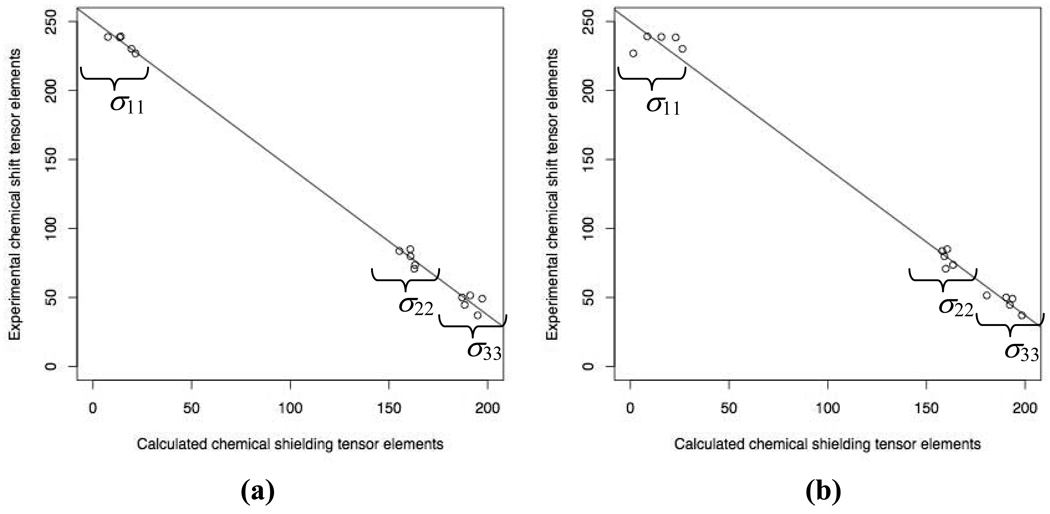
Experimental data for all three principal components of GB3’s 15N chemical shift tensors are not available. However, these data exist for most residues of protein GB1 (Wylie et al. 2007), which is highly homologous to GB3. In fact, all helical residues of GB3 are present in GB1, except for E24 and A29, which are an alanine and a valine, respectively, in GB1. Therefore we compared our calculated principal values of the 15N chemical shielding tensor for A26, E27, K28, K31, and Y33 in GB3 with the corresponding values of the chemical shift tensor of these residues in GB1, obtained by solid-state NMR measurements (Fig. 5). We found that the individual principal values of the calculated chemical shielding tensor are in good agreement with the experimental data. Over the whole range of variation in the tensor’s principal values, the difference between the results of “Model C neutral” and “Model C” calculations is small (Fig. 5).
Fig. 5.
Comparison of the principal values of the calculated 15N chemical shielding tensor for GB3 with the corresponding values of the experimental chemical shift tensor for GB1 (from solid-state NMR measurements (Wylie et al. 2007)). The model used and the parameters of the regression line are as follows: (a) Model C, intercept = 250.88 ± 2.24 ppm, slope = −1.07 ± 0.02; (b) “Model C neutral”, intercept = 249.98 ± 4.11 ppm, slope = −1.07 ± 0.03
CFP calculations
The difference between a vacuum calculation and a CFP calculation is a useful indicator of whether all necessary electrostatic effects are taken into account in the vacuum calculation. For example, when using a “three-fragment” model (Model B) there are large differences between the CFP calculation and the vacuum calculation (Table 1). This suggests that the fragment that is used in the vacuum calculation is too small. When using Model C which includes every residue from the direct hydrogen bonding partner to the indirect hydrogen bonding partner, not only the difference between vacuum and CFP calculations becomes smaller in general (Table 1 and Fig. 4b) but also the correlation between the vacuum calculation and the experiment becomes better, with a |r| value of 0.93, compared to 0.68 for Model B vacuum calculation and 0.54 for “Model B CFP” calculation (E27 was not included in this analysis).
From Table 1 and Fig. 4b, we observe that a simple CFP calculation for one model is close to a vacuum calculation for the next-complexity-level model. That is, Model A CFP calculation is very similar to Model B vacuum calculation and, likewise, Model B CFP is in general very close to Model C vacuum calculation. Although the CFP calculations include all point charges representing the atoms from the rest of the protein, only certain charges that are close enough to the fragment under consideration can influence the distribution of the electrons by perturbing the wave function and hence potentially affect the 15N chemical shielding. For example, Model B CFP calculation shows on average ~7 ppm deshielding of 15N compared to the Model B calculation, but including only point charges for the remaining helical residues from Model C yields most of the deshielding effect already (Table 1).
Conclusions
We performed density functional calculations of backbone 15N chemical shielding tensor for selected helical residues in protein G (GB3) and compared the isotropic chemical shielding and the principal values of the shielding tensor with experimental chemical shift data. We explored the effect of electrostatic interactions in a protein on the calculated 15N chemical shielding and found that:
To calculate the chemical shielding of backbone 15N in residue i, the hydrogen bonding partners and the residues that contribute to the helical dipole need to be included. Their side chains, when not charged, do not influence much the chemical shielding of 15N of interest; when charged, however, they can introduce an additional source of variation to the calculated 15N chemical shielding.
To accurately predict 15N chemical shielding when adopting charged forms of the ionizable side chains, it is important to include all charges that can potentially influence the 15N chemical shielding.
Tensor elements calculation yeilds a good correlation with experiments in general and the slope is close to the ideal value of −1. The variation exists mainly in the σ11 and σ33 components while σ22 is less affected by the charge states of the ionizable side chains that surround the amide nitrogen site.
CFP calculation can serve as an indicator of whether all relevant long-range electrostatic effects have been accounted for in the vacuum calculation. In the example of GB3, the rest of the protein does not seem to exert much of an effect, and the “long-chain” model (Model C) in vacuum seems to be adequate for computing 15N chemical shielding in the α-helix.
Note that this study focused on an α-helix, where the spatial relationship between various atoms is different from that in, for example, extended conformation. Therefore these conclusions apply specifically to helical residues and may or may not be applicable to other secondary structures. Similar calculations (currently underway) for the other parts of the protein are expected to address this issue. Although this study covered different residues in the helix, it is inevitably limited by the amino acid composition of GB3. Comparison with experimental data for a broad range of proteins is required in order to reach a better understanding of the accuracy of the computational approaches used here and the ways to improve them.
Supplementary Material
Acknowledgements
Supported by NIH grant GM065334 to DF and by American Chemical Society Petroleum Research Fund (44481-G6) and Francqui Foundation to DSK. We thank Gabriel Cornilescu, Chad Rienstra, and Ben Wylie for making available detailed experimental chemical shift data for comparison.
References
- Bader R. Utilizing the charge field effect on amide N-15 chemical shifts for protein structure validation. J Phys Chem B. 2009;113:347–358. doi: 10.1021/jp807362v. [DOI] [PubMed] [Google Scholar]
- Becke AD. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys Rev A. 1988;38:3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- Becke AD. Density-functional thermochemistry. III. The role of exact exchange. J Chem Phys. 1993;98:5648–5652. [Google Scholar]
- Cai L, Fushman D, Kosov DS. Density functional calculations of N-15 chemical shifts in solvated dipeptides. J Biomol NMR. 2008;41:77–88. doi: 10.1007/s10858-008-9241-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chesnut DB, Rusiloski BE, Moore KD, Egolf DA. Use of locally dense basis-sets for nuclear magnetic resonance shielding calculations. J Comp Chem. 1993;14:1364–1375. [Google Scholar]
- Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. A second generation force-field for the simulation of proteins, nucleic acids, and organic molecules. J Am Chem Soc. 1995;117:5179–5197. [Google Scholar]
- Cornilescu G, Delaglio F, Bax A. Protein backbone angle restraints from searching a database for chemical shift and sequence homology. J Biomol NMR. 1999;13:289–302. doi: 10.1023/a:1008392405740. [DOI] [PubMed] [Google Scholar]
- de Dios AC, Laws DD, Oldfield E. Predicting C-13 nuclear magnetic resonance chemical shielding tensors in zwitterionic L-threonine and L-tyrosine via quantum chemistry. J Am Chem Soc. 1994;116:7784–7786. [Google Scholar]
- de Dios AC, Oldfield E. Methods for computing nuclear magnetic resonance chemical shielding in large systems - multiple cluster and charge field approaches. Chem Phys Lett. 1993;205:108–116. [Google Scholar]
- de Dios AC, Pearson JG, Oldfield E. Chemical shifts in proteins - an ab initio study of C-13 nuclear magnetic resonance chemical shielding in glycine, alanine, and valine residues. J Am Chem Soc. 1993a;115:9768–9773. [Google Scholar]
- de Dios AC, Pearson JG, Oldfield E. Secondary and tertiary structural effects on protein NMR chemical shifts: An ab initio approach. Science. 1993b;260:1491–1496. doi: 10.1126/science.8502992. [DOI] [PubMed] [Google Scholar]
- Ditchfield R. Self-consistent perturbation theory of diamagnetism .1. Gauge-invariant LCAO method for NMR chemical shifts. Mol Phys. 1974;27:789–807. [Google Scholar]
- Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JA, Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. Gaussian 03, Revision C.02. Wallingford, CT: Gaussian, Inc.; 2004. [Google Scholar]
- Fushman D, Cowburn D. Nuclear magnetic resonance relaxation in determination of residue-specific N-15 chemical shift tensors in proteins in solution: Protein dynamics, structure, and applications of transverse relaxation optimized spectroscopy. Meth Enzym. 2001;339:109–126. doi: 10.1016/s0076-6879(01)39312-6. [DOI] [PubMed] [Google Scholar]
- Fushman D, Tjandra N, Cowburn D. Direct measurement of N-15 chemical shift anisotropy in solution. J Am Chem Soc. 1998;120:10947–10952. [Google Scholar]
- Gronenborn AM, Filpula DR, Essig NZ, Achari A, Whitlow M, Wingfield PT, Clore GM. A novel, highly stable fold of the immunoglobulin binding domain of streptococcal protein G. Science. 1991;253:657–661. doi: 10.1126/science.1871600. [DOI] [PubMed] [Google Scholar]
- Hall JB, Fushman D. Variability of the 15N chemical shielding tensors in the B3 domain of protein G from 15N relaxation measurements at several fields. Implications for backbone order parameters. J Am Chem Soc. 2006;128:7855–7870. doi: 10.1021/ja060406x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey W, Dalke A, Schulten K. VMD - Visual Molecular Dynamics. J Mol Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Le HB, Oldfield E. Ab initio studies of amide-N-15 chemical shifts in dipeptides: Applications to protein NMR spectroscopy. J Phys Chem. 1996;100:16423–16428. [Google Scholar]
- Lee CT, Yang WT, Parr RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron-density. Phys Rev B. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- Lipsitz RS, Tjandra N. 15N chemical shift anisotropy in protein structure refinement and comparison with NH residual dipolar couplings. J Magn Reson. 2003;164:171–176. doi: 10.1016/s1090-7807(03)00176-9. [DOI] [PubMed] [Google Scholar]
- Nadaud PS, Helmus JJ, Jaroniec CP. C-13 and N-15 chemical shift assignments and secondary structure of the B3 immunoglobulin-binding domain of streptococcal protein G by magic-angle spinning solid-state NMR spectroscopy. Biomol. NMR Assign. 2007;1:117–120. doi: 10.1007/s12104-007-9041-0. [DOI] [PubMed] [Google Scholar]
- Shen Y, Bax A. Protein backbone chemical shifts predicted from searching a database for torsion angle and sequence homology. J Biomol NMR. 2007;38:289–302. doi: 10.1007/s10858-007-9166-6. [DOI] [PubMed] [Google Scholar]
- Shen Y, Lange O, Delaglio F, Rossi P, Aramini JM, Liu GH, Eletsky A, Wu YB, Singarapu KK, Lemak A, Ignatchenko A, Arrowsmith CH, Szyperski T, Montelione GT, Baker D, Bax A. Consistent blind protein structure generation from NMR chemical shift data. Proc Natl Acad Sci USA. 2008;105:4685–4690. doi: 10.1073/pnas.0800256105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Y, Vernon R, Baker D, Bax A. De novo protein structure generation from incomplete chemical shift assignments. J Biomol NMR. 2009;43:63–78. doi: 10.1007/s10858-008-9288-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulmer TS, Ramirez BE, Delaglio F, Bax A. Evaluation of backbone proton positions and dynamics in a small protein by liquid crystal NMR spectroscopy. J Am Chem Soc. 2003;125:9179–9191. doi: 10.1021/ja0350684. [DOI] [PubMed] [Google Scholar]
- Vila JA, Scheraga HA. Factors affecting the use of 13C(alpha) chemical shifts to determin,refien, and validate protein structures. Proteins. 2007;71:641–654. doi: 10.1002/prot.21726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolinski K, Hinton JF, Pulay P. Efficient implementation of the Gauge-independent toamic orbital method for NMR chemical-shift calculations. J Am Chem Soc. 1990;112:8251–8260. [Google Scholar]
- Wylie BJ, Schwieters CD, Oldfield E, Rienstra CM. Protein structure refinement using 13C alpha chemical shift tensors. J Am Chem Soc. 2009;131:985–992. doi: 10.1021/ja804041p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wylie BJ, Sperling LJ, Frericks HL, Shah GJ, Franks WT, Rienstra CM. Chemical-shift anisotropy measurements of amide and carbonyl resonances in a microcrystalline protein with slow magic-angle spinning NMR spectroscopy. J Am Chem Soc. 2007;129:5318–5319. doi: 10.1021/ja0701199. [DOI] [PubMed] [Google Scholar]
- Xu XP, Case DA. Automated prediction of N-15, C-13(alpha), C-13(beta) and C-13' chemical shifts in proteins using a density functional database. J Biomol NMR. 2001;21:321–333. doi: 10.1023/a:1013324104681. [DOI] [PubMed] [Google Scholar]
- Xu XP, Case DA. Probing multiple effects on 15N, 13C alpha, 13C beta, and 13C ' chemical shifts in peptides using density functional theory. Biopolymers. 2002;65:408–423. doi: 10.1002/bip.10276. [DOI] [PubMed] [Google Scholar]
- Zuiderweg ERP. Mapping protein-protein interactions in solution by NMR Spectroscopy. Biochemistry. 2002;41:1–7. doi: 10.1021/bi011870b. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.