Single-molecule Force Spectroscopy Approach to Enzyme Catalysis

Abstract

Enzyme catalysis has been traditionally studied using a diverse set of techniques such as bulk biochemistry, x-ray crystallography, and NMR. Recently, single-molecule force spectroscopy by atomic force microscopy has been used as a new tool to study the catalytic properties of an enzyme. In this approach, a mechanical force ranging up to hundreds of piconewtons is applied to the substrate of an enzymatic reaction, altering the conformational energy of the substrate-enzyme interactions during catalysis. From these measurements, the force dependence of an enzymatic reaction can be determined. The force dependence provides valuable new information about the dynamics of enzyme catalysis with sub-angstrom resolution, a feat unmatched by any other current technique. To date, single-molecule force spectroscopy has been applied to gain insight into the reduction of disulfide bonds by different enzymes of the thioredoxin family. This minireview aims to present a perspective on this new approach to study enzyme catalysis and to summarize the results that have already been obtained from it. Finally, the specific requirements that must be fulfilled to apply this new methodology to any other enzyme will be discussed.

Introduction

Enzymes are one of the main actors in a living organism, as they are able to specifically catalyze a great number of chemical reactions necessary for life. Enzyme-catalyzed reactions can proceed 10¹⁰–10²³ times faster than the corresponding uncatalyzed counterparts (1). In the last decades, the mechanisms that sustain catalytic activity have been inspected by increasingly sophisticated techniques, from bulk biochemistry assays to high-resolution x-ray crystallography or NMR. These studies have identified many structural features and conformational changes necessary for the catalytic activity of enzymes. As a consequence, different pictures of how enzymes work have emerged. From the primigenious “lock and key” model to the current transition state theory, a considerable improvement in our knowledge of the mechanisms of enzyme catalysis has been achieved (2). Unfortunately, we are still far from a definitive description of enzymatic activity, as demonstrated by the systematic reduced catalytic efficiency shown by de novo designed enzymes (3). New approaches to the study of enzyme catalysis are required to fill the gaps that still exist.

In the last decades, it has been postulated that enzyme dynamics may play an important role in catalysis (4–7). In particular, the ability to distort substrates may be considered as a dynamic property of enzymes (1, 8). As most proteins, enzymes are dynamic entities whose conformation is not rigid but fluctuates (9). Experimentally, two types of conformational fluctuations with different time scales have been found for enzymes, i.e. those on the nano- to picosecond time scale and those on the milli- to microsecond time scale (10). The latter are coincident with the time scales reported for most catalytic cycles. Even though the proposal that enzyme dynamics is important for catalysis is not free from controversy (11), it is supported by a number of experimental evidences. For example, it has been observed that the theoretically predicted hinge centers in most enzymes colocalize with their catalytic sites (12). In addition, the fact that mutations far from the catalytic site are able to reduce the catalytic rate of enzymes has been related to the hampering of motions important for catalysis (13, 14). Furthermore, NMR experiments have identified multiple conformations in the catalytic pathways of different enzymes whose proportions change as the reaction develops (15, 16). Accordingly, single-molecule fluorescence and fluorescence energy transfer assays have been able to correlate changes in the catalytic rate of an enzyme with conformational fluctuations (17, 18). Still, exploring the dynamic sub-angstrom rearrangements of the atoms participating in catalysis is experimentally challenging (10).

One method especially suited to the investigation of the dynamics of proteins over a wide range of time scales with atomic resolution is NMR (19, 20); however, with NMR, there is no easy means to separate the motions relevant to catalysis from those that are not (21). In addition, NMR determinations usually require working under steady-state conditions, which are accessible only for reversible reactions (20). Combined quantum mechanics/molecular mechanics methods are used to study the relevance of specific enzyme motions in the catalytic activity (10). Even though quantum mechanics/molecular mechanics simulation techniques will presumably be improved over the coming years (22), important limitations remain. For instance, it is not likely that simulations can reach the time scales of most enzymatic reactions in the near future. Therefore, there is a need to develop new assays able to explore the dynamics of enzymes during catalysis, providing new information that complements the results obtained by existing experimental approaches (1). In this regard, force is a highly appropriate probe if it can be used to dynamically alter the system on a relevant scale. The application of force to a substrate could, in that case, explain motions that are important for catalysis. In fact, simple chemical reactions are modulated by force as a consequence of the spatial rearrangements of the participating atoms (23). What scale is relevant for these interactions? As the stiffness of a covalent bond is on the order of ∼10 nN/Å (24)⁴ and the transition state distance for a chemical reaction typically is a fraction of an angstrom, this necessitates an appropriate force probe to be in the range of ∼100 pN up to ∼1 nN per bond, which is specially suited for atomic force microscopy (AFM) determinations. Taking into account that force is a vector and not a scalar, measuring the effect of force on bulk reactions cannot be easily achieved (23). The appearance of single-molecule techniques has overcome this limitation. For example, both fluorescence and optical tweezers have been extensively used to detect forces and motions of molecular motors (25, 26). Only recently has it become possible to measure the influence of force on the enzymatic cleavage of covalent bonds. In particular, single-molecule force spectroscopy has emerged as a useful tool to study the force dependence of the reduction of disulfide bonds by different thioredoxins (Trxs) (14, 27). In this approach, a mechanical force is directly applied to the substrate disulfide bond. It has been shown that the force dependence of the reaction is directly related to the sub-angstrom rearrangements of enzyme and substrate during catalysis. This minireview aims to present a perspective on this new methodology to study enzyme catalysis.

Disulfide Bond Reduction Studied by Single-molecule Force Spectroscopy

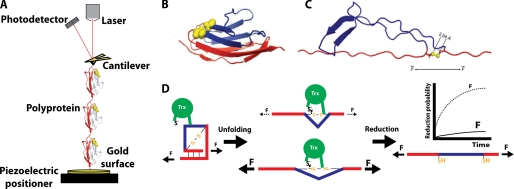
Single-molecule force spectroscopy by AFM has proven useful to study the force dependence of the reduction of disulfide bonds both by chemicals and by different Trxs (27, 28). In the standard assay, a polyprotein composed of several copies of an immunoglobulin domain from human cardiac titin (I27) is held between the tip of an AFM cantilever and a gold surface on top of a piezoelectric positioner (Fig. 1A). Polyproteins composed of eight I27 modules are usually employed. Each one of the I27 modules includes an engineered disulfide bond between residues 32 and 75, (I27_G32C-A75C)₈ (Fig. 1B). In the force-clamp mode of AFM, it is possible to set the force exerted to the polyprotein up to several hundreds of piconewtons (29). In this mode of operation, the deflection of the cantilever is held constant because of an electronic feedback system that controls the extension of the polyprotein via the piezoelectric positioner (30). Response times of ∼5 ms can be easily achieved with the current instrumentation.

FIGURE 1.

Single-molecule force spectroscopy assay for the detection of single reduction events by the enzyme Trx. A, in the standard assay, (I27_G32C-A75C)₈ is stretched between the tip of an AFM cantilever and a gold surface. In the force-clamp mode, the signal received by the photodetector is kept constant by an electronic feedback system that controls the extension of the polyprotein via the piezoelectric positioner. Note that, for the sake of simplicity, only three monomers of the polyprotein are depicted in the diagram. B, shown is the I27 monomer, with the residues forming the disulfide bond indicated in yellow (Protein Data Bank code 1TIT). C, shown is the structure of one I27_G32C-A75C module after unfolding according to molecular dynamics simulations (27). Because of the presence of the disulfide bond, only part of the protein unfolds (shown in red). D, as long as the modules remain folded, the disulfide bond in each I27_G32C-A75C domain cannot be reduced by Trx. The unfolding event acts as a steric switch that allows the disulfide bond to be accommodated into the active site of Trx and be reduced. Concomitant to the reduction, a second length increase is detected, as the trapped residues extend (shown in blue). The probability of reduction drastically depends on the applied force as a consequence of the dynamics of enzyme and substrate during catalysis.

The behavior of both I27 and I27_G32C-A75C upon application of mechanical loads has been thoroughly examined by AFM (31, 32). The unfolding rate of I27_G32C-A75C at ∼200 pN is high (30 s⁻¹) (28). Thus, a double-pulse protocol is employed to detect the reduction of disulfide bonds. A first pulse of force (160–190 pN during 0.3–1.0 s) unfolds the domains of the polyprotein. In these experiments, the disulfide bonds act as force transducers; therefore, the I27_G32C-A75C modules extend only up to the disulfide bonds (Fig. 1, C and D), as forces higher than 1 nN are required to cleave covalent bonds (33). The individual unfolding events can be unambiguously detected as step increases of ∼10.8 nm in the length of the polyprotein, which give rise to a well defined staircase in a length versus time plot (Fig. 2A). Each step in size is accompanied by a sudden decrease in the force, which is rapidly compensated by the feedback (Fig. 2A). Therefore, this series of unfolding steps serves as a well defined fingerprint that unambiguously distinguishes the polyprotein of interest from any other spurious interactions. In addition, the unfolding events promote a steric switch that now allows the disulfide bonds that were buried in the protein to be reduced by reducing agents contained in the solution (Fig. 1D) (27, 28, 34). After the unfolding of the domains, a second pulse of force is applied for up to minutes to monitor single-disulfide reductions. When a disulfide bond is reduced, the region of the protein whose unfolding was hampered by the disulfide bond now extends. These extensions are recorded as a second series of steps of ∼13.2 nm/disulfide bond reduction (Fig. 2A). As in the unfolding steps, a sudden decrease in the force accompanies the reduction events (Fig. 2A). Generally, 15–50 traces, as shown in Fig. 2A, are accumulated per force. In the more straightforward analysis, the traces are averaged and fitted with a single exponential with time constant τ (Fig. 2B). From this fit, it is possible to obtain the reduction rate at a given force (r = 1/τ) (28). It has been observed that, as a consequence of the detachment kinetics of the polyprotein from the surface or the cantilever, the results can be biased to faster rates. To avoid this artifact, only traces with long detachment times should be included in the analysis (35). As an alternative to exponential fits, a dwell time analysis technique has been implemented recently for the study of single-molecule mechanochemical reactions (36). This procedure overcomes the limitations of exponential fits when multiple-reaction pathways occur simultaneously; however, a large pool of events (>1000) needs to be collected.

FIGURE 2.

Single-molecule force spectroscopy as a probe to study chemical reactions and enzyme catalysis. A, when (I27_G32C-A75C)₈ is pulled at 165 pN, a series of 10.8-nm steps is detected, reflecting the rapid unfolding of the modules up to the disulfide bond (see inset). If a reducing agent such as the enzyme Trx is present in solution (red trace), a second series of 13.2-nm steps is detected. These correspond to the reduction of the disulfide bonds and the subsequent release of the residues from 32 to 75. No reduction happens if there is no reducing agent in the solution (blue trace). Note the sharp peaks in the force trace reflecting the fast response of the feedback system after the unfolding and reduction events. B, 15–50 traces as that shown in Fig. 2A are averaged per force, and a single exponential is fitted to each averaged trace (smooth line) to get the reduction rates (r). C, shown is the force dependence of the reduction rate for a small reducing agent (l-Cys, 12.5 mm; blue circles), human Trx (10 μm; red squares), and E. coli Trx (10 μm; green triangles). Error bars were obtained by bootstrapping methods (27). D, the diagram represents the energy landscape for the thiol/disulfide exchange reaction under force. The application of force reduces the activation energy by F·Δx. Force-clamp determinations indicate the distance to the transition state (Δx) with sub-angstrom resolution. E, the schematic shows the Trx-catalyzed reduction of a disulfide bond in a stretched polypeptide. To acquire the correct geometry for an S_n2 reaction, the substrate disulfide bond has to rotate by angle θ, which causes a contraction of the substrate against the pulling force. It has been hypothesized that this contraction is responsible for the negative Δx obtained in single-molecule force spectroscopy experiments (see text).

Chemical Reactions under Force at the Single-molecule Level

To better understand the effects of force on a reaction catalyzed by an enzyme, let us first consider the case of more simple uncatalyzed chemical reactions. It has been shown that the rate of reduction of the disulfide bonds in (I27_G32C-A75C)₈ by small reducing agents such as dithiothreitol (DTT) or l-Cys is exponentially dependent on the applied force (Fig. 2C) (28, 37, 38). The exponential dependence is given by a Bell-like (39) relationship: r(F) = A·exp((F·Δx − E_a)/k_B·T). In this expression, A is the attempt frequency, Δx is the distance to the transition state of the reaction, E_a is the activation energy barrier for the reaction, k_B is the Boltzmann constant, and T is the absolute temperature. Fitting the experimental results for the reduction by DTT to the equation above yields Δx = 0.34 Å (28). Interestingly, theoretical calculations have suggested that the length of the disulfide bond at the transition state of a simple S_n2 thiol/disulfide exchange reaction increases by ∼0.37 Å (40). These results then indicate that the changes in distance between the sulfur atoms at the transition state are responsible for the force dependence of the reaction. Indeed, when different reducing agents are used, the measured distances to the transition states of the corresponding reactions are in agreement with the physicochemical characteristics of the reactants (37, 38). For thiol-initiated disulfide bond reductions such as DTT, β-mercaptoethanol, or glutathione, Δx = 0.31 ± 0.05 Å. When phosphine-based reducing agents are employed, Δx is significantly higher (0.44 ± 0.03 Å). Such an increase in the distance to the transition state for the latter compounds is again in agreement with quantum chemical calculations, which show that the distance between sulfur atoms in the transition states of phosphine-based reactions is longer than that in thiol-initiated reductions (37). In addition, it has been demonstrated for phosphine-initiated reductions that Δx decreases when glycerol is incorporated into the aqueous solution (37). This result provides a direct test of theoretical calculations of the role of solvent molecules in the transition state of a bimolecular S_n2 reaction. In summary, the force-clamp experiments using small reducing agents show that the mechanical force imposes a one-dimensional reaction coordinate for the reaction (Fig. 2D). In this context, Δx reports on the progression along that reaction coordinate with sub-angstrom resolution, providing valuable information about the geometry of the transition state. In addition, the information gained about the transition state from force-clamp determinations is probably independent of its lifetime. The rational behind this is that, no matter how short- or long-lived a transition state is, it will always be subjected to force. Thus, in theory, the force spectroscopy methodology applied to chemical reactions might be able to inspect the geometric properties of transition states independently of their lifetimes.

Force as a New Probe of Enzyme Catalysis

From the experiments using small reducing agents, it is clear that chemical reactions resulting in changes in bond distance will be force-dependent and that single-molecule force spectroscopy is able to provide sub-angstrom information about the transition state of the reaction. The same approach has also been employed to investigate the mechanism of disulfide bond reduction by members of the Trx family of enzymes (14, 27). Trxs show a highly conserved active site (CXXC) that catalyzes the reduction of target disulfide bonds involved in a multitude of cellular processes (41, 42). Several methods based on bulk spectrophotometry have been widely used to determine the activity of Trxs. These methods are based on the oxidation of NADPH in the presence of Trx reductase or ribonucleotide reductase (43, 44); the increase in turbidity of insulin solutions concomitant with the reduction of the disulfide bonds in that peptide (43); or the use of Ellman's reagent (5,5′-dithiobis(nitrobenzoic acid)), which generates colored products upon reduction by thiol groups (41). The change in the intrinsic fluorescence of Trx has also been used to measure rates of enzyme oxidation and reduction (45). Although highly effective in monitoring the overall activity of Trx enzymes, these methods do not probe the chemical mechanisms underlying their catalysis. The main reason is that many factors influence the measurements, such as the kinetics of reduction of Trx by Trx reductase and the kinetics of insulin aggregation after disulfide bond reduction (14, 46). In addition, they have the limitations inherent to bulk assays, as they provide only average measurements of activity. In the case of the single-molecule force spectroscopy assays, the enzyme is kept in the reduced form because of the presence of Trx reductase and NADPH (the so-called Trx system). Therefore, the amount of oxidized Trx is negligible, and the measured activity reflects only the reduction of the disulfide bond in (I27_G32C-A75C)₈ at a given Trx concentration.

In contrast to DTT and other small reducing agents, human Trx-mediated disulfide reduction is strongly inhibited by force, with Δx = −0.79 Å (Fig. 2C) (27). A molecular interpretation of this result has been obtained from the crystal structure of human Trx in complex with a substrate peptide (Protein Data Bank code 1MDI). A peptide-binding groove is identified on the surface of the protein close to the catalytic cysteine. It is known that the reduction of a disulfide bond proceeds via an S_n2 mechanism, in which the three participating sulfur atoms form an ∼180° angle (47, 48). Given the fact that the disulfide bond in 1MDI forms an angle of ∼70° with respect to the axis of the groove, it is evident that the target disulfide bond must rotate with respect to the pulling axis to acquire the correct geometry for reaction (Fig. 2E). Taking into account the orientation of the disulfide bond with respect to the pulling force, it can be estimated that a 0.77-Å shortening of the substrate polypeptide is needed to align the participating sulfur atoms, in extraordinary agreement with the experimental Δx (−0.79 Å). This interpretation is supported by molecular dynamics simulations and a theoretical model that treats the substrate backbone as a freely jointed chain (27). Therefore, it appears that, different from what is observed for the reductions by small reducing agents, the change in bond distance at the transition state is not the main determinant of the force dependence for enzyme-catalyzed reactions. On the contrary, the dynamics of enzyme and substrate during catalysis are the main contributors to the measured Δx.

When Trx from Escherichia coli was assayed, a similar force dependence up to 200 pN was observed. However, this enzyme shows a second chemical pathway that becomes apparent only at higher forces (27). The two pathways seem to be independent of each other because mutants P34H and G47S selectively inhibit only the first pathway (14, 27). The second pathway of E. coli Trx is force-accelerated with Δx = 0.22 Å (Fig. 2C) (27). This catalytic mode might be explained by the reduction occurring without the peptide binding the groove; in this regard, the second pathway would be similar to the reduction by agents such as DTT and l-Cys (Fig. 2C).

In summary, the application of single-molecule force spectroscopy to the study of catalysis by Trxs, in combination with molecular dynamics simulations, provides detailed information about the dynamics of enzyme and substrate during catalysis. This information has been used to detect residue co-evolution in enzymatic activity, which would have gone unnoticed using standard bulk assays (14). Future work will address the relevance of the peptide-binding groove in the different catalytic pathways (49) and how the different Trx catalytic mechanisms have been shaped by evolution.

Single-molecule Force Spectroscopy Assays for Other Enzymatic Activities

The results obtained with Trx suggest that it will be highly informative to apply the single-molecule force spectroscopy methodology to other enzymes. In principle, the single-molecule assay for the reduction of disulfide bonds by Trx might be adapted to any other enzyme that catalyzes the cleavage of covalent bonds. This would allow a deeper understanding of different mechanisms of catalysis. Proteases, esterases, phosphodiesterases, glycosidases, and glycosyltransferases are enzymes with the ability to cleave covalent bonds (50). From what has been learned from the single-molecule assay for disulfide bond reduction, it is clear that any new experimental setup aimed at studying single-molecule bond cleavage under force should fulfill the following requirements. (i) The substrate should be incorporated into a macromolecule providing an unambiguous fingerprint after mechanical unfolding. (ii) The rate of substrate cleavage by the enzyme should be low when put together in solution so that no significant cleavage occurs in the time scale needed to conduct AFM experiments. (iii) The unfolding of the macromolecule should promote a steric switch in the substrate, rendering it sensitive to cleavage. (iv) Cleavage should be translated into a new increment in length of the macromolecule. It is conceivable that new substrates complying with the above checklist will be presented in the future and will be employed to gain insight into the catalytic mechanisms of enzymes other than Trx.

Conclusions

In this minireview, we have provided an overview of single-molecule force spectroscopy as an emerging method to probe the catalytic mechanisms of enzymes. So far, this approach has been used to study the reduction of disulfide bonds by Trx. From the force dependence of the reaction rate, new light has been shed on the dynamics of enzyme and substrate during catalysis. In particular, the Δx parameter, which is derived from exponential fits to the measured force dependence, reports on the spatial rearrangements of the participating atoms at the transition state of the reaction. These rearrangements can be dissected at the sub-angstrom scale in a manner unachievable by any other current experimental technique. When used in appropriate combination with other methods, single-molecule force spectroscopy has the promise of revealing new details in our quest to understand how enzymes truly work.