Bayesian Mediation Analysis

Abstract

This article proposes Bayesian analysis of mediation effects. Compared to conventional frequentist mediation analysis, the Bayesian approach has several advantages. First, it allows researchers to incorporate prior information into the mediation analysis, thus potentially improving the efficiency of estimates. Second, under the Bayesian mediation analysis, inference is straightforward and exact, which makes it appealing for studies with small samples. Third, the Bayesian approach is conceptually simpler for multilevel mediation analysis. Simulation studies and analysis of two datasets are used to illustrate the proposed methods.

Mediation analysis is a statistical method that help researchers understand the mechanisms underlying the phenomena they study. It has wide applications in psychology, prevention research, and other social sciences. The basic mediation framework involves a three variable system in which an independent variable causes a mediating variable, which, in turn, causes a dependent variable (Baron & Kenny, 1986; MacKinnon, 2008). The aim of mediation analysis is to determine whether the relation between the independent variable and the dependent variable is due, wholly or in part, to the mediating variable.

Considerable research has been conducted in mediation analysis, including that of Judd and Kenny (1981), James and Brett (1984), Baron and Kenny (1986), MacKinnon and Dwyer (1993), Collins, Graham and Flaherty (1998), MacKinnon, Krull and Lockwood (2000), MacKinnon et al. (2002), Kraemer, Wilson, Fairburn and Agras (2002), and Shrout and Bolger (2002), among others. These works mainly focus on the single-level mediation model that is suitable for analyzing independent data. Recently, there is emerging interest in multilevel mediation analysis that is useful for analyzing hierarchical and repeated measures data. See, for example, the work of Kenny, Kashy, and Bolger (1998), Krull and MacKinnon (1999, 2001), Raudenbush and Sampson (1999), Kenny, Korchmaros and Bolger (2003), and Bauer, Preacher and Gil (2006). Comprehensive reviews on mediation analysis can be found in publications by MacKinnon, Fairchild and Fritz (2006) and MacKinnon (2008). In this growing literature, no research has yet focused on mediation analysis from the Bayesian perspective.

This article proposes Bayesian analysis of mediation effects in both single-level and multilevel models. Compared to conventional frequentist mediation analysis, the Bayesian approach has several advantages. First, it allows researchers to incorporate available prior information into the mediation analysis. This is a useful way of incorporating the information psychologists usually have before conducting experiments to test a mediation process. Such prior information arises from pilot studies or other related studies, and often includes information about limits (or distribution) on values of regression coefficients between the independent variable, the mediating variable, and the dependent variable. Incorporating such prior information into the mediation analysis is an efficient use of resources, and also improves the efficiency of estimates.

The second advantage of Bayesian mediation analysis is the ability to construct credible intervals for indirect effects for simple as well as complex mediation models in a straightforward manner. More important, such inferences are exact in finite samples, i.e., they do not impose restrictive normality assumptions on sampling distributions of estimates and do not rely on large sample approximations (Robert, 2007). This property makes the Bayesian approach especially appealing for studies with small samples. In contrast, the statistical inference of the indirect effects can be rather involved in conventional mediation analyses, as the sampling distribution of the estimate of the indirect effect does not follow a simple parametric distribution (MacKinnon et al., 2002). For convenience, a normal approximation is often used to construct confidence intervals, in which the standard error of the estimate of the indirect effect is estimated by the first-order or second-order Taylor expansion (Sobel, 1982; Aroian, 1947). However, as the sampling distribution of the estimate of the indirect effect actually is not normal (Bollen & Stine, 1990; Stone & Sobel, 1990; MacKinnon & Dwyer, 1993), the resulting inference is problematic for small samples. Several approaches have been proposed to address this problem. MacKinnon, Lockwood, Hoffman, West and Sheets (2002) proposed constructing confidence intervals based on the distribution of the product of two random variables. Other researchers (Bollen & Stine, 1990; Mackinnon, Lockwood & Williams, 2004; Shrout & Bolger, 2002) advocated a bootstrap approach without imposing any distribution assumption on the estimate of the indirect effect.

The third advantage of using a Bayesian perspective is that it provides a more natural and simpler mediation analysis in multilevel models (Gelman & Hill, 2007). As parameters are treated as random variables instead of fixed values, mediation analysis in multilevel models is conceptually natural in the Bayesian framework. Computationally, Markov chain Monte Carlo (MCMC) methods provide a unified tool that enables researchers to fit almost any complex multilevel model. In contrast, conventional multilevel mediation analysis is often burdened by difficulties of computation and estimation (Kenny, Korchmaros & Bolger, 2003).

Bayesian inference has drawn great attention in scientific research (Ashby, 2006; Malakoff, 1999). Bayesian inference has many strengths, and seems ideal for mediation analysis, especially for complex multilevel mediation analysis. The primary objective of this paper is to propose an alternative approach to conventional mediation analysis that is capable of incorporating prior information and making inference in a relatively convenient way, especially for complex multilevel models. For an accessible and excellent introduction to Bayesian statistics, see texts by Gelman, Carlin, Stern and Rubin (2003) and Gill (2008).

Conventional estimation of the mediated effect in a single-level mediation model

Let Y denote the dependent (or outcome) variable, X denote the independent variable, and M denote the mediating variable (or mediator). A single-level mediation model (Figure 1) can be expressed in the form of three regression equations:

$$Y={\beta }_1+\tau X+e_1$$ (1)

$$M={\beta }_2+\alpha X+e_2$$ (2)

$$Y={\beta }_3+\beta M+{\tau }^{\prime }X+e_3$$ (3)

where τ quantifies the relation between the independent variable and dependent variable, τ′ quantifies the relation between the independent variable and dependent variable after adjusting for the effect of the mediating variable, β quantifies the relation between the mediating variable and dependent variable after adjusting for the effects of the independent variable, and α measures the relationship between the independent variable and mediating variable. It is assumed that residuals e₁, e₂ and e₃ follow normal distributions with mean 0 and variance ${\sigma }_1^2,{\sigma }_2^2\text{and}{\sigma }_3^3$, respectively. The three mediation equations are clearly related. If we plug equation (2) into (3), and then compare the resulting equation with equation (1), some relationships among these equations are obvious. For example, β₁ = β₃ + ββ₂, αβ = τ − τ′, and e₁ = βe₂ + e₃. Actually, as discussed in below, to calculate the mediated effect, only two out of the three equations are needed.

Figure 1.

Diagram of the single-level mediation model.

The mediated effect can be calculated in two ways (MacKinnon & Dwyer, 1993). The first one is based on equation (1) and equation (3), and estimates the mediated effect by τ̂ − τ ^′ (Judd & Kenny, 1981), where τ̂ and τ ^′ are least-squares or maximum-likelihood estimates of τ and τ′. The second method involves equation (2) and equation (3), and estimates the mediated effect by α̂β̂. These two estimators of the mediated effect are equivalent in ordinary least squares regression for the single-level mediation model (MacKinnon, Warsi, & Dwyer, 1995), but are generally different in multilevel mediation models. In this paper, we focus on estimating αβ, but our method directly applies to estimating τ − τ′, as well.

There are several estimators of the standard error and approaches to constructing the confidence interval (CI) for the mediated effect (MacKinnon et al., 2002). A commonly used estimate of the standard error due to Sobel (1982) has the form

$${\widehat{\sigma }}_{\widehat{\alpha }\widehat{\beta }}=\sqrt{{\widehat{\alpha }}^2{\widehat{\sigma }}_{\widehat{\beta }}^2+{\widehat{\beta }}^2{\widehat{\sigma }}_{\widehat{\alpha }}^2}$$

where ${\widehat{\sigma }}_{\widehat{\alpha }}^2\text{and}{\widehat{\sigma }}_{\widehat{\beta }}^2$ are sampling variances of α̂ and β̂ , and a 95% CI for the mediated effect based on normal approximation is then given by α̂β̂ ± 1.96σ̂_α̂β̂. However, this symmetric CI does not perform well because the distribution of α̂β̂ is actually skewed. MacKinnon et al. (2004) discussed several improved CIs by taking into account the fact that α̂β̂ is not normally distributed, including the CI based on the distribution of the product of two normal random variables, and the CI based on the bootstrap method (Bollen & Stine, 1990; Shrout & Bolger, 2002).

Bayesian inference

Bayes theorem

The basic strategy of Bayesian inference is intuitive: after observing data from the current study, knowledge on an unknown parameter, say θ, is updated to incorporate newly obtained information. Central to Bayesian philosophy is the recognition that in addition to the data being quantified as a distribution, the unknown parameters are also quantified as distributions. In the Bayesian framework, all knowledge and uncertainty about unknown parameters are measured by probabilities. In contrast, conventional (or frequentist) statistical inference treats unknown parameters as unknown fixed values.

Before a study is conducted, researchers usually have some prior knowledge about an unknown parameter θ based on previous studies or expert opinions. Such prior information is routinely used to calculate statistical power and determine the sample size at the study design stage. In the Bayesian framework, the prior knowledge of θ is quantified by a probability distribution called the prior distribution, denoted by p(θ). After observing new data from the study, knowledge of θ is updated through Bayes Theorem:

$$p(\theta |\text{data})=\frac{p(\theta ,\text{data})}{p(\text{data})}=\frac{p(\theta )p(\text{data}|\theta )}{p(\text{data})}$$ (4)

where p(·|·) denotes a conditional distribution, p(data) = ∫ p(θ)p(data|θ)dθ, and p(data|θ) is the sampling distribution (or likelihood) of the data given the parameter. The resulting density p(θ |data) is referred to as a posterior distribution because it reflects probability beliefs on θ posterior to, or after, seeing the data. An equivalent form of (4) is obtained by omitting the factor p(data) that does not depend on θ and can thus be considered a constant. The posterior distribution of θ given the data is the product of prior information and likelihood of the data given θ, as follows

$$p(\theta |\text{data})\propto p(\theta )p(\text{data}|\theta )$$

Symbolically, it can be written as

$$\mathit{\text{Posterior}}\propto \mathit{\text{Prior}}\times \mathit{\text{Likelihood}}$$

Thus, the posterior distribution is computed (up to a proportionality constant) by multiplying the likelihood of data given the parameter by the prior density assigned to the parameter, thereby combining the prior information with data information.

One way of understanding the Bayesian combination of prior information and observed data is through the notion of shrinkage (Gelman et al., 2003). To illustrate the idea, suppose that we are interested in estimating the mean of depression score µ of a population based on n subjects with observations x₁, …, x_n, which follow a normal distribution with an unknown mean μ and a known variance σ². We further suppose that based on the prior information, the best estimate of μ, a priori, is µ₀. A convenient prior distribution of µ to quantify such prior information is a normal distribution centering at µ₀, say $N({\mu }_0,{\sigma }_0^2)$, where the value of ${\sigma }_0^2$ is chosen to reflect the uncertainty regarding the prior knowledge of the value of µ, i.e., µ₀. Applying Bayes Theorem, it can be shown that the posterior distribution of µ is a normal distribution,

$$\begin{array}{cc}p(\mu |x_1,\cdots ,x_n)\hfill & =N\left(\frac{{({\sigma }^2/n)}^{-1}\overline{x}+{\sigma }_0^{-2}{\mu }_0}{{({\sigma }^2/n)}^{-1}+{\sigma }_0^{-2}},\frac{1}{{({\sigma }^2/n)}^{-1}+{\sigma }_0^{-2}}\right)\hfill \\ \hfill & =N\left((1-\lambda )\overline{x}+\lambda {\mu }_0,\frac{1}{{({\sigma }^2/n)}^{-1}+{\sigma }_0^{-2}}\right)\hfill \end{array}$$

where $\lambda ={\sigma }_0^{-2}/[{\sigma }_0^{-2}+{({\sigma }^2/n)}^{-1}]$ is a fraction between 0 and 1, measuring the relative precision of the prior distribution and the observed mean x¯. A natural estimate of µ is its posterior mean (1 − λ)x¯ + λµ₀. This estimate is called a shrinkage estimate because it shrinks the classical maximum likelihood estimate x¯ toward the prior mean µ₀. The degree of shrinkage is controlled by the relative precision (i.e., the inverse of the variance) of observations and the prior distribution. For example, with strong prior information on µ, i.e., there is confidence that the true value of parameter µ is close to µ₀, a small value of ${\sigma }_0^2$ should be chosen so that the estimate shrinks more toward µ₀. If the prior information on µ is weak, we may assign a large value to ${\sigma }_0^2$ so that the shrinkage becomes negligible, and the estimate is essentially the maximum likelihood estimate x¯. Figure 2 shows how the posterior distribution is affected by the strength of the prior information (or distribution). It is clear that stronger prior information (i.e., small value of ${\sigma }_0^2$) causes more shrinkage of posterior distribution toward the prior distribution.

Figure 2.

Panel 1a–c show the prior, likelihood and posterior under weak prior information (µ ~ N(6, 100²)). In this case, the prior information has negligible effect on the posterior distribution. Panel 2a–c show the prior, likelihood and posterior under moderate prior information (µ ~ N(6, 6²)). The posterior distribution is shrunk toward the prior distribution. Panel 3a–c show the prior, likelihood and posterior under strong prior information (µ ~ N(6, 2²)). In this case, the prior information has strong effect on the posterior distribution. The likelihood is that x¯ ~ N(16, 4²).

Bayes estimates

From the Bayesian perspective, all knowledge about a parameter after observing the data is contained in the posterior distribution (O’Hagan & Forster, 2004). The most informative way to present results is to plot the posterior distribution of the parameter. However, some summary measures of the posterior distribution are often very useful in practice. In particular, a commonly used point estimate of the parameter θ is its posterior mean, given by

$$\widehat{\theta }=E(\theta |\mathit{\text{data}})={\displaystyle \int \theta f(\theta |\mathit{\text{data}})\mathrm{d}\theta .}$$

Alternatively, the posterior mode can also be used as a point estimate of θ, especially when the posterior distribution is skewed. Similar to the conventional standard error, the posterior standard deviation provide a Bayesian measure of estimation uncertainty, and is given by

$${\sigma }_{\theta }=\sqrt{\mathit{\text{Var}}(\theta |\mathit{\text{data}})}=\sqrt{{\displaystyle \int {(\theta -\widehat{\theta })}^{2}f(\theta |\mathit{\text{data}})\mathrm{d}\theta .}}$$

In addition to these point estimates, it is nearly always important to report interval summaries. Analogous to conventional confidence intervals, credible intervals are Bayesian interval summaries of parameters. The (1 − w)% credible interval is often defined as (q_w/2, q_1−w/2) where q_w/2 denotes the w/2 quantile of the posterior distribution. For example, a 95% credible interval is (q_0.025, q_0.975).

However, the interpretation of Bayesian credible intervals is fundamentally different from that of conventional confidence intervals (Casella & Berger, 2001). Bayesian credible intervals have more natural probability interpretations than confidence intervals. A 95% credible interval means that there is a 95% chance that the credible interval contains the true value of the parameter based on the observed data. In comparison, the frequentist confidence interval does not have such an intuitive interpretation, although practitioners often misinterpret it in this way. A 95% confidence interval actually means that if we repeatedly sample a population, and a confidence interval is calculated from each sample, then, on average, 95% of these intervals contain the true value of the parameter. The interpretation of confidence interval is based on repeated sampling, which involves repeating the same experiment under the exact same conditions many times. However, this is not the case in practice. Even if we repeat the experiment, it is almost impossible to conduct it under the exact same conditions, especially in the social sciences. For this reason, Bayesian credible intervals are more meaningful and relevant to scientific practice.

When the posterior density of θ has a closed form, the calculation of the posterior mean, variance and credible interval is straightforward. However, except in some simple cases, posterior distributions do not have analytic forms, especially in complex models such as generalized linear models or multilevel models. In these situations, a general approach is to simulate samples from the posterior distribution, and then make inference based on these posterior samples. For example, the posterior mean, variance and credible interval can be estimated by the sample mean, sample variance and sample quantile based on posterior draws.

A general class of methods for simulating from arbitrary posterior distributions is the Markov chain Monte Carlo (MCMC) method (Gamerman, 1997). Using an MCMC algorithm, a correlated sequence of random variables is simulated in which the jth value in the sequence, say θ^(j), is sampled from a probability distribution dependent on the previous value θ^(j−1). Under conditions that are generally satisfied, the sequence of sample values converge to the posterior distribution of interest as j becomes large. Essentially, MCMC algorithms produce a random walk over a probability distribution. If we take a sufficient number of steps in this random walk, the simulation visits various regions of the state space according to the target posterior distribution. The MCMC algorithm usually takes a certain number of iterations to reach convergence. To make inference, we generally discard these early iterations, and focus on iterations when approximate convergence is reached. The practice of discarding early iterations in MCMC simulations is referred to as burn-in. The number of burn-in iterations depends on the application. In the context of mediation analysis, a few hundred burn-in iterations are often adequate.

A very useful property of random samples is that a function of posterior samples of parameters is the posterior samples of the function of the parameters (Gelman et al., 2003). Precisely, let g(θ) be a function of a parameter vector θ = (θ₁, …, θ_k), and assume that ${\mathit{\theta }}^{(t)}=({\theta }_1^{(j)},\cdots ,{\theta }_k^{(j)})$ are jth posterior draws of θ obtained from the MCMC algorithm, then g(θ^(j)) is a random draw from the posterior distribution of g(θ). As we will show, this property can be conveniently employed to make inference for the mediated effect αβ or τ − τ′, and relative mediation effects such as the proportion mediated αβ/(αβ + τ′), which are all functions of regression parameters. A program called WinBUGS (a Windows version of Bayesian inference using Gibbs sampling) can be used to implement Bayesian computation. Users only need to specify the model and input data, and the program will conduct the MCMC algorithm and output posterior draws of the parameters. This software is available for free downloading at the BUGS project website (http://www.mrc-bsu.cam.ac.uk/bugs).

When the MCMC algorithm is used, it is important to assess its convergence to ensure that the random draws are actually coming from to the posterior distribution of interest. A very useful informal approach is to visually inspect the plot of posterior draws against the iteration (e.g., see Figure 5 (a)), the so-called trace plot. A stable well-mixed trace plot, such as Figure 5 (a), is often the indication of the convergence of the chain. Gelman and Rubin (1992) proposed a formal diagnostic method by running a small number (e.g., m = 3) of independent chains with different starting points. The basic idea is that although the chains look different at early iterations due to different starting points, when the MCMC algorithm is converged, the chains should mix together and are indistinguishable from each other, as they converge to the same posterior distribution. Formally, the convergence of the MCMC algorithm is monitored by the estimated scale reduction factor R^,

$$\widehat{R}=\frac{n-1}{n}+\frac{1}{n}\frac{B}{M}$$

where B/n is the variance between the means from the m independent chains with the length n, and W is the average of the m within-chain variances. If the value of R^ is close to 1, for example less than 1.2, we may conclude that the MCMC algorithm reasonably converges; otherwise the algorithm may fail to converge. This convergence diagnosis method has been implemented as the routine CODA in open source statistical computing and graphics software called R (R development core team, 2008). This routine can be used jointly with WinBUGS to assess the convergence of the MCMC algorithm. A comprehensive discussion of convergence diagnosis can be found in Cowles and Carlin (1996).

Figure 5.

Trace plot (a) and the Gelman-Rubin convergence statistic R (b) for posterior samples of the mediated effect αβ for the Bayesian single-level mediation analysis of the firefighter health promotion data.

Bayesian inference of the mediated effect in a single-level mediation model

We now discuss how to apply the foregoing Bayesian inference to the single-level mediation model defined by equation (1), equation (2) and equation (3). First, consider the estimation of equation (2). The Bayesian inference starts with specifying the prior distribution for unknown parameters θ, in this case, $\theta =\{{\beta }_2,\alpha ,{\sigma }_2^2\}$. For linear regression, we often use normal distributions as priors of regression coefficients β₂ and α, and use an inverse gamma distribution as the prior of the variance ${\sigma }_2^2$. The inverse gamma distribution is adopted to guarantee a positive value of the variance. Assuming these priors are independent a priori, the joint prior distribution of these parameters can be expressed as

$$p({\beta }_2,\alpha ,{\sigma }_2^2)=N({\mu }_{{\beta }_2},{\sigma }_{{\beta }_2}^2)N({\mu }_{\alpha },{\sigma }_{\alpha }^2)\mathit{\text{IG}}(a,b)$$ (5)

where IG(a, b) denotes an inverse gamma distribution with a shape parameter a and a scale parameter b. Parameters of prior distributions, such as ${\mu }_{{\beta }_2},{\sigma }_{{\beta }_2}^2,{\mu }_{\alpha },{\sigma }_{\alpha }^2,a,\text{and}b$, are called hyperparameters. In Bayesian inference, the values of hyperparameters are known, reflecting prior information on these parameters.

A general way to specify values of hyperparameters is to let the mean of the prior distribution equal the prior estimate of the parameter, and to set the variance of the prior distribution at a value that reflects the uncertainty of the prior estimate. For example, suppose that based on prior information, the investigator expects that the most plausible value of α is 4, then we can set µ_α as 4 to center the prior distribution of α at 4. The value of ${\sigma }_{\alpha }^2$ is set to reflect the uncertainty about the prior knowledge of α = 4. If the prior information is strong (or weak), we may assign a relatively small (or large) value to ${\sigma }_{\alpha }^2$. For example, if σ_α = 2, we assert that α = 4 is about 1.6 times as likely as α = 2 or 6, and about 7.4 times as likely as α = 0 or 8. A plot of the prior distribution provides a helpful guidance to specify an appropriate value of σ_α.

Historical data from pilot or previous studies are very useful to specify the prior distribution of parameters in mediation analysis. As historical data are available, one natural approach is to fit the historical data and use the resulting posterior distribution of parameters as the prior distribution. This approach assumes that the historical and current observations are exchangeable, meaning that these observations come from a same distribution, or more rigorously, meaning that the joint distribution of the observations is invariant to permutations of the observation indexes. Unfortunately, the assumption of exchangeability rarely holds in practice because various characteristics of the current study are often different from those of previous studies, such as the study design, study population, and experimental facilities. To accommodate this uncertainty, the variance of the posterior distribution is often inflated by a certain degree before using it as the prior distribution in the current study. Information is borrowed from previous studies but it is important that the borrowed information does not dominate the observed data. The inflation of posterior variances can also be viewed as a way to discount the number of observations in the historical data (Spiegelhalter, Abrams & Myles, 2004). For example, if we inflate the posterior variance by 4, in a certain sense, we downweight the historical data from 100 subjects to be equivalent to that from 25 subjects.

Another type of prior information often available is limiting values of parameters. For example, based on the subject matter, the investigators may expect the regression parameter (or correlation) between the mediator and independent variable to be between 0.1 and 0.4. If the investigators believe that any value between the limiting values is equally likely, then a uniform distribution ranging from 0.1 to 0.4 can be employed as a prior distribution to incorporate the prior information. On the other hand, if the investigators also have prior belief that certain values are more likely than other values within the limiting values, then we may use a distribution with negligible probabilities outside of the limiting values as the prior distribution. For example, a normal distribution with mean 0.25 and standard deviation 0.05 assigns negligible probability outside of the range (0.1, 0.4). Note that the uniform prior with specified limits precludes the parameter taking any values outside of the limits a priori, which may be a strong assumption in some situations. Without strong prior knowledge to support the limits, it is sensible to use a normal prior with a reasonable variance to cover all plausible values of the parameter.

For the variance parameter ${\sigma }_2^2$, less prior information is usually available. In this case, small values can be assigned to a and b, such as a = b = 0.001, so that the prior distribution has a large variance and is flat over a wide range of values. Of course, if relatively good information about the variance is available, we can determine the value of a and b so that the inverse gamma prior distribution has a mean that is centered at the expected value with a reasonable dispersion. Again, if limiting values of ${\sigma }_2^2$ are available, a uniform distribution or an inverse gamma distribution with most probability distributed within the range of the limiting values can serve as the prior distribution.

In some cases, there may be no or very vague prior information about the parameter values, or the investigators may prefer that the prior information has the least effect on the results. In these situations, the following uniform prior can be used:

$$f({\beta }_2,\alpha ,\mathit{\text{log}}({\sigma }_2^2))\propto \mathit{\text{Unif}}(-\infty ,\infty )$$ (6)

where Unif(−∞,∞) denotes a uniform distribution from −∞ to ∞. As σ² cannot take negative values, the logarithm of ${\sigma }_2^2$ is used in (6) so that all values between −∞ and ∞ can be attained. The uniform distribution assumes that all values between −∞ and ∞ have the same probability of being the value of the parameters a priori. It does not favor any outcome over another, thus often called a noninformative prior. The rationale for using a noninformative prior distribution is to let data speak for themselves so that inferences are unaffected by information external to the current data. Mathematically, the noninformative prior (6) is equivalent to the following distribution in the original scale of ${\sigma }_2^2$:

$$f({\beta }_2,\alpha ,{\sigma }_2^2)\propto {\sigma }_2^{-2},$$ (7)

which is a limiting distribution of the prior distribution (5) by setting ${\sigma }_{{\beta }_2}^2,{\sigma }_{\alpha }^2$ and variance of the inverse gamma distribution at infinity (Gelman et al., 2003). Note that the noninformative prior as above is not a proper distribution in the sense that it does not integrate to 1. However, as long as the resulting posterior densities are proper (i.e., the integration of the posterior densities equals 1), inferences are usually correct.

When using the noninformative prior, the posterior means of β₂ and α are exactly the same as the conventional frequentist estimates. However, the Bayesian approach automatically takes into account the uncertainty associated with estimating the variance parameter ${\sigma }_2^2$, and the resulting posterior distribution of β₂ and α is a t distribution. One may question that if the noninformative prior should not offer any information, why do we employ Bayesian analysis with the noninformative prior. For one reason, as we will show below, the Bayesian analysis enables us to draw inference without making restrictive distributional assumptions, such as normality, on the estimates. This feature is particularly appealing for studies with small samples. There are also other more fundamental reasons to favor Bayesian analysis, see Robert (2007) for detailed discussions.

It is possible to analytically derive the posterior distribution of $\{{\beta }_2,\alpha ,{\sigma }_2^2\}$ under simple linear regression by using certain priors. However, a more general approach, which also directly applies to more complex models such as multilevel mediation models, is to simulate posterior draws using MCMC methods. A particularly useful MCMC algorithm for regression models is Gibbs sampling, also called the alternating conditional sampling, which updates parameters alternatively based on their conditional distributions. Gibbs sampling is an iterative algorithm. For regression model (2), we let ${\beta }_2^{(t-1)},{\alpha }^{(t-1)},{\sigma }_2^{2(t-1)}$ denote the simulated value at the (t − 1)th iteration. To get the next iteration, parameters are sampled according to the following two steps:

1. Generate ${\beta }_2^{(t)}$ and α^(t) from their conditional distribution $f({\beta }_2,\alpha |{\sigma }_2^{2(t-1)},\mathit{\text{data}})$, which is a bivariate normal distribution.

2. Generate ${\sigma }_2^{2(t)}$ from its conditional distribution $f({\sigma }_2^2|{\beta }_2^{(t)},{\alpha }^{(t)},\mathit{\text{data}})$, which is an inverse gamma distribution.

The WinBUGS software can be used to implement the above Gibbs sampling algorithm to obtain the posterior draws of β₂, α and ${\sigma }_2^2$. In a similar manner, equation (3) can be fitted after specifying the appropriate priors to the parameters $\{{\beta }_3,{\tau }^{\prime },\beta ,{\sigma }_3^2\}$. Particularly, the noninformative prior for these parameters is

$$p({\beta }_3,{\tau }^{\prime },\beta ,{\sigma }_3^2)\propto {\sigma }_3^{-2}.$$ (8)

The WinBUGS code for the single-level mediation analysis is given in the Appendix.

After obtaining posterior draws of the parameters $\mathit{\theta }=\{{\beta }_2,\alpha ,{\sigma }_2^2,{\beta }_3,{\tau }^{\prime },\beta ,{\sigma }_3^2\}$, inference can be easily made for any function of these parameters. Let ${\mathit{\theta }}^{(t)}=\{{\beta }_2^{(t)},{\alpha }^{(t)},{\sigma }_2^{2(t)},{\beta }_3^{(t)},{{\tau }^{\prime }}^{(t)},{\beta }^{(t)},{\sigma }_3^{2(t)}\}$ denote the tth posterior draw of θ for t = 1, …, T, and g(θ) be a function of θ of interest, then {g(θ^(t)); t = 1,…, T} form T random draws from the posterior distribution of g(θ). Based on these posterior draws, Bayesian inference for g(θ) is obtained. In particular, the posterior draws of the mediated effect αβ are {α^(t)β^(t); t = 1, …, T}, and the point estimate of αβ is given by

$$\widehat{\alpha \beta }=\frac{1}{T}{\displaystyle \sum _{t=1}^T{\alpha }^{(t)}{\beta }^{(t)}}$$ (9)

The posterior variance of αβ is given by

$$\mathit{\text{Var}}(\alpha \beta |\mathit{\text{data}})=\frac{1}{T-1}{\displaystyle \sum _{t=1}^T{({\alpha }^{(t)}{\beta }^{(t)}-\widehat{\alpha \beta })}^2}$$ (10)

The 95% credible interval of αβ is given by $(q_{0.025}^{*},q_{0.975}^{*})$ where $q_{0.025}^{*}\text{and}{q}_{0.975}^{*}$ denote the 0.025 and 0.975 sample quantiles of the posterior draws of αβ, respectively. The inference for the relative mediation effects αβ/(αβ +τ′) or any function g(θ) can be obtained in the same way. In comparison, using the frequentist approach, the point estimate of g(θ) is easily obtained by plugging in the maximum likelihood estimate of θ; however, it is generally more difficult to obtain the corresponding sampling variance and distribution for g(θ).

Single level simulation study

Simulation description

It is well known that Bayesian inference is exact for small samples (Gelman et al., 2003). Provided that the Bayesian model (including priors) is correctly specified, Bayesian estimates are consistent, and Bayesian credible intervals have exact nominal coverage rates regardless of sample size. Given these facts, it is redundant to conduct a simulation study to evaluate the performance of Bayesian estimates from the Bayesian perspective (i.e., in the simulation, both data and parameters are treated as random variables). However, it is of interest to conduct a simulation study to evaluate the performance of the proposed Bayesian mediation analysis from the frequentist point of view. That is, in the simulation, parameters are fixed and only resample the data.

The purpose of this simulation study is to evaluate the frequentist performance of the Bayesian mediation analysis and demonstrate the potential efficiency gain by incorporating prior information. Note that because the simulation is conducted from the frequentist perspective, it intrinsically favors the frequentist mediation approach.

Following MacKinnon et al. (2002), we considered four values of parameters α, β and τ′: 0, 0.14, 0.39 and 0.59, corresponding to no, small, medium and large effect sizes, respectively, and five values of the sample size, N = 25, 50, 100, 200 and 1000. This generated 20 scenarios. Without loss of generality, we assumed that β₂ = β₃ = 0 and σ₂ = σ₃ = 1 for convenience. To generate data under each scenario, a sample of X of size N from the standard normal distribution was generated, then conditional on the values of X, we simulated M and Y according to equation (2) and equation (3), where residuals e₂ and e₃ were generated from independent standard normal distributions. A total of 1,000 data sets were generated under each scenario.

For each simulated data set, both frequentist mediation analysis and Bayesian mediation analysis were applied. In frequentist approach, the distribution of the product method (MacKinnon, Lockwood & Williams, 2004) was used to construct the 95% confidence interval of αβ.

Bayesian approach was considered under three types of prior information commonly encountered in practice. The first type of prior information is limiting values of regression parameters. For example, based on pilot studies, investigators may expect a small effect size in the current study, and thus expect that the values of regression parameters are between 0 and 0.39. To reflect such prior information, we assigned uniform prior distributions Unif(−0.14, 0.14), Unif(0, 0.39), Unif(0.14, 0.59) and Unif(0.39, 0.79) to regression parameters { α, β, τ′} for zero, small, medium and large effect sizes, respectively. That is, it was assumed that for a small effect size, any effect size between no effect size (i.e., 0) and a medium effect size (i.e., 0.39) is equally likely to be the value of regression parameter a priori; and for a medium effect size, any effect size between a small effect size (i.e., 0.14) and a large effect size (i.e., 0.59) is equally likely to be the value of regression parameter a priori; and so on. The Bayesian analysis based on these uniform priors is denoted as BUNI. For other parameters that appear in the mediation regression equations, noninformative prior distributions were used to reflect relatively weaker prior information on these parameters.

The second type of prior information often available to researchers is the knowledge that some values of parameters are more likely than other values. For example, based on the subject matter, the researchers might expect a moderate effect size, and believe that α = 0.4 would be more likely than α = 0.2 or α = 0.6. In this case, a normal distribution centered at 0.4 can serve as the prior distribution of α. Prior distributions of α and β used in the simulation are displayed in Figure 3. The Bayesian analysis based on the normal priors is denoted as BNOR.

Figure 3.

Informative normal prior distributions for α and β when the mediated effect size is zero, small, medium and large in the single level mediation simulation study.

The third case is one in which researchers have no specific prior information on the parameters, or they prefer that the inference is not affected by information outside of the study. The noninformative prior (7) and (8) was used in our Bayesian mediation analysis, and denoted this Bayesian analysis as BNIN.

In the Bayesian approach, 10,000 posterior samples of the model parameters were recorded after 1,000 burn-in iterations. The convergence of the MCMC was monitored by graphical inspection and the method of Gelman and Rubin (1992).

Empirical bias, relative mean square error (RMSE), and coverage rate of 95% credible (or confidence) intervals were calculated based on estimates from 1,000 simulated data sets. Letting MSE₀ denote the mean square error of the estimate of the mediated effect based on frequentist mediation analysis, then the RMSE of an estimate of the mediated effect is defined as MSE/MSE₀, where MSE denotes the mean square error of the estimate based on another method. The coverage rate of the 95% credible (or confidence) interval is the proportion of estimates that fall within the 95% credible (or confidence) interval across 1,000 simulations.

Simulation results

Table 1 shows the empirical bias (×10,000), RMSE, and coverage rate of the 95% credible intervals (or confidence intervals), respectively. As expected, both frequentist and Bayesian point estimates of the mediated effect have minimal bias, as we know theoretically that the two estimates are unbiased. However, by incorporating prior information (BUNI and BNOR in Table 1), the mean square error of the Bayesian estimate of the mediated effect is dramatically decreased. This gain is especially prominent when the sample size is small or moderate (e.g., less than 200). For example, under a sample size of 100 and the intermediate mediated effect size (α = β = 0.39), the MSE decreases by 50% for the Bayesian analysis with the knowledge of limiting values of parameters, and by 65% for the Bayesian analysis with the informative normal prior. Under the large sample size (e.g., N=1,000), we observe much less efficiency gain because in that case the information contained in the data dominates the prior information. In other words, under the large sample, the prior information contributes relatively little information to the inference, with respect to the strong data information. Nevertheless, a certain decrease in the MSE in the Bayesian approach when N = 1,000 is observed.

Table 1.

Empirical bias (×10,000), relative mean square error (RMSE), and coverage rate (%) of the 95% credible interval (or confidence interval) for Bayesian estimates and frequentist estimates for the mediated effect. FREQ denotes the results from the frequentist approach, and BNIN, BUNI and BNOR denote the Bayesian results under a noninformative prior, (informative) uniform prior, and (informative) normal prior, respectively.

	α = β = 0			α = β = 0.14			α = β = 0.39			α = β = 0.59
Method	Bias	RMSE	Cov	Bias	RMSE	Cov	Bias	RMSE	Cov	Bias	RMSE	Cov
						N=25
FREQ	22.2	100.0	99.7	21.7	100.0	98.2	69.3	100.0	91.2	−16.3	100.0	92.9
BNIN	−21.7	100.0	99.7	15.0	98.4	99.2	50.0	98.8	94.9	−44.8	99.3	96.1
BUNI	0.5	0.03	100.0	133.9	7.9	100.0	−130.7	8.1	99.7	−0.8	6.3	100.0
BNOR	−0.1	0.04	100.0	7.4	6.2	100.0	−3.5	6.0	99.9	1.3	6.9	100.0
						N=50
FREQ	4.1	100.0	99.8	6.7	100.0	93.3	63.8	100.0	93.0	−20.6	100.0	94.3
BNIN	5.6	100.0	99.9	7.4	99.9	99.6	64.0	100.0	94.5	−20.3	100.0	95.1
BUNI	0.2	0.39	100.0	95.7	22.8	99.9	−99.3	21.1	98.9	11.1	16.0	99.8
BNOR	0.3	0.47	100.0	−1.1	19.7	100.0	−14.0	14.8	100	8.3	15.6	99.9
						N=100
FREQ	−1.5	100.0	99.6	2.4	100.0	89.6	−11.8	100.0	94.0	−36.5	100.0	94.5
BNIN	−0.4	100.0	99.8	2.5	99.6	98.2	−12.8	99.9	95.3	−37.7	100.0	95.2
BUNI	−0.1	2.9	100.0	60.8	43.7	99.3	−32.9	49.8	97.3	−7.0	38.9	98.9
BNOR	−0.5	2.9	100.0	0.2	41.1	98.4	7.9	34.5	98.6	−4.8	31.9	99.3
						N=200
FREQ	−0.5	100.0	99.8	−1.3	100.0	91.5	14.5	100.0	94.4	21.3	100.0	94.5
BNIN	0.6	100.0	100.0	−0.7	99.8	97.4	14.4	99.9	95.9	20.7	100.0	95.4
BUNI	−0.2	15.8	100.0	22.8	68.9	99.1	−25.7	74.5	95.2	17.8	72.0	95.6
BNOR	−0.2	12.1	100.0	−2.3	63.5	98.5	−11.4	49.9	97.7	11.5	54.0	97.8
						N=1000
FREQ	0.1	100.0	99.8	−2.3	100.0	94.3	−9.4	100.0	95.1	−5.7	100.0	95.1
BNIN	0.4	100.0	100.0	−2.0	100.0	99.1	−8.8	100.0	96.4	−4.8	100.0	95.1
BUNI	0.2	96.0	100.0	−2.3	96.1	99.4	2.6	97.7	95.6	16.6	89.6	96.9
BNOR	0.2	59.6	100.0	−2.4	89.2	99.4	2.4	93.3	96.3	15.5	76.8	97.0

In the case without prior information, the performance of the Bayesian approach (i.e., BNIN in Table 1) is comparable to that of the frequentist approach, even from a frequentist perspective. The mean square errors of the BNIN are essentially the same as those of the frequentist mediation analysis. This result is expected because noninformative priors (7) and (8) are used in the Bayesian approach, thus the point estimate of the mediated effect from the Bayesian mediation analysis is essentially the same as the one from the frequentist mediation analysis.

The coverage rate of the 95% Bayesian credible interval and the 95% frequentist confidence interval depend on both the sample size and the size of the mediated effect. For example, when there is no mediation (α = β = 0), both the Bayesian credible interval and frequentist confidence interval provide coverage rates larger than the nominal value of 95.0%. However, under the small mediated effect (α = β = 0.14) and large sample sizes (N = 200 or 1,000), the Bayesian credible interval tends to provide overcoverage of the true value of the mediated effect size, while the confidence interval tends to provide undercoverage of the true value of the mediated effect size. When the mediated effect size is medium or large (α = β = 0.39 or 0.59), under small samples (e.g., N = 25 or 50), the conventional confidence interval undercover the true value, and the Bayesian credible interval overcover the true value. When the sample size is large (N = 1,000) and the mediated effect size is medium or large (α = β = 0.39 or 0.59), the coverage rates of both the Bayesian credible interval and confidence interval are close to the nominal value. In general, the coverage rate of the Bayesian credible interval is larger than the frequentist confidence interval in our simulation. Note that as the simulation is conducted from the frequentist perspective, it intrinsically favors the frequentist approach. If the data were generated based on a Bayesian model, the coverage of the Bayesian credible interval would exactly match the nominal value, no matter the sample size or the size of the mediated effect.

Based upon this simulation, the Bayesian mediation analysis could substantially improve the quality of estimates (e.g., decreasing MSE) by incorporating prior information. This is particularly important when the sample size is small or moderate. Even without prior information, the Bayesian estimates have frequentist properties that are comparable to those of conventional mediation analysis.

Single level mediation example

The Bayesian mediation procedures were applied to data from a study of health promotion of firefighters (Elliot et al., 2007) where X represents randomized exposure to an intervention, the mediator M is change from baseline to followup in knowledge of the benefits of eating fruits and vegetables, and the dependent variable Y is reported eating of fruits and vegetables. Our analysis was based on the single-level mediation model described by equation (1), equation (2) and equation (3), and the parameter of interest was the mediated effect αβ. The conventional mediation analysis yielded an estimate of αβ of 0.056 with a standard error of 0.026. The 95% confidence interval based on the distribution of the product method (MacKinnon, Lockwood & Williams, 2004) was (0.013, 0.116).

We began the Bayesian mediation analysis without using any prior information, i.e., noninformative priors were used for unknown parameters in the mediation model. We used 1,000 iteration to burn in and collected the 10,000 posterior draws to make inference. The posterior distribution of αβ is displayed in Figure 4. The posterior mean and posterior standard error of αβ are 0.056 and 0.027, respectively. The 95% credible interval for the mediated effect is (0.011, 0.118). The Bayesian point estimate of the indirect effect is essentially the same as the conventional estimate, but there are slight differences between the 95% confidence interval and the 95% Bayesian credible interval. As shown in Figure 4, the posterior distribution of αβ is clearly skewed, and Bayesian inference based on the posterior distribution automatically takes this feature into account.

Figure 4.

Posterior distribution of the mediated effect (left panel) and the corresponding normal quantile-quantile plot (right panel) for the Bayesian single-level mediation analysis of the firefighter health promotion data.

To assess the convergence of the MCMC algorithm, Figure 5 shows the trace plot for the posterior samples of the mediated effect αβ. Posterior draws of αβ were quite stable after hundreds of iterations, suggesting the convergence of the MCMC chain and adequacy of our choice of 1,000 burn-in iterations. As a formal examination of convergence, three independent chains with over-dispersed starting values (i.e., −500, 0, 500 as starting values for β₂, β₃, α, β and τ′) were simulated, based on which the Gelman-Rubin convergence statistic R was calculated for the mediated effect αβ (Figure 5). Clearly, after 1,000 burn-in iterations, the value of R has been very close to 1, also supporting the convergence of the algorithm.

Under the Bayesian approach, available prior information can be used to improve the efficiency of the estimate. Based on the historical data, we assumed that the posterior mean and standard error of α were 0.35 and 0.1, and the posterior mean and standard error of β were 0.1 and 0.05. To account for the possible heterogeneity between the current study and previous studies, we inflated the posterior variance by 4 times, and used N(0.35, 0.2²) or N(0.1, 0.1²) as the prior distribution of α and β, respectively. Under these priors, the resulting posterior mean and standard error of αβ are 0.051 and 0.023, respectively, and the 95% credible interval is (0.013, 0.102). Compared to the noninformative approach, the width of the credible interval is decreased by 16%.

Under the Bayesian paradigm, the information contained in the current data can be used as prior information for future studies. For example, posterior distributions of parameters obtained from the current data can be used to construct prior distributions of future large-scale studies and for data analysis. That is, the Bayesian approach allows the cumulation of scientific evidence as more studies are conducted, which is another attractive feature of Bayesian inference.

Bayesian inference of indirect effects in the multilevel mediation model

In psychological and social research, data are often collected at more than one level, typically at the individual and group levels such as schools, classrooms, hospital, communities, and families. Because individuals from the same group are likely to share characteristics, they are more likely to respond in the same way on research measures compared with individuals in other groups. As a result, data from subjects in the same group are correlated. Such type of data sometimes is called clustered data. Longitudinal data (or repeated measures) can be viewed as a specific case of clustered data, in which groups are individuals and the longitudinal measures are the observations in the groups defined by individual subjects. For the correlated data, the single-level mediation analysis described in the previous section is not appropriate. Using the single-level mediation model leads to biased estimates of standard errors and confidence intervals, as the assumption of independent observations is violated (Barcikowski, 1981).

Multilevel models are useful tools to analyze clustered data and repeated measures (Hox, 2002; Raudenbush & Bryk, 2002). These models assume that there are at least two levels in data, an upper level and a lower level. The lower level units (e.g., individuals) are often nested within the upper level units (e.g., groups). Multilevel models have several advantages over single-level models when modeling correlated data. First, multilevel models appropriately account for correlation among the lower level observations by introducing random effects, therefore valid statistical inference can be obtained. Second, multilevel models can accommodate unbalanced data and missing data. Third, multilevel models allow for making inference at the lower level and higher level separately. Because of these advantages, multilevel modeling is of substantial interest to researchers in the behavioral and social sciences.

Mediation in multilevel modeling, multilevel mediation, is more complex than single-level mediation, both conceptually and computationally. In multilevel mediation, different types of mediation effects can occur across multiple levels. Kenny, Kashy and Bolger (1998) distinguished upper level and lower level mediation. In upper level mediation, the initial causal variable for which the effect is mediated is an upper level variable. In lower level mediation, the initial causal variable is a lower level variable. Krull and MacKinnon (1999, 2001) investigated upper level mediated effects. Kenny, Korchmaros, and Bolger (2003) studied lower level mediation for cases in which mediation links vary randomly across upper level units.

Estimation is significantly more difficult for multilevel models than for single-level models. For multilevel models, ordinary least squares methods are not applicable because data are correlated, and maximum likelihood methods and/or empirical Bayes methods are needed. Among parameters in multilevel models, the estimation of covariance between random effects is particularly challenging, as it involves two mediation regression equations with different dependent variables (outcome Y and mediator M). Kenny et al. (2003) described these difficulties and proposed an ad hoc method to obtain an approximate estimate of the covariance between random effects. Bauer, Preacher and Gil (2006) extended the work of Kenny et al. (2003), and proposed a method to yield consistent estimates of the variance components by simultaneously fitting the two mediation regression equations using a selection variable. A general approach is now available in the Mplus programming language (Muthén and Muthén, 2007) as described in MacKinnon (2008; Chapter 9).

Bayesian inference is particularly advantageous in analyzing complex multilevel mediation (Gelman & Hill, 2007). In addition to the ability to incorporate prior information, Bayesian inference has several other important advantages. First, multilevel modeling is conceptually natural under the Bayesian framework, in which parameters are treated as random variables instead of fixed values. By assigning distributions to the lower level parameters, the upper level model is obtained. Second, estimation in multilevel modeling is relatively straightforward under the Bayesian framework. MCMC methods, especially Gibbs sampling, are well developed to fit almost any complex multilevel models. For example, when adjusting from two-level models to three-level or four-level models, just a few extra steps are added to draw the conditional posterior distribution of the parameters (of the third or fourth level) when using Gibbs sampling. Finally, as mentioned earlier, Bayesian inference is exact for small samples. It does not rely on asymptotic approximations and does not assume the normality of estimates. In conventional approaches, we may use nonparametric methods such as bootstrapping to avoid making distribution assumptions in simple single-level modeling. However, in complex multilevel models, the computational burden of bootstrapping is extensive (Bauer, Preacher & Gil, 2006).

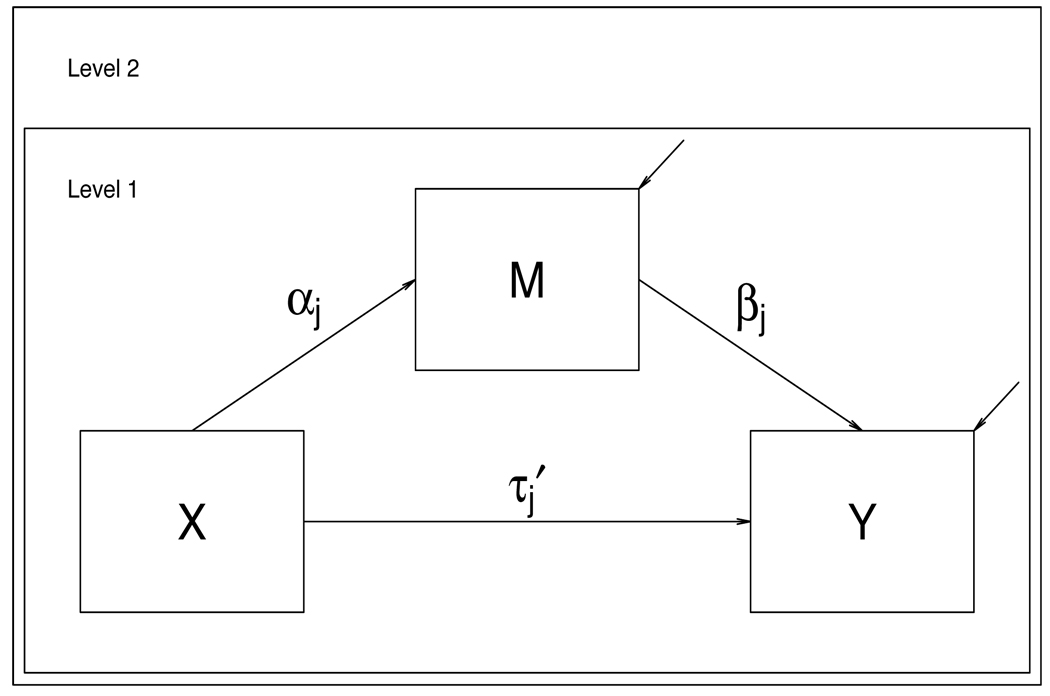
For notational simplicity and clarity, we use a simple two-level mediation model, as shown in Figure 6, to illustrate Bayesian inference of multilevel models. Our approach is immediately applicable to mediation models of higher levels. Let i be index units of the first level and j be index units of the second level. A two-level mediation model can be expressed as follows: at the first level,

$$\begin{array}{cc}{M}_{\mathit{\text{ij}}}\hfill & ={\beta }_{2j}+{\alpha }_j{X}_{\text{ij}}+e_{2\mathit{\text{ij}}}\hfill \\ Y_{\mathit{\text{ij}}}\hfill & ={\beta }_{3j}+{\beta }_j{M}_{\mathit{\text{ij}}}+{\tau }_j^{\prime }{X}_{\text{ij}}+e_{3\mathit{\text{ij}}}\hfill \end{array}$$

and at the second level,

$$\begin{array}{cc}\hfill {\beta }_{2j}& ={\beta }_2+u_{1j}\hfill \\ {\alpha }_j\hfill & =\alpha +u_{2j}\hfill \\ {\beta }_{3j}\hfill & ={\beta }_3+u_{3j}\hfill \\ {\beta }_j\hfill & =\beta +u_{4j}\hfill \\ {\tau }_j^{\prime }\hfill & ={\tau }^{\prime }+u_{5j}.\hfill \end{array}$$

Figure 6.

Diagram of the two-level mediation model.

In the first-level model, the terms e_2ij and e_3ij are residuals of M and Y; the parameters β_2j and β_3j are random intercepts, and α_j, β_j and ${\tau }_j^{\prime }$ are random slopes. The specification of random intercepts and slopes allows different first-level units, say groups, to have different regression intercepts and slopes. In particular, for the jth group, α_j quantifies the relationship between the mediating variable and independent variable, and β_j measures the relationship between the dependent variable and mediating variable after adjusting for the effects of the independent variable. In the second-level model, α and β are population (or average) slopes, which specify the average effect of the independent variable on the mediating variable, and the average effect of the mediating variable on the dependent variable after controlling the independent variable, respectively. The parameters β₂ and β₃ are population (or average) intercepts. We assume that for simplicity there is no level two predictor for the random effects. The extension to include level two predictors is straightforward.

In multilevel modeling, the first-level residuals e_2ij and e_3ij are assumed to be independent and follow normal distributions,

$$\begin{array}{cc}{e}_{2\mathit{\text{ij}}}\hfill & \sim N(0,{\sigma }_2^2)\hfill \\ e_{3\mathit{\text{ij}}}\hfill & \sim N(0,{\sigma }_3^2)\hfill \end{array}$$

and the second-level residuals u_j = (u_1j, u_2j, u_3j, u_4j, u_5j)^T follow a multivariate normal distribution

$${\mathit{u}}_j\sim N(\mathbf{0},\mathbf{\Sigma })$$

where 0 is a vector of 0, and Σ is a 5 × 5 covariance matrix.

In multilevel mediation, the average indirect effect in the population is often of primary interest. Under the above two-level model, the average indirect effect is given by

$$\mathit{\text{ab}}=E({\alpha }_j{\beta }_j)=\alpha \beta +{\sigma }_{{\alpha }_j{\beta }_j},$$

where σ_αjβj denotes the covariance between α_j and β_j. Another useful measure of the indirect effect is the relative indirect effect which is defined as the proportion mediated which is the ratio of the indirect effect to the overall effect (MacKinnon, 2008). Kenny et al. (2003) showed that the total effect in a fully random, lower level mediated multilevel model is

$$c={\tau }^{\prime }+\alpha \beta +{\sigma }_{{\alpha }_j{\beta }_j}$$ (11)

Therefore, the relative average indirect effect may be expressed as

$$\mathit{\text{ab}}/c=\frac{\alpha \beta +{\sigma }_{{\alpha }_j{\beta }_j}}{{\tau }^{\prime }+\alpha \beta +{\sigma }_{{\alpha }_j{\beta }_j}}.$$ (12)

All these quantities are functions of the average slopes α and β, and the covariance between α_j and β_j.

To conduct Bayesian multilevel modeling, priors are assigned to all unknown parameters in the model, including regression parameters (i.e., β₂, τ′, β, β₃, α), first-level variance parameters(i.e., ${\sigma }_2^2\text{and}{\sigma }_3^2$), and second-level variance parameters (i.e., Σ). For the regression parameters, depending on how much prior information is available on these parameters, either assign these parameters independent normal prior distributions with appropriate hyperparameters as described in previous sections, or simply assign them independent noninformative uniform priors as follows,

$$p({\beta }_2,\alpha ,{\beta }_3,\beta ,{\tau }^{\prime })\propto \mathit{\text{Unif}}(-\infty ,\infty ).$$ (13)

For the first-level variance parameters ${\sigma }_2^2\text{and}{\sigma }_3^2$, a convenient prior is an inverse gamma distribution. Alternatively, if prior information is not available, as is often the case in practice, use the following noninformative prior,

$$p({\sigma }_2^2,{\sigma }_3^2)\propto {\sigma }_2^{-2}{\sigma }_3^{-2}.$$ (14)

For the second-level covariance matrix Σ, a commonly used prior distribution is the inverse Wishart distribution, which is indexed by a degree of freedom parameter ν and a scale matrix parameter S. The inverse Wishart distribution is a multivariate generalization of the inverse gamma distribution. To represent vague prior knowledge, choose the degree of freedom to be as small as possible (i.e., 5, the rank of Σ), and set the scale matrix as a diagonal matrix with small values, such as 0.001, at the diagonal. Once the prior distributions of unknown parameters are specified, the normal hierarchical model can be easily fitted by Gibbs sampling.

Based on posterior draws of the parameters, it is straightforward to make inference for the average indirect effect. We first obtain posterior draws of the average indirect effect from the posterior draws of the model parameters, as follows:

$${\mathit{\text{ab}}}^{(t)}={\alpha }^{(t)}{\beta }^{(t)}+{\sigma }_{{\alpha }_j{\beta }_j}^{(t)}t=1,\dots ,T$$

where ${\alpha }^{(t)},{\beta }^{(t)},\text{and}{\sigma }_{{\alpha }_j{\beta }_j}^{(t)}$ denote the ith posterior draws of these parameters. Then the posterior mean and variance of the average indirect effect are given by

$$\begin{array}{ccc}\widehat{\mathit{\text{ab}}}\hfill & =E(\mathit{\text{ab}}|\text{data})\hfill & =\frac{1}{T}{\displaystyle \sum _{i=1}^T{\mathit{\text{ab}}}^{(t)}}\hfill \\ \hfill & \mathit{\text{Var}}(\mathit{\text{ab}}|\text{data})\hfill & =\frac{1}{T-1}{\displaystyle \sum _{i=1}^T({\mathit{\text{ab}}}^{(t)}-\widehat{\mathit{\text{ab}}})}\hfill \end{array}$$

The 95% credible interval of the average indirect effect is determined based on the sample quantiles of ab^(t). In the same manner, we can easily make inference for any function of the model parameters, such as the total effect c in (11) and relative mediated effect ab/c in (12), which could be a difficult task if we were to use the frequentist approach.

Multilevel mediation example

We used simulated data provided by Kenny et al. (2003) to illustrate the Bayesian multilevel mediation analysis. The data consisted of 200 subjects with 10 measures for each subject for each variable X, M and Y. For ease of exposition, MacKinnon (2008) added some context to the data set, as follows: Assume a study of a special exercise program for depression, where the independent variable X was the continuous measure of how conducive the person’s lifestyle and environment was to exercise; the mediating variable M was a measure of fitness; and the dependent variable Y was the measure on a happiness scale. These variables were measured on 10 different days for each subject. The researchers were interested in whether the exercise program would enhance happiness. They further hypothesized that the person’s exercises would work by changing the fitness level of each person, which, in turn, would decrease depression and increase happiness.

We applied the lower level multilevel mediation model to the data set. Following Kenny et al. (2003), we assumed that α_j and β_j were correlated and followed a bivariate normal distribution with the mean vector $\left(\begin{array}{c}\alpha \hfill \\ \beta \hfill \end{array}\right)$ and covariance matrix

$$\mathrm{\Sigma }=\left(\begin{array}{c}{\sigma }_{{\alpha }_j}^2,{\sigma }_{{\alpha }_j{\beta }_j}\hfill \\ {\sigma }_{{\alpha }_j{\beta }_j},{\sigma }_{{\beta }_j}^2\hfill \end{array}\right).$$

Other second-level random effects β_2j, β_3j, and ${\tau }_j^{\prime }$ were independent of α_j and β_j and mutually independent.

We further supposed that the researchers wanted the data to speak for themselves, and preferred that the inference was unaffected by information external to the current data. Thus, it was appropriate to use the noninformative prior (13) for the regression parameters and (14) for the first-level variance parameters. We used a Wishart distribution with a degree of freedom of 2 and a scale matrix parameter $\left(\begin{array}{c}0.001,0\hfill \\ 0,0.001\hfill \end{array}\right)$ to reflect vague prior information on the covariance matrix Σ. For variances of β_2j, β_3j, and ${\tau }_j^{\prime }$, we applied the following noninformative prior

$${\sigma }_{{\beta }_{2j}},{\sigma }_{{\beta }_{3j}},{\sigma }_{{{\tau }^{\prime }}_j}\sim \mathit{\text{Unif}}(0,\infty )$$ (15)

where σ_β2j, σ_β3j and ${\sigma }_{{{\tau }^{\prime }}_j}$ denote standard deviations of β_2j, β_3j and ${\tau }_j^{\prime }$, respectively. In practice, a large number can replace ∞. Note that for the second-level variance parameters, in order to obtain proper posteriors, we assigned uniform priors to the standard deviations rather than logarithm of the variances as (14) for the first-level variance parameters. In the case that the number of second-level units is very small (e.g., < 5), Gelman (2006) recommend half t prior, the absolute value of a Student-t distribution centered at zero. We used 1,000 iterations to burn in and 10,000 posterior draws to make inference. The WinBUGS code to fit the Bayesian lower level multilevel mediation model is given in the Appendix.

The results of the Bayesian analysis are reported in Table 2. For comparison, we also list the results of a conventional multilevel mediation analysis by using the method of Bauer et al. (2006) in Table 2. In general, the Bayesian estimates are similar to the results from the conventional analysis. However, by taking a Bayesian approach, in addition to the point estimates, we automatically obtain the posterior standard errors and 95% confidence intervals, and those inferences do not depend on a large sample approximation. Comparatively, it is more involved to obtain interval estimates in conventional multilevel mediation analysis. Bauer et al. (2006) proposed an approach to estimate the indirect effect ab and c in multilevel models, and derived formulas of the standard error of these estimates and confidence intervals. However, these standard error formulas is complex and rely on large sample Taylor approximation. Their accuracy may be compromised in small samples.

Table 2.

Estimates of a lower level mediation model based a conventional analysis and a Bayesian analysis. The results of the conventional analysis are obtained by using the method of Bauer et al. (2006).

		Conventional Analysis			Bayesian Analysis
Effect	Population	Estimate	SE	95% CI	Estimate	SE	95% CI
ab	0.473	0.500	0.041	(0.422, 0.581)	0.510	0.040	(0.435, 0.594)
c	0.672	0.677	0.046	(0.589, 0.768)	0.678	0.045	(0.590, 0.769)
ab/c	0.703	0.739	0.035	(0.673, 0.808)	0.752	0.035	(0.687, 0.823)
α	0.600	0.589	0.032	(0.526, 0.651)	0.589	0.031	(0.528, 0.649)
β	0.600	0.632	0.036	(0.561, 0.703)	0.631	0.035	(0.563, 0.699)
τ′	0.200	0.177	0.027	(0.124, 0.230)	0.168	0.027	(0.116, 0.218)
${\sigma }_{{\alpha }_j}^2$	0.160	0.133	0.020	(0.094, 0.172)	0.122	0.019	(0.088, 0.162)
${\sigma }_{{\beta }_j}^2$	0.160	0.174	0.024	(0.127, 0.221)	0.168	0.023	(0.127, 0.218)
${\sigma }_{{\alpha }_j{\beta }_j}^2$	0.113	0.127	0.018	(0.092, 0.162)	0.138	0.018	(0.105, 0.176)
${\sigma }_{{\tau }_j^{\prime }}^2$	0.040	0.057	0.013	(0.032, 0.082)	0.060	0.014	(0.036, 0.090)

As an example, consider the inference of relative average mediation effect ab/c = (αβ + σ_αjβj)/(τ′+ αβ + σ_αjβj). In a conventional approach, the point estimate of the relative average mediation effect is simply âb̂/ĉ = (α̂β̂ + σ̂_αjβj)/(τ ^′ + α̂β̂ + σ̂_αjβj), where α̂, β̂, σ̂_αjβj and τ̂′ are maximum likelihood estimates of these parameters. However, it is not immediately clear how we would calculate the standard error of this estimate, and it is more difficult to derive the exact distribution of âb̂/ĉ in order to construct confidence intervals under finite samples. Bauer et al. (2006) suggested using the parametric bootstrap to construct the confidence interval and calculate the standard error for complex functions of parameters. The standard error and confidence interval of the estimate of ab/c in Table 2 were obtained in this way. However, the parametric bootstrap tends to yield narrow confidence intervals because it ignores the uncertainty associated with the estimation of parameters, i.e., the estimates, such as α̂, β̂, and σ̂_αjβj, rather than true values, of the parameters are used in the parametric bootstrap. Comparatively, in a Bayesian approach, there is virtually no extra work. Once we obtain posterior draws of parameters in the model, we can simply plug the posterior draws into (12) for inference on the relative average mediated effect. More important, as what we plug in is the random posterior draws, rather than fixed point estimates, the Bayesian approach automatically takes into all uncertainties associated with the estimation.

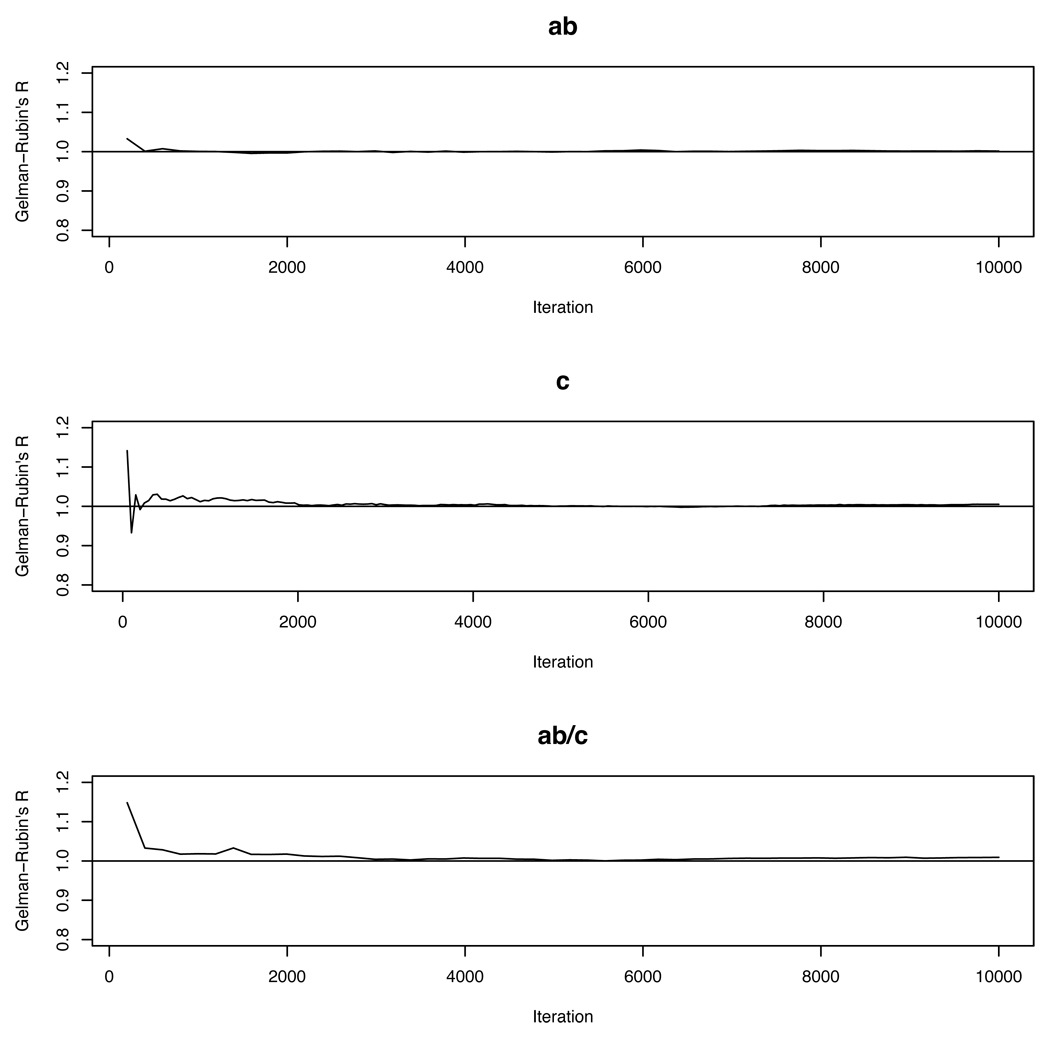
As a diagnosis of the convergence of the MCMC algorithm, Figure 7 shows the trace plot of the posterior samples for the quantities of primary interest, including the indirect effect ab, total effect c and relative average indirect effect ab/c. After 1,000 burn-in iterations, posterior draws of these parameters are very stable, suggesting the convergence of the MCMC chains. Figure 8 shows the Gelman-Rubin convergence statistic R for each of the quantities of interest. The values of R are very close to 1, further confirming the convergence of the MCMC chains. Alternatively, the convergence of the indirect effect, total effect and relative average indirect effect can be assessed simultaneously using the method of Brooks and Gelman (1998), a multivariate generalization of the Gelman-Rubin convergence statistic.

Figure 7.

Trace plot of posterior samples of the indirect effect ab, total effect c and relative average indirect effect ab/c for the example of the multilevel mediation model.

Figure 8.

The Gelman-Rubin convergence statistic R for the indirect effect ab, total effect c and relative average indirect effect ab/c in the example of the multilevel mediation model.

In the context of multilevel mediation analysis, we have primarily emphasized the conceptual and computational simplicity of Bayesian inference, as computational and conceptual difficulties are main hurdles of the application of multilevel mediation models. The Bayesian approach is also attractive for its ability to incorporate prior information. More efficient estimates can be obtained by using prior information in multilevel mediation analysis. For the above hypothetical large data set, incorporating prior information may not be particularly helpful as the likelihood of data is deemed to dominate the prior information. However, for typical multilevel mediation studies that have small or moderate sample sizes, the incorporation of prior information through a Bayesian approach can be very useful to improve the accuracy of estimates.

Multilevel mediation simulation study

Simulation description

Like the simple mediation analysis, Bayesian multilevel mediation analysis does not rely on asymptotic approximation, and inferences are exact. The purpose of this simulation study was also to assess frequentist properties of the proposed Bayesian multilevel mediation analysis.

The simulation study was based on those presented by Bauer et al. (2006) and Kenny et al. (2003). Data were simulated based on the two-level mediation model. The random intercept for the M equation, β_2j, was assumed to follow a normal distribution with a mean of β₂ = 0 and a variance of 0.6, and the random intercept for the Y equation, β_3j, followed a normal distribution with a mean of β₃ = 0 and a variance of 0.4. Those two random intercepts were independent of each other and independent of the other random effects in the model. We set the residual of the M and Y equation as e_2ij ~ N(0, 0.65) and e_3ij ~ N(0, 0.45), respectively. We assumed that the random slope ${\tau }_j^{\prime }$ followed a normal distribution with a mean of τ′ = 0.2 and a variance of 0.04, and was independent of other random effects.

To generate different simulation scenarios, three design factors were manipulated: the mean of the random slopes α_j and β_j, the covariance between α_j and β_j, and the sample sizes. Following Bauer et al. (2006), we set α = β = 0.3 or α = β = 0.6 to simulate different effect sizes of the average indirect effect, and we set the covariance between α_j and β_j as −0.113, 0, or 0.113 to generate negative, zero, and positive correlations. Three sample sizes (N₁=4, 8 or 16) for the first level and three sample sizes (N₂=25, 50 and 100) for the second level were studied. The factorial design of the above three factors yielded a total of 54 scenarios. For each scenario, 1,000 data sets were generated and fitted each of the data sets by the Bayesian method. In the MCMC algorithm, we used 1,000 iterations to burn in and collected 10,000 posterior draws to make inference. The results focus on making inference on the average indirect effect and covariance between α_j and β_j.

Simulation results

Table 3 shows the empirical bias and coverage rate of the 95% credible interval for the Bayesian estimates of the indirect effects. Overall, the results are comparable to the frequentist results reported in Bauer et al. (2006). Across all scenarios, the point estimate of the indirect effects shows negligible bias. However, the coverage rate of the 95% credible interval depends on the sample size. When the sample size is small, the credible interval tends to have coverage rates that are less than the nominal rates. For example, in the case with 4 first-level units within each of 25 second-level units, coverage rates are generally under 90% at different settings of α, β and σ_αjβj. When the sample size become large, such as 16 first-level units within each of 100 second-level units, coverage rates are close to the nominal level.

Table 3.

Empirical bias (×1,000) and coverage rate (%) of 95% credible interval of Bayesian estimates of the indirect effect. N₁ and N₂ denote the sample size of the first-level units and second-level units, respectively. Numbers in the parentheses are coverage rates.

	α = β = 0.3			α = β = 0.6
N1	σαjβj = −0.113	σαjβj = 0	σαjβj = 0.113	σαjβj = −0.113	σαjβj = 0	σαjβj = 0.113
	N2 = 25
4	2 (86.1)	0 (88.8)	−12 (87.1)	7 (90.6)	4 (90.9)	−10 (89.7)
8	−19 (91.3)	4 (82.7)	17 (91.5)	16 (89.1)	4 (88.5)	12 (91.8)
16	−22 (90.1)	−3 (91.2)	22 (92.0)	19 (89.9)	0 (93.4)	21 (94.2)
	N2 = 50
4	6 (88.6)	1 (81.4)	6 (91.5)	−7 (89.7)	−8 (86.8)	6 (92.6)
8	−19 (90.4)	−1 (88.6)	17 (91.3)	−13 (91.7)	−1 (93.1)	12 (94.4)
16	13 (94.0)	1 (94.4)	13 (94.0)	−11 (93.0)	−4 (93.4)	11 (94.5)
	N2 = 100
4	−11 (93.6)	2 (85.6)	12 (93.1)	−10 (90.5)	−2 (90.1)	12 (94.0)
8	12 (92.3)	−1 (93.7)	12 (92.3)	−10 (93.6)	−1 (95.5)	8 (95.8)
16	−5 (94.8)	0 (94.3)	6 (95.3)	−4 (94.5)	0 (94.8)	4 (95.1)

As shown in Table 4, the simulation results for the Bayesian estimate of σ_αjβj are similar to those described above. Specifically, the point estimate shows very little bias, but the coverage rate is sensitive to the sample size. Under small sample sizes, the 95% credible interval tends to cover the true value of the parameter under the nominal value, and when the sample size is large, the coverage of the 95% credible interval is quite close to the nominal value.

Table 4.

Empirical bias (×1,000) and coverage rate (%) of 95% credible interval of Bayesian estimates of the covariance between α_j and β_j. N₁ and N₂ denote the sample size of the first-level units and second-level units, respectively. Numbers in the parentheses are coverage rates.

	α = β = 0.3			α = β = 0.6
N1	σαjβj = −0.113	σαjβj = 0	σαjβj = 0.113	σαjβj = −0.113	σαjβj = 0	σαjβj = 0.113
	N2 = 25
4	−23 (79.5)	2 (88.7)	−23 (79.5)	18 (80.3)	0 (86.9)	−20 (81.1)
8	−9 (90.3)	3 (76.3)	10 (90.9)	−8 (89.5)	−2 (74.6)	7 (88.9)
16	−13 (92.6)	−2 (87.2)	11 (91.7)	−12 (92.7)	1 (89.0)	12 (91.4)
	N2 = 50
4	2 (87.8)	0 (73.9)	1 (89.9)	−2 (89.6)	−2 (74.9)	4 (89.2)
8	−14 (91.9)	0 (85.4)	12 (92.2)	−12 (91.9)	−1 (88.2)	12 (92.0)
16	−6 (92.5)	0 (92.3)	6 (93.8)	−7 (93.7)	0 (92.9)	7 (92.9)
	N2 = 100
4	−11 (92.5)	0 (80.7)	12 (91.7)	−11 (92.5)	−3 (80.0)	11 (91.5)
8	−10 (91.5)	−2 (91.9)	9 (91.9)	−10 (93.1)	0 (95.2)	9 (91.1)
16	−3 (94.5)	0 (94.1)	2 (94.7)	−2 (94.7)	0 (94.5)	3 (95.5)

Discussion

The purpose of this paper was to propose a Bayesian approach to mediation analysis, and to describe several attractive features of this approach. Bayesian mediation analysis enables researchers to incorporate prior information collected from the literature or from pilot studies into the current mediation analysis, thereby improving the statistical power of the analysis. The Bayesian approach is especially useful for multilevel mediation analysis, which is not easily handled through a conventional frequentist approach. Bayesian multilevel mediation analysis is not only conceptually natural, but also has computational advantages. Well-developed MCMC methods, along with the powerful software WinBUGS, enable researchers to easily fit very complex hierarchical models. Another important feature of the proposed Bayesian mediation analysis is that the inference does not depend on large-sample approximation. The inference is exact for small samples. This feature makes the Bayesian approach especially appealing for studies with small sample size. Simulation studies showed that the Bayesian mediation analysis also possesses favorable frequentist properties. And Bayesian analysis with noninformative priors yields similar results as frequentist methods. Bayesian mediation analysis may be especially useful for testing sensitivity to assumed priors by evaluating how different priors change results. And Bayesian methods naturally incorporate prior research allowing for the accumulation of knowledge of mediated effects across research studies. These methods may also be ideal for mediation analysis with small samples where statistical power to detect even medium sized effects may be very low and prior information can be used to decrease standard errors.

This article focuses on certain forms of prior densities, such as widely used noninformative priors and conjugate priors, for model parameters in the single-level and multilevel mediation models. A large variety forms of prior densities can also be used. For example, a t or Cauchy distribution (Johnson, Kotz, & Balakrishnan, 1994), rather than the normal distribution, may be used as priors for regression coefficients in mediation models. However, when the likelihood of data dominates prior information, as often the case in practice, the exact form of the prior density usually has minor impact on the Bayesian inference (Gelman et al, 2003). The priors discussed in this article are often adequate and convenient to use in practice.

An important issue in Bayesian inference is the misspecification of prior information. When prior information is inappropriately specified, estimates based on Bayesian mediation models can be biased. To avoid such bias, it is critical to carefully scrutinize prior information and elicit appropriate prior density to summary the available prior information. Spiegelhalter et al. (2004, Chapter 5) provide useful techniques and procedures to elicit prior opinions and prior densities. As a general guideline, when quantifying prior information, scientists should pay specific attention to the uncertainty associated with the prior information. For example, historical data may often need to be discounted when using them to elicit priors. A strong prior that dominates the likelihood usually is not recommended. The inference should be mostly driven by currently observed data. In practice, dispersed priors can often be used to achieve this goal and guard Bayesian inference from bias. Alternatively, the noninformative prior may be used to minimize the impact of prior information and let data speak for themselves. In addition, sensitivity analysis can always be conducted to assess the influence of different specifications of priors on the inference.

In the Bayesian paradigm, priors offer a natural and coherent way to incorporate prior information, such as historical data, into the mediation analysis. Within a non-Bayesian framework, meta-analysis provides a method to combine information across multiple studies by pooling data or summary statistics from the studies (Cooper and Hedges, 1994). Similarly, Mulaik, Raju, and Harshman (1997) suggests incorporating previous evidence into new studies in the form of point hypotheses. Although these methods accomplish something similar to Bayesian priors, they are quite different from using priors. Meta-analysis typically assumes that the studies to be combined are exchangeable, at least after controlling study characteristics. In contrast, prior does not impose this restrictive assumption. When the exchangeable assumption is in question, as often the case in practice, historical data can be discounted to reflect this uncertainty as discussed previously. Moreover, prior can also be used to incorporate experts’ opinions and prior knowledge that do not necessarily take an explicit form of data or summary statistics. Bayesian methods can be used in meta-analysis to account for heterogeneity of studies and incorporate prior information. Actually, Bayesian meta-analysis is a very active topic in meta-analysis (Hartung, Knapp, & Sinha, 2008; Sutton, Abrams, Jone, Sheldon, & Song, 2000).

One important topic we have not covered in this article is hypothesis testing. An approximation is that we may test the null hypothesis of no mediation effect based on whether the 95% credible interval contains zero or not. However, this approach has more of the flavor of conventional frequentist hypothesis testing. Strict Bayesian hypothesis testing is based on Bayes factor, which is essentially the odds of the null hypothesis being true versus the alternative hypothesis being true, conditional on the observed data. Conventional hypothesis testing based on the p value of 0.05 has been criticized from several perspectives (Berger & Sellke, 1987; Goodman, 1999a, 1999b). For example, conventional hypothesis testing tends to always reject the null hypothesis when the sample size is large. The use of Bayesian hypothesis testing to address these pitfalls would be a reasonable future research topic in Bayesian mediation analysis.

Appendix

WinBUGS code for single-level mediation analysis

model {
   # y[i], m[i] and x[i] denote data vectors of dependent variable, mediating variable
   # and independent variable, respectively. N is the number of observations
   for(i in 1:N)
   {
      # specify the mediation model M = β2 + αX + e2; dnorm(µ, σ) denotes a
      # normal distribution with the mean µ and precision of σ (or a variance of 1/σ).
      m[i] ~ dnorm(mean.m[i], prec.m)
      mean.m[i] < − beta2 + alpha*x[i]

      # specify the mediation model Y = β3 + βM + τ′ X + e3;
      y[i] ~ dnorm(mean.y[i], prec.y)
      mean.y[i] < − beta3 + beta*m[i] + tau.prime*x[i]
   }
   # prior distribution of parameters. Huge variances, essentially noninformative.
   beta2 ~ dnorm(0, 1.0E-6)
   beta3 ~ dnorm(0, 1.0E-6)
   alpha ~ dnorm(0, 1.0E-6)
   beta ~ dnorm(0, 1.0E-6)
   tau.prime ~ dnorm(0, 1.0E-6)

   # dgamma (a, b) is a gamma distribution with the shape parameter a and
   # inverse scale parameter b.
   prec.y ~ dgamma(0.001, 0.001)
   prec.m ~ dgamma(0.001, 0.001)

   # define the mediated effect as function of parameters
   theta < − alpha*beta
}

WinBUGS code for multilevel mediation analysis

model
{
   # specify the multilevel model
   # N1 and N2 are the number of first-level units and second-level units, respectively.
   for( j in 1:N2){
      for(i in 1:N1){
         # Specify the first-level model: Mij = β2j + αjXij + e2ij
         m[j, i] ~ dnorm(mean.m[j, i], prec.m)
         mean.m[j, i] < − Beta2[j] + AlphaBeta[j, 1]*x[j, i]

         # Specify the first-level model: Yij = β3j + βjMij + τ′jXij + e3ij
         y[j, i] ~ dnorm(mean.y[j, i], prec.y)
         mean.y[j, i] < − Beta3[j] + AlphaBeta[j, 2]*m[j,i] + Tau.p[j]*x[j, i]
      }
      # Specify the second-level models
      Beta2[j] ~ dnorm(beta2, prec.beta2)
      Beta3[j] ~ dnorm(beta3, prec.beta3)
      Tau.p[j] ~ dnorm(tau.p, prec.taup)

      # bivariate normal distribution for αi and β i
      AlphaBeta[j, 1:2] ~ dmnorm(alphabeta[ ], prec.ab[,])

   }

   # vague bivariate normal prior for α and β
   alphabeta[1:2] ~ dmnorm(mean[ ], prec[,])
   mean[1] < − 0
   mean[2] < − 0
   prec[1,1] < − 1.0E-6
   prec[1,2] < − 0
   prec[2,1] < − 0
   prec[2,2] < − 1.0E-6

   # vague inverse-Wishart prior for the covariance of αj and β j;
   # dwish(·) is the Wishart distribution
   prec.ab[1:2 , 1:2] ~ dwish(Omega[,], 2)
   Omega[1,1] < − 0.001
   Omega[1,2] < − 0.0
   Omega[2,1] < − 0.0
   Omega[2,2] < − 0.001

   # vague normal priors for β2, β3 and τ′
   beta2 ~ dnorm(0.0, 1.0E-6)
   beta3 ~ dnorm(0.0, 1.0E-6)
   tau.p ~ dnorm(0.0, 1.0E-6)

   # vague inverse-gamma prior for variances of the first level model
   prec.y ~ dgamma(0.001, 0.001)
   prec.m ~ dgamma(0.001, 0.001)

   # vague uniform priors for standard deviations of the second level model
   sigma.beta2 ~ dunif(0, 100)
   sigma.taup ~ dunif(0, 100)
   sigma.beta3 ~ dunif(0, 100)
   prec.beta2 < − 1/(sigma.beta2*sigma.beta2)
   prec.taup < − 1/(sigma.taup*sigma.taup)
   prec.beta3 < − 1/(sigma.beta3*sigma.beta3)

   ## define quantities of interest
   # covariance matrix of αi and βi
   var.ab[1,1] < − prec.ab[2,2]/(prec.ab[1,1]*prec.ab[2,2]-prec.ab[1,2]*prec.ab[2,1])
   var.ab[1,2] < − -prec.ab[1,2]/(prec.ab[1,1]*prec.ab[2,2]-prec.ab[1,2]*prec.ab[2,1])
   var.ab[2,1] < − -prec.ab[2,1]/(prec.ab[1,1]*prec.ab[2,2]-prec.ab[1,2]*prec.ab[2,1])
   var.ab[2,2] < − prec.ab[1,1]/(prec.ab[1,1]*prec.ab[2,2]-prec.ab[1,2]*prec.ab[2,1])

   # average mediated effect ab, total effect c and relative mediated effect r = ab/c
   ab < − alphabeta[1]*alphabeta[2]+ var.ab[1,2]
   c < − alphabeta[1]*alphabeta[2]+ var.ab[1,2]+tau.p
   r < − ab/c
}