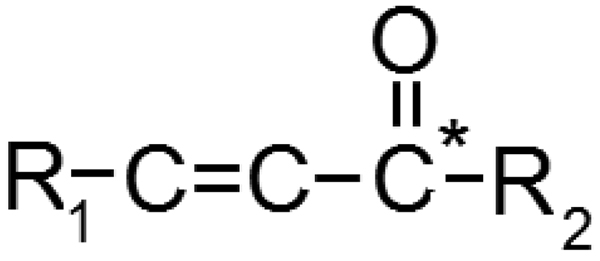Optimal transfer of spin-order between a singlet nuclear pair and a heteronucleus

Abstract

Intramolecular spin-order transfer is a useful technique for signal enhancement of insensitive and low-concentration molecular species. We present a closed-form, optimized pulse sequence which maximizes the efficiency of transfer between a singlet (para) nuclear pair and a vicinal heteronucleus. Neglecting the decay of coherences while the nuclei are in the transverse plane, the scheme is unity efficient for all combinations of internuclear scalar couplings. Efficiency loss due to T₂-like decay is also minimized by keeping the sequence as short as possible. We expect this result to be useful for hyperpolarization experiments in which the spin-order originates in parahydrogen, as well as studies of singlet state decay aimed at longer-term storage of spin-order in hyperpolarized Magnetic Resonance Imaging.

I. Introduction

Nuclear magnetic resonance is an enormously versatile tool that is used in a wide variety of chemical analysis and medical imaging applications. Many of its most useful applications arise from NMR’s unique sensitivity to the chemical environment. In the context of medical imaging, however, tests that take advantage of this attribute are not commonly performed, even though the detection and quantification of specific molecular species and transformations would be of great benefit. This is largely because the NMR signal is not sufficiently sensitive to the chemical environment when the target nucleus is the proton, and detection of any other nucleus is impractical due to an unacceptably low signal-to-noise.

During the past several years, nuclear alignment techniques collectively known as ‘hyperpolarization’ have been developed to address the limited signal from heteronuclei. One of these techniques, Parahydrogen-Induced Polarization (PHIP), makes use of the spin-order inherent in the parahydrogen molecule, which is then transferred to a heteronucleus after a hydrogenation chemical reaction. This order transfer relies on a sequence of NMR pulses that control the post-hydrogenation spin evolution to maximize heteronuclear alignment. Spectroscopy or imaging is then performed before the nuclear state returns to thermal equilibrium.

We present a general formula for calculating the optimum pulse choice and timing. In the absence of T₂-like relaxation or imperfect pulses, the sequence always yields complete heteronuclear alignment. Since the prediction and discovery of the PHIP effect [1,2], other schemes for order transfer have been proposed [3–7]. All are based on either static field cycling or are related to the INEPT pulse sequence for polarization transfer between thermally polarized nuclei. This work builds in particular on the recent publication by Goldman, et al. [5], extending the geometrical analogy to the entire evolution period, and solving the resulting equations to arrive at a closed-form optimal sequence.

II. Background

Parahydrogen is a form of ordinary hydrogen gas (H₂) in which the two protons are in the antisymmetric singlet state. Using density matrix formalism, this state is shown in eq. 1. After hydrogenation of an alkene or alkyne bond using a molecular catalyst, the proton spin order is often conserved, although subsequent spin evolution now includes couplings to nearby nuclei. In nearly all circumstances, the two hydrogen atoms are added by a catalyst to neighboring carbon atoms. As noted in section III, spin order transfer to another nucleus is quick and efficient if the protons’ coupling to the target nucleus differs substantially. This condition is often found in molecules of the form shown in fig. 1. Note that maximally efficient spin order transfer requires that there only be couplings between the parahydrogen protons and the target nucleus, although this configuration is well-approximated by real molecules in which other nearby protons are either absent or have been replaced by deuterons (²H). In the following analysis, we refer to the two proton spins as S₁ and S₂, and the nearby heteronucleus as I. It is possible to doubly hydrogenate an alkyne bond, leading to two para proton pairs, although this case is not amenable to closed-form analysis.

$${\rho }_{{\mathit{\text{pH}}}_2}=\frac{1}{4}-S_1·S_2$$ eq. 1

Figure 1.

Typical precursor structure for successful hydrogenation and spin order transfer. R₁ and R₂ are general structures, chosen for biological interest or to minimize coupling to hydrogenated protons. C^* refers, in this case, to a ¹³C-labeled position.

In general, the state of the hydrogenated, dissolved molecule is described by a Zeeman energy for each nucleus and a scalar coupling between each pair of nuclei:

$$\frac{H}{\hslash }={\omega }_H(S_{1Z}+S_{2Z})+{\omega }_C{I}_Z+2\pi (J_{12}{S}_1·S_2+J_{1C}I·S_1+J_{2C}I·S_2)$$ eq. 2

This may be simplified somewhat by noting that during periods of free evolution, the effect of terms that cause transitions between states of substantially different energy (e.g., I₊S₁₋) is suppressed by a factor of ~(ω_H − ω_C)/J. Under typical conditions of interest, this factor is approximately 10⁴, and all of these terms may be ignored. This leads to eq. 3.

$$\frac{H}{\hslash }={\omega }_H(S_{1Z}+S_{2Z})+{\omega }_C{I}_Z+2\pi (J_{12}{S}_1·S_2+J_{1C}{I}_Z{S}_{1Z}+J_{2C}{I}_Z{S}_{2Z})$$ eq. 3

In the state space which includes the heteronucleus, post-hydrogenation evolution then begins from the density matrix of eq. 4, and is governed by the Schrödinger equation.

$$\rho (0)=\frac{1}{8}-\frac{S_1·S_2}{2}$$ eq. 4

As in the INEPT polarization transfer sequence, the evolution may be thought of in terms of two steps; step one maximizes the coherence between the para protons and the heteronucleus, and step two transforms this coherence into a heteronuclear state change by putting the heteronucleus in the transverse plane. The two evolution periods are amenable to the same simplifications and geometric interpretations, and may be treated identically.

In solving the Schrödinger equation, it is convenient to expand ρ(t) in terms of the sixty-four orthogonal Liouville space superoperators that span the three-spin space. Of these, only eight (defined below in eq. 5) are required to describe the full motion.

$$\begin{array}{cc}{\rho }_0=I_o\otimes (S_{1o}\otimes S_{2o}-S_{1z}\otimes S_{2z})\hfill & {\rho }_4=I_y\otimes (S_{1o}\otimes S_{2o}-S_{1z}\otimes S_{2z})\hfill \\ {\rho }_1=I_o\otimes (-S_{1x}\otimes S_{2x}-S_{1y}\otimes S_{2y})\hfill & {\rho }_5=I_x\otimes (S_{1o}\otimes S_{2z}-S_{1z}\otimes S_{2o})\hfill \\ {\rho }_2=I_z\otimes (S_{1x}\otimes S_{2y}-S_{1y}\otimes S_{2x})\hfill & {\rho }_6=I_x\otimes (S_{1y}\otimes S_{2x}-S_{1x}\otimes S_{2y})\hfill \\ {\rho }_3=I_z\otimes (S_{1o}\otimes S_{2z}-S_{1z}\otimes S_{2o})\hfill & {\rho }_7=I_z\otimes (S_{1o}\otimes S_{2o}-S_{1z}\otimes S_{2z})\hfill \end{array}$$ eq. 5

The subscript o refers to ½ × the unit operator, and x, y, and z denote the spin-½ operators, or ½ × the corresponding Pauli matrices. Note that ρ₇ corresponds to the fully polarized heteronuclear state, making it a suitable hyperpolarized target.

We may therefore define the density matrix at any time t as

$$\rho (t)={\displaystyle \sum c_i{\rho }_i}$$ eq. 6

subject to the initial conditions

$$c_0(0)=c_1(0)=1,c_{2..7}(0)=0$$ eq. 7

Substitution of (2) and (6) into the Schrödinger equation yields the coupled differential equations:

$$\begin{array}{ccc}{\mathit{ċ}}_0=0\hfill & {\mathit{ċ}}_1=\pi (J_{1C}-J_{2C})c_2\hfill & {\mathit{ċ}}_4=\pi (J_{1C}-J_{2C})c_5\hfill \\ \hfill & {\mathit{ċ}}_2=-\pi (J_{1C}-J_{2C})c_1-2\pi J_{12}{c}_3\hfill & {\mathit{ċ}}_5=-\pi (J_{1C}-J_{2C})c_4-2\pi J_{12}{c}_6\hfill \\ \hfill & {\mathit{ċ}}_3=2\pi J_{12}{c}_2\hfill & {\mathit{ċ}}_6=2\pi J_{12}{c}_5\hfill \end{array}$$ eq. 8

Free evolution of the system does not yield the desired polarized heteronuclear state. However, as with INEPT, a sequence can be devised that makes use of periods of free evolution punctuated by selective rotations of the heteronucleus. Inspection of eq. 5 shows the effect of such pulses, which is summarized in figure 2.

Figure 2.

A schematic representation of controlled evolution during the spin-order transfer pulse sequence. The system begins in a state characterized by c₁ = 1. Evolution proceeds among c₁, c₂ and c₃ at the rates shown (thin arrows), and is controlled by selective inversion of c₂ and c₃ using π_y pulses. Once c₁ has been eliminated, a π/2_y pulse transfers the system to another subspace (c₆ = −c₂, c₅ = c₃). Evolution continues, controlled by inversion of c₅ and c₆ using π_y pulses, until the state characterized by c₄ = 1 is reached. A final π/2_x pulse achieves the fully aligned heteronuclear state.

It is now possible to conceptually describe the pulse sequence that will take us from the initial state of eq. 4 to one in which the probability is concentrated in the hyperpolarized heteronuclear state (c₇ = 1). This can be done in four steps:

1. Evolution initially proceeds inside the subspace spanned by ρ₁, ρ₂, ρ₃, and is steered by inversions of the heteronucleus.

2. When c₁ has been eliminated, a π/2_y pulse transfers the system to the subspace spanned by ρ₄, ρ₅ and ρ₆.

3. A similar sequence of heteonuclear pulses steers to a state in which c₄ and c₅ have been eliminated, and

4. A final π/2_x pulse transfers the state to the fully aligned heteronuclear state in which c₀ = c₇ = 1.

III. Results: Geometric analogy and closed-form solution

In devising the optimal pulse sequence to control the evolution as described above, it is helpful to note that differential equations describing the motion of the system (eq. 8) are identical to those which describe the motion of a fictitious dipole K with a gyromagnetic ratio of 1 under the influence of a magnetic field

$$\mathbf{B}=\frac{J_{1C}-J_{2C}}{2}\stackrel{⌢}{x}+J_{12}\stackrel{⌢}{z},$$ eq. 9

fixed at an angle

$$\theta ={\text{tan}}^{-1}\left(\frac{|J_{1C}-J_{2C}|}{2J_{12}}\right)$$ eq. 10

with respect to the z axis. A similar correspondence was pointed out for the evolution of step 1 in ref. [5], but we note here that it applies to step 3 as well. We may therefore picture the dynamical behavior of the 3-spin system in terms of a precession of K at rate

$$\omega =2\pi \sqrt{{J_{12}}^2+\frac{{(J_{1C}-J_{2C})}^2}{4}}$$ eq. 11

around B. As can be seen from inspection of eq. 5, the applied pulses can be interpreted geometrically in this analogous system as well; the application of heteronuclear inversion pulses has the effect of rotating K by π around ẑ, and the π/2_y pulse is equivalent to a π/2 rotation of K around ẑ. With this correspondence in place, it becomes possible to visualize and calculate the optimal pulse sequence that achieves steps 1–4 above using rotations in ordinary 3-space rather than the less intuitive full product space of the nuclear system. Such a sequence will consist of a series of delays Δ(τ_i) followed by heteronuclear pulses such that

$$\mathit{\nu }=\left({\displaystyle \prod _i\mathrm{\Lambda }{R}_y(\theta )R_z(\omega {\tau }_i)R_y(-\theta )}\right)\widehat{z}$$ eq. 12

lies in the x-y plane (step 1). Another series of delays is chosen such that

$$\left({\displaystyle \prod _j\mathrm{\Lambda }{R}_y(\theta )R_z(\omega {\tau }_j)R_y}(-\theta )\right)R_z(\pi /2)\mathit{\nu }=\widehat{z}.$$ eq. 13

In the expression above, $\mathrm{\Lambda }=-\widehat{x}\widehat{x}-\widehat{y}\widehat{y}+\widehat{z}\widehat{z}$ ; multiplication by this operator reflects K around the z axis. Although any ν in the x-y plane is in principle a suitable intermediate state, a particularly straightforward sequence is arrived at if the τ_i are chosen such that the intermediate state makes an angle of π/4 with the x and y axes, i.e., $\mathbf{v}•\widehat{x}=\pm 1/\sqrt{2}$. This is because the π/2 rotation corresponding to step 2 maintains the same relationship to the x and y axes, and a symmetric set of pulses can be employed for steps 1 and 3. Additionally, we find that the total evolution time is either equal to or negligibly longer than (within a few percent of) the minimum possible for complete order transfer.

The form of this optimal or near-optimal sequence depends on the relative strengths of the three internuclear couplings, but a solution can always be found and is specified for all cases below. Note that each period of evolution referred to below as Δ(τ) must be refocused by including an inversion of all spins at the midpoint of the delay, or through another equivalent scheme. These refocusing pulses are omitted below for brevity.

$$\mathit{\text{Case}}\mathit{1}\mathit{:}\text{tan}(\theta )=\sqrt{2}$$

In this fortuitous case (corresponding to approximately $\frac{|J_{1C}-J_{2C}|}{2J_{12}}=1.4142$), the transfer of spin-order is particularly simple because initial and final states make the same angle with the fictitious field (that is, $\widehat{z}•\mathbf{B}=(\widehat{x}-\widehat{y})/\sqrt{2}•\mathbf{B}$). Therefore, a simple precession causes the desired transitions in steps 1 and 3. The optimal pulse sequence consists only of two heteronuclear pulses and two identical waiting periods:

$$\mathrm{\Delta }({\tau }_1)-{\frac{\pi }{2}}_{C,y}-\mathrm{\Delta }({\tau }_1)-{\frac{\pi }{2}}_{C,x}$$ eq. 14

in which the waiting period τ₁ = 2π / 3ω. In practice, this simple sequence is acceptably efficient in the range $1<\frac{|J_{1C}-J_{2C}|}{2J_{12}}<2$, achieving a singlet to aligned nucleus spin-order transfer of > 0.9 in all such cases.

$$\mathit{\text{Case}}\mathit{2}\mathit{:}\text{tan}(\theta )<\sqrt{2}$$ eq. 15

$$\mathit{\text{Case}}\mathit{2}a\mathit{:}\frac{\sqrt{2}}{2\sqrt{2}\text{sin}(2\theta )+1}\le \text{tan}(\theta )<\sqrt{2}$$ eq. 16

In these implicitly defined cases (corresponding to approximately $0.4526\le \frac{|J_{1C}-J_{2C}|}{2J_{12}}<1.4142$), the target state of step 1 can be achieved with a single inversion pulse. Explicitly solving for the delays using eq. 12, we find that two different delays are required, yielding a sequence of the form

$$\mathrm{\Delta }({\tau }_1)-{\pi }_{C,y}-\mathrm{\Delta }({\tau }_2)-{\frac{\pi }{2}}_{C,y}-\mathrm{\Delta }({\tau }_2)-{\pi }_{C,y}-\mathrm{\Delta }({\tau }_1)-{\frac{\pi }{2}}_{C,x}$$ eq. 17

with unequal delays

$${\tau }_1=\frac{1}{\omega }{\text{cos}}^{-1}\left(1-\frac{\sqrt{2}\text{cos}(\theta )-\text{sin}(\theta )}{\sqrt{2}\text{sin}(\theta )\text{sin}(2\theta )}\right)$$ eq. 18

$${\tau }_2=\frac{1}{\omega }{\text{cos}}^{-1}\left(-\frac{\text{sin}\left(\theta \right)}{1+{\text{cos}}^2(\theta )}\left\{\sqrt{2}\text{cos}(\theta )[1-\text{cos}(\omega {\tau }_1)]+\sqrt{2}\text{sin}(\omega {\tau }_1)+\text{sin}(\theta )\right\}\right)$$ eq. 19

$$\mathit{\text{Case}}\mathit{2}b\mathit{:}\text{tan}(\theta )<\frac{\sqrt{2}}{2\sqrt{2}\text{sin}(2\theta )+1}$$ eq. 20

For cases in which the couplings between the heteronucleus and each member of the singlet pair are sufficiently similar $(\frac{|J_{1C}-J_{2C}|}{2J_{12}}<0.4526)$, two or more heteronuclear inversions are required to achieve complete transfer of spin-order. In the geometric analogy, the sequence must be modified to develop sufficient separation between K and B that a final precession can lead to the final state of eq. 12. As with a precessing magnetic moment, separation is obtained most efficiently by modulating the transverse field component (inverting the heteronucleus) synchronously with the unmodified precession; this corresponds to a series of refocused delays of length π / ω. Although it does not affect the final sequence length, we find that the closed-form expressions are simplest if the additional periods are inserted in the middle of the sequence. As |J_1C − J_2C| approaches zero, an increasingly long sequence is required, which is analogous to the increasing NMR pulse length needed as the transverse field strength is decreased. In a generalization of eq. 16, a solution requiring n additional evolution periods can be found if

$$\text{tan}(\theta )\ge \frac{\sqrt{2}}{2\sqrt{2}\text{sin}(2\theta )+\text{cos}(2n\theta )+\text{sin}(2n\theta )\sqrt{2{\text{csc}}^2(\theta )-1}}$$ eq. 21

The appropriate sequence has the form

$$\mathrm{\Delta }({\tau }_1)-{\pi }_{C,y}-\mathrm{\Delta }({\tau }_2)-{\pi }_{C,y}\cdots \mathrm{\Delta }({\tau }_{n+2})-{\frac{\pi }{2}}_{C,y}-\mathrm{\Delta }({\tau }_{n+2})-{\pi }_{C,y}-\mathrm{\Delta }({\tau }_{n+1})-{\pi }_{C,y}\cdots \mathrm{\Delta }({\tau }_1)-{\frac{\pi }{2}}_{C,x}$$ eq. 22

and the delays τ_1..n+2 which achieve maximal spin-order transfer are

$${\tau }_1=\frac{1}{\omega }{\text{cos}}^{-1}\left(1-\frac{\sqrt{2}\text{cos}(\theta )-\text{sin}(\theta )\text{cos}(2n\theta )-\text{sin}(2n\theta )\sqrt{2-{\text{sin}}^2(\theta )}}{\sqrt{2}\text{sin}(\theta )\text{sin}(2\theta )}\right)$$ eq. 23

$${\tau }_2=\frac{1}{\omega }\left(\pi +{\text{tan}}^{-1}\left[\frac{\text{sin}(\theta )\text{sin}(\omega {\tau }_1)}{\text{sin}(2\theta )\text{cos}(\theta )-\text{cos}(\omega {\tau }_1)\text{sin}(\theta )\text{cos}(2\theta )}\right]\right)$$ eq. 24

$${\tau }_{3..n+1}=\frac{\pi }{\omega }$$ eq. 25

$${\tau }_{n+2}=\frac{1}{\omega }{\text{tan}}^{-1}(-\text{sec}(\theta ))$$ eq. 26

In the expressions above, note that the value of the tan⁻¹ should be chosen such that it is always between 0 and π.

$$\mathit{\text{Case}}\mathit{3}:\text{tan}(\theta )>\sqrt{2}$$ eq. 27

Although it is less immediately apparent, a similar trend toward increasingly long sequences is found as |J_1C − J_2C| becomes large. This situation is less common in molecular systems of interest, but is included below for completeness. We find that the resulting expressions are simplest if the delays analogous to eq. 25 are at the beginning of the sequence:

$$\mathit{\text{Case}}\mathit{3}a:\text{tan}(\theta )>\sqrt{2}\text{ and tan}(\theta )\ge \frac{\sqrt{2}}{2\sqrt{2}\text{sin}(2\theta )-1}\text{ and sin}(2\theta )>\frac{1}{2\sqrt{2}}$$ eq. 28

In these cases, corresponding to approximately $1.4142\le \frac{|J_{1C}-J_{2C}|}{2J_{12}}<3.8923$, the sequence consists of

$$\mathrm{\Delta }({\tau }_1)-{\pi }_{C,y}-\mathrm{\Delta }({\tau }_2)-{\frac{\pi }{2}}_{C,y}-\mathrm{\Delta }({\tau }_2)-{\pi }_{C,y}-\mathrm{\Delta }({\tau }_1)-{\frac{\pi }{2}}_{C,x}$$ eq. 29

in which

$${\tau }_1=\frac{1}{\omega }{\text{cos}}^{-1}\left(1-\frac{\sqrt{2}\text{cos}(\theta )+\text{sin}(\theta )}{\sqrt{2}\text{sin}(\theta )\text{sin}(2\theta )}\right)$$ eq. 30

$${\tau }_2=\frac{1}{\omega }{\text{cos}}^{-1}\left(\frac{\text{sin}(\theta )}{1+{\text{cos}}^2(\theta )}\left\{\sqrt{2}\text{cos}(\theta )[1-\text{cos}(\omega {\tau }_1)]+\sqrt{2}\text{sin}(\omega {\tau }_1)-\text{sin}(\theta )\right\}\right)$$ eq. 31

$$\mathit{\text{Case}}\mathit{3}b:\text{tan}(\theta )>\sqrt{2}\text{ and }(\text{tan}(\theta )<\frac{\sqrt{2}}{2\sqrt{2}\text{sin}(2\theta )-1}\text{or sin}(2\theta )<\frac{1}{2\sqrt{2}})$$ eq. 32

For cases in which $\frac{|J_{1C}-J_{2C}|}{2J_{12}}>3.8923$, a solution using n additional evolution periods can be found as long as ${(-1)}^n\text{cos}((2n+3)\theta )\le -\text{sin}(\theta )/\sqrt{2}$. The sequence will have the form

$$\mathrm{\Delta }({\tau }_1)-{\pi }_{C,y}-\mathrm{\Delta }({\tau }_2)-{\pi }_{C,y}\cdots \mathrm{\Delta }({\tau }_{n+2})-{\frac{\pi }{2}}_{C,y}-\mathrm{\Delta }({\tau }_{n+2})-{\pi }_{C,y}-\mathrm{\Delta }({\tau }_{n+1})-{\pi }_{C,y}\cdots \mathrm{\Delta }({\tau }_1)-{\frac{\pi }{2}}_{C,x}$$ eq. 33

with

$${\tau }_{1..n}=\frac{\pi }{\omega }$$ eq. 34

$${\tau }_{n+1}=\frac{1}{\omega }{\text{cos}}^{-1}\left(-\frac{\sqrt{2}\text{cos}((2n+1)\theta )\text{cos}(2\theta )+{(-1)}^n\text{sin}(\theta )}{\sqrt{2}\text{sin}((2n+1)\theta )\text{sin}(2\theta )}\right)$$ eq. 35

$${\tau }_{n+2}={\text{cos}}^{-1}\left(\frac{-\text{cos}(\theta )}{\sqrt{2-{\text{sin}}^2(\theta )}}\right)-{\text{tan}}^{-1}\left(\frac{\text{sin}(\omega {\tau }_{n+1})\text{tan}((2n+1)\theta )}{\text{cos}(\omega {\tau }_{n+1})\text{tan}((2n+1)\theta )\text{cos}(2\theta )-\text{sin}(2\theta )}\right)$$ eq. 36

In the above expression, the value of tan⁻¹ is again chosen to be positive.

IV. Discussion

The sequences presented in section III apply to all possible combinations of scalar couplings among the three-spin system and constitute the fastest possible method for complete spin order transfer from a singlet nuclear pair to an aligned heteronucleus. Barring unusual circumstances, in which the intermediate coherences decay at significantly different rates, it is likely the most efficient sequence as well. It can of course also be used in reverse to create singlet spin order from an aligned (thermally or otherwise) heteronucleus.

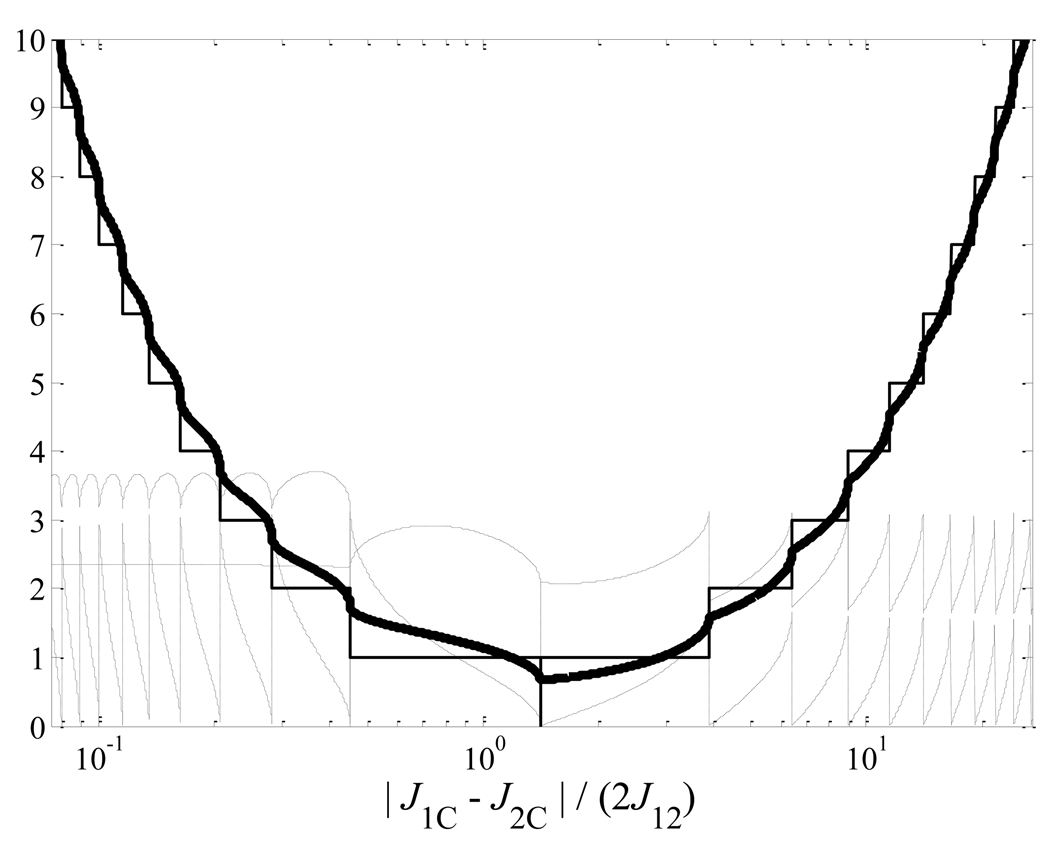
However, there are three potential limitations to consider when implementing the sequence. First, the scalar couplings J_1C and J_2C must differ. This can be seen immediately by noting that we seek a transition from a symmetric (singlet, unaligned) state to an antisymmetric (hyperpolarized) one; the source of the asymmetry must be the Hamiltonian. In fact, although not as immediately apparent, the Hamiltonian must have symmetric features as well. As noted in section III, case 1, the perfectly ‘mixed’ Hamiltonian occurs when $(J_{1C}-J_{2C})/J_{12}=\pm 2\sqrt{2}$ and results in the fastest order transfer; departure from this condition by more than approximately an order of magnitude requires a sequence that is likely too long compared to expected coherence decay rates to be of practical value. The increase in the number of pulses and total delay time as the couplings become purely symmetric or antisymmetric is demonstrated in more detail in fig. 3. As a practical matter, J₁₂ in saturated analogs of fig. 1 is typically ~4–8 Hz [8], implying efficient spin-order transfer when |J_1C − J_2C| > 0.5–1 Hz. This is usually the case in biological molecules of interest.

Figure 3.

As the ratio of scalar couplings |J_1C−J_2C| / (2J₁₂) departs significantly from ~1, spin-order transfer requires increasingly more time and RF pulses. The thin, solid trace shows the number of evolution periods required to effect transfer. In the range of approximately 0.1 to 10, a sequence of reasonable total length is possible (solid, thick trace, in units of 1/(πω) ). The dotted traces show the required values of the unequal delays, shown in units of 1/ω. Note that the total pulse sequence duration is approximately nπ/ω, and thus ranges from ~100 ms to ~1 second over the range shown for typical molecular scalar coupling values.

Second, it is important to minimize any other sources of singlet-triplet conversion within the singlet pair both before and during the transfer pulse sequence. Chief among these sources is the chemical shift difference, which must be removed by choosing chemically identical environments for the singlet pair, lowering the field to the point at which the frequency difference is much less than ω [9], or interspersing decoupling/spin-locking pulses during hydrogenation and the delay periods of the transfer sequence [10]. It is also important to minimize the departure from the isolated three-spin system, either through deuteration of vicinal protons [11–15] or the choice of an inherently well-isolated system. This isolation may be achieved either by choosing a precursor molecule with no non-zero spins except the label (e.g., acetylenedicarboxylate, demonstrated in [16]), or by ensuring that spins to which coupling would ordinarily be expected are sufficiently distant (e.g., 2-hydroxyethyl acrylate, described in [12–13,15], in which the nearest nonzero, non-deuterated spin is three bonds away from the three-spin system of interest).

Finally, it should be noted that while order transfer from a singlet pair to an aligned heteronucleus can in principle be performed with unit efficiency, the maximum efficiency for the reverse sequence is ½ due to the inherently greater order of the singlet pair (1 of 4 possible states) as compared to that of the single aligned nucleus (1 of 2 possible states). An equal mixture of the singlet and triplet m=0 states is produced by the reversed sequence.

V. Conclusion

We have derived a closed-form sequence that causes optimally or near-optimally efficient spin-order transfer between a singlet nuclear pair and a heteronucleus in dissolved molecular systems. In the absence of coherence decay, this sequence is always lossless and is reversible (although with reduced efficiency), and is likely maximally efficient in all cases. Measurement of the three internuclear scalar couplings is sufficient to specify the sequence. As long as the potential limitations noted above are ameliorated, efficient transfer can be achieved in most systems of interest. Applications of this result include production of hyperpolarized nuclei through spin-order transfer from parahydrogen, and the creation of intramolecular singlet pairs with the potential for extended storage of spin-order.