Pitch, Harmonicity and Concurrent Sound Segregation: Psychoacoustical and Neurophysiological Findings

Abstract

Harmonic complex tones are a particularly important class of sounds found in both speech and music. Although these sounds contain multiple frequency components, they are usually perceived as a coherent whole, with a pitch corresponding to the fundamental frequency (F0). However, when two or more harmonic sounds occur concurrently, e.g., at a cocktail party or in a symphony, the auditory system must separate harmonics and assign them to their respective F0s so that a coherent and veridical representation of the different sounds sources is formed. Here we review both psychophysical and neurophysiological (single-unit and evoked-potential) findings, which provide some insight into how, and how well, the auditory system accomplishes this task. A survey of computational models designed to estimate multiple F0s and segregate concurrent sources is followed by a review of the empirical literature on the perception and neural coding of concurrent harmonic sounds, including vowels, as well as findings obtained using single complex tones with “mistuned” harmonics.

Introduction

Many of the sounds that are important to humans and other animals are harmonic or quasi-harmonic. The frequencies of the spectral components of such sounds are all roughly integer multiples of a common low frequency, which is known as the “fundamental frequency” or “F0”. Harmonic sounds are usually perceived as a coherent entity, rather than as a simultaneous collection of unrelated pure tones. This simple observation suggests that the auditory system tends to “group” or “bind” together components that are presented simultaneously and are harmonically related. A second important observation concerning harmonic complex tones is that they evoke a pitch that corresponds, in most cases, to that of a pure tone with a frequency corresponding to the F0 of the complex tone. This “virtual pitch” is perceived even when spectral energy at the F0 of the complex tone is absent, or masked. Together, these two observations have led to the hypothesis that the same underlying mechanisms are responsible for the perceptual grouping of harmonically related components, and for the perception of virtual pitch. A corollary of the hypothesis that the auditory system uses harmonicity to group together frequency components that belong to a common F0, and presumably arose from a single source, is that differences in F0 can be used to separate concurrent sounds, which are then perceived as having different pitches.

In this article, we review psychophysical findings concerning the ability of normal-hearing listeners to use F0 differences, or deviations from harmonicity, to segregate concurrent sounds. Although there have been excellent reviews of the role and effects of harmonicity in the perceptual organization of sounds in the past (e.g., Bregman, 1990, chapter 3; Darwin and Carlyon, 1995), there has been increased interest and activity in this area over the last decade. Some of these studies involving both simultaneous and sequential segregation were reviewed by Carlyon and Gockel (2008). Here we focus only on the perceptual organization of simultaneous sounds, and the role played by harmonicity and spectral regularity. We review psychophysical studies as well as physiological studies, where neural responses to concurrent harmonic sounds have been measured at various levels of the auditory system, including single-unit studies in animals, and evoked-potential studies in humans.

Before delving into these empirical investigations, we consider briefly how auditory models, which were initially designed to model the perception of isolated harmonic complex sounds, have been extended or modified in an attempt to deal with concurrent sounds. A more exhaustive survey of computational models of F0 extraction and F0-based segregation can be found in de Cheveigné (2005) and de Cheveigné (2006), respectively.

1. Modeling the perception of multiple concurrent pitches and F0-based segregation

1.1 Segregation and F0 estimation from a single representation

Most models of pitch perception (e.g., Cohen et al., 1995; Goldstein, 1973; Meddis and Hewitt, 1991a, 1991b; Meddis and O’Mard, 1997; Shamma and Klein, 2000; Terhardt, 1979; Wightman, 1973) were originally designed to account for psychophysical data obtained using single sounds presented in isolation. However, these models can be presented with mixtures of sounds, in the hope that their output will not only provide evidence for multiple periodicities, but also allow these periodicities to be estimated. For instance, the autocorrelation function (ACF) of a harmonic complex sound usually exhibits peaks at delays (or “lags”) corresponding to integer multiples of the stimulus period (Cariani and Delgutte, 1996; Meddis and Hewitt, 1991b) (Figure 1a). When two sounds with different F0s are mixed together, the ACF of the combined waveform will exhibit peaks that reflect both F0s (Figure 1b), provided the two F0s are not too close to each other, or in octave relationship. Under such “ideal” circumstances, it is possible to estimate more than one F0 by applying the same algorithm (i.e., peak-picking) multiple times on the same representation. Weintraub (1985) devised a system for estimating the F0s of concurrent voices based on this principle.

Figure 1.

Autocorrelation functions (ACFs) for a) a single harmonic complex tone with an F0 of 250 Hz and b) two concurrent harmonic complexes with F0s of 250 and 263 Hz. The ACF of the single complex displays peaks at integer multiples of the F0 period, 4 ms. The ACF of the complex mixture displays peaks at integer multiples of both F0 periods, 3.8 and 4 ms.

A similar approach may be pursued with “spectral” or “place” representations, also known as “excitation patterns” (EPs) (Glasberg and Moore, 1990). These EPs represent the energy (or a monotonically related quantity) at the output of simulated cochlear filters as a function of the filter center frequency (CF). Provided that the harmonics in a complex tone, or a mixture of two complex tones, evoke detectable EP peaks (Figure 2), the frequencies of these harmonics can be determined (using “peak-picking”, or a more physiologically plausible algorithm), and the corresponding F0(s) estimated. Most “place” models of pitch perception rely on this. However, relying solely on EP peaks has some disadvantages. The peak-to-valley ratios in EPs evoked by multi-component complexes decrease with decreasing frequency resolution (as determined by the bandwidths of the simulated cochlear filters), and with decreasing frequency spacing between the stimulus components. Although the relative bandwidths (bandwidth, relative to the CF) of the cochlear filters may remain constant or even decrease with increasing CF, the absolute bandwidths (in Hz) of the cochlear filters increase. As a result, “place” models of pitch perception based on EPs can usually only be applied to relatively low-numbered harmonics (below about the 10^th). These low-ranked harmonics, which produce salient peaks in EPs, are said to be “resolved”. The likelihood that a harmonic is resolved decreases when two, equal-level spectrally overlapping complex tones with flat spectral envelopes are presented simultaneously, as this reduces the average spacing between spectral components by a factor of two. With three or more such complexes in the same spectral region, the likelihood of several well-detectable peaks being present in the EP is low. Therefore, the performance of models that rely solely on peaks in EPs to estimate multiple pitches is likely to drop rapidly as the number of sounds increases. However, it is important to note that these observations apply specifically to concurrent complexes with approximately equal levels and flat spectral envelopes. Obviously, if one of the sounds has a substantially higher level than the others, its harmonics may remain “resolved” even after other sounds are added, as they dominate the mixture (see: Micheyl et al., 2005). For sounds with sparse spectra or strongly modulated spectral envelopes, such as vowels, harmonics of one sound may dominate and be resolved in one spectral region, while harmonics of the other sound may dominate and be resolved in a different spectral region.

Figure 2.

Excitation patterns (EPs) evoked by a) a single harmonic complex consisting of the first 15 harmonics of a 250 Hz F0, and b) a mixture of two harmonic complexes consisting of the former tone plus the first 7 harmonics of a 526 Hz F0. The solid vertical lines show the harmonics of the 250 Hz-F0 complex; the dashed lines show the harmonics of the 526 Hz F0.

A further point that is often overlooked is that the absence of salient peaks in EPs evoked by sound mixtures does not imply that a place-based approach is necessarily doomed. Features other than peaks may be present in the EPs evoked by mixtures of complex sounds. For instance, a harmonic close in frequency to a higher-level component can manifest itself as a “shoulder” next to the main peak. Similarly, by analyzing the shapes of spectral or EP peaks, a system may be able to detect peaks that were produced by more than one component, and to estimate the frequencies of these components. Parsons (1976) took advantage of such features to estimate accurately the frequencies of overlapping harmonics in the spectra of concurrent vowels [however, see de Cheveigné (2006) for an illustration of certain difficulties with this approach, due to the influence of the relative phases of the components on the shape of short-term magnitude spectra]. Recently, Larsen et al. (2008) were able to estimate accurately the F0s of two concurrently presented harmonic complexes based on rate-place profiles derived from cat auditory-nerve responses. As discussed in more detail in the section devoted to neurophysiological data, the estimation algorithm that they employed makes use of features other than just peaks.

1.2 Segregation based on F0 or channel suppression

Some approaches to separating sources and estimating F0s have used an iterative procedure, where the initial estimation of sources or F0s leads to an alteration of the stimulus representation to facilitate the processing of the remaining sources. The algorithm of Parsons (1976), mentioned above, is one of the first examples. Parson’s algorithm involves the following steps. First, peaks are extracted from the spectral representation of a mixture of two vowels. Second, these are used to compute a Schroeder histogram (Schroeder, 1968), which is obtained by dividing the frequencies of spectral peaks by successive small integers (e.g., from 1 to 20), and by sorting the resulting values into relatively small bins; if the bins are sorted in increasing order from right to left based on their center frequencies, the center frequency of the rightmost bin corresponding to a mode of the histogram is the F0 estimate (see: 2005 for details and an example). Parsons used the first F0 derived from the Schroeder histogram of all peaks in the combined spectrum as an estimate of one of the two F0s present in the mixture. He then used this estimate to “tag” spectral peaks corresponding to that first F0. Finally, he recomputed a Schroeder histogram using solely untagged peaks, in order to estimate the F0 of the second voice.

While Parsons’ algorithm operates directly on the spectrum, authors of later studies applied the estimation-suppression-estimation idea in the context of more realistic auditory models. For instance, Scheffers (1983b) adapted Duifhuis et al.’s (1982) implementation of Goldstein’s (1973) optimum processor theory of pitch perception to better estimate the F0 of harmonic sounds partially masked by noise or another harmonic sound. Scheffers used his model to segregate two concurrent vowels. In general, his model was able to identify one of the two constituent vowels, but not both. Moreover, the model failed to predict the improvement in identification performance with increasing F0 separation observed in human listeners (Assmann and Summerfield, 1990; Scheffers, 1983a; Zwicker, 1984). Assmann and Summerfield (1990) extended Scheffers’ work. They tested different pattern-matching procedures, based on EPs, for the identification of double vowels with the same F0. Importantly, they introduced the idea of computing similarity measures between EPs evoked by isolated vowels and EPs evoked by double vowels, in order to predict identification performance.

1.3 From purely time- or place-based models to place-time models

Assmann and Summerfield (1990) systematically evaluated the performance of various place and place-time models in the identification of vowels with different F0s. Both types of models involved an initial stage simulating cochlear filtering, but while place-only models discarded temporal fluctuations at the output of the peripheral filters, place-time models used this information to estimate the F0s of the two vowels. The main finding was that place-time models substantially outperformed place-only models, and came closer to predicting human performance. These findings played an important part in orienting subsequent efforts to model the perception of double vowels away from purely place-based analyses, and towards temporal analyses. Nevertheless, even the place-time models had difficulties reproducing the gradual improvement in performance with increasing F0 separation observed in human listeners.

To remedy this problem, Meddis and Hewitt (1992) devised a more sophisticated place-time model. Similar to those considered by Assmann and Summerfield (1990), Meddis and Hewitt’s model also involved initial filtering of the input signal by a bank of bandpass filters, and computation of ACFs at the output of each filter. The summed ACF was used to estimate one F0, and then each filter was sorted into one of two groups, depending on which periodicity was most dominant in that filter channel. These two groups of channels were then used to identify the two presented vowels. Importantly, the vowel-identification procedure was applied separately on each group of channels, so that the identification of one vowel was not contaminated by information from channels that responded primarily to the other vowel. Clearly, meaningful segregation of the channels into two groups based on F0 is only possible when the F0s of the two input vowels differ. Moreover, as F0 separation increases, the segregation becomes more robust. Thus, this type of model predicts increases in identification performance with increasing F0. In fact, simulation results showed a rapid increase in predicted identification performance as the F0 difference increased from 0 to 1 semitone, and little or no further improvement beyond 1 semitone, as found in human listeners. As explained below, the view that the increase in performance below 1 semitone is mediated by a periodicity-guided channel-segregation process such as that proposed by Meddis and Hewitt (1992) has been challenged (Culling and Darwin, 1994). Nonetheless, the idea that the auditory system uses periodicity information in the F0 range to segregate peripheral channels, and that this F0-guided separation may facilitate the identification of concurrent sounds such as vowels, is an important one, which has inspired the interpretation of both psychophysical and neural data.

1.4 Timing nets

A remarkable example of how successful schemes for the separation of concurrent vowels – and, more generally, concurrent periodicities – can be build based solely or primarily on temporal information cues is provided by “timing nets” (Cariani, 2001, 2004). The basic processing element of timing nets is an array of coincidence detectors connected via tapped delay lines (as illustrated in Cariani, 2001). This processing unit acts as a “temporal sieve”, which extracts common or recurrent spike patterns in its inputs. Depending on the time scale of the spike patterns, timing nets can subserve F0-guided extraction, as well as timbre-based extraction, where “timbre” denotes spectral details conveyed in the temporal fine structure (TFS) of spike patterns. Thus, timing nets provide a powerful and flexible tool for the automatic separation of concurrent vowels on different or identical F0s. They may also prove instrumental in modeling the perceptual separation of concurrent vowels or other periodic sounds by humans. However, so far, the extent to which a model of sound separation based on timing nets can replicate existing psychophysical data on the perception of concurrent harmonic sounds has not been evaluated in any great detail.

1.5 F0-based enhancement and F0-based cancellation

An interesting and important idea, which was suggested and supported in several studies by de Cheveigné and colleagues (de Cheveigné, 1993; de Cheveigné et al., 1995; de Cheveigné et al., 1997) is that harmonicity can be used not only to enhance a harmonic target in the presence of a harmonic or inharmonic masker, but also to suppress a harmonic masker in the presence of a harmonic or inharmonic target. Canceling the dominant periodicity then allows for a more accurate estimation of the other periodicity present in the mixture.

1.6. Summary

As this survey suggests, most existing models of the perception of concurrent harmonic sounds have been designed primarily to account for the identification of double vowels. Considering that extracting concurrent F0s and segregating peripheral channels based on F0 was a sub-problem in the design of such models, it would appear that the problem of modeling the perception of concurrent pitches with harmonic complexes other than vowels has already been solved. However, as the review of psychophysical data in the following section will show, more work remains to be done in this area.

2. Psychoacoustic findings

Several psychoacoustic studies have examined the role of harmonicity (or spectral regularity) in the perception of concurrent sounds. These studies can be divided into two main categories: studies with synthetic vowels, and studies with harmonic complex tones other than vowels. These two categories are reviewed separately below.

2.1. Double-vowel studies

2.1.1 Summary of the main findings

In a “double vowel” experiment, the listener is presented simultaneously with two synthetic vowels, which can have either the same or different F0s. The task is to identify the vowels. Usually, identification performance (percent correct) is measured as a function of the F0 difference between the two vowels. The results can be summarized as follows. Firstly, even when the two vowels have the same F0, performance is usually above chance. This indicates that whatever pattern-recognition process is at work, it can identify vowels with some degree of success based on the overall spectral shape, or composite waveform, of the mixture. Examples of how this may be achieved can be found in the work of Assmann and Summerfield (1989), which evaluated four pattern-matching procedures for the identification of concurrent vowels with the same F0. Secondly, performance usually increases with F0 separation (Assmann and Summerfield, 1990; Scheffers, 1983a; Zwicker, 1984). In most cases, all or most of the improvement occurs for F0 differences of 1 semitone or less. As the F0 separation increases beyond 1 semitone, little additional benefit is observed. The results of a study by Culling and Darwin (1993), in which synthetic vowels containing an F0 difference between the first formant and higher formants were mixed together, indicate that the improvement in identification with increasing F0 separation at small separations is mediated mostly by information in the region of the first formant. This may be explained by considering that, at least for listeners with normal peripheral frequency selectivity, the harmonics of concurrent sounds are likely to be better resolved by the auditory system at low frequencies than at higher frequencies, where the absolute bandwidths of the auditory filters are wider.

2.1.2 Improvements in concurrent-vowel identification with increasing F0 separation: F0-based segregation or waveform interactions?

At face value, the increase in identification performance with increasing F0 separation is consistent with the idea that as the F0s of the two vowels become more different, the vowels become easier to segregate perceptually. As the two vowels become easier to segregate, they also become easier to identify. The finding that the effect depends primarily on F0 differences in the region of the first formant (Culling and Darwin, 1993) suggests that the operation of the segregation mechanism may be limited by cochlear frequency resolution. Some of the models described in the previous section have this property. This is the case for place-based models, which operate on EPs (Assmann and Summerfield, 1990; Parsons, 1976; Scheffers, 1983b). However, such models have often been found not to be sensitive enough to account for the performance of human listeners at small F0 separations, below 1 semitone. Place-time models based on the autocorrelation function are more successful at predicting human performance (Assmann and Summerfield, 1990; Meddis and Hewitt, 1992). To the extent that these models do not separate harmonics that fall into the passband of the same auditory filter, their success at separating the harmonics from concurrent vowels should depend on the presence of resolved harmonics in the mixture.

One problem with the view that improvements in concurrent vowel identification with increasing F0 separation are related to F0-based segregation comes from the observation that, while most of the improvement occurs below 1 semitone, listeners do not usually hear two distinct sources and distinct pitches until larger F0 separations are used. For instance, Assmann and Paschall (1998) found that listeners could reliably adjust the F0 of a harmonic complex to match the individual pitches of concurrent vowels that have F0s separated by 4 semitones or more, whereas at smaller separations they heard and matched only a single pitch. Summerfield (personal communication cited by Culling and Darwin, 1994) found that listeners were very poor at ranking the pitches of concurrent vowels with F0s differing by 1 semitone or less, even when only trials on which the two vowels had been successfully identified were included in the analysis.

Culling and Darwin (1994) proposed an explanation for the improvement in identification performance at small F0 separations, which does not necessarily involve F0-based segregation per se. According to this explanation, beats between harmonics of the two vowels result in relatively slow fluctuations in the temporal envelope of the composite stimulus. Although these modulations may be detrimental in some cases (Assmann and Summerfield, 1990), more generally, they may aid performance by making important spectral features temporarily more prominent. In fact, they may result in the mixture sounding more like one vowel at one time, and like the other vowel at another time. To test whether the improvement in identification performance with increasing F0 separation was mediated by such spectro-temporal fluctuations, rather than by a harmonicity-based grouping mechanism, Culling and Darwin used synthetic vowels, which were devised specifically to produce beating patterns similar to those evoked by harmonic vowels, but which each consisted of inharmonic components. Consistent with the hypothesis that listeners can take advantage of cues produced by beating, they found that identification performance for these inharmonic vowels improved as “F0” separation increased from 0 to 1/2 semitone. A computational model involving a bank of auditory filters, followed by temporal integration, and a neural classification network for the recognition stage, was able to reproduce subjects’ ability to take advantage of changes in spectral information over the course of the stimulus.

Culling and Darwin’s (1994) “beat” explanation was questioned by de Cheveigné (1999) based on both theoretical and empirical considerations. He manipulated the starting phases of the harmonics in each vowel, and presented different segments of the resulting waveform to the listeners. Although identification performance varied somewhat across segments, the magnitude of these effects (averaged across all vowel pairs) was relatively small compared to that of F0 separation. Moreover, identification performance improved as F0 separation increased from 0 to as small as 0.4%, regardless of which segment was used. Based on these results, de Cheveigné concluded that improvements in concurrent-vowel identification with increasing F0 separation are unlikely to be due primarily to beats, and that the results were more consistent with an F0-guided segregation mechanism such as that proposed by Meddis and Hewitt (1992), or with de Cheveigné’s (1997b) “cancellation” model.

In summary, the question of how human listeners identify concurrent vowels remains a complex problem, with several possible solutions. The finding that listeners can identify vowels at well above chance levels even when these vowels have exactly the same F0 indicates that F0 differences are only one factor. At least two explanations have been proposed for why performance improves when F0 differences are introduced: F0-based segregation, and waveform interactions (beats). The latter has been criticized on the grounds that it only works for specific starting-phase relationships between the harmonics. However, this does not rule out the possibility that listeners can take advantage of envelope fluctuations (via “glimpsing”) whenever such fluctuations provide a useful cue for identification. The F0- or harmonicity-based segregation explanation has been criticized based on the observation that most of the improvement occurs over a range of F0 separations over which listeners do not perceive the two vowels as separate sounds with distinct pitches. However, it is possible that harmonicity-based separation starts to benefit vowel identification before listeners start to perceive two separate sounds. A more general criticism of the two-vowel paradigm is that it presents a rather artificial situation, in which two sources are gated on and off completely synchronously, and in which there are no F0 or amplitude fluctuations in the sources over time. Such conditions rarely occur in the real world, meaning that cues, such as beating, which may mediate performance in these experiments, may be only rarely available in real listening situations.

2.2. Studies with concurrent harmonic complexes other than vowels

2.2.1. Identifying the pitches of concurrent notes

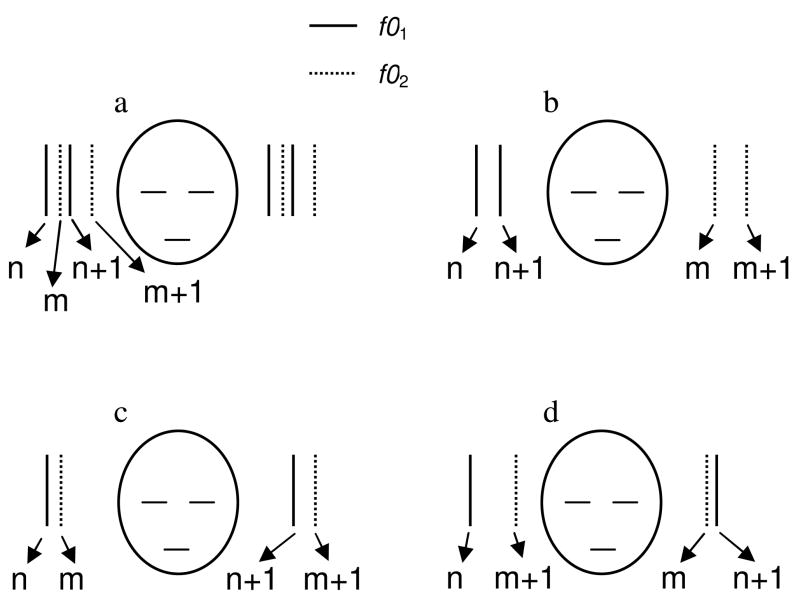
In two of the earliest studies of the concurrent perception of simultaneous harmonic complexes, Beerends and Houtsma (1986, 1989) measured listeners’ ability to identify the pitches of two simultaneously presented synthetic tones. Each tone consisted of only two consecutive harmonics of an F0, which was chosen from five possible values (200, 225, 250, 267, and 300 Hz) corresponding to the musical notes do, re, mi, fa, and sol in just temperament. The rank of the lower harmonic in one of the two notes was systematically varied between 2 and 10. The rank of the lower harmonic in the other note was varied over the same range, independently from that of the first note. All possible combinations of rank assignments were tested. On each trial, subjects were asked to indicate which two notes were presented by pressing two out of five buttons on a response box. The percentage of trials on which listeners correctly identified one or both of the two presented notes was computed. Depending on the condition being tested, either both notes were presented simultaneously in both ears (diotic presentation mode), or two harmonics (one from each note) were presented in the same ear, while the remaining two harmonics were presented in the opposite ear (Figure 3).

Figure 3.

Stimulus conditions tested by Beerends and Houtsma (1990). All conditions involved the simultaneous presentations of two “notes”, each consisting of two consecutive harmonics (n and n+1 for the first note, m and m+1 for the second note) of two F0s (f0₁ for the first note, f0₂ for the second note). In one of the conditions, the notes were presented diotically; this is shown in panel a. In all other conditions, the notes were presented dichotically, as illustrated in panels b (one note in each ear), c (lower harmonics from each note in the same ear, upper harmonics in the opposite ear), and d (lower harmonic from one note and upper harmonic from the other note in the same ear, the remaining two harmonics in the opposite ear).

These two studies yielded two important results. First, performance was found to depend only weakly on how the partials were distributed between the two ears. This is consistent with models in which pitch is determined centrally, after information concerning the individual frequencies of harmonics has been pooled across the two ears (Houtsma and Goldstein, 1972). Second, when the frequencies of the two components in each ear were too close to be “resolved” in the cochlea, performance was substantially worse than when at least one component from each tone was resolved. Note that the second observation qualifies the first: the mode of presentation of the components mattered inasmuch as components with frequencies close to each other were peripherally unresolved only when presented to the same ear.

These findings drew attention to the possible role of cochlear frequency resolution in concurrent sound segregation. However, caution must be exercised in interpreting these results. First, the complexes contained only two components each. Such tones do not elicit a strong pitch sensation, and the weakness in pitch may have been compounded by mixing two such notes together. Thus, even though Beerends and Houtsma’s listeners were musically experienced, and could readily identify the pitch of each note in isolation, their pitch identification performance with the mixtures may not have been representative of the performance that might be achieved with complexes containing more than two harmonics. A second methodological factor, which may have also limited listeners’ performance, is that the ranks of the harmonics of the two notes varied randomly across trials over a relatively wide range (from 2 to 11). This presumably resulted in marked timbre differences across trials, which may have distracted the listeners and prevented them from focusing on the relevant virtual pitch dimension. Results of Laguitton et al. (1998) indicate that when complex tones contain only two components, virtual pitch is less salient than spectral pitch. When three or four harmonics are present, the converse is observed. Therefore, it would be interesting to replicate Beerends and Houtsma’s identification studies using complex tones that contain more than two harmonics. However, to our knowledge, their study remains the only one that actually measured pitch and musical interval identification. The few remaining studies that have investigated pitch in concurrent sounds, discussed below, have all concentrated on the discrimination of small pitch differences.

2.2.2. Discriminating the F0 of a harmonic target in the presence of a spectrally overlapping harmonic masker

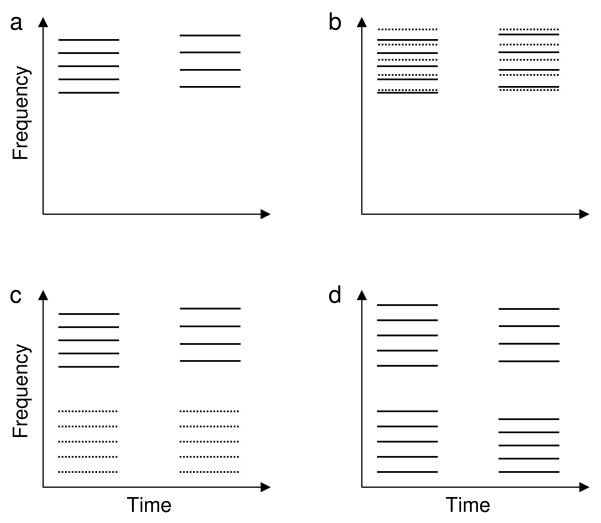
Carlyon (1996b) measured listeners’ sensitivity (d′) to the direction of changes in the F0 of a harmonic complex in the absence (Figure 4a) and presence (Figure 4b) of another, spectrally overlapping complex (“masker”) presented simultaneously in the same ear. The target and masker complexes were filtered identically into a “low” (20-1420 Hz) or a “high” (3900–5400 Hz) spectral region. The F0 of the masker was constant, and equal to either 62.5 or 210 Hz. The F0s of the two target complexes presented on a trial were centered geometrically on the masker F0. These combinations of spectral region and F0s were chosen to yield conditions in which the target complexes contained resolved harmonics in their passband (“low” spectral region, 210-Hz F0), and conditions in which they did not (“high” spectral region, 210-Hz F0, and, according to Carlyon, also the “low” spectral region, 62.5 Hz F0). The masker was either gated synchronously with the target, or it was gated on 150 ms before, and off 150 ms after, the target.

Figure 4.

Schematic spectrograms of the stimuli used in various experiments referred to in the text. a) Basic F0 discrimination experiment with two bandpass-filtered harmonic complex tones presented sequentially on each trial. The task of the listener is to indicate which observation interval contains the higher F0 (in the example shown here, the correct answer is “second interval”). b) F0 discrimination between two “target” harmonic complexes with a harmonic masker (represented by dotted lines) filtered in the same spectral region. These types of stimuli were used by Carlyon (1996), and Micheyl et al. (2006). c) F0 discrimination between two bandpass-filtered harmonic complex tones in the presence of a simultaneous “interferer” complex filtered in a non-overlapping, and in this example, lower, spectral region. These types of stimuli were used by Gockel et al. (2004, 2005), and Micheyl and Oxenham (2007) to measure “pitch discrimination interference” (PDI). d) Detection of F0 differences (or “mistuning”) between two harmonic complexes presented simultaneously into non-overlapping spectral regions. Note that in one observation interval (in this case, the first), the two simultaneous complexes have the same F0. The listener’s task is to indicate in which observation interval the two complexes have different F0s. This stimulus setup was used by Carlyon and Shackleton (1994) and Brochert et al. (submitted).

The results revealed that when the complexes were filtered into the “low” spectral region and had an F0 around 210 Hz (a condition in which the target complex contained resolved harmonics), the masker affected performance only moderately, regardless of whether it was synchronous or asynchronous with the target. A very different pattern of results was observed when the complexes were filtered into the “high” spectral region, or filtered into the low spectral region but with an F0 of 62.5 Hz (conditions in which the target complex contained only unresolved harmonics). In these conditions, listeners did not distinguish two pitches, even when the target and masker F0s differed by about 25%. Instead, they heard the target and masker mixture as a unitary noise-like sound, or “crackle”. This was reflected in their F0 discrimination performance, which was much worse in the presence of the asynchronous masker than in its absence. Surprisingly, even in those high-spectral region or low-F0 conditions, the masker only had a moderate detrimental effect on performance when it was gated synchronously with the target. Carlyon (1996b) suggested that, in this condition, listeners perhaps based their responses on temporal envelope peaks in the composite stimulus waveform at the output of peripheral auditory filters excited by multiple harmonics. Such temporal envelope peaks or “pitch pulses”, which were enhanced by summing all harmonics with the same starting phase (0 degrees), provided listeners with a “mean rate” cue: a higher overall pulse rate signaled a higher target F0. Using this cue, listeners could in principle identify which observation interval contained the higher-F0 target, even though they could not perceptually segregate the target from the masker. This explanation was explored and supported in a subsequent study (Carlyon, 1997), in which the “mean rate” cue was manipulated by selectively removing individual pulses in pulse trains, which were bandpass-filtered to contain only unresolved harmonics. Under such circumstances, performance in the F0 discrimination of a target pulse train was at chance when a spectrally overlapping masker train was presented simultaneously.

Carlyon’s (1996) results revealed that when two harmonic complexes, each containing no resolved harmonics, were presented simultaneously in the same ear, listeners could not segregate them, and did not hear two separate pitches. When both complexes contained some resolved harmonics, the pitch perception of one was less affected by the presence of the other. However, it remained unclear whether it was harmonic resolvability before or after mixing that determined performance.

The results of a later study by Micheyl et al. (2006) provided more information on this issue. Using a different approach from both and Beerends and Houtsma (1989) and Carlyon (1996), these authors measured the target-to-masker ratio (TMR) required for listeners to correctly identify (with either ~70% or ~80% accuracy) the direction of changes in the F0 of a target complex in the presence of a simultaneous, spectrally overlapping masker. The F0 difference between the two target complexes presented on each trial was fixed at two or four times the listener’s F0 discrimination threshold for the same target without interference. The target and masker complexes were identically bandpass-filtered between 1200 and 3600 Hz. Different resolvability conditions were produced by varying the average or “nominal” F0s of the target and masker from 100 to 400 Hz, in octave steps. The nominal F0 of the masker was either equal to, 7 semitones below, or 7 semitones above that of the two targets. To limit listeners’ ability to use global properties of the mixture (e.g., Carlyon’s “mean rate cue”), which would have allowed them perform the task without necessarily hearing out the target F0, the actual F0s presented on each trial were roved over a relatively wide (6-semitone) range across trials (for the target), or across intervals (for the masker). In addition, the starting phases of the harmonics were selected at random on each presentation, limiting the use of envelope cues, such as pitch-pulse asynchronies (Carlyon, 1997).

In conditions in which the nominal F0 of the target was equal to 100 Hz, the target complex contained no “resolved” harmonics according to commonly used criteria (Shackleton and Carlyon, 1994), even before mixing with the masker. In those conditions, threshold TMRs were always positive, and usually above 3 dB. At such TMRs, the mixture was dominated by the target, and the target F0 could be heard without listeners having to “extract” it from the mixture through segregation. This is consistent with Carlyon’s (1996b) finding that when two harmonic complexes that already contain no resolved harmonics when presented in isolation are presented simultaneously in the same spectral region, at approximately the same level, listeners are essentially unable to distinguish two F0s. The conditions involving a 200 Hz or 400 Hz target F0 are more informative. In those conditions, the target contained some resolved harmonics before mixing. However, after mixing, the target almost never contained resolved harmonics – one exception being the 400-Hz target F0 condition with the masker nominal F0 set 7 semitones above that of the target, for which it was estimated that at least one target harmonic was resolved in about one third of the trials. Nonetheless, in many of these conditions, negative TMRs were obtained, suggesting that listeners were able to reliably discriminate the F0 of the target in the presence of a higher-level masker, and no resolved target harmonic was present in the mixture.

The conclusion that resolved harmonics may not be necessary for the successful separation of concurrent harmonic complexes is supported by the results of a recent study by Bernstein and Oxenham (2008). This study showed that if the odd harmonics in a complex tone containing only unresolved harmonics were mistuned by 3%, listeners’ performance in an F0 discrimination task was considerably improved, to the point that it nearly equaled that measured with resolved harmonics present. This was the case even though the 3% mistuning was not sufficiently large to make the odd harmonics resolved – as indicated by the lack of performance improvement in a task involving frequency discrimination of individual harmonics inside the complex. One interpretation of these results is that the 3% deviation between the odd and even harmonics was sufficient to allow their perceptual segregation into two sounds with different pitches. Consistent with this, in a pitch-matching experiment, listeners matched the pitch of complexes to an F0 that was either close to, or an octave above, the F0 of the complex. Matching to the upper octave may be understood by considering that after the odd and even harmonics have been segregated, the frequency spacing between consecutive harmonics within each group is equal to twice their F0.

Another question, which is closely related to the issue of whether or not resolved harmonics are necessary for perceptual segregation, is whether or not resolved harmonics are necessary for accurate perception of the F0s of concurrent complexes. As pointed out by Carlyon (1996b), relatively accurate perception of the F0s of concurrent complexes can be achieved even in conditions where listeners do not hear the target and simultaneous masker as two separate sounds, based on “global” features of the mixture. In a recent study, Micheyl et al. (submitted) measured F0 discrimination thresholds for target complexes in the presence of a spectrally overlapping masker. The target and masker were identically bandpass-filtered into either a “low” (800–2400 Hz) or a “high” spectral region (1600–3200 Hz). As in Carlyon’s (1996) study, the F0 of the masker was constant across the two intervals, and the two target F0s presented on a trial were always centered on the masker F0. The difference between the two target F0s was varied adaptively, so that the F0 separation between the target and the simultaneous masker decreased with decreasing F0 difference between the two targets. The target F0s of 100, 200, and 400 Hz were tested in both spectral regions, yielding varying degrees of harmonic resolvability before and after mixing. After the psychophysical experiment, EPs evoked by target-and-masker signals similar to those used in the experiment were simulated. In these simulations, the F0 difference between the two targets was equal to the mean F0 discrimination threshold measured in the listeners (for the corresponding experimental condition).

The comparison between the psychophysical data and model simulations suggested that the conditions in which masked thresholds were relatively low (less than 2%), indicating relatively accurate perception of the target F0 (compared to other masked conditions in which thresholds were usually larger than 10%), corresponded to those in which the EPs evoked by the target-plus-masker mixture displayed relatively salient peaks, with peak-to-valley ratios of 2 dB or more. Importantly, in some of the conditions, none of these peaks was produced by a single target component; instead, corresponding harmonics of the target and masker were so close to each other that each pair evoked a single EP peak. One interpretation is that the presence of salient peaks in the mixture allowed template-matching mechanisms to operate, and that these mechanisms could reliably estimate the target F0 relatively precisely even though, strictly speaking, none of the target harmonics was individually resolved. This template-based approach was used by Parsons (1976), and more recently in a physiological study by Larsen et al. (2008), as described below. On the other hand, the observation that salient EP peaks are associated with relatively small masked thresholds for the discrimination of the target F0 is not inconsistent with a temporal mechanism, the operating of which is constrained by peripheral filtering. The presence of salient peaks in EPs evoked by target-plus-masker mixtures are usually an indication that relatively few frequency components are present in some auditory channels. Temporal periodicity-separation mechanisms (e.g., Cariani, 2001, 2004; de Cheveigné, 1993) may be able to benefit from such circumstances. Therefore, while the results of Carlyon (1996b) and Micheyl et al. (2006; submitted) concur to indicate that frequency resolution plays a role in listener’s ability to discriminate changes in the F0 of a target harmonic complex in the presence of another, they should not be taken to imply that this ability necessarily relies on place-based pattern-matching mechanisms.

2.2.3. Implications for hearing-impaired listeners

The question of whether harmonic resolvability plays a role in the segregation of simultaneous harmonic sounds is not merely of theoretical interest. Listeners with sensorineural hearing loss often have reduced frequency selectivity (Moore, 1995). As a result, spectral components that are resolved by normal-hearing listeners can be unresolved for hearing-impaired listeners. Reduced access to resolved harmonics may explain some of the difficulties experienced by these listeners with concurrent sounds, including concurrent speech (e.g., Arehart, 1998; Arehart et al., 1997; Arehart et al., 2005; Gilbert and Micheyl, 2005; Qin and Oxenham, 2003, 2006; Rossi-Katz and Arehart, 2005), music, and other sounds that contain harmonic or quasi-harmonic components. Considering that perception of the F0s of concurrent harmonic sounds is often more accurate when either resolved harmonics, or salient EP peaks, are present in the mixture, signal-processing algorithms that enhance spectral contrasts and harmonic resolvability selectively may provide a benefit in concurrent F0 perception.

2.2.4. Discriminating the F0 of a harmonic target in the presence of a spectrally non-overlapping harmonic masker

The studies considered so far have involved harmonic complexes that were presented in the same spectral region. Other studies, beginning with Gockel et al. (2004), have measured F0 discrimination performance for a target harmonic complex in the presence of an interferer harmonic complex that is filtered into a different spectral region (Figure 4c). In contrast to situations where the spectra of the two stimuli overlap, any interference in the non-overlapping cases is unlikely to be due to peripheral spectral resolution. The results from the Gockel et al.’s studies showed that when the masker F0 was similar to that of the target, performance was significantly worse than when the masker was absent, or when its F0 was remote from that of the target. However, even with an F0 separation of 30% between target and masker, performance in the presence of the masker was still not as high as achieved without the masker. Gockel et al. (2004) coined the expression “pitch discrimination interference” (PDI) to describe these effects.

In the Gockel et al. (2004; 2005) studies the target was always filtered into a higher spectral region than the masker, and it never contained resolved harmonics. As discussed earlier, the pitch evoked by unresolved harmonics is generally much weaker, and less accurately discriminated, than that evoked by resolved harmonics. Micheyl and Oxenham (2007) showed that PDI could also be observed between two groups of resolved harmonics, and the target complex produced a strong pitch percept in isolation. This conclusion was confirmed in a subsequent study of Gockel et al. (2009). In addition, Micheyl and Oxenham (2007) found that when both the target and interferer contained resolved harmonics, listeners had difficulties ignoring the interferer when it was filtered into a lower spectral region than the target, especially when the F0 difference between the two targets was equal to approximately 14%. However, Gockel et al.’s (2009) study revealed that, with specific training and/or cueing, listeners could learn to ignore the lower-region interferer, provided its F0 differed by more than about 4% from that of the target. More recently, Gockel et al. (2009) found that PDI could occur even when the target and interferer were presented in opposite ears.

Further evidence for the existence of significant interactions across spectral regions in the perception of pitch was obtained by Krumbholz et al. (2005). In their study, listeners’ ability to discriminate between temporally regular and irregular trains of bandpass-filtered clicks (using 150^th order Blackmann-windowed FIR filters with a 200-Hz bandwidth centered on 1.6 kHz) was measured in the presence of an irregular train filtered in the same spectral band (“masker”), and with a temporally regular or irregular train in a separate frequency band (“flanker”). The target trains had a click repetition rate of 100 Hz, which given the relatively high center-frequency of the target band yielded unresolved harmonics. The temporally irregular masker and flankers also had an average click repetition rate of 100 Hz which, depending on the center frequency of the flanker band (0.4, 0.57, 0.8, 1.13, 2.26, 3.2, 4.53, or 6.40 kHz), could yield resolved harmonics or not. The main results of the study was that thresholds were lower in the presence of the temporally regular flanker than in the presence of the temporally irregular flanker, even when the regular flanker was delayed relative to the regular target, or when the target and flanker bands were widely separated in frequency.

Given that PDI was discovered relatively recently, it is perhaps not surprising that not much work has yet gone into reconciling the effect with the various models of pitch perception. PDI appears to result from the integration of spectro-temporal information from both the target and interferer into a single pitch estimate. Such integration of F0 information across spectral regions appears to occur mostly under conditions in which the target and interferer are perceptually grouped into a single auditory object. The effects of perceptual grouping may explain why PDI effects are reduced by large differences in F0 between the target and interferer exist, or by gating the target and masker asynchronously. In principle, these results could be mimicked by models of pitch perception, provided that these models incorporate grouping and segregation mechanisms.

2.2.5. Detecting F0 differences (mistuning) between simultaneous harmonic complexes in non-overlapping spectral regions

The tasks used in PDI experiments involve attending to one spectral region while trying to ignore another. Such tasks are probably involved in the real world when hearing out one source against the background of another. Another real-world challenge is to process two simultaneous sources (such as two voices singing in harmony) and be able to attend to them both. Such tasks have been studied in the laboratory by asking subjects to compare the pitches of two simultaneous sounds and to judge whether the sounds have the same or different F0s (Figure 4d).

An early study (e.g., Carlyon and Shackleton, 1994) concluded that such simultaneous comparisons of F0 across spectral regions may be achieved by the same mechanisms that are presumably used to make pitch comparisons of sequential sounds, namely that one F0 is extracted and compared with the F0 of the second sound. However, this conclusion has been questioned on multiple grounds (Gockel et al., 2004; Micheyl and Oxenham, 2004, 2005). In fact, when performance in Carlyon and Shackleton’s simultaneous and sequential tasks was compared using a consistent model of signal detection, it seemed that performance in the simultaneous task was considerably better than that predicted from performance in the sequential task (Micheyl and Oxenham, 2005). Micheyl and Oxenham (2005) proposed various explanations for this outcome, including the possibility that the sequential F0 discrimination and the detection of F0 differences between simultaneous complexes involve different cues and mechanisms. A similar idea was proposed earlier by Demany and Semal (1990), who stated that simultaneous and sequential pitch comparisons may involve “quite separate neural mechanisms”.

This idea was tested more directly in a recent study by Borchert et al. (submitted), who measured listeners’ performance in two tasks involving F0 comparisons between two groups of resolved harmonics that were filtered into separate spectral regions. In one case, the two groups of harmonics were presented sequentially twice, once on the same F0, once on different F0s, and listeners’ task was to indicate in which pair of tones the F0s differed. In another experiment, the two groups of harmonics were presented simultaneously, and listeners had to indicate which of the two sequentially presented pairs of simultaneous tones sounded “mistuned”. Unlike in Carlyon and Shackleton’s (1994) earlier study, these two (sequential and simultaneous) F0-comparison tasks involved the same number of tones: two pairs of tones on each trial. Moreover, the same complex tones were used in the sequential and simultaneous conditions; in both cases, listeners compared the F0s of tones filtered into different spectral regions, to ensure that the results in the simultaneous and sequential tasks were directly comparable. The results showed markedly higher performance in the simultaneous across-region F0-comparison task than in the corresponding sequential task. This outcome is consistent with the hypothesis that listeners’ ability to detect F0 differences across spectral regions relies on different cues, depending on whether the two sounds being compared are sequential or simultaneous. In the sequential case, each tone evokes a pitch, and listeners compare these pitches to decide if they are the same or different. Most listeners find it difficult to compare the pitches of tones that differ markedly in timbre (Micheyl and Oxenham, 2004; Moore and Glasberg, 1990), as is the case for tones filtered into completely different spectral regions. In the simultaneous case, listeners can identify the different-F0 pair based on differences in the overall sensation evoked by the same-F0 and different-F0 pair. Listeners report that the different-F0 pair usually sounds less “fused”, less “consonant”, or “rougher”, than the same-F0 pair. Since the two groups of harmonics were filtered into non-overlapping spectral region, and peripheral interactions across the two regions were masked using background noise, the “roughness” sensation presumably reflects the detection of “beats” generated centrally, perhaps similar to the “beats of mistuned consonance” that are observed for some combinations of pure tones (Feeney, 1997). These cues may be detected even when the F0 difference is not large enough for the two simultaneous groups of harmonics to be heard as separate tones with distinct pitches. Therefore, unlike in the sequential case, performance may not be limited by interactions (or confusions) between pitch differences and timbre differences. In fact, performance on the simultaneous F0 comparison may not rely on explicit pitch comparisons at all, but rather a judgment of perceived fusion.

If listeners rely on perceived “fusion” to detect F0 differences between simultaneous tones, their performance in this task should be impaired by stimulus manipulations that promote perceptual segregation of the tones. In order to test this hypothesis, Brochert et al. (submitted) introduced a 200-ms onset asynchrony between the two groups of harmonics in the simultaneous F0-comparison task, while increasing their duration (from 400 ms to 600 ms) to ensure that the tones were simultaneously presented for 400 ms, as in their main experiment. As a result, the two groups were simultaneous for as long as in the main experiment, but because of the onset asynchrony, they were heard as two separate tones. This manipulation caused a significant drop in listeners’ performance, consistent with the hypothesis that the detection of simultaneous F0 differences across spectral regions depends on perceived fusion. This made an explanation based on perceived beats less likely, because such beats might be expected to persist despite the differences in perceived grouping. Further evidence for this explanation was obtained in a subsequent experiment, in which the lower-region complex was preceded by four copies of itself, causing its capture into a perceptual “stream” separate from the simultaneous complex in the higher spectral region. This segregation-promoting manipulation also produced a drop in performance.

To summarize, based on the limited data currently available, it appears that listeners’ ability to detect simultaneous across-frequency differences in F0 (a form of mistuning) cannot be explained simply based on their performance in the detection or discrimination of differences in F0 between sequential tones filtered into the same or different spectral regions. Instead, listeners appear to be more sensitive to F0 differences between two groups of resolved harmonics filtered into separate spectral regions when the two groups are presented simultaneously than when they are presented sequentially. This can be understood by considering that the detection of F0 differences between groups of harmonics presented simultaneously in separate spectral regions may involve different cues and mechanisms than the detection of F0 differences between sequential sounds filtered into the same or different spectral regions. Whereas the latter ability appears to require explicit pitch comparisons, the former may rely on the degree of perceived “fusion”. Further study is needed in order to determine precisely what cue(s) listeners are using in the simultaneous case, as well as how, and at what level of the auditory system, this cue is extracted.

2.2.6 “Mistuned harmonic” studies

The previous section was devoted to the detection of mistuning between two simultaneous groups of harmonics. In this section, we consider another form of mistuning, which is obtained by shifting the frequency of a single component in an otherwise harmonic tone. Many studies have measured the detectability of such mistuning, and its influence on the pitch of the mistuned component, or that of the complex remainder. Some studies have also measured the percepts associated with this mistuning. While these studies do not qualify as using concurrent complexes, their results have undeniably contributed to further our understanding of the role of deviations from harmonicity (or spectral regularity) in the perception of concurrent sounds.

The basic findings of mistuned-harmonic studies can be summarized as follows. If the amount of mistuning exceeds 1–2%, the mistuned harmonic usually “pops out” from the complex, and is heard as separate tone (Brunstrom and Roberts, 2001; Hartmann et al., 1986; Hartmann et al., 1990; Lin and Hartmann, 1998; Moore et al., 1986; Roberts and Brunstrom, 1998; Roberts and Holmes, 2006). However, the mistuned harmonic continues to contribute to the pitch of the complex for mistunings of up to 3% (Darwin et al., 1994; Moore et al., 1985). These observations have been explained in terms of a “harmonic sieve” (de Cheveigné, 1997a; Duifhuis et al., 1982). According to this explanation, spectral components are perceptually grouped if their frequencies fall within a certain range around integer multiples of a common F0; spectral components that fall outside of that range are rejected. It is worth pointing out that although the notion of a harmonic sieve has often been suggested in the context of place-based models of pitch perception (Duifhuis et al., 1982; Goldstein, 1973), it applies equally well to estimates of component frequencies derived from temporal information (Srulovicz and Goldstein, 1983).

The view that the simultaneous grouping of spectral components depends on harmonicity per se has been questioned by Roberts and colleagues (Roberts and Bregman, 1991; Roberts and Bailey, 1993a; Roberts and Bailey, 1993b). These authors have found that the key factor is regular spectral spacing. They arrived at this conclusion based on the results of experiments in which listeners were asked to rate how clearly they could “hear out” odd or even harmonics in a complex tone composed of only odd harmonics with the addition of a single even harmonic. Listeners generally gave higher clarity ratings to the even harmonics than to the odd harmonics. This result was all the more surprising as even harmonics were closer in frequency to other (odd) components in the complex than odd harmonics; thus, they should have been more easily masked. The authors suggested that this unexpected result could be explained by considering that even harmonics were easier to hear out because they violated the regular spectral pattern formed by the odd-harmonic “base”. This conclusion was further supported by the results of subsequent studies, in which components were selectively removed from the “base” complex in order to weaken spectral regularity, and promote segregation (Roberts and Bailey, 1996a, 1996b). More recently, Roberts and Brunstrom (1998, 2001) garnered further evidence for a role of regular spectral spacing by asking listeners to match the pitch of a component that deviated from its original frequency in an inharmonic but spectrally regular complex. The stimulus was produced by shifting all component frequencies in an originally harmonic complex by the same amount in Hz (which is known as “frequency shifting”), or by increasing the frequency spacing between consecutive components by a cumulative amount from low to high (which is known as “spectral stretching”). The results revealed that listener’s ability to match the frequency of a “deviating” component within these frequency-shifted or spectrally stretched complexes was not appreciably worse than for harmonic complexes. This led Roberts and Brunstrom (1998) to conclude that much of the perceptual fusion associated with harmonic complexes may be due to their inherent spectral regularity rather than their harmonicity per se.

Roberts and colleagues’ results challenge the widespread view that the simultaneous grouping of spectral components is governed by a harmonic sieve. The results obtained with spectrally stretched complexes, the components of which are both inharmonic and unequally spaced, can be interpreted as suggesting that grouping is based on local, rather than global, deviations from equal spectral spacing. Deviations from equal spacing that result from the application of a moderate spectral stretch are large only over large spectral distances, i.e., across widely separated components. The conclusion that simultaneous grouping depends on local spectral mechanisms is consistent with results of Lin and Hartmann (1998). According to this view, the overall strength of perceptual fusion for a complex tone would emerge from the combination, or “chaining”, of local groupings between adjacent groups of spectral components (Roberts and Brunstrom, 2001). How this process may be implemented is not entirely clear. Roberts and Brunstrom (2001) pointed out that the autocorrelograms of harmonic, frequency shifted, or spectrally stretched complexes containing a “deviating” component exhibit a salient local perturbation, which takes the form of a “kink” in the vertical “spine” in the autocorrelogram, and corresponds to channels primarily excited by the deviating component. They suggested that this feature provides a potential cue to the presence and frequency of the deviating component, which might be detected by a central pattern analyzer, and used for perceptual segregation. To our knowledge, this idea has not yet been evaluated quantitatively.

To summarize this section, an important conclusion from Roberts and colleagues’ studies is that the mechanisms responsible for the perceptual grouping and segregation of simultaneous spectral components are distinct from the mechanisms responsible for the perception of virtual pitch. While virtual pitch perception appears to involve a harmonic sieve (Duifhuis et al., 1982; Goldstein, 1973) or an aggregation of periodicity information across channels (Meddis and Hewitt, 1991a, 1991b; Meddis and O’Mard, 1997), simultaneous grouping appears to rely also on local spectral regularity, or on a comparison of periodicity information across nearby auditory channels.

3. Neural basis of the perception of concurrent harmonic sounds

In recent years, there has been an upsurge in interest in the neural coding of concurrent complex sounds, including concurrent vowels, harmonic complexes differing in F0, and complex tones with a mistuned harmonic. These studies have used techniques ranging from single-unit recordings in anesthetized animals to auditory evoked potentials in humans. In this section, we review the main findings of these studies.

3.1 Neural responses to concurrent vowels

While numerous studies have been devoted to characterizing auditory-nerve responses to single vowels (e.g., Delgutte and Kiang, 1984; Miller et al., 1997; Palmer et al., 1986; Sachs and Young, 1979; Young and Sachs, 1979), very few studies have measured neural responses to double vowels. One of the main findings of studies with single vowels is that place- and rate-based representations convey sufficient information to allow identification at low sound levels in quiet, but degrade rapidly with increasing sound level, or in the presence of wideband background noise (Sachs and Young, 1979; Sachs et al., 1983). In contrast, temporal aspects of the discharge patterns were found to be relatively robust in the face of background noise, or level changes (Delgutte, 1980; Sachs et al., 1983). This led Palmer (1988; 1992) to investigate temporal representations of concurrent vowels in the auditory nerve (AN). These studies involved recording the responses of auditory-nerve fibers in anesthetized guinea pigs to synthetic vowels presented in isolation or concurrently. The vowels had F0s of 100 or 125 Hz. The results obtained using single vowels showed that, depending on the relationship between the characteristic frequency (CF) of the unit and the position of the formants, the temporal pattern of neural discharges tended to reflect the frequencies of individual harmonics, or the F0. In general, strong phase locking to the frequency of individual harmonics was observed for units with a CF close to a high-level formant peak, which were dominated by a single component. Units with a CF between two formant peaks showed modulation at the F0, reflecting beating between several harmonics that fall within the passband of peripheral auditory filters. The responses to double vowels showed a similar, albeit more complex, pattern with responses synchronized to either or both of the two F0s present, or to individual harmonics. Importantly, Palmer demonstrated that the responses of auditory-nerve fibers to double vowels contained sufficiently accurate temporal information for the two F0s to be reliably identified. In addition, he showed that the fact that the responses of some units reflected one F0, while others reflected the other F0, could be used to segregate the two constituent vowels and infer their amplitude spectra.

Even fewer studies have explored neural responses to double vowels beyond the AN. Keilson et al. (1997) measured the responses of single units (primary-like and chopper cells) in the ventral cochlear nucleus (VCN) of cats to concurrent vowels with different F0s (around 100 Hz), and F0 separations (ranging from 11%, which is close to 2 semitones, to 27%, which is somewhat larger than 4 semitones). The two vowels were selected so that one vowel had a formant frequency below the unit’s CF, while the second vowel had a formant frequency above CF. The position of the formant peaks was then shifted relative to the unit’s CF by varying the stimulus sampling frequency – which is equivalent to multiplying all frequencies in the stimulus by a constant. Unsurprisingly, the discharge rate of the units was found to increase with the energy of the stimulus within the receptive field. Neural discharges showed synchrony to either or both F0s. In the latter case, responses were synchronized more strongly to the F0 of the “dominant” vowel, i.e., the vowel with a greater amount of energy within the unit’s receptive field. Keilson et al. (1997) suggested that the auditory system could in principle take advantage of such “periodicity tagging” for segregating the two vowels. They proposed a scheme to reconstruct the spectral profiles of the two vowels by apportioning the discharge rates of VCN units based on their relative synchronization to the two F0s.

The studies of Palmer and Keilson et al. demonstrate that the responses of neurons at low levels of the auditory system contain enough temporal information to allow accurate estimation of the F0s of concurrent vowels and, subsequently, F0-based segregation of these vowels. This provides a neurophysiological basis for models of concurrent-vowel segregation based on the ACF, such as the one proposed by Meddis and Hewitt (1992).

Information concerning the neural processing of concurrent vowels at higher levels of the auditory system was provided by Alain et al. (2005a). Using electroencephalography (EEG), these authors recorded auditory event-related potentials (ERPs) while participants were presented with pairs of concurrent synthetic vowels at different F0 separations, ranging from 0 to 4 semitones. In one condition, the participants were instructed to ignore the auditory stimuli, and to focus on watching a silent movie. In the other condition, they were assigned the task of identifying the vowels. The behavioral results were consistent with those of earlier studies of double-vowel perception, showing increases in correct identification performance with increasing F0 separation, mostly over the 0–1 semitone range. The electrophysiological data revealed the presence of a negative wave superimposed on the N1 and P2 deflections, with a peak around 140 ms after sound onset, which was maximal over midline central electrodes. This wave, which was present regardless of whether listeners were listening passively to the sounds or actively identifying the vowels, increased in magnitude as the F0 difference between the two vowels increased from 0 to 4 semitones. Alain and colleagues pointed out that the characteristics of this negative wave were similar to those of the “object related negativity” (ORN), which had been observed using mistuned harmonics in earlier ERP studies (see below). The observation of a similar negativity in response to concurrent vowels differing in F0 in their current study suggested that the ORN may index the automatic detection, by the central auditory system, of significant discrepancies between an incoming stimulus and the best-fitting harmonic template, indicating the presence of more than one sound source in the environment.

In addition to this “early” negativity, a later negativity, which peaked around 250 ms and was largest over the right and central regions of the scalp, was observed only under the “active” listening condition, in which listeners had to identify the vowels. Alain and colleagues pointed out that this later ERP component had characteristics similar to the N2b wave, which is commonly thought to reflect stimulus-classification and decision processes controlling behavioral responses in discrimination tasks (Ritter et al., 1979). Based on the observed sequence of neural events, ORN followed by N2b, they proposed a two-stage model of concurrent-vowel processing, in which constituent vowels are first extracted automatically by a harmonic template-matching system, then matched effortfully against representations in working memory for identification.

In another study, Alain et al. (Alain et al., 2005b) used event-related functional magnetic resonance imagining (fMRI) to measure, and localize more precisely than with EEG, brain activity while participants were listening to concurrent vowels, which they had to identify. The results revealed bilateral activation in the thalamus and superior temporal gyrus (STG), as well as in the left anterior temporal lobe, and the left inferior temporal gyrus. Moreover, the left thalamus, Heschl’s gyrus (HG), STG, and planum temporale (PT) were found to be differentially activated depending on whether listeners had identified correctly both vowels, or only one. Enhanced activity in the latter areas during the activation of both vowels was interpreted as reflecting the “extra computational work” needed to segregate and identify successfully the two vowels. The authors concluded that auditory cortex areas located in or near HG and PT, especially on the left side, are actively involved in the segregation and identification of concurrent vowels.

In summary, neural responses to concurrent vowels have been recorded at various levels of the auditory system, ranging from the AN to the AC. Single-unit studies at the level of the AN and of the CN have identified potential cues for the F0-based separation of simultaneous vowels based on place-based and/or temporal aspects of neural responses. EEG and fMRI studies have started to reveal neural activation in thalamus and auditory cortex, which appears to be related to automatic or effortful segregation and/or identification of concurrent vowels.

3.2 Neural responses to concurrent harmonic complexes other than vowels

3.2.1 Responses to concurrent harmonic complexes in the auditory nerve

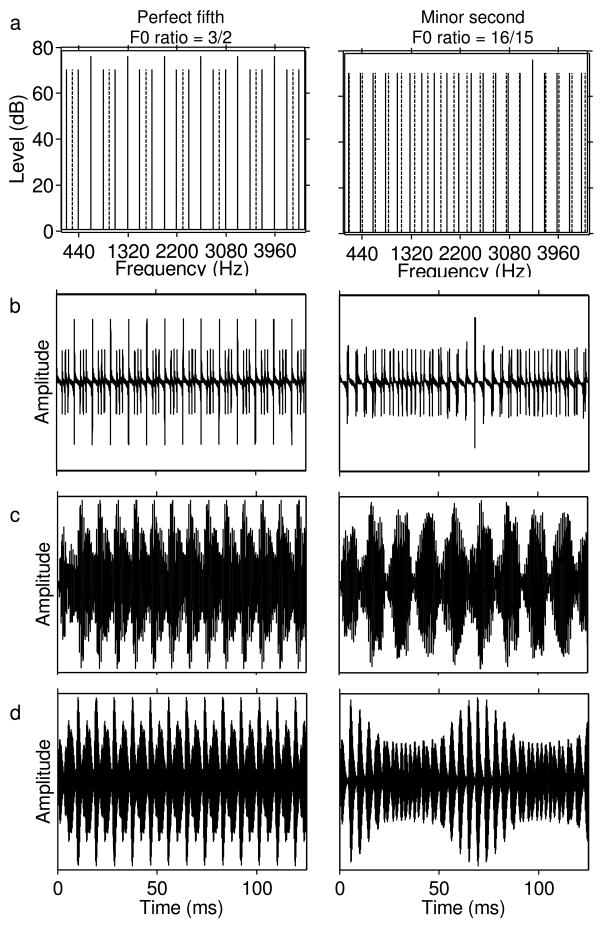
Very few studies have characterized neural responses to concurrent harmonic complexes other than vowels in the AN. Tramo et al. (2001) compared the responses of cat AN fibers to a pair of complex tones, the F0s of which were chosen to form either a consonant musical interval (perfect fifth or fourth) or a dissonant interval (minor second or tritone). They found that, for consonant intervals, temporal response patterns followed the F0s of the two notes, as well as “bass notes” related to the missing F0 of a harmonic interval. For dissonant intervals, the temporal response patterns showed slow modulations, which did not correspond to either F0 or to bass notes. This pattern of results can be explained relatively simply by looking at the spectra of stimuli with consonant and dissonant intervals (Figure 5a). The latter contain components whose frequencies differ only by a few Hz. This results in slow envelope modulations (beats), both in the stimulus waveform (Figure 5b), and at the output of auditory filters within which these components interact (Figures 5c–d).

Figure 5.

Example spectra, waveforms, and simulated auditory-filter outputs for a consonant (perfect fifth, left) and a dissonant (minor second, right) musical interval. a) Magnitude spectra. Solid lines indicate harmonics of the F0 of the first note, 220 Hz. Dashed lines indicate harmonics of the second F0, which was equal to 3/2 times 220 Hz (i.e., 330 Hz) for the fifth, and 16/15 times 220 Hz (i.e., 234.67 Hz) for the minor second. Some of the harmonics of the second F0 coincide with harmonics of the first. The corresponding dashed lines are not visible, but the solid lines are longer, reflecting a higher level. b) Stimulus waveforms. c) Waveforms at the output of a gammatone filter with a center frequency equal to the frequency of the fifth harmonic of the 220 Hz F0, i.e., 1100 Hz. d) Waveforms at the output of a gammatone filter with a center frequency equal to the frequency of the fifteenth harmonic of the 20 Hz F0, i.e., 3300 Hz. The slow temporal envelope fluctuations in the response of this filter to the dissonant interval reflect “beating” between adjacent harmonics from the two tones. In general, dissonant intervals results in more complex, and less coherent, temporal response patterns across auditory filters.

In a more recent study, Larsen et al. (2008) explored the extent to which the F0s of two simultaneously presented harmonic complexes could be estimated using either spike-rate or spike-timing information contained in the responses of ANFs in anesthetized cats. Taking advantage of the principle of scaling invariance (Zweig, 1976), Larsen et al. used the responses of single ANFs to isolated complex tones and pairs of complex tones with a wide range of F0s to infer the responses of a population of AN fibers with different CFs to a pair of complex tones with constant F0s. The range of F0s presented to an ANF was selected based on the measured CF of that fiber, in such a way that the “neural harmonic number” (CF/F0) varied from approximately 1.5 to 5.5 in steps of 1/8. When two complex tones were presented simultaneously, the F0 of one complex was set at 15/14 time (i.e., approximately 7%, or slightly more than a semitone above) or 11/9 times (i.e., approximately 22%, or slightly less than four semitones above) the F0 of the other complex. In order to determine how well simultaneous F0s could be estimated based on place information or temporal information, Larsen et al. (2008) performed both rate-based and interspike-interval analyses. The rate-based analysis involved three steps. First, the responses to single complexes were fitted using a phenomenological model of ANF responses, which involved a gammatone filter (Patterson et al., 1995) followed by a saturating nonlinearity representing the dependence of discharge rate on level (Sachs and Abbas, 1974). The parameters of the model (including the filter bandwidth and center frequency, as well as the spontaneous, medium, and saturation rates) were fitted based on the recorded responses to the single complex. In the second step, the principle of scaling invariance was used to convert the best-fitting single-fiber model into a model of responses from an array of fibers tuned to different CFs. In the third step, the responses of the latter model to all combinations of simultaneous F0s used in the experiment were generated, and a fit was computed between these simulated responses and the measured rate profile. The results of this fit were used to estimate the two presented F0s, and to quantify the error of these estimates. The interspike interval analysis involved the computation of a “pseudo-pooled” interspike interval histogram, with the time axis normalized to accommodate the pooling of responses evoked by different F0s.

Using these analyses, Larsen et al. (2008) found that the accuracy of concurrent-F0 estimates based on rate information increased with CF. This can be explained by the gradual improvement in the relative frequency selectivity of ANFs with increasing CF (Kiang et al., 1965; Liberman, 1978). For CFs above 2–3 kHz, the F0s of the two simultaneous complexes could be estimated with an accuracy of less than 2% based on spike-rate profiles. In contrast, the accuracy of F0 estimates based on interspike interval histograms was found to decrease with increasing CF. This decrease is attributable to the weakening in phase-locking toward higher CFs. F0s could only be accurately estimated (with errors of less than 3%) based on interspike intervals for CFs lower than about 2–4 kHz. As was the case for rate-based estimates, the ratio of constituent F0s had little effect on estimation performance. Surprisingly, estimates of the two F0s based on rate profiles were not less accurate for the smaller F0 separation (a ratio of 15/14, approximately 7%) than for the larger separation (a ratio of 11/9, approximately 22%).

Larsen et al.’s (2008) findings are remarkable in that they demonstrate that by using more information than just peak positions in spike-rate profiles, the F0s of concurrent complex tones can be recovered accurately, in principle, even when the profiles do not exhibit peaks corresponding to individual harmonics of either constituent sound. This is a very important result, which challenges the view that resolved harmonics must be present in a sound mixture in order for the F0s of constituent sounds to be accurately estimated using only place information. However, it is important to note that, as the authors of that study themselves pointed out, this conclusion is based on observations at the level of the AN. Information-processing constraints at higher stages of the auditory system may limit perceptual performance. This might explain why the psychophysical studies that were reviewed above have generally found that human listeners’ ability to perceive concurrent F0s accurately is usually worse under stimulus conditions in which place representations (EPs) do not exhibit salient peaks corresponding to resolved harmonics than under conditions in which such peaks are present (Carlyon, 1996a, 1996b; Micheyl et al., 2006; Micheyl et al., submitted). Further research is needed to clarify why, and where in the central auditory system, limitations on the ability to extract the F0s of concurrent sounds arise.

3.2.2 Responses to concurrent harmonic complexes in the cochlear nucleus and the inferior colliculus

McKinney et al. (2001) measured the responses of single units in the inferior colliculus (IC) of anesthetized cats to two simultaneous pure or complex tones. The frequencies, or F0s, of the two simultaneous tones were chosen to form either consonant or dissonant musical intervals. The authors examined both average spike rates, and temporal fluctuations in spike rate, which were quantified as the standard deviation of smoothed post-stimulus-time histograms. Averaged across neurons (including either Sustained and Onset units or just Onset units), these two measures correlated well with subjective ratings of dissonance in humans: both the psychophysical and the neural measures showed a peak corresponding to the minor second, and a smaller peak corresponding to the tritone. Smaller values were observed for the unison, the perfect fifth, and the fourth, which are all normally considered consonant.

Sinex and coworkers (Sinex, 2008; Sinex and Li, 2007) measured responses to concurrent harmonic complexes in the IC and cochlear nucleus (CN) of anesthetized chinchillas. In the IC, the responses to double harmonic complexes showed little or no synchrony to individual harmonics, and usually followed envelope fluctuations resulting from beats between adjacent components (Sinex and Li, 2007). In the CN, responses depended qualitatively on the type of unit sampled. Primary-like units displayed synchrony to individual stimulus components, as observed in ANFs. In contrast, Chopper neurons exhibited little synchrony to individual components, and tended to follow envelope fluctuations resulting from interactions between adjacent components (Sinex, 2008). Based on these results and earlier ones, which showed that ANFs typically synchronized to individual components in harmonic complex tones or complex tones containing a mistuned component (Sinex et al., 2003), Sinex (2005, 2008) suggested that neural responses to complex tones undergo a major transformation at the level of the lower brainstem, which results in qualitatively different responses to harmonic and inharmonic stimuli below and above the CN. Below the CN, neurons usually synchronize to individual components in a complex tone, regardless of whether these components are harmonically related or not. Above CN, neural responses mainly reflect envelope fluctuations resulting from interactions between two or more components. However, as mentioned above, Tramo et al. (2001) found that neural responses to double complex tones at the level of the AN could already show qualitatively different response patterns with, in some cases, discharges synchronized to the period of individual components, and in other cases, slow fluctuations in spike counts following beats between nearby components. In Sinex’s (2003) study, low-frequency modulations of spike counts reflecting beats between high-frequency components were more rarely observed. This difference between the two studies could be due to the use of different stimuli: a single harmonic complex with no or one mistuned component in Sinex’s (2003) study, versus two concurrent harmonic complexes in Tramo et al.’s (2001) study, which usually resulted in strong peripheral interactions, especially when the interval was dissonant.

3.2.3 Responses to concurrent harmonic complexes in the auditory cortex

Fishman et al. (2001) measured neural responses (multiunit activity and auditory evoked potentials) to simultaneous complex tones with F0s selected to yield varying degrees of consonance and dissonance in the primary auditory cortex (A1) of awake macaques. In addition, they measured responses to similar chords in the auditory cortex (Heschl’s gyrus and planum temporale) of two human subjects, who were undergoing surgical evaluation for epilepsy. For dissonant chords (minor and major seconds), the neural responses showed significant oscillations corresponding to frequency differences between nearby components (i.e., beats). In contrast, responses evoked by consonant chords, such as octaves and perfect fifths, displayed little or no such oscillations. This pattern of results is strongly reminiscent of that observed at lower levels of the auditory system in the studies of Tramo et al. (2001) and McKinney et al. (2001). A similar pattern was observed in human Heschl’s gyrus. In contrast, responses in the planum temporale displayed no significant oscillations related to beats, suggesting a functional differentiation between this area and Heschl’s gyrus. An interesting question is whether and how these neural response patterns observed in AC are used by the central nervous system to decide that more than one source is present in the environment. Slow neuronal oscillations reflecting low-frequency beats could be used as a cue to the presence of more than one source, and the absence of such oscillations could be used to promote perceptual fusion across frequency. Additional studies are required to answer these questions.

3.3 Neural responses to mistuned harmonics

3.3.1 Single unit responses in the AN, CN, and IC

Sinex and coworkers (Sinex, 2005, 2008; Sinex et al., 2002; Sinex et al., 2005; Sinex et al., 2003) performed several studies to investigate differences in neural responses to harmonic complex tones and complex tones with a mistuned component, at various levels of the auditory system (AN, CN, and IC). Some of these studies overlap with the “double complex tones” studies by the same authors, as discussed above. The results reveal that responses to complex tones with a mistuned component in the IC are generally larger and more sustained than responses to corresponding harmonic complexes with no mistuned component (Sinex, 2005; Sinex et al., 2002). In addition, IC responses to complex tones with a mistuned component exhibit marked fluctuations, some of which correspond to beats between the mistuned component and a nearby harmonic. Other fluctuations can also be present in the response, which do not correspond to simple differences between the frequencies of components in the stimulus, but reflect second-order interactions – for instance, between two response components corresponding to first-order frequency differences (for details see: Sinex et al., 2002). As a result, the responses of IC neurons to complex tones containing a mistuned harmonic often exhibit a “richer” temporal pattern that is harder to predict than the responses to harmonic complexes. Such strong qualitative differences in responses to harmonic and mistuned-harmonic complex tones are not typically observed at the level of the AN. Instead, the responses of ANFs usually show phase-locking to individual frequency components, regardless of whether they are mistuned or not (Sinex et al., 2003). As with double complexes, responses to harmonic and mistuned-harmonic complexes in the CN are either similar to those observed in the AN (for Primary-like units) or more similar to those observed in the IC (for Chopper units). Most of these differences in response patterns between IC and AN units can probably be explained by a combination of relatively broad receptive fields and across-frequency integration, reduced phase-locking to the temporal fine structure (which results in envelope-following responses), and temporally patterned inhibitory and excitatory inputs in IC cells (Sinex, 2005).

It is not entirely clear how these neurophysiological findings relate to the perception of mistuned harmonics. Differences in response patterns to harmonic and mistuned complex tones are usually most apparent at relatively large mistunings, which have been found to evoke a segregated percept in psychophysical experiments. This suggests that the perceptual segregation of the mistuned component may be associated, at the neural level, with strongly modulated and partially incoherent temporal response patterns induced by interactions between the mistuned component and nearby harmonics. One way to model this involves grouping across-frequency responses that reflect coherent periodicities, and segregating responses that are temporally incoherent (Roberts and Brunstrom, 1998).

3.3.2 Auditory evoked potentials from auditory cortex

Alain and colleagues (Alain, 2007; Alain and Izenberg, 2003; Alain and Bernstein, 2008; Alain et al., 2001; Alain et al., 2002; Dyson and Alain, 2004) recorded auditory evoked potentials (AEPs) in response to harmonic complex tones and complex tones with a mistuned component. They found that, under conditions in which the amount of mistuning was large enough for listeners to perceive the mistuned component as a separate sound, a biphasic wave peaking between 150 and 350 ms after sound onset was present. They termed the early negative component of this wave “the object-related negativity” (ORN). The ORN was observed regardless of whether subjects were actively attending to the auditory stimuli, or listening passively (e.g., watching a silent movie). In addition, with long-duration tones, sustained potentials were observed, which were present only when participants attended to the stimuli, and were greater in amplitude when the mistuned harmonic was perceptually segregated. Based on these observations, the authors proposed a two-stage model of auditory scene analysis: a first, automatic stage, followed by a second stage, under attentional control. The observation that the ORN and the positive wave were present even with short duration sounds suggests that the underlying processes depend on transient neural responses, which may reflect the detection of a mismatch between the stimulus and harmonic internal templates. It is not yet known whether the ORN can also be produced by violations of regular spacing between logarithmically-spaced or stretched frequencies, as used in the psychophysical studies of Roberts and colleagues (Roberts and Bailey, 1996a, 1996b; Roberts and Brunstrom, 1998, 2001).

Summary

The perceptual segregation of concurrent harmonic sounds, such as vowels or musical notes, is an important aspect of auditory scene analysis. Over the last fifteen years, psychophysical and neurophysiological studies using double vowels, concurrent harmonic complexes, or harmonic complexes with a mistuned harmonic, have started to unravel the cues and mechanisms that may be used by the auditory system to accomplish this formidable task. Several important points have emerged from the results of these studies:

• - F0 differences between simultaneous harmonic complexes usually promote perceptual segregation, and facilitate the extraction of the pitch (and, in the case of vowels, phonemic identity) of the constituent sounds. The mechanisms responsible for these effects of F0 separation, including the possible influence of beats between neighboring components and “glimpsing”, are still debated.

• - Listeners’ ability to identify or discriminate the F0 of a target harmonic complex in the presence of a spectrally overlapping harmonic masker, and to take advantage of F0 differences between target and masker, generally appears to be constrained by peripheral frequency resolution. However, some studies indicate that relatively accurate perception of the target F0 may be possible even in conditions in which none of the target harmonics are “resolved” in peripheral place-based representations of the target-plus-masker mixture.

• - To the extent that peripheral frequency selectivity facilitates the segregation and estimation of concurrent F0s, the reduced frequency selectivity found in hearing-impaired and cochlear-implant listeners may play an important role in the difficulties they experience in complex acoustic environments.

• - The perception of the pitch of a harmonic complex tone can be impaired by the simultaneous presentation of another harmonic complex even when the two sounds do not overlap spectrally. Such across-frequency pitch-discrimination interference effects have not yet been incorporated into models of pitch perception, and their underlying mechanisms are not currently known.

• - Listeners’ sensitivity to F0 differences or “mistuning” between groups of harmonics presented simultaneously in non-overlapping spectral regions appears to rely on the detection of cues that depend on perceived segregation, and does not always require pitch comparisons. This may explain why listeners, who often find it difficult to compare the pitches of sounds that differ markedly in timbre, have little trouble detecting even small F0 differences across spectral regions when the sounds are presented simultaneously. The neural mechanisms that mediate this ability remain largely unknown. However, neural correlates of the perceived segregation of a single mistuned component within a harmonic complex tone have already been identified in the central auditory system.

• - The perceptual grouping of simultaneous spectral components appears to involve mechanisms that are at least partly different from those responsible for perception of virtual pitch, and are sensitive to various forms of spectral regularity, not just harmonicity. Neural mechanisms that can support such sensitivity to various forms of spectral regularity have yet to be identified within the central nervous system.