Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Aug 1.
Published in final edited form as: J Struct Biol. 2010 Apr 4;171(2):142–153. doi: 10.1016/j.jsb.2010.03.018

High-Performance Iterative Electron Tomography Reconstruction with Long-Object Compensation using Graphics Processing Units (GPUs)

Wei Xu 1, Fang Xu 1, Mel Jones 2,3, Bettina Keszthelyi 2,3, John Sedat 3, David Agard 2,3, Klaus Mueller 1
PMCID: PMC2885506  NIHMSID: NIHMS200242  PMID: 20371381

Abstract

Iterative reconstruction algorithms pose tremendous computational challenges for 3D Electron Tomography (ET). Similar to X-ray Computed Tomography (CT), graphics processing units (GPUs) offer an affordable platform to meet these demands. In this paper, we outline a CT reconstruction approach for ET that is optimized for the special demands and application setting of ET. It exploits the fact that ET is typically cast as a parallel-beam configuration, which allows the design of an efficient data management scheme, using a holistic sinogram-based representation. Our method produces speedups of about an order of magnitude over a previously proposed GPU-based ET implementation, on similar hardware, and completes an iterative 3D reconstruction of practical problem size within minutes. We also describe a novel GPU-amenable approach that effectively compensates for reconstruction errors resulting from the TEM data acquisition on (long) samples which extend the width of the parallel TEM beam. We show that the vignetting artifacts typically arising at the periphery of non-compensated ET reconstructions are completely eliminated when our method is employed.

Keywords: Tomography, Reconstruction, Image Processing, Parallel Processing

1 Introduction

Electron Tomography (ET) (see for example Frank, 2006, or Luic et al., 2005) uniquely enables the 3D study of complex cellular structures, such as the cytoskeleton, organelles, viruses and chromosomes. It recovers the specimen’s 3D structure via computerized tomographic (CT) reconstruction from a set of 2D projections obtained with Transmission Electron Microscopy (TEM) at different tilt angles. ET can be accomplished using exact analytical methods (weighted back-projection WBP (Radermacher, 2006) and more recently electron lambda-tomography (Quinto et al., 2009)) or via iterative schemes, such as the Simultaneous Algebraic Reconstruction Technique (SART) (Andersen and Kak, 1984), the Simultaneous Iterative Reconstruction Technique (SIRT) (Gilbert, 1972), and others. The dominant use of the analytical methods is most likely due to their computational simplicity and consequently fast reconstruction speed. Iterative methods, however, have the advantage that additional constraints can be easily and intuitively incorporated into the reconstruction procedure. This, for example, can be exploited to better compensate for noise (Skoglund et al., 1996) and to perform alignment corrections (Castano-Diez et al., 2006; Frank and McEwen, 1992; Lawrence, 1992) during the iterative updates. Additional challenges are imposed by the fact that the projection sinogram is vastly undersampled, both in terms of angular resolution (due to dose constraints) and in terms of angular range (due to limited sample access). These types of scenarios can be handled quite well using iterative reconstruction approaches (Andersen, 1989).

Thus, iterative approaches have great potential for ET. However, as data collection strategies (Zheng et al., 2004) and electron detectors improve, the push has been to reconstruct larger and larger volumes (20482 × 512 pixels and beyond). Although the benefits are significant, the major obstacle preventing the widespread use of iterative methods in ET so far has been the immense computational overhead associated with these, leading to reconstruction times on the order of hours to days for practical data scenarios. As in many other scientific disciplines, the typical solution to meet these high computational demands has been the use of supercomputers and large computer clusters (Fernández, 2008; Fernández et al., 2004; Zheng et al., 2006), but such hardware is expensive and can also be difficult to use and gain access to. Fortunately, the recently emerging graphics processing units (GPUs) offer an attractive alternative platform, both in terms of price and performance. GPUs are available at a price of less than $500 at any computer outlet and, driven by the ever-growing needs and tremendous market capital of computer entertainment, their performance has been increasing at triple the rate of Moore’s law, which governs the growth of CPU processors. For example, the recent NVIDIA GPU board GTX 280 has a peak performance of nearly one Trillion floating point operations per second (1 TFlop), which is 1–2 orders of magnitude greater than that of a state-of-the-art CPU.

The great performance of GPUs comes from their highly parallel architecture, and the vast potential of these boards for general high performance computing has given rise to the recent trend of General Purpose Computing on GPUs (GPGPU) (Owens et al., 2005). In the past, GPU-programming was only possible via graphics APIs, such as CG, GLSL and HDSL, which required programmers to have some background in computer graphics. In order to make the hardware more accessible to non-graphics programmers, a C-like parallel computing programming interface called CUDA (Compute Unified Device Architecture) has recently been introduced by GPU manufacturer NVIDIA. A similar but more general API called OpenCL has also become available. We have used GLSL for our implementation.

The high potential of GPUs for accelerating Computed Tomography (CT) has been recognized for quite some time in the field of X-ray CT (Cabral et al., 1994; Chidlow and Möller, 2003; Kole and Beekman, 2006; Mueller and Xu, 2006; Schiwietz et al., 2006; Wang et al., 2005; Xu and Mueller, 2005; Xu and Mueller, 2007; Xu et al., 2010, Xue et al., 2006), and more recently also for ET (Castano-Diez et al., 2007; Castano-Diez et al., 2008; Lawrence et al., 2009; Schoenmakers et al., 2005; Schmeisser et al., 2009). The majority of GPU algorithms developed for X-ray CT have focused on 3D reconstruction from data acquired in perspective (cone- and fan-beam) viewing geometries, using flat-panel X-ray detectors in conjunction with X-ray point sources. This poses certain constraints on how computations can be managed (pipelined) given the highly parallel SIMD (Single Instruction Multiple Data) architecture of GPUs. However, data acquisition in ET is typically posed within a parallel-beam configuration, and this allows for additional degrees of freedom in the implementation, which are not available in the cone- and fan-beam configurations. Our approach exploits these opportunities to derive a novel high-performance GPU-accelerated iterative ET reconstruction framework.

The GPU method proposed by Castano-Diez et al. can be viewed as a first step towards achieving high-performance ET. Our framework is a substantial advance of their method, speeding up their calculations by an order of magnitude. Such speedups are especially significant when it comes to 3D reconstructions, which are the ultimate goal of ET. The method of Castano-Diez at al. enables only 2D iterative reconstructions to be accomplished at reasonable speeds (where reasonable is defined here as being on the order of minutes). However, reconstructions at the same resolution, but in 3D, still take hours to compute. Our framework, on the other hand, obtains these 3D reconstructions in an order of minutes, on comparable hardware. Finally, the latest generation of GPU hardware enables further considerable speed increases, which may be valued as another demonstration of the immense potential GPUs have for iterative ET.

SIRT is a commonly used reconstruction algorithm in ET and has been shown to produce good reconstruction results. On the other hand, SART has been shown to converge at considerably faster rates, but generating somewhat noisier reconstructions. This occurs since each update/correction is only based on a single projection and therefore does not enjoy the stabilizing effect of a global SIRT update which deals better with noise. We have recently shown (in Xu and Mueller, 2008) that a special caveat is imposed by the SIMD architecture of GPUs where one must carefully choose the number of parallel threads for optimal performance. Since the number of parallel threads grows with the number of projections (or better, the number of pixels they contain) it turns out that iterations with SIRT are considerably faster than those with SART. However, since the slower convergence rate requires a larger number of iterations in SIRT this does not necessarily yield gains in real-time performance.

To find a mechanism to express a compromise between SART and SIRT, we presented (in Xu et al, 2008, Xu et al., 2010) an Ordered Subsets SIRT (OS-SIRT) algorithm in which SART has N subsets of 1 projection each, and SIRT has 1 subset of N projections (with N being the number of projections acquired). A similar compromise has been introduced as OS-SART by (Wang and Jiang, 2004). The rational was similar to that of (Hudson and Larkin, 1994) who devised OS-EM, an ordered subsets algorithm for the Expectation Maximization (EM) algorithm (Shepp and Vardi, 1982). In OS-EM, the best subset size is one that most optimally balances the noise compensation offered by larger subsets (many projections in one subset) and the smaller number of iterations required for convergence offered by smaller subsets (many corrective updates within one iteration). However, for our OS-SIRT the focus was to provide a mechanism by which one can balance GPU runtime performance (which is convergence as measured in wall-clock time) with noise cancelation (for better reconstruction quality). For the work presented in this paper we have applied this framework to CT reconstruction from TEM data and show that OS-SIRT also provides a favorable algorithm here. We note that the study of OS-SIRT and its optimization for TEM data is not the focus of this paper – this is subject of future work. Rather, in the current work we have aimed to provide more insight into GPU-accelerated computing for ET reconstruction.

Finally, an important issue in CT is the “long object” reconstruction problem. It arises in spiral CT when the goal is to reconstruct a region-of-interest (ROI) bounded by two trans-axial slices, using a set of axially truncated cone-beam projections corresponding to a spiral segment long enough to cover the ROI, but not long enough to cover the whole axial extent of the object (Defrise et al., 2000). Essentially, in this situation some rays used for ROI reconstruction also traverse object regions not within the ROI, and these rays are sometimes called “contaminated” rays. This problem is similar to the “local tomography” problem in ET. While for ET the data acquisition trajectory is orthogonal to the one in spiral CT, ray contamination occurs whenever the object contains material not covered by every projection (that is, only a sub-region of the object is exposed to electrons in a local view). These areas are then incompletely reconstructed in the iterative procedure, which is evidenced by vignetting – a brightness fall-off in the peripheral regions of the reconstructed object. We derive a method, within our iterative framework, which effectively compensates for this effect, correcting the contaminated rays for the missing information.

Our paper is structured as follows. Section 2 presents relevant background both on reconstruction algorithms and on GPU hardware. Section 3 describes our various contributions, that is, the advanced GPU acceleration framework, the extension to the OS-SIRT mechanism, and the long-object compensation method. Section 4 presents results and Section 5 ends with conclusions.

2 Background

Before detailing the contributions of this paper, we first give a brief overview over the implemented – and then accelerated and extended – reconstruction algorithms and the relevant intricacies of GPU hardware. In this paper, we have only considered algebraic reconstruction algorithms, but the hardware acceleration generalizes readily to expectation maximization (EM) type procedures (for more information, see (Xu and Mueller, 2005)).

2.1 Iterative Algebraic Reconstruction: theory and practice

Most iterative CT techniques use a projection operator to model the underlying image generation process at a certain viewing configuration (angle) φ. The result of this projection simulation is then compared to the acquired image obtained at the same viewing configuration. If scattering or diffraction effects are ignored, the modeling consists of tracing a straight ray ri from each image element (pixel) and summing the contributions of the volume elements (voxels) vj. Here, the basis function wij determines the contribution of a vj to ri. The projection operator is given as:

ri=∑j=1Nvj·wij  i=1,2,…,M (1)

Here, M and N are the number of rays (one per pixel) and voxels, respectively. One can cast the choice of the weighting factors wij as an interpolation problem, where the rays traverse a field of basis functions (kernels) wij, each centered at a voxel vj (Mueller et al., 1999). The most efficient basis functions for GPUs are the nearest-neighbor and linear interpolation functions, in conjunction with point sampling. We have shown in earlier work (Xu and Mueller, 2006) that for 3D iterative reconstruction (with SART) this type of sampling is sufficient. There we showed that the error function was similar to the one obtained with Siddon’s line and area/volume integration schemes which assume lower-quality nearest-neighbor kernels (but integrate them). A similar observation was also made for SIRT (Benson and Gregor, 2005).

Once M and N are sufficiently large, it becomes infeasible to store the wij as a pre-computed array. In fact, since GPUs are heavily optimized for computing and less for memory bandwidth (which is consequence of general semi-conductor technology), computing these wij on the fly is by far more efficient. This is even more so, since linear interpolation up to three dimensions and up to 32-bit floating-point precision is implemented on GPUs in special extra-fast ASIC circuitry. As it turns out, on the latest GPU cards there is almost no difference in performance for nearest-neighbor and bi-linear interpolation. This is fortunate, since iterative algorithms are very sensitive to the accuracy of the projector and thus bi-linear interpolation is a requirement for high-quality reconstructions (see Section 4). This sensitivity comes from the need for accurate correction factors to be used for the iterative updates. Here, linear interpolation strikes a good balance between aliasing and smoothing. The correction update for projection-based algebraic methods is computed with the following equation:

vj(k+1)=vj(k)+λ∑pi∈OSspi−ri∑l=1Nwil∑i=1Nwij   ri=∑l=1Nwil·vl(k) (2)

We have written this equation as a generalization of the original SART and SIRT equations to support ordered subsets for the OS-SIRT. Here, the pi are the pixels in the P/S acquired images that form a specific subset OSs where P is the total number of projection images, S is the number of subsets, and 1 ≤ s ≤ S. The factor λ is a relaxation factor, which will be chosen as a function of subset size (for SIRT where S=P, λ=1). The factor k is the iteration count, where k is incremented each time all P projections have been processed. In essence, all voxels vj on the path of a ray ri are updated (corrected) by the difference of the projection ray ri and the acquired pixel pi, where this correction factor is first normalized by the sum of weight encountered by the (back-projection) ray ri. Since a number of back-projection rays will update a given vj, these corrections need also be normalized by the sum of (correction) weights. Note that for SIRT, these normalization weights are trivial.

2.2 Graphics hardware: architecture and programming model

GPUs have their origin as dedicated graphics processors. In graphics, high visual detail (when geometric detail is not needed) can be generated by simply mapping an image of sufficient resolution onto a large polygon. This requires two units. First, one needs a high-performance parallel polygon rasterizer, since each such polygon potentially affects many screen pixels onto which the image must be mapped. Second, with each rasterized pixel giving rise to a fragment one also requires a high-performance parallel fragment processor, able to process the oncoming front of fragments efficiently. Traditionally, each such fragment computation was just an interpolation of the mapped image at the coordinates attached to the fragment by the rasterizer. But now these computations can be much more involved, such as generating sophisticated lighting effects, driving complex physical simulations, or, in a GPGPU application, the execution of an arbitrary program (called shader). The key to a successful GPGPU implementation is that these computations can be cast as parallel operations, executed in lock-step (SIMD = Single Instruction Multiple Data) on the parallel fragment processors. This puts certain constraints on both data flow and programming model, which often requires a creative re-organization of the existing CPU program to enable optimal utilization of all parallel GPU resources.

The NVIDIA G70 chip (which forms the GPU in the 7800 GTX and in the Quadro FX 4500) has 24 SIMD fragment processors (and 8 vertex processors), 512MB of DDR memory, and 165 GFlops performance. On the other hand, the recent GTX 280 has 240 generalized processors, 1GB of DDR memory, and nearly 1TFlops performance (for further detail on these chips and boards the reader is referred to the corresponding Wikipedia pages). As mentioned, up to recently, the only way to interface with GPU hardware was via a graphics API, such as OpenGL or DirectX, and using CG, GLSL, or HDSL for coding the shader programs to be loaded and run on the fragment processors. With CUDA, the GPU can now directly be perceived as a multi-processor, and a suitable programming interface is available for this model where fragments become the CUDA (SIMD) computing threads and the shader programs become the computing kernels, which can be launched by a single instruction

Textures are the data structures utilized most frequently in GPU graphics programming (and they can also be used with CUDA). Textures are essentially 1D–3D arrays supporting data types of various precisions ranging from 8-bit fixed point to 32-bit floating point. Among those, 2D floating point textures are most suitable for general purpose computing due to their complete support of all data formats and interpolation schemes. Conceived within a graphics context, textures are designed to contain up to four channels (RGBA) of data, where RGB is (red, green, blue) color and the A (alpha) channel carries the opacity (1-transparency) value. This feature provides additional data parallelism, in addition to the intrinsic pipeline parallelism described above. However, in order to achieve this parallelism one needs to fulfill even stronger requirements than just SIMD.

Understanding the GPU memory hierarchy is the key to maximizing computational performance. On the GPU, memory is organized in register, shared, texture, and global memory. Registers and shared memory are fastest and on-chip, while texture and global memory is maintained as slower DDR memory and on-board. Shared memory stores recently accessed data blocks for use by parallel threads, and each memory miss causes 100 or more wait clock cycles. Fortunately, GPUs hide these latencies by replacing any waiting thread by another thread that (already) has the data it needs to compute the current SIMD instruction. It is therefore desirable to (a) maintain data locality among neighboring threads in order to prevent costly cache misses overall, (b) launch a sufficient number of threads (many more than the number of available microprocessors) so the latencies incurred by cache misses can be hidden by overlapping the memory waits with computation, and (c) keep the kernel program sufficiently long to amortize setup cost, minimize synchronization overhead, and promote efficient instruction and data flow.

3 Methods

Most relevant in a GPU-accelerated CT reconstruction framework is to have an efficient projection and back-projection operator. The remaining operations, such as the correction computations, are simple vector operations of low complexity and can be implemented on the GPU by subtracting two 2D textures, the texture holding the acquired projections and the texture computed during projection. In the following we (a) describe an efficient parallel framework that accelerates these operations, and (b) present a new method that efficiently deals with the effects of the limited specimen coverage of the detector.

3.1 Acceleration of forward and backward projection

We begin our discussion by writing the projection procedure in form of a typical CPU implementation. Assuming S exclusive subsets and P projections in total, the pseudo-code for projection is shown in Figure 1 (the backprojection is interleaved for each subset, but not shown here). A ray steps across a slice, interpolates the slice at the sample positions (which results in the weights), sums these contributions (and the weights) and finally divides the ray sum by the sum of weights for normalization. We pre-compute this sum of weights in a pre-processing step and store into a texture.

Figure 1.

Figure 1

Open in a new tab

Forward projection loop of a straightforward CPU implementation.

From the code in Figure 1 we observe that (i) the projection procedure has 5 nested loops (indicated in blue), and (ii) the body of the final level is the longest in terms of operations. The implementation of Castano-Diez et al. maps this loop structure directly to the GPU. The body of loop (4) as well as loop (5) and its body are executed in the fragment shader, while the head of loop (4) itself is parallelized by generating a raster of fragments, one for each loop instantiation. A polygon of size T×1 is created (where T is the number of pixels within a projection) and this polygon is rasterized to the screen. Since each volume slice is processed separately, the projection data is just a set of 1D lines drawn from the set of 2D projections. This process generates one fragment per pixel and for each pixel the fragment program is executed. Given this decomposition, executing all instantiations of loop (4) then encompasses a single parallel operation (called pass in GLSL), and therefore one gets VS·P such passes. Furthermore, due to then-existing limits on the number of instructions that could be executed in one kernel, Castano-Diez et al. were forced to break each volume slice into TL tiles and computed the rays sum for each tile in a separate pass, adding the results in the end. Thus the final number of passes became even higher, that is, VS·P·TL. Assuming SIRT and P=85, VS=1024 slices, and TL=4 tiles, this would then result in 348k passes, causing significant overhead.

This early implementation does not promote the rules set forward at the end of Section 2.2 which hampers performance and also scalability. There is only little parallelism, there are only few threads per pass, and the threads themselves are short. We have improved on this as follows, referring to the pseudo code given in Figure 2:

  • Minimize synchronization overhead: We do not subdivide the domain into tiles, but trace all rays from entry to exit. Optionally, we pre-compute for each ray its starting locations (rx, ry,) at the slice boundary as well as its direction vector (rdx, rdy) and store these four values into a ray texture TXray.

  • Encourage latency hiding: We launch all rays in a subset at the same time. Thus the number of threads can be controlled by the subset configuration. It is this flexibility that makes our OS-SIRT scheme so attractive and powerful for high-performance GPU computing. For this, we group all |OS| 1D projections in a subset (corresponding to a certain volume slice) into a single 2D sinogram texture TXproj. Then, during projection, we create a polygon of size T×|OS|, and use TXsim as a rendering target. This generates rays/fragments for all angles and pixels in the currently processed subset, and eliminates loop (3).

  • Exploit RGBA channel parallelism: For this to work, all fragments in these parallel channels must exhibit the exact same mapping function – all that can be different are the data and the rendering target, with each such simultaneous pair being stored in the RBGA channels. Such a strong parallelism is readily exposed in parallel projection, and we can achieve it by storing and processing a consecutive 4-tuple of volume slices and associated projection data in the RGBA channels of their corresponding textures. This reduces the number of required passes theoretically by a factor of 4, but in practice this factor is about 3. GLSL provides a better interface than CUDA for accessing these functionalities since RGBA color is typically used for graphics rendering.

Figure 2.

Figure 2

Open in a new tab

Pseudo code for sinogram-based forward projection. The first two gray lines are executed on the CPU, while the remainder is GPU-resident fragment code. Note that a fragment in this code is the equivalent of a CUDA thread.

All put together, we can reduce the number of passes required for one iteration to VS/4∙S. For example, assuming classic SIRT with S=1 and VS=1024 slices as before, we would have 256 passes (if less passes are desired we could also combine equivalent rays in multiple slices). This is less than 0.1% of the implementation of Castano-Diez et al., which has a significant impact on reconstruction performance.

Equivalent to the projection code, Figure 3 lists the pseudo fragment code for back-projection. Similar to Castano-Diez.et al., the final two loops of the above pseudo codes are explicitly controlled and executed on the GPU and are rendered in a single pass. However, in addition, we also exploit the RGBA 4-way parallelism, reducing the total number of required passes to VS/4·S.

Figure 3.

Figure 3

Open in a new tab

Pseudo code for sinogram-based back-projection. The first two gray lines are executed on CPU, while the remainder is GPU-resident fragment code.

Note that the major difference of backprojection and forward projection is that in the former the pixel rays are processed in parallel (forming a pixel-driven operator), while in the latter the voxels form the threads (yielding a voxel-driven operator). This makes both projectors gathering operations which are more efficient than scattering operations in which every interaction would be a spreading instead of an interpolation. More concretely, a voxel-driven forward projector would have to splat (scatter, distribute) a kernel function onto the detector plane, while a pixel-driven backprojector would have to splat the corrective updates into the reconstruction grid. These already expensive operations would have to be written as kernel code, while interpolation is accelerated in special super-fast hardware circuits. Although this forms an unmatched projector-backprojector pair it has been shown by (Zeng and Gullberg, 2000) to work very well in practice.

Finally, since our backprojector uses linear interpolation where the weights always sum to 1.0 for each projected voxel the post-weighting normalization in equation (2) simplifies to a division by |OSs|, which is the number of projections in subset s. Equation (2) is then written as:

vj(k+1)=vj(k)+λ∑pi∈OSspi−ri∑l=1Nwil|OSs|   ri=∑l=1Nwil·vl(k) (3)

This reduces the need for keeping track of the sum weights in the backprojection and saves on memory and calculations.

3.2 Limited detector problem compensation

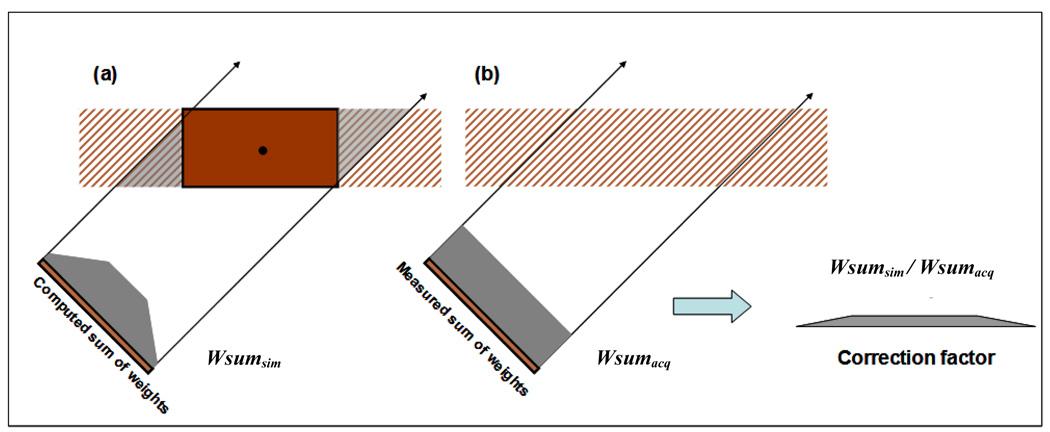
During the data collection stage only a small portion of the sample is imaged to obtain the tilt projections. This results in the “limited detector” or “long-object” problem as discussed in Section 1, and an illustration is shown in Figure 4a. Here an off-center acquired projection image contains ray integrals across the whole sample, but the simulated projection at the same angle does not have the complete integral since the reconstruction volume must be limited (typically by a box). In other words, voxels residing in the shadow area of the original complete sample (shown shaded in grey) participate in the projection formation during imaging, but due to the restricted reconstruction area (shown in solid red), they do not contribute in the value formation of any pixels during the reconstruction, resulting in severe vignetting effects if we do not compensate for this.

Figure 4.

Figure 4

Open in a new tab

Limited detector/long object problem: (a) the shadowed area indicated regions not reconstructed, but participating in the image formation, (b) area for acquired sum of weights term.

This vignetting effect is shown for three datasets in Figure 5a. The top row shows the reconstruction of a long slab of uniform density, while the others show two TEM datasets – a tobacco mosaic virus and the HPCcere2 dataset (see below) – all after one iteration with SART. Note that these raw CT slices are vertical cross-sections of the stack of slices typically displayed for visualizing the salient biological structures – we present these more familiar cross-sectional images in Section 4. We observe that while the vignetting effects are most prominent for the slices at the top and bottom ends of the stack, all slices are principally affected (see the bow-tie like structures which will cause density fall-off within all cross-sectional slices).

Figure 5.

Figure 5

Open in a new tab

Limited detector effect: (a) without compensation, and (b) with compensation during iterative reconstruction. Top to bottom row: a uniform slab, the tobacco mosaic virus, and the HPCcere2 dataset.

We propose a weight correction scheme that effectively resolves this problem for iterative ET – other compensations exist for analytical algorithms (Sandberg et al., 2003) based on Filtered backprojection, where an extended area of around double the length of the region of interest (ROI) is used as the reconstruction target to prevent sampling artifacts. While the over-sampling approach resolves the edge problem, it introduces an extra amount of computation. Our approach does not require these extra computations, as we compensate for the missing target regions on the fly.

In a typical iterative algebraic framework, at a particular tilt angle (see Figure 4), the corrective update is derived as:

Correction=Pacq−PsimWsumsim=PacqWsumsim−PsimWsumsim (4)

Here the acquired projection is denoted as Pacq and the simulated projection as Psim. The problem with using this equation to derive a correction is that the computed sum of weights Wsumsim is calculated based on the bounding box which does not exist (in this closed form) in the acquired data. Therefore, this sum should not be applied towards the acquired projection Pacq. Instead, the acquired sum of weights Wsumacq (shown in Figure 4b) is the correct value that should be used. Using these arguments, we derive an updated correction equation as follows:

Correction=PacqWsumacq−PsimWsumsim=Pacq·Wsumsim−Psim·WsumacqWsumacq·Wsumsim=Pacq·WsumsimWsumacq−PsimWsumsim (5)

Consequently, an additional correction factor determined by dividing Wsumsim over Wsumacq should be computed to pre-weight the acquired projection Pacq before it participates in the regular correction stage. In practice, we assume that the true extent of the specimen falls within a box extending the box bounding the reconstruction region. The ratio Wsumsim/Wsumacq could then be obtained as the ratio of the length of the parallel rays clipped to the reconstruction region’s bounding box and the length of these rays fully intersecting the extended box at the given tilt angle. The latter can be computed by L=d/cos(α) where d is the thickness of the specimen (typically the number of voxels in that dimension assuming unit cell size) and α is the tilt angle. While using a metric ray length L to normalize Pacq has been already described in (Kak and Slaney, 1988 and Gilbert, 1972), these authors only used this formulation as a measure more accurate than a sum of discrete weights W. They did not differentiate the sum of weights to be used for weighting Pacq and Psim within a limited detector scenario.

To reduce computational overhead we pre-compute L for each tilt angle and store its reciprocal into a constant texture. The ratio for a given ray is then computed by multiplying this constant by the ray’s actual sum of weights Wsumsim obtained from the weight sum texture (see Section 3.1). Alternatively we may also pre-compute and store the ratios themselves as a (constant) texture.

The reconstruction results (again after one iteration with SART) presented in Figure 5b show that this approximation is reasonably accurate, and we find that by applying the new correction the strong vignetting artifacts present in Figure 6a are effectively removed.

Figure 6.

Figure 6

Open in a new tab

(Top row) Reconstruction results for a tobacco mosaic virus dataset using the extreme OS configurations (SIRT and SART) and OS-SIRT 5, all taking about 30s to reconstruct (intensity windowing was applied in each to boost contrast). (Bottom row) Zooming into a specific detail (again with intensity windowing). The number of projections was 61, the tilt angle 120°, the volume size 680×800×100, and λ was set to 1.0 for SIRT, 0.5 for OS-SIRT 5, and 0.03 for SART.

4 Results

We have experimented with two TEM datasets: (1) a cryo dataset of a frozen hydrated tobacco mosaic virus, comprised of 61 projections of size 680×800 each and obtained at uniform spacing over a tilt angle of around 120° and (2) a brain synapse (the HPFcere2 dataset from the Cell Centered Database http://www.ccdb.ucsd.edu), comprised of 61 projections of size 2,242×3,340 each and obtained at uniform spacing over a tilt angle of 120° (these are double tilt data, but we only used a single tilt). In order to align all projections, we cropped them to size 1,424×2,024. Next we show results we have obtained with our GPU-accelerated SIRT, SART, and OS-SIRT algorithm. We first show reconstructions we obtained, then present the timing results, and end with further results on our limited-detector artifact compensation scheme.

4.1 Reconstruction quality, in the context of computational performance

For OS-SIRT we experimentally determined that OS-SIRT 5 gave the best reconstruction quality in the shortest wall clock time for the TEM datasets we tested. We used λ=1 for SIRT in all cases. For SART we used a fixed λ=0.3 for the brain synapse dataset and λ=0.05 for the noisier tobacco mosaic virus. Figure 6 displays reconstruction results for the tobacco mosaic virus, with all 800 slices (resolution 680×100) reconstructed via the two extreme OS configurations (SIRT and SART) and OS-SIRT 5. Here we found, similar to Dietz et al. that a single iteration was sufficient for SART to converge and that SIRT will eventually reach convergence as well with similar results, but requires many more iterations (50 or more). The top row shows the full slice view of (a linear intensity window was applied to maximize contrast) of the reconstructed volume, and the bottom row shows a detail view of the same slice (with intensity windowing). All reconstructions were obtained at the same wall-clock time of 30s, matching the time required for one iteration with SART (using the more versatile single-channel implementation, see below). It appears that OS-SIRT 5 provides somewhat better detail and feature contrast than both SART and SIRT – the tube channels seem better preserved for OS-SIRT 5. Figure 7 shows a similar series for the HPFcere2 dataset (with 506 slices at 356×148 resolution) obtained at a wall clock time of about 22s, with similar observations. SIRT produces significantly less converged (blurrier) images at this wall clock time. They improve (sharpen) if further iterations are allowed, which we study in Figure 8. There we see that 20 iterations appear to be sufficient to match the reconstruction result obtained with OS-SIRT 5 (but at more than triple the time).

Figure 7.

Figure 7

Open in a new tab

Reconstruction results for the HPFcere2 dataset using the extreme OS configurations (SIRT and SART) and OS-SIRT 5, all taking about 22s to reconstruct (intensity windowing was applied in each to boost contrast). The number of projections was 61, the tilt angle 120°, volume size 356×506×148, and λ was set to 1.0 for SIRT, 1.0 for OS-SIRT 5, and 0.3 for SART.

Figure 8.

Figure 8

Open in a new tab

Reconstruction results for the HPFcere2 dataset comparing the results obtained with extended iterations with SIRT and OS-SIRT 5 (intensity windowing was applied in each to boost contrast). The number of projections was 61, the tilt angle 120° and the volume size 356×506×148. We observe by visual inspection that 20 iterations with SIRT yield similar results than 6 iterations with OS-SIRT, but at double the wall-clock time. The relaxation factor λ was set to 1.0 for both SIRT and OS-SIRT 5.

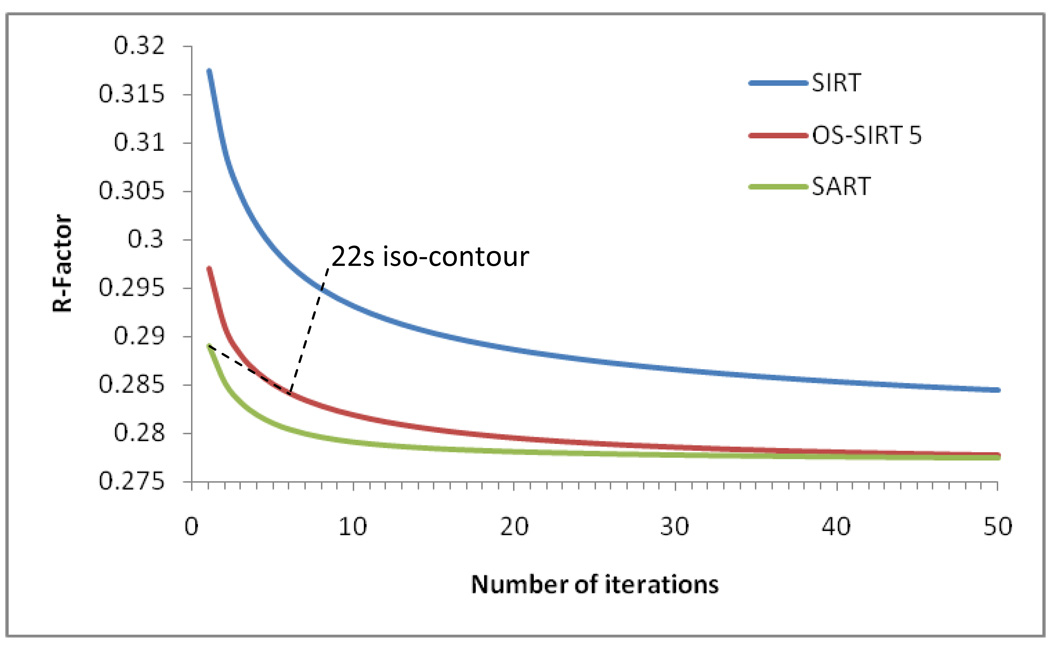
Figure 9 compares the three different algorithms (SRT, OS-SIRT 5, and SIRT) quantitatively using the R-factor. Although the R-factor still improves beyond the images we have shown here, we found that these improvements are not well perceived visually and so we have not shown these images here. To visualize the aspect of computational performance in the context of a quantitative reconstruction quality measure (here, the R-factor) we have inserted into Figure 9 a metric which we call the ‘computation time iso-contour’. Here we used 22s for this contour – the approximate time required for 1 SART, 6 OS-SIRT, and 8 SIRT iterations (see Figure 7) which yielded reconstructions of good quality for OS-SIRT 5. We observe that OS-SIRT 5 offers a better time-quality performance than SART, and this is also true for other such time iso-contours (although not shown here) since the time per iteration for OS-SIRT is roughly 1/6 of that for SART. SIRT, on the other hand converges at a much higher R-factor.

Figure 9.

Figure 9

Open in a new tab

Comparison of SART, OS-SIRT 5, and SIRT in terms of quality (R-factor) and performance (22s iso-contour).

Finally, Figure 10 presents detail results obtained from higher resolution reconstructions with OS-SIRT 5 (of the HPFcere2 dataset). We confirm that crisper detail can be obtained with higher resolution, and we will present the time overhead required in the following section.

Figure 10.

Figure 10

Open in a new tab

Reconstruction results for the HPFcere2 dataset using 8 iterations with OS-SIRT 5 and for increasing resolution. The number of projections was 61, the tilt angle 120°, but the data used was at matching resolution. The relaxation factor λ was set to 1.0 for all reconstructions.

4.2 Absolute computational performance

We now discuss the general performance of our optimized GPU-accelerated ET-framework. First, to illustrate the benefits of our new projection/backprojection scheme in general, we provide Table 1 which compares the running times obtained via our framework with those reported in (Castano-Diez et al., 2007). The timings presented here refer to a 2D slice reconstruction with SIRT, using projection data from 180 tilt angles, including the time to transfer the data to the GPU. We have run our framework on GPU hardware comparable to the one employed by Castano-Diez et al., that is, the NVIDIA G70 chip (this chip forms the core of both the Quadro 4500 and the GeForce 7800 GTX boards, with only minor performance differences). Since then, newer generations of NVIDIA chips have emerged, with the latest being the G200 chip (available as the GTX 280 board) for which we also report timings. More detail on these two architectures was already presented in Section 2.2. We observe that the significant decrease in passes of our GPU-algorithm leads to consistent speedups of nearly an order of magnitude across all resolutions and iteration numbers (7800 GTX columns). The newer platforms yield further speedups mainly founded in hardware improvements (GTX 280 columns).

Table 1.

Timings for the reconstruction of a single volume slice at different resolutions using SIRT and parallel projections acquired at 180 tilt angles, comparing different implementations and platforms.

Number of
iterations		 Slice
resolution		 (Diez et al.)
Quadro 4500		 7800GTX Speedup GTX 280 Speedup
10 256×256 N/A 0.41s N/A 0.13s N/A
50 256×256 N/A 2.05s N/A 0.66s N/A
10 512×512 9s 1.23s 7.3 0.34s 26.0
50 512×512 39s 5.32s 7.3 1.75s 22.2
10 1024×1024 32s 4.30s 7.5 1.23s 25.8
50 1024×1024 146s 21.89s 6.7 6.44s 22.7
10 2048×2048 123s 17.39s 7.1 5.06s 24.3
50 2048×2048 567s 85.30s 6.7 26.94s 21.0
Open in a new tab

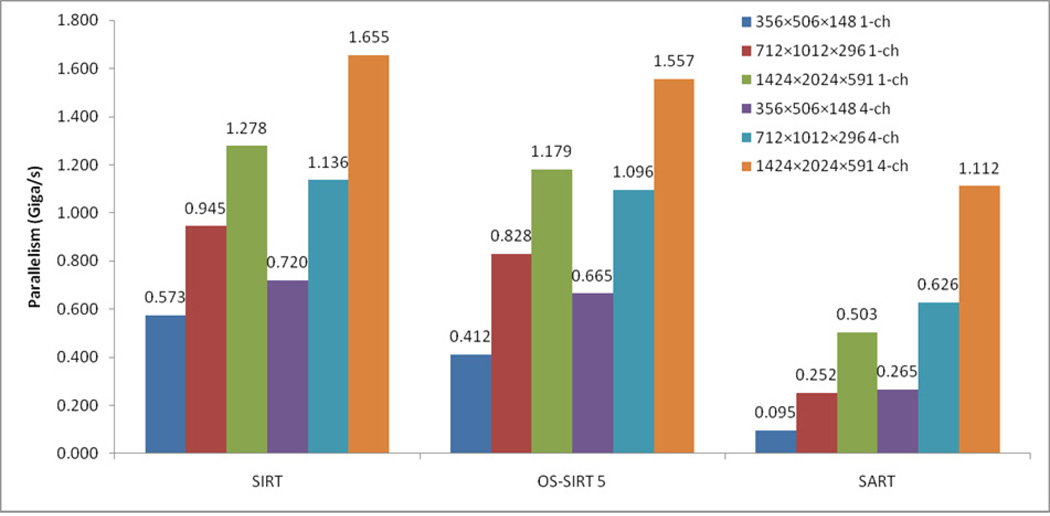
Table 2 studies the performance per iteration for SART, SIRT, and OS-SIRT 5 for different volume sizes/resolutions (assuming the same number of projections). In this table we also compare the timings obtained for the more versatile single-channel implementation with the RGBA (4) channel solution implemented with GLSL. We make two observations. First, we see that the 4-channel scheme pays off more as the number of subsets increases, with SART being the extreme case where it can achieve speedups between 2 and 3. Second, we observe that the performance gap of SIRT, OS-SIRT, and SART narrows (but more so for the 4-channel implementation) with increasing volume size, with eventually SIRT being only 1.5 times as fast than SART (for one iteration) in the 4-channel configuration. Since in ET practice the volume slice resolution tends to be at the order of 2k to 4k and larger, this means that the choice of subsets will be mainly determined by the traditional tradeoff between speed of convergence and noise cancelation. Figure 11 shows similar trends with a more standardized metric, the number of voxels (multiplied by the number of projections in the subset) processed per second. This yields a metric for the overall task complexity measured in gigavoxels/s.

Table 2.

Running time for 1 iteration for the reconstruction of volumes of different sizes (resolutions) using SIRT, OS-SIRT 5 and SART, with the 1-channel and 4-channels schemes, and parallel projections acquired at 61 tilt angles.

Volume resolution SIRT OS-SIRT 5 SART
1-ch 4-ch 1-ch 4-ch 1-ch 4-ch
356×506×148 2.642 2.103 3.672 2.278 15.867 5.712
712×1012×296 12.822 10.665 14.625 11.053 47.993 19.341
1424×2024×591 75.708 58.471 82.055 62.135 192.337 87.042
Open in a new tab

Figure 11.

Figure 11

Open in a new tab

Reconstruction performance expressed in Gigavoxels/s for different volume sizes, algorithms and the 1-channel and 4-channel scheme.

4.3 Limited detector problem compensation

Our final results present the impact of our compensation scheme on reconstruction quality. Section 3.2 has already shown that artifacts are effectively removed in the reconstructed thick specimen slab (which is a portion of a much wider and longer sheet). We have also mentioned that in most cases this slab is re-sliced orthogonally and then the grey level densities reversed and windowed, which yields the images typically visualized and also shown in our Figures 8, 9, and 10. In Figure 12 we present the center slices of the re-sliced slabs of Figure 5 (center row, the HPFcere2 dataset) before and after grey-level reversal (top and bottom row, respectively) and without and with compensation (left and right column, respectively) after one iteration with SART. We observe, in the uncompensated images, the peripheral density fall-offs at the left and right edge and we also observe a slight vertical stripe artifact due to the bow-tie border. Both artifacts are effectively removed with our compensation scheme.

Figure 12.

Figure 12

Open in a new tab

Comparing reconstruction results obtained for the HPFcere2 dataset without and with limited-detector compensation for 1 iteration with SART (at the same settings than for Fig. 7).

5 Conclusions

We have described new contributions and presented confirming results for these within three major areas of 3D Electron Tomography (ET): (i) the iterative reconstruction framework using algebraic methods in different subset configuration schemes, (ii) the compensation for the limited angle at which projections can be obtained, and (ii) the acceleration of ET via commodity graphics hardware (GPUs). For the latter, we have presented a novel data decomposition scheme that minimizes the number of GPU passes required, yielding speedups of nearly an order of magnitude with respect to present GPU-acceleration efforts. We also compared acceleration with a versatile single-channel scheme that is available with any GPU API with a 4-channel scheme (currently) only available with graphics APIs, such as GLSL, which offers additional speedups of up to 2 for large practical datasets (more for smaller datasets). Our GPU-accelerated framework allows full-size 3D ET reconstructions to be performed on the order of minutes, using hardware widely available for less than $500.

Our GPU-accelerated ET platform allows ET researchers to achieve a major task which has so far been infeasible without expensive and extensive hardware: the iterative reconstruction of full-size 3D volumes. We have shown that it is now possible to reconstruct a 20482×100 volume within a few minutes, while Castano-Diez et al. report nearly an hour or more for this task. A CPU-based reconstruction would take on the order of days. We emphasize that all of our results were obtained with a single GPU solution (of a cost of less than $500) – a multi-GPU configuration would provide even higher performance. We believe that the impact of gaining such capabilities is great, as it enables demanding iterative schemes crucial for the improvement of image resolution and contrast, such as iterative projection alignment and registration, and we are planning to further our efforts in this direction.

Current work is directed towards determining a framework that can automatically optimize the number of subsets and determine the best relaxation factor λ for a given imaging scenario, as expressed in SNR, imaged specimen, and imaging platform. We have already obtained encouraging initial results in this direction, as recently reported in (Xu and Mueller, 2009).

Acknowledgements

This work was partially funded by NIH grant R21 EB004099-01 and GM31627 (DAA) and the Keck Foundation, and the Howard Hughes Medical Institute (DAA).

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Andersen A. Algebraic reconstruction in CT from limited views. IEEE Transactions on Medical Imaging. 1989;8:50–55. doi: 10.1109/42.20361. [DOI] [PubMed] [Google Scholar]
  2. Andersen AH, Kak AC. Simultaneous Algebraic Reconstruction Technique (SART): a superior implementation of the ART algorithm. Ultrason. Img. 1984;6:81–94. doi: 10.1177/016173468400600107. [DOI] [PubMed] [Google Scholar]
  3. Benson TM, Gregor J. Modified simultaneous iterative reconstruction technique for faster parallel computation. IEEE Nuclear Science and Medical Imaging Symposium; 2005. pp. 2715–2718. [Google Scholar]
  4. Cabral B, Cam N, Foran J. Accelerated volume rendering and tomographic reconstruction using texture mapping hardware. ACM Symposium on Volume visualization; 1994. pp. 91–98. [Google Scholar]
  5. Castano-Diez D, Moser D, Schoenegger A, Pruggnaller S, Frangakis AS. Performance evaluation of image processing algorithms on the GPU. J. Struct. Biol. 2008;164:153–160. doi: 10.1016/j.jsb.2008.07.006. [DOI] [PubMed] [Google Scholar]
  6. Castano-Diez C, Seybert A, Frangakis AS. Tilt-series and electron microscope alignment for the correction of the non-perpendicularity of beam and tilt-axis. Journal of Structural Biology. 2006;154:195–205. doi: 10.1016/j.jsb.2005.12.009. [DOI] [PubMed] [Google Scholar]
  7. Castano-Diez D, Mueller H, Frangakis AS. Implementation and performance evaluation of reconstruction algorithms on graphics processors. Journal of Structural Biology. 2007;157(1):288–295. doi: 10.1016/j.jsb.2006.08.010. [DOI] [PubMed] [Google Scholar]
  8. Chidlow K, Möller T. Rapid emission tomography reconstruction. Proceedings of the 2003 Eurographics/IEEE TVCG Workshop on Volume graphics; ACM Press; Tokyo, Japan. 2003. pp. 15–26. [Google Scholar]
  9. Defrise M, Noo F, Kudo H. A solution to the long-object problem in helical cone-beam tomography. Physics in Medicine and Biology. 2000;45:623–644. doi: 10.1088/0031-9155/45/3/305. [DOI] [PubMed] [Google Scholar]
  10. Fatahalian K, Houston M. A closer look at GPUs. Communications of the ACM. 2008;51(10):50–57. [Google Scholar]
  11. Fernández J-J, Carazo J-M, García I. Three-dimensional reconstruction of cellular structures by electron microscope tomography and parallel computing. Journal of Parallel and Distributed Computing. 2004;64:285–300. [Google Scholar]
  12. Fernández JJ. High performance computing in structural determination by electron cryomicroscopy. Journal of Structural Biology. 2008;164:1–6. doi: 10.1016/j.jsb.2008.07.005. 2008. [DOI] [PubMed] [Google Scholar]
  13. Fernando R, Kilgard MJ. The Cg Tutorial: The Definitive Guide to Programmable Real-Time Graphics Addison-Wesley Professional. 2003 [Google Scholar]
  14. Frank J, McEwen BF. Alignment by Cross-Correlation. In: Frank J, editor. Electron Tomography. Plenum Press; 1992. pp. 205–214. [Google Scholar]
  15. Frank J, editor. Electron Tomography: Methods for Three-Dimensional Visualization of Structures in the Cell. 2nd ed. New York: Springer; 2006. [Google Scholar]
  16. Gilbert P. Iterative methods for the 3D reconstruction of an object from projections. J. Theor. Biol. 1972;76:105–117. doi: 10.1016/0022-5193(72)90180-4. [DOI] [PubMed] [Google Scholar]
  17. Hudson H, Larkin R. Accelerated Image Reconstruction Using Ordered Subsets of Projection Data. IEEE Transaction of Medical Imaging. 1994;13:601–609. doi: 10.1109/42.363108. [DOI] [PubMed] [Google Scholar]
  18. Kak AC, Slaney Malcolm. Principles of Computerized Tomographic Imaging. IEEE Press.1988. [Google Scholar]
  19. Kole JS, Beekman FJ. Evaluation of accelerated iterative X-ray CT image reconstruction using floating point graphics hardware. Phys. Med. Biol. 2006;5:875–889. doi: 10.1088/0031-9155/51/4/008. [DOI] [PubMed] [Google Scholar]
  20. Lawrence MC. Least-squares method of alignment using markers. In: Frank J, editor. Electron Tomography. Plenum Press; 1992. pp. 197–204. [Google Scholar]
  21. Lawrence A, Phan S, Singh R. Parallel Processing and Large-Field Electron Microscope Tomography. WRI World Congress on Computer Science and Information Engineering; 2009;3:339–343.
  22. Lucic V, Forster F, Baumeister W. Structural studies by electron tomography: from cells to molecules. Annu Rev Biochem. 2005;74:833–865. doi: 10.1146/annurev.biochem.73.011303.074112. [DOI] [PubMed] [Google Scholar]
  23. Mueller K, Xu F. Practical considerations for GPU-accelerated CT. IEEE International Symposium on Biomedical Imaging (ISBI); Arlington, VA. 2006. pp. 1184–1187. [Google Scholar]
  24. Mueller K, Yagel R, Wheller JJ. Anti-aliased 3D cone-beam reconstruction of low-contrast objects with algebraic methods. IEEE Transactions on Medical Imaging. 1999;18:519–537. doi: 10.1109/42.781017. [DOI] [PubMed] [Google Scholar]
  25. Owens JD, Luebke D, Govindaraju N, Harris M, Kruger J, Lefohn AE, Purcel T. A Survey of General-Purpose Computation on Graphics Hardware. Eurographics Association; Eurographics 2005. 2005:21–51.
  26. Quinto ET, Skoglund U, Oktem O. Electron lambda-tomography. Proc Natl Acad Sci USA. 2009 doi: 10.1073/pnas.0906391106. In press. http://www.pnas.org/cgi/doi/10.1073/pnas.0906391106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Radermacher M. Weighted back-projection methods. In: Frank J, editor. Electron Tomography: Methods for Three-Dimensional Visualization of Structures in the Cell. 2nd ed. Springer; 2006. pp. 245–273. [Google Scholar]
  28. Sandberg K, Mastronarde DN, Beylkina G. A fast reconstruction algorithm for electron microscope tomography. Journal of Structural Biology. 2003;144:61–72. doi: 10.1016/j.jsb.2003.09.013. [DOI] [PubMed] [Google Scholar]
  29. Schiwietz T, Chang T, Speier P, Westermann R. MR image reconstruction using the GPU. Proc. SPIE; 2006. pp. 1279–1290. [Google Scholar]
  30. Schmeisser M, Heisen BC, Luettich M, Busche B, Hauer F, Koske T, Knauber KH, Stark H. Parallel, distributed and GPU computing technologies in single-particle electron microscopy. Acta Crystallogr. D Biol. Crystallogr. 2009;65:659–671. doi: 10.1107/S0907444909011433. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Schoenmakers RHM, Perquin RA, Fliervoet TF, Voorhout W, Schirmacher H. New software for high resolution, high throughput electron tomography. Microscopy and Analysis. 2005;19(4):5–6. [Google Scholar]
  32. Shepp L, Vardi Y. Maximum likelihood reconstruction for emission tomography. IEEE Transaction of Medical Imaging. 1982;1:113–122. doi: 10.1109/TMI.1982.4307558. [DOI] [PubMed] [Google Scholar]
  33. Skoglund U, Ofverstedt LG, Burnett RM, Bricogne G. Maximum-entropy three-dimensional reconstruction with deconvolution of the contrast transfer function: a test application with adenovirus. J Structural Biology. 1996;117:173–188. doi: 10.1006/jsbi.1996.0081. [DOI] [PubMed] [Google Scholar]
  34. Wang Z, Han G, Li T, Liang Z. Speedup OS-EM image reconstruction by PC graphics card technologies for quantitative SPECT with varying focal-length fan-beam collimation. IEEE Transactions on Nuclear Science. 2005;52:1274–1280. doi: 10.1109/TNS.2005.858231. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wang G, Jiang M. Ordered-subset simultaneous algebraic reconstruction techniques (OS-SART) Journal of X-Ray Science and Technology. 2004;12:169–177. [Google Scholar]
  36. Xu F, Mueller K. Accelerating popular tomographic reconstruction algorithms on commodity PC graphics hardware. IEEE Transactions on Nuclear Science. 2005;52:654–663. [Google Scholar]
  37. Xu F, Mueller K. A comparative study of popular interpolation and integration methods for use in computed tomography. IEEE International Symposium on Biomedical Imaging (ISBI); Arlington, VA. 2006. pp. 1252–1255. [Google Scholar]
  38. Xu F, Mueller K. Real-Time 3D Computed Tomographic Reconstruction Using Commodity Graphics Hardware. Physics in Medicine and Biology. 2007;52:3405–3419. doi: 10.1088/0031-9155/52/12/006. [DOI] [PubMed] [Google Scholar]
  39. Xu F, Mueller K, Jones M, Keszthelyi B, Sedat J, Agard D. On the Efficiency of Iterative Ordered Subset Reconstruction Algorithms for Acceleration on GPUs. New York: MICCAI (Workshop on High-Performance Medical Image Computing & Computer Aided Intervention); 2008 doi: 10.1016/j.cmpb.2009.09.003. [DOI] [PMC free article] [PubMed]
  40. Xu F, Xu W, Jones M, Keszthelyi B, Sedat J, Agard D, Mueller K. On the Efficiency of Iterative Ordered Subset Reconstruction Algorithms for Acceleration on GPUs. Computer Methods and Programs in Biomedicine. 2010 doi: 10.1016/j.cmpb.2009.09.003. (to appear, available online at http://linkinghub.elsevier.com/retrieve/pii/S0169260709002521). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Xu W, Mueller K. Learning Effective Parameter Settings for Iterative CT Reconstruction Algorithms. China: Beijing; Fully 3D Image Reconstruction in Radiology and Nuclear Medicine. 2009 September;
  42. Xue X, Cheryauka A, Tubbs D. Acceleration of fluoro-CT reconstruction for a mobile C-Arm on GPU and FPGA hardware: a simulation study. Proc. SPIE; 2006. pp. 1494–1501. [Google Scholar]
  43. Zeng G, Gullberg G. Unmatched projector/backprojector pairs in an iterative reconstruction algorithm. IEEE Transactions on Medical Imaging. 2000;19(5):548–555. doi: 10.1109/42.870265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Zheng QS, Braunfeld MB, Sedat JW, Agard DA. An improved stategy for automated electron microscopic tomography. Journal of Structural Biology. 2004;147:91–101. doi: 10.1016/j.jsb.2004.02.005. [DOI] [PubMed] [Google Scholar]
  45. Zheng SQ, Keszthelyi B, Branlund E, Lyle JM, Braunfeld MB, Sedat JW, Agard DA. UCSF tomography: An integrated software suite for real-time electron microscopic tomographic data collection, alignment, and reconstruction. Journal of Structural Biology. 2006;157:138–147. doi: 10.1016/j.jsb.2006.06.005. [DOI] [PubMed] [Google Scholar]

RESOURCES