Composite RF pulses for $B_1^{+}-\text{insensitive}$ volume excitation at 7 Tesla

Abstract

A new class of composite RF pulses that perform well in the presence of specific ranges of B₀ and $B_1^{+}$ inhomogeneities has been designed for volume (non-selective) excitation in MRI. The pulses consist of numerous (~ 100) short (~ 10µs) block-shaped sub-pulses each with different phases and amplitudes derived from numerical optimization. Optimized pulses are designed to be effective over a specific range of frequency offsets and transmit field variations and are thus implementable regardless of field strength, transmit coil configuration, or the subject-specific spatial distribution of the static and RF fields. In the context of 7T human brain imaging, both simulations and phantom experiments indicate that optimized pulses result in similar on-resonance flip-angle uniformity as BIR-4 pulses but with the advantages of superior off-resonance stability and significantly reduced average power. The pulse design techniques presented here are thus well-suited for practical application in ultra-high field human MRI.

1. Introduction

The problem of inhomogeneous transmitted RF $(B_1^{+})$ fields in ultra-high field MRI (1) has previously been addressed by various RF pulse designs (e.g., spectral-spatial excitations (2) and adiabatic pulses (3; 4; 5)) and hardware modifications (e.g., parallel transmit coils (6) and traveling-wave antennae (7)). Such techniques have practical limitations in that field maps must be acquired for a specific imaging slice prior to the design of the RF pulse, specific absorption rate (SAR) requirements hinder implementation at ultra-high field, pulse durations are impractical, or non-standard hardware configurations must be implemented. New methods that improve flip-angle uniformity in the presence of large $B_1^{+}$ inhomogeneities while simultaneously addressing or avoiding such shortcomings are therefore of interest.

The design scheme introduced here can be used to generate composite pulses for volume (non-selective) excitation that are executable on commercial quadrature transmit coils within the practical limits of maximum RF amplitude and pulse duration of current ultra-high field human MRI. Using numerical techniques, pulses are optimized to produce uniform flip angles over a range of $B_1^{+}$ and static (B₀) field variations designated during the design process. When such field inhomogeneities can be estimated to lie within a given range, pre-designed composite pulses can be used without the time-consuming acquisition of $B_1^{+}$ and B₀ field maps and the subsequent design of a tailored RF pulse.

The main objectives of this study were (1) to determine relevant $B_1^{+}$ and ΔB₀ ranges to be targeted for 7T volume excitation of the human brain and a dielectric phantom of similar size; (2) to design optimized pulses as series of block-shaped sub-pulses with amplitudes and phases determined by numerical optimization; (3) to investigate the dependence of the performance of optimized composite pulses on such factors as average power, pulse duration, sub-pulse duration, and the number of component sub-pulses; (4) to compare the performance of selected optimized composite pulses to that of suitable block-shaped and adiabatic counterparts by way of simulations based on phantom and in vivo data acquired at 7T; and (5) to validate the efficacy of optimized composite pulses in improving flip-angle homogeneity in phantom experiments at 7T. Simulations and experiments demonstrate that this approach to pulse design is suitable for immediate practical application. Similar $B_1^{+}$- and ΔB₀-insensitive composite RF designs have been reported (8; 9; 10; 11; 12) but differ from this study in available RF time resolutions, maximum RF amplitude limits, and optimization methodologies. The present study therefore introduces new strategies for the design of $B_1^{+}$- and ΔB₀-insensitive pulses specifically for use in ultra-high field human imaging.

2. Methods

The design process for generation of the composite pulses in this study is summarized in the following steps:

1. perform experiments to determine the distribution of static and RF field magnitudes in volumes of interest (Section 2.1)

2. choose ranges of $B_1^{+}$ and ΔB₀ values for which pulses are targeted to perform (Section 2.2)

3. choose number and duration of component sub-pulses (Section 2.3)

4. optimize sub-pulse phases and amplitudes via a minimization algorithm (Section 2.4)

5. determine average power (P̄) and minimum repetition time (T_R,min) for each optimized pulse (Section 2.7)

Also in this section are descriptions of the block-shaped and adiabatic pulses used for performance comparisons (Sections 2.5 and 2.6) and details of methods used for simulation of the Bloch equations (Section 2.8). Lastly, the experimental procedures used for validation of optimized pulses are presented (Section 2.9).

2.1. Field mapping

A key design aim is the tailoring of pulses for a specific range of field inhomogeneities found in practice. Prior to determination of suitable ranges of $B_1^{+}$ and ΔB₀ values for which pulses are to be optimized, measurements were made of typical variations in these fields throughout particular volumes of interest—a 17 cm dielectric phantom (Function Biomedical Information Research Network, FBIRN) and the human brain. Two volunteer subjects were recruited from the community, and written informed consent was obtained according to the guidelines of the local Institutional Review Board. All experimental data were acquired with a single-channel, volume quadrature transmit/receive head coil (Nova Medical, Wilmington, MA, USA) and a 7T MR scanner (Philips Healthcare, Best, The Netherlands).

Protocols for estimating $B_1^{+}$ distributions were 1) a 3D spoiled steady-state actual flip-angle imaging (AFI) sequence (13) and 2) a series of 11 single-slice gradient recalled echo (GRE) images acquired at flip angles ranging from 10° to 210° in 20° increments. Due to its superior data collection efficiency, the former technique was used to estimate the $B_1^{+}$ field throughout the 3D volume, while the latter technique was used to give a more accurate measure of the same quantity in a single imaging slice (14). The AFI data were referenced in choosing the range of $B_1^{+}$ values to be targeted by the optimized pulses as well as for multi-slice simulations, and the GRE series data were used for single-slice phantom and in vivo simulations.

Data for $B_1^{+}$ and ΔB₀ scans were acquired in 3 mm isotropic voxels within a 240 × 192 mm axial field of view, with the 3D scan spanning 153 mm in the cephalo-caudal direction. Both sequences also used identical second-order volume shimming with a targeted shim volume corresponding roughly to the largest cubic volume that could be inscribed within the imaging volume. The AFI sequence employs interleaved acquisitions with alternating T_R values of 20 ms and 100 ms, an echo time (T_E) of 1.70 ms, and a nominal flip angle (α₀) of 60°. The voxel-by-voxel ratio of signals acquired at the different values of T_R can be related to the actual flip angle (α) at a given spatial location. The value of α/α₀ then gives an estimate of the relative magnitude of the $B_1^{+}$ field. The series of GRE images was acquired for a single slice corresponding to the central axial slice of the 3D AFI scan, thus placing the slice location for the in vivo scans just superior of the corpus callosum. Imaging geometry was identical to that of the AFI sequence, with T_R and T_E respectively set to 5000 ms and 2.7 ms. Given a GRE signal intensity represented by

$$S_i=\beta |\text{sin}(\lambda {\alpha }_{0i})|,$$ (1)

with β representing the product of the received RF field $B_1^{-}$ and the initial magnetization (M₀) and λ indicating the ratio of the actual transmitted RF field magnitude $(B_1^{+})$ to the corresponding field magnitude $(B_{1,\text{nom}}^{+})$ associated with the nominal flip angle α_0i of the i-th image in the series, a least-squares fit of the parameters β and λ to the S vs. α₀ curve for each voxel in the imaging slice results in a measure of λ (i.e., the relative magnitude of the $B_1^{+}$ field) (2; 15). Axial $B_1^{+}$ maps obtained with this technique are shown in Fig. 1b.

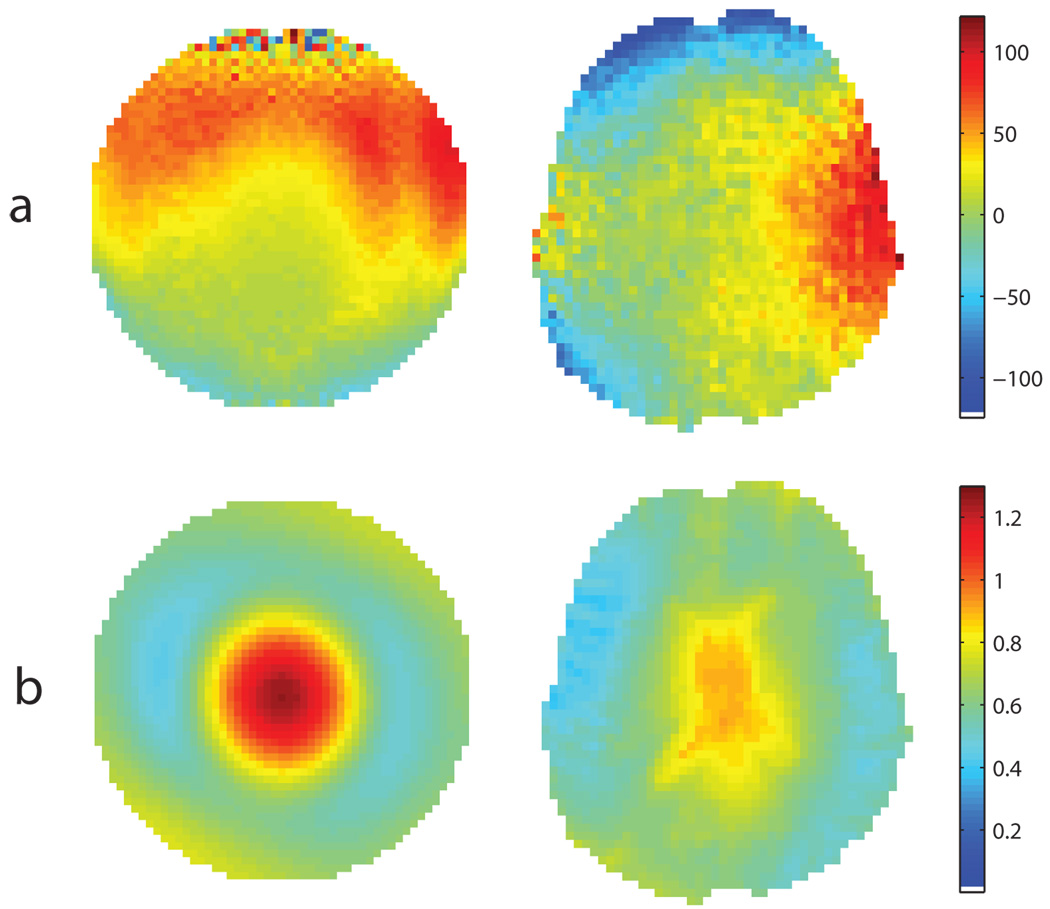
Figure 1.

ΔB₀ (row a) and $B_1^{+}$ (row b) maps for the central axial slice of a phantom and the human brain at 7T. ΔB₀ values are reported in Hz while $B_1^{+}$ magnitude is indicated as a ratio to that of $B_{1,\text{nom}}^{+}.B_1^{+}$ maps are those obtained with the multi flip-angle technique (Eq. 1).

Static field variations (ΔB₀) were mapped via a 3D spoiled GRE sequence with a double-echo acquisition (ΔT_E = 0.5 ms). Frequency offsets for all voxels were then calculated from the difference in magnetization phase at the two echo times (ΔB₀ = Δϕ/(2πΔT_E)). The value of ΔT_E was chosen short enough that no phase wrapping existed in the phase difference data and that T₂ effects were minimized but long enough that phase differences remained large compared to the noise in the phase images. Although the respective T_R and α₀ values of 5.3 ms and 10° resulted in considerable T₁-weighting in the magnitude images, the phase data, and therefore the ΔB₀ measurements, did not reflect tissue boundaries (see Fig. 1a). Geometric imaging parameters were set identically to those of the AFI sequence such that corresponding measurements of ΔB₀ and α/α₀ were collected for all voxels in the 3D volume. Fig. 2 shows ΔB₀ and corresponding AFI measurements throughout the spherical phantom and throughout the volume of the brain approximately superior to the red nucleus. Regions inferior to the midbrain are not included in Fig. 2 since reduced coil sensitivity in the area significantly undermines the accuracy of AFI measurements. Central axial slices of phantom and in vivo ΔB₀ maps are presented in Fig. 1a above the corresponding multi flip-angle $B_1^{+}$ data.

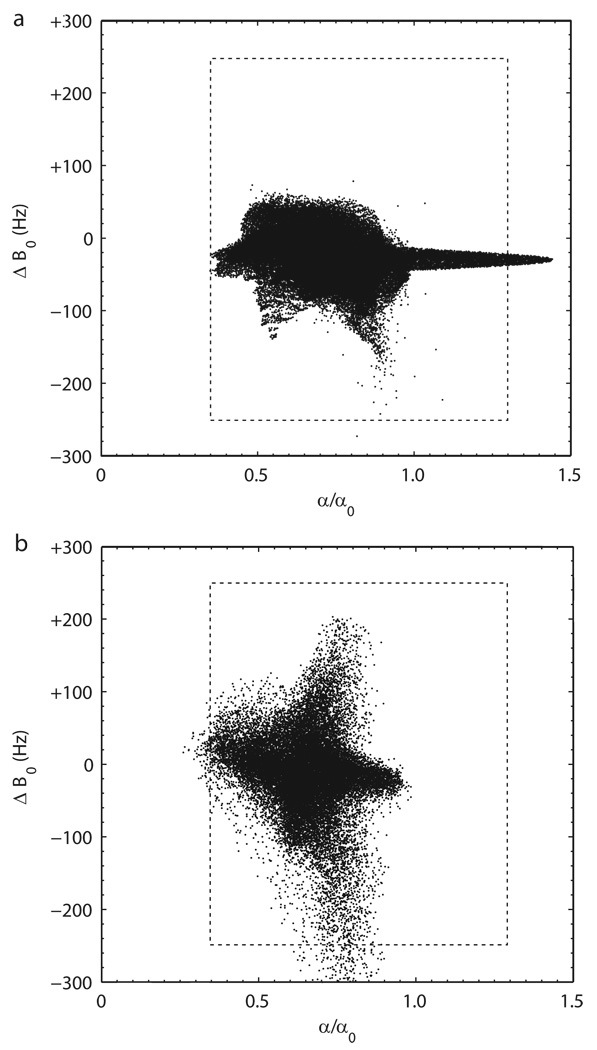
Figure 2.

ΔB₀ values (y-axis) and corresponding actual flip-angle measurements (x-axis, given as the ratio of the actual flip angle α to the nominal flip angle α₀) throughout the volume of (a) a 17 cm dielectric spherical phantom and (b) the in vivo human cerebrum at 7T. Each point represents a single imaging voxel and the entire distribution is plotted on the same coordinate system in which the composite pulses of this study are optimized. These data were used in selecting the ranges of $B_1^{+}$ and ΔB₀ values (indicated by dashed boxes) to be targeted by the optimized pulses.

2.2. $B_1^{+}-\mathrm{\Delta }{B}_0$ grids

The next step in pulse design is the designation of a parameter space representing the ranges of the possible combinations of the $B_1^{+}$ and ΔB₀ values for which pulses are to be optimized (9; 16; 17). A target flip-angle map is generated by specifying the desired flip angle at each point in the $B_1^{+}-\mathrm{\Delta }{B}_0$ space. In the subsequent optimizations of this study, uniform flip angles of 30°, 60°, 90°, and 180° were targeted over the entire parameter space. For all examples presented in this work, respective $B_1^{+}$ and ΔB₀ ranges of 0.35 – 1.30 and ±250 Hz were selected to represent typical variations throughout the human cerebrum and the spherical phantom at 7T (Fig. 2). Selected ranges reflect only an approximation to the total field variations of the brain and phantom but include the large majority of data points. $B_1^{+}$ and ΔB₀ ranges were respectively discretized into 20 and 21 evenly-spaced values, resulting in a grid of 420 points, a $B_1^{+}/B_{1,\text{nom}}^{+}$ step size of 5%, and a ΔB₀ step size of 25 Hz. An odd number of ΔB₀ steps was selected so that the on-resonance response of the pulse could be specifically monitored. The chosen level of $B_1^{+}$ and ΔB₀ discretization reflects a compromise between the desired response of the pulse and the computing time associated with the optimization, and the practical validation of a given $B_1^{+}-\mathrm{\Delta }{B}_0$ grid comes with evaluating the experimental performance of the resulting optimized pulse.

2.3. Anatomy of optimized composite pulses

Prior to optimization, the basic structure of the amplitude and phase modulation waveforms must be defined. All pulses considered here are a composite of block-shaped sub-pulses executed in immediate succession with the amplitude and phase of each sub-pulse being subject to numerical optimization. Designations of the number (N_s) and duration (Δt_s) of sub-pulses, as well as the maximum and minimum allowed RF amplitudes, are prerequisites to pulse optimization. These choices effectively fix the number of free parameters and their constraints for the numerical optimization. Composite pulses with N_s = 16, 32, 48, 64, 80, 96, 112, and 128 were generated. In each case, Δt_s values were fixed to 6.4, 12.8, 19.2, 32.0, 64.0, 128.0, 192.0 and 320.0 µs, thus yielding a total of 64 optimized pulses for each target flip angle. The time increment of 6.4 µs, of which all sub-pulse durations are common multiples, reflects a typical electronics dwell time on commercial human MR scanners (i.e., the smallest time increment by which the output of the RF amplifier can be updated). Maximum and minimum parameter constraints were respectively set to 0 and 15 µT for sub-pulse amplitude and ±π for sub-pulse phase. The maximum amplitude of 15 µT was chosen in accordance with typical performance limits on commercial RF coils in practical imagers.

2.4. Optimization of composite pulses

Routines were written in Matlab to optimize the sub-pulse amplitudes A = {A₁, A₂,…, A_k} and phases ϕ = {ϕ₁, ϕ₂,…, ϕ_k} of composite pulses via minimization of the function

$${\delta }_{\alpha }(\mathbf{A},\varphi )=\frac{1}{\mathit{\text{mn}}}{\displaystyle \sum _{i,j=1}^{m,n}\left|\frac{{\alpha }_{i,j}^S(\mathbf{A},\varphi )-{\alpha }_{i,j}^T}{{\alpha }_{i,j}^T}\right|,}$$ (2)

where i is the $B_1^{+}$ index on the $B_1^{+}-\mathrm{\Delta }{B}_0$ grid, j is the ΔB₀ index on the $B_1^{+}-\mathrm{\Delta }{B}_0$ grid, and α is the flip angle given by cos⁻¹ (M_z/M₀) with S and T denoting simulated and target values. The value of function δ_α represents the average deviation of simulated flip angles from the target flip angle over the entire $B_1^{+}-\mathrm{\Delta }{B}_0$ grid and is expressed as a fraction of the target flip angle. With the goal of finding a minimum of Eq. 2, the non-linear constrained minimization algorithm (18; 19) (Matlab function fmincon) iteratively calculates a quasi-Newtonian estimate of the Hessian of the Lagrangian defined by the second partial derivatives of Eq. 2 with respect to the k amplitudes and k phases of the RF waveform. The algorithm is seeded by a composite pulse in which the k amplitudes and phases conform to an even probability distribution within the prescribed limits of 0–15 µT and ±π rad, respectively. A termination condition is satisfied if the minimization algorithm fails to decrease the value of δ_α by at least a factor of 10⁻⁶ over the course of a single iteration. The phase of the magnetization is not considered in the cost function, since phase is not crucial to pulse performance. In the context of volume excitation, phase must only be a smoothly and slowly varying function of $B_1^{+}$ and ΔB₀ so as to avoid intravoxel dephasing. After the pulse design process, variations in phase were examined across the $B_1^{+}-\mathrm{\Delta }{B}_0$ grid to ensure minimal impact on the resulting signal.

Although the indices of ${\alpha }_{i,j}^T$ signify that composite pulses for which target flip-angles vary across the $B_1^{+}-\mathrm{\Delta }{B}_0$ grid could be designed without modification of the cost function (Eq. 2), each of the pulse compositions described in Section 2.3 was optimized with target flip angles on the $B_1^{+}-\mathrm{\Delta }{B}_0$ grid uniformly set to 30°, 60°, 90°, and 180° as described in Section 2.2. A subset of four optimized pulses (see Fig. 6) was selected for explicit comparison with block-shaped and adiabatic pulses with equivalent nominal flip angles.

Figure 6.

The ratio of actual to nominal flip angle as simulated on the 20 × 21 $B_1^{+}-\mathrm{\Delta }{B}_0$ optimization grid (columns 1, 3, and 5) along with RF amplitude and phase modulation waveforms (columns 2, 4, and 6). Columns 1 and 2 are maximum-bandwidth block pulses; columns 3 and 4 are BIR-4 pulses (ΔT = 4.096 ms); columns 5 and 6 are select optimized composite pulses (ΔT = 4.096 ms); rows correspond to different nominal flip angles (indicated at left). Maps reflect the on-resonance $B_1^{+}-\text{insensitivity}$ of BIR-4 and optimized pulses while optimized pulses result in significantly improved off-resonance behavior.

2.5. Maximum-bandwidth block pulses

The central lobe of the frequency spectrum of a block-shaped pulse has a bandwidth inversely proportional to the pulse duration; therefore, block pulses can affect a range of ΔB₀ offsets limited only by the minimum possible pulse duration. The flip-angle (α) of a block pulse is determined solely by the pulse amplitude (A) and duration (ΔT) such that

$$\alpha =2\pi \gamma {\displaystyle {\int }_0^{\mathrm{\Delta }T}\left|B_1^{+}\right|\mathit{\text{dt}}=2\pi \gamma A\mathrm{\Delta }T,}$$ (3)

with γ = 42.57 MHz/T (for hydrogen), hence a block pulse with the largest possible bandwidth can be determined by choosing the shortest ΔT given the maximum allowed value of A (A_max = 15 µT) and the desired flip-angle (α₀). Parameters for all block pulses in this study were chosen according to this condition of maximum bandwidth while simultaneously requiring ΔT to be an integer multiple of the electronics dwell time (d = 6.4 µs). The integer number of dwell times (N_d) in a maximum-bandwidth block pulse is then uniquely given by

$$N_d=\text{ceil}\left(\frac{{\alpha }_0}{2\pi \gamma A_{\text{max}}d}\right),$$ (4a)

where ceil denotes the operation of rounding to the next highest integer. Actual values of A and ΔT were then defined via the relations

$$\mathrm{\Delta }{T}_{\text{actual}}=N_{d}d$$ (4b)

and

$$A_{\text{actual}}=\frac{{\alpha }_0}{2\pi \gamma \mathrm{\Delta }{T}_{\text{actual}}}.$$ (4c)

Using this protocol, block pulses serving as metrics for the performance of optimized pulses were generated for α₀ values of 30°, 60°, 90°, and 180°.

2.6. $B_1^{+}-\text{insensitive}$ adiabatic pulses

Four-part $B_1^{+}-\text{insensitive}$ rotations (BIR-4) are composites of four adiabatic pulse segments. These pulses are capable of producing arbitrary flip angles and have been shown to improve flip-angle uniformity in the context of volume (non-selective) excitation (4; 5); therefore, BIR-4 pulses provide a suitable basis for comparison when evaluating the performance of the optimized composite pulses produced in this study. Flip-angle maps for 4.096 ms BIR-4 pulses with nominal flip angles of 30°, 60°, 90°, and 180° were simulated for specific comparison with the subset of four 4.096 ms optimized pulses subject to additional analysis in Section 3.2. Simulation of the Bloch equations (Section 2.8) was carried out in an identical manner to that of optimized pulses; however, BIR-4 pulses were divided into as many d = 6.4µs block-shaped sub-pulses as possible (n = 640) given the total pulse duration (ΔT = 4.096 ms). This reflects the typical way pulses with continuous waveforms are executed digitally on an amplifier for which d = 6.4µs. BIR-4 amplitude and frequency modulations were designated according to Staewen et al. (4), with A_max = 15 µT and a frequency sweep of ±250 Hz.

2.7. Average power and minimum T_R

The specific context in which a given RF pulse is implemented usually dictates the optimal value of T_R, thus providing a restriction on the average power (P̄) of the RF excitation. To maintain generality, P̄ was therefore not directly incorporated into the design of the optimized pulses; however, P̄ was indirectly limited by the maximum allowed RF amplitude and fixed duration of each pulse. With average power calculated as

$$\overline{P}=\frac{1}{\mathrm{\Delta }T}{\displaystyle {\int }_0^{\mathrm{\Delta }T}{\left|B_1^{+}\right|}^2\mathit{\text{dt}}}$$ (5a)

for a pulse of length ΔT, practical limitations associated with RF power of each pulse were quantified by calculation of a minimum value of T_R via the relationship

$$T_{R,\text{min}}=\frac{C\overline{P}\mathrm{\Delta }T}{{\text{SAR}}_{\text{max}}},$$ (5b)

where C = 1.41 W/kg/µT² is a coil-specific constant representing the rate of energy dissipation of 298 MHz radiation in human brain tissue, SAR_max is set to the value of 3 W/kg corresponding to the SAR threshold for significant risk in the human head according to the Food and Drug Administration (FDA) (20), and ΔT is the time duration of the given RF pulse. T_R,min therefore represents the minimum repetition time for a pulse sequence in which the optimized excitation is the only RF component (such as in a GRE imaging experiment or a pulse-and-acquire spectroscopy experiment). Values are unique to both the magnitude of the static field and the specific volume head coil used in this study but may serve as useful guidelines when using similar coil configurations at 7T.

2.8. Simulation of the Bloch equations

Magnetization response to a composite of k sub-pulses with constant phase and amplitude was modeled as a series of rotations (R_j, where j = 1,…, k), each representing the operation due to a relaxation-independent form of the Bloch equations (21). With each rotation corresponding to one of the k individual sub-pulses, the collective operation of all components of a composite pulse is described by

$${\mathbf{M}}^f=R_k{R}_{k-1}{R}_{k-2}\dots R_1{\mathbf{M}}^0,$$ (6)

where M⁰ is the magnetization vector preceding the pulse and M^f is the magnetization vector following the pulse. For all cases in this study, the initial magnetization was taken to be in the z-direction such that the components of M⁰ were given by $(M_x^0,M_y^0,M_z^0)=(0,0,1)$.

2.9. Phantom experiments

A spoiled, 3D, echo-planar, GRE sequence (T_R = 500 ms, T_E = 5 ms, 3 mm isotropic voxels, EPI factor 3) was used to image the entire volume of the 17 cm FBIRN phantom with the same hardware configuration described in Section 2.1. This experiment was carried out with the 4.096 ms excitation pulses shown in the first row of Fig. 6: a 30° maximum-bandwidth block pulse, a 30° BIR-4 pulse, and a 30° optimized composite pulse. For each excitation pulse, data were acquired both for the case of second-order static field volume shimming and the case in which all static field shimming gradients were turned off. Respectively, these ΔB₀ shimming scenarios allowed for the evaluation of excitation pulse performance when (1) in-slice static field variations were similar to those found in the well-shimmed human brain at 7T (e.g., compare the in vivo ΔB₀ map of Fig. 1a with the unshimmed phantom ΔB₀ map of Fig. 12) and when (2) in-slice static field variations were minimal.

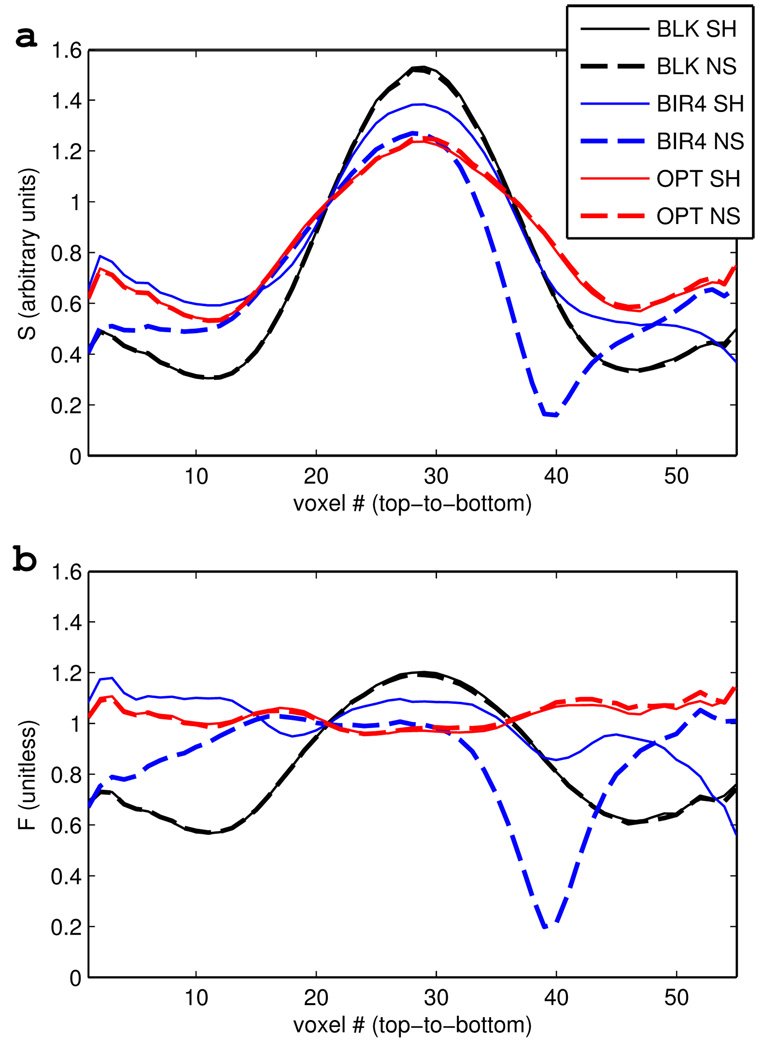
Figure 12.

Vertical line profiles through the images (a) and F maps (b) found in Fig. 11, with orientation of the line corresponding to the dashed white line in the first image of Fig. 11. Voxels are numbered from top to bottom, corresponding to the direction in which the static field predominantly increases (see field maps in Fig. 1). The case of static field shimming (SH) is indicated by solid lines while the case of no static field shimming (NS) is indicated by dashed lines. Comparison of solid and dashed lines of a given color reveals the superior off-resonance stability of maximum-bandwidth block (black) and optimized composite (red) pulses as compared to the BIR-4 pulse (blue). Of the three pulses, the optimized composite pulse is closest to producing the ideal combination of B₀- and $B_1^{+}-\text{insensitivity}$, which would be characterized in (b) by both solid and dashed lines having the constant value F(α) = 1.

Data for calculation of the parameter β (Eq. 1) in a 2D axial slice corresponding to the central slice of the 3D volume were obtained according to the protocol described in Section 2.1. Since the steady-state signal (S_ss) can be expressed as a product of $B_1^{-}-\text{ and }{B}_1^{+}-\text{dependent}$ factors β and F such that

$$S_{\mathit{\text{ss}}}=\beta F,$$ (7a)

with F being explicitly given by

$$F(\lambda ,T_1,T_2^{*};{\alpha }_0,T_R,T_E)=\frac{|\text{sin}(\lambda {\alpha }_0)|(1-e^{-T_R/T_1})e^{-T_E/T_2^{*}}}{1-|\mathit{\text{cos}}(\lambda {\alpha }_0)|e^{-T_R/T_1}},$$ (7b)

and

$$\lambda =B_1^{+}/B_{1,\text{nom}}^{+},$$ (7c)

central-slice images from the 3D acquisitions were divided by the calculated map of β. This procedure resulted in six maps of F (three excitation pulses with two static field shimming schemes) which were then compared in terms of uniformity. To avoid signal scale discrepancies arising from the fact that S_ss values were acquired with a 3D sequence while β values were calculated from 2D sequence data, S_ss and β were normalized prior to the calculation of F such that S_ss = β = 1 for voxels with λ = 1.

3. Results

3.1. Optimized pulses

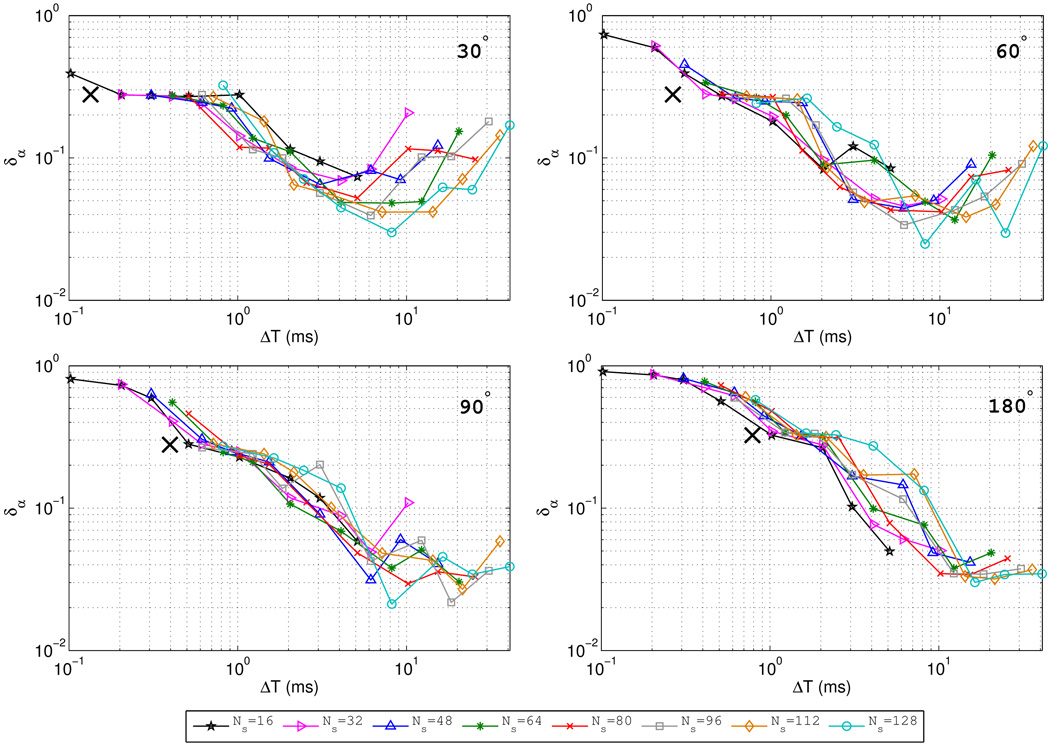
The 4 flip angles (30°, 60°, 90°, 180°), 8 N_s values (16, 32, 48, 64, 80, 96, 112, 128), and 8 Δt_s values (6.4, 12.8, 19.2, 32.0, 64.0, 128.0, 192.0, 320.0 µs) for which composite pulses were optimized resulted in a total of 256 composite pulses produced for this study. In Fig. 3, δ_α values (Eq. 2) for each of these pulses are plotted as a function of total pulse duration (ΔT) for all values of N_s. In Fig. 4, the same information is presented but organized according to pulses with a given Δt_s. While these data indicate the sensitivity of pulse performance to the design parameters N_s and Δt_s, they firstly illustrate the radical improvement in flip-angle uniformity that is possible with optimized composite pulses as compared to maximum-bandwidth block pulses (the performance of which is indicated by a ‘×’ symbol in each sub-plot of Figs. 3 and 4). In general, composite pulse performance clearly increases (i.e., δ_α decreases) with increasing ΔT. One obvious exception to this trend occurs for 30° pulses with ΔT ≳ 5 ms. For most values of N_s in Fig. 3, δ_α clearly reaches a minimum value when ΔT is between 2 and 10 ms. Smaller N_s values lead to δ_α minima at the lower end of this range while larger N_s values lead to δ_α minima at the upper end of this range. Similar behavior in the ΔT -dependence of δ_α can be seen to a lesser degree as α₀ increases. Examination of δ_α vs. ΔT in light of Δt_s (Fig. 4) reveals that shorter Δt_s pulses rather consistently provide increased performance when ΔT is long (≳ 5 ms). For shorter ΔT, Δt_s appears to make little difference in pulse performance.

Figure 3.

Cost function value (δ_α, Eq. 2) as a function of overall pulse duration (ΔT), with each sub-plot corresponding to a different target flip angle as indicated in the upper right corner. Line colors indicate optimized pulses with different numbers of sub-pulses (N_s). The ‘×’ symbol indicates performance of maximum-bandwidth block pulses for each flip angle. For short pulse durations, optimization tends to result in similar pulse performance for the various values of N_s due to the limited available RF power. Longer pulses tend to result in better pulse performance but with δ_α depending more noticeably on the value of N_s.

Figure 4.

Cost function value dependence on ΔT as in Fig. 3 but with line colors corresponding to optimized pulses with different sub-pulse durations (Δt_s). As in Fig. 3, the performance of shorter pulses is similar for the various values of Δt_s due to the limited available RF power. Longer pulses tend to result in better pulse performance with δ_α often being lower for smaller values of Δt_s. This likely reflects the reduced bandwidth associated with longer Δt_s values.

Absolute minimum values of δ_α are found at the following combinations of N_s and Δt_s, respectively: 128 and 64 µs for 30°, 60°, and 90° pulses; 128 and 128 µs for 180° pulses. By this measure alone, performance of pulses appears limited simply by N_s, while the ideal value of Δt_s depends on both the optimal bandwidth of the component sub-pulses and the available RF power for the entire composite pulse. From this, it can be inferred, given the objective of the optimization, that the ideal composite pulse would have the maximum value of N_s within the limits of the optimization algorithm and the shortest value of Δt_s as long as ΔT is sufficiently long. While these findings are consistent with the optimal control studies of Skinner et al. (22), further interpretation of the N_s, Δt_s, and ΔT dependencies of δ_α are saved for the discussion section.

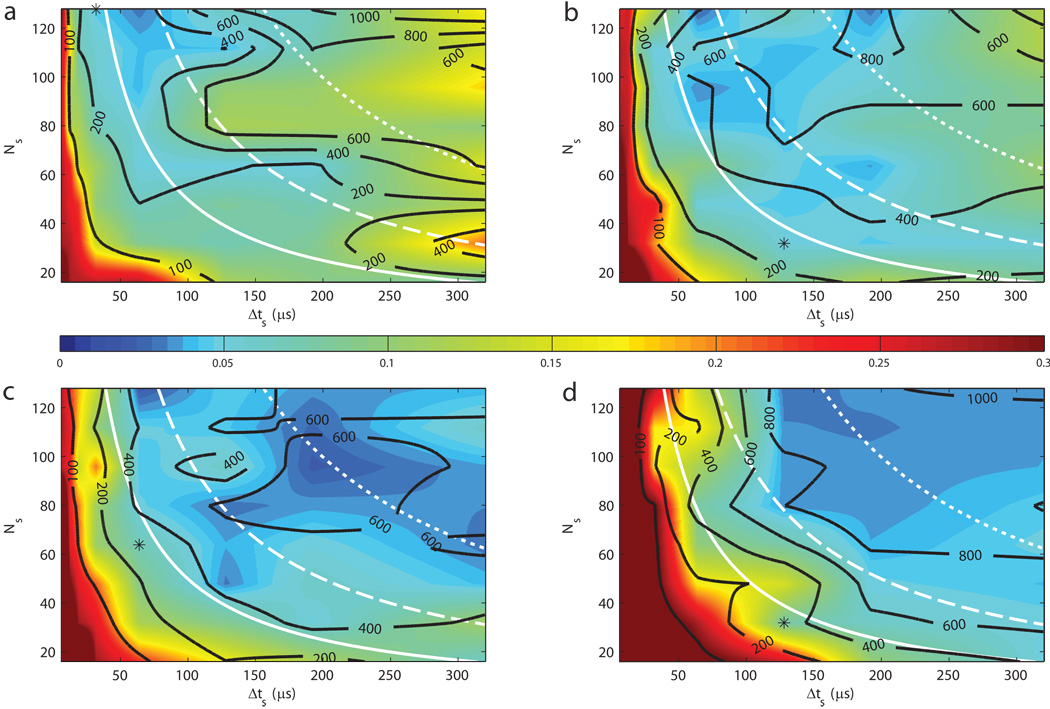
Based on a 2D linear interpolation of the data in Figs. 3 and 4, Fig. 5 provides a visual representation of pulse performance in the near-continuous parameter space of N_s vs. Δt_s. Using a linearly weighted average of the four nearest data points, both δ_α and T_R,min data for each of the four flip angles were interpolated from an 8 × 8 (N_s × Δt_s) grid to a 128 × 3136 grid resulting in respective interpolated parameter step sizes of 1 sub-pulse and 0.1 µs. The value of composite pulses is again obvious given that all colors other than the darkest red in Fig. 5 signify an improvement in flip-angle uniformity as compared to maximum-bandwidth block pulses. In the context of Fig. 5, the strong correlation between values of δ_α (colors), T_R,min (black contours), and ΔT (white lines) also becomes apparent. These relationships emphasize that little improvement in flip-angle uniformity can be achieved when the available RF power is too limited. Such a power threshold is, however, noticeably reduced for smaller α₀. For example, 30° composite pulses can drastically improve flip-angle uniformity for T_R values less than 200 ms while 180° pulses offer significantly reduced benefits under the same restriction. Conversely, the regions in which pulses perform the best don’t necessarily correlate well with regions of high P̄ (i.e., highest T_R,min values). This effect is most easily observable for the lower α₀ pulses (i.e., 30° and 60°). For example, the lowest δ_α values for 30° pulses occur in the T_R,min range of 200 – 400 ms. Similarly, there is no significant advantage to be gained in selecting 60° pulses with T_R,min > 400 ms, and, in fact, many such pulses perform significantly worse than their lower P̄ counterparts.

Figure 5.

Results of composite pulse optimizations interpolated across the 2D parameter space of sub-pulse duration (Δt_s) and the number of sub-pulses (N_s) with sub-figures (a), (b), (c), and (d) corresponding respectively to α₀ values of 30°, 60°, 90°, and 180°. Color scale indicates the minimized function value (δ_α); black contours give corresponding minimum repetition times (T_R,min) in milliseconds; solid, dashed, and dotted white lines are isocontours of total pulse duration (ΔT) at 5, 10, and 20 ms, respectively. Black asterisks indicate the values of N_s and Δt_s for the optimized pulses specifically compared to block and BIR-4 pulses in Figs. 6, 7, and 8 and Table 1. Data indicate that the lowest values of δ_α migrate toward the top right corner of the parameter space with increasing α₀—thus reflecting increased power requirements. At lower α₀, δ_α minima tend to be found in the upper left, suggesting that the maximum number of short-duration sub-pulses yields the best performance given that a certain power threshold is satisfied.

3.2. General performance comparison of select optimized pulses to maximum-bandwidth block pulse and BIR-4 counterparts

In order to facilitate comparison of optimized composite pulses to block and BIR-4 pulses of the same α₀, a subset of four optimized pulses was identified according to the practical criterion of ΔT = 4.096 ms. Given this total duration, the composite pulse with the lowest δ_α value was selected for each α₀. The respective N_s and Δt_s values for these pulses are 128 and 32 µs for 30°, 64 and 64 µs for 90°, and 32 and 128 µs for both 60° and 180° and are indicated by asterisks in Fig. 5. Simulated flip angles on the $B_1^{+}-\mathrm{\Delta }{B}_0$ optimization grid are shown in Fig. 6 for these four selected composite pulses along with the optimized amplitude and phase modulation waveforms. Also given in this figure are the corresponding simulated results for maximum-bandwidth block pulses and 4.096 ms BIR-4 pulses. Upon visual inspection of Fig. 6, optimized composite pulses appear to outperform the other pulse types in terms of flip-angle uniformity but also quantitatively demonstrate their increased performance when normalized mean (ᾱ/α₀), mean-normalized standard deviation (σ_α/ᾱ), and coefficient of variations (c_v = σ_α/ᾱ) are compared (Table 1). Depending on the nominal flip angle, composite pulses show a ~ 4-fold reduction in δ_α values as compared to block pulses. Block pulses exhibit the expected linear relationship between actual flip angles and $B_1^{+}$ field strength (Eq. 3) while BIR-4 pulses demonstrate strong $B_1^{+}-\text{insensitivity}$ for static field strengths very close to resonance. It is in areas of off-resonance, especially at low $B_1^{+}$ field strengths, that composite pulses designed in the manner of this study offer a distinct advantage over their adiabatic counterparts. Although the colors in Fig. 6 are thresholded at δ_α = 1.3, BIR-4 pulses actually result in δ_α values as high as 5.0 (i.e., α is 500% of α₀) for α₀ = 30°. This fact is reflected in the large standard deviation for this BIR-4 pulse as simulated on the $B_1^{+}-\mathrm{\Delta }{B}_0$ grid (Table 1).

Table 1.

Quantitative comparison of pulses featured in Figs. 6 and 7. Nominal flip angle (α₀) and pulse type are indicated in columns 1 and 2. Columns 3 – 5 show the mean flip angle (normalized to α₀), standard deviation (normalized to the mean), and coefficient of variation for three contexts in which pulse performance was evaluated: the $B_1^{+}-\mathrm{\Delta }{B}_0$ optimization grid, the central axial slice through a spherical phantom, and the central axial slice of the human brain. Column 6 gives the minimum repetition time (T_R,min), while columns 7 and 8 respectively show the average power (P̄) and the ratio of P̄ to the average power of the corresponding block pulse (P̄_BLK) with the same α₀.

α0	pulse	grid	phantom	brain	TR,min (ms)	P̄ (µT2)	P̄/P̄BLK
	BLK	0.82 ± 0.28(±35%)	0.67 ± 0.17(±26%)	0.62 ± 0.11(±18%)	13	7	1.0
30°	BIR-4	1.31 ± 0.86(±66%)	0.94 ± 0.03(±4%)	0.93 ± 0.08(±8%)	382	198	29.4
	OPT	0.98 ± 0.07(±8%)	1.00 ± 0.03(±3%)	0.99 ± 0.05(±5%)	274	142	21.1
	BLK	0.82 ± 0.28(±35%)	0.67 ± 0.17(±26%)	0.62 ± 0.11(±18%)	27	14	1.0
60°	BIR-4	1.01 ± 0.31(±30%)	0.95 ± 0.03(±3%)	0.92 ± 0.07(±7%)	382	198	14.1
	OPT	0.98 ± 0.08(±8%)	1.00 ± 0.03(±3%)	1.01 ± 0.05(±5%)	261	136	9.7
	BLK	0.82 ± 0.28(±35%)	0.67 ± 0.17(±26%)	0.62 ± 0.11(±18%)	40	21	1.0
90°	BIR-4	0.92 ± 0.16(±17%)	0.95 ± 0.03(±3%)	0.92 ± 0.07(±8%)	382	198	9.6
	OPT	0.97 ± 0.10(±10%)	1.01 ± 0.07(±7%)	0.96 ± 0.09(±10%)	256	132	6.4
	BLK	0.82 ± 0.28(±35%)	0.67 ± 0.17(±26%)	0.62 ± 0.11(±18%)	80	42	1.0
180°	BIR-4	0.75 ± 0.13(±18%)	0.92 ± 0.03(±4%)	0.86 ± 0.10(±12%)	382	198	4.8
	OPT	0.92 ± 0.10(±11%)	0.93 ± 0.05(±5%)	0.93 ± 0.06(±6%)	344	179	4.3

Optimized pulse phase modulations in Fig. 6 have been unwrapped from the ±π rad constraints of the optimization according to the Matlab function unwrap in order to emphasize the tendency of optimized modulation functions to be characterized by a frequency sweep coupled with a near-constant amplitude. A frequency sweep can be described in general terms of phase modulation as a smoothly varying and cyclic function. Such behavior in the amplitude and phase modulation is evidence of the quasi-adiabatic nature of the optimized composite pulses. In other words, pulses appear to be largely functioning by way of a gradual change in the direction of the effective field $({\overrightarrow{B}}_{\text{eff}}={\overrightarrow{B}}_1^{+}+{\overrightarrow{\mathrm{\Delta }B}}_0)$ and a simultaneous spin-lock achieved through a high RF amplitude, although the adiabatic condition is, in general, not satisfied throughout the pulse. Similar phase modulation in the context of composite pulses has been previously reported (10) while the strongly modulated pulses of Boulant et al. (11; 12) appear to implicitly incorporate similar behavior into their design.

3.3. Phantom and in vivo simulations of maximum-bandwidth block, BIR-4, and optimized composite pulses

Simulated flip-angle maps (normalized to α₀) are shown in Fig. 7 for the single axial slices of both the spherical phantom and the in vivo human brain. These simulations are based on the 7T multi flip-angle $B_1^{+}$ maps and the corresponding slices of the 3D ΔB₀ maps described in Section 2.1. Flip-angle maps for maximum-bandwidth block pulses are characterized by a central hot spot due to the combination of attenuation and constructive interference of the $B_1^{+}$ field and the flip angle’s linear dependence on the time-integrated magnitude of this field (1). This effect is somewhat reduced in vivo due to geometrical asymmetry and the resulting incoherences in the transmitted field. BIR-4 pulses do not rely on a linear relationship between flip angle and $\int B_1^{+}\mathit{\text{dt}}$ but instead on the process of adiabatic spin-locking. The resulting improvement in flip-angle uniformity is dramatic when compared to that of the block pulse. In the phantom, static field shimming appears sufficient such that the undesirable off-resonance behavior of BIR-4 pulses seen on the $B_1^{+}-\mathrm{\Delta }{B}_0$ grid (Fig. 6) does not effect flip angles in the central axial slice. In this context, performance of BIR-4 and optimized composite pulses is remarkably similar, with BIR-4 pulses even outperforming optimized pulses in terms of flip-angle c_v values at 90° and 180° (Table 1). In vivo simulation, however, begins to emphasize the significant advantage of the optimized pulses. In the in vivo case, with B₀ shimming being more challenging, BIR-4 pulses result in much reduced flip-angle uniformity as compared to the phantom. In particular, it is the low-$\text{low}-B_1^{+}$ off-resonance areas (roughly corresponding to the right side and upper left of the axial brain slice) in which flip-angles deviate the most (compare column 5 of Fig. 7 to column 2 of Fig. 1). Although optimized pulse performance also suffers somewhat in the lowest $B_1^{+}$ regions, these pulses are not as susceptible to variations in the static field. The in vivo results of Table 1 indicate significant improvements in flip-angle mean and c_v for optimized pulses, with the lone exception being c_v for the 90° pulse. It is noteworthy that such increases in performance as compared to BIR-4 pulses can be attained while simultaneously reducing P̄ (or equivalently, T_R,min) values by an average of 23% (Table 1).

Figure 7.

Flip-angle maps (expressed as a ratio of actual to nominal values) simulated in the central axial slice of a 17 cm phantom (left side) and the human brain (right side) for block (BLK), BIR-4, and optimized composite (OPT) pulses. Simulations are based on multi flip-angle $B_1^{+}$ and 3D ΔB₀ maps acquired at 7T. Colors denote flip angles normalized to the nominal values indicated at the beginning of each row. Optimized and BIR-4 pulses show superior flip-angle uniformity to that of block pulses while in vivo simulations highlight the increased susceptibility of BIR-4 pulses to off-resonances. Optimized pulses appear to combine desirable features of the other pulse types—the high effective bandwidth of the block pulses and the $B_1^{+}-\text{insensitivity}$ of BIR-4 pulses.

Although $B_1^{+}$ field maps may be less accurate than the multi flip-angle data set used in Fig. 7, 3D AFI data were used to simulate flip-angle response to 30° block, BIR-4, and optimized composite pulses in eight adjacent axial slices in the brain (Fig. 8). These results are convincing in their illustration of the improvements possible with optimized pulses. Inferior slices in this stack are proximal to many air-tissue interfaces (such as the frontal sinus) with magnetic susceptibility changes giving rise to sharp variations in B₀. As expected due to its large effective bandwidth, the block pulse appears least affected by these off-resonances but nonetheless suffers from dramatic $B_1^{+}-\text{induced}$ flip-angle variations. The BIR-4 pulse drastically improves flip-angle uniformity in the superior slices and the central regions of inferior slices; however, undesirable off-resonance effects are obvious in most slices and especially so in the inferior-most regions. In fact, the outline of the shim volume (a cuboid) is visibly recognizable in the central slices (Fig. 8, row 2, columns 1–5), again emphasizing that the BIR-4 pulse performs well only under an ideal B₀ shimming scenario. The optimized composite pulse is considerably more resilient to static field variations than the BIR-4 pulse, with undesirable flip angles appearing in much more confined regions of the inferior-most slices. In fact, the optimized pulse decidedly outperforms the block and BIR-4 pulses in terms of flip-angle uniformity across all ten slices presented in Fig. 8 (compare statistical measures beneath each sub-plot).

Figure 8.

Flip-angle maps simulated in 8 axial slices of the brain for the 30° block, BIR-4, and optimized composite pulses shown in Fig. 6. Simulations are based on 3D ΔB₀ and AFI maps acquired at 7T. Results indicate improved on-resonance flip-angle uniformity but lower effective bandwidth of BIR-4 and optimized pulses as compared to block pulses. Relative to optimized pulses, increased sensitivity of BIR-4 pulses to variations in the static field is apparent in all slices. Below each sub-figure are the nomalized mean, the mean-normalized standard deviation, and the coefficient of variation for the simulated flip-angle distributions in the given slice.

3.4. Time-evolution and off-resonance simulations of BIR-4 and optimized pulses

In addition to simulated flip-angle maps following the execution of the pulse, the performances of 30° BIR-4 and optimized pulses were investigated by simulating the time evolution of the magnetization throughout the pulse duration as well as the off-resonance behavior out to ±5 kHz. Plots of α vs. time are shown for BIR-4 and optimized pulses in Fig. 9 for different combinations of $B_1^{+}$ and ΔB₀. Although the amplitude of fluctuations in α(t) are considerably larger for the BIR-4 pulse, the oscillatory behavior of α(t) shows some resemblances between the two pulse types. For example, local minima are apparent in the neighborhood of t = −1, 0, and +1 ms. Such similarities may be indicative of the quasi-adiabatic nature of the optimized pulse. The analytical design of BIR-4 pulses, relying on adiabatic manipulation of the magnetization, results in smooth and predictable changes in the magnetization with time. The optimized composite pulses were designed to produce uniform flip angles at the conclusion of the pulses with no regard for what happens along the way. For this reason, optimized pulses are free to take advantage of adiabatic spin-locking but only to the extent that best satisfies the minimization condition (Eq. 2). The α(t) curves of Fig. 9 are suggestive of such quasi-adiabatic behavior. This figure also clearly demonstrates the way in which magnetization vectors for BIR-4 and optimized pulses converge to the target flip angle at the end of the pulse, regardless of the $B_1^{+}$ and B₀ offsets. The one exception to this behavior is for the BIR-4 pulse when off-resonance at low $B_1^{+}$. This serves as a good example of the loss of adiabatic behavior responsible for the undesirable off-resonance effects illustrated in Figs. 6, 7, and 8.

Figure 9.

Flip angle as a function of time simulated for the 30° BIR-4 (a) and optimized composite (b) pulses of Fig. 6. Solid, dashed, dotted, and dash-dotted lines indicate flip-angle behavior at the $B_1^{+}/B_{1,\text{nom}}^{+},\mathrm{\Delta }{B}_0$ coordinates respectively given by (0.5,+150 Hz), (0.5, 0 Hz), (1.2, 0 Hz), and (1.2,+150 Hz). At the end time of the pulse, the four trajectories would ideally converge at the target flip-angle value of 30°. The objective of the optimization in this study is to design a composite pulse that simultaneously forces such behavior for all 420 points on the $B_1^{+}-\mathrm{\Delta }{B}_0$ grid. The lower effective bandwidth of BIR-4 pulses relative to optimized pulses is evident in the solid line of (a) which terminates at a flip angle more than twice the target value.

Terminal flip-angle values for the same BIR-4 and composite pulses of Fig. 6 are shown in Fig. 10 for ±5 kHz and nominal $B_1^{+}$. These data indicate qualitative similarities in the magnetization response to both BIR-4 and optimized pulses, again suggesting the quasi-adiabatic nature of the latter. Off-resonance data also emphasize that both pulse types (in their current form) are truly limited to volume excitations since large flip angles are produced very far from the target bandwidth.

Figure 10.

Nominal $B_1^{+}$, off-resonance behavior out to ±5 kHz for the (a) 30°, (b) 60°, (c) 90°, and (d) 180° BIR-4 (dashed lines) and optimized composite (solid lines) pulses of Fig. 6. Vertical dashed lines denote the ±250 Hz optimization region. At nominal $B_1^{+}$, both pulses show remarkably similar off-resonance behavior and are obviously unsuitable for slice-selection.

3.5. Phantom experiments

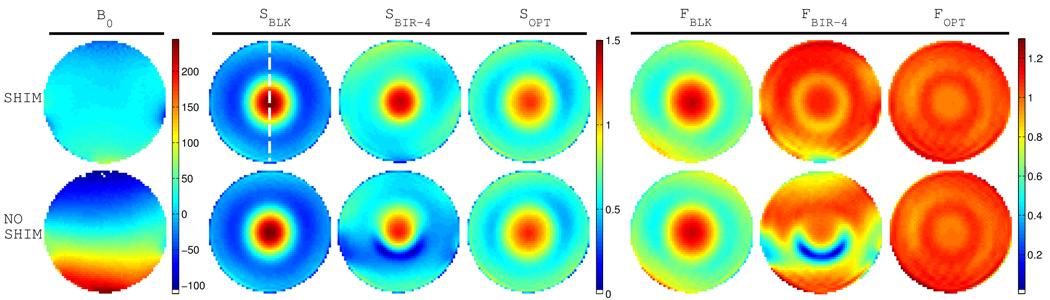
Results from phantom experiments using 30° excitation pulses in a 3D gradient echo sequence are shown in Fig. 11 with line profiles given in Fig. 12 and relevant statistical measures presented in Table 2. In the case of second-order static field shimming (first row of Fig. 11), the calculated maps of the $B_1^{+}-\text{dependent}$ factor F (Eq. 7b) are consistent with the phantom flip-angle map simulations presented in Fig. 7, thus lending further credibility to the other simulated results presented in this work. In experiment, both BIR-4 and optimized composite pulses perform very well in terms of the uniformity of F when static field shimming is applied. In contrast, the maximum-bandwidth block pulse results in highly $B_1^{+}-\text{dependent}$ values of F, as anticipated. In the case that the static field shimming gradients are turned off, the F maps in Fig. 11 indicate the sensitivity of the BIR-4 pulse to off-resonance effects and the insensitivity of both the maximum-bandwidth block pulse and the optimized pulse to the same changes in B₀. Thus, the optimized composite pulse combines the desirable qualities of the maximum-bandwidth block pulse and the BIR-4 pulse in that the resulting excitation is highly insensitive to variations in the both the static field and the transmitted RF field. Vertical line profiles for the images and F maps of Fig. 11 are given in Fig. 12 and provide a different perspective on the same results. The intensity profiles in Fig. 12a reflect the fact that $B_1^{+}-\text{insensitive}$ pulses still result in images with considerable intensity variations due to the inhomogeneous $B_1^{-}$ field associated with the receiving coil while Fig. 12b shows the component of the signal dependent on $B_1^{+}$ (i.e., F). A comparison of solid and dotted lines allows for an evaluation of off-resonance sensitivity for a given pulse type. In Table 2, the distributions of F values for each combinations of pulse type and B₀-shimming scheme are described quantitatively. When comparing c_v values, the optimized pulse can be seen to perform roughly twice as well as the BIR-4 pulse when B₀ shimming is applied and about four times better in the case of no B₀ shimming. The latter case more closely reflects anticipated performance in the human brain at 7T.

Figure 11.

Phantom signal intensity (S) from experiment and calculated steady-state $B_1^{+}-\text{dependent}$ factor (F in Eq. 7b) values for the cases of second-order static field shimming (first row) and no static field shimming (second row). Static field maps are shown in column 1, and S and F maps for the three pulse types are indicated at the top of the other columns. When static field shimming is active, the BIR-4 and optimized composite pulses result in significant improvement in flip-angle uniformity as compared to the block pulse. When no static field shimming is present (and B₀ variations are similar in range to that of the human brain at 7T), the BIR-4 pulse results in much reduced flip-angle uniformity while optimized pulse performance is similar to the case when static field shimming is applied. The dashed vertical line in the first image indicates the position of the line profiles plotted in Fig. 12.

Table 2.

Distribution statistics for the experimental phantom maps of the $B_1^{+}-\text{dependent}$ factor F found on the right side of Fig. 11. The mean of F, standard deviation of F, and the sc_v value are given for 30°, 4.096 ms maximum-bandwidth block (BLK), BIR-4, and optimized composite (OPT) pulses. In terms of the width of the distribution of F, the optimized pulse performs slightly better that BIR-4 pulse when ΔB₀ variations are minimal. When no B₀ shimming is applied, the optimized pulse demonstrates superior flip-angle uniformity.

ΔB0	BLK	BIR-4	OPT
SHIM	0.69 ± 0.16(±23%)	1.00 ± 0.09(±9%)	1.03 ± 0.05(±5%)
NO SHIM	0.69 ± 0.16(±23%)	0.83 ± 0.20(±24%)	1.04 ± 0.06(±6%)

4. Discussion

The results of this feasibility study into the applicability of numerically optimized composite pulses for 7T demonstrate the possibility of marked gains in flip-angle uniformity as compared to block and BIR-4 pulses. Simulations and phantom experiments straightforwardly signify improved off-resonance behavior of the optimized pulses relative to BIR-4 pulses and dramatically improved excitation homogeneity relative to block pulses. The optimized waveforms in their current form are implementable for volume excitation on commercial human MR systems and, although designed specifically for a volume head coil at 7T, can directly be used at other field strengths and for other coil/field configurations for which the $B_1^{+}$ field is highly inhomogeneous (e.g., surface coils or 3T torso imaging).

The optimized pulses of this study are specifically designed for arbitrary flip-angle volume excitation within the practical limits dictated by a commercial 7T MR imager. Comparisons of flip-angle uniformity between RF pulse classes (e.g., block, adiabatic, and optimized composite pulses) are complicated by the array of intended applications. For example, although emphasis in this analysis has been placed on comparison with BIR-4 pulses, it should be noted that the optimized composite pulses presented here do not in general result in plane rotations as achieved by BIR-4 pulses and, therefore, cannot be used for refocusing. For this application, composite pulses would have to be specifically designed by changing the minimization condition of Eq. 2 to include the reversal of one or both orthogonal transverse magnetization components. For the purposes of excitation and inversion, it would be useful for future studies to compare the flip-angle uniformity of optimized composite pulses to that of other $B_1^{+}-\text{insensitive}$ waveforms such as hyperbolic secant (3) and chirp (23) pulses within the context of 7T human imaging. Of particular interest would be a direct comparison with the offset-independent adiabaticity (OIA) representation of such pulses (24; 25). While some such pulses offer the advantages of high bandwidth and sharp frequency profiles thus making them potentially more suitable for spectroscopy and slice-selective imaging, composite pulses could be optimized via the methods of this study with slice-selection or high bandwidth being the primary objective. The performance of such pulse designs is presently unknown.

While the phase of the transverse magnetization is unconstrained in the optimization in order to increase the resulting flip-angle uniformity, phase should in general be monitored such that variations with respect to $B_1^{+}$ and ΔB₀ do not result in signal loss from intravoxel dephasing. While the experiments in this study (with 3 mm isotropic voxels) did not appear affected by magnetization phase variations, use of optimized composite pulses could potentially result in signal intensity fluctuations in regions where the static field changes rapidly with respect to voxel dimensions. Examples of scenarios that might lead to such conditions are the use of larger voxels, the presence of extreme magnetic susceptibility fluctuations, or the use of strong gradients for suppression of signal arising from beyond the imaging volume. In such scenarios, variations in the phase of transverse magnetization produced by optimized composite pulses may warrant further scrutiny.

In addition to demonstrating notable excitation uniformity in the context of 7T human brain imaging, data from the present study illuminate several ways in which the design process for composite pulses could be altered to produce further improvements for in vivo applications. The remainder of this discussion addresses the potential of data-driven alterations to composite pulse anatomy, the optimization grid, incorporation of SAR limits into the optimization algorithm, utilization of competing minimization strategies, and hardware modifications.

The performance of the optimized composite pulses relies on the combination of pulse parameters ΔT, N_s, and Δt_s in ways that are not always obvious. Perhaps the most straightforward dependence is the general trend of improved performance with increasing ΔT. Since optimized pulses tend to be characterized by high amplitudes sustained for large fractions of the pulse length, the dependence of performance on ΔT can be interpreted as a need for high average power of the total RF waveform. This idea is consistent with the adiabatic interpretation of magnetization behavior since adiabatic pulses utilize high RF amplitudes to maintain spin-locking conditions so that the direction of the effective magnetic field may be slowly varied by way of a phase or frequency sweep. As ΔT values increase, pulse performance also generally becomes more dependent on the parameters N_s and Δt_s, suggesting that a power threshold necessary for adiabatic behavior is satisfied. This effect does appear to be somewhat dependent on the target flip angle given that the minimum δ_α values in Figs. 3 and 4 favor higher ΔT values as the target flip angle is increased. When the influence of N_s is visible in the data, it is usually the case that higher N_s lead to increased pulse performance for a given ΔT, although individual exceptions can certainly be found. The value of Δt_s appears to have a more subtle influence on pulse performance, but shorter Δt_s do appear somewhat favorable when comparing pulses of a given length. The effects of Δt_s are likely related to the bandwidth of the individual sub-pulses and may influence results only slightly since all Δt_s investigated in this study correspond to bandwidths much larger than the target range of ΔB₀ values (e.g., the bandwidth of a 320 µs sub-pulse is ~ 3.1 kHz). Lastly, the bandwidth associated with the total pulse length ΔT may be an additional factor affecting pulse performance. For example, the eventual reduction in performance at large ΔT seen in lower flip-angle data of Fig. 3 could be fostered by the fact that the bandwidth associated with the overall pulse length is actually narrower than the target ΔB₀ range of ±250 Hz (e.g., the effective bandwidth of a 10 ms block pulse is ±100 Hz). Such an effect would certainly seem relevant in the case that the amplitude modulation waveform approximates a that of a block pulse with the same duration.

Although the distribution of in vivo $B_1^{+}-\mathrm{\Delta }{B}_0$ values of Fig. 2b are representative of only a single subject, the data are suggestive that there are large regions of the chosen optimization grid that are not relevant to 7T volume excitation of the human brain. Furthermore, areas in which in vivo pulse performance is worst (e.g., Fig. 8, near the frontal sinus) have resonance offsets of as much as ±700 Hz, again suggesting that the optimization region for composite pulses could be defined more suitably for uniform volume excitation of the brain. Instead of simply choosing limits for the $B_1^{+}-\mathrm{\Delta }{B}_0$ grid based on the maxima and minima of both phantom and brain data, only the relevant combinations of in vivo $B_1^{+}$ and ΔB₀ values could be identified. Ideally, such an analysis would be based on data from multiple subjects with differing head sizes and geometries. Such a customized optimization grid could result in better pulse performance at low $B_1^{+}$ values or at large resonant offsets.

Consistency of simulated flip-angle maps across the contexts of optimization grids (Fig. 6) and phantom/brain data (Fig. 7) indicates that discretization of the grids is sufficient to represent true variations in the underlying fields. Thus, the behavior of the magnetization for a given combination of $B_1^{+}$ and ΔB₀ is sufficiently represented by the corresponding values of neighboring points on the grid. Consequently, there appears to be no need for further discretization while reduced discretization may be possible for the sole purpose of saving computational time.

Since specific applications were not targeted in this study, P̄ constraints were not incorporated into the optimization algorithm. The disadvantage of this approach is that a given pulse with a certain T_R,min is not necessarily the best pulse for a specific target application—that is, there may be a different combination of N_s and Δt_s that results in the same P̄ but with a lower value of δ_α. A specific P̄ limit could easily be incorporated in the optimization scheme by calculating P̄ at every iteration and comparing that value to the prescribed constraint.

Solutions to optimization problems like the one investigated in this study are only as good as the underlying minimization technique. Given that subsequent optimizations for a pulse with particular N_s and Δt_s result in different waveforms due to the differing random initial conditions, it can be concluded that the minimization algorithm utilized here (Section 2.4) is not in general successful at finding a global minimum—thus, resulting pulses may not be the best possible ones given the design criteria. It is unknown if optimal control theory as implemented by Skinner et al. (9) is better suited for finding a global minimum. The condition of a uniquely defined phase for the final magnetization vector in that work would need to be relaxed to facilitate a comparison of optimization methods given that the lone condition of flip-angle uniformity in the present study does not constrain the phase of the magnetization; however, the relaxation of this phase condition does not appear straightforward. In a future study, the two algorithms (optimal control and fmincon) could be directly compared in the context of RF pulse design given that the final phase of the magnetization is specified. This would at least allow for a general performance comparison and an analysis of the sensitivity to initial conditions inherent in both methods. In the context of the same minimization problem, optimal control theory has the advantage of efficiently handling very large numbers of free parameters, thus allowing for the design of composite pulses with arbitrarily short Δt_s. Indeed, the present study (Section 3.1) and others (22) have shown that pulses with short Δt_s are more likely to produce superior results. In light of these comments on the efficacy of minimization algorithms, it is worth stating that the primary objective of this work is to design a pulse that provides a practical solution to the given optimization problem, and, although algorithms with improved efficiency and performance are always preferable, determination of a global minimum is not a priority.

As alluded to in Section 3.3, potential for numerically optimized composite pulses should be re-evaluated in light of any relevant hardware advancements. Since sensitivity to off-resonance is apparently a relevant design issue for optimized composite and BIR-4 pulses alike, it is a noteworthy conclusion of this work that both pulse types would potentially benefit greatly from improved B₀ shimming schemes such as dynamic shimming (26) due to the corresponding reduction in the minimum required RF bandwidth (i.e., the range of ΔB₀ represented on the optimization grid). Not only would better B₀ shimming result in enhanced performance of both existing BIR-4 and optimized composite pulses but would also likely reduce the power requirements for the latter class—thus, increasing optimized pulse performance for short-T_R applications. This observation serves to emphasize the interconnected relevance of inhomogeneities in the static and RF fields. As for transmission coil technology, composite pulses should be re-designed to ensure the best possible performance if maximum RF amplifier outputs above 15 µT are available. Indications from this study are that limited RF amplitude is a significant inhibitory factor in pulse performance given that many optimized amplitude modulation functions utilize the maximum available amplitude for a large fraction of the pulse duration (see Fig. 6).

5. Conclusion

An optimization algorithm for producing composite excitation pulses with $B_1^{+}-\text{insensitivity}$ has been investigated in the context of human brain imaging at 7T. In addition to demonstrating significant improvements of optimized pulses over block and BIR-4 pulses, this study has documented the performance of these existing methods of volume excitation. When compared to block-shaped pulses, optimized composite pulses are capable of dramatic enhancement of flip-angle uniformity at the costs of increased power, duration, and susceptibility to static field variations. Given the measured distribution of ΔB₀ values and estimated SAR values at 7T, these drawbacks seem workable, especially if applications are identified for which pulse sequence repetition times are sufficiently long (≳ 100 ms). When compared to BIR-4 pulses of the same duration, optimized composite pulses also show compelling gains in flip-angle uniformity, primarily with respect to off-resonance sensitivity, and do so with reduced power requirements. Further customization to the optimization grid and direct incorporation of power constraints into the optimization algorithm may result in pulses with better in vivo performance and suitability to short-T_R applications. Despite such possible improvements, the pulses generated for this study already demonstrate the convincing way in which $B_1^{+}$ inhomogeneity problems at high field can be addressed through the numerical optimization of composite RF waveforms for a single channel transmitter.