Transport and Equilibrium Uptake of a Peptide Inhibitor of PACE4 into Articular Cartilage is Dominated by Electrostatic Interactions

Abstract

The availability of therapeutic molecules to targets within cartilage depends on transport through the avascular matrix. We studied equilibrium partitioning and non-equilibrium transport into cartilage of Pf-pep, a 760 Da positively charged peptide inhibitor of the proprotein convertase PACE4. Competitive binding measurements revealed negligible binding of Pf-pep to sites within cartilage. Uptake of Pf-pep depended on glycosaminoglycan charge density, and was consistent with predictions of Donnan equilibrium given the known charge of Pf-pep. In separate transport experiments, the diffusivity of Pf-pep in cartilage was measured to be ~1×10⁻⁶ cm²/s, close to other similarly-sized non-binding solutes. These results suggest that small positively charged therapeutics will have a higher concentration within cartilage than in the surrounding synovial fluid, a desired property for local delivery; however, such therapeutics may rapidly diffuse out of cartilage unless there is additional specific binding to intratissue substrates that can maintain enhanced intratissue concentration for local delivery.

1. INTRODUCTION

In this study, we focused on the effects of Donnan partitioning and matrix binding interactions on the transport and uptake of a small (760 Da) positively charged peptide inhibitor of paired amino acid converting enzyme-4 (PACE4). PACE4 is a Ca²⁺-dependent serine endoprotease belonging to the subtilisin-like proprotein convertase family, and is a key proprotein convertase responsible for extracellular activation of aggrecanases from their inactive latent forms within cartilage [1]. ADAMTS-4 (aggrecanase-1) and ADAMTS-5 (aggrecanase-2) are synthesized as latent zymogens [2, 3] by chondrocytes, and their catalytic activity depends on the removal of their prodomains [1, 4, 5]. Both aggrecanases cleave the aggrecan core protein at multiple sites (e.g., Glu³⁷³, Glu¹⁵⁴⁵, Glu¹⁷¹⁴, Glu¹⁸¹⁹, and Glu¹⁹¹⁹ [6, 7]), resulting in the release of aggrecan fragments from cartilage in vitro [8, 9] and into the synovial fluid of osteoarthritic (OA) knees [10, 11] in vivo. Since the proteolytic activities of ADAMTS-4 and ADAMTS-5 are believed to play a crucial role in the pathogenesis of OA [12], PACE4 is regarded as a potential therapeutic target for OA. Therefore, studying the physicochemical mechanisms that govern the penetration and transport of such charged peptide inhibitors into cartilage will help to understand their potential therapeutic benefits.

Since adult articular cartilage is avascular and alymphatic, therapeutic agents must be delivered to intratissue targets through the extracellular matrix (ECM) [13], which constitutes ~20–40% of the wet weight of the tissue [14]. Transport through cartilage is regulated by the collagen fibrils and proteoglycans of the ECM, primarily, which accounts for ~60–70% and ~15–25% of the dry weight of the tissue, respectively [15]. The negatively charged glycosaminoglycan (GAG) chains of aggrecan play a unique role in determining the transport properties of the cartilage. The pioneering studies of Maroudas and co-workers [13, 15, 16] showed that the partitioning of free (unbound) electrolyte ions into cartilage (e.g., Na⁺ and Cl⁻) is governed by Donnan equilibrium between the tissue and its bathing solution, associated with electrostatic interactions between matrix GAGs and these ionic solutes. Uptake of free cations into cartilage was enhanced by Donnan equilibrium, whereas anions were largely excluded, and partitioning was further affected by the ion valence in a manner predicted by Donnan theory.

In addition, electrostatic interactions between soluble protein factors and GAGs can regulate transport and binding of these soluble proteins within cartilage. For example, insulin-like growth factor-1 (IGF-1) is a basic protein (pI ~8.5) that partitions into cartilage on the basis of size (steric interactions) and charge (Donnan equilibrium); in addition, IGF-1 binds to specific IGF binding proteins (IGFBPs) that are contained within the ECM [17, 18]. Recently, an HB-IGF-1 fusion protein consisting of native IGF-1 with the heparin-binding (HB) domain of heparin-binding epidermal growth factor-like growth factor (HB-EGF) was designed, purified [19] and found to bind specifically to chondroitin sulfate (CS) GAGs of aggrecan as well as heparin sulfate (HS) GAGs of HS-proteoglycans [20]. The high concentration of positively charged lysine residues within the heparin-binding domain thereby conferred higher uptake and binding of HB-IGF-1 within cartilage ECM and long-term delivery to chondrocytes compared to wild-type IGF-1 [19], even after the HB-IGF-1 was removed from the medium. Similarly, cationized bovine serum albumin (BSA), had increased uptake and prolonged retention via binding within murine cartilage compared to native BSA [21–23].

Interestingly, however, augmenting the net positive charge of a given small or large solute does not necessarily result in binding interactions to negatively charged ECM molecules. Since binding and Donnan partitioning can independently increase the intratissue uptake of a basic protein, experimental methods to characterize each separate mechanism are needed. One approach involves the use of competitive binding assays in which radiolabeled and unlabeled ligands compete for the same binding sites within cartilage tissue, such that the uptake of the labeled ligand changes dramatically as the concentration of unlabeled ligand is varied over a wide range. This method was used to characterize binding of IGF-1 to IGFBPs, while Donnan partitioning of IGF-1 was found to play a far less important role [18, 24]. It is important to note that binding to ECM not only increases total solute uptake in cartilage but can slow the initial diffusion kinetics until a final steady concentration profile within the tissue is achieved, giving rise to a diffusion-binding lag time [18, 24]. To understand the transport of charged solutes into cartilage, binding and partitioning must be distinguished from each other, since these two mechanisms affect the uptake and transient diffusion in very different ways.

To achieve this goal, our objectives were (1) to quantify the equilibrium partitioning and non-equilibrium diffusion of the peptide inhibitor Pf-pep in cartilage, and (2) to assess the extent of binding of the peptide to sites within the tissue. The effect of charge-charge interactions and tissue heterogeneity on uptake and transport were examined. Experimental results were compared to theoretical models of Donnan equilibrium partitioning, reversible binding, and non-equilibrium diffusive transport in cartilage.

2. MATERIALS AND METHODS

2.1 Tissue harvest

Cartilage explants were harvested from the femoropatellar grooves of three 18–24 months old cows (Bertolino Beef, Boston, MA) and a 1–2 weeks bovine calf (Research 87, Marlborough, MA) [18]. Briefly, 9-mm diameter cartilage-bone cylinders were cored, mounted on a microtome and sliced sequentially from the top surface to divide explants into level-1 (L1, ~400 μm with superficial zone intact) and level-2 (L2, ~400 μm below L1). To measure time-dependent diffusive transport of the inhibitor into and across cartilage, the 9-mm diameter slices were used as cut. For equilibrium uptake studies, four 3-mm diameter disks were punched from each of the 9-mm slices and distributed evenly into groups from among different harvest sites along joint surfaces. All cartilage specimens were equilibrated overnight at 4°C in 1× phosphate buffered saline (PBS) supplemented with 0.1% bovine serum albumin (BSA), 0.01% sodium azide (NaN₃) and protease inhibitors (Complete, Roche Applied Science, Indianapolis, IN) prior to experiments.

2.2 Solute structure and preparation

Pf-pep is a 760 Da, basic (trivalent) peptide inhibitor of PACE4 having the sequence Arg-Tyr-Lys-Arg-Thr, pI = 11, and an IC₅₀ = 2 μM measured by screening the peptide against recombinant rat PACE4 and monitoring activity using a peptide substrate as previously described [1]. Radio-iodinated ¹²⁵I-Pf-pep and unlabeled Pf-pep were provided by Pfizer (St. Louis, MO). For the iodinated species, the tyrosine residue was labeled using lactoperoxidase labeling [25]. Before all experiments using ¹²⁵I-Pf-pep, Sephadex G10 chromatography was used to separate and remove any small ¹²⁵I-species that may have resulted from degradation of ¹²⁵I-Pf-pep, (0.7 × 50 cm columns using an elution buffer of 1×PBS buffer with 0.1% BSA and 0.01% NaN₃, and the void volume collected for the desired ¹²⁵I-Pf-pep) [18].

2.3 Equilibrium uptake of Pf-pep

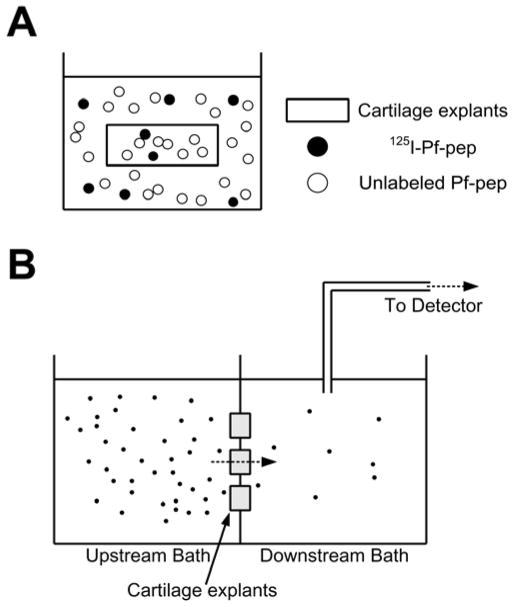
In order to measure equilibrium partitioning of Pf-pep into cartilage and to determine whether Pf-pep may bind to sites within the tissue [24], disks were equilibrated in a buffer containing a fixed amount of ¹²⁵I-Pf-pep (0.127 nM, specific activity 2000 Ci/mmol) and graded amounts of unlabeled Pf-pep (0.5, 1, 2, 4, 8, 16, 32, and 64 nM, shown schematically in Fig. 1a). The buffer consisted of 1×PBS supplemented with 0.1% BSA, 0.01% NaN₃ and protease inhibitors at 4°C. After 48 hours, disks were removed from the bath and briefly rinsed in fresh PBS buffer (equilibrium was reached by 48 hours; see Results below). The surface of each disk was quickly blotted with Kimwipes and the wet weight was measured. The ¹²⁵I-radioactivity of each cartilage disk and aliquots of the equilibration baths were quantified individually using a gamma counter. Disks were then lyophilized and the dry weight was measured; the water weight of each disk was calculated from the tissue wet and dry weights. The inhibitor uptake ratio was calculated as the concentration of the ¹²⁵I-Pf-pep in the cartilage disks (per intratissue water weight) normalized to the concentration of ¹²⁵I-Pf-pep in the equilibration bath. Radio-labeled and unlabeled Pf-pep were assumed to partition into the cartilage in an identical manner.

Figure 1.

(a) Schematic diagram showing incubation of cartilage explants with labeled and unlabeled Pf-pep in the bath. (b) Transport chamber consisting of two compartments, upstream bath and downstream bath. Solutes only could transport through three 9-mm diameter cartilage slices clamped between two compartments. The downstream bath was recirculated through the detector to measure the radioactivity of downstream in real-time.

The disks were then digested with proteinase-K (Roche Applied Science, Indianapolis, IN) and the sulfated glycosaminoglycan (sGAG) content of each disk was measured using the dimethylmethylene blue (DMMB) dye binding assay [26]. Samples from the baths were again analyzed by Sephadex G10 chromatography to determine whether any small labeled species (e.g., ¹²⁵I) may have accumulated from degradation of ¹²⁵I-Pf-pep during each experiment. The uptake ratio was corrected to take into account the presence of any such small labeled species, assuming the small species to be ¹²⁵I [27]. In a separate control experiment, the uptake ratio of ¹²⁵I alone was measured to calibrate the correction factor, which was ~0.6.

To investigate the possibility that Pf-pep may bind to specific sites within the cartilage tissue, we compared the measured uptake ratio to a theoretical model based on a first-order, reversible, bimolecular reaction involving one dominant family of binding sites. The form of this model has been used previously, for example, to characterize the reversible binding of IGF-1 to a single dominant binding site within cartilage [18], and the reversible binding of H⁺ ions to negative carboxyl groups of reconstituted collagen fibrils [28]:

$$R_u=\frac{C_B+C_F}{C_{\mathit{bath}}}=K\left(1+\frac{N}{K_d+C_F}\right)=K\left(1+\frac{N}{K_d+{KC}_{\mathit{bath}}}\right)$$ (1)

where, in the present case, R_u is the uptake ratio, C_B is the concentration of Pf-pep bound to sites within cartilage, C_F is the concentration of free (unbound) Pf-pep in cartilage, C_bath is the bath concentration of Pf-pep, K is the partition coefficient, N is the density of binding sites, and K_d is the dissociation constant. In general, measurement of the uptake ratio (R_u) over a range of bath concentrations of unlabeled Pf-pep (C_bath) would enable a fit of the model to the experimental data and thereby provide best-fit estimates of K and the binding parameters N and K_d using Eq. (1) [18]. However, if there is no significant change in the measured uptake ratio over a wide range of bath concentrations of unlabeled Pf-pep, it is most likely that intratissue binding of Pf-pep to specific sites is negligible (i.e., N = 0 in Eq. (1)) and the measured uptake ratio is then identical to the partition coefficient of the solute into the tissue (R_u = K).

To further test the relation between uptake of the positively charged peptide Pf-pep and matrix fixed charge density, cartilage disks were treated with trypsin to mimic aspects of matrix degradation. Plugs were incubated for 24 hours with 0.1 mg/ml trypsin at 4°C and then washed at least three times in fresh buffer (total wash time was ~48 hours). To determine the decrease in cartilage sGAG content caused by trypsin treatment, sGAG was measured in tissue disks at the end of the experiments (via the DMMB dye binding assay as described above), and sGAG released to the medium by treatment was also measured. To minimize any residual enzymatic activity after trypsin treatment during the uptake measurements, a protease inhibitor cocktail (Complete, Roche Applied Science, Indianapolis, IN) was added to the equilibration buffer containing ¹²⁵I-Pf-pep to inhibit serine, cysteine, and metallo- proteases as well as calpains.

2.4 Diffusive transport measurements

Real-time measurement of diffusive transport of the inhibitor into and through adult bovine cartilage slices (with intact superficial zone) was measured using a diffusion chamber consisting of two compartments, shown schematically in Fig. 1b [24, 29]. Groups of three 9-mm diameter cartilage slices were clamped in parallel by 3 pairs of O-rings positioned at the outer periphery of each disk; the disks were held between the two compartments in such a way that transport between compartments could only occur through the cartilage tissue. Both compartments were filled with 1×PBS supplemented with 0.1% BSA, 0.01% NaN₃ and protease inhibitors, and maintained at 20°C. Both chambers were magnetically stirred to minimize the effects of stagnant films on transport across the cartilage-buffer interfaces [30]. After addition of ¹²⁵I-Pf-pep to the upstream compartment, the downstream bath concentration of ¹²⁵I-Pf-pep was measured continuously by recirculating the bath through a gamma detector (A500 Radiomatic, Packard, Meriden, CT). To correct for any small labeled species (e.g., ¹²⁵I) that may have accumulated from degradation of ¹²⁵I-Pf-pep during diffusive transport experiments, we used experimental and analytical methods described in detail previously [27]. Aliquots from the baths were analyzed using Sephadex G10 chromatography before and after each experiment to determine the amount of any accumulated free ¹²⁵I. At the end of the experiment, free ¹²⁵I was injected into the upstream bath and the total radiolabel flux (attributed to the combination of ¹²⁵I-Pf-pep and free ¹²⁵I) was measured. Using an analytical expression for the total radiolabel flux (Eqn. (1) of [27]) in conjunction with chromatographic assessment of ¹²⁵I concentration, the contribution of any free ¹²⁵I present could be estimated for correction.

2.5 Statistical analysis

2-way ANOVA was used to evaluate the effects of unlabeled Pf-pep concentration and tissue layer on the uptake ratio. Relationships among tissue sGAG content, tissue hydration, and uptake ratio were tested by linear regression analysis. The effects of tissue layer on tissue sGAG density and tissue hydration were evaluated by t-test. The effects of removal of proteoglycans and ionic strength on uptake ratio were examined by 1-way ANOVA followed by post hoc Dunnett’s test. For all statistical analyses, P values less than or equal to 0.05 were considered significant. Systat 12 software (Richmond, CA) was used to perform all analyses.

3. RESULTS

3.1 Equilibrium uptake of ¹²⁵I-Pf-pep into adult bovine cartilage

The equilibrium uptake of ¹²⁵I-Pf-pep in the more superficial (L1) and middle-deep zone (L2) explants of adult bovine cartilage was measured. The uptake of ¹²⁵I-Pf-pep was significantly higher in L2 compared to L1 cartilage overall (2-way ANOVA, effect of the tissue layer, p<0.0001, Fig. 2). If ¹²⁵I-Pf-pep bound to sites in cartilage, we postulated that increasing amounts of unlabeled Pf-pep would compete with ¹²⁵I-Pf-pep for these binding sites, resulting in uptake of ¹²⁵I-Pf-pep that would vary with the concentration of unlabeled Pf-pep [18, 24]. However, the results of Fig. 2 show that there was no significant change in the uptake ratio of ¹²⁵I-Pf-pep with the concentration of unlabeled Pf-pep over the entire range tested for both L1 and L2 tissue (2-way ANOVA, no significant effect of the Pf-pep concentration or the interaction between tissue layer and concentration). These results suggest that there is little or no binding of Pf-pep to sites within the tissue (i.e., N = 0 in Eq. (1)). Under this assumption, these results suggest a ~2–4-fold upward partitioning of Pf-pep into adult bovine cartilage in a depth-dependent manner (with the partition coefficient, K, taken to be the measured R_U of Fig. 2).

Figure 2.

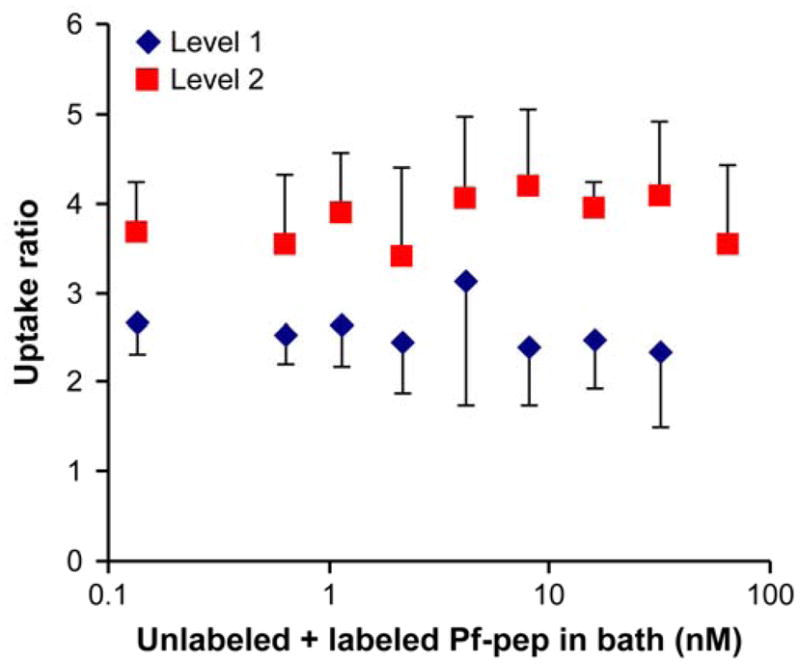
Concentration-dependent uptake ratio of ¹²⁵I-Pf-pep in adult bovine cartilage after 48 hr at 4°C in 1×PBS buffer. Graded amount of unlabeled Pf-pep was added with fixed amount of ¹²⁵I-Pf-pep (< 1 nM). The uptake ratio of ¹²⁵I-Pf-pep did not vary significantly with the concentration of unlabeled Pf-pep over the entire range of concentration for both L1 and L2 tissue (1-way ANOVA, p = 0.825 with L1, p = 0.831 with L2). The uptake of ¹²⁵I-Pf-pep was significantly higher in L2 compared to L1 cartilage overall (2-way ANOVA, p <0.0001). Mean ± SD (n = 4 disks per condition)

As a positive control for the interpretation of concentration-dependent binding, we also measured the uptake ratio of ¹²⁵I-IGF-1 in both L1 and L2 explants using the same methods [18]. We observed that the uptake ratio of ¹²⁵I-IGF-1 in both L1 and L2 explants decreased dramatically by 30-fold as the bath concentration of unlabeled IGF-1 was increased from 10 nM to 100 nM (data not shown), consistent with the known binding of IGF-1 to IGF binding proteins (IGFBPs) located within the cartilage extracellular matrix (ECM) [18, 24].

For each of the 68 cartilage specimens that comprise the data-set of Fig. 2, we plotted the measured uptake ratio as a function of the specimen’s individually measured sGAG content (Fig. 3a) and hydration (Fig. 3b, where hydration is defined here as water weight/dry weight [27, 31]). Uptake of Pf-pep increased with tissue sGAG content (Fig. 3a, linear regression, r² = 0.637, p<0.0001) and with decreasing tissue hydration (Fig. 3b, linear regression, r² = 0.353, p<0.0001). We also note that cartilage from the deeper region (L2) generally had higher GAG density (t-test, p<0.0001) and lower hydration (t-test, p=0.00016) than L1 tissue, consistent with previously reported trends for adult articular cartilage [32]. Therefore, L2 cartilage had higher fixed charge density (FCD) compared to the more superficial L1 tissue.

Figure 3.

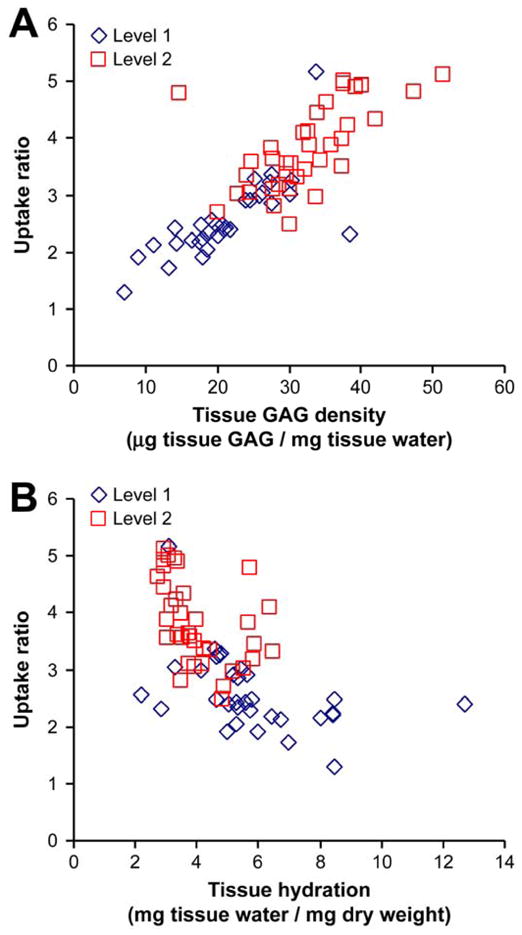
Dependence of the uptake ratio of ¹²⁵I-Pf-pep on (a) tissue GAG density (μg GAG content/mg tissue water) and (b) tissue hydration (mg tissue water/mg dry weight). Uptake of ¹²⁵I-Pf-pep increased with increasing tissue sGAG content and with decreasing tissue hydration (linear regression, p <0.0001). Cartilage from the deeper region (L2) generally had higher GAG density (t-test, p <0.0001) and lower hydration (t-test, p = 0.00016) than L1 tissue. Each data point represents one of the 68 cartilage specimens that comprise the data-set of Fig. 2.

3.2 Uptake of ¹²⁵I-Pf-pep followed Donnan equilibrium partitioning

The data of Figs. 2 and 3 suggest that the uptake of the positively charged ¹²⁵I-Pf-pep was enhanced by the charge-charge interactions with the negative ECM. For small, positively charged species that do not to bind within cartilage tissue, such as Na⁺ [15], partition coefficients in cartilage have been reported to be greater than 1, and to increase with FCD of the ECM in a manner that typically follows Donnan equilibrium [15]. To test whether the intratissue concentration of Pf-pep obeyed Donnan equilibrium, the net charge of Pf-pep was estimated by fitting the predictions of Donnan theory to the data of Fig. 3a, and then compared to the known charge of +3. Donnan theory predicts that the partition coefficient of Pf-pep (K_pep = C̄_pep/C_pep) is related to the partition coefficient of Na⁺ (K_Na = C̄_Na⁺/C_Na⁺) by a power law having the form,

$$\frac{{\overline{C}}_{\mathit{pep}}}{C_{\mathit{pep}}}={\left(\frac{{\overline{C}}_{{Na}^{+}}}{C_{{Na}^{+}}}\right)}^Z$$ (2)

where Z is the net charge of Pf-pep, C̄_i is the intratissue concentration (mole per liter of intratissue water) and C_i is the bath concentration of the i^th species (see details of the theoretical model in the Appendix). By combining the laws of Boltzmann equilibrium and electroneutrality, we calculated the Donnan partitioning of bath Na⁺ ions using the measured GAG density of each specimen (see Eq. A.5). The partition coefficient of ¹²⁵I-Pf-pep was assumed to be equal to the measured uptake ratio in Fig. 3. That is, all the radioactivity within the disks was assumed to be free (not bound) and assumed to be able to partition according to the Donnan equilibrium. Fig. 4 shows a plot of the calculated partition coefficients of ¹²⁵I-Pf-pep versus that of Na⁺ for each individual cartilage disk; the solid lines are predicted theoretical curves for Pf-pep charge Z = 1 through Z = 4. To calculate the net charge of Pf-pep from these data, the partition coefficients of ¹²⁵I-Pf-pep and Na⁺ were inserted into Eq. (2) and a robust nonlinear least squares method (MATLAB) was used to calculate the best fit value of Z; the bisquare function was used as the weighting function to reduce the effect of outliers. The resulting best fit Z = +2.87 (r² = 0.763) corresponds well to the known charge of the trivalent peptide, Z = +3, and is consistent with the assumption of Donnan partitioning and the assumption that all intratissue radioactivity is mobile and thus does not bind to sites that immobilize radioactive counts.

Figure 4.

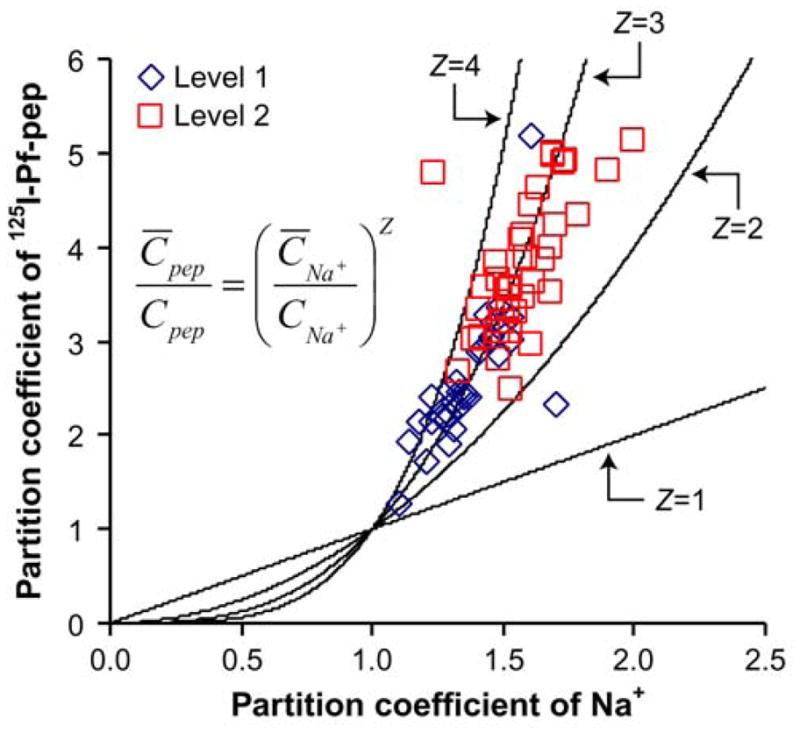
Estimate of the net charge (Z) of Pf-pep using Donnan equilibrium theory. Donnan theory predicts that the partition coefficient of ¹²⁵I-Pf-pep will follow the power-law relation with the partition coefficient of Na⁺ by the exponent Z. The partition coefficient of Na⁺ was calculated from the measured GAG density of each individual specimen (A.5) and the partition coefficient of ¹²⁵I-Pf-pep was assumed to be equal to the measured uptake ratio in Fig 3. The solid lines are the predicted theoretical curves for Pf-pep charge (Z = 1–4). The best fit value of Z was + 2.87, which corresponds well to the known charge of Pf-pep (+3). Each data point represents one of the 68 cartilage specimens that comprise the data-set of Fig. 2.

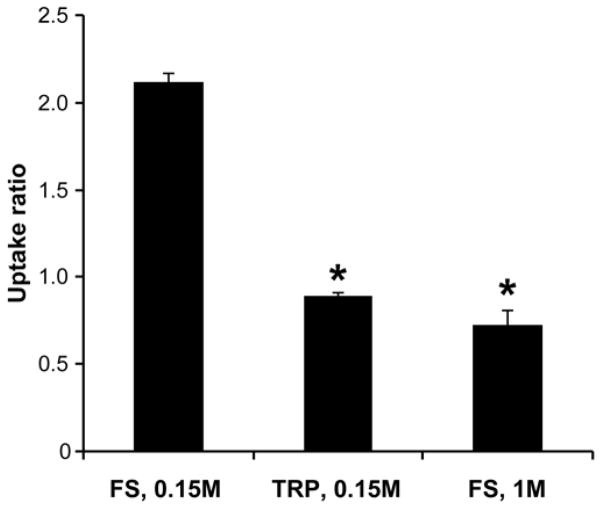
To further test the role of electrostatic interactions between the small peptide inhibitor and cartilage ECM, we examined the effect of loss of tissue GAG or screening GAG charge on the uptake of ¹²⁵I-Pf-pep into newborn bovine calf cartilage L2 disks. For GAG depletion studies, disks were incubated for 24 hours with 0.1 mg/ml trypsin at 4°C prior to the measurement of uptake of ¹²⁵I-Pf-pep. This trypsin treatment removed approximately 60% of the GAG from these L2 disks. For studies of the effects of charge screening, the NaCl concentration of the bath was increased to 1M at neutral pH [33]. Treated and control disks were then equilibrated with Pf-pep for 48-hours. Untreated control disks equilibrated in physiologic ionic strength (0.15M NaCl) showed significantly higher uptake of ¹²⁵I-Pf-pep than that observed in either trypsin-treated explants in 0.15M NaCl or untreated explants in 1M NaCl bath (Fig. 5, data shown for L2 disks, 1-way ANOVA post hoc Dunnett’s test, vs. control group “FS, 0.15 M”, p<0.0001), indicating that electrostatic interactions between Pf-pep and ECM are primarily responsible for the enhanced uptake.

Figure 5.

Effects of trypsin depletion of GAG (TRP, 0.15M NaCl) or screening of GAG electrostatic interactions (FS, 1M NaCl) on the uptake of ¹²⁵I-Pf-pep in L2 bovine calf cartilage disks. Untreated control disks in physiological ionic strength (FS, 0.15M NaCl) showed significantly higher partition coefficients compared to the two treated groups (*p<0.0001 by 1-way ANOVA post hoc Dunnett’s test, vs. control group “FS, 0.15 M”). Mean ± SEM (n = 3 disks per condition)

3.3 Diffusive transport of ¹²⁵I-Pf-pep across adult bovine cartilage

Using the transport cell arrangement of Fig. 1b, the diffusive flux of ¹²⁵I-Pf-pep within and across disks of adult bovine cartilage was measured in order to estimate the diffusivity of Pf-pep within cartilage ECM (Fig. 6). At time t ~ 50 min, ¹²⁵I-Pf-pep was introduced into the upstream bath, and, with rapid mixing, a concentration gradient was quickly established across the disks. Previous studies have shown that binding of solutes to sites within cartilage in this geometry can dramatically slow transport across the disks and into the downstream bath, consistent with a significant decrease in the solute’s effective diffusivity. In contrast, in the absence of binding, the concentration gradient of Pf-pep across cartilage slices between the two compartments of Fig. 6 would generate only passive diffusive flux of ¹²⁵I-Pf-pep through cartilage, and a more rapid emergence of the solute into the downstream bath. A typical result showing transport of ¹²⁵I-Pf-pep across a group of three cartilage disks is shown in Fig. 6; the measured downstream concentration of ¹²⁵I-Pf-pep was normalized to the upstream concentration. After an initial lag time of ~10 minutes, the slope from t ~ 60 minutes to t ~ 720 minutes represents the steady state flux of ¹²⁵I-Pf-pep.

Figure 6.

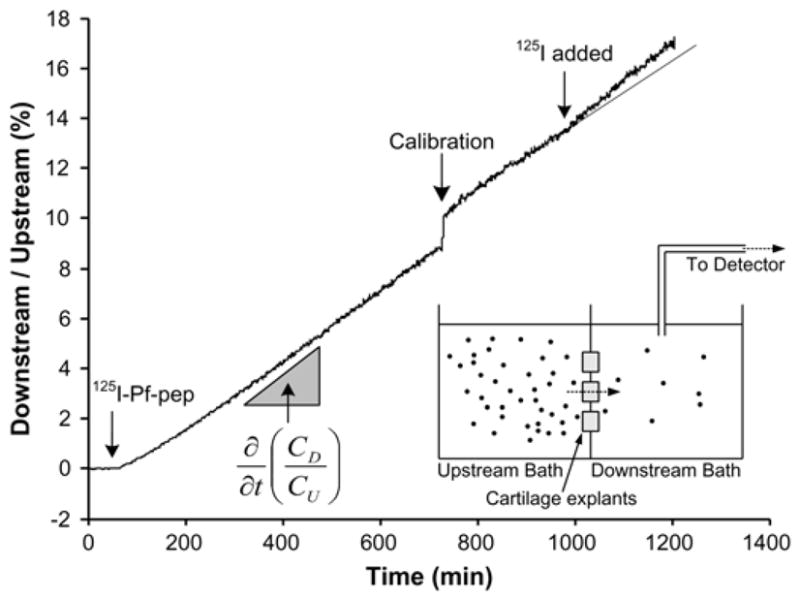
Non-equilibrium diffusion of ¹²⁵I-Pf-pep across groups of three adult bovine cartilage disks (data shown for L1 disks), plotted as the measured downstream concentration versus time, normalized to the applied upstream concentration. At t = 50 minutes, ¹²⁵I-Pf-pep was introduced to the upstream bath. The diffusivity of Pf-pep was calculated from the measured diffusive flux of ¹²⁵I-Pf-pep (i.e., the slope of the concentration vs. time data as shown). At t = 728 minutes, a 300 μl aliquot from the upstream bath (20 ml) was transferred to the downstream bath (20 ml) to calibrate the concentration. At t = 980 minutes, unbound ¹²⁵I was added to the upstream bath to estimate the contribution of unbound ¹²⁵I to the total flux and to correct for the presence of such ¹²⁵I in the calculated diffusivity of ¹²⁵I-Pf-pep. The solid line at the end of experiment shows the predicted flux which would be present if ¹²⁵I were not added.

The data of Fig. 6 were used to estimate the intratissue diffusivity of ¹²⁵I-Pf-pep using established methods [18]. Since the upstream concentration of ¹²⁵I-Pf-pep is much higher than the downstream concentration during the initial ~700 minutes in Fig. 6, the steady-state flux, Γ, of ¹²⁵I-Pf-pep across the cartilage disks is given by,

$$\mathrm{\Gamma }=\phi KD\frac{C_U-C_D}{\delta }\cong \phi KD\frac{C_U}{\delta }$$ (3)

where φ is the tissue porosity, K is the partition coefficient, D is the diffusivity, C_U is the upstream concentration, C_D is the downstream concentration, and δ is the average thickness of the three tissue disks. The time derivative (slope) of the normalized downstream concentration (C_D/C_U) can be related to the steady-state flux by,

$$\frac{\partial }{\partial t}\left(\frac{C_D}{C_U}\right)=\frac{A\mathrm{\Gamma }}{V_{DS}{C}_U}\cong \frac{\phi \mathit{KDA}}{\delta V_{DS}}$$ (4)

where A is the total exposed area of the cartilage-disks, and V_DS is the volume of downstream bath. The diffusivity was thereby calculated from the steady-state flux using Eq. (4) [18].

The presence of mobile ¹²⁵I that may have accumulated during a diffusion experiment would artifactually increase the estimated tracer flux into the downstream bath and thereby alter the estimate of the diffusivity of ¹²⁵I-Pf-pep [27]. Sephadex G10 chromatography showed that small labeled species (i.e., ¹²⁵I) constituted less than 10% of total radioactivity of the bath (data not shown). In addition, when ¹²⁵I was directly added to the upstream bath near the end of the experiment (e.g., at t ~ 980 minutes in Fig. 6), the steeper slope observed immediately after addition of ¹²⁵I gave a direct measurement of the effect of a known amount of ¹²⁵I on the calculated flux and the resulting diffusivity. (The diffusivity of ¹²⁵I was independently measured to be ~3×10⁻⁶ cm²/s). These results were combined with the independently measured partition coefficient of ¹²⁵I-Pf-pep (and unbound ¹²⁵I) to give a final estimate of the diffusivity of Pf-pep, using methods described previously [27]. The diffusion coefficients for L1 and L2 disks were 1.6×10⁻⁶ cm²/s and 0.95×10⁻⁶ cm²/s, respectively.

Finally, given an estimate of the diffusivity of Pf-pep, we can estimate the time needed to reach equilibrium in the uptake experiments of Figs. 2–5. The characteristic time constant τ for 1-dimensional diffusion of a solute into a disk of thickness δ given by δ²/(π²D), where δ is the disk thickness and D is the solute diffusivity [34]. Using a value of D measured in L1 and L2 disks ~1×10⁻⁶ cm²/s and δ = 400 μm, the calculated diffusion time constant is τ ~ 2.7 min, and diffusion equilibrium would be attained by 3–5 time constants [34]. Therefore, in the uptake experiments of Figs. 2–5, the concentration of Pf-pep within the tissue would certainly reach equilibrium by 24–48 hours.

4. DISCUSSION

The results of this study indicate that Pf-pep, a small positively charged peptide inhibitor of PACE4, did not show measurable binding to the negatively charged GAG chains in cartilage; however, charge-charge interactions were critically important in determining the intratissue distribution of Pf-pep, which had a higher concentration in the tissue compared to the bath. Partitioning correlated significantly with tissue GAG density, supporting a major role for matrix composition in the uptake of Pf-pep.

The equilibrium distribution of Pf-pep between cartilage and the surrounding bath followed Donnan equilibrium (Fig. 4), which resulted in a partition coefficient K > 1 (Fig. 2). This enhanced uptake of Pf-pep was associated with tissue GAG density (Fig. 3a), but was not due to intratissue binding (Fig. 2). The uptake of Pf-pep was lower in the surface zone (L1) than deeper (L2) tissue (Fig. 2), consistent with the lower GAG density and higher hydration of L1 tissue (Fig. 3). One caveat in comparing the uptake ratio in L1 and L2 is that L2 disks have one more cut surface than L1 tissue, which could affect the uptake ratio due to altered tissue hydration. Eisenberg [35] measured the swelling properties of middle zone (L2) adult bovine femoropatellar groove cartilage by changing the ionic strength of the bath, and found that this tissue showed minimal (< 3%) changes in swelling under hypotonic conditions (0.01M NaCl). This suggests that the additional cut surface of L2 disks would likely not affect tissue hydration.

Furthermore, depletion of GAG and the concomitant lowering of tissue fixed charge density following trypsin treatment dramatically decreased uptake of Pf-pep (Fig. 5), which is notable since trypsin treatment has been used to mimic certain aspects of cartilage degradation [36–40]. Taken together, we suggest that there would be less uptake of Pf-pep in areas of cartilage undergoing aggrecan loss as observed in OA. Compared to normal cartilage, OA cartilage has lower GAG content and higher hydration than healthy tissue [32], especially in the superficial zone. Thus, the beneficial effect of electrostatic interactions on uptake of Pf-pep would be lessened with progression of disease.

While uptake of this 760 Da peptide appeared dominated by Donnan equilibrium, steric exclusion may also be important to consider as the size of the solute increases. Maroudas included the effects of steric exclusion for larger solutes by incorporating Ogston’s theory for the partitioning of spherical molecules into a hydrated matrix of linear fibers [41–44]. Based on the values of the solute radius and inter-fiber spacing, Ogston’s theory would predict a decrease in the partition coefficient of a given neutral solute with increasing cartilage GAG density, rather than the increase in partition coefficient with GAG density observed here for Pf-pep. Modeling of the combined effects of steric exclusion and electrostatic partitioning for charged solutes has not been well studied in cartilage. For the general case of charged gels, Johnson and Deen extended Ogston’s model by introducing a Boltzmann factor for the electrostatic partitioning of a spherical charged solute within a charged fiber matrix [45]. Using this model, ongoing studies are focused on including the role of excluded volume on intratissue partitioning of solutes having a range of effective radii.

In the absence of binding interactions, non-equilibrium transport of smaller solutes (e.g., Pf-pep) across cartilage is dominated by passive diffusion (Fig. 6). The characteristic time lag, τ, for diffusive penetrating into a tissue of thickness, L, is τ = L²/6D [34], where D is the solute diffusivity. Using a value of D on the order of that measured in L2 tissue (~1×10⁻⁶ cm²/s), τ ~ 27 min for L = 1mm. This is consistent with the order of magnitude time lag observed in Fig. 6 (~10 min) starting after the addition of Pf-pep at t ~ 50 min. Thus, Pf-pep can quickly diffuse into the cartilage, which would be a desired property for an intra-articular OA therapeutic. However, when a therapeutic agent is introduced into the synovial fluid and is intended for targets within cartilage, the synovial fluid concentration must be maintained to enable accumulation of the agent at its needed concentration within the tissue. If clearance from the synovial fluid by the circulation is rapid [46], and the agent does not bind to sites and thereby remain at high enough concentration near the intended target (e.g., cell receptors, proteases or in the present case, PACE4), then such a small solute could quickly diffuse out of the cartilage without a sustained inward concentration gradient. For example, intra-articularly injected small non-steroidal anti-inflammatory drugs such as paracetamol (151 Da), diclofenac (296 Da), and salicylate (413 Da), were cleared from synovial fluid in 1–5 hrs; the rate of clearance depended on the size of molecules and their binding to albumin [47]. For comparison, the diffusive loss of Pf-pep from cartilage can be predicted using the estimated diffusivity (Fig. 6), which would then motivate the choice of an appropriate dosing frequency for intra-articular therapy. Assuming that the thickness of cartilage is of order ~1 mm, and that a ~10 mM concentration of Pf-pep could be quickly achieved in the cartilage after an initial intra-articular dose, the intratissue concentration of Pf-pep would fall below the IC₅₀ of 2 μM by ~10 hrs, suggesting that daily treatment would be necessary. For Pf-pep, the effect of its positive charge was limited to enhancing partitioning (Fig. 2), but not to altered diffusive transport rates (Fig. 6) since Pf-pep did not bind to GAG chains. While the absence of binding to GAGs or other non-specific sites beneficial for achieving fast inward diffusion, there would be no long-term “sustained delivery” from such intratissue binding sites to the desired intratissue target (e.g., PACE4).

The diffusivity of ¹²⁵I-Pf-pep (~1×10⁻⁶ cm²/s) was consistent with values found previously for similarly sized small molecules. For example, diffusivities of ³H-thymidine (242 Da), ³H-L696,418 (476 Da) and ³H-raffinose (594 Da), in adult bovine cartilage were 3.2×10⁻⁶ cm²/s, 0.72×10⁻⁶ cm²/s and 2.9×10⁻⁶ cm²/s, respectively [29]. It is well documented that the intratissue diffusivity of large solutes in cartilage is greatly affected by GAG density which, in turn, is a function of tissue depth [42, 48], static compression [16, 49–51], and enzymatic degradation [36, 52, 53]. While fluid convection caused by dynamic compression is also well known to affect the transport of large solutes, diffusive transport dominates convection for small solutes [29, 54–56]. There is mixed evidence on the dependence of small solute diffusivity on the matrix density. Diffusivities of urea (60 Da) and glucose (180 Da) did not vary significantly with tissue depth [42]; static compression, however, which increases solid volume fraction, reduced the diffusivities of Na⁺ and SO₄²⁻ ions [16] and tetramethylrhodamine (TMR, 430 Da) [49, 50]. Removal of proteoglycans using trypsin did not affect the diffusion coefficient of glucose [36], but did change that of gadolinium-DTPA (530 Da) [39]. These differences may be associated with the different methods used in these various studies. It is possible, therefore, that the diffusivity of Pf-pep could also be affected by changes in matrix density associated with compositional variations, compression or degradation.

Our diffusion experiments were carried out at room temperature for practical reasons: since the diffusion chamber was connected to a large flow-through gamma detector, it would be extremely difficult to control the temperature of the entire setup at 37°C. In order to calculate the diffusivity that would be found at 37°C, several previous investigators have found that the Stokes-Einstein relation gives an appropriate estimate for the effects of temperature on diffusivity in this temperature range [57, 58]. Assuming that intratissue diffusion of Pf-pep follows the Stokes-Einstein relation, the diffusion coefficient of Pf-pep would increase by a factor of ~1.4.

In summary, our results with Pf-pep suggest that a small, positively charged molecule will have a higher concentration within cartilage than in the surrounding synovial fluid; however, they may not be retained within the tissue unless there is additional specific binding to intratissue substrates that can maintain enhanced concentration. Since small non-binding solutes have a higher diffusivity, such solutes can quickly penetrate and diffuse into cartilage and achieve an intratissue concentration that is enhanced by Donnan partitioning. However, they can also diffuse back out to the synovial fluid at the same rate due to nonequilibrium diffusion unless their intratissue concentration is maintained. Extensive loss of negatively charged GAG chains due to OA can lead to the loss of enhanced uptake of a positively charged therapeutic, even though such GAG loss, along with increased tissue hydration, would increase solute diffusivity.

ABBREVIATIONS

PACE4

paired amino acid converting enzyme-4

ECM

extracellular matrix

GAG

glycosaminoglycan

ADAMTS

a disintegrin and metalloproteinase with thrombospondin motif

FCD

fixed charge density

IGF-1

insulin-like growth factor-1

IGFBP

insulin-like growth factor binding protein

DMMB

dimethylmethylene blue

OA

osteoarthritis

APPENDIX

Donnan equilibrium predicts the distribution of Pf-pep with charge, Z, to be related to Na and Cl ion concentrations by,

$${\left(\frac{{\overline{C}}_{\mathit{pep}}}{C_{\mathit{pep}}}\right)}^{\frac{1}{Z}}=\frac{{\overline{C}}_{{Na}^{+}}}{C_{{Na}^{+}}}=\frac{C_{{Cl}^{-}}}{{\overline{C}}_{{Cl}^{-}}},$$ (A.1)

where C̄_pep, C̄_Na⁺, and C̄_Cl⁻ are intratissue concentration of Pf-pep, Na⁺, and Cl⁻, respectively, and C_pep, C_Na⁺, and C_Cl⁻ are bath concentration of Pf-pep, Na⁺, and Cl⁻, respectively. Since the bath was PBS buffer with physiological ionic strength, the bath concentration of Na⁺ and Cl⁻ are given by

$$C_0=C_{{Na}^{+}}=C_{{Cl}^{-}}=0.15M.$$ (A.2)

Charge neutrality requires the sum of all charges becomes net zero as given by

$$\rho +{\overline{C}}_{{Na}^{+}}-{\overline{C}}_{{Cl}^{-}}+{\overline{C}}_{\mathit{pep}}=0,$$ (A.3)

where ρ is the fixed charge density, which has a negative value in cartilage. We can safely neglect C̄_pep in Eq. (A. 3), since Pf-pep is a minor carrier compared to Na⁺ or Cl⁻. Combining Eq. (A. 1) and Eq. (A. 2) to eliminate C̄_Cl⁻ in Eq. (A.3) gives

$$\rho +{\overline{C}}_{{Na}^{+}}-\frac{C_0^2}{{\overline{C}}_{{Na}^{+}}}=0.$$ (A.4)

Eq. (A. 4) is quadratic equation for C̄_Na⁺ and the solution is given by

$${\overline{C}}_{{Na}^{+}}=\frac{-\rho +\sqrt{{\rho }^2+4C_0^2}}{2},$$ (A.5)

where only one solution is valid since C̄_Na⁺ cannot be negative. The charge density, ρ, can be converted from the GAG density by assuming −2 moles of charge per 1 mole of disaccharide unit in GAG chains. Then ρ (mol/L) is given by,

$$\rho =-2·\frac{\text{GAG}\text{content}(\mu \text{g})}{M{W}_{\mathit{GAG}}·\text{Tissue}\text{water}(\mu \text{l})},$$ (A.6)

where MW_GAG is 458 g/mol [59]. Rearranging Eq. (A.1) gives

$$Z=\frac{log\left(\frac{{\overline{C}}_{\mathit{pep}}}{C_{\mathit{pep}}}\right)}{log\left(\frac{{\overline{C}}_{{Na}^{+}}}{C_{{Na}^{+}}}\right)},$$ (A.7)

and Z can be computed for individual explants using the known partition ratios on the right side of Eq. (A.7). The average value of Z calculated from the 68 explants was +3.07 ± 0.74 (SD). The best fit value of Z corresponding to the 68 specimen population was obtained from a robust nonlinear least squares method (MATLAB) used to iteratively calculate the value of Z which minimized the least squares error from an initial guess; the bisquare function was used to down weight large residuals. The resulting best fit was Z = +2.87 (r² = 0.763).