A Signal-to-Noise Standard for Pulsed EPR

Abstract

A 2 mm diameter by 10 mm long cylinder of fused SiO₂ (quartz) γ-irradiated to 1 kGy with ⁶⁰Co contains about 2×10¹⁶ spins/cm³. It is proposed as a standard for monitoring signal-to-noise (S/N) performance of X-band pulsed EPR spectrometers. This sample yields S/N of about 25 on modern spin echo spectrometers, which permits measurement of both signal and noise under the same conditions with an 8-bit digitizer.

Introduction

There is need for a standard sample for monitoring the performance of pulsed EPR spectrometers. Many components of pulsed EPR spectrometers change with time: power amplifiers, limiters, switches, and detectors age; resonators can be damaged. If something seems to be going wrong, it is convenient to use a standard sample under standard conditions to determine whether spectrometer hardware or operating parameters are the problem. Performance of pulsed EPR spectrometers has improved so much that the sample described in 1993 [1] is now too intense to be a useful signal-to-noise (S/N) standard for most purposes at X-band. That fused quartz (SiO₂) sample was γ-irradiated to 250 kGy (25 MRad), which is well into the saturation region where the EPR signal does not increase linearly with increased dose [2]. This high-dose sample, which is available from Wilmad Glass (part number WGSR-01-4), remains useful for many purposes in CW and pulsed EPR, including monitoring the automatic frequency control system [3] and checking many pulsed EPR functions. The long relaxation times (ca. 200 µs T₁ and 25 µs T₂ at room temperature) [1, 4] and high S/N make the 25 MRad quartz sample very useful for demonstrating relaxation-dependent EPR phenomena. With normal pulse conditions on home-built [5] or Bruker E580 pulsed EPR spectrometers, a single 2-pulse echo from that quartz sample is strong enough that the noise is less than one bit in the 8-bit digitizers typically used in pulsed spectrometers. Although one can change gains to optimize use of the digitizer, the effective noise bandwidth of an amplifier can depend on the gain, so it is desirable to decrease the signal amplitude such that both signal and noise can be measured under the same conditions.

The present paper describes a sample that is designed to have S/N in a range that can be measured well with current spectrometer signal detection modules, and to provide for future improvements. Samples of clear fused quartz rod (2 mm o.d. by 10 mm long) were purchased from Wilmad Glass and irradiated by NIST with ⁶⁰Co γ-radiation to a dose of 1.00 kGy ± 2%. This is a different batch of quartz than was used for the previous standard sample [1].

1. Methods

1.1 Experiments

The home-built X-band spectrometer was described in [5] and upgrades of the detection system were detailed in [6]. Pulses were formed by a locally-built Programmable Timing Unit (PTU) [7], and recorded in a LeCroy 9310 300 MHz bandwidth digital oscilloscope, which has an 8-bit digitizer. The Bruker BioSpin spectrometer used in Denver is an E580 with E585 PatternJet and E587 SpecJet. The E580-1010 X-band microwave bridge was built in ca. 1994 as part of an E380 pulse spectrometer and has been modified to include a Gunn diode source and the microwave and signal routing capabilities to implement pulsed double electron-electron resonance (DEER), and for pulsed Q-band EPR, with E580-400-u and SuperQFT-u modules. The E580 used in Billerica is a more modern instrument, incorporating an E5803000 bridge, PatternJetII and SpecJetII. Both Specjet modules use 8-bit digitizers. Since the resonator is a key contributor to the system comparison, measurements were performed using a Bruker BioSpin FlexLine ER4118X-MS-5 split-ring resonator on each spectrometer. The irradiated quartz sample was contained in a 4 mm o.d. quartz tube, centered in the 5 mm diameter resonator. Hence, the filling factor was the same for all of the measurements. A 1 kW pulsed TWT amplifier was used in each spectrometer. Since the TWT output is off at the time of the echo formation, and detection is via a double-balanced mixer, there should be no contribution from the microwave source to the noise. Q was calculated from the power ring-down following a microwave pulse. Measurements were performed at ambient temperature, which was about 293 K.

Since the power required for a 90° pulse increases as Q decreases, power was adjusted as Q was decreased by overcoupling. The irradiated quartz signal is narrow enough that all spins are turned by a 20 ns pulse, which was demonstrated as follows. When the spectrometer was set for a 90-τ-180-τ-echo pulse sequence, and then the pulse width was doubled, the echo is almost exactly nulled, as expected if the spins all experienced a 180-τ-360-τ-echo pulse sequence.

T₁ was measured by inversion recovery on the E580 and by saturation recovery on a home-built instrument with a rectangular resonator and Q ~ 2000 [8]. The number of spins in the sample was determined by CW measurements.

2.2 Data Analysis

Echo amplitude was measured with cursors on a digital oscilloscope or by the Bruker Xepr software. The noise value in the denominator of the S/N calculation was standard deviation noise, which was calculated using at least 100 data points, either by mathematical routines within the digital oscilloscope or in locally written software.

2. Results and Discussion

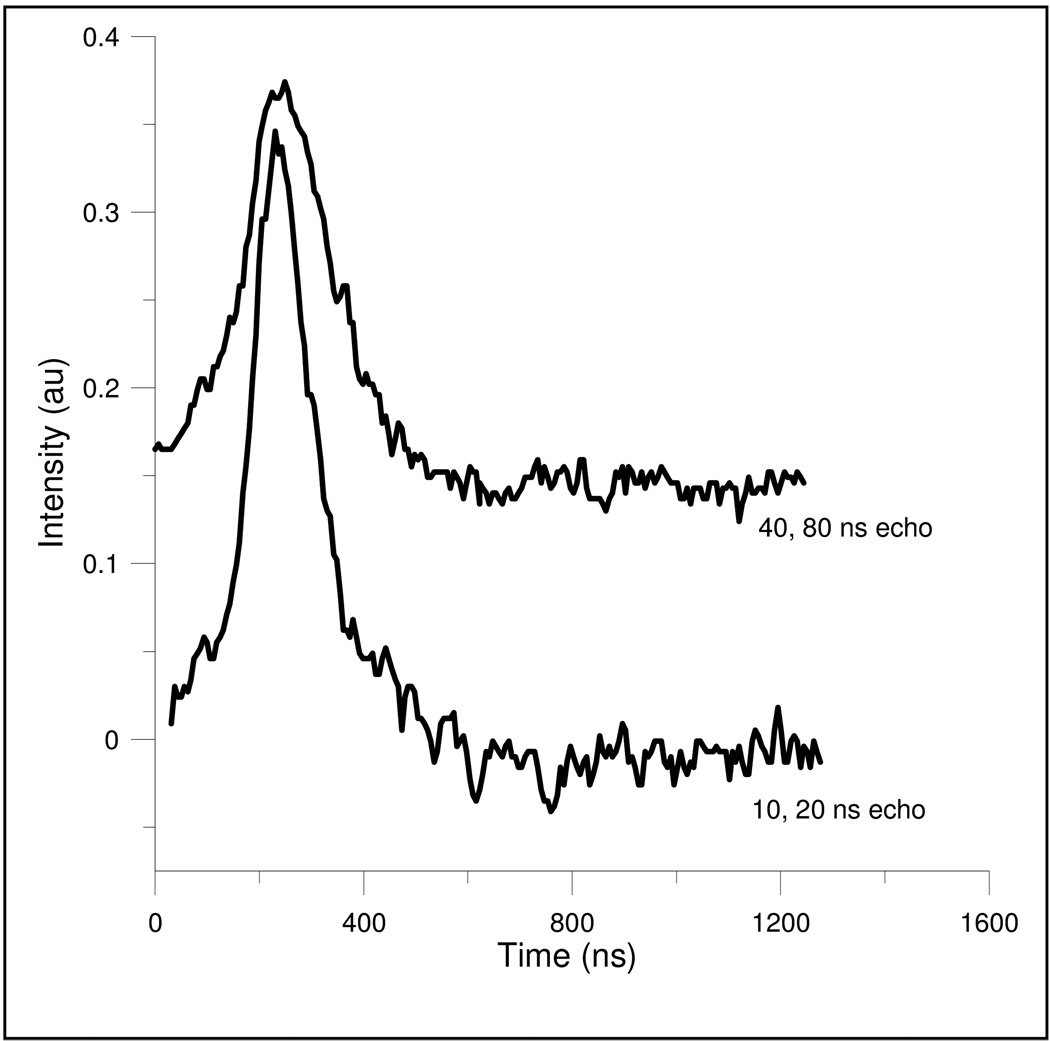
By reducing the radiation dose, the spin echo signal intensity was reduced to the extent that the echo and the noise could be digitized in the same scan with an 8-bit digitizer to yield statistically meaningful noise for S/N calculations. Example spin echoes, which were recorded without signal averaging, are shown in Fig. 1.

Figure 1.

Electron spin echoes from the 2 mm diameter, 10 mm long, fused quartz sample irradiated to 1 kGy, show the effect on the echo shape of the bandwidth of the microwave B₁. The echo in the lower curve was created with 10, 20 ns pulses, which excited the entire spectrum, and the echo in the upper curve was created with more selective 40, 80 ns pulses.

The echo amplitude is proportional to the filling factor, the portion of the spins excited and detected, and the square root of resonator Q [6]. The noise is proportional to the temperature of the sample and any lossy components in the signal path (“thermal noise”), the noise factor (F) of the detection system (noise factor is the ratio of S/N input to output, so for a perfect amplifier F = 1, see p 19 in [9]), and the square root of the bandwidth of the detection system. By keeping the sample and resonator constant, using enough power to excite the full spectrum, and doing all measurements at room temperature, the S/N comparisons become functions of Q, noise factor, and bandwidth [6, 10].

$$\frac{S}{N}\alpha \frac{\sqrt{Q}}{F\sqrt{\mathit{\text{bandwidth}}}}$$

The functional dependence predicted by Eq. 1 was demonstrated for a range of resonator Q and detector bandwidth settings. Discrepancies were in the direction expected for incomplete excitation of the spectrum at higher Q. Each spectrometer has capabilities for several signal gain and detection path bandwidths. Measurements at several settings confirmed the expected dependences (Eq. (1)) to within the accuracy with which actual gains and effective noise bandwidths are known for each spectrometer. See [6, 10] for a discussion of these points.

3.1 S/N of the Spin Echo

Following a high-power microwave pulse, a strong spin echo can be observed with intensity well above the residual decay of pulse power from the resonator, after about 20 resonator ring-down time constants. The time constant, TC, for resonator power ring down is given by the expression Q = 2πνTC, where Q is the loaded Q of the resonator and ν is the resonant frequency. One reason for selecting the irradiated quartz sample as a S/N standard is that the T₂ relaxation time is long enough that a strong two-pulse echo can be observed with interpulse spacings (τ) of several µs. The long relaxation time permits measuring S/N using a critically-coupled resonator, and some labs might want to establish test conditions that exploit the long relaxation time in this way. However, high Q also limits the bandwidth of excitation. We advocate overcoupling the resonator to reduce Q, as in the usual operation of the spectrometer for spin echo measurements, so that a larger fraction of the quartz spectrum is excited. With the irradiated quartz sample in a 4 mm o.d. quartz tube in the Bruker ER4118X-MS-5 resonator, the critically coupled Q was ca. 1150. For Q of ca. 1200, the echo should be observable, well above ring-down, after about 400 ns or more. To be conservative, τ = 1 µs and Q ~ 400 were chosen for the measurements reported in this paper, and is recommended as a standard.

Comparison of S/N of the fused quartz sample irradiated to 1 kGy on three spectrometers is presented in Table 1. Absolute values of the signal amplitude and of the noise depend on overall system gain, so they are not of fundamental interest and are not reported here. The ratio of echo signal amplitude to standard deviation noise, which should be independent of system gain, is denoted S/N, and reported in Table 1. Since measurements of signal and noise were made with the spectrometer system at room temperature (ca. 293 K), the primary noise sources probably are the thermal noise of the sample and resonator, and the noise added by amplifiers and mixers in the detection system. The ASE Model 117 1 kW output TWT has a signal gain of 60 dB, and the three units used had noise figures of 30, 38, and 45 dB. The on/off ratio is 80 dB. The noise measured did not depend on whether the TWT was operating. The signal is reduced by losses between the resonator and the amplifiers.

Table 1.

Experimental S/N Measurements on Three Spectrometers

	Denver home-built	Denver E580	Bruker E580
resonator Q	356	436	440
detector bandwidth (MHz)	21 (3 dB); 26.4 (NEB)	20 MHz at 6 dB point	20 MHz at 6 dB point
90° pulse length	20	20	20
S/N	27	24.8 ± 0.2	24.6 ± 1.8

It is important to correct for differences in bandwidths in the various comparisons, and to distinguish 3 dB bandwidths and Noise Effective Bandwidths (NEB). A correction to the noise measurements can be made on the basis that noise voltage in dB is proportional to 20 log (BW) where BW is the bandwidth of the noise being measured, usually established by a low-pass filter but sometimes by video amplifier characteristics. NEB is always somewhat larger than the nominal 3 dB bandwidth established by a low-pass filter and depends on the characteristics of the filter. It is measured by integrating the noise voltage contribution for frequencies beyond the nominal cut-off of the filter, adding this contribution to the in-band noise and then assigning a bandwidth that would produce this total noise voltage. For purposes of comparison between spectrometers it is sufficient to use nominal bandwidth numbers as the difference between nominal and NEB is likely to be similar in both cases.

The home-built spectrometer [5] uses a limiter with a loss of 1.5 dB to protect the first stage microwave preamplifier, which has a noise figure of 1.14 dB. The noise figure of the entire detection system in the home-built spectrometer is 4–5 dB. The E580 uses a defense switch to protect the microwave preamplifier, and has additional switching for experimental versatility, which may account for the small differences in S/N between the spectrometers.

These S/N values were only achieved after careful sample positioning. The sample is 10 mm long, which is of the order of the length of the resonator. The B₁ field distribution varies along the length of the resonator, whether cavity resonator or split-ring resonator, so the maximum echo signal requires positioning the sample to optimize interaction with the B₁ field distribution. Data were collected with the center of the quartz sample in the center of the resonator. Also, if the quartz sample does not fill the whole EPR tube, it leans against the wall of the tube. The angle of the quartz cylinder relative to the resonator gap also affects the S/N measurement. Without careful positioning we achieved a S/N on the Denver E580 spectrometer of about 21.

3.1.1 Fraction of spectrum excited

A 90° pulse with microwave field strength B₁ will rotate about “B₁ gauss” of the spectrum by 90° [11]. The pulse turning angle is θ = γB₁t_p , where γ is the gyromagnetic ratio of the electron (1.7608×10⁷ rad s⁻¹ G⁻¹) and t_p is the microwave pulse length. Thus, a 20 ns 90° pulse has B₁ = 4.5 G. The width of the EPR spectrum of the irradiated quartz sample is largely due to g anisotropy. At X-band most of the intensity of the spectrum is encompassed within about 2.5 G. Thus, a 90° pulse that is shorter than about 40 ns excites the full spectrum. High resonator Q can decrease the spectral extent that is fully excited. For example, Q of 1200 at 9.6 GHz corresponds to a 3 dB bandwidth of 8 MHz, which is ca. 2.9 G. Thus, if the magnetic field is selected to be at the center of the spectrum, the excitation of the outer portions of the irradiated quartz signal is decreased to about 1/√2 relative to the center of the spectrum (B₁ is proportional to square root of power). As the Q is lowered, bandwidth increases, and more of the spectrum is excited uniformly. If, in addition, the pulse is shorter, so that the spectrum of B₁ is larger, the shape of the echo changes from a smooth decay to showing the structure due to the g anisotropy. As shown in Fig. 1, the more selective the pulse, the wider the echo.

3.1.2 Narrower detection bandwidth increases S/N

The noise is proportional to the square root of the bandwidth. Detection of the spin echo does not require very high bandwidth, since the T₂* is about 250 ns. With 40, 80 ns pulses the echo is ca. 190 ns wide at half height (Fig. 1). The Bruker pulsed EPR spectrometer video amplifier bandwidths were settable to 20, 50, 100, and 200 MHz in early versions, and 20 and 200 MHz in later versions. The current 20 MHz bandwidth is 20 MHz at the 6 dB point. The bandwidths of the home-built system in Denver were detailed in [6] for several gain and filter settings. The closest equivalence between this system and the E580 is gain = 20 and no filter capacitor, which results in a 3 dB bandwidth of 21 MHz (Table 3 in [6]). The Denver system uses a single-pole RC filter, which quickly reaches a slope of 6 dB/octave after the 3 dB point.

3.2 Spin concentration

The spin concentration in the 1 kGy sample was estimated by comparison with the 250 kGy sample, which had previously been estimated to have 5 to 7 ×10¹⁷ spins/cm³ [1]. The long relaxation times make it impossible to obtain a proper CW spectrum on a standard EPR spectrometer, but both spectra were equivalently saturated, so the comparison should be reasonably useful. CW spectra were obtained with a TE₁₀₂ cavity resonator, 10 kHz magnetic field modulation frequency, and the lowest power available on a Varian E9 spectrometer, which is 60 dB below ca. 200 mW, roughly 0.2 µW. At higher incident powers the mixing of dispersion with absorption [3] made integration of the spectra extremely inaccurate. Multiple scan averaging was used to obtain useful S/N. In addition to comparing integrated spectra, multiples of the stronger (essentially noise-free) spectrum were subtracted from the weaker spectrum to estimate relative amplitudes. The two methods agreed within 8%. The 1 kGy sample has ca. 2×10¹⁶ spins/cm³ or ca. 6.3×10¹⁴ total spins in the 2 mm diameter by 10 mm long cylinder. The spin concentration was also measured on a Bruker spectrometer using an ER 4119HS resonator, 100 kHz modulation and 60 dB microwave power attenuation (below 200 mW), and the Bruker “Xenon” quantitative EPR software. This measurement yielded a concentration of 1.94 ×10¹⁶ spins/cm³. The good agreement between the two independent measurements, one of which is relative to a 16-year old sample, also testifies to the long-term stability of the samples.

3.3 Relaxation Times

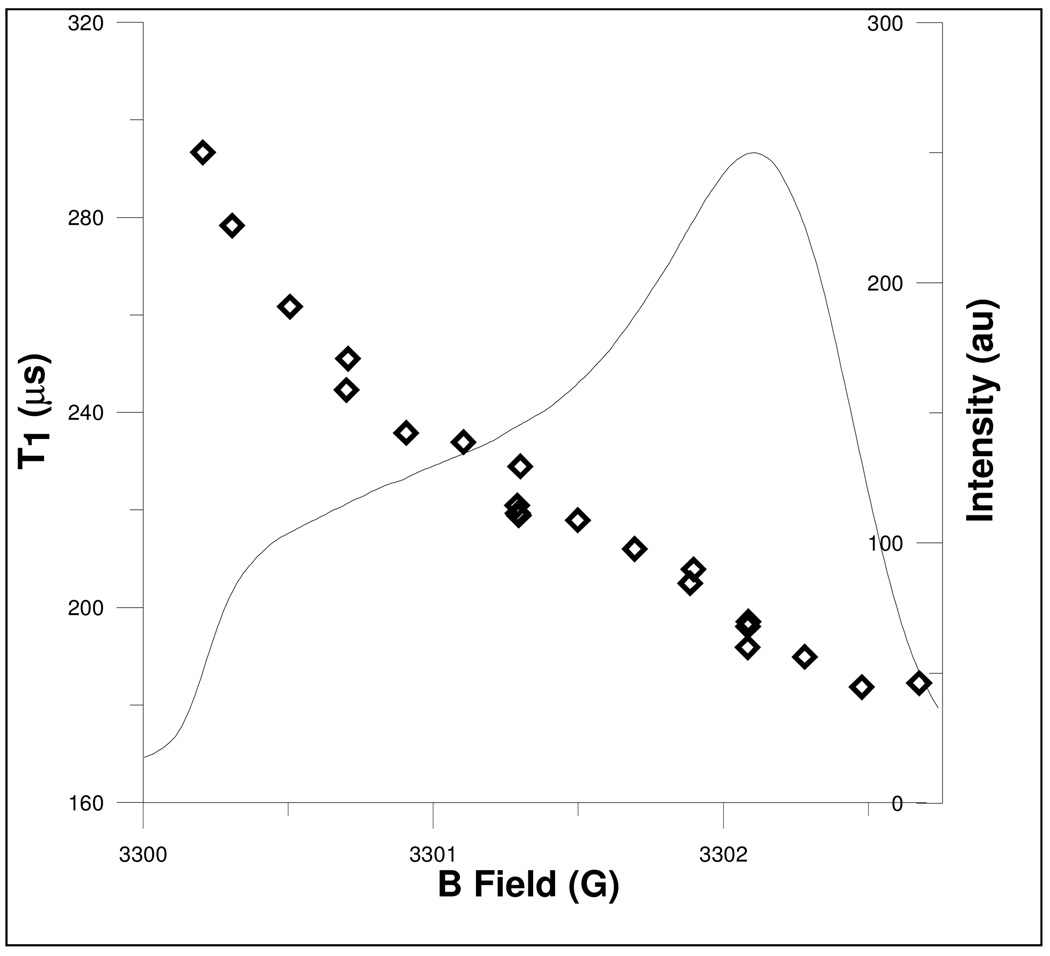
For the 1 kGy quartz sample, T₁ measured by inversion recovery is 204 µs, which is an average over almost all of the spins in the sample. Saturation recovery involves fixed-frequency CW detection, which has a narrower detection bandwidth and therefore is more orientation selective. For the highly-irradiated (250 kGy) sample, T₁ has been shown to decrease from ca. 240 to 160 µs from low-field to high-field across the spectrum [1]. The T₁ for the 1 kGy irradiated quartz sample was measured by saturation recovery as a function of field. The field was varied from 3300.1 to 3302.7 and T₁ was measured every 0.2 G (see Fig. 2). T₁ decreases from 293 to 185 µs from low-field to high-field across the spectrum. This orientation dependence (parallel vs. perpendicular) is attributed to the anisotropy of vibrational modes which has been discussed elsewhere [12].

Figure 2.

T₁ measured at several positions along the EPR spectrum, which is displayed as the first integral of the derivative spectrum.

For a sample with high spin concentration, instantaneous diffusion shortens T_m for an echo decay recorded with a 90, 180° pulse sequence. The weaker the pulses, the longer the measured T_m, until the limiting value (true T₂) is attained. The T_m extrapolated to low pulse turning angles was about 25 µs for the highly-irradiated quartz sample [1]. The low-turning angle T_m for the 1 kGy sample was about 100 µs. Since T₂ previously was estimated to be due to electron spin dipolar interaction, it should be longer for the 1 kGy sample, as observed. The spin concentration is about a factor of 30 lower in the 1 kGy sample than in the 250 kGy sample. Bloch [13] and Bloembergen et al. [14] estimated that T₂ would be proportional to the cube of the distance to neighboring spins. To within the accuracy of these estimates, we can assume that the spins are on a dilute cubic lattice, so the distance, r, between spins is approximately the cube root of the concentration [15]. For the 250 kGy sample this yields T₂ = 20 µs, compared with the measured 25 µs. For the 1 kGy sample this simple formula yields T₂ = ca. 600 µs, which is much longer than the measured T₂ (100 µs). At this low electron spin concentration, the 4.7% natural abundance ²⁹Si spins may become significant contributors to T₂. The calculated value of 600 µs also is longer than T₁ (about ca. 200 µs), so T₁ may contribute to T₂.

The single 2-pulse echo S/N measurement described here is only one of many criteria for quality of a pulsed EPR spectrometer. For many applications, critical features would include for example, the ability to acquire and average multiple pulse responses (FID or echo) quickly, and the long-term stability of the spectrometer.

3.4 Comparison with CW S/N

The standard conditions for CW S/N measurement of weak pitch involve an acquisition that takes about 168 seconds and use a 1.3 s filter time constant. The pulse S/N reported here used 20 MHz bandwidth and 2 ms acquisition time, which was based on the repetition time required to fully relax the spins. Noise is proportional to the square root of the bandwidth, and to the square root of the number of scans. Adjusting for these differences between the CW and pulse measurements, the pulse measurement could achieve a sensitivity of ca. 3×10⁷ spins by averaging for 168 s and decreasing the bandwidth to ca. 1 Hz by post-acquisition processing. The best X-band CW S/N reported so far has been 9×10⁸ spins [16]. It is hard to justify this kind of comparison because the experiments are so different, but it is presented here because comparison between CW and pulse is frequently requested. Rinard et al. [10] estimated that for a somewhat analogous set of assumptions, including that one could use all available microwave B₁ in the CW measurement (ca. 0.5 G B₁ in a TE₁₀₂ cavity), and that the modulation amplitude was equal to the line width, the CW/echo intensity ratio would be ca. 0.2 for a line 2.5 G wide. The CW and pulse intensities were both normalized to the voltage appearing at the end of the transmission line. The pulse S/N measurement performed here differs from CW S/N measurements in several ways. The CW S/N measurement is designed to evaluate low-frequency microphonics as part of a measure of spectrometer system performance, whereas the single-echo pulse measurement is insensitive to spectral noise densities in that frequency range. In addition, the noise of the pulse measurement is established by the noise figure of the first stage microwave preamplifier, which is lower than the noise figure of the input stages of a CW bridge, which include the crystal detector demodulator and the amplifier after it.

3.5 Suitability of Irradiated SiO₂ as a Standard

Radiation-produced defect centers in natural quartz are used for geochronology. One paper reports that at 20 °C the mean lifetime of the EPR signal in crystalline quartz is about 10⁸ years [17]. However, it is also true that exposure to UV and high temperatures (above ca. 100 °C) can create and destroy the E’ defect center, and fused quartz could be different from crystalline quartz. For the known range of quartz samples there are many possible complications. Usually, increased temperature anneals out the defects, but there are also cases known in which heating increases the EPR signal (see, e.g, [18]). However, if a sample is stored at room temperature and protected from UV light or higher energy radiation, the EPR signal will be stable for a very long time. Clear fused quartz, including Wilmad EPR tubes, has been proposed as a radiation dosimetry material [19–21]. The 250 kGy sample [1] has been stable for over 16 years.

Absolute reproducibility of defect centers in fused quartz is unlikely if the type of quartz is changed. General knowledge of the field [22, 23] suggests that the concentration of defect centers depends on the nature (synthetic vs. natural) and purity of the quartz, and especially the metal impurities and OH group content (see, e.g. [24]). For example, Heralux was found to be two orders of magnitude more sensitive than Suprasil to ⁶⁰Co gamma radiation [19]. The samples used in the present study were made of “clear fused quartz”, purchased from Wilmad in May 2007. Measurements were made on different samples from the same batch, and were measured in different labs. One might expect that samples from a different batch of quartz could give different signal intensities, but Wilmad purchases the quartz from a supplier that prepares it from natural quartz with impurities specified at the ppm level. It is reasonable to expect that irradiation of “clear fused quartz” tubes or rods from Wilmad for special applications would yield samples that would be closely comparable to those available from this study. For calibration, signals in samples prepared from different batches of quartz can be compared.

3. Summary

As a standard procedure, we recommend using a fused quartz sample γ-irradiated to 1 kGy, in a high filling factor resonator, such as the ER4118X-MS-5 resonator, overcoupled to Q < 500, a 20 ns 90° pulse, τ= 1 µs, detection system bandwidth = 20 MHz. Measurement of a single echo (no signal averaging), and measurement of the standard deviation noise in the baseline following the echo should be used to calculate S/N. The echo should be created after a delay time of about 2 ms to ensure that the magnetization is at equilibrium prior to the 2-pulse echo sequence. With these conditions, an X-band spin echo spectrometer should achieve S/N > 20.

Since the echo was formed by on-resonance excitation, any FID would be nearly exponential, with very low frequency oscillations due to those spins not exactly on resonance, so there is some possibility that the slope after the main intensity of the echo could be due to residual FID. This can be removed by an 8-step phase cycle to remove the effects of FID after both the first and the second pulse. There are other instrumental artifacts that can contaminate single-pulse measurements, but most of these are eliminated by measuring the echo with τ= 1 µs. Phase cycling would add signal averaging to the measurement, but would still result in sufficient noise to define a meaningful S/N. One could also collect data out to a sufficiently long time after the echo that the FID has decayed, and measure the noise there.

Fifty of these irradiated quartz standard samples have been prepared, and are available from the Eaton lab. For labs with access to irradiation facilities, a standard 4 mm o.d. quartz sample tube, irradiated to the same level, would serve as a slightly different, but convenient local performance standard and would be less dependent on sample position. In the future, similar samples of the correct size could be produced for smaller diameter resonators at X-band (such as the ER4118X-MS-3), and for the smaller resonators used at higher frequencies. We also expect that it will be useful as a standard for rapid scan EPR. Such applications will be reported separately.