Distance measurements in model Bis-Gd(III) complexes with flexible “bridge”. Emulation of biological molecules having flexible structure with Gd(III) labels attached

Abstract

In this work, we continue to explore Gd(III) as a possible spin label for high field Double Electron Electron Resonance (DEER) based distance measurements in biological molecules with flexible geometry. For this purpose, a bis-Gd(III) complex with a flexible “bridge” was used as a model. The distances in the model were expected to be distributed in the range of 5-26 Å, allowing us to probe the shortest limits of accessible distances which were found to be as small as 13 Å. The upper distance limit for these labels was also evaluated and was found to be about 60 Å. Various pulse duration setups can result in apparent differences in the distribution function derived from DEER kinetics due to short distance limit variations. The advantages, such as the ability to perform measurements at cryogenic temperatures and high repetition rates simultaneously, the use of very short pumping and observation pulses without mutual interference, the lack of orientational selectivity, as well as the shortcomings, such as the limited mw operational frequency range and intrinsically smaller amplitude of oscillation related to dipolar interaction as compared with nitroxide spin labels are discussed. Most probably the use of nitroxide and Gd based labels for distance measurements will be complementary depending on the particulars of the problem and the availability of instrumentation.

Introduction

In the last decade, Pulsed Dipolar (ESR) Spectroscopy (PDS) [1] has become a widespread technique for mapping distances in variety of biomolecules such as enzymes, DNA and RNA. A few recent excellent reviews [2-5] and articles [6-8] provide clear descriptions of the achievements and possibilities on one hand while pointing to some yet existent problems on the other. We recapitulate them briefly below.

PDS is based on the measurement of the dipolar interaction between paramagnetic centers, mostly spin labels, mainly by Double Electron-Electron Resonance (DEER) or Double Quantum Coherency (DQC) techniques. The spin labels, with few exceptions, are nitroxide radicals attached to the molecule of interest either by site directed spin labeling [9-11] in the case of proteins or by chemical modifications in the case of nucleic acids [12]. The distances accessible to DEER [1-8] are typically between (15-20) Å on the low side to (50-60) Å on the high side. The DQC based measurements probe wider range of distances (from ∼12 Å to ∼70 Å). The minimal concentration of spin labeled molecules is typically not less than 0.1mM [13-18], and sample volume needed is 30-80 μL although the measurements at lower concentrations were also recently reported [19-21]. The acquisition time required to obtain good quality time domain patterns at low concentrations is reported up to 10-20 hours [13-23]. The most challenging systems are those with flexible structures where the separation between the spin labels is distributed over a wide range of distances. In these cases, the time domain traces do not show the dipolar related oscillations and therefore the determination of distances and their distribution becoming complicated. Furthermore, in a system with a broad and unknown distance distribution, it is difficult a priori to optimize acquisition parameters (time interval and dwell time). In order to obtain reliable information on distance distributions, therefore, the signal to noise ratio (S/N) has to be substantially higher than that for a single fixed distance, thus requiring an increase in acquisition time and/or concentration. These issues were discussed and analyzed while solving similar problems [24,25].

The limit on the short distance end (15-20) Å in DEER is determined primarily by the allowed minimal pulse durations. In turn, the latter depends on instrument parameters such as available mw power and resonator design as well as the intrinsic properties of spin label such as the width of the EPR spectrum. In properly applied DEER, the excitation profiles of the pumping and observing pulses have to be well separated to avoid complications that are due to pulse interferences [2-7,26,27]. The characteristic width of the EPR spectrum of nitroxide radicals at the most commonly used spectrometer microwave (mw) frequencies (from S- to Ka -band, 2-32 GHz) does not exceed 160 MHz. Accordingly, the applied pulses have to be longer than ∼15 ns (assuming that instrument is up to the task) to avoid spectral overlap. This limits the shortest distance that can be probed by ∼15Å [7]. The long distance limit, [2-5], is dictated by sensitivity arguments and is determined by the combination of such factors as the need for a long time interval, reasonable duration of the acquisition time and respectively, low concentration of labeled molecules. All these arguments are generally valid for DQC based techniques as well, except some particularities [2,5].

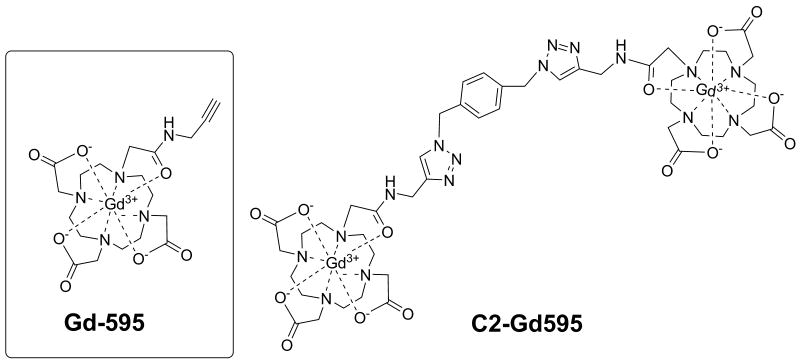
To expand the distance range accessible by DEER, clearly the pulse durations should decrease and sensitivity should increase. The obvious solution is to perform DEER measurements in the W- band frequency range or higher (≥95 GHz) where the width of the nitroxide EPR spectrum increases significantly [16] and thus provides enough room to accommodate pulses as short as <10ns. The only reason that such a simple idea has not been implemented yet is that at present, the mw power amplifiers of W-band spectrometers used for PDS are not powerful enough to generate a π -pulse shorter than ∼ 20ns [28], [FN]. On the other hand, the concentration sensitivity of nitroxide spin labels does not improve beyond the Ka-band either (see Supporting Information, SI), and the long distance limit for distance measurements in the W-band remains unchanged. (Nonetheless, the small amount of sample required, 1-2 μL, compared to ∼100-50 μL remains attractive). The options to increase the distance range using nitroxide labels, therefore, seems to be limited. This, despite the widespread employment of nitroxide spin labels and the impressive developments in their use for distance measurements, provides incentives to search for another family of spin labels which may suffer less from the above mentioned restrictions. One alternative of new spin labels are the Gd-based spin labels suggested earlier [30]. From the start it was clear that Gd(III) is essentially a “high field” item, however, for the same input mw power for a matched resonator the higher transition probability of the −½ ↔½ transition as compared to a S=½ system allows for a decrease in pulse duration (∼2.5:1) (see SI). Consequently, even with the existing mediocre power available at W-band [28], the π- pulse duration for this transition can be reduced to ∼8 ns in standard cavities, while in the Ka-band a π- pulse of ∼5ns can be readily achieved. The potential to quantify shorter distances is therefore evident. Because the Gd(III) spectrum usually spreads over 6,000 MHz [31], it provides more than sufficient room to set up a 400 MHz separation between the carrier frequencies of pumping and observation pulses thus accommodating pulses as short as 5 ns without interference. The short distance limit in DEER using Gd(III) labels, therefore, can potentially be reduced from ∼15Å to ∼8 Å once the resonator bandwidth is adjusted. The long distance limit (as compared to nitroxides) may also increase. Indeed, unlike nitroxides, the full width of EPR spectrum of Gd(III) remains unchanged with increase of operational frequency, while the width of the sub-spectrum of the -½↔½ transition becomes even more narrow. The concentration sensitivity for Gd(III) is therefore expected to increase (see SI) from, e.g., the Ka to W-band, resulting accordingly in an increase in the long distance limit. The next intrinsic feature of Gd(III) is the relatively fast spin lattice relaxation at cryogenic temperatures. This allows the measurements at high pulse repetition rates (up to 100 kHz when the mw amplifier allows) and low temperature (∼10-15K). For the latter, such a combination of low temperature and high repetition rate is problematic because of their long spin lattice relaxation time at low temperatures [2-5]. The Gd-based labels, therefore, may offer substantial advantages that warrant their development. As for attaching them to biological molecules, a number of new methods have been developed for bio macromolecular ligation/labeling with fluorescent lanthanide tags in vivo or ex vivo [32-36]. In addition, tags bearing lanthanides have been developed for paramagnetic NMR spectroscopy [37]. This can be adapted for attaching Gd(III) spin labels. Among these methods, “click” chemistry stands out as being fast, facile, and orthogonal to other reactive functionalities [38-41]. As was demonstrated in literature, “click” chemistry has been successfully applied for the synthesis of a variety of n-mers of Gd(III)-based complexes with flexible “bridges” in which singular Gd(III) complexes are assembled on a benzyl core [41]. While our first demonstration of a distance determinations between two Gd(III) ions using DEER was done on a rigid molecule [30], in this work we focus on a bis- Gd(III) complex (referred as C2-Gd595) with a flexible “bridge” in which two singular Gd(III) complexes are assembled on a benzyl core, as it is shown in Fig. 1. This assembly can serve as a primitive model for flexible proteins having Gd(III) as the spin label, and for which the distance is expected to be distributed in the range of (5- 10) –(25-28) Å.

Fig. 1.

A schematic presentation of the structures for the compounds used in this work.

Here we present DEER measurements that were carried out in the Ka- and W-bands. The short distance limit is explored under the currently available mw power and resonator designs. We show that under the condition of a small crystal field interaction (cfi) as compared to the Zeeman interaction, the DEER results can be analyzed essentially in the same way as for a virtual S=½ system. We also discuss some specifics related to asymptotic DEER decay and to the role of the pseudosecular term of the dipolar interaction. Finally, we will discuss possible applications of Gd(III)-based labels in biological structural investigations.

2. Experimental

2.1 Sample preparation

The synthesis of mono- and bis Gd(III) (Fig. 1) is described in the SI. Solutions of 0.5 and 0.1 mM in water-glycerol (1:1v:v) of Gd595 and C2-Gd595 were prepared for the Ka- and W-band measurements respectively. The total volumes of sample in these bands are ∼30 μL and ∼2 μL.

2.2 DEER measurements

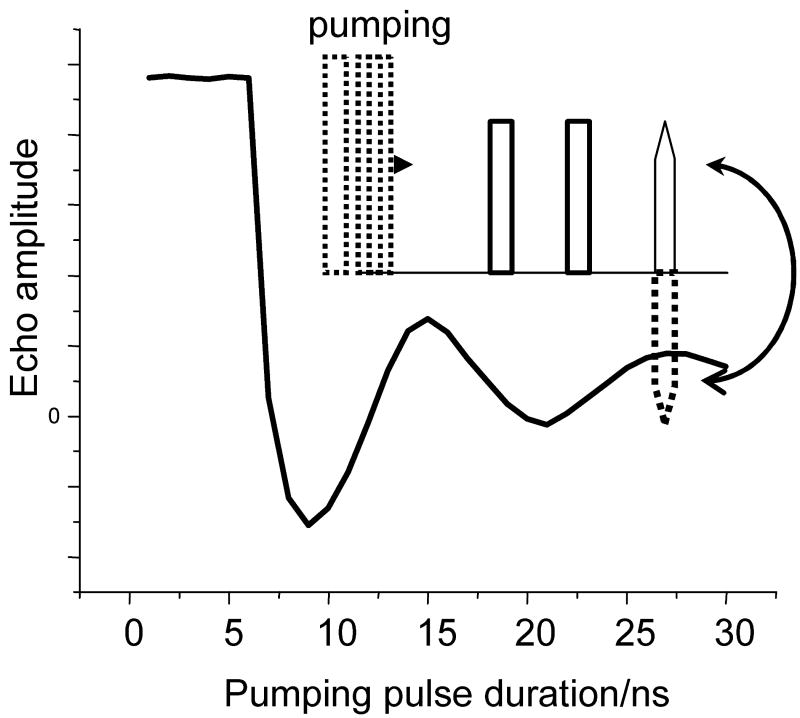
The Ka-band (∼30 GHz) and W-band (95 GHz) measurements were performed using the in-house built spectrometers described earlier [28,42]. The resonator bandwidth in the Ka-band measurements was increased slightly modifying the existing resonator, placing Teflon inserts in the original ∼37 GHz cylindrical cavity (TE₀₁₁). Due to this modification, the resonance frequency decreased to ∼30 GHz and the bandwidth of the loaded and critically coupled resonator became ∼200 MHz. The modified cavity was adequate to accommodate π pulses of 10ns and longer. An example nutation pattern that demonstrates resonator performance is shown in Fig. 2.

Fig. 2.

Test of the Ka-band resonator performance by means of the nutation experiment. The pulse sequence is shown in the insert. The sample used in this experiment was 0.25 mM C2-Gd595 in water-glycerol (1:1, v:v) solution. Experimental conditions: B₀=1.0806 T (maximum of −½↔½ transition); operational frequency: 29.964 GHz; temperature: 15K; durations of second and third pulses: 20 ns; separation between first and second pulses: 500 ns. The absence of a pumping pulse during the initial seven nanoseconds is due to an insufficient switching speed of the TTL driver. The effective duration of the π-pulse is given by the position of the first minimum and is approximately equal to 9ns.

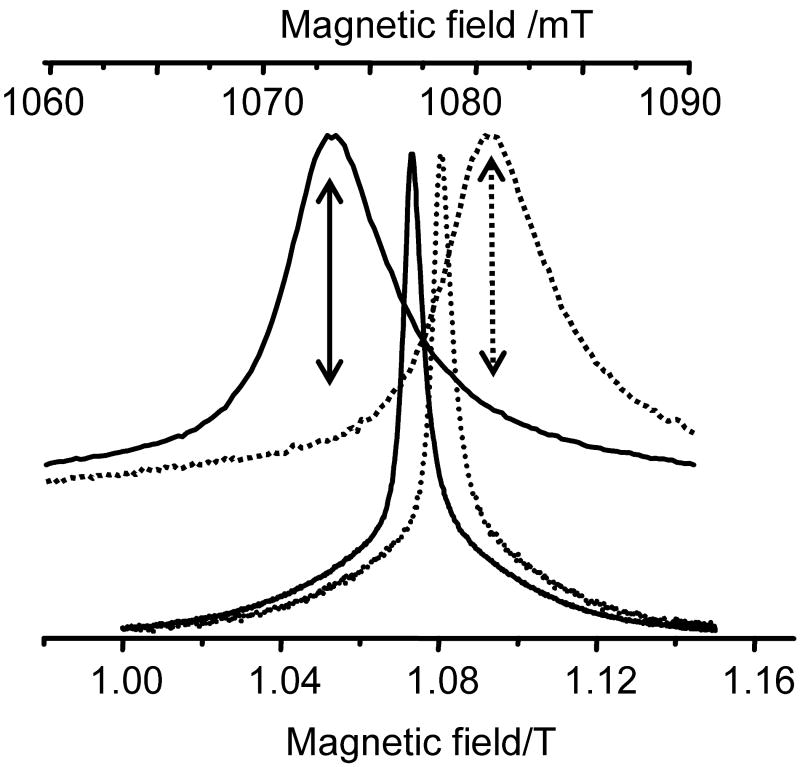
A “zero” dead-time, four-pulse DEER sequence [43] was used in all DEER measurements. Typical frequency separations, Δν, between observation, ν₀, and pumping, ν_p, frequencies were ∼170-200 MHz in the Ka- band, as illustrated in Fig. 3, and ∼75 MHz in the W-band measurements. In the majority of Ka- band experiments, the duration of the pumping π-pulse was varied from 12ns to 40 ns, while that of the observation pulses was kept constant and equal to 30ns for π pulses. In the W-band measurements, the observation π pulse duration was 40 ns and the π pumping pulse was 25ns. The measurement temperature was ∼15 K in the Ka-band and ∼25 K in the W-band. At these temperatures, the relative population of central transitions was close to the high-temperature limit.

Fig. 3.

ESE detected Ka-band spectra of C2-Gd595 collected at pumping (ν_p=29.964 GHz) and observation (ν₀=29.764 GHz) frequencies (dashed and solid lines, respectively) shown at two different scales. The relative field shift of these spectra which is clearly seen from the extended upper panel is ∼70 G. This is in agreement with the 200 MHz difference between ν_p and ν_o. The observation position in spectrum when the pumping frequency is at the maximum for the -½ ↔ ½ transition is shown by a dashed arrow in the upper panel. To evaluate background time domain patterns (vidae infra), the experiments were performed at fields shifted from the maximum by ±70 G. One such field position is shown in the top panel by a solid arrow. All other conditions are pulse durations: 20ns; pulse separation: 200ns; temperature: 15K; Gd(III) concentration: ∼0.5 mM.

3. Theoretical background

3.1 The spin Hamiltonian and the EPR spectrum

The spin Hamiltonian for a Gd(III)-Gd(III) dimer can be written in the form

$$H=\sum _{i=1}^2{g}_i\beta \overrightarrow{B_0}\cdot S_i+H_{\mathit{\text{FS}}}+H_{\mathit{\text{dd}}}$$ (1)

where H_FS is the fine structure Hamiltonian, which, to good accuracy, can be characterized by two cfi parameters, D and E,

$$H_{\mathit{\text{FS}}}=D\mathit{(}{S}_{Z_C}^2-\frac{1}{3}S\mathit{(}S+1\mathit{)}\mathit{)}+E\mathit{(}{S}_{X_C}^2-S_{Y_C}^2\mathit{)}$$ (2)

The H_dd in Eq. 1 is the part of the Hamiltonian responsible for dipolar interactions between the Gd(III) ions. In Eqs. 1 and 2, g_i are the electronic g-factors, β is the Bohr magneton and B_o is the external magnetic field. The index “c” is related to the crystal field. The cfi parameters of the higher order terms, Sⁿ, n>2, in H_FS are small [44] and can be safely neglected.

For D≪gβB₀, a condition which is satisfied for all known Gd(III) complexes at Ka-band frequencies and higher [31], the EPR spectrum of a single Gd(III) consists of an intense central peak corresponding to the -½↔½ transition and a broad background due to all other transitions [31] (Fig.3). The -½ ↔½ transition is subjected to broadening due to H_FS only in the second order of perturbation theory. For axial symmetry, E=0, the width of the central peak, δ, is [45,46]:

$$\delta \approx \mathit{(}10-13\mathit{)}\frac{D^2}{g\beta B_0},$$ (3)

The characteristic width for each sub-spectra related to transitions m_s ↔ m_s+1 is

$$\Delta B_{\text{o}}=\left|\frac{3}{2g\beta }\cdot D\mathit{(}2m_S+1\mathit{)}\right|$$ (4)

The width varies from 9D/gβ (±7/2↔ ±5/2 transitions) to 3D/gβ (±3/2↔ ±1/2) transition. The total spectrum, therefore, spreads over ±6D/gβ and is the sum of the sub- spectra of various transitions. In Gd(III) complexes, the cfi tensor can be approximated the sum of the 7-9 tensors of the individual ligands [31]. The resulting spectrum of all transitions, except the narrow -½↔½ transition, in glassy frozen solutions is, therefore, featureless and smooth and lacks orientation selectivity [47].

3.2 Effect of the cfi and the high spin on the dipolar interaction detected by DEER

For commonly used spin labels, S=½, in which the magnitude of the components of the dipolar interaction tensor, |A_ij|, is substantially smaller than the difference of resonance frequencies |ω_0,1-ω_0,2| of the interacting spins, both spins are quantized along the external magnetic field, B₀. For this case, H_dd in Eq. (1) can be represented in a simple truncated form where only the secular part of the dipolar Hamiltonian remains:

$${\mathit{\text{H}}}_{\mathit{\text{dd}}}=\hslash A_{\mathit{\text{ZZ}}}{S}_{Z,\mathit{1}}{S}_{Z,2}$$ (5)

where

$$\begin{array}{cc}{A}_{\mathit{\text{ZZ}}}=A_0\mathit{(}1-3{\mathit{\text{cos}}}^2\vartheta \mathit{)};& {\omega }_{\mathit{\text{dd}}}\equiv A_0=\frac{g_a{g}_b{\mu }_B^2{\mu }_0}{4\pi h}\end{array}{r}^{-3}$$ (6)

and ϑ is the angle between radius vector r connecting the two spins and the external magnetic field.

In contrast to S=½ systems, for a substantial cfi the quantization axis of high spin systems may deviate from Z‖B₀. The effect of this for D/gβB₀ ≪1 has been accounted for by the introduction of effective projection operators using perturbation theory in the context of ENDOR and ESEEM [47, 48]. It was shown that the corrections to the effective projection operator <S_Z,_i> are proportional to (D/gβB₀)² and are, therefore, negligible for Gd(III) in the Ka- and W-bands [30,47]. The corrections to <S_X,i> and <S_Y,i> are more significant because they are proportional to (D/gβB₀), therefore, to evaluate the corrections to the dipolar interaction, the S_X,i and S_Y,i components should be reintroduced into the Hamiltonian of the dipolar interaction. Second order perturbation theory shows, however, that the shift of the respective energy levels due to terms involving <S_{X, Y}> does not result in a correction of ω_dd [30,47]. The exact solutions show that for systems used in our experiments (D/gβB₀≅0.02 in Ka-band) this correction, although not exactly zero, can be safely neglected. As calculations have shown, the correction depends on the angle between the principal axes of the cfi tensor and the external magnetic field. On average, it amounts to only 1-2% of the nominal value of ω_dd.. Since all currently known Gd(III) complexes have D/gβ≤ 400G [31], the apparent DEER modulation frequency can deviate from ω_dd by not more than 3-5% if the measurements performed in the Ka-band or higher. A detailed derivation of ω_dd for a high spin system using perturbation theory is given in SI. While the effects of the cfi on ω_dd in high field experiments are negligible the role of the pseudo-secular term in dipolar interactions becomes increasingly important. The effects related to the pseudosecular term are discussed in the SI.

3.3 Evaluation of the spin flip probability

The probability of flipping the spin by the pumping pulse, λ_n, is an important parameter for a quantitative description of DEER time domain patterns. In particular, the asymptotic decay of the time domain pattern, V_ia(t), due to static dipolar interactions between spins (S= ½) in the pair randomly oriented in space is [49] :

$${V{(t)}_{\mathit{\text{ia}}}|}_{t\to \infty }\equiv V{(t)}_{\mathit{\text{ia}}}^a=1-{\lambda }_n$$ (7)

In turn, the λ_n depends only on the pumping pulse parameters (duration, t_p, and amplitude, ω₁=γB₁), and on the spectral density of the spins, g(Δω) (the EPR lineshape) [50]:

$$\begin{array}{l}{\lambda }_n=\int \frac{{\omega }_1^2}{{\Omega }^2}{\mathit{\text{sin}}}^2\frac{{\Omega }_{tp}}{2}g(\Delta \omega )d(\Delta \omega )\\ {\Omega }^2={\omega }_1^2+\Delta {\omega }^2\end{array}$$ (8)

and does not depend on distance or the distribution of distances in pairs. The λ_n, therefore, can always be evaluated independently. In the case of Gd(III), spin flip probability can be evaluated in the same manner [30] while taking into account that the Gd(III) spectrum is composed of sub-spectra, each of which having a different effective B₁. The total flip probability can be calculated by summing the partial spin flip probabilities λ_n^(k) of each sub-spectrum. Although somewhat cumbersome, this approach can be implemented since the sub-spectra can be found from simulations [31]. For Gd(III), however, this complicated method may not be necessary since the sub- spectrum of -½ ↔ ½ transitions, g_|½|(Δω), is quite different from all the others. It is narrow, intense and can be easily separated from broad, smooth and featureless background (see Experiment). This allows one to deal only with -½↔½ transition. Evaluation of the flip probability, λ_n^(½), for this transition requires only a substitution in Eq. 8 of g(Δω) by g_|½|(Δω) and taking into account the population of states, p's :

$$\begin{array}{l}{\lambda }_n^{(1/2)}=p\int \frac{{\omega }_1^2}{{\Omega }^2}{\mathit{\text{sin}}}^2\frac{{\Omega }_{tp}}{2}{g}_{\left|½\right|}(\Delta \omega )d(\Delta \omega )\\ p=p(\stackrel{1}{}/\underset{2}{})+p(-\stackrel{1}{}/\underset{2}{})\end{array}$$ (8')

Another way to evaluate λ_n^(½) is completely experimental and does not need an extraction of g_|½|(Δω). This method is based on measurements and the consequent processing of time domain patterns due to dipolar interaction of randomly distributed spins. For pairs randomly distributed in space, the time pattern, V(t), is the product of two patterns, V(t)_ia and V(t)_ir, resulting from intra- (ia) and inter- (ir) pair dipolar interactions:

$$V\mathit{(}t\mathit{)}=V{\mathit{(}t\mathit{)}}_{\mathit{\text{ia}}}V{\mathit{(}t\mathit{)}}_{\mathit{\text{ir}}}$$ (9)

For S= ½ (to a good accuracy)

$$V_{\mathit{\text{ir}}}\mathit{(}t\mathit{)}=\mathit{\text{exp}}\mathit{\{}-\mathit{(}\lambda C\ast t\mathit{)}\mathit{\}}$$ (10)

where C is the spin concentration (mM) and t is the time interval (μs). The flip probability, λ, therefore, can be evaluated from the experimental time domain DEER trace V(t)_ir as

$$\lambda =-\{\mathit{\text{ln}}{V}_{\mathit{\text{ir}}}(t)\}/(C\ast t)$$ (11)

Likewise, λ_n^(½) can be estimated from the experimental time domain DEER trace V(t)_ir,_½ stemming from the inter Gd(III) dipolar interaction for known concentrations.

3.4 Determination of the distance distribution from time domain patterns

There are two simple approaches that can be used in combination or separately to determine the approximate pair distribution function, both of which are based on processing the DEER time domain pattern. One processes the entire time domain trace of V(t)_ia while the other makes use of the dependence of the asymptotic decay $V{(t)}_{\mathit{\text{ia}}}^a$ on pulse durations. In the following, we briefly describe both methods as they were applied to pairs composed of S= ½ centers.

If the pulse durations used in DEER are short (1/t_p≫ω_dd), then V(t)_ia of pairs which have an intrapair distance distribution, f(r), and are randomly oriented with respect to the magnetic field is:

$$V{\mathit{(}t\mathit{)}}_{\mathit{\text{ia}}}\propto 1-{\lambda }_n\mathit{(}1-\underset{0}{\overset{\infty }{\int }}\mathit{\text{drf}}\mathit{(}r\mathit{)}\underset{1}{\overset{-1}{\int }}\mathit{\text{cos}}\mathit{(}{A}_{\mathit{\text{ZZ}}}t\mathit{)}\mathit{\text{dx}}\mathit{)}=1-{\lambda }_n\mathit{(}1-\underset{0}{\overset{\infty }{\int }}\overline{\mathit{\text{cos}}\mathit{(}{A}_{\mathit{\text{ZZ}}}t\mathit{)}}f\mathit{(}r\mathit{)}\mathit{\text{dr}}\mathit{)}$$ (12)

where A_zz is defined by Eq.6 and x ≡cosϑ. The kernel $\overline{cos({\text{A}}_{\text{zz}}\text{t})}\equiv \overline{cos\text{Z}}$ of the integral equation, Eq.12, approaches zero as Z→∞. The decrease of the echo amplitude, therefore, is limited by (1 − λ_n) which is called the asymptotic decay $V{\mathit{(}t\mathit{)}}_{\mathit{\text{ia}}}^a$ (Eq.7). The simplest way to solve Eq.12, as was already demonstrated in [51] is to approximate $\overline{cos\text{Z}}$ by step function, T(Z),

$$\text{T}(\text{Z})\equiv \{\begin{array}{cc}1& \text{Z}<{\text{Z}}^{\ast }\\ 0& \text{Z}\ge {\text{Z}}^{\ast }\end{array}$$ (13)

positioning the step at $\overline{cos\text{Z}}=½$, where Z*≡ ω_ddt* ≈ 0.2 [51,52]. The step position defines the relationship between r* and t* :

$$r\ast =6.4\times {(t\ast )}^{1/3}$$ (14)

where r* is in Ǻ and t* is in ns. After substituting $\overline{cos\text{Z}}$ with T(Z) in Eq. 13, it can be re-written as

$$V{(t\ast )}_{\mathit{\text{ia}}}\propto 1-{\lambda }_n(1-{\int }_{r\mathit{(}t\ast \mathit{)}}^{\infty }f(r)\mathit{\text{dr}})=1-{\lambda }_n{\int }_0^{r\mathit{(}t\ast \mathit{)}}f(r)\mathit{\text{dr}}$$ (15)

The distribution function, f(r), can be derived by taking the derivative of Eq. 15 and using Eq. 14:

$${f(r)|}_{r\ast }\propto -t^{2/3}\frac{d(V{(t)}_{\mathit{\text{ia}}})}{\mathit{\text{dt}}}{|}_{t\ast }$$ (16)

Equally, the distribution function can be derived by processing the TDPs via direct solution of the integral equation (Eq. 12), a truncated SVD method [52], or by using various approaches such as Tikhonov regularization with and without the maximum entropy option [53,54], approximate Pake transformation (APT) and Gaussian fitting which are implemented in free software, such as DeerAnalysis [55] or the software of the National Biomedical Center for Advanced Electron Spin Resonance Technology [56].

The λ₀ measured experimentally may or may not, be equal to nominal value λ_n. The deviation of λ₀ from λ_n is an indication that either the pulses chosen were too long and, as a result, the short distance part of f(r) is missing, or the time interval that was chosen for data collection was too short and so the long distance part of f(r) is missing.

While the effects of the finite pulse duration are unwanted, they can be used to evaluate the distance distribution function. One way to perform such experiments is to keep the duration of observation pulses constant and carry out a set of measurements as a function of t_p. As was already reported in [6, 57], the ratio λ_o/λ_n depends on the relationship between the dipolar interaction, pulse amplitude and duration. As a result, such experiments can yield the distance distribution as well.

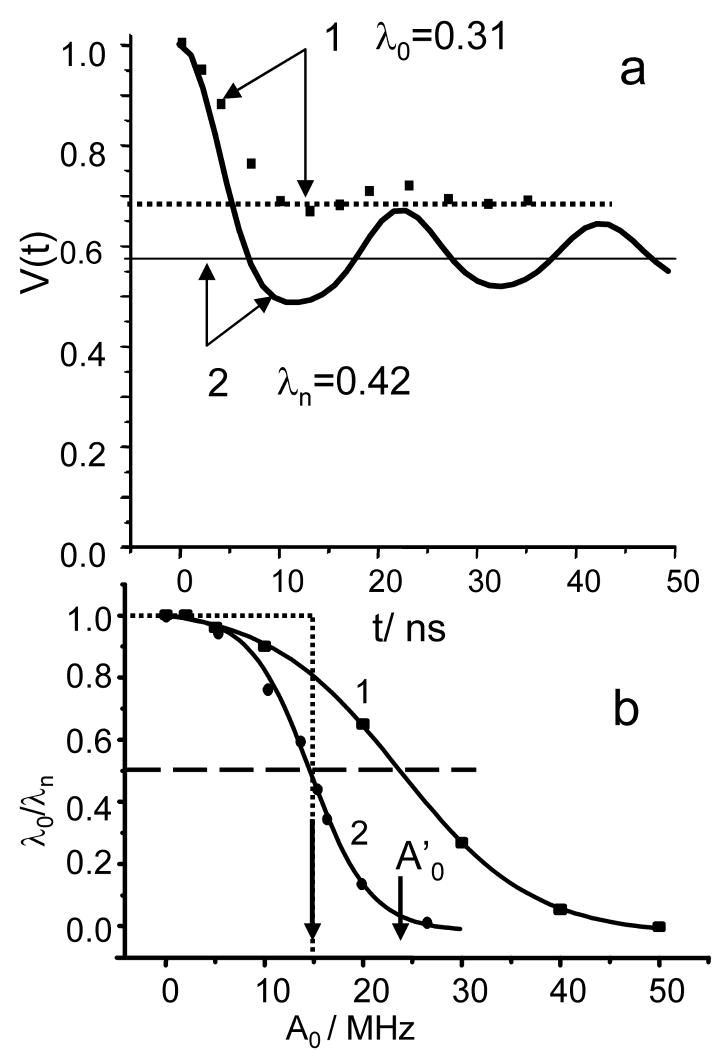
Some quantitative evaluations of the effect have been already presented in literature [6, 57]. To evaluate the effect for our particular set of experimental conditions, we carried out calculations of V(t)_ia as generated by the four pulse DEER sequence using the density matrix formalism in which the dipolar interaction, A_zz (Eq.6) and Δω were included in the rotational (pulse) operators during pumping as well as during observation. The line shape, g(Δω), for simplicity, was chosen to be rectangular. Its width was kept substantially larger than 2A₀ and 2/t_p. The possible interference between pumping and observation pulses was excluded explicitly. The calculations were performed in 2D format where one time coordinate, t′, was the coordinate of echo shape and the other, t, was the position of pumping pulse. Each V(t,t′) was the result of averaging over Δω and cos ϑ. The V(t,t′) was then integrated in a “window” the width of which was chosen to be about half of the echo width, similar to boxcar integrator set up used in the experiments. Numerous calculations were performed for various pulse durations, pulse amplitudes and magnitudes of dipolar interaction. For each set of parameters, the calculations yield time domain patterns similar to one presented in Fig. 4a. In the same figure we also presented the time domain pattern which one would expect for complete excitation of dipolar interaction with the given pulse parameters. It is evident from Fig. 4a that for the particular set of parameters used in the calculations, the loss of asymptotic decay is ∼30%, corresponding to λ_o/λ_n∼0.7. Notably, the oscillation amplitude decreases more quickly than asymptotic decay. Not only distance distributions, therefore, can decrease the amplitude of oscillation but a finite duration of pulses can as well. Repeating such calculations at fixed pulse parameters and various values for dipolar interaction, A₀, allows us to obtain the dependence of λ_o/λ_n on A₀ as it is shown in Fig. 4b. As is evident from Fig. 4b, this dependence is a sigmoid type curve, σ(A₀,t_p,t_o). The inflection point of the curve for each A₀ depends on t_p and t_o. In a simple situation, when the observation pulses are so short that A₀t_o≪1, σ(A₀,t_p,t_o) can be presented as a function of the single parameter, σ(X≡ Rt_p^-1/3), as it is shown in the SI.

Fig. 4.

(a). (1) The time domain pattern (squares) calculated for finite pumping and observation pulse durations in the four- pulse experiment. For the data presented, the observation π pulse was 5 ns, the pumping π- pulse was 10 ns and A₀=50 MHz. The line shape in the calculations was taken as rectangular, having a 200 MHz width. The level of asymptotic decay, λ_o=0.31, is represented by a dashed, straight line. (2) The time domain pattern represented by a solid line is calculated as $1-{\lambda }_n\mathit{(}1-\overline{\mathit{\text{cos}}\mathit{(}{A}_{\mathit{\text{ZZ}}}t\mathit{)}}\mathit{)}$ and corresponds to the complete excitation of the dipolar interaction. The asymptotic decay for this case, λ_n=0.42 (straight solid line), was evaluated using Eq.8.

(b) The dependences of λ₀/λ_n on the magnitude of the dipolar interaction, A₀, for the following parameters: t₀:15ns (π/2 pulse), t_p(π): 12 ns (1), and t_p:40 ns (2). The solid lines are sigmoids drawn through dots. The arrows show the shift of A₀ ≡A₀′ with a t_p variation at the level of λ₀/λ_n=0.5. An example of the step-function used to substitute a sigmoid is represented by a dotted line.

This discussion shows that to reconstruct the detectable part of a distribution function in a rigorous way, one needs to substitute the analytical kernel of integral equation Eq(12), $\overline{cos\text{Z}}$, by a numerical kernel, V(t,t′,A₀(r)), and then proceed as usual. The volume of calculations as a result increases considerably and it requires substantial efforts and time to develop an efficient software package. Modification of widely used existing software is not an option because it is written in MatLab, which is convenient but notoriously slow. We should also take note that with DeerAnalysis [55] to account for a finite length of pumping pulse the modified kernel $\overline{exp(-A_0^2/\Delta {\omega }^2)cos(A_{0}t)}$ was introduced into Eq. 12. Here, the Δω is a function of some pre-determined pumping pulse durations. Unfortunately, even with this option, DeerAnalysis could not be directly used here to process TDPs for a variety of reasons. One of them, for instance, is the lack of 2D output, V(t,t′), which one needs for the correct normalization of TDPs collected with various durations of observation pulses. Since the development of the new software package was certainly a project of its own, for this work we continue to employ an approach similar to that used above: the calculated σ(A₀,t_p,t_o)s were substituted by a step function as shown in Fig.4b. Such a substitution cuts off some still observable short distances in distribution function. The short distance limit in this kind of processing, therefore, is underestimated. Such a shortcoming is compensated for by the convenience of having direct relationship between the characteristic distance (r′) and the pulse durations (t_p, t_o) used in the experiment. As our numerous calculations show, the relationship between r′ and t_p can be presented empirically for fixed duration observation pulses and for rather broad t_p variations as

$$r^{\prime }\cong r_0^{\prime }\times {\{\frac{a+t_p}{b}\}}^{1/3}$$ (17)

where r′₀, a and b are adjustable parameters dependent on the duration of observation pulses. As the step-function approximation implies that pairs having a distance less than r′ do not contribute to dipolar related decay of the TDP, Eq.13 has to be modified, respectively:

$$\text{V}{(\text{t})}_{\text{ia}}\propto 1-{\lambda }_{\text{n}}(1-\underset{0}{\overset{{\text{r}}^{\prime }(\text{tp})}{\int }}\text{f}(\text{r})\text{dr})+\underset{{\text{r}}^{\prime }(\text{tp})}{\overset{\infty }{\int }}\overline{cos({\text{A}}_{\text{ZZ}}\text{t})}\text{f}(\text{r})\text{dr})$$ (18)

The long time decay limit becoming

$$V{\mathit{(}t\mathit{)}}_{\mathit{\text{ia}}}^a\propto 1-{\lambda }_n\mathit{(}1-\underset{0}{\overset{r^{\prime }}{\int }}f\mathit{(}r\mathit{)}dr\mathit{)}=1-{\lambda }_n\underset{r^{\prime }}{\overset{\infty }{\int }}f\mathit{(}r\mathit{)}dr=1-{\lambda }_o$$ (18')

and therefore ${\lambda }_o/{\lambda }_n=\underset{r^{\prime }}{\overset{\infty }{\int }}f\mathit{(}r\mathit{)}dr$ This relationship directly links the relative asymptotic decay and distribution function.

Finally, as follows from Eq. 18, the distribution function still can be determined using Eq.16. but the starting distance has to be shifted respectively, in accordance with Eq. 17.

4. Results and Discussion

4.1 The EPR spectra

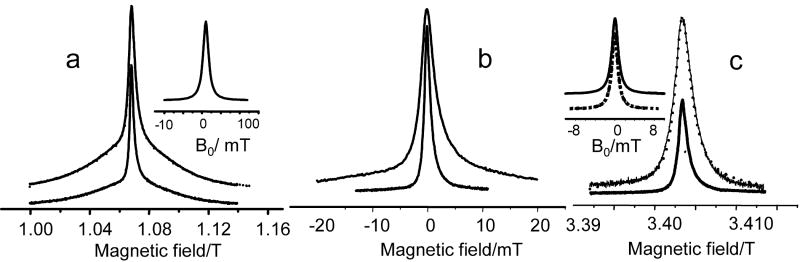
The Ka-band echo detected EPR spectra of Gd595 and C2-Gd595 are shown in Fig. 5a. The spectra consist of a central narrow line, g_|½|(Δω), due to a -½↔½ transition superimposed on a broad background due to all other transitions. The cfi parameter D/gβ can be readily evaluated from the characteristic width of g_|½|(Δω) of Gd595 by means of Eq.3, and was found to be about 180 G. This value, although small, is still within the range of D values known for various Gd complexes. The central parts of the Ka- and W-bands spectra of Gd595 are shown in Fig. 5b. It shows that the characteristic line width decrease from ∼30 G in the Ka-band to 13 G in the W –band which is nearly inversely proportional to the operational frequencies. This observation confirms that the line shape of the -½↔½ transition is primarily determined by the cfi while all other sources of line shape broadening such as unresolved hfi are secondary, justifying our evaluation of D.

Fig. 5.

(a). Solid lines: Ka-band ESE detected EPR spectra of C2-Gd595 (top) and Gd595 (bottom). Experimental conditions: same as in Fig. 3. The dotted line is the result of the convolution monomer spectrum (bottom) with the Lorenzian broadening function, f_B(ν′), shown in the insert.

(b) The central part of the ESE-detected EPR spectrum of Gd595 collected in the Ka-band (top) and W-band (bottom). For W-band measurements, pulse durations: 20ns, frequency: 94.9 GHz, temperature: 25K. c) Solid lines: W-band ESE-detected EPR spectra of C2-Gd595 (top) and Gd595 (bottom). Experimental conditions: same as in (b). The dotted line results from the convolution of the monomer Gd595 spectrum with Lorenzian broadening function, f_B(ν′), shown in the insert. The f_B(ν′), calculated directly from the model distance distribution function presented in Fig. 8 is also shown in the insert by a dotted line.

The spectra of the bis-complex, C2-Gd595, are presented in Figs. 5 a,c along with spectra of Gd595. As is evident from Fig. 5, the central part of the C2-Gd595 spectrum is considerably broader than the central part of the latter. Because of the same local structure around the Gd(III) in both complexes, it is unlikely that the increased width is associated with an increase in D, but rather that it originates from the static dipolar interaction between the two Gd(III) ions. Indeed, at a distance of ∼20 Å, a static dipolar interaction between Gd(III) ions in states m_s=1/2 and m_s=7/2 is already ∼17G and increases to ∼140 G as the distance decreases to ∼10 Å. The attribution of the broadening to static dipolar interactions can be substantiated by comparing the Ka- and W-band spectra of C2-Gd595 and Gd595. The broadening caused by dipolar interactions should remain the same in the Ka- and W-band because cfi effects on the dipolar interaction are negligible.

Evidently, to compare such broadening in a rigorous way, one needs to reconstruct dipolar-broadening related line shapes f_B(ν′) in these mw bands, which is a complicated problem on its own. One can, however, use a simplified approach. It is reasonable to expect f_B(ν′) to be smooth, without explicit singularities, due to the interspin distance distribution in C2-Gd595 and to a variation of the dipolar interactions from complex to complex arising from the presence of different spin states. Any smooth broadening function, therefore, can be used as a probe function. For instance, we were able to reproduce the C2-Gd595 spectra by convoluting the Ka-and W-band Gd595 spectra with simple Lorenzian lines shapes. The widths of the Lorenzians used in the convolutions were very close, ∼10G and ∼9G respectively, as it is shown in Figs. 5a,c. The close similarity of f_B(ν′) for the two bands support the idea that differences in a line shapes between mono- and bis-complexes are mostly due to dipolar interactions. Finally, we built an f_B(ν′) for the -½↔½ transition by taking into account the populations of the spin states, the model distance distribution, which will be discussed later and random orientations of the pairs. Apparently, this f_B(ν′) can be well approximated by a Lorentzian line having a width of ∼8G. As presented in Fg.5c, there is good agreement with the broadening functions used in convolutions.

4.2. Evaluation of the spin flip probability and the asymptotic DEER effect

In the Theoretical Background, we have described how the flip probability, λ_n^(½), can be determined. The λ_n^(½) calculated for particular experimental conditions are presented in Table 1. The main concern in these evaluations is that in the case of C2-Gd595, the static dipolar broadening may result in a line shape with extended tails, which is hard to correctly discern from the background. If the tails are missed in g_|½|, then the λ_n^(½) calculated using Eq. 10 will be overevaluated. There are two ways to address this concern. First, as was suggested in [58], g_|½|(Δω) can be extracted with substantially higher accuracy if the extraction is based on the intensity of proton ENDOR lines rather than what a simple background subtraction would allow, although this procedure is extremely time consuming. Second, as was already mentioned, the λ_n^(½) can be evaluated independently from the analysis of the DEER inter-pair time domain pattern (Eq. 11). These experiments were performed and λ_n^(½) values found from the V(t)_ir,½ processing are presented in Table 1 as well. (In the SI we also presented the complete set of data which shows excellent correlation between λ_n^(½) for various pumping pulse durations evaluated using these two methods). As it evident from Table 1, the two methods of evaluating λ_n^(½) yield similar results. The small difference of less than 20% could be caused by plethora of technical issues.

Table 1.

Nominal λ_n^(½) values calculated for Ka- and W-band using Eq. 11 as compared to that obtained from processing V(t)_ir,½ (shown in parenthesis) The pumping pulse is nominally π pulse.

mw-band	tp/ns	λn(½)
Ka	12	0.055 (0.064)
W	25	0.085 (0.10)

4.3 DEER measurements and their analysis

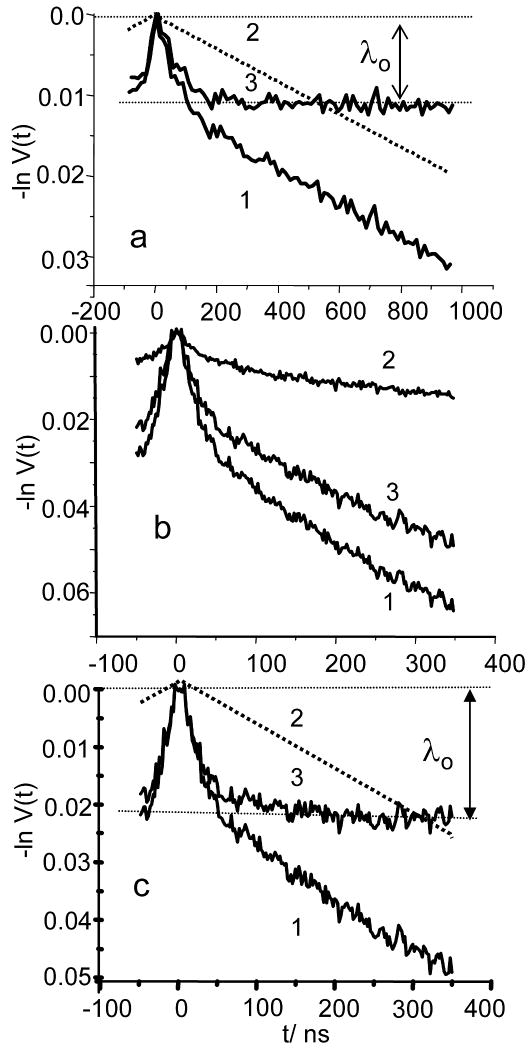
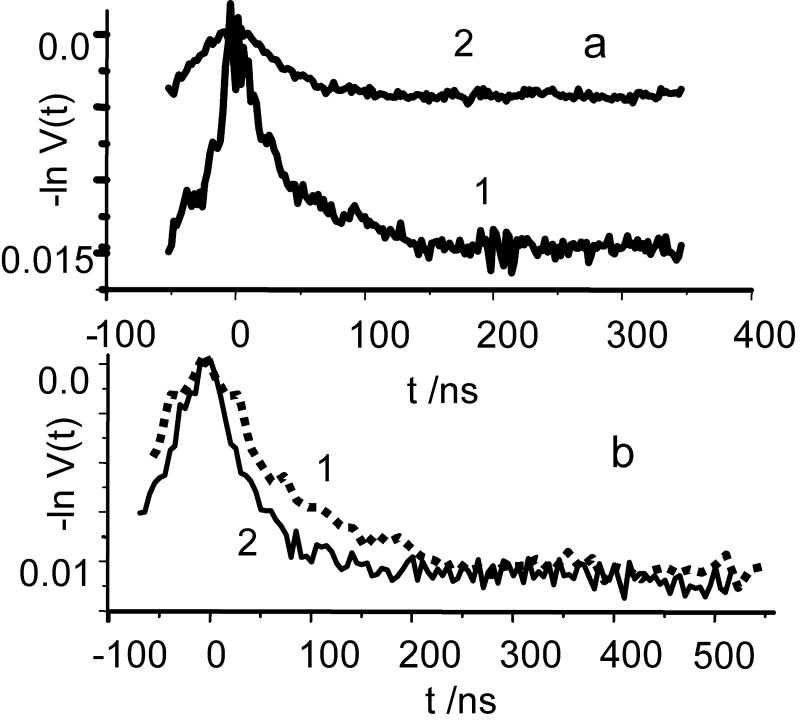
Fig. 6a presents a typical W- band DEER trace of C2-Gd595. The trace consists of an initial steep drop which apparently lasts about 150 ns, followed by a long, substantially slower decay. In Gd595 (trace not shown), the initial steep decay is absent, which allows us to ascribe the latter to intra-pair interaction. The separation of V(t) into intra and inter pair traces, V(t)_ia and V(t)_ir, is shown in Fig. 6a. The V(t)_ia trace shows an initial drop (∼1.1-1.2%) during first ∼200 ns, and then remains constant. The value of this drop, λ₀, however, is about an order of magnitude less than the nominal asymptotic decay value, λ_n^(½) (see Table 1). The V(t)_ia trace is also smooth and does not show any dipolar related periodic oscillations except for the initial fast decay. The Ka-band DEER measurements yield qualitatively similar results. In the Ka-band, however, the relative magnitude of the spectral background becomes more significant than in the W- band. Consequently, the pumping pulse, when set to the maximum of the central transition (see Fig. 3), flips a substantial number of pairs where both spins are in states m_S≠|1/2|. To measure the contribution of the latter, additional DEER measurements were performed in which the pumping pulse was set outside of the central transition. Fig. 6b depicts the initial V(t) traces for the pumping pulse applied to the maximum of the central transition, -200MHz away from maximum and the difference of these traces, V(t)_½. The last trace is decomposed into its V(t)_½,ia and V(t)_½,ir contributions as shown in Figs. 6c. From the V(t)_{½, ia} presented in Fig 6a, c one can immediately conclude that the asymptotic decay λ_o in the Ka-band is about twice of that found in the W-band (2.2% vs 1.1%), despite the fact that λ_n^(½) in the Ka-band is smaller. Nonetheless, even the 2.2% observed for shortest pumpimg pulse is only ∼40% of the estimated λ_n^(½) (see Table 1), while ratio λ_o/λ_n^(½) for the W-band is somewhere between 0.14- 0.11. A closer look at the W-band TDP (see Fig 7b) shows that although the time domain patterns in the W and Ka- bands have similar behavior, the asymptotic decay in the W-band is reached around 250 ns as compared to 180 ns in the Ka- band and the initial decay in the W- band time domain pattern is more gradual. The additional measurements performed in Ka-band (see Fig 7) with longer pumping pulse show a decrease in λ_o and λ_o/λ_n^(½) as well, while asymptotic value are still reached at around 180 ns as far as noise allows to judge.

Fig.6.

(a) (1) W-band DEER time domain pattern of C2-Gd595 (0.1 mM) and it separation into V(t)_ir (2) and V(t)_ia (3). The observed asymptotic decay is denoted as λ_0. Experimental conditions: ν_p: 94.9 GHz and ν_o=ν_p+78MHz; t_p:25ns; t_o:40 ns for the π-pulse; temperature: 25K; repetition rate: 10kHz; total accumulation time:1h 25min. Pumping frequency corresponds to the maximum for the −½↔ ½ transition at a magnetic field of 3.4038 T.

(b)DEER traces of C2-Gd595 (0.5 mM) collected in the Ka band for different field positions of the pumping pulse. (1) Pumping pulse applied to the maximum for the -½↔½ transition, shown in Fig.3. (2) Pumping pulse applied at -70 G from the maximum -½↔½ transition, marked by a solid arrow in Fig. 3. (3) Difference between curves (1) and (2). Pulse durations: t_p=12 ns, t_o=30 ns for π-pulse, ν_p=29.964GHz, ν_o= 29.764 GHz. Repetition rate=1 kHz, total accumulation time=2 hours, temperature=15K. (c)Separation of the DEER trace the of -½↔½ transition (curve 1) into V(t)_ir,_½ (2) and V(t)_{ia, ½} (3) in the same manner as in (a).

Fig.7.

(a) Examples of V(t)_{½, ia} collected in the Ka band for different pumping pulse durations; t_p=16 ns, trace 1, and t_p=32 ns, trace 2. All other experimental conditions are the same as in Fig.6b.

(b) 1-dashed line: extended view of TDP collected in W-band and presented in Fig. 6a, curve 3; 2- solid line : V(t)_{½, ia} collected in the Ka band at the same pulse setting, as was used in W-band. The scale for this TDP is increased by a factor of 2. All other experimental for collecting these data are the same as in Fig.6b.

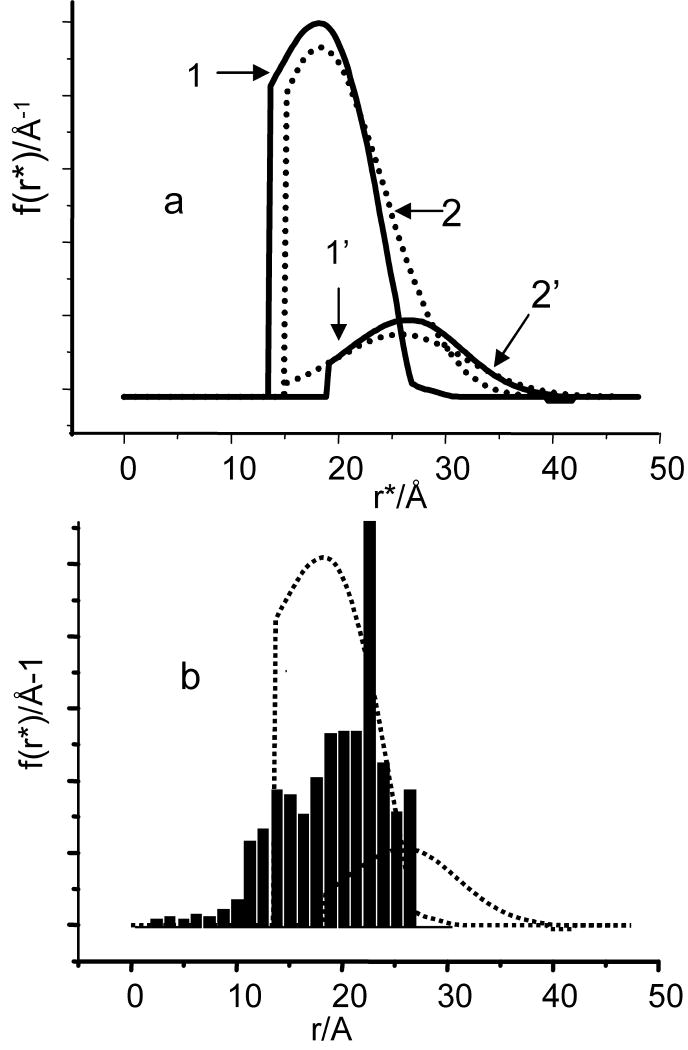
To summarize, three main observed features of the DEER traces for C2-Gd595 in both bands are: the lack of detectable dipolar related oscillations, the magnitudes of the λ_o's, that are small as compared to λ_n^(½) and the completion of the decay at a time interval of no longer than ∼250 ns. We also note a minor feature: some slight difference in the shapes of the TDPs collected in the Ka and W-bands. While all three main features are quite understandable, the the difference is yet to be explained although some plausible hypotheses will be offered later. Here, we continue a discussion of the main features. The lack of a distinctive oscillation pattern can definitely be caused by the broad Gd(III)^- - Gd(III) distance distribution which completely smears the periodic oscillation [52]. The second feature has been already discussed in the Theoretical Background and it is due to the presence of short distances in the pair distance distribution for which ω_ddt_p≥1. The loss in the asymptotic decay is an indication of the fact that a substantial proportion of the pairs (∼60% even for the shortest pulses used) are situated at distances beyond detection. In the “step-function” approximation (see Theoretical Background), these distances are below ∼13Å. The third feature, the completion of decay at times of no longer than 250 ns, is an indication that long distances in the pair distance distribution are limited and that this apparent distance border is about 23-25Å. This crude evaluation, therefore, shows that under the best currently available experimental settings, only about 40% are observable and they are situated at distances somewhere between 13Å and 25Å. Generally, at this point this evaluation is satisfactory to describe distribution function. It is possible to use a more complicated approach as described in the Theoretical Background based on processing the V(t)_ia's using Eq.16 to obtain the distance distribution. This processing requires the differentiation of a DEER pattern which is highly susceptible to the presence of noise. The derivatives, therefore, were taken from spline fitted to time domain patterns. As we processed two different TDPs, collected in the Ka and W- bands, two distribution functions were obtained. These distribution functions normalized to the number of observed pairs are shown in Fig. 8a. The distribution function f(r) obtained from processing Ka band TDP represents about 40% of the configurations. It is close to rectangular, showing distances between 13 and 26 Å. The first moment of this function is about 19Å. The distribution function f(r) obtained from processing the W band TDP represents, at most, 14% of the configurations. It spans between 19Å and 35Å and partially overlaps with f(r). As our analysis shows at least 93%-95% of all configurations are situated at distances of less than 26Å. The difference between the W and Ka-band distribution functions in an integral sense is only ∼5%, due to the part which apparently spans from 26Å to 35Å. Such a difference is insignificant and may be an artifact related to the peculiarities of processing [52].

Fig.8.

(a) Solid lines, 1 and 1′: the parts of the distance distribution functions between the two Gd(III) ions in C2-Gd595, derived by processing intrapair TDPs presented in Fig.6a and c, curves 3. The TDPs were processed in accordance with Eq. 16. The functions are normalized to 0.4 and 0.11. First moment of these functions are 19.2Å and 25Å respectively. Dashed lines: The distribution functions (2 and 2′) obtained by processing the above mentioned TDPs by DeerAnalysys, Gaussian fit option. The functions are normalized accordingly. First moments of these functions were found 21A and 26.5A, respectively. The distribution functions derived by means of two other options, approximate Pake pattern and Tikhonov regularization and simulated TDP are presented in SI.

(b) (bars) The histogram of the distance distribution between Gd(III) ions in C2-Gd595. The details of the distribution modeling are presented in the text. Dashed lines are distribution functions shown in solid lines in (a).

Still, the W-band is expected to be more engaged in DEER measurements in distances below 20Å when hardware adjustment will allow operation with short pulses. If the difference observed in shapes of TDP in W- band and Ka band is due to physical phenomenon it is therefore sensible to consider some apparent explanations to avoid complications in future. So far, a reason which could be provided for the observed phenomenon may be spectral diffusion caused by spin diffusion. Spectral diffusion causes random flips of pumped spins, which may lead to the distortion of the shape of TPD and decrease of the asymptotic decay value. For spectral diffusion to be efficient, at least two conditions must be satisfied. The flip-flop process should be more or less resonant and respective channel in spin-lattice interaction should exist to funnel excess energy. The former occurs when the pseudosecular term in the dipolar interaction (see SI) is comparable to the inhomogeneous line width. Since at the W-band the intrinsic line width becomes more narrow, the spin diffusion and the accompanied spectral diffusion are expected to be substantially more efficient than that at Ka-band. A deeper understanding of the issue will require a separate investigation which using extensive experiments with models of different distances between Gd(III), at different temperatures, etc. If this hypothesis happens to be valid, additional deliberation regarding the choice of mw band for optimal measurements will be required. The choice should be based on the balance between population of ½, - ½ states vs efficiency of spin lattice relaxation, and line width of central transition vs dipolar interaction.

At this point it is perhaps sensible to compare information on distance distribution obtained from processing TDP and from independent source such as molecular geometry simulations. A preliminary examination of the molecule’ geometry shows that distances between two Gd(III) in C2-Gd595 can be anywhere between 10 and 30A. This is certainly in a range of distances covered by the distribution functions found from TDP processing. To obtain more detailed information, we sought to generate distribution functions using standard package for molecular dynamics simulations such as Amber-9. It however turned out to be too complicated and did not yield reliable results. We realized it lacks necessary input parameters for Gd(III) and determination of these parameters is rather complicated. Therefore, we compromise and develop the model for distance distribution simulations in which the flexible bridge composition was approximated as being segments with fixed lengths and angles within the segments. The dihedral angles between two segments were then assigned some arbitrary values. This describes a situation where the rotations around certain bonds in the molecule are free as opposed to the stretching and bending of bonds that are “frozen”. The geometry of the inorganic fragment without the Gd(III) crowns has been optimized at a B3LYP level of theory with a 6-31g* basis set using Gaussian 98. The bond lengths and angles were taken from this optimized geometry and the Gd(III)-O distances of the crown were added later. The histogram of the distance distribution, presented in Fig. 8b, shows that the Gd(III)-Gd(III) distances are in the range of 5-26 Å with an expected maximum around 18-24 Å. The distances below 5Å have low probability and are a consequence of neglecting the size of the atoms. For the sake of comparison, this function presented together with those found from processing of experimental TDPs. As it is evident from Fig.8 all the functions are situated in the same range of distances.

We already discussed above that if the standard software packages [55,56] applied “as is” for processing of our data, it will result in incorrect output information. They however certainly can be used for illustrative purposes. To demonstrate this we processed our data by means of DeerAnalysis [55]. The software has three different options to derive f(r). The results of processing using all three options are presented in Fig. 8a and in SI. While comparing these results with distribution functions derived above, one should keep in mind that (i) the normalization of the distribution function has to be performed independently; (ii) the distribution function can only be related to observed part of molecule configurations; (iii) the cut off distance in DeerAnalysys is internal parameter of the program and can not be changed without proper code modification. Since the shape of TDP which does not have discernable oscillations is determined mainly by first and second moments of distribution function, the shapes of distribution functions obtained by different way of processing are expected to be different but with close values of first moments. Indeed, the first moments of f(r) obtained using three options (Gauss fitting, APT and Tikhonov regularization) were 21Å, 19.4Å and 19.1Å respectively and all close to first moment of f(r), 19.2Å, determined by step-function approximation.

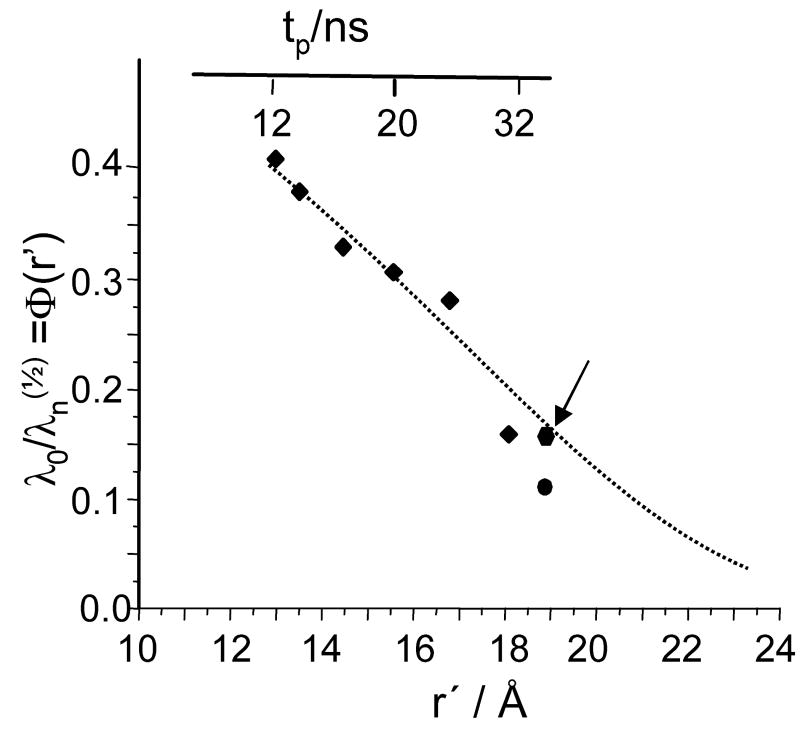
Finally, as mentioned earlier, additional information about distance distribution function can be obtained from the dependence of the asymptotic decay on the pumping pulse duration. The examples of V(t)_ia,_½ collected at various durations of pumping pulses are presented in Fig. 7. The dependence of λ_o/λ_n^(½) on t_p as derived from these kinetics is presented in Fig. 9. This approach to evaluating the distribution function is more experimentally demanding because it requires numerous measurements of time domain patterns at various pulse durations followed by their respective processing. Nonetheless, because it provides independent cross-sections of the distribution function, it is worthwhile to perform this kind of measurements on a one-time basis. In the step-function approximation, λ₀/λ_n^(½) represents the probability of finding C2-Gd595 complexes for which the Gd-Gd distance exceeds a given r′, i.e. $\Phi ({\text{r}}^{\prime })={\int }_{{\text{r}}^{\prime }}^{\infty }\text{f}(\text{r})\text{dr}$, (see Eq. 18′). The λ₀/λ_n^(½) ratio is presented in Fig.9 along with Φ(r′) which is evaluated from the integration of f(r) found as described above by means of processing V(t))_ia,½ (Fig. 8). As is evident from Fig. 9 the Φ(r′) value found by either method are in satisfactory agreement.

Fig. 9.

The part of distribution function, λ_o/λ_n^(½), observable for various pulse settings. Squares are datapoints found from Ka-band measurements, performed at mostly used experimental conditions (as in Figs 6b,8a) The pumping pulse durations, t_p for these datapoints are presented on the top axes while the respective distances, r′, on the bottom axes. The relationship between t_p and r′ for these particular pulse settings are r′≅ 13×{t_p/12}^1/3 (r′in Å, t_p in ns). The circle is a data point obtained from W-band measurements. The diamond (shown by arrow) is the datapoint obtained from the Ka-band measurements for the same pulse settings which were used in W-band. The dotted line was obtained from the integration of f(r), shown in Fig. 8a, curve 1. For comparison datapoints obtained in W-band and in Ka-band one has to take into account absolute accuracy which includes, in addition to common experimental errors, absolute uncertainty in determination λ_n^(½).

As a final reminder, we would like to reiterate that the ultimate goal of this work was to show the general features of Gd based labels linked by flexible linker rather than the particular details of the shape of the distance distribution. Accordingly, the data analysis was deliberately limited to application of a simple, straightforward, step-function approximation. More sophisticated approximations [53,54] can be implemented as well after development of respective software. This step could be necessary if Gd based labels will found widespread applications comparable to that of nitroxide based labels.

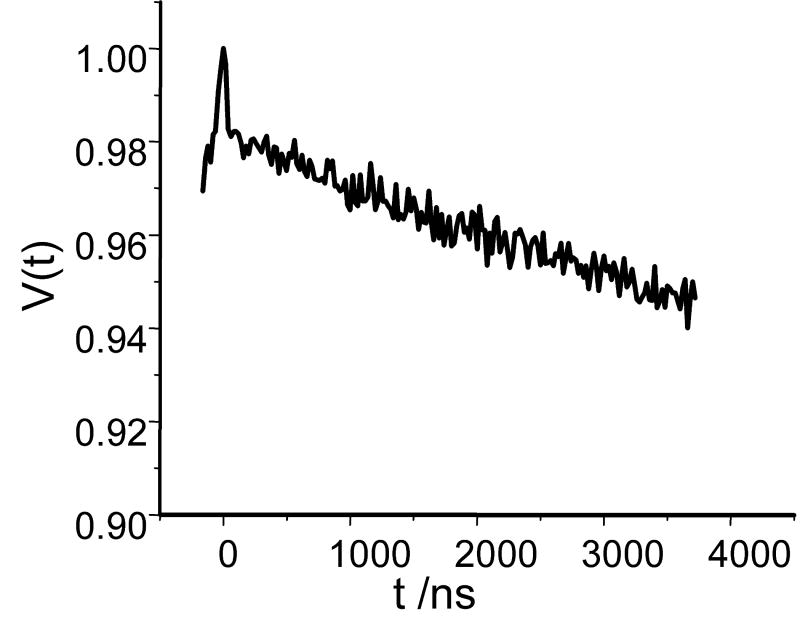
Sofar, all our experiments and discussions girated around the problem of short distances measurements. Preliminary evaluation of the long distance limit in DEER measurements for Gd-based labels is equally desirable since it allows to set broader perspective on their applications. Since we did not have at hand the molecule with large separation between Gd(III)s we used for our evaluations the same molecule C2-Gd595. For this experiment the solution concentration was 0.1mM and the TDP collected with pulse separation of ∼4 μs is presented in Fig. 10. The dwell time was 20ns which was more than adequate to measure long period oscillations but it was too coarse to correctly reproduce the initial decay which amplitude was as a result slightly distorted. Note, that even without distortion the initial decay is only about 40% of expected asymptotic decay as was discussed above. Nevertheless, even in such a worst case scenario the intra-pair decay was about same magnitude that decay due to inter-pair dipolar interaction as required for unambiguous background adjustment. To estimate long distance limit we assume, as usual, that pulse separation should accommodate one period of dipolar related oscillations. Simple calculations then show that distance of ∼60Å is readily accessible. The duration of experiment was 1h 10min and the reslting S/N was about 4:1. Usually, 10:1 S/N is considered a good starting point for data processing. Such S/N can be reached in about 8 hours. Even in Ka-band, therefore, present experimental set up performance Gd based labels is comparable to that for standard nitroxide labels. The W-band performance with respect to distance below 20Å should be better after some instrumental improvements.

Fig.10.

The TDP collected in the Ka-band. The separation between second and third pulses, 4 μs. Pulse durations: t_p=12 ns, t_o=30 ns for π-pulses, ν_p=29.964GHz, ν_o= 29.764 GHz; repetition rate, 3kHz; dwell time, 20 ns; temperature, 10K; concentration, 0.1mM of C2-595; the duration of experiment, 1h 10 min.

5. Conclusion and outlook

In this work, we began to explore the possible advantages of Gd(III) as a spin label for DEER distance measurements in biological molecules with the emphasis on a flexible geometry. The cfi parameter D/gβ for all known Gd(III) ions does not exceed ∼200-400 G. For measurements performed in Ka-band and higher, this allows us to treat, in most cases, this label as an effective S=1/2 system, i.e., the DEER data can be analyzed using the usual expressions for the DEER traces employed for S=1/2. The difference, however, between the Gd(III) DEER and a proper S=1/2 system is in magnitude of the nominal asymptotic decay which for the central transition can not exceed one quarter as compared to unity for proper S=1/2 systems. This occurs as a result of the distribution of populations over a multiplicity of spin states and other particulars of the experiment. While this feature can be regarded as a major shortcoming that lowers the sensitivity of the measurements, it is a drawback for which is compensated by a significant improvement in signal intensity, a more efficient use of mw power permitting the application of shorter mw pulses, and a faster accumulation rate at a lower temperature.

Although all of the possible advantages of Gd-based spin labels stated in the Introduction were not completely realized in this work, the path to achieve them is certainly paved. We have shown that compared to nitroxide spin labels, an improvement in terms of the short distance limit may be obtained. This is afforded by the possibility of generating shorter (π) pulses using same power amplifier and using a large frequency separation between the pump and observe pulses. In terms of long distance limits, we have shown that the Ka-band DEER traces can be easily measured with a time interval of ∼4 μs while a S/N=4 is achieved within ∼70 min at a concentration as low as 0.1 mM. The obvious and straightforward hardware modification should allow to perform measurements at lower concentration and larger pulse separations Another factor that is relevant to the sensitivity issue is the value of D. A larger D will broaden the central transition, reducing the signal intensity and flip probability. The symmetry of the Gd(III) chelator when designing Gd(III) tags for biomolecule labeling has to therefore be considered.

We also acknowledge that despite all of the realized and potential advantages, Gd(III) ions are certainly not universal labels. Firstly, there are indications that Gd(III) based labels are more prone to lose their observable dipolar oscillations versus nitroxides, even in a rigid structure. Their use, by this reason, may be primarily beneficial for distance measurements in flexible biological objects in which distances between labels are distributed in wide limits. In such objects, the oscillations are already non-existent and the advantages of Gd(III) based labels are apparent. Secondly, the Gd(III) based labels can only be used efficiently within a limited range of microwave frequencies, roughly between the Ka and W-bands. At operational frequencies below the Ka-band, sensitivity is lost due to broadening of the central transition, a more complex description of dipolar interactions is required and the extraction of the correct distances becomes complicated. At frequencies higher than 95 GHz and at cryogenic temperatures which are prerequisite to working with Gd-based labels the population of the |½| states becomes substantially lower, leading to a severe loss of pumping efficiency. Higher temperatures cannot, however, be used due to Gd(III) relaxation and possible development of spectral diffusion. As a result of these Gd(III) spin label limitations and the limitations imposed on nitroxide labels described in the Introduction, the use of both of these types of labels. can be complementary in the determination of distance measurements of rigid and flexible biological molecules.

Finally, this work emphasizes that while working with systems having a broad distance distribution (either nitroxide labels or Gd(III)), the setup of pulse durations have to be adequate to measure the distances of interest. Use of too long pulses for TDP acquisitions coupled with the lack of monitoring of asymptotic decay, followed by improper application of standard software for TDP processing may result in apparently different distribution functions for different pulse settings.