Skip to main content
NCBI home page
RNA logoLink to RNA
. 2010 Jul;16(7):1340–1349. doi: 10.1261/rna.1837410

On the significance of an RNA tertiary structure prediction

Christine E Hajdin 1, Feng Ding 2, Nikolay V Dokholyan 2, Kevin M Weeks 1
PMCID: PMC2885683  PMID: 20498460

Abstract

Tertiary structure prediction is important for understanding structure–function relationships for RNAs whose structures are unknown and for characterizing RNA states recalcitrant to direct analysis. However, it is unknown what root-mean-square deviation (RMSD) corresponds to a statistically significant RNA tertiary structure prediction. We use discrete molecular dynamics to generate RNA-like folds for structures up to 161 nucleotides (nt) that have complex tertiary interactions and then determine the RMSD distribution between these decoys. These distributions are Gaussian-like. The mean RMSD increases with RNA length and is smaller if secondary structure constraints are imposed while generating decoys. The compactness of RNA molecules with true tertiary folds is intermediate between closely packed spheres and a freely jointed chain. We use this scaling relationship to define an expression relating RMSD with the confidence that a structure prediction is better than that expected by chance. This is the prediction significance, and corresponds to a P-value. For a 100-nt RNA, the RMSD of predicted structures should be within 25 Å of the accepted structure to reach the P ≤ 0.01 level if the secondary structure is predicted de novo and within 14 Å if secondary structure information is used as a constraint. This significance approach should be useful for evaluating diverse RNA structure prediction and molecular modeling algorithms.

Keywords: RMSD, RNA modeling, P-value, tertiary structure

INTRODUCTION

There is likely to be a large universe of biologically important RNAs with true three-dimensional tertiary folds mediated by long-range and higher-order interactions. Only a small fraction of these structures have been visualized at high resolution. Moreover, there exist many functionally important RNA states, including folding intermediates and elements containing flexible motifs, whose structures cannot be established by direct high-resolution structure determination approaches. Structure–function relationships for these RNAs can, in principle, be addressed by accurate three-dimensional RNA structure modeling.

The field of RNA modeling is developing rapidly and many new ideas have been introduced for obtaining useful structures. Strategies for three-dimensional RNA structure prediction and modeling differ in whether they use all-atom or simplified representations of RNA structure, allow or require expert user intervention, facilitate incorporation of experimental information, or are designed for small versus large RNA motifs (for reviews, see Shapiro et al. 2007; Jonikas et al. 2009). Ultimately, the goal of all modeling approaches is the same: to generate an accurate structural model that is useful for designing, testing, confirming, or rejecting chemical and biological hypotheses.

RNA molecules are built up from just four nucleotide building blocks and form a single predominant secondary structure, the A-form RNA duplex. Thus, RNA structure prediction might be easier than for proteins (Tinoco and Bustamante 1999). Even with these simplifying features, a given RNA can fold into a very large number of potential structures. An RNA of N nucleotides can form roughly 1.8N base-paired secondary structures (Zuker and Sankoff 1984) and a large number of tertiary folds.

The best way of summarizing the quality of an RNA structure model will vary depending on the prediction goals and methods. The quality of a tertiary structure model at the level of its overall fold can be summarized in a simple way as the root-mean-square deviation (RMSD) between predicted and accepted RNA structures over a representative set of atoms; typically, a ribose atom or the phosphate position. A strength of using the RMSD to characterize structure prediction is that this metric can be applied to both simplified and all-atom models. Other metrics are necessary to characterize the accuracy of local interactions. For example, local base pairing and stacking interactions are sensitive to the all-atom RMSD, the global distance test (GDT) (widely used to assess template-based models of protein structure) (Zemla 2003; Keedy et al. 2009), or the recently introduced interaction network fidelity (INF) that applies specifically to RNA (Parisien et al. 2009). The decision to focus on the global fold versus local interactions depends on the specific modeling objective. For longer RNAs with long-range tertiary interactions, it currently remains a major challenge to predict the overall architecture correctly, whereas predictions for small helical RNAs, or of individual motifs within large RNAs, can sometimes correctly identify many individual hydrogen-bonding and base-stacking interactions.

In this work, we develop an approach for evaluating algorithms designed to predict the overall architecture of relatively large RNAs (50–200 nucleotides [nt]) characterized by extensive long-range interactions that involve more than individual helices (for example, Fig. 1A). We focus on metrics for assessing the global fold of an RNA at roughly “nucleotide resolution,” which is also the level of RNA structural information that is obtained from most biochemical experiments when applied to large RNAs. This class of experiments includes chemical probing, through-space cleavage and cross-linking, and solution hydrodynamic measurements. To this end, we address the magnitude of RMSD that constitutes a successful prediction as opposed to models that are not significantly different from those expected by chance. Throughout this work, we compare structures based on RMSDs calculated over all phosphate positions, although our conclusions apply to correlations calculated at any backbone position.

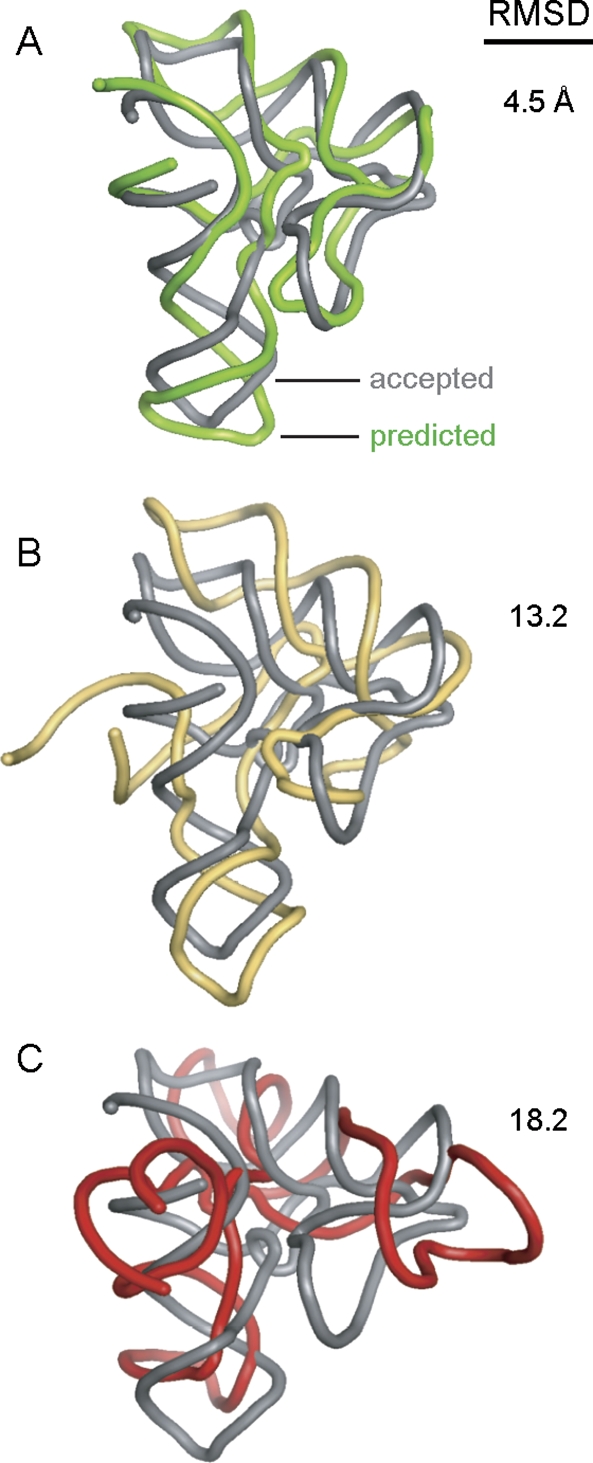
FIGURE 1.

FIGURE 1.

Open in a new tab

Comparison of an accepted RNA structure with modeled tertiary structures as a function of RMSD similarity. The experimentally determined (Montange and Batey 2006) and simulated structures of the SAM riboswitch (94 nt, 2gis) are shown as gray and colored backbones, respectively (A–C).

Success and failure for tertiary structure prediction are obvious at the extremes. For example, for an RNA of moderate size like the SAM-I riboswitch (94 nt) (Winkler et al. 2003), a model with 4.5 Å RMSD relative to the crystallographically determined structure (Montange and Batey 2006) clearly corresponds to a good prediction, whereas a prediction at 18 Å RMSD is unlikely to be helpful in generating strong, testable biological hypotheses (Fig. 1A,C). At 13.2 Å RMSD, a model for this RNA clearly resembles the experimentally determined structure (Fig. 1B). However, given the intrinsic rigidity of RNA helices and the limited number of nucleotide building blocks, it is not clear whether a model that differs from the accepted structure by 13.2 Å RMSD constitutes a successful prediction, especially if the secondary structure is used as a constraint during modeling.

RNA chain length is an important variable in establishing the RMSD value that describes a nonrandom prediction. The range of RMSD values that correspond to similar RNA structures increases with chain length. For example, two RNAs with a 4.5 Å RMSD are similar if their lengths are 94 nt (Fig. 1A), but are dissimilar if they comprise short base-paired duplexes. This feature is common to both protein (Cohen and Sternberg 1980; Reva et al. 1998) and RNA structure prediction, but may be more pronounced with RNA for two reasons. First, structured RNAs tend to be more elongated and less globular compared with proteins of similar mass. Second, stacked helices comprise the major structural building block for RNA, are relatively rigid, and can span large linear dimensions. If a helix is modeled to be in roughly the right place, but is angled relative to the correct orientation, this error can propagate to produce large RMSD values with modest degrees of angular deflection.

A second criterion distinctive to RNA structure prediction is that the pattern of base pairing that comprises an RNA secondary structure is often known with perfect or near-perfect accuracy prior to three-dimensional modeling. Accurate RNA secondary structures can be obtained from comparative sequence analysis (Michel and Westhof 1990; Gutell et al. 2002; Roth and Breaker 2009) and experimentally constrained prediction (Deigan et al. 2009). Most RNA helices, including those that incorporate mismatched and noncanonical base pairs, will show good (<2 Å RMSD) alignments if the structure is simply assumed to be A-form. For large RNAs, enforcement of native-like base pairing dramatically reduces the allowed conformational space. RMSD values for predicted structures should therefore be significantly smaller if information regarding base-pair constraints is included in the modeling algorithm.

In this work we develop a framework for assessing the confidence that a predicted RNA tertiary structure is significantly different from a chance prediction. We generate a large number of decoy structures using replica exchange discrete molecular dynamics (DMD) simulations and then calculate the magnitude of RMSD that indicates any two structures are more similar than two randomly generated, but still RNA-like, chains. We also establish an empirical power-law relationship for mean RMSD as a function of chain length that makes it possible to define analytical expression for the significance and nonrandomness of RNA structure prediction.

RESULTS

Selection of target structures

RNA structures, ranging in size from 27 to 161 nt, were obtained from the RCSB structure database (Table 1). RNA structures were required to (1) be solved at a resolution of 3.3 Å or better; (2) have nontrivial higher-order tertiary interactions, defined as having close helix packing, long-range intrastrand interactions, or a pseudoknot; (3) contain a single complete or nearly complete chain; and (4) form a stable tertiary structure in the absence of protein binding. We excluded RNAs that form simple A-form helices or stem–loops or that form Y-shaped structures without significant long-range tertiary interactions. For RNAs with multiple structures, the example with the best resolution or that was the most complete was selected. The RNA structures were also chosen to be distributed evenly over the 27–161-nt length range, given the examples available in the current RCSB database (Berman et al. 2000).

TABLE 1.

RNA targets with decoy structures generated by DMD

graphic file with name 1340tbl1.jpg

Open in a new tab

Generation of decoy structures by DMD

Ideally, the quality of an RNA tertiary structure prediction would be determined by comparing the agreement between a predicted versus an experimentally determined model. This similarity would then be compared with the differences observed between members of a diverse group of experimentally determined decoy structures of similar size. Unfortunately, even with the recent increase in high-resolution structures, there are still too few known RNA structures to serve as a statistically valid set of decoys in any given size range.

We therefore used replica exchange DMD simulations (Ding et al. 2008a) to generate decoy structures for representative RNAs. RNA decoys were generated by DMD using a coarse-grained model in which each nucleotide is represented as three pseudo-atoms corresponding to the phosphate, sugar, and base moieties (Ding et al. 2008a). Interactions between pseudo-atoms include bonded, nonbonded, and loop entropy terms. This coarse-grained RNA model yields topologically reasonable RNA-like folds for a large number of small RNAs (Ding et al. 2008a) and for tRNA when constrained by pairwise experimental information (Gherghe et al. 2009). Replica exchange DMD makes it possible to efficiently overcome energy barriers in a rugged energy landscape and to explore conformational space broadly while simultaneously maintaining conformational sampling in a regime that corresponds to a physically relevant free energy surface (Zhou et al. 2001; Okamoto 2004).

A priori knowledge of the secondary structure dramatically increases the correlation (and therefore reduces the RMSD) between simulated and experimentally determined structures. We therefore also generated decoy structures for each target RNA in which the DMD pseudo-atoms corresponding to the bases were constrained to pair. In all cases, we selected for compact decoy structures by requiring that the radius of gyration be within 1.2-fold of the native structure.

Analysis of RNA decoy structures

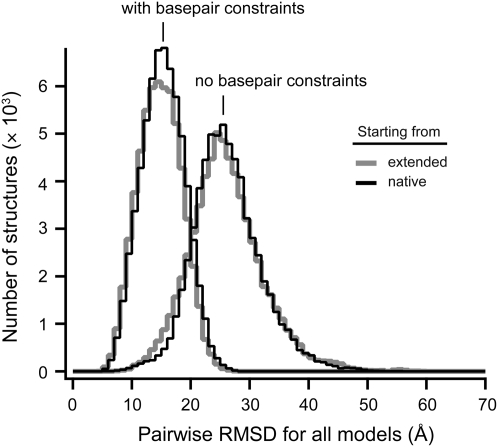
To generate an ensemble of statistically significant decoy structures, the replica exchange DMD simulations must reach equilibrium in conformational sampling. We therefore evaluated whether the DMD ensembles generated from different starting states converged. We initiated simulations starting from two very different starting states, the experimentally determined native structure and a linear, extended, structure generated in silico for seven of the target RNAs (Table 1, 1q9a, 1l2x, 1xjr, 1u8d, 2gis, 1nbs, 1gid). Both the pairwise RMSD distributions (Fig. 2) and DMD energies (data not shown) were nearly identical for simulations initiated from either the native or fully extended states. This similarity in the final distribution of structures holds independent of whether the native pattern of base pairing is imposed during the simulation (Fig. 2). Thus, replica exchange DMD yields fully equilibrated sets of RNA decoy structures for RNAs as large as 161 nt.

FIGURE 2.

FIGURE 2.

Open in a new tab

Replica exchange DMD simulations as a function of starting state and of enforcing native base pairing. Simulations were initiated either from the crystallographic structure or from a linear, extended state for the purine riboswitch (67 nt, 1u8d) (Batey et al. 2004).

We then used replica exchange DMD to generate decoy structures for our complete set of RNAs (Table 1) and calculated RMSD values for all pairwise combinations of decoy structures. Representative RMSD distributions for a viral RNA pseudoknot (28 nt), the purine riboswitch (67 nt), and the specificity domain of RNase P (155 nt) are shown in Figure 3. These profiles have three critical features.

FIGURE 3.

FIGURE 3.

Open in a new tab

Distributions of decoy structures. RNA decoy structures were stimulated using replica exchange DMD starting from fully extended linear structures either without or with constraints that enforce the native pattern of base pairing (solid gray lines). Distributions show good Gaussian-like behavior (dashed lines). RNAs shown are a viral RNA pseudoknot (28 nt), the purine riboswitch (67 nt), and the specificity domain of RNase P (155 nt) (Egli et al. 2002; Krasilnikov et al. 2003; Batey et al. 2004; Gherghe et al. 2008). Standard deviations are ∼1.8 ± 0.3 Å in all cases, with the exception of the narrower distribution for the 28-nt pseudoknot RNA with base-pair constraints.

First, the pairwise RMSD distributions are Gaussian-like (Fig. 3, cf. solid and dashed lines). A Gaussian-like distribution in pairwise RMSD distribution is consistent with the Central Limit Theorem that holds that the sum of a large number of random variables (structures) should be normally distributed. Gaussian-like behavior also means that each distribution can be characterized by its mean RMSD value and a standard deviation.

Second, mean RMSD values increase as a function of chain length (Fig. 3; Table 1). Hence, no single RMSD value represents a nonrandom prediction. An RNA modeling algorithm must therefore produce structures with comparatively smaller RMSD values for short RNAs if these structures are to be better than those expected by chance.

Third, imposing the native pattern of base pairing has a large effect on the RMSD distributions. Constraining structures to have native base pairing biases the distribution to smaller RMSD values by 4–15 Å, depending on RNA length (Fig. 3; Table 1).

A power-law relationship for the radius of gyration and chain length in RNA

Given the mean and standard deviation distribution for each RMSD profile, we will derive below an analytical expression relating RMSD to chain length (N). We therefore sought to determine the proper mathematical form for this relationship. The mean RMSD for protein structure prediction is approximately proportional to the radius of gyration. This relationship reflects that the distances between corresponding atoms in two structures scale with the overall dimensions of the macromolecule (Reva et al. 1998). We expect that the mean RMSDs will also scale in a similar way with chain length and the radius of gyration for RNA.

We calculated the radius of gyration, Rg, for all of the RNAs in our target set (Table 1) plus a set of additional RNAs to more fully populate the Rg versus N curve (Fig. 4). The best fit gives:

graphic file with name 1340equ1.jpg

The key result is the exponent, 0.41, which lies between the values expected for a molecule composed of closely packed spheres (1/3) and for a self-avoiding chain (3/5) (Doi 1996). This exponent is different from a prior analysis that suggested Rg for RNA scales with an exponent of 0.33 (Hyeon et al. 2006). The earlier work did not filter simple helices of 25 nt or less and included the 16S and 23S ribosomal RNAs, which achieve their structures only as ribonucleoprotein complexes. Excluding these two sets of RNAs from the Hyeon et al. (2006) data set yields an exponent consistent with this work.

FIGURE 4.

FIGURE 4.

Open in a new tab

Dependence of radius of gyration on chain length for compact RNAs with higher-order tertiary structure interactions. Fits to the 0.33 and 0.60 exponents (but not to the 0.41 exponent) show systematic deviations from the points.

Both Pearson's correlation coefficient and the nonparametric Wald–Wolfowitz test indicate that the 0.41 exponent better fits the Rg data than either of the other two limits (Fig. 4). This result is intrinsically satisfying because it suggests that folded RNAs are more structured than random self-avoiding chains, but do not fully maximize their packing density. This exponent is also slightly larger than the 0.33 value found for proteins (Reva et al. 1998), consistent with the less-globular structures of most RNAs relative to proteins of the same mass (Holbrook 2008).

DISCUSSION

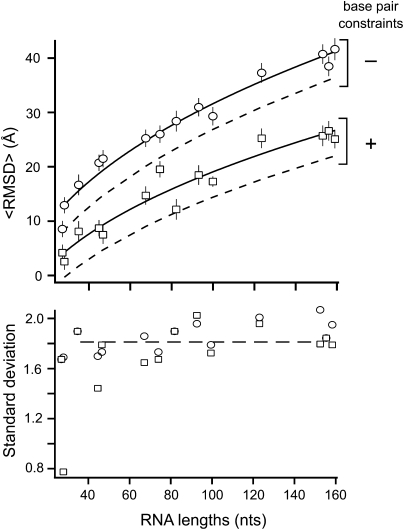
We have used DMD to calculate statistically significant sets of decoy structures for a representative set of RNAs. These decoy structures correspond to compact, RNA-like, but largely incorrect structures for each target RNA. Mean RMSD values increase with chain length, both when base pairing was allowed to vary or was constrained to correspond to that in the accepted structure (Fig. 5, top). In both cases, these distributions are well fit by a power-law relationship, a N0.41 – b, where the exponent 0.41 is derived from Rg and N (Fig. 4; Box 1). Since the mean RMSDs defined by the empirical relationship with respect to RNA length should be positive, the RNA length should be N > Nc = (b/a)1/0.41. The critical length, Nc, is ∼5.3 when no base-pair information is imposed during modeling and 16 Å when base-pair constraints are enforced (a and b for a chance prediction are given in Box 1). These values are sensible and correspond to the minimal lengths of RNA with significant secondary and tertiary structures. Mean RMSD values increase by roughly fivefold as chain length increases from 27 to 161 nt.

FIGURE 5.

FIGURE 5.

Open in a new tab

Mean pairwise RMSD as a function of RNA chain length. Decoy structures either constrained to form base pairs found in the experimentally determined native structure or allowed to form any energetically favorable set of base pairs are shown. Solid lines correspond to distributions expected for RNA-like, but chance, folds. Dashed lines indicate the RMSD cutoff corresponding to a prediction better than that expected by chance at the P < 0.01 level. Lines indicate fits to the power-law relationship 〈RMSD〉 ≈ a N0.41-b ; a and b values are given in Box 1. The mean and standard deviation for each distribution are shown with symbols and error bars.

BOX 1.

Significance (P-value) analysis for RNA tertiary structure prediction

graphic file with name 1340tbl2.jpg

Open in a new tab

In contrast, the standard deviation in RMSD for each distribution is approximately constant at 1.8 Å (Fig. 5, bottom). It is not clear what physical property of RNA governs the relative invariance of the standard deviation in RMSD; interestingly, a similar behavior appears to hold for protein structure (Reva et al. 1998).

These distributions (Fig. 5) represent a measure of the agreement between any two structure predictions for an RNA of a given size as expected by chance. Although we generated these distributions based on a specific DMD model for the RNA decoy structures, available evidence suggests these relationships are general. First, the DMD model captures the driving forces of RNA folding and is able to predict the native structures of many small RNAs from a large set of competitive decoys (Ding et al. 2008a). Second, the replica exchange simulation efficiently samples RNA conformational space, which is populated by many thermodynamically viable decoy structures with competitive base pairing and higher-order packing interactions. Third, similar distributions are obtained by creating decoys using an alternative approach, by threading short RNA sequences onto the structures of longer RNA molecules (see Materials and Methods). Critically, analysis of the effect of enforcing the native pattern of base pairing on pairwise RMSD (Fig. 3) is only possible with the DMD-based approach for generating decoys.

Using the empirical relationships for RMSD distribution as the function of RNA length (Fig. 5), it is possible to create a scoring function for the significance of an RNA tertiary structure prediction given the chain length (N) and the RMSD relative to the accepted structure (Box 1). This assessment of RNA tertiary structure prediction can be summarized as a P-value. Smaller P-values correspond to predicted structures with greater statistical significance.

The P-value calculation provides a broad measure of prediction quality for RNAs between 35 and 161 nt. These P-values can be used to evaluate predictions for both small and large RNAs and for algorithms that make use of prior information about base pairing versus those that predict all interactions de novo.

The mean and standard deviation obtained for each distribution can also be used to calculate the RMSD between a known and predicted three-dimensional structure that corresponds to a predicted structure which differs from a random prediction at a chosen confidence level. We suggest that P < 0.01 represents a successful prediction (Fig. 5, top, dashed lines). Analytical expressions for the RMSD that corresponds to a chance prediction versus that for a successful prediction at the P < 0.01 level are given in Box 1.

Our laboratories are developing accurate and efficient methods for modeling complex RNA structures (Badorrek et al. 2006; Ding et al. 2008a; Sharma et al. 2008; Deigan et al. 2009; Gherghe et al. 2009; Lavender et al. 2010). Many other laboratories are also making innovative contributions to the RNA modeling field (Massire and Westhof 1998; Tan et al. 2006; Das and Baker 2007; Das et al. 2008; Parisien and Major 2008; Yu et al. 2008; Jonikas et al. 2009). We undertook the present study in order to create a framework for benchmarking any RNA modeling algorithm. We illustrate the usefulness of the P-value approach outlined here by considering two recent studies that have focused on refining the tertiary fold of tRNA.

For an RNA the size of yeast tRNAAsp (75 nt), a model should have an RMSD over all phosphate atoms of 10.0 Å or better to reach P ≤ 0.01 if the native pattern of base pairing is enforced during modeling. For comparison, RMSD values between tRNAAsp and two unrelated RNAs of similar size, the HDV and thi-box RNAs, are 23 and 27 Å, which correspond to the near-maximal P-value of 0.99. In contrast, the free tRNAAsp and its energetically accessible protein-bound conformation superimpose with an RMSD of 6.5 Å (P = 0.00001) (Fig. 6).

FIGURE 6.

FIGURE 6.

Open in a new tab

Use of P-values to benchmark RNA tertiary structure models. (A) Spheres represent P-values for seven models (indicated with Mx) of tRNAAsp based on experimentally derived tertiary structure information, refined by DMD (Gherghe et al. 2009). (Squares) P-values for three refinements (indicated with Nx) of tRNA using a one-bead model for RNA and filtering by hydroxyl radical and SAXS data using the NAST program (Jonikas et al. 2009). P-values for comparison of tRNAAsp (2tra, 75 nt) (Westhof et al. 1988) with two unrelated RNAs of similar size, the HDV ribozyme (1vby, 76 nt) (Ke et al. 2004), and the Thi-box riboswitch (3d2g, 77 nt) (Thore et al. 2008), plus tRNAAsp as it exists when bound by its synthetase (1asy) (Ruff et al. 1991), are shown as a horizontal bar and a filled circle, respectively. RMSDs are calculated over all phosphate positions with the exception of the NAST models, which correspond to the C3′ atom. (B) Comparison of RMSD and GDT-TS values for the seven Mx tRNA models (open circles), plus the comparison between the 2tra and 1asy structures (filled circle).

In one approach, native-like tertiary structures for yeast tRNAAsp were obtained given only the sequence and using a combination of SHAPE chemistry (Merino et al. 2005; Wilkinson et al. 2006) and pairwise constraints generated using a sequence-directed cleavage agent. This biochemical information was then refined using DMD (Gherghe et al. 2009). The cleavage agent was placed at nucleotide positions 4, 49, and 67 in tRNAAsp, and structures were refined using the tertiary constraints provided by any one, two, or all three experiments for seven possible total refinements (Fig. 6A, summarized as spheres). Of the seven refinements, five yielded models with P-values significantly lower than 0.01 (Fig. 6A). These refinements correspond to P-values of 2.0 × 10−5 to 2.0 × 10−3 (calculated given the correct pattern of base pairing as established by SHAPE). Two structures refined to RMSDs of ∼10.8 Å, corresponding to a P-value of 0.03, which represent fair predictions, but not equivalent to the P < 0.01 level.

In a second approach, tRNA was modeled by representing each nucleotide as a single bead centered at the C3′ atom, enforcing base pairing, and filtering structures based on hydroxyl radical cleavage and SAXS data using the NAST program. Resulting models for E. coli tRNAPhe (76 nt) had RMSDs of 8.0, 13.6, and 15.8 Å (Jonikas et al. 2009). Although these RMSD values were calculated at the C3′ position, comparison with the framework developed here is appropriate because RNA backbone atom positions are highly correlated (see Materials and Methods). These RMSD values correspond to P-values of 0.00023, 0.36, and 0.80 (Fig. 6A, squares); the first of these represents a prediction at the P < 0.01 level. Overall, this analysis of two recent and different approaches for refining RNA structure models makes clear that experimentally constrained modeling of complex RNA structures has substantial promise for refining structures to P-values ≤0.01, but that additional effort is required to reach this level consistently.

An alternative to the RMSD, the GDT is a good indicator of similarity between two structures. The GDT total score (GDT-TS), as implemented in the LGA program (Zemla 2003), has been widely used to rank protein models (Keedy et al. 2009; Zhang 2009) and, recently, to evaluate RNA structures (Jonikas et al. 2009; Parisien et al. 2009). LGA uses multiple alignments and calculates the largest set of atoms that deviate by less than a user-defined cutoff. GDT scores span a uniform scale with zero equal to no similarity and 100 indicating near perfect agreement. It had not been determined what GDT-TS score corresponds to a significant tertiary fold prediction for tRNA. We find that RMSD and GDT-TS are highly correlated (r2 = 0.86) for RNA models at medium resolution (Fig. 6B, open circles). A GDT-TS value ≥37 indicates a strong prediction, with a P-value >0.01 (as defined in Box 1). However, the GDT-TS increases rapidly as structures become highly similar. This is exemplified in the comparison of free tRNAAsp with it synthetase-bound form. Of the 75 nt that comprise these two structures, 70 positions have RMSDs <5 Å. The remaining nucleotides have large variations, with RMSDs >10 Å. This gives a GDT-TS of 51, whereas the overall RMSD is 6.5 Å (Fig. 6B, filled circle). Thus, for very detailed analyses involving threading, homology modeling, or evaluating single site mutations, the GDT-TS is more discriminating. However, for evaluating RNA modeling at the level of the global fold, especially for RNAs with long-range tertiary interactions, the RMSD and GDT-TS are both good metrics for determining similarity.

Returning to our original example oulined in Figure 1, a 4.5 Å RMSD for an RNA of 94 nt using an algorithm that enforces native base pairing (Fig. 1A) corresponds to a highly significant prediction (P ≤ 10−6). In contrast, a 18.2 Å RMSD (Fig. 1C) is readily identified as a poor prediction by its P-value = 0.74. For an RNA of 94 nt, the 13.2 Å prediction falls at the P = 0.016 level. Inspection of the agreement between this structure and the accepted structure (Fig. 1B) supports the view that this prediction lies near the lower limit at which the model might be useful for designing instructive biological hypotheses. P-value significance testing should prove broadly useful in ongoing efforts to benchmark and improve RNA tertiary structure prediction and modeling algorithms.

MATERIALS AND METHODS

Target RNAs and analysis of power-law relationships for RNA

RNA structures were obtained from the RCSB structure database (Berman et al. 2000). For RNAs with multiple structures, the example with the best resolution or that was most complete was selected. If the U1A protein was present to facilitate crystallization (Ferré-D'Amaré and Doudna 2000), this protein component was removed. To establish a power-law relationship between the radius of gyration and RNA length, we calculated the radius of gyration (Rg) for the structures in Table 1, plus the following (listed by PDB code): 1ato, 1nem, 2tob, 1q9a, 1l2x, 437d, 1eht, 1rnk, 1fmn, 1q8n, 1mme, 1xjr, 2qwy, 3e5c, 1kh6, 2goz, 1u8d, 1y26, 1eov, 1tra, 1vby, 3d2g, 2hoj, 2gis, 1z43, 2gcs, 1nbs, 1gid, 2qbz, 1u9s, 3djz, 1u6b, 1x8w, 3bwp, and 2a64. The radii of gyration were fit to Equation 1. We used both Pearson's correlation coefficient, r, and the nonparametric Wald–Wolfowitz test to evaluate whether the best fit exponent of 0.41 is better than the limits for closely packed spheres (0.33) or a self-avoiding chain (0.60). P-values for the latter two values were 0.0096 and 0.0003, which indicate statistically significant deviations; in contrast, the P-value for the 0.41 exponent was 0.24, indicating no significant deviation from the proposed power-law model. We also calculated the exponent for a complete data set of all RNA structures in the RCSB database (as described by Hyeon et al. 2006). The exponent over all deposited structures is 0.33, exactly as reported previously; however, if short (<25 nt) and ribosomal RNAs are excluded and only single-chain RNAs are considered, the exponent is 0.46, in agreement with the analysis shown in Figure 4.

Generation of RNA decoys by replica exchange DMD

We used replica exchange DMD (Ding et al. 2008a,b) to explore RNA conformational space and generate statistically valid ensembles of decoy structures. Each RNA nucleotide is represented as three pseudo-atoms representing the phosphate, sugar, and base moieties (Ding et al. 2008a). Bonded terms included bond angles and dihedrals; nonbonded terms included base pairing, stacking, hydrophobic, and phosphate–phosphate repulsion interactions; an explicit term was included for loop entropy. Replica DMD simulations were performed in parallel over temperatures ranging from low (T = 0.20) to high (T = 0.24); this temperature range covers the folding temperatures of the coarse-grained RNA model (Ding et al. 2008a). Replicas with neighboring temperature values were periodically (every 2000 time units [tu]) exchanged in a Metropolis manner. Temperatures were exchanged between two replicas, i and j, at temperatures Ti and Tj, and with energies Ei and Ej according to the exchange probability ρ, where ρ = 1 if Δ = (1/kBTi - 1/kBTj)(Ej - Ei) ≤ 0, and ρ = exp(-Δ), if Δ > 0. Simulations were carried out for 800,000 tu, yielding 12,000 structures. Decoy generation for a 150-nt RNA requires ∼20 h on a single-core equivalent Xenon CPU (2.3 GHz). Individual structures were accepted for pairwise analysis subject to the following: (1) simulations were allowed to equilibrate for 200,000 tu to exclude structures that reflected residual memory of the starting state; (2) frames were required to be different by 200 steps to exclude correlated consecutive structures; and (3) structures were required to be compact and have a radius of gyration that was within 1.2-fold of the accepted structure.

Generation of RNA decoys by threading

As an alternative to using replica exchange DMD to generate decoy structures, we also generated decoys by threading the SARS pseudoknot (47 nt) and the guanine riboswitch (67 nt) onto a set of longer RNA structures (1u8d, 1gid, 1nbs, 1xjr, 1z43, 2gcs, 2tra, 2qbz, 3irw, 3gx3, 3d0u, 3d2g, and 3kc4 3kcr). Decoys, corresponding to 47 or 67 nt segments in the long RNAs, were filtered by the structures that (1) have Rg values within 1.2-fold of the test RNAs and (2) initiate at positions at least 10 nt apart. The limitations of this approach are that the number of decoy structures is small and a subset does not have realistic secondary structures. It is also not possible to use threading to constrain the secondary structure to be native-like nor to generate realistic decoys for structures much larger than 70 nt, given the current structure database. RMSD distributions for the pseudoknot and riboswitch RNAs are 18.7 ± 2.4 and 22.2 ± 2.6 Å, in good agreement with the decoys generated by DMD.

Pairwise RMSD and Gaussian distribution calculations

RMSD was calculated as:

graphic file with name 1340equ2.jpg

where A is an arbitrary rotation matrix. The calculation was performed using the Kabsch algorithm (Kabsch 1976) over all phosphate positions in each RNA. RMSD distributions were fit to a Gaussian curve,

graphic file with name 1340equ3.jpg

where A is the amplitude, x0 is the mean, and σ is the standard deviation.

Effect of calculating RMSD values over other RNA atoms

We calculated RMSDs for free tRNAAsp (2tra) (Westhof et al. 1988) relative to this tRNA as bound by the tRNA synthetase (Ruff et al. 1991) (RNA molecule in 1asy). RMSD values as a function of atom are: phosphate, 6.80 Å; C3′, 6.37 Å; C4′, 6.66 Å; N1, 6.59 Å; N3, 6.68 Å; and over all atoms, 7.11 Å. The single-atom RMSD values are essentially identical; the all-atom value is larger by 0.3–0.6 Å.

Calculation of confidence intervals

The P < 0.01 line in Figure 5 was calculated from a standard Z-score relationship. For P < 0.01, the RMSD value is obtained as:

graphic file with name 1340equ4.jpg

The RNA prediction significance, or P-value, is also calculated from the Z-score, given a predicted structure that differs from an accepted structure by an RMSD of m:

graphic file with name 1340equ5.jpg

where 〈RMSD〉 is the expected RMSD obtained from the best-fit relationship in Box 1 and is a function of chain length, N; σm is the standard deviation for decoy structures of length N (Fig. 5, bottom). For predictions of RNAs with lengths ≥35 nt, this value is approximately constant at 1.8 Å. The statistical probability of obtaining a given RMSD value is estimated as the P-value:

graphic file with name 1340equ6.jpg

where erf(x) is the standard Gauss error function and Z is given by Equation 5. A simplified summary of this calculation is provided in Box 1. The lower limit on P-value is capped at ≤10−6. We provide a spreadsheet for calculating the RNA tertiary structure prediction significance P-value, given N and the RMSD between the predicted and accepted structure (Supplemental Material). This calculation and source code are also available at the iFoldRNA server (http://iFoldRNA.dokhlab.org) (Sharma et al. 2008).

SUPPLEMENTAL MATERIAL

Supplemental material can be found at http://www.rnajournal.org.

ACKNOWLEDGMENTS

We thank P. Kota for setting up the P-value calculation as a web service, A. Zemla for assistance with the LGA program, and C. Hyeon and D. Thirumalai for sharing their Rg data for all RNA structures in the RCSB database. This work was supported by grants from the US National Institutes of Health to K.M.W. (GM064803) and N.V.D. (GM080742 and CA084480), and by an ARRA supplement (to K.M.W. and N.V.D.).

Footnotes

Article published online ahead of print. Article and publication date are at http://www.rnajournal.org/cgi/doi/10.1261/rna.1837410.

REFERENCES

  1. Badorrek CS, Gherghe CM, Weeks KM 2006. Structure of an RNA switch that enforces stringent retroviral genomic RNA dimerization. Proc Natl Acad Sci 103: 13640–13645 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Batey RT, Gilbert SD, Montange RK 2004. Structure of a natural guanine-responsive riboswitch complexed with the metabolite hypoxanthine. Nature 432: 411–415 [DOI] [PubMed] [Google Scholar]
  3. Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE 2000. The Protein Data Bank. Nucleic Acids Res 28: 235–242 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Cohen F, Sternberg MJE 1980. On the prediction of protein structure: The significance of the root-mean-square deviation. J Mol Biol 138: 321–333 [DOI] [PubMed] [Google Scholar]
  5. Das R, Baker D 2007. Automated de novo prediction of native-like RNA tertiary structures. Proc Natl Acad Sci 104: 14664–14669 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Das R, Kudaravalli M, Jonikas MA, Laederach A, Fong R, Schwans JP, Baker D, Piccirilli JA, Altman RB, Herschlag D 2008. Structural inference of native and partially folded RNA by high-throughput contact mapping. Proc Natl Acad Sci 105: 4144–4149 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Deigan KE, Li TW, Mathews DH, Weeks KM 2009. Accurate SHAPE-directed RNA structure determination. Proc Natl Acad Sci 106: 97–102 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Ding F, Sharma S, Chalasani V, Demidov V, Broude NE, Dokholyan NV 2008a. Ab initio RNA folding by discrete molecular dynamics: From structure prediction to folding mechanisms. RNA 14: 1164–1173 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Ding F, Tsao D, Nie H, Dokholyan NV 2008b. Ab initio folding of proteins with all-atom discrete molecular dynamics. Structure 16: 1010–1018 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Doi M 1996. Introduction to Polymer Physics. In Oxford Science Publications, pp. 10–12 Clarendon Press, Oxford, UK [Google Scholar]
  11. Egli M, Minasov G, Su L, Rich A 2002. Metal ions and flexibility in a viral RNA pseudoknot at atomic resolution. Proc Natl Acad Sci 99: 4302–4307 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Ferré-D'Amaré AR, Doudna JA 2000. Crystallization and structure determination of a hepatitis delta virus ribozyme: Use of the RNA-binding protein U1A as a crystallization module. J Mol Biol 295: 541–556 [DOI] [PubMed] [Google Scholar]
  13. Gherghe CM, Mortimer SA, Krahn JM, Thompson NL, Weeks KM 2008. Slow conformational dynamics at C2′-endo nucleotides in RNA. J Am Chem Soc 130: 8884–8885 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gherghe CM, Leonard CW, Ding F, Dokholyan NV, Weeks KM 2009. Native-like RNA tertiary structures using a sequence-encoded cleavage agent and refinement by discrete molecular dynamics. J Am Chem Soc 131: 2541–2546 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Gutell RR, Lee JC, Cannone JJ 2002. The accuracy of ribosomal RNA comparative structure models. Curr Opin Struct Biol 12: 301–310 [DOI] [PubMed] [Google Scholar]
  16. Holbrook SR 2008. Structural principles from large RNAs. Annu Rev Biophys 37: 445–464 [DOI] [PubMed] [Google Scholar]
  17. Hyeon C, Dima RI, Thirumalai D 2006. Size, shape, and flexibility of RNA structures. J Chem Phys 125: 194905 doi: 10.1063/1.2364190 [DOI] [PubMed] [Google Scholar]
  18. Jonikas MA, Radmer RJ, Laederach A, Das R, Pearlman S, Herschlag D, Altman RB 2009. Coarse-grained modeling of large RNA molecules with knowledge-based potentials and structural filters. RNA 15: 189–199 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kabsch W 1976. A solution for the best rotation to relate two sets of vectors. Acta Crystallogr A 32: 922–923 [Google Scholar]
  20. Ke A, Zhou K, Ding F, Cate JH, Doudna JA 2004. A conformational switch controls hepatitis delta virus ribozyme catalysis. Nature 429: 201–205 [DOI] [PubMed] [Google Scholar]
  21. Keedy DA, Williams CJ, Headd JJ, Arendall WB, Chen VB, Kapral GJ, Gillespie RA, Block JN, Zemla A, Richardson DC, et al. 2009. The other 90% of the protein: Assessment beyond the Cαs for CASP8 template-based and high-accuracy models. Proteins (Suppl 9) 77: 29–49 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Krasilnikov AS, Yang X, Pan T, Mondragón A 2003. Crystal structure of the specificity domain of ribonuclease P. Nature 421: 760–764 [DOI] [PubMed] [Google Scholar]
  23. Lavender CA, Ding F, Dokholyan NV, Weeks KM 2010. Robust and generic RNA modeling using inferred restraints: A structure for the hepatitis C virus IRES pseudoknot domain. Biochemistry 49(in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Massire C, Westhof E 1998. MANIP: An interactive tool for modelling RNA. J Mol Graph Model 16: 197–205 [DOI] [PubMed] [Google Scholar]
  25. Merino EJ, Wilkinson KA, Coughlan JL, Weeks KM 2005. RNA structure analysis at single nucleotide resolution by selective 2′-hydroxyl acylation and primer extension (SHAPE). J Am Chem Soc 127: 4223–4231 [DOI] [PubMed] [Google Scholar]
  26. Michel F, Westhof E 1990. Modeling of the three-dimensional architecture of group I catalytic introns based on comparative sequence analysis. J Mol Biol 216: 585–610 [DOI] [PubMed] [Google Scholar]
  27. Montange RK, Batey RT 2006. Structure of the S-adenosylmethionine riboswitch regulatory mRNA element. Nature 441: 1172–1175 [DOI] [PubMed] [Google Scholar]
  28. Okamoto Y 2004. Generalized-ensemble algorithms: Enhanced sampling techniques for Monte Carlo and molecular dynamics simulations. J Mol Graph Model 22: 425–439 [DOI] [PubMed] [Google Scholar]
  29. Parisien M, Major F 2008. The MC-Fold and MC-Sym pipeline infers RNA structure from sequence data. Nature 452: 51–55 [DOI] [PubMed] [Google Scholar]
  30. Parisien M, Cruz JA, Westhof E, Major F 2009. New metrics for comparing and assessing discrepancies between RNA 3D structures and models. RNA 15: 1875–1885 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Reva BA, Finkelstein AV, Skolnick J 1998. What is the probability of a chance prediction of a protein structure with an RMSD of 6 Å? Fold Des 3: 141–147 [DOI] [PubMed] [Google Scholar]
  32. Roth A, Breaker RR 2009. The structural and functional diversity of metabolite-binding riboswitches. Annu Rev Biochem 78: 305–334 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Ruff M, Krishnaswamy S, Boeglin M, Poterszman A, Mitschler A, Podjarny A, Rees B, Thierry JC, Moras D 1991. Class II aminoacyl transfer RNA synthetases: Crystal structure of yeast aspartyl-tRNA synthetase complexed with tRNA(Asp). Science 252: 1682–1689 [DOI] [PubMed] [Google Scholar]
  34. Shapiro BA, Yingling YG, Kasprzak W, Bindewald E 2007. Bridging the gap in RNA structure prediction. Curr Opin Chem Biol 17: 157–165 [DOI] [PubMed] [Google Scholar]
  35. Sharma S, Ding F, Dokholyan NV 2008. iFoldRNA: Three-dimensional RNA structure prediction and folding. Bioinformatics 24: 1951–1952 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Tan RKZ, Petrov AS, Harvey SC 2006. YUP: A molecular simulation program for coarse-grained and multiscaled models. J Chem Theory Comput 2: 529–540 [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Thore S, Frick C, Ban N 2008. Structural basis of thiamine pyrophosphate analogues binding to the eukaryotic riboswitch. J Am Chem Soc 130: 8116–8117 [DOI] [PubMed] [Google Scholar]
  38. Tinoco I, Bustamante C 1999. How RNA folds. J Mol Biol 293: 271–281 [DOI] [PubMed] [Google Scholar]
  39. Westhof E, Dumas P, Moras D 1988. Restrained refinement of two crystalline forms of yeast aspartic acid and phenylalanine transfer RNA crystals. Acta Crystallogr A 44: 112–123 [PubMed] [Google Scholar]
  40. Wilkinson KA, Merino EJ, Weeks KM 2006. Selective 2′-hydroxyl acylation analyzed by primer extension (SHAPE): Quantitative RNA structure analysis at single nucleotide resolution. Nat Protoc 1: 1610–1616 [DOI] [PubMed] [Google Scholar]
  41. Winkler WC, Nahvi A, Sudarsan N, Barrick JE, Breaker RR 2003. An mRNA structure that controls gene expression by binding S-adenosylmethionine. Nat Struct Biol 10: 701–707 [DOI] [PubMed] [Google Scholar]
  42. Yu ET, Hawkins A, Eaton J, Fabris D 2008. MS3D structural elucidation of the HIV-1 packaging signal. Proc Natl Acad Sci 105: 12248–12253 [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Zemla A 2003. LGA: A method for finding 3D similarities in protein structures. Nucleic Acids Res 31: 3370–3374 [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Zhang Y 2009. Protein structure prediction: When is it useful? Curr Opin Struct Biol 19: 145–155 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Zhou R, Berne BJ, Germain R 2001. The free energy landscape for β hairpin folding in explicit water. Proc Natl Acad Sci 98: 14931–14936 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Zuker M, Sankoff D 1984. RNA secondary structures and their prediction. Bull Math Biol 46: 591–621 [Google Scholar]

Articles from RNA are provided here courtesy of The RNA Society

RESOURCES