A two-length-scale polymer theory for RNA loop free energies and helix stacking

Abstract

The reliability of RNA secondary structure predictions is subject to the accuracy of the underlying free energy model. Mfold and other RNA folding algorithms are based on the Turner model, whose weakest part is its formulation of loop free energies, particularly for multibranch loops. RNA loops contain single-strand and helix-crossing segments, so we develop an enhanced two-length freely jointed chain theory and revise it for self-avoidance. Our resulting universal formula for RNA loop entropy has fewer parameters than the Turner/Mfold model, and yet simulations show that the standard errors for multibranch loop free energies are reduced by an order of magnitude. We further note that coaxial stacking decreases the effective length of multibranch loops and provides, surprisingly, an entropic stabilization of the ordered configuration in addition to the enthalpic contribution of helix stacking. Our formula is in good agreement with measured hairpin free energies. We find that it also improves the accuracy of folding predictions.

INTRODUCTION

Accurate prediction of macromolecular structure from a primary sequence is one of the grand challenges of computational biology. The secondary structure of RNA, defined by a set of canonical GC, AU, or GU base-pair interactions of the cis Watson–Crick/Watson–Crick-type (Leontis and Westhof 2001) contributes the great majority of the total free energy. Tertiary interactions, such as nonlocal hydrogen bonds, divalent-counterion stabilization, or helix stacking, account for the remainder.

The Turner rules (Xia et al. 1998; Mathews et al. 1999) are the basis for many RNA secondary structure prediction algorithms including Mfold (Zuker 2003), ViennaRNA (Hofacker 2003), Sfold (Ding and Lawrence 2003), and others. RNAstructure (Mathews et al. 2004) has systematically incorporated revisions to the rules (Kim et al. 1996; Diamond et al. 2001; Mathews and Turner 2002; Mathews et al. 2004; Tyagi and Mathews 2007). The Turner rules are based largely on physical–chemical measurements, with tabulated free energies for base-pair stacks and hairpin and interior loops.

Loop free energies are the most uncertain part of the Turner model, with large statistical errors for hairpin loops and systematic errors in the model of multibranch loops. The authors of Mfold confess (Zuker et al. 1999), “Because so little is known about the effects of multibranch loops on RNA stability, we assign free energies in a way that makes the computations easy.” The Mfold algorithm assumes a linear dependence of multibranch loop free energy on loop dimensions (Zuker and Sankoff 1984). Several statistical–mechanical approaches (Chen and Dill 2000; Zhang and Chen 2002) have since rejected this unphysical, albeit computationally efficient, treatment of multibranch loops.

The entropy of RNA loops has been computed recently by enumerating backbone configurations to simulate loop regions (Cao and Chen 2005; Zhang et al. 2008) based on a virtual bond representation of the backbone (Olson and Flory 1972; Olson 1975). These studies give fairly accurate numerical representations of the entropies of different loops, but their extrapolation formulas do not provide the physical insight that our theoretical framework can provide.

In this study, we describe RNA loops in terms of a two-length-scale polymer physics model with single-strand and helix-crossing segments. We derive the self-avoiding loop-closure free energy for this model, arriving at a simple functional form, which greatly reduces the number of parameters that appear in the Turner model or enumerative simulations. The standard errors for multibranch loops are 10 times smaller for our model than for Mfold's when compared with simulations. Our formula also neatly passes through the large experimental error bars for hairpin free energies.

We also introduce the surprising physical insight that the coaxial stacking of adjacent helical segments provides an entropic free energy benefit, in addition to the energetic stabilization currently incorporated in secondary structure prediction algorithms (Mathews et al. 2004). This situation marks a rare exception to the classic tradeoff between energy and entropy. This novel phenomenon may have widespread implications in determining the stability of RNA structures. Finally, in addition to simplifying the Turner model, we will show that our formula increases the accuracy of Mfold predictions.

MATERIALS AND METHODS

Polymer theory

One key observation is that RNA loops have two length scales: a = 6.2 Å for monomer separation in single-strand regions, and b = 15 Å to cross a helix (Aalberts and Hodas 2005). The properties of such a polymer can be understood by extending the freely jointed chain (FJC) model from one up to two step lengths. In our FJC2, each segment has length r_i ∈ {a, b}. Randomly distributed unit vectors obey for i ≠ j, and 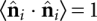. The total end-to-end separation is 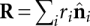. If there are N links of length a and M links of length b,

this defines the characteristic spatial extent of the chain. If there is only one segment length type, Equation 1 reduces to the familiar FJC result (Grosberg and Khohklov 1994).

Loops are formed when the polymer walk returns near to its starting point. If we use a characteristic volume ΔV to define “near” the origin, the loop probability scales like

For self-avoiding polymers, the classic Flory result (Grosberg and Khohklov 1994) is that the chain extension scales with a larger power, 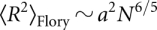. The self-avoiding FJC2 analogy is

The probability of end-to-end separation for a self-avoiding polymer adopts an asymptotic scaling form (Grosberg and Khohklov 1994):

when the dimensionless chain extension is small. To form a loop, is small, and after combining 1/2, 5/18, and 3/2 exponents,

Thus, the FJC2 loop-closure free energy is

with C reflecting the possibility of a different criterion for being near.

Sequence dependencies of loops are largely ignored in the Turner rules (Mathews et al. 1999, 2004); exceptions include stacking bonuses of the bases adjacent to a helix, a list of stable tetraloops (hairpin loops with n = 4 bases), and interior loops with up to 2 × 3 mismatched bases—we include these sequence dependences identically to Mfold in our testing. Implicit in neglecting sequence dependences is the approximation that the entropy of configurations dominates the free energy, particularly for long loops. This “athermal” approximation of ignoring enthalpic effects is explicit in enumerations of chain configurations (Cao and Chen 2005; Zhang et al. 2008) and in our derivation of loop free energies.

Coaxial stacking

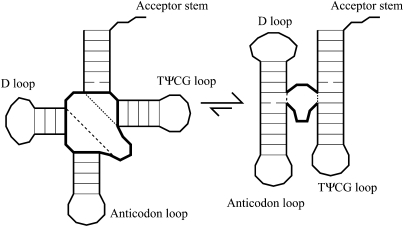
Although coaxial stacking refers to the tertiary organization of secondary structure elements, it is included in secondary structure folding algorithms (Mathews et al. 1999, 2004; Zuker 2003). If no bases intervene between two helices, they may adopt a coaxially stacked orientation; a free energy change equal to making a conventional base-pair stack is assigned in Mfold for coaxially stacked helices (Mathews et al. 1999). If there is an unpaired base between the helices, Mfold essentially recruits a base from the loop to make an intervening mismatch (Kim et al. 1996; Tyagi and Mathews 2007). Figure 1 shows examples of each type—the acceptor stem and TψCG helix stack coaxially, while the anticodon and D stems are separated by one base.

FIGURE 1.

The secondary structure of tRNA includes four base-paired stems meeting at a central multibranch loop. In the multibranch loop and hairpin loops, the effective backbone is comprised of a combination of N single-strand links of length a and M helix-crossing segments of length b. Coaxial stacking orients helices, reducing the effective multibranch loop size.

An important fact that has not been noticed is the effect of orienting the helices on the remainder of the multibranch loop. Basically, two of the long b segments are removed from the effective loop in the ordered configuration. Since the free energy cost to make a loop is less for a shorter chain, the stacked configuration is not only the low enthalpy state it is also the more stable state of the loop.

To get a sense of the magnitude of this surprising loop entropy stabilization, consider a typical tRNA (see Fig. 1) with a (N = 12, M = 4) multibranch loop. After coaxial stacking of the TψCG loop and the acceptor stem, and orienting the stems leading to the D and anticodon loops, M_eff = 0. The free energy benefit is

Our M_eff benefit comes in addition to the conventional stacking free energy (which we treat identically to Mfold's efn2); its origin is the entropic benefit of shortening a loop. It is known from rubber elasticity that there are more chain configurations when the two ends are near. Stacking reduces the separation of dashed and dotted lines in Figure 1, so the stacked state has the greatest chain entropy. Terminal stacking of unpaired bases adjacent to helices could be treated in an analogous manner, but the magnitude of the effect is much smaller because it relates primarily to the shorter length scale; consequently we did not incorporate this at this stage.

Simulations

We also compute the probability of loop formation by performing FJC2 simulations. The parameters of the simulations, a = 6.2 Å and b = 15 Å, come from analyzing the 4′ carbon coordinates (Aalberts and Hodas 2005) of PDB files. To enforce self-avoidance we use hard-core beads with radius r = 2.4 Å, consistent with our observation that adjacent C_4′-to-C_4′ unit vectors satisfy 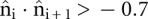and with Turner's requirement of at least three bases (N > 4 segments) for a hairpin loop. Helix lengths contain interior beads (see Fig. 2). At least one single-stranded link always separates helices (see Fig. 1), so consecutive steps of length b are prohibited. Loops with N < 3 at M = 0, N < 4 at M = 1, or N < M are all disallowed geometrically.

FIGURE 2.

In simulations, the backbone is represented as hard-core beads of radius r = 2.4 Å. For single-stranded links the separation is a = 6.2 Å. For helix-crossing links the separation is b = 15 Å, with (hatched) intermediate beads to provide self-avoidance. A hairpin loop (M = 1 helical lengths) with three bases (N = 4 single-strand links) is depicted.

We compute the loop probability p_loop(N, M), in simulations with 10⁸ chains. After M steps of length b and (N − 1) steps of length a, chosen at random, we measure the probability density of end separation in 0.1 Å bins, using the average bin density around end-to-end separation a. The Boltzmann formula,

again converts probability to free energy.

RESULTS AND DISCUSSION

Multibranch loops

We begin with the interesting case of multibranch loops with N single-stranded segments (or n = N − M bases) and M > 2 stems. Our polymer-physics-based formula, Equation 2, correlates beautifully with simulations for a range of N, M values (see Fig. 3C).

FIGURE 3.

As a function of G_sim, for N ≤ 20 and M ≤ 6, we plot: (A) the Mfold initial run (Equation 5); (B) the re-evaluated free energies of Mfold's efn2 (Equation 6); (C) our G_FJC2 formula (Equation 2); and (D) the best linear fit to simulation data G_linear = (4.3 + 0.07N + 0.2M)kcal/mol. It is clear that G_FJC2 best approximates G_sim, demonstrating that FJC2 captures the correct polymer physics lacking in the Mfold formulas. The quality of the agreement allows us to incorporate hairpin loops on the same footing as multibranch loops and to consider coaxial stacking as a change in the effective M.

The Mfold approach to multibranch loops is rather arbitrary and peculiar. In the initial Mfold run, a linear function is used

Mfold uses Equation 5 to generate a set of optimal and suboptimal folds.

Mfold then recomputes the free energies of the set of folds using the efn2 function:

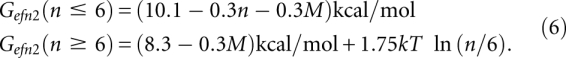For the multibranch free energy, Mfold reports the efn2 value from Equation 6, along with any free energy changes due to terminal mismatches or dangling bases.

It is clear from Figure 3 that our multibranch formula is in excellent agreement with simulations, while both Mfold approaches are poorly correlated. The standard errors per data point are: s = 0.08 kcal/mol for G_FJC2, s = 0.28 kcal/mol for G_linear, s = 0.37 kcal/mol for G_affine, and s = 0.80 kcal/mol for G_efn2. Incidentally, Zhang et al. (2008) and Cao and Chen (2005) use extrapolation formulas with multiple adjustable constants for each M. In our formula, the disparity of a and b lengths elegantly explains why chains with larger M have higher free energy and lower apparent slope with respect to changes in N.

Because our polymer theory uses exponents derived for the long chain limit, while these are relatively short chains, some systematic errors are observed. Altering the exponents could improve agreement slightly, but with errors already reduced to the same 0.1 kcal/mol range as base-pair stacking parameters, we prefer to avoid introducing additional fitting parameters for marginal improvement.

It is also not surprising that G_FJC2 deviates the most from G_sim for very short hairpins (M = 1 and N = 4, 5), as self-avoidance greatly stretches these loops. Corrections to the free energies of stretched chains can be introduced (Marko and Siggia 1995), but to avoid complication we simply use G_FJC2 rather than including corrections for the observed differences between G_sim and G_FJC2. Andronescu et al. (2007) have achieved improvements in prediction accuracy simply by reparametrizing the Turner model.

Mathews and Turner (2002) proposed (9.3 − 0.9M + 0n)kcal/mol on the basis of a set of experiments on M = 3,4 multibranch loops. They indicated that their observation that M = 4 loops are more stable than M = 3 loops might arise from whether M is even or odd; in our framework, this can be explained as stacked helices reducing an M = 4 effective loop size to M_eff = 0 but M = 3 only to M_eff = 1. In the limit of large M, the negative slope with respect to M is unphysical because longer chains have more configurations and are thus less likely to form loops. The Mathews and Turner (2002) formula produces a standard error of s = 2.2 kcal/mol against G_sim. An additional term related to the asymmetry of loops was also proposed in Mathews and Turner (2002); however, the functional form of this term has prohibited implementation in folding algorithms. Asymmetry is likely a proxy for the possibility of helix stacking discussed above.

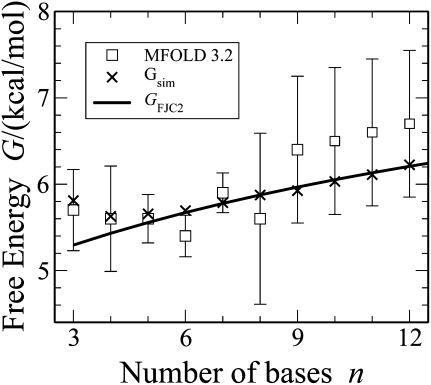
Hairpin loops

Hairpin loops contain M = 1 helices and N single-stranded segments (or n = N − 1 bases). We find that our polymer theory is also consistent with the Turner values (Mathews et al. 1999). In Figure 4, our M = 1 theory and simulation results are compared with experiment (Mathews et al. 1999). Turner quotes values for each n, while we believe fitting all the data to a model context is preferable, especially when extrapolating to long loops. The smoothness of Mfold's “experimental” curve for n > 9 is misleading as it is a Jacobson–Stockmayer extrapolation (Jacobson and Stockmayer 1950), while the actual experiments are for 3 ≤ n ≤ 9. Our smooth theory and simulation curves generally fall within the large error bars of Turner.

FIGURE 4.

The free energies of hairpin loops as a function of the number of bases are given for Mfold/Turner rules (Mathews et al. 1999); for Monte Carlo simulations (Equation 4); and our theoretical expression (Equation 2) with C = −0.8 kcal/mol. Note that Mfold values for n > 9 are inferred from the Jacobson–Stockmayer theory using n = 9 as a reference point even though the data are not smooth for n ≤ 9. The experimental errors for loop energies are much larger than the ±0.1 kcal/mol for base pairs.

Testing G_FJC2 with Mfold

We test the performance of Mfold with its hairpin (M = 1) and multibranch (M > 2) loop free energies replaced by G_FJC2. The interior or bulge loop (M = 2) free energies were not altered because sequence dependencies for mismatched bases have been tabulated. For hairpins, the first mismatch and the sequence-specific tetraloop and triloop free energies were also retained. The values of C for the multibranch and hairpin forms of G_FJC2 are set to 0.0 kcal/mol and −1.1 kcal/mol, respectively; these values ensure that G_FJC2 hairpin and multibranch free energies are similar to their efn2 counterparts. This similarity is important for the maintenance of relative free energy levels among the different secondary structure motifs and prevents systematic biasing toward certain types of motifs.

No Mfold default settings were changed except for the percent-suboptimality parameter, which was increased from P = 5 to P = 30 to generate a set of suboptimal folds within 30% of the minimum free energy. (For the relatively short hammerhead ribozyme sequences, P = 100.) This set of optimal and suboptimal folds, based on Equation 5, is rank ordered by free energy. The free energies for these Mfold affine structures are recomputed with efn2, Equation 6. We do the same with our G_FJC2 formula, Equation 2. This procedure facilitates the most direct comparison of results. Because recomputing with efn2 or G_FJC2 does not predict any new structures, changes in the accuracy are manifested as changes in the rank ordering of predicted folds.

We first tested using 569 tRNA sequences, previously used in a study by Gutell and coworkers (Doshi et al. 2004). This set of sequences represents a diverse collection of tRNAs corresponding to different amino acids in a wide variety of organisms. The Gutell group also makes available comparatively determined structure information for every sequence. Modified bases are represented as N and, as such, are not allowed to pair.

Each structure from the Mfold list is compared with Gutell's “correct” structure. The “most accurate” structure is the one with the most correct base pairs; but while this structure is the same for G_FJC2, affine, and efn2, its rank among the list may change as the relative energies of the folds change. The number of “most accurate” structures at the optimal position shows a statistically significant increase from 203 with efn2 to 245 with G_FJC2 (see Table 1).

TABLE 1.

The number of times the “most accurate” structure is predicted to have the minimum free energy (MFE) is compared between the models for five RNA classes

We further tested a large set of 5S ribosomal RNA sequences used in a previous evaluation of Mfold (Mathews et al. 1999), a set of SRP RNA from the SRP database (Andersen et al. 2006), and hammerhead ribozyme and cis-regulatory RNA elements from the Rfam database (Griffiths-Jones et al. 2005). The SRP, hammerhead, and cis-regulatory sequences were obtained via the RNA strand website (Andronescu et al. 2008). Performance of G_FJC2, measured by the percentage of times the “most accurate” structure for each sequence appears with the lowest free energy, remains similar to that of Mfold for these classes (see Table 1).

CONCLUSIONS

Our major conclusions are these: (1) RNA loops are built from two different lengths, so we introduce the FJC2 model. We encourage others to respect the a/b ratio in drawing two-dimensional representations. (2) The free energy of RNA loops can be derived from polymer physics principles (Equation 2). The 10 parameters for hairpins and multibranch loops in the Turner model reduce to only two adjustable constants in our model. (3) G_FJC2 (N, M) is in good agreement with experiment and simulation (see Figs. 3, 4), while the Mfold formulations for multibranch loops are poor. (4) Helix stacking lowers the enthalpy as expected, but surprisingly also increases the likelihood of loop formation, because there are relatively more loop configurations for shorter effective chains. We suspect that the previously reported effect of asymmetry within loops (Mathews and Turner 2002; Zhang et al. 2008) can be understood better in terms of the entropic benefit of coaxial stacking. (5) We have shown that FJC2 produces a statistically significant increase in the accuracy of tRNA predictions while performing on par with Mfold for other RNA classes (see Table 1). (6) Our improved loop free energy function can readily be calculated if the secondary structure is known. A linear approximation of our formula as in Figure 3D, along with an M_eff correction, can be incorporated in all of the RNA folding algorithms based on the Turner model. (7) We believe that the FJC2 formalism is a good springboard for including stacking of single-stranded bases (Aalberts et al. 2003) in the future.