Optimal matrix rigidity for stress fiber polarization in stem cells

Abstract

The shape and differentiation of human mesenchymal stem cells is especially sensitive to the rigidity of their environment; the physical mechanisms involved are unknown. A theoretical model and experiments demonstrate here that the polarization/alignment of stress-fibers within stem cells is a non-monotonic function of matrix rigidity. We treat the cell as an active elastic inclusion in a surrounding matrix whose polarizability, unlike dead matter, depends on the feedback of cellular forces that develop in response to matrix stresses. The theory correctly predicts the monotonic increase of the cellular forces with the matrix rigidity and the alignment of stress-fibers parallel to the long axis of cells. We show that the anisotropy of this alignment depends non-monotonically on matrix rigidity and demonstrate it experimentally by quantifying the orientational distribution of stress-fibers in stem cells. These findings offer a first physical insight for the dependence of stem cell differentiation on tissue elasticity.

Recent research has shown that the regulation of important cellular processes such as proliferation, differentiation and apoptosis, is controlled by the mechanical properties and geometry of the cells and their environment [1–11]. Cell differentiation and other cellular processes were shown to optimize in a range of matrix rigidities that is characteristic of the native tissue environment [4–8]. Engler et al. [7] have shown that the rigidity of the environment can direct the shape and lineage specification of stem cells. When plated on substrates whose rigidity mimicked that of brain, muscle and bone, differentiation markers corresponding to these tissue-cells were expressed in the stem cells after few days and showed a maximum on the respective substrates. Significant differences in cell morphology, however, emerge within the first 24 hours. The extent of cell elongation (aspect ratio) depended non-monotonically on the rigidity of the matrix [7], adopting the characteristic polarized morphology of muscle cells only when placed on a matrix whose rigidity matched the typical stiffness of muscle tissue (E ≈ 10 kPa).

In this paper, we focus on the alignment of the contractile, acto-myosin stress-fibers in the cytoskeleton of adhering cells since they were shown to play an essential role in the active, mechano-sensitivity of cells [12], particularly in the determination of cell shape [13] and differentiation [14]. We predict theoretically and demonstrate experimentally that the matrix rigidity and the cell shape regulate the polarization of stress-fibers in cells, and dictate the preferential alignment of the stress-fibers along the long axis of the cell [15–17]. We show that the alignment of stress-fibers in stem cells depends non-monotonically on the matrix rigidity, attaining a maximum value when the cell and matrix rigidity are similar.

We model the cell as an active, elastic inclusion in an infinite, homogeneous and isotropic medium and consider both 2D and 3D geometries. The theory includes both the passive forces arising from the elasticity of the cell and the surrounding medium as well as the active forces generated and regulated by the cells; this extends the treatment of passive inclusions in solids to living matter. We show that a small asymmetry in the early-time shape of an adhering cell (see Supplementary figure 2) results in a symmetry breaking of the elastic stress in the cell that in turn, may direct the spontaneous polarization of the stress-fibers in the cell. We invoke the use of an active cell polarizability that reflects the feedback between the elastic stresses in the cell and the active forces that the cell generates to predict the anisotropic polarization of the forces in the cell and its dependence on the cell shape and elastic characteristics.

Experiments were carried out to systematically analyze the alignment of stress-fibers in human mesenchymal stem cells (hMSCs) as a function of the cell shape and the rigidity of the environment. Cells were cultured on substrates of varying stiffness and sorted by their aspect ratio. We show a quantitative analysis of stress-fiber polarization in cells by staining for both actin and non-muscle myosin IIa (NMMIIa) and applying a segmentation algorithm to map their spatial organization in the cell.

Our results suggest a generic mechanical coupling between the cell shape, the rigidity of the surroundings and the organization of stress-fiber in the cytoskeleton of stem cells. This elucidates a mechanical property of cells – stress-fiber polarization – that is maximized at an optimal substrate rigidity, analogous to the optimal rigidity found in stem cell differentiation (e.g., to muscle cells).

I. THEORY OF CELL ADHESION AND ACTO-MYOSIN POLARIZATION

The anchoring of a cell to the extracellular matrix as well as the active spreading of a cell on a surface involve a shape and volume deformation that produces elastic stresses in the cell and the matrix [17–22]. Nascent protein adhesion complexes (often termed focal complexes [12]) that anchor the cell to the surrounding matrix, grow in response to these forces [23] providing mechanical support for stronger, organized and more prominent acto-myosin stress-fibers in the cell. The theory shows how the adhesion-induced stresses can initiate a feedback that controls the amount and alignment of the stress-fibers in the cell; we begin with a simple 1D spring model [24] and then extended it in full elastic 2D and 3D models.

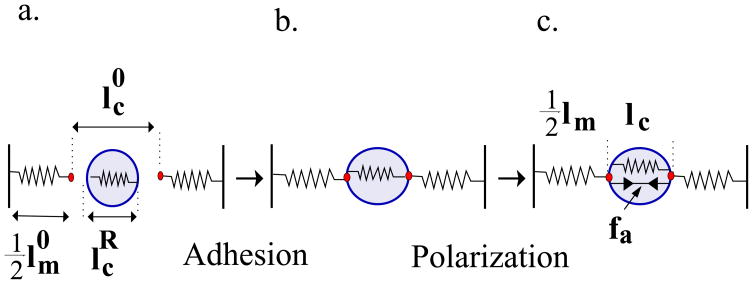
In the spring model (Fig. 2), the passive elasticity of the cell and the matrix are represented by springs with rigidities, k_c and k_m, respectively. We denote by $l_c^R$ the relaxed length of the cellular spring as it would exist in a soft environment of vanishing rigidity. This length is determined, in part, by active forces, f⁰, (not shown in Fig. 2) arising from the initial, isotropic distribution of myosin motors that locally compresses the cytoskeleton. We begin with the first stage of cell adhesion (Fig. 2a→b) where the cell anchors to the matrix or spreads isotropically [18] on a surface and an elastic stress develops in the cell. Experiments show that the spreading area and the force exerted by cells increase with the matrix rigidity [4, 6, 16, 25]. We denote by $-\mathrm{\Delta }{l}_c^0=l_c^0-l_c^R>0$ the elastic deformation that would arise if the cellular springs were maximally stretched, as appropriate to spreading on a substrate of infinite rigidity; where $l_c^0$ denotes the fully stretched size of the cellular spring as it exist in an infinitely rigid matrix.

Figure 2.

Cell adhesion and polarization represented by a 1D spring model. Springs with constants k_c and k_m represent the elasticity of the cell and matrix respectively. Elastic morphological changes upon cell adhesion (a → b) are represented here by a change in the cellular spring length $-\mathrm{\Delta }{l}_c^0=l_c^0-l_c^R>0$. This triggers an internal feedback mechanism (b→c) that results in an enhancement of the active forces (see Eq. 2).

We now consider the equilibrium spring lengths, l_c and l_m, including the matrix deformation, but not yet including the feedback that leads to well developed acto-myosin stress fibers (Fig. 2b). To calculate the equilibrium spring lengths we solve the force balance equation: $k_c(l_c-l_c^R)=k_m(l_m-l_m^R)$ along with the (boundary) condition $l_c+l_m=l_c^0+l_m^R$; here $l_m^R$ is the equilibrium length of the matrix spring. This results in the following relation: $\mathrm{\Delta }{l}_c=[k_c/(k_c+k_m)]\mathrm{\Delta }{l}_c^0$, where $\mathrm{\Delta }{l}_c=l_c-l_c^0$.

A simple feedback mechanism is next included in which the modulation of the active actomyosin force exerted by the cell, f^a = f − f⁰, due to the assembly of organized anisotropic stress-fibers in the cell, is proportional to the stress within the cell; f is the total acto-myosin force. We write this feedback as follows: $f^a=-\alpha k_c(l_c-l_c^R)=-\alpha k_c(\mathrm{\Delta }{l}_c-\mathrm{\Delta }{l}_c^0)$. Here, α > 0, is a phenomenological “polarizability” that relates the stress in the cytoskeleton to the number, size and orientation of the stress-fibers and focal adhesions in the cell. In the presence of these active forces, the force balance equation reads: $k_c(l_c-l_c^R)=k_m(l_m-l_m^R)+f^a$. This allows us to predict the magnitude of the average force and strain that develop in a cell as a function of the cell and matrix rigidity (Fig. 2c). For the cellular strain we find:

$$\frac{\mathrm{\Delta }{l}_c}{l_c^0}=\frac{{\stackrel{\sim }{k}}_c}{({\stackrel{\sim }{k}}_c+k_m)}\frac{\mathrm{\Delta }{l}_c^0}{l_c^0}.$$ (1)

Here, k̃_c = (1 + α) k_c is the effective rigidity of the cell; an active cell is effectively more rigid (for α > 0) since the stretching by the matrix springs enhances the active contractile forces in the cell that further opposes the matrix stretch. In addition, the net, anisotropic polarized acto-myosin force is given by:

$$\frac{f^a}{f^0}=\alpha \frac{k_m}{{\stackrel{\sim }{k}}_c+k_m}.$$ (2)

This expression correctly captures the experimentally observed monotonic increase and saturation of the contractile cellular force with the matrix rigidity, see Supplementary figure 3 and Ref. [16].

The 1D spring model is useful for understanding the increase in cell contractility but is unable to account for the anisotropic polarization of the forces in the cell. To this end, we use approaches from solid mechanics, and generalize the well-known inclusion problem [26, 27] to include the “live” nature of cells, that is their ability to actively regulate their forces. We do this both for 2D and 3D systems; see Supporting Information for details.

We model the cell as an isotropic and homogeneous ellipsoid embedded in an infinite 3D matrix; the same formalism applies to an elliptical cell embedded in a 2D sheet under conditions of generalized plane stress [28, 29]. We denote by C_c and C_m the mean elastic moduli of the cell and the matrix, respectively. Bold face letters are used to designate fourth-rank tensors and a product of the form Ag_ij denotes A_ijkl g_kl, and similarly AB g_ij = A_ijmnB_mnkl g_kl, where summation over repeated indices is implied. The isotropic modulus, C_c, refers to the cell elasticity upon adhesion, as it exists before the stress-fibers have become numerous and oriented; this includes contributions from other cytoskeletal components and from actin that is in an isotropic, gel state. We denote by $-u_{ij}^0>0$ the early time strain associated with cell adhesion and spreading in an infinitely rigid environment (analogous to $-\mathrm{\Delta }{l}_c^0$ in the spring model); this produces a restoring stress ${\mathbf{C}}_c{u}_{ij}^0<0$ in the cytoskeleton that initiates the polarization response.

The active acto-myosin forces in the cytoskeleton are modeled by a local distribution of “force dipoles” [30–32] that arise from the equal and opposite forces exerted by myosin motors at two nearby points on actin filaments. These are represented by a tensor quantity 〈p_ij〉 which is the average (active) dipole density per unit volume. We assume that these force-dipoles polarize in response to the local stress in the cell, changing their magnitude and orientation from their average, isotropic initial value $\langle p_{ij}^0\rangle$. We denote by, $\langle p_{ij}^a\rangle =\langle p_{ij}\rangle -\langle p_{ij}^0\rangle$, the anisotropic polarization tensor of the force dipoles in the cytoskeleton and in analogy to the spring model, we assume a feedback response of the form:

$$\langle p_{ij}^a\rangle =-\mathit{\alpha }{\mathbf{C}}_c(u_{ij}^c-u_{ij}^0),$$ (3)

where α denotes the active cellular polarizability (see Supporting Information) and ${\mathbf{C}}_c(u_{ij}^c-u_{ij}^0)$, is the mean stress developed in the cell [26]. The strain and the forces that develop in the cell due to this feedback response are given by the self-consistent solution of the elastic equations along with the feedback effect of Eq. 3. This predicts that the strain and the cell force are given by:

$$u_{ij}^c=[\stackrel{\sim }{\mathbf{A}}({\mathbf{S}}_m-\mathbf{I})+\mathbf{I}]u_{ij}^0$$ (4)

and

$$\langle p_{ij}^a\rangle =-\mathit{\alpha }{\mathbf{C}}_c\stackrel{\sim }{\mathbf{A}}({\mathbf{S}}_m-\mathbf{I})u_{ij}^0$$ (5)

with, $\stackrel{\sim }{\mathbf{A}}={[\mathbf{I}+{\mathbf{S}}_m({\stackrel{\sim }{\mathbf{C}}}_c-{\mathbf{C}}_m){\mathbf{C}}_m^{-1}]}^{-1}$; I is the unit tensor. The quantity C̃_c = (I + α) C_c is the effective elastic modulus of the cell (analogous to k̃ in the spring model). This tensor embodies the “live” properties of cells via the cell polarizability, α. The tensor, S_m is the Eshelby tensor [26, 27], a function of the cell shape and the Poisson ratio of the matrix. Eqs. 4 and 5 allow us to explore the relation between the cell shape and the polarization of the forces, and to predict how anisotropic stress fibers first arise. While the establishment of cell shape and polarization of stress-fibers occur on a time scale of hours to days, during which the elastic properties of cytoskeleton and cell shape vary, the final steady-state of the cell, emerges from an early time breaking of symmetry, whose origin and mechanical consequences are described by our model.

II. PREDICTIONS AND EXPERIMENTAL OBSERVATIONS

Experimentally, focal adhesions and stress-fibers have been shown to grow and develop parallel to the direction of an applied force [33], consistent with the more general observation that cells tend to polarize in the direction of stronger elastic resistance [34]. We thus consider the simplest model in which a cell responds to stresses by locally modulating its active actomyosin forces only in directions parallel to the local stress. In this case, the isotropic fourth rank tensor, α, can be replaced by a single positive scalar quantity, α, and $\langle p_{ij}^a\rangle =-\alpha {\mathbf{C}}_c\mathrm{\Delta }{u}_{ij}^c$ (see Eq. 3). In the Supporting Information we discuss an alternative form for α, but the conclusions of the main body of the paper are unaltered in that model as well.

To illustrate how the shape of the cell alone can be responsible for the polarization anisotropy, we assume, for simplicity, and in line with experiments [18] that the initial-time adhesion-induced stress, ${\mathbf{C}}_c{u}_{ij}^0$, is isotropic, including the contribution arising from the early-time, force dipoles, i.e., $\langle p_{xx}^0\rangle =\langle p_{yy}^0\rangle =\langle p_{zz}^0\rangle =p^0$. Nevertheless, the global shape change (elongation of the cell) that accompanies the polarization of stress-fibers in the cell may involve an additional axial stretching of the cytoskeleton. This effect is considered below, but we first focus on the consequences of the isotropic forces exerted by the cell. While the actual proportion of isotropic dipolar forces, $\langle p_{ij}^0\rangle$, in the total stress exerted by the cell, ${\mathbf{C}}_c{u}_{ij}^0$, is unknown, for simplicity, and without loss of generality we use ${\mathbf{C}}_c{u}_{ij}^0=\langle p_{ij}^0\rangle$ in the calculations presented below. We model cells in 3D as spheroids whose long axis (taken to be in the z direction) has a length c and whose short axis (taken to be in the x − y plane) has a radius a. Similarly, in our 2D model the cell is modeled by an ellipse with long and short axes c and a respectively; in both cases r = c/a is the aspect ratio of the cell.

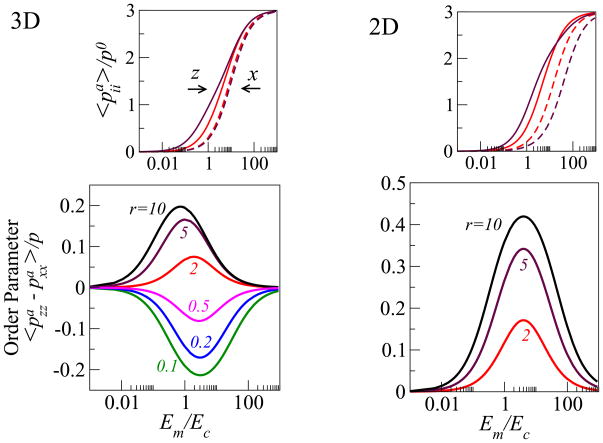
Figure 3 shows our results for both the 2D and 3D systems. In the upper panels we plot the normalized dipole elements $\langle p_{zz}^a\rangle /p^0$ and $\langle p_{xx}^a\rangle /p^0$, as a function of the ratio of the Young’s modulus of the matrix and the cell, E_m/E_c; for two values of the aspect ratio r. Consistent with experiment [16], our 1D spring model, and our estimate of the total myosin content in the stress-fibers (Supplementary figure 3) we find that the magnitude of the cellular forces in both the x and z directions, increases monotonically with the rigidity of the matrix up to the same saturation value, $\langle p_{zz}^a\rangle /p^0=\langle p_{xx}^a\rangle /p^0=\alpha$. For intermediate values of the matrix rigidity, the matrix tractions that oppose the cellular forces turn out to be stronger along the long axis of the cell. This fact, which is entirely due to the anisotropic shape of the cell, is responsible for the stronger polarization of the forces along the long axis of the cell. Thus for rod-like cells oriented parallel to the z axis, we find that $\langle p_{zz}^a\rangle >\langle p_{xx}^a\rangle$. The preferential alignment of stress-fibers (as well as of the sarcomeres in muscle cells) parallel to the long axis of cells is a common experimental observation [15–17], that has not been explained theoretically.

Figure 3.

Cell polarization as a function of the ratio of the Young’s modulus of the matrix, E_m, and the cell, E_c, in both our two- and three-dimensional models; the plots are shown for different values of the cellular aspect ratio, r. The upper panels show (magenta: r = 5, red: r = 2) the normalized average dipole elements $\langle p_{zz}^a\rangle$ (solid lines) and $\langle p_{xx}^a\rangle$ (dashed lines) corresponding to the forces in the directions that are respectively parallel (ẑ) and perpendicular (x̂) to the long axis of the cell. The bottom panels show the calculated orientational order parameter of the stress-fibers that is given by the normalized difference $(\langle p_{zz}^a\rangle -\langle p_{xx}^a\rangle )/p$. The color coding indicates the aspect ratio. In this plot the Poisson ratio of the matrix and the cellular domain are taken to be, ν_m = 0.45, ν_c = 0.3 and the magnitude of the polarizability is α = 3.

Our theory shows that the polarization of the stress-fibers in the cell should depend non-monotonically on the matrix rigidity. To illustrate this behavior we plot in the main panel of Fig. 3 the normalized difference, $S=(\langle p_{zz}\rangle -\langle p_{zz}\rangle )/p=(\langle p_{zz}^a\rangle -\langle p_{xx}^a\rangle )/p$, that can be shown to be equal to the orientational order parameter of the dipoles; here p is the trace of the mean dipole tensor, 〈p_ij〉. In both 2D and 3D we find the same, generic, Lorentzian-type (i.e., a Lorentzian multiplied by the linear factor E_m/E_c) of functional dependence for S as a function of the Young’s moduli ratio: S = a(E_m/E_c)/[b ((E_m − E₀)/E_c)² + 1]; where a, b, E₀ are complicated functions of the aspect ratio, cell polarizability, Poisson ratio of the cell and matrix and dimensionality of the system.

We find that the polarization of the forces in the cell is maximal at an optimal ratio of the matrix and cell rigidities, (E_m/E_c)^★. The explanation for this important feature is the following. Consider the two extreme limits of a cell in an infinitely rigid and infinitely soft matrix. In the former case, since the matrix exerts strong tractions that completely oppose the initial, isotropic, inward pulling forces of the cell, $f_i^0={\mathbf{C}}_c{u}_{ij}^0{n}_j$, the early-time (tensile) stress that develops, ${\mathbf{C}}_c(u_{ij}^{c,0}-u_{ij}^0)=-{\mathbf{C}}_c{u}_{ij}^0$, is also isotropic (cf. Eq. 6 in the Supporting Information); this results in an isotropic polarization of the stress-fibers because $\langle p_{ij}^a\rangle ={\sigma }_{ij}^c/\alpha$ (where ${\sigma }_{ij}^c={\mathbf{C}}_c(u_{ij}^c-u_{ij}^0)$). In the opposite limit of an infinitely soft matrix, the matrix resistance, and consequently the cellular stress, drops to zero in all directions, thus providing no orientational cue for the polarization of stress-fibers in the cell. Between these two limits, the forces in different directions increase with different rates with the matrix rigidity as seen in the upper panels of Fig. 3. Because the saturation values are independent of direction the difference in the polarization, parallel and perpendicular to the long axis of the cell, has a maximum at a certain value of the matrix rigidity.

Interestingly, we predict that the optimal ratio, (E_m/E_c)^★, scales as $\sim \sqrt{1+\alpha }$ (see Supporting Information). Since α is, in general a cell-type specific parameter this scaling suggest that different cell types would possess a different level of sensitivity to the anisotropy of the stress in the cell. In addition, our theory shows that the stress-fiber polarization in 2D is larger by a factor of ≈ 2 compared with 3D. In 3D the cell is surrounded by a matrix that more strongly suppresses the anisotropy of the elastic stress in the cell. In the Supporting Information we present a more quantitative analysis of these arguments.

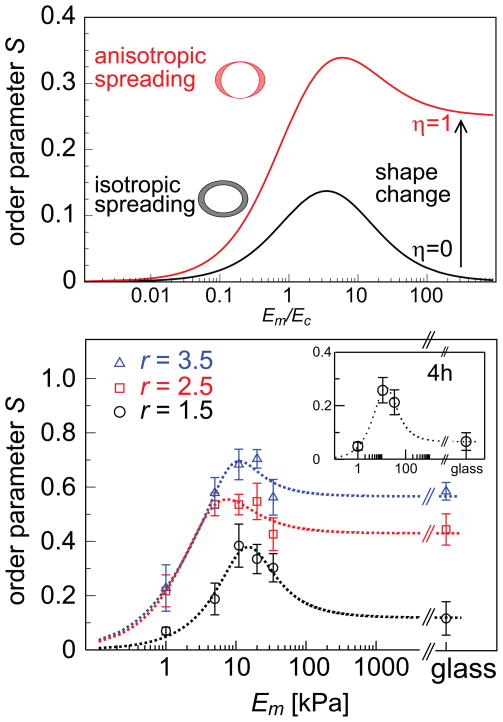
Thus far we considered the sole effect of the stress anisotropy that results from the cell shape. This gives rise to a non-monotonic dependence of stress-fiber polarization on the matrix rigidity. The stress-fiber polarization however is often accompanied by a simultaneous narrowing and elongation of the cell; see Fig. 1. To model the consequences of the stress associated with cell elongation we include an axial contribution to the early-time elastic stress ${\mathbf{C}}_c{u}_{ij}^0$ exerted by the cell and calculate its effect on the polarization of stress-fibers in the cell. We note that this is an approximation since the cell shape changes continuously but nevertheless it captures an important elastic consequence of cell spreading anisotropy. We thus write ${\mathbf{C}}_c{u}_{ij}^0=p^0({\delta }_{ij}+\eta {\delta }_{iz}{\delta }_{jz})$ where the second term is an axial stress along the z-axis - the direction of cell elongation. Like the separate elements of the stress tensor ${\sigma }_{xx}^c$ and ${\sigma }_{zz}^c$ in the previous case, the stress resulting from this axial contribution increases with the matrix rigidity. The upper panel of Fig. 4 shows the predicted effect of this axial stress on the polarization of the stress-fibers in the cell. Rather than dropping to zero as the matrix rigidity increases, the order parameter saturates to a finite value given by ηα/(ηα + d + dα) where d = 2, 3 is the dimensionality.

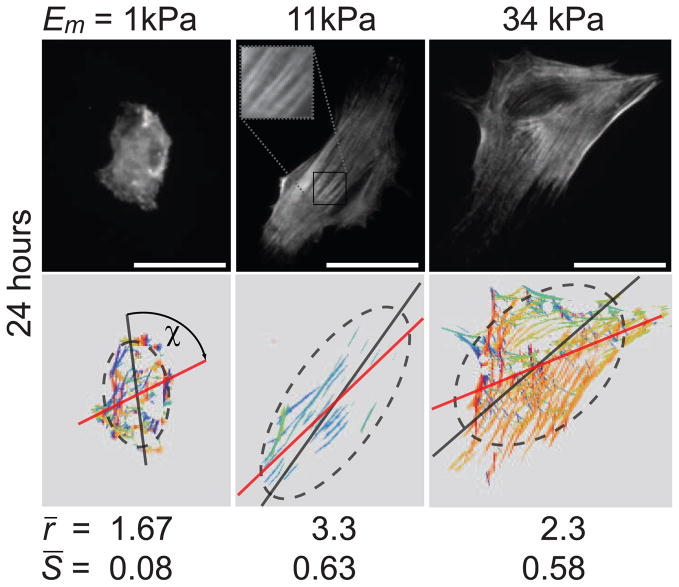
Figure 1.

Acto-myosin stress-fiber alignment in hMSCs sparsely plated on 2D substrates of different elasticity. The top row shows hMSCs immuno-stained for non-muscle myosin IIa (NMMIIa) 24 hours after plating on elastic substrates with a Young’s modulus E_m of 1 kPa, 11 kPa, and 34 kPa that are the most representative cells of the mean values obtained for cell area A, aspect ratio of long to short axis r, and stress-fiber order parameter S = 〈cos2θ〉; where θ is the angle between each stress-fiber in the cell and the long axis of the fitted ellipse. The bottom row shows the respective orientational plots, where the different orientations of myosin filaments are depicted with different colours. The dark gray dashed ellipses are best fits to the cell edge and the red line indicates the mean orientation of the stress-fibers as determined by the automated algorithm. ξ is the angle between the mean stress-fiber orientation and the principal axis of the ellipse. From symmetry considerations we need only consider the absolute value of ξ between 0 and π/2; thus, a completely random distribution has an average ξ = π/4. Values given for r and S are the mean values of at least 60 cells per condition. All scale bars represent 50 μm.

Figure 4.

The effect of axial cell elongation on stress-fiber polarization and experimental values of the order parameter S for different elastic substrates. Upper panel shows a calculation of the 2D order parameter as a function of the matrix rigidity, for two cases: (i) (black curve) the cell spreads isotropically on the substrate, η = 0, and (ii) (red curve) the cell spreads anisotropically on the substrate, η = 1, see text. The two illustrations left of the curves show top views over the cell, before (shown as blank) and after (shown as shaded) cell spreading. In the asymmetric spreading case, r corresponds to the cell shape in an infinitely rigid matrix. For both curves we used r = 2, α = 2 and Poisson ratios as in Fig. 3. The bottom panel shows the experimental values of the stress-fiber order parameter, S = 〈cos2θ〉, 24 hours after plating the cells, for the three groups of cells (of aspect ratios r = 1.5, 2.5, 3.5) as a function of the Young’s modulus of the matrix, E_m; θ is the angle between each stress-fiber in the cell and the long axis of the fitted ellipse. Within each of the different groups, S is maximal for E_m = 11 kPa and generally increases with aspect ratio r, in agreement with our theoretical predictions. Error bars denote the standard error of the mean and theory curves (dotted lines) calculated from the simplified expansion of S (supporting Information) are shown to guide the eye.

To test the predictions of our model we imaged actin and NMMIIa in hMSCs sparsely grown on substrates of different elasticities. The overall aspect ratio r of the cell and the orientation of the contractile stress-fibers have been determined; to quantify the polarization response we calculated the order parameter S = 〈cos2θ〉, where θ is the angle between each stress-fiber in the cell and the long axis of the fitted ellipse. see Methods section for details.

Cells imaged one hour after plating on the substrate showed aspect ratios, r, slightly greater than unity (see Supplementary Figure 2), and although some stress fibers already developed there was no significant polarization yielding order parameters S close to zero. This situation clarifies 4 hours after plating the cells; the order parameter S increases and shows a non-monotonic behavior as a function of the matrix rigidity, as shown in the inset of Fig. 4.

After 24 hours, both the morphology of the cells and cytoskeletal organization is significantly different (p < 0.05) on the substrates of 1, 11, and 34 kPa. Fig. 1 shows that cells on the 11 kPa substrate, whose rigidity is comparable to that of the cells, show an elongated, spindle-like morphology and exhibit a closer alignment of the stress-fibers with the major axis of the cell, as predicted by our model. In contrast, the cells on the 1 kPa and 34 kPa substrates are more isotropic in their overall shape and their stress-fibers are less well aligned with the long axis of the cell.

Fig. 4 shows the mean values of the order parameter, S, for different substrate elasticities E_m, 24 hours after the cells were plated on the substrate. Because of the natural variation of the shape of the cells, we regrouped the cells for each matrix elasticity E_m according to their different aspect ratios r = 1.5, 2.5, and 3.5. For each of these subgroups the order-parameter plots show a non-monotonic dependence on the matrix rigidity and in general S is higher for cells with higher aspect ratio r. The non-monotonic dependence however is most pronounced for cells with low aspect ratio, r = 1.5. For the groups with higher aspect ratio, the curves saturate to higher values. This is likely to reflect the axial stress resulting from the concurrent cell elongation, as predicted by our model. Our simplified models thus capture the correct qualitative behavior of stress-fiber polarization in stem cells as seen in Figs. 3 and 4. Our findings thus suggest a mechanism that allows stem cells to adopt different internal structures in different mechanical environments and may provide a physical basis for the mechanosensitivity of stem cell differentiation [7].

III. METHODS

Elastic polyacrylamide (PA) gels with a Young’s elastic modulus E_m of 1, 5, 11, 20, and 34 kPa were prepared as reported elsewhere [7, 35, 36]. Additionally, hyaluronic acid (HA) gels with a stiffness of 5 and 20 kPa and glass slides were prepared as described earlier [7]. The elasticity of the matrix was verified by force indentation measurements with an atomic force microscope (MFP-3D, Asylum Research) using a modified Hertz model. We performed force indentation curves at ten different spots (10 curves each) to ensure a homogeneous elastic modulus E_m throughout the whole gel. For cell adhesion, collagen type I (rat tail, BD Biosciences) was covalently attached to the hydrogels and to amino-silane coated glass with the bifunctional cross-linker Sulfo-SANPAH (Pierce) assuring the same ligand density on substrates of different stiffness. Scanning force microscopy of the surface after coating revealed a homogeneous smooth surface without structured inhomogeneities. hMSCs, obtained from Lonza, were cultured in standard tissue culture treated plastic flasks (Corning) using MSC growth medium (low glucose DMEM (Invitrogen) supplemented with 10 % fetal bovine serum (Sigma) and 1 % penicillin/streptomycin (Invitrogen)). 500 cells per cm² were plated on the substrates to ensure cells being. For immuno-staining and imaging the cells were fixed with a 10 % solution of formaldehyde (Sigma) in PBS and subsequently permeabilized with a 0.5 % solution of Triton X 100 (Sigma) in PBS. NMMIIa was immunostained with a primary antibody produced in rabbit (Sigma) followed by a secondary antibody (Alexa Fluor 488 donkey anti-rabbit IgG, Invitrogen) and F-actin was visualized using rhodamine-phalloidin (Fluka). The nucleus was stained with a Hoechst stain (#33342, Invitrogen). Fluorescence images were taken on an inverted microscope (IX 71, Olympus) equipped with a 20x phase contrast objective using a 1.6x post magnification lens. To obtain unbiased cell images single nuclei were searched that looked healthy and had no close neighbors. Only then actin and NMMIIa images were taken. Supplementary figure 1 shows a composite fluorescence image (A) and the raw fluorescence intensity image of NMMIIa (B) that is used to determine cytoskeletal organization. In order to obtain sufficient statistics at least 60 cells per condition were analyzed.

Image Analysis

Cell area, orientation and the major and minor axes of the cell were computed from the moments up to the second order of the thresholded binary image of the cell using NIH ImageJ [37]; the aspect ratio r is the ratio of major to minor axis.

Segmentation and orientation analysis of cell stress-fibers was performed using a custom automated image analysis algorithm written in Mathematica (Wolfram Research, Champaign, IL). The segmentation uses a series of elongated Laplace of Gaussian (eLoG) kernels [38]. These are generated from n anisotropic Gaussians of the form

$$G=\frac{1}{2\pi {\sigma }_x{\sigma }_y}exp(-\left(\frac{x^2}{2{\sigma }_x}+\frac{y^2}{2{\sigma }_y}\right))$$

that are each rotated in steps of π/n where n goes from 0 to π − π/n. For the results presented here we used n = 15. The Gaussian kernels are then convolved with a Laplacian filter given by

$$L=\left(\begin{array}{ccc}0& -1& 0\\ -1& 4& -1\\ 0& -1& 0\end{array}\right).$$

The n eLoG kernels are each convolved with the original images producing n response images. The maximum over the n response images at each xy–pixel is then used to create a single maximum response image. The segmentation shown in Supplementary Figure 1C is the maximum response image after it has been thresholded using the Otsu method [39], which determines a threshold based only on the image intensity histogram and so does not introduce any experimenter bias. Finally, connected circular spots with a diameter greater than 10 pixels are removed from the thresholded image to reduce the contribution of bright non-fibrous points in the original image that lead to isotropic spots to the filtered image because the response of each eLoG kernel survives the threshold if the intensity in the original image is sufficiently high. The rotation angle of the filter that gave the maximum response at each pixel is taken as that pixels orientation and is represented as the different colors. The average fiber orientation and order parameter are determined from the histogram of the individual pixel orientations.

To compare the alignment of the stress-fibers for a single cell shape, the cells were regrouped according to their aspect ratios and the averaged orientational order parameter of the stress-fibers S has been determined for each of these groups. These values are plotted in Fig. 4 and are listed in table I:

TABLE I.

Order parameter S and standard error of the mean (SEM) for cell groups of different aspect ratio r on substrates of different elasticity E_m.

Em =	1 kPa S ± SEM	5 kPa S ± SEM	11 kPa S ± SEM	20 kPa S ± SEM	34 kPa S ± SEM	glass S ± SEM
r = 1.5	0.07 ± 0.01	0.19 ± 0.06	0.38 ± 0.08	0.33 ± 0.05	0.30 ± 0.05	0.12 ± 0.06
r = 2.5	0.22 ± 0.06	0.54 ± 0.04	0.54 ± 0.04	0.55 ± 0.07	0.43 ± 0.06	0.44 ± 0.06
r = 3.5	0.23 ± 0.09	0.58 ± 0.06	0.68 ± 0.06	0.70 ± 0.03	0.56 ± 0.07	0.58 ± 0.03

To determine the amount of NMMIIa, we used thresholded binary images of the determined stress-fibers as a mask for the fluorescence images of NMMIIa. The total intensity after multiplication of the mask with the fluorescence image gives an estimate of the active contractile NMMIIa in stress fibers without including the diffuse background intensity from cytosolic NMMIIa. This is a measure of the total amount of contractile dipoles in the cell that increases with increasing substrate stiffness (see Supplementary Figure 3).