Ecological Inference in the Social Sciences

Abstract

Ecological inference is a problem of partial identification, and therefore reliable precise conclusions are rarely possible without the collection of individual level (identifying) data. Without such data, sensitivity analyses provide the only recourse. In this paper we review and critique approaches to ecological inference in the social sciences, and describe in detail hierarchical models, which allow both sensitivity analysis and the incorporation of individual level data into an ecological analysis. A crucial element of a sensitivity analysis in such models is prior specification, and we detail how this may be carried out. Furthermore, we demonstrate how the inclusion of a small amount of individual level data can dramatically improve the properties of such estimates.

1 Introduction

In this paper the problems of making individual-level inference from ecological data is considered. In particular suppose we have a set of R × C tables in which the margins only are observed, for concreteness we suppose each table corresponds to a different geographical area. This problem arises in many disciplines including political science (Achen and Shively, 1995; King, 1997), sociology (Goodman, 1953, 1959; Duncan and Davis, 1953)) and spatial epidemiology (Richardson and Montfort, 2000; Wakefield, 2008); King (1997) and Cleave et al. (1995) describe further application areas. However, the exact nature of the inferential question differs importantly across these disciplines, see Salway and Wakefield (2004) compare objectives and approaches to inference in the social sciences and epidemiology.

In epidemiological applications the usual aim is to estimate a risk contrast between exposed and unexposed individuals in a certain population and time period. This contrast can then be used to predict the number of new cases in a future time period (for public health provision, for example) or to make causal inferences. Since the data are usually observational, to estimate the causal effect of the exposure an attempt must be made to control for confounding variables (for example, one or more of age, gender, race, and smoking history) that are responsible for differences in risk, beyond those due to exposure, of the study populations. Hence in ecological studies in epidemiology there is never a single predictor and the data are not simply in the form of a series of 2 × 2 tables, since within each area there will (typically) be multiple confounders for which to control. Control for confounders in ecological studies is more difficult than in individual studies, since the multivariate distribution of exposures/confounders within and between areas is needed (Richardson et al., 1987; Greenland and Robins, 1994; Prentice and Sheppard, 1995; Plummer and Clayton, 1996; Lasserre et al., 2000; Wakefield, 2008).

By contrast, in the social sciences, ecological inference can have causal and non-causal inferential purposes. In many cases, social scientists have concentrated on imputing the missing cells in the constituent 2×2 or R×C tables. This type of ecological inference is often referred to as EI (named after the software package that accompanies King’s famous 1997 book). For example, in political science, a typical analysis will examine the differences between racial voting patterns in a specific region. This query can be answered by imputing the number of votes by race for a particular party or candidate, by area. Hence, viewed in this way, prediction rather than causality is the aim. However, in many recent cases, EI is followed by a second stage analysis that utilizes the imputed data, often as the dependent variable in a regression (Herron and Shotts, 2003b) and may be implicitly causal. For example, Burden and Kimball (1998) use EI to analyze ticket splitting rates across congressional districts, and then use these rates in a second stage analysis to determine why voters are splitting their tickets. This type of analysis is often referred to as EI-R.

Although the shortcomings of ecological inference in the EI and epidemiological contexts have been documented (Achen and Shively, 1995; Greenland and Robins, 1994; Cho, 1998; Freedman et al., 1998; Gelman et al., 2001; Wakefield, 2008), the continued use of ecological data can be attributed to: the increased sample sizes and predictor ranges they provide; their routine availability; their increased reliability when a sensitive question is asked; and the impossibility of further data collection in historical contexts. Furthermore, King (1999) argues that EI is a reasonable approach and will only be unreliable in the following circumstances:

If the assumptions are wrong and the bounds and diagnostics are not sufficiently informative, and the researcher has no time to collect qualitative knowledge, then EI will perform poorly.

The difficulties of ecological inference may however become compounded when ecological estimates are used as data in second stage analyses in EI-R (Herron and Shotts, 2003b), and although extensions to the EI can alleviate some of these problems (Adolph and King, 2003; Herron and Shotts, 2003a; Adolph et al., 2003), there are still concerns over the use of the technique (Herron and Shotts, 2004; Cho and Gaines, 2004).

Given the aforementioned difficulties of ecological inference, the ecological analyst will benefit from a method that possesses the following properties: 1) produces only logically consistent estimates that respect the Duncan and Davis (1953) bounds, 2) allows the incorporation of qualitative information, 3) provides a means for carrying out sensitivity analysis, 4) allows the inclusion of individual level data and characterizes the gains to be made from such an inclusion. In this paper, we demonstrate that the hierarchical convolution likelihood model described in Wakefield (2004a) has all of these properties.

The outline of this paper is as follows. In Section 2 we describe the fundamental difficulties of ecological inference, and describe a data set that will be used to illustrate the various issues raised throughout the paper. In Section 3 we describe the so-called convolution likelihood. Section 4 describes the Bayesian approach to inference, including subsections on prior specification and predictive distributions. The latter links the parameters of the model to the observables (unobserved counts), and is of great importance in political science applications (where there has been confusion between unobservable probabilities in a hypothetical super population model, and the samples fractions in the study population, which are potentially observable) as emphasized above. Section 5 describes the various computational schemes that have been suggested in the context of ecological inference. Section 6 presents a sensitivity analysis in the context of the Louisiana data, while we consider the combination of aggregate and individual data in Section 7. A concluding discussion rounds out the paper in Section 8.

2 The Fundamental Difficulty of Ecological Inference

To motivate our discussion we introduce a specific data set for which Y = 0/1 represents the event Democrat/Republican registration, and X = 0/1 the event Black/White. The data were collected in the U.S. state of Louisiana in 1990 and are available in each of the 64 counties of that state. These data are ideal for illustration of methods, since they are one of the few sources for which the individual level data are available.

Figure 1 gives an initial look at the ecological data. In panel (a) we give a histogram of the fraction black, and observe that in the majority of counties this fraction is less than 0.5. Panel (b) gives the proportion registered Republican against the fraction black, with a least squares line added to indicate the linear association. The general trend is that the proportion registered Republican decreases as the proportion black increases. The obvious explanation is that blacks are less likely to register Republican. Alternative explanations exist, however, in particular the same pattern could be observed if whites are less likely to register Republican if in a predominantly black county, if blacks are more likely to register Republican in a predominantly white county, or if individual race is an unimportant predictor of registration behavior, and instead an individual’s behavior, whether black or white, is predicted by the proportion of blacks in the area. In each of these scenarios the proportion black/white in an area is an example of a contextual variable, a variable reflecting characteristics of individuals in a shared environment. To help explain the results that follow panels (c) and (d) give the fractions black and white who register Republican against the fraction black, again with least squares lines added. Note that it would not have been possible to produce these two plots without the individual level data which we have in this special case. We see that the fraction black who register Republican decreases across counties as the fraction black in the counties increases, hence it seems plausible that some contextual variable is driving black Republican registration (e.g. income). We also see that the proportion white who register Republican increases across counties as the fraction black in the counties increases. This is consistent with the explanation that whites in areas with large numbers of blacks are more fearful of affirmative action policies, and register/vote accordingly.

Figure 1.

Across 64 counties of Louisiana: (a) Histogram of fraction of population that are black; (b) fraction registered Republican versus fraction black, (c) fraction black registered Republican versus fraction black, (d) fraction white registered Republican versus fraction black.

Hence Figure 1(b) understates the extent to which blacks are less likely to register Republican than whites, which is an example of what Selvin (1958), called the ecological fallacy: incorrect inference concerning individual effects gleaned from aggregate data. In an extreme case, the aggregate relationship could be the reversal of the true individual relationship, a phenomenon closely related to Simpson’s paradox (Simpson, 1951), see Wakefield (2004c) for further discussion. The ecological fallacy had been discussed in the sociology literature before 1950, but Robinson (1950) provided an extremely lucid account, which explained the subsequent influence of the paper, in deterring the analysis of ecologic data. Recently, Robinson’s paper has been revisited, within a multilevel framework (Subramanian et al., 2009b,a) and critiqued (Oakes, 2009; Firebaugh, 2009; Wakefield, 2009).

We now introduce some notation, in the context of the Louisiana data, in order to ease description of models that have been suggested for ecologic data. For a generic individual, Y = 0/1 will denote the event that an individual is unregistered/registered (the response), and X = 0/1 the event that an individual is of black/white race (the predictor). Table 1 describes the notation that we will use throughout the paper; Y_0i, Y_1i are the Y = 1 individuals from covariate group X = 0, 1, respectively, in area i. In an aggregate situation we do not observe the internal counts Y_0i, Y_1i. The fundamental difficulty of ecological inference is that we are interested in these two quantities, but it is their sum Y_i only, that we observe.

Table 1.

Table summarizing data in area i; in an ecological study the margins only are observed.

	Y = 0	Y = 1
x = 0		Y0i	N0i
x = 1		Y1i	N1i
	Ni − Yi	Yi	Ni

In the social science ecological inference literature the inference problem has often been treated as the imputation of the missing data, Y_0i, Y_1i, and due to this perspective approaches have often implicitly adopted a finite sampling view. Here we utilize a hypothetical infinite population of exchangeable blacks and whites within each area as the primitive modeling object, and define the parameter p_ji to be the fraction of race j in area i that register. With this viewpoint an estimate of this probability, p̂_ji, is not equal to the true (but unobserved) fraction registered, Y_ji/N_ji, which we denote by p̃_ji. In a finite sample view if Y_ji were observed then inference is complete since the population has been observed. In contrast, in the infinite population view, even if Y_ji is observed, uncertainty concerning p_ji will remain (though may be small if N_ji is large). However, while the infinite population model takes p_ji to be the primary parameter of interest, note that this model can still be used to make predictions about the fractions p̃_ji if these are of interest. Section 4.3 discusses this in greater detail.

To see the indeterminacy of ecological inference more clearly we write, for area i,

$$\frac{Y_i}{N_i}=\frac{Y_{0i}+Y_{1i}}{N_i}=\frac{Y_{0i}}{N_{0i}}\times \frac{N_{0i}}{N_i}+\frac{Y_{1i}}{N_{1i}}\times \frac{N_{1i}}{N_i}$$

which may be rewritten as

$${\stackrel{\sim }{q}}_i={\stackrel{\sim }{p}}_{0i}\times x_i+{\stackrel{\sim }{p}}_{1i}\times (1-x_i),$$ (1)

where q̃_i is the fraction registered, p̃_0i and p̃_1i are the black and white fractions registered, and x_i and 1 − x_i are the proportions black and white respectively. In an ecological data set, q̃_i and x_i are observed while p̃_0i and p̃_1i are not. From (1) we see that the observed q̃_i are consistent with many true fractions p̃_0i, p̃_1i. The bounds of Duncan and Davis (1953), may be written in terms of q̃_i and x_i:

$$\begin{array}{l}max\left\{0,\frac{{\stackrel{\sim }{q}}_i-(1-x_i)}{x_i}\right\}\le {\stackrel{\sim }{p}}_{0i}\le min\left\{1,\frac{{\stackrel{\sim }{q}}_i}{x_i}\right\}\\ max\left\{0,\frac{{\stackrel{\sim }{q}}_i-x_i}{1-x_i}\right\}\le {\stackrel{\sim }{p}}_{1i}\le min\left\{1,\frac{{\stackrel{\sim }{q}}_i}{1-x_i}\right\}\end{array}$$

In terms of the underlying probabilities p_ji, there is no constraint beyond 0 < p_ji < 1. This is a crucial difference between the finite sample and infinite sampling views. Figure 2 shows the admissible ranges for p̃_0i and p̃_1i for the Louisiana data via a so-called tomography plot. We see that for the blacks in particular there is a great deal of uncertainty. The open circles correspond to the true fractions, which are available for these data.

Figure 2.

Tomography lines for Louisiana data.

Two extreme explanations are consistent with (1). First, following Goodman (1953, 1959) we may assume that p̃_0i and p̃_1i are such that

$$E[{\stackrel{\sim }{p}}_{ji}\mid x_i]=p_j,$$ (2)

j = 0, 1 so that the fractions are uncorrelated with x_i. The expectation here is with respect to repeated sampling in areas with proportion of blacks x_i. We then have

$$E[{\stackrel{\sim }{q}}_i\mid x_i]=p_0\times x_i+p_1\times (1-x_i)=a+{bx}_i,$$ (3)

where a = p₁ and b = p₀ − p₁. Although it is only the expectations of the fractions that are considered constant in (2), the usual way of imputing the internal fractions is to simply take p̃_ji = p_j, which is equivalent to a model in which the fractions themselves are constant. This model has sometimes been described as Goodman regression, but the name ecological regression is more appropriate as Goodman did not encourage general use of the approach, and in particular was aware that the ‘constancy assumption’ (2) would often be inappropriate. The assumption of constancy allows the mean to be derived, but to formulate an estimation method it would be desirable to derive the variance and covariance of Y_i = N_iq̃_i. In general it has been assumed that counts in different areas are independent, and various forms for the variance have been considered. As we will describe in detail in Section 3, a plausible likelihood leads to Y_i following a convolution distribution with variance that depends on p_0i and p_1i.

A very simple model, termed the ‘nonlinear neighborhood model’ (Freedman et al., 1991), is to assume that p_0i = p_1i = q_i, i.e. to assume that registration and individual race are independent. This allows the table to be collapsed, and inference is straightforward. Freedman (2001) states that in this model, ‘…behavior is determined by geography not demography’. A specific version of the nonlinear neighborhood model, the ‘linear neighborhood’ model, was also described by Freedman et al. (1991) and makes the assumption that E[p_0i|x_i] and E[p_1i|x_i] are identical but depend on the proportion black via the linear form

$$E[p_{0i}\mid x_i]=E[p_{1i}\mid x_i]=E[q_i\mid x_i]=a+{bx}_i,$$ (4)

which is identical to (3) though the interpretation and imputed internal cells are drastically different under the two models, which was the motivation for Freedman et al. (1991) to introduce the model, to illustrate the fundamental unidentifiability of ecological inference. Other regression-type approaches, with a non-parametric flavor, are described by Chambers and Steel (2001).

The assumption that q̃_i is uncorrelated with x_i may be a major problem in some applications; see Freedman et al. (1998, 1999); Freedman (2001)) for examples. A further problem with ecological regression is the assumption that the estimated fractions are not allowed to vary across areas so that between-area variability is not acknowledged. Least squares procedures are known to provide consistent estimates of regression parameters under a range of distributions of the errors, but are also known to be very poor at providing predictions of observable quantities. For prediction some knowledge of the distribution of the error terms is required. The great benefit of the hierarchical approach that was popularized by King (1997) is that between-area differences in fractions are assigned a distribution, so allowing variability in the estimates of race-specific fractions across areas.

To conclude, in this section we have reviewed how two competing explanations with vastly different interpretations and inferential implications lead to an identical mean function. To overcome this unidentifiability and estimate 2m quantities from m observables, it is clear that any approach that is considered must make assumptions (or incorporate additional information). It is not immediately apparent, but also true that some of the assumptions from any approach will be uncheckable from the aggregate data alone. In all observational studies untestable assumptions such as ‘no unmeasured confounding’ are required for causal interpretations (e.g. even Figures 1(c) and (d) are not sufficient to derive the full causal story). If causal inference is the goal of an ecological study, this problem is particularly acute since the amount of information concerning quantities of interest is much smaller than in typical individual-level observational studies (e.g. Figure 1(b) provides less information than Figures 1(c) and (d)).

3 The Convolution Likelihood

In the previous section we simply derived the form of the marginal mean of the fraction registered Republican under various assumptions. In this section we describe a likelihood function under a plausible sampling scheme, and compare this with various (often implicit) likelihoods that have been used in the ecological literature. Recall that

$$p_{0i}=Pr(Y=1\mid x=0,i)\text{and}{p}_{1i}=Pr(Y=1\mid x=1,i)$$ (5)

are the population probabilities in area i, i = 1, …, m. Returning to Table 1 we first note that if Y_0i and Y_1i were observed then if we were to assume that each of the N_0i black individuals in area i have independent Bernoulli responses with probability p_0i, and each of the N_1i white individuals in area i have independent Bernoulli response with probability p_1i, then

$$Y_{ji}\mid p_{ji}\sim \text{Binomial}(N_{ji},p_{ji}),$$

j = 0, 1, i = 1, …, m. Under this sampling scheme, if Y_0i and Y_1i are unobserved then the sum Y_i follows a convolution of these binomial distributions:

$$Pr(Y_i\mid p_{0i},p_{1i})=\sum _{y_{0i}=l_i}^{u_i}\left(\begin{array}{c}{N}_{0i}\\ y_{0i}\end{array}\right)\left(\begin{array}{c}{N}_{1i}\\ Y_i-y_{0i}\end{array}\right)p_{0i}^{y_{0i}}{(1-p_{0i})}^{N_{0i}-y_{0i}}{p}_{1i}^{Y_i-y_{0i}}{(1-p_{1i})}^{N_{1i}-Y_i+y_{0i}}$$ (6)

where

$$l_i=max(0,Y_i-N_{1i}),u_i=min(N_{0i},Y_i).$$ (7)

These values correspond to the admissible values that Y_i can take, given the margins in Table 1. McCullagh and Nelder (1989) consider this likelihood under the assumption that p_0i = p₀ and p_1i = p₁, see also Achen and Shively (1995, p. 46).

We now briefly examine the shape of the likelihood for a single table. Plackett (1977) showed that the maximum likelihood estimate of the log odds ratio in a single table in which the margins only are observed is ±∞, which corresponds to p_0i = 0 or 1 and/or p_1i = 0 or 1. Steele et al. (2004) work with the convolution directly and report that the maximum likelihood estimator lies at the endpoint of the tomography line.

In King et al. (1999) the alternative model

$$Y_i\mid P_{0i},p_{1i}\sim \text{Binomial}\{N_i,P_{0i}{x}_i+p_{1i}(1-x_i)\}$$ (8)

was considered. As in King (1997), this produces a likelihood that is constant along the tomography line (an intuitively appealing feature given the implicit lack of information on the internal cells of the table). However, the underlying model should be viewed as an approximation in this context since it assumes sampling independently N_i individuals each with probability p_0ix_i + p_1i(1 − x_i).

In contrast, the convolution likelihood assumes that we sample N_0i individuals with probability p_0i and N_1i individuals with probability p_1i, i = 1, …, m. As N_i → ∞ with x_i and q̃_i constant, this convolution likelihood function becomes concentrated along the tomography line with an asymmetric U-shape, with the maximum at one endpoint. At first, this non-constancy of the likelihood may seem counterintuitive (given the lack of information). However, an MLE on the boundary of the parameter space is an alternative indication for a lack of information. Furthermore, if uniform priors are placed on the probabilities p_0i and p_1i, this likelihood implies a flat posterior predictive distribution for p̃_0i and p̃_1i along the associated tomography line. Therefore, the convolution likelihood produces constancy in exactly the space that we would expect ({p̃_0i, p̃_1i} instead of {p_0i, p_1i}), and only produces constancy when the appropriate assumption of “no information” is made about p_0i and p_1i.

It is clear that the data in one table alone gives limited information concerning p_0i, p_1i or p̃_0i, p̃_1i, since we only have a single observation, Y_i. However, in most applications, ecological data from multiple areas is available.

4 Bayesian Inference

4.1 Priors

Following King (1997) a number of authors have developed hierarchical approaches in which, rather than reduce the dimensionality of the models as was described in the previous section, the full 2m parameters are retained but the probabilities/fractions, are assumed to arise from a bivariate distribution.

At the second stage of the King (1997) model it is assumed that the pair p̃_0i, p̃_1i arise from a truncated bivariate normal distribution, hence imposing identifiability. King (1997) views the truncated bivariate normal distribution as the likelihood while we have referred to the tomography lines as providing the first stage of the model, with the truncated bivariate normal the second stage of the model. Inference is initially carried out via MLE for the five population parameters, using numerical integration, and then simulation is used to make more refined inference. Priors may be placed on the population parameters (that characterize the truncated normal) to give a Bayesian model. In common with the majority of approaches, it is assumed that the pairs of fractions form an independent sample from the second stage distribution (here the truncated bivariate normal), see Haneuse and Wakefield (2004) for a hierarchical model with spatial dependence between the probabilities. The model in its most basic form also assumes that the fractions are uncorrelated with x_i. The latter may be relaxed (see, King 1997, Chapter 9), via the introduction of contextual effects (in King et al. (2004) it is recommended that such effects be included), but reliable estimation of both individual and contextual effects is crucially dependent on the existence of substantive prior information (see the example in Wakefield (2004c), for a further demonstration of this). The freely-available EzI software (Benoit and King, 1998) may be used to implement the truncated normal model, and its extensions.

At the second stage, King et al. (1999) assume that p_0i and p_1i are independent with

$$p_{ji}\mid a_j,b_j{\sim }_{\mathit{iid}}\text{Beta}(a_j,b_j).$$ (9)

The third and final stage of the model consists of exponential priors, Exp(λ) on a_j, b_j, j = 0, 1, where λ⁻¹ is the mean of the exponential. Specifically, in the example considered it was assumed that these exponential priors had mean 2 (λ = 0.5), a choice which is not desirable in many instances because it often produces a prior for each probability which is very strongly U-shaped (since beta priors with a_j < 1, b_j < 1 are themselves U-shaped, and an exponential with mean 2 has a 0.39 probability of being less than one). This is discussed more fully in Wakefield (2004c), in particular see Figure 6. Choosing much smaller values of λ, for example, λ = 0.01, produces almost uniform priors on the probabilities, though we would not universally recommend a particular hyperprior, given the sensitivity of inference it should be context specific. As the number of tables decreases and the x distribution becomes more asymmetric this problem becomes more and more acute. The ideal situation is for substantive information to be available for prior specification. The strong dependence on the third stage prior is in stark contrast to the usual generalized mixed model case for which there is far less dependence (except for priors on variance components, where again care must be taken with small numbers of units). Here we emphasize that the form of the prior should be examined through simulation. Specifically, for generic second stage, p(p|φ, and third stage, p(φ):

1. For fixed φ, simulate φ^(s) ~ p(φ), for s = 1, …, S.

2. Simulate p^(s) ~ p(p|φ^(s)), for s = 1, …, S.

3. Examine graphical and numerical summaries of the collection {φ ^(s), s = 1, …, S}.

This procedure will be illustrated shortly.

The model given by (9) does not allow dependence between the two random effects (note this is distinct from the independence between pairs of random effects in different areas, which is also assumed) though it is conjugate (giving a marginal distribution for the data that is beta-binomial) which may offer some advantage in terms of computation. The model also allows area-level covariates to be added at the second stage.

Wakefield (2004c) proposed, as an alternative to the beta model, a second stage in which the logits of the registration probabilities arose from a bivariate normal distribution; this model was introduced for the analysis of a series of 2 × 2 tables when the internal cells were observed by Skene and Wakefield (1990). Specifically, a reasonably general form is

$$\begin{array}{l}{\theta }_{0i}=log\left(\frac{p_{0i}}{1-p_{0i}}\right)={\mu }_0+{\beta }_0{z}_i+{\delta }_{0i}\\ {\theta }_{1i}=log\left(\frac{p_{0i}}{1-p_{0i}}\right)={\mu }_1+{\beta }_1{z}_i+{\delta }_{1i}\end{array}$$ (10)

with

$${\delta }_i\sim N_2(0,\mathrm{\sum }),$$

where

$${\delta }_i=\left[\begin{array}{c}{\delta }_{0i}\\ {\delta }_{1i}\end{array}\right]\text{and}\mathrm{\sum }=\left[\begin{array}{cc}{\mathrm{\sum }}_{00}& {\mathrm{\sum }}_{01}\\ {\mathrm{\sum }}_{10}& {\mathrm{\sum }}_{11}\end{array}\right].$$ (11)

Hence θ_0i and θ_1i denote the logits of the probabilities p_0i and p_1i in table i, so that p_ji = exp(θ_ji)/{1 + exp(θ_ji)}, j = 0, 1. In the specification (10), z_i represent area-level characteristics (and may, in principle, include x_i) and β₀, β₁ are (ecological) log odds ratios associated with these variables.

A third stage hyperprior adds priors on μ₀, μ₁ and Σ (and β₀, β₁ if there are covariates). It is difficult to gain information on the covariance term Σ₀₁ and so from this point onwards we assume that Σ₀₁ = 0. Without substantive information for the registration-race data, Wakefield (2004c) chose logistic priors with location 0 and scale 1 for μ₀ and μ₁, since these induce uniform priors on exp(μ_j)/{1 + exp(μ_j)} (the median of the registration probability for race j across the population of areas). Since G(z) ≈ (cz) with $c=16\sqrt{3}/(15\pi )$ and where G(z) = (1 + e^−z)⁻¹ is the CDF of a logistic random variables, as an alternative we may specify normal priors with mean 0 and standard deviation 1/c.

For the precisions ${\mathrm{\sum }}_{00}^{-1},{\mathrm{\sum }}_{11}^{-1}$ we specify gamma distributions Ga(a, b) (where the parameterization is such that the mean is given by a/b). In the WinBUGS manual the priors Ga(0.001, 0.001) are often used for precisions within a hierarchical model. This choice is not to be recommended in general (that is, for all applications); here it is a very poor one (and leads to marginal priors for the probabilities that are highly U-shaped). We follow a previously suggested procedure (Wakefield, 2009) which we briefly describe for a generic log odds ratio in area i, δ_i ~_iid N(0, Σ) with Σ⁻¹ ~ Ga(a, b). We integrate over S to find the marginal distribution p(δ_i) which is a t distribution with d = 2a degrees of freedom, location zero, and scale Σ = b/a. To construct a prior distribution we require a careful interpretation of δ_i, or more informatively, exp(δ_i) which is the perturbation of the odds of Republican registration from the median of the distribution of the odds of Republican registration across all areas. Hence we may refer to exp(δ_i) as a residual odds, since it is relative to the median odds across areas. We give a range for exp(δ_i). In particular, for the range (1/R, R) we use the relationship $\pm t_{0.025}^d\sqrt{\sigma }=\pm logR$, where $t_r^d$ is the 100 × r-th quantile of a Student t random variable with d degrees of freedom, to give a = d/2, $b={(logR)}^{2}d/2{(t_{1-(1-q)/2}^d)}^2$. We choose d = 1, to give a Cauchy marginal distribution. As an example, for a 95% range of [0.1, 10] we obtain a = 0.5, b = 0.0164.

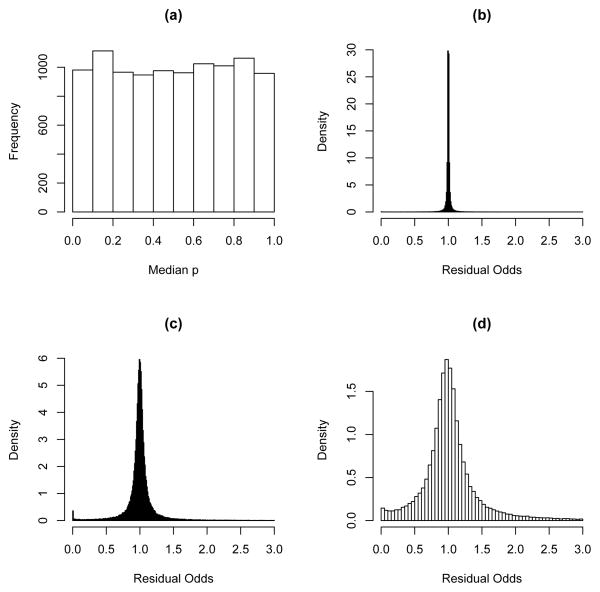
We illustrate the prior simulation strategy with the priors μ ~ N(0, 1/c²), Σ⁻¹ ~ Ga(0.5, b), with θ_i = μ + δ_i, and δ_i ~ N(0, Σ). We take three values of b, corrsponding to 95% ranges of [0.9, 1.1], [0.5, 2] and [0.1, 10] (which correspond to b = 0.000028, 0.00149, 0.0164, respectively). Figure 3(a) gives the marginal distribution of $\text{median}(p)=\frac{exp(\mu )}{1+exp(\mu )}$, which is close to uniform, in line with the theory outlined above. These priors are applied in Section 6.

Figure 3.

Simulations from the N(0, 1/c²) × Ga(0.5, b) prior. Panel (a) gives the marginal distribution of the median odds of Republican registration. Panels (b), (c) and (d) gives the residual odds of Republican registration (across areas) with ranges [0.9, 1.1], [0.5, 2] and [0.1, 10], respectively.

4.2 Derivation of the posterior distribution

In the Bayesian approach all unknown quantities are assigned prior distributions and the posterior distribution reflects both these distributions and the information in the data that is contained in the likelihood. In the hierarchical models described in Section 4.1 two stage priors are specified, with the first stage of the prior assuming a common form for the pairs of probabilities, and the second stage assigning hyperpriors to the parameters of this form. Letting p_i represent the pair of table specific probabilities, and φ a generic set of hyperparameters upon which the second stage of the prior depends, we have:

$$\pi ({\mathit{p}}_1,\dots ,{\mathit{p}}_m,\mathit{\phi }\mid y_1,\dots ,y_m)\propto p(y_1,\dots ,y_m\mid {\mathit{p}}_1,\dots ,{\mathit{p}}_m,\mathit{\phi })\times \pi ({\mathit{p}}_1,\dots ,{\mathit{p}}_m,\mathit{\phi })$$

with

$$p(y_1,\dots ,y_n\mid {\mathit{p}}_1,\dots ,{\mathit{p}}_m,\mathit{\phi })=\prod _{i=1}^{m}p(y_i\mid {\mathit{p}}_i),$$

by conditional independence of counts in different areas, and

$$\pi ({\mathit{p}}_1,\dots ,{\mathit{p}}_m,\mathit{\phi })=\pi ({\mathit{p}}_1,\dots ,{\mathit{p}}_m\mid \mathit{\phi })\times \pi (\mathit{\phi }),$$

to give the two-stage prior. Under the assumption of independence of the table-specific parameters (which would not be true if we assumed spatial dependence between these parameters), we may further write

$$\pi ({\mathit{p}}_1,\dots ,{\mathit{p}}_m\mid \mathit{\phi })=\prod _{i=1}^m\pi ({\mathit{p}}_i\mid \mathit{\phi }).$$

Hence, under these assumptions, we have the posterior distribution

$$\pi ({\mathit{p}}_1,\dots ,{\mathit{p}}_m,\mathit{\phi }\mid y_1,\dots ,y_m)\propto \prod _{i=1}^{m}p(y_i\mid {\mathit{p}}_i)\times \prod _{i=1}^m\pi ({\mathit{p}}_i\mid \mathit{\phi })\times \pi (\mathit{\phi }).$$

Inference follows via consideration of marginal posterior distributions, and predictive distributions. For example π(p_i|y₁, …, y_m) is the marginal posterior distribution for the pair of probabilities of Republican registration from table i.

4.3 The Posterior Predictive Distribution

We may also be interested in imputing the missing counts in area i. In particular, this is often the goal of ecological inference in the social sciences. This type of inference may be carried out via examination of the predictive distribution

$$Pr(Y_{0i}\mid y_1,\dots ,y_m)=\int Pr(Y_{0i}\mid {\mathit{p}}_i,N_{0i},N_{1i},N_i-y_i,y_i)\times \pi ({\mathit{p}}_i\mid y_1,\dots ,y_n)d{\theta }_i.$$

Note that we only need the distribution for Y_0i since the distribution of Y_1i = Y_i − Y_0i, which is immediately available. The integral averages the distribution of Pr(Y_0i|p_i, N_0i, N_1i, N_i − y_i, y_i) with respect to the posterior. The distribution of Y_0i given the row and column margins and the table probabilities, is a non-central (sometimes referred to as an extended) hypergeometric distribution, see for example, McCullagh and Nelder (1989). Suppose the odds ratio in the table is given by ψ_i = p_0i(1 − p_1i)/p_1i(1 − p_0i); then Y_0i has a non-central hypergeometric distribution if its distribution is of the form

$$Pr(Y_{0i}=y_{0i}\mid {\psi }_i,N_{0i},N_{1i},N_i-y_i,y_i)=\{\begin{array}{cc}\frac{\left(\begin{array}{c}{N}_{0i}\\ y_{0i}\end{array}\right)\left(\begin{array}{c}{N}_{1i}\\ y_i-y_{0i}\end{array}\right){\psi }_i^{y_{0i}}}{{\sum }_{u=l_i}^{u_i}\left(\begin{array}{c}{N}_{0i}\\ u\end{array}\right)\left(\begin{array}{c}{N}_{1i}\\ y_i-u\end{array}\right){\psi }_i^u}& y_{0i}=l_i,\dots ,u_i,\\ 0& \text{otherwise}\end{array}$$ (12)

where l_i = max(0, y_i − N_1i) and u_i = min(N_0i, y_i). Hence the predictive distribution is an overdispersed non-central hypergeometric distribution. The above predictive distribution produces (y_0i/N_0i, y_1i/N_1i) pairs that lie along the tomography line, and with flat priors on the probabilities, this distribution is uniform along the tomography line Wakefield (2004d). This provides a link with the likelihoods of King (1997) and King et al. (1999), but we emphasize that the flat distribution is with respect to the fractions, and not for the underlying probabilities.

5 Computation

Given the lack of identifiability in the posterior distribution, it is not surprising that computation is not straightforward for ecological inference, when analyzed using hierarchical models. In Wakefield (2004c) an “obvious” augmented data scheme was utilized.

Auxiliary Variable Sampling

For the missing data y_0i, the distribution is an extended hypergeometric distribution with margins N_0i, N_1i, y_i, N_i − y_i, i = 1, …, m:

$$\text{Pr}(Y_{0i}=y_{0i}\mid {\psi }_i,N_{0i},N_{1i},y_i)=\{\begin{array}{cc}\frac{\left(\begin{array}{c}{N}_{0i}\\ y_{0i}\end{array}\right)\left(\begin{array}{c}{N}_{1i}\\ y_i-y_{0i}\end{array}\right){\psi }_i^{y_{0i}}}{{\sum }_{u=l_i}^{u_i}\left(\begin{array}{c}{N}_{0i}\\ u\end{array}\right)\left(\begin{array}{c}{N}_{1i}\\ y_i-u\end{array}\right){\psi }_i^u}& y_{0i}=l_i,\dots ,u_i,\\ 0& \text{otherwise}\end{array}$$ (13)

where l_i = max(0, Y − N_1i) and u_i = min(N_0i, Y) and ψ_i = p_0i(1− p_1i)/p_1i(1− p_0i) is the odds ratio in the table. This discrete distribution may be sampled from in an obvious fashion, but in typical political science/sociology applications the margins are large and so generation is highly inefficient due to the summation over a large number of terms, each of which contains factorials. The mode is available in closed form, however, which may be exploited to produce an improved scheme, see Wakefield (2004c) for details.

Posterior Probability Sampling

Here we are required to sample from the conditional distribution for i = 1, …, m. If we assume p_ji|a_j, b_j ~ Be(a_j, b_j), then this conditional distribution corresponds to the product

$$\text{Be}(y_{0i}+a_0,N_{0i}-y_{0i}+b_0)\text{Be}(y_{1i}+a_1,N_{1i}-y_{1i}+b_1),$$ (14)

for i = 1, …, m, and is straightforward to sample from. With a normal second stage distribution for the logits, the conditional distribution is no longer of standard form but a Metropolis-Hastings step is easy.

For large table Wakefield (2004c) proposed a normal approximation to the convolution. WinBUGS code for ecological inference using this normal approximation was given in the Appendix of Wakefield (2004b). In the JAGS (Just Another Gibbs Sampler) software (Plummer (2009)) there is a a novel distribution dsum that may be used in the ecological inference context. It may be used in the following way (Plummer, personal communication). The specification y ~ dsum (y0, y1) where y is observed and y0, y1 are unobserved discrete-valued stochastic nodes creates an MCMC sampler that will simultaneously update y0 and y1, while respecting the constraint y0 + y1== y. In typical social science applications there are too many possible values of y0 (or y1) to use inversion and so the sampler uses discrete slice sampling (Neal, 2003) as an alternative.

The R package MCMCpack package (Martin et al., 2009) contains a function MCMChierEI to implement the hierarchical model of Wakefield (2004c) with the normal approximation to the convolution likelihood implemented along with slice sampling. An extension to this work to the R × C table case is available in the R package RxCEcolInf (Greiner et al., 2009). This package contains functions to analyze both ecological data alone, or ecological data supplemented with individual-level data, which is a very important extension, as we discuss further in Section 7. The methodological extension to the 2 × 2 table cases is described in Greiner and Quinn (2009). An additional R package, eco is also available and fits models described in Imai et al. (2008). These models include a close relative of the parametric model of Wakefield (2004c) and a non-parametric model in which the second stage distribution is a Dirichlet process prior.

With sampling-based inference, if we can simulate from Pr(Y_0i, Y_1i|θ_i, N_0i, N_1i, N_i − y_i, y_i) then it is straightforward to simulate from the predictive distribution, once samples ${\mathit{p}}_i^{(s)}$ are available from π(p_i|N_0i, N_1i, N_i − y_i, y_i), via

$$\frac{1}{S}\sum _{s=1}^{S}Pr(Y_{0i},Y_{1i}\mid {\mathit{p}}_i^{(s)},N_{0i},N_{1i},N_i-y_i,y_i).$$

6 Illustrative Analysis

We analyze the Louisiana data using the hierarchical normal model, and investigate the sensitivity of inference to the choice of the gamma prior on the precisions of the random effects distribution. Specifically, following the procedure outlined in Section 4.1 we pick ranges of: [0.1, 10], [0.2, 5], [0.5, 2], [0.9, 1.1], for the residual odds of Republican registration. These range from a prior that expexts the probabilities across areas to be tightly clustered around the median, to one in which there is much larger variability. In all cases we specify $N(0,{(15\pi /16\sqrt{3})}^2)$ priors for μ_j, j = 1, 2.

We used the MCMChierEI function to carry out inference, and ran the Markov chains for 10⁶ iterations, after discarding 10⁵ iterations as burn-in. We summarize the accuracy of inference in terms of S₀ and S₁ where S_j = Σ_i |p̂_ji − p̂_ji|/p̂_ji, j = 0, 1. For the black probabilities we obtain S₀ = 76.1, 72.8, 78.9, 81.6 while for the white probabilities S₁ = 4.4, 4.2, 4.6, 4.7. The first thing to note is that inference for the blacks is much less accurate for the blacks, as we might expect from Figure 2, since there is far less information available. The empirical distribution of the residual odds may be calculated here (since the individual data are available), and give 95% ranges for blacks and whites of [0.33,2.3] and [0.41,2.9], respectively so that the second prior is most consistent with the data, which explains the above summaries of S₀ and S₁. Figure 4 gives the posterior medians of the fractions registered Republican for blacks and whites, versus the true fractions based on the individual data. The top row is under the prior with residual odds in the range [0.9,1.1] and the bottom row is under the prior with range [0.1,10]. We see that the black/white fractions tend to be overestimated/underestimated. The effect of the prior is most apparent for the black fractions; under the narrower prior the estimates are virtually identical for all counties. In Figure 2 we saw that in many counties the bounds on the black fractions were wide, indicating the lack of information.

Figure 4.

(a) Estimated black fraction registered Republican (RR) versus black fraction RR under the narrow prior, (b) estimated white fraction RR versus white fraction RR under the narrow prior, (c) estimated black fraction RR versus black fraction RR under the wide prior, (d) estimated white fraction RR versus white fraction RR under the wide prior.

7 Combination of Individual and Aggregate Data for the Posterior Predictive

We now consider the situation in which survey data are available, Table 2 illustrates the notation in this case, the observed counts in area i are z_0i, z_1i and y_i, i = 1, …, m. When such survey data are available on a subset of individuals within particular areas then the resultant product of binomial distributions may be simply combined with the aggregate data likelihood, with each term being independent, i.e.

Table 2.

Summary of notation for the situation in which we have both individual survey data with sample sizes m₀i and m_1i, and aggregate marginal data in area i There are N_i individuals in area i, with y_i responding Y = 1, and N_0i, N_1i individuals with x = 0, 1 respectively.

	Survey Data			Aggregate Data
	Y= 0	Y= 1		Y = 0	Y = 1
x = 0		z0i	m0i			N0i − m0i
x = 1		z1i	m1i			N1i − m1i
	mi − zi	zi	mi	Ni − mi − (yi − zi)	yi − zi	Ni − mi

$$L(p_{0i},p_{1i})=p(z_{0i}\mid p_{0i})\times p(z_{1i}\mid p_{1i})\times p(y_i^{★}\mid p_{0i},p_{1i}),$$

where $y_i^{\ast }=y_i-z_i$, and each of the first two terms is binomial and the third is the convolution likelihood.

Wakefield (2004c) illustrated the benefits of adding individual (survey) data to the ecological data to gain identifiability. A number of discussants to the paper (Best, 2004; Jackson, 2004; Salway, 2004) suggested that smaller sample sizes may be all that is needed, and that the design of the survey is an important topic. Here we touch upon these issues by investigating a number of scenarios.

The first 4 rows of Table 3 report S₀ and S₁ for survey samples within each area of sizes 1000, 500, 300, 100, respectively. Two sets of results are given in each row, the first set correspond to the use of the individual-level data only, and the second to the combined individual-ecologic data. All results were obtained using the AnalyzeWithExitPoll function within the RxCEcolInf package. Each MCMC run began with a burn-in of 10⁵, with 10³ samples collected subsequently over 10⁶ iterations. In all cases inference is greatly improved when individual-level data supplement the ecologic data. Examination of the resultant estimates of the probabilities revealed that for low sample sizes bias existed in the estimates but this was more than offset by the reduction in variance.

Table 3.

Summaries for the combined survey/ecologic setting. Rows two through five of the main body show the effects of adding samples of the stated sizes to all areas. Error measures associated with the individual data only are also given for these rows. The last three rows report situations in which individual samples of size 500 were sampled from the reported proportion of areas.

	Individual		Combined
Data Source	S0	S1	S0	S1
Ecologic Only	—	—	78.9	4.6
1000 Samples	22.1	4.0	16.7	0.9
500 Samples	26.2	6.1	15.9	0.8
300 Samples	40.4	8.1	21.7	1.1
100 Samples	73.1	13.4	31.1	1.7
Samples in Half	—	—	22.0	1.3
Samples in Quarter	—	—	24.9	1.6
Samples in Eighth	—	—	29.5	1.6

Viewed in the opposite direction to the emphasis of this paper, an important observation is that inference based on the individual data only can be greatly improved by supplementing the survey data with ecologic information.

In the second stage of our investigation we now fixed the sample size at 500 but only sampled 1/2, 1/4 and 1/8 of areas. Again we see that in all cases inference is hugely improved over the ecologic only analysis. In fact, note that with samples of size 500 from 8/64 tables (4000 sample size), we achieve better results than with samples of 300 from 64/64 tables (19,200 sample size). Given the additional cost effectiveness of sampling within fewer tables, this result implies the potential for considerable savings from sampling design in this context.

In Figure 5 we plot the estimates versus the “true” fractions. In the top row these comparisons are for the areas with survey data, while in the second row the comparisons are in areas with no survey data. Although there is clearly bias in the estimates for blacks in particular, it is far less than in the ecologic only case (compare with Figure 4). This improvement in estimation with no survey data is due to the hierarchical model which is common to all areas, thus allowing the areas with surveys to positively impact the areas with no data.

Figure 5.

Analysis based on subsamples in the first 16 areas only: (a) Estimated black fraction registered Republican (RR) versus black fraction RR in areas with survey data, (b) estimated white fraction RR versus white fraction RR in areas with survey data, (c) estimated black fraction RR versus black fraction RR in areas with no survey data, (d) estimated white fraction RR versus white fraction RR in areas with no survey data.

8 Discussion

In this paper, we have shown that it can be unreliable to estimate the p_ji or p̃_ji values with ecological data. We have also shown that the inclusion of individual level data in the analysis can mitigate these problems, and that only a small amount of data from a small number of tables may be necessary.

Furthermore, while we have focused on the estimation of p_ji or p̃_ji in this paper, it is straightforward to see that the estimation of contextual parameters is not possible from ecological data alone. Let p_ji be the proportion of individuals of race j in area i and suppose the individual-level model is:

$$p_{ji}=a_{ji}+b_{ji}{x}_i$$

so that we have both effects due to race in area i, a_0i and a_1i, and contextual effects, b_0i and b_1i. Upon averaging across individuals, to give ecological data we obtain the marginal area-level probability

$$p_i=x_i\times p_{0i}+(1-x_i)p_{1i}=a_{1i}+x_i(a_{0i}+b_{1i}-a_{1i})+x_i^2(b_{0i}-b_{1i})$$

which clearly shows the identifiability problem. With a non-linear model (for example a logistic model), the parameters become identifiable, but only due to the non-linearity and different non-linear forms will give different answers.

Data and code for all of the examples of the paper are available at: http://faculty.washington.edu/jonno/cv.html

In Section 7 we showed the benefits of small amounts of individual-level data. In the simulations we sampled individuals without replacement from black and white populations to produce a representative sample. In practice selection bias may be present, and without further information on the nature of this bias, a sensitivity study is the only recourse. However, within the framework we have described such a study is straightforward.