Disease Dynamics in a Dynamic Social Network

Abstract

We develop a framework for simulating a realistic, evolving social network (a city) into which a disease is introduced. We compare our results to prevaccine era measles data for England and Wales, and find that they capture the quantitative and qualitative features of epidemics in populations spanning two orders of magnitude. Our results provide unique insight into how and why the social topology of the contact network influences the propagation of the disease through the population. We argue that network simulation is suitable for concurrently probing contact network dynamics and disease dynamics in ways that prior modeling approaches cannot and it can be extended to the study of less well-documented diseases.

Introduction

A question of fundamental importance to epidemiology is determining which characteristics of a population are most salient in dictating the manner in which a disease will spread through that population. That is, what is it about the demographics and connectivity of an underlying contact network that creates the most prominent features of the landscape in which the disease travels, and moreover how do changes to that landscape affect the dynamic behavior of the disease? An extensive body of work has explored this question, demonstrating, for example, that a global demographic such as population size can have profound effects on epidemic occurrence, leading to large, regular epidemics with few fadeouts (periods during which no one is infected) in populations above a certain threshold size, while populations whose size is below this threshold experience only small, chaotic epidemics [1]. The large amount of work on childhood diseases such as measles has shown that dynamic trends in the underlying social structure--for example, the change in aggregation among schoolchildren with the onset and end of the school term--create dynamic trends in epidemic profiles (epidemics tend to occur when children aggregate [1-3]). In addition, an increase in birthrate can cause a shift in epidemic periodicity from biennial to annual in populations above a certain threshold [1, 2].

To date much of the mathematical modeling explaining epidemiological data has employed fully mixed compartmental models [1, 2, 4, 5]. In the simplest of these models—the basic SIR model—the population is understood to consist of individuals who are either susceptible (S), infected/ infectious (I), or recovered/immune (R). The population is assumed to mix fully, and interactions are governed by coupled differential equations such that the rate of change in the number of susceptible individuals is proportional to -βSI, where β is the contact rate, and individuals recover at a rate γ per unit time, such that the rate of change in the number of infected individuals is proportional to βSI-γI (see, for example, the supplement in [3]). This basic SIR model is quite successful in reproducing and explaining the real-world behaviors of large and even some intermediate-sized populations for which the assumption of full mixing is a good approximation. In fact, a handful of the model's more complex variants capture some of the nuances of more complicated populations for which full mixing is not a fair assumption [6, 7]. However, as useful as fully mixed compartmental models are for large populations, their utility tends to be drastically reduced as population size decreases and as population structure (e.g. heterogeneity in connectivity) increases, since the assumption of full mixing fails to hold and the mathematics needed to describe the heterogeneities in mixing becomes intractable. Compartmental models also tend to do poorly at describing the initial or final stages of an outbreak, when few individuals are involved in transmission and stochastic person-to-person effects play an important role.

New avenues in epidemic modeling involving individual-based in-silico simulation of the propagation of disease address some of the shortcomings of compartmental modeling [8, 9]. For example, stochastic, spatially-structured, individual-based simulations were used to model highly-contagious, aerosol-transmitted diseases, such as influenza [10, 11]. Transmission in these models is based on co-location of individuals in schools, in workplaces, on public transportation etc. Generally these models define mixing groups such as households, schools, workplaces, neighborhoods and communities, and each mixing group is assumed to be (close to) well-mixed. Network-based models, on the other hand, simulate disease propagation in person-to-person contact networks, without adopting a well-mixed assumption, and therefore enabling an analysis of the relationships between the topology of contact networks and disease dynamics at multiple scales. The work of Newman on epidemic spreading in random networks [12], for example, revealed that the probability of a major epidemic depends on the average degree (connectivity) of the network. Pastor-Satorras and Vespignani showed that epidemics are always possible in populations whose interpersonal contacts are power law-distributed [13]. Realistic and highly-structured contact networks formed from real-world statistics for population composition were constructed to model SARS transmission in Vancouver, Canada [8] and to capture the movement of individuals between locations in a city [14].

Most individual-based and contact network models (including those mentioned previously) are demographically static representations; i.e. the implicit assumption is that demographic changes such as births, deaths and marriages will not affect the structure of the mixing groups or contact network, or will affect it at a rate much slower than the rate of disease spread in the network. The question therefore arises whether the dynamics of a disease on a demographically dynamic contact network will differ from the dynamics of the disease on such a network's static counterpart. We explore answers to this question by simulating realistic and detailed underlying topologies that are built from relevant statistical data and that are allowed to evolve according to rates collected from statistical (demographic) data for real societies. With this framework, we can then observe directly, for any population size, how the dynamics of the topology is influenced by demographic changes, and how, in turn, demographic dynamics affect the dynamics of disease.

Here, we simulate a contact/social network that is a conglomerate of family networks, work networks, school and preschool networks, and individuals, and that grows and changes according to salient real-world statistical rates. We track both the dynamics (demographic and topological) of the population and the dynamics of a disease propagating through this population. Simulations have been generated for measles, and we present a comparison of our findings to data found in [1-3]. We demonstrate agreement both in long-term epidemic profiles as well as in a multitude of epidemiological measures for a range of population sizes from 10,000 to ∼250,000 individuals. Furthermore, our results provide unique insight into how and why the social topology of the contact network influences the propagation of the disease through the population.

Simulating social networks and disease dynamics

In our simulations individuals are represented by vertices (nodes) and their most salient social interactions (familial, working, and (pre)school) are indicated by edges. Each node is characterized by the age and gender of the corresponding individual, and has edges to family members, classmates (if it is of school age) or work colleagues (if it is an adult). The social network grows and changes over time due to births, marriages, deaths, immigration, and to individuals joining and leaving schools and workplaces. The rates of these events are estimated from statistical data such as age distributions, birth rates, marriage rates, immigration and unemployment rates, etc. The social network algorithms are interlinked with the disease algorithm, and two dominant timescales are adopted in the simulations: a yearly timescale for “slow” social processes—i.e. marriages, formation of work groups and (pre)school groups—and a weekly timescale for “fast” or distributed social processes—i.e. births, deaths, immigration-- and for (most) disease updates. While statistical data is abundant for node-related quantities in social networks, it is almost non-existent in regard to social edges in large social networks. It is therefore necessary to establish logical rules that are based on observation and “reverse-engineering” of the social underpinnings of social institutions (e.g. families, workplaces, (pre)schools) to account for how and why people are connected (in terms of having “social edges” between them) in a population. In the following subsections we briefly describe the major social network algorithms we employed in our population model as well as the disease algorithms (tailored for childhood diseases, such as measles) included in our simulations.

Dominant social processes

Basic demographics and social processes: births, deaths, age distribution and immigration

For a simulated population of size N, an initial age distribution is adapted from the vital statistics of London [15] and New York City [16], which have been interpolated and averaged in order to determine values for each age between 0 and 95 in an arbitrary population. The age of each individual in the population is incremented yearly, and for simplicity, all individuals age simultaneously. During each yearly time step, women (roughly half the total population) between the ages of 15 and 45 are eligible to have children, and the number of children born to women of each age i in this range is determined according to documented fertility rates (a rate per 1000 women of age i) [15, 16]. Each newborn is represented by a new node, and this node is integrated into the contact network by connections to his/her mother, father and siblings (if any). The week at which each baby will be added to the population is randomly chosen, as are the women who will become new mothers. Similarly, the number of people of age i who will die in the current year is determined according to the documented death rate of people of age i [15, 16]. Individuals are randomly selected for death (unless their age exceeds 95, in which case they are automatically removed from the population), and the week of their removal is randomly determined. After death the corresponding node and all of its edges are deleted from the network.

To allow an average annual population growth rate of roughly 0.6%, with simultaneously maintaining a stable age distribution, both close to what is observed in many large western cities [15, 16], immigration rates were adapted from [15, 17], and were interpolated and averaged in order to find a rate for each age between 0 and 95. The number of people of age i who are added to (or subtracted from) the population at time (year) t is equal to the product of the number of people of age i-1 at time t-1 and the immigration rate for age i: n_i(t) = r_in_i–1(t – 1). Nodes corresponding to adult immigrants are connected to workplaces, in accordance with the (un)employment rate, at the next updating of workplaces, while school-aged immigrants are immediately added to school groups. It is required that individuals under the age of 18 leave the population with a family group, and to the extent that it is possible to satisfy the immigration-by-age distribution, entire family groups are moved out of the population if any family member is randomly chosen as an emigrant. The week at which an individual will enter or leave the population is randomly determined; however, if the individual is moving with a family, his or her entire family group will move at the same time.

Marriages and family graphs

Family groups form the first of four broad classes of social subnetwork within the larger simulated population. In these simulations, a family group must contain at least one, and no more than two (one male and one female) adults, and any number of children. To simulate marriage, approximately 54% of the population over the age of 18 will be paired with a person of the opposite gender at any given time[15, 16]. Marriage is not a necessary condition for childrearing in our simulations, as single women can have children. Each individual in a family group is connected to every member of the immediate family (the subgraph is fully-connected) and remains so until the child(ren) turn 18; at this point only the mother and father will remain connected. Because it occurs very infrequently, children whose parents die are not reassigned to new families. The average family size is 3-4.

Work graphs

Work groups comprise the second of the four broad classes of social subnetwork within the larger simulated population. Individuals have the option to enter the workforce at age 18, and must exit from the workforce at age 65. Each year, based on (un)employment statistics [15, 18] approximately 6.8% of current 18-year olds will remain unemployed, and all others will enter the workforce. The initial number of workplaces is approximately 1% of the total population size [15, 18], and is allowed to grow over time. Workplace sizes are power-law distributed between a minimum size of four workers and a maximum size equal to 1% of the total workforce. Each initial workplace is a hub-and-spoke graph—in essence, a boss and employees. Each new worker joins a randomly-selected, existing workplace, or initiates a new workplace whose size will be in keeping with the power-law distribution. As new workers are added to the workplaces, they are attached uniformly randomly to a minimum of three and a maximum of all other workers in the workplace. For computational efficiency, for childhood diseases, where clustered populations of adults do not greatly affect the transmission of the disease, we update the work groups only once per year.

Preschool graphs

A large preschool network, consisting of children between the ages of 2 and 5, forms the third of the four social subnetworks within the larger population. To implement the fact that preschool-aged children can have a variety of group settings, from daycare centers to informal playgroups, children in this age group are randomly connected to between 0 and 10,000 N_2–5/N other children, where N_2-5 is the number of children between the ages of 2 and 5 and N is the total number of people in the population. This connection scheme leads to preschool-aged children having degrees that are exponentially distributed between 0 and 100, with a mean degree of k=41.

School graphs

School groups form the final, and in the case of measles, arguably the most important class of social subnetwork within the larger simulated population. All children between the ages of 6 and 18 are included in the school subnetwork. This subnetwork consists of fully-connected, age-specific classes of maximum size equal to 40, that are, in turn, interconnected by additional edges. Until every child of a given age has been assigned to a class, classes containing children of that age will continue to be formed, so long as all other classes of that age have already been filled to capacity. The interclass edges represent connections between children who attend different classes in the same school, or social ties between children in different geographic regions of the city resulting from extracurricular activities, such as soccer clubs and church groups. The interclass edges of each child are selected randomly (from a truncated normal distribution) according to the following rule: children between the ages of 6 and 13 (elementary/middle school age children) can have a maximum of 0.5*(size of their class) connections to children in other classes in this age range; children between the ages of 14 and 18 (high school age children) can have a maximum of 0.75*(size of their class) connections to other classes in this age range; all children have at least .25*(size of their class) connections to other classes. This difference in school edge distribution that occurs when children reach the age of 14 accounts both for the fact that they join middle schools, and for the fact that their extracurricular interests often change in ways that allow them to make more social contacts. We tested the aforementioned linking parameters for robustness with respect to their impact on disease dynamics. So long as no school-aged children are without intraclass links, and so long as no child in the 6-13 year age range has more than 0.8*(size of his/her class) intraclass links, the disease dynamics are robust; therefore, the parameters chosen for these simulations fall within the stable range.

Each year, 5% of school edges are severed from the beginning of April until the end of June, and again from the beginning of September until the beginning of December, to represent a lower transmission season during which children might spend more time outdoors, in less proximity to one another. In addition, all school edges are severed from the beginning of July through the end of August, to simulate summer vacation. Only from December through March, when children are forced to be in enclosed spaces with one another due to colder weather, are all the school edges in place. With this scheme of seasonal edge removal and reinstitution which is also applied to the preschool subpopulation, we are able to approximate school-term forcing [2, 3].

We note that we have implemented hierarchical clustering rules for school-aged children that do not explicitly address the idea of school groups. That is, in our model, classrooms are not agglomerated into school groups. We have instead assumed that links between children in different schools are indistinguishable from links between children in different classrooms, and all interclass links are therefore established with the same probability. For measles, this assumption is justified: the by-age transmission rate for the disease is so high between children of age 6 or 7, that a susceptible child of this age need only be connected to two other infected children of the same age group to have more than a 90% chance of acquiring the disease. Thus, whether or not classrooms are grouped into school compartments, infection of children in one classroom of 6 or 7-year olds has a high probability of spreading infection to other classrooms of the same age group. The population model would likely need to include an added level of clustering to properly capture the dynamics of diseases for which the by-age transmission rate is more homogeneous for all children between the ages of 6 and 18. One could, for example, group classrooms into schools and assume that the probability of connection between classes in the same school is less than the probability of connection between classes in different schools.

Disease processes

Initial immunity by age, loss of maternally-acquired immunity, spread and recovery

The initial immunity profile (i.e. what portion of the population, by age, has initial immunity to the disease) should be tailored on a by-disease basis. The immunity profile (by age) for measles was adapted from [4] and is a set of input parameters at time t=0. For developed nations, the immunity profile for measles is linearly distributed from 0% to 90% between the ages of 0 and 11; it is assumed that 99% of the population over the age of 11 is immune to the disease [4]. The susceptibility of immigrants is assumed to be higher (3.5%) than it is in the native population (1%) [17].

All newborns are assumed to be immune to the disease for (in the case of measles) up to six months after the week of birth. The specific week during this six month period at which maternally-acquired immunity will be lost is randomly chosen from a Gaussian distribution with mean equal to 12 weeks and standard deviation equal to two weeks.

Disease can spread from an infected individual to a susceptible individual if there is an edge (contact) between the two. The probability of infection is also dependent on an age-specific transmission rate, β, that is obtained from a matrix, called the Who Aquires Infection From Whom (WAIFW) matrix, whose (a,b) entry represents a contact between an infected individual in age group a and a susceptible individual in age group b. Therefore, at each disease time step, t, the probability p_j that a susceptible individual in age group b will become infected by its infectious neighbors depends on the age-specific transmission rates between its neighbors and itself, such that p_j(t) = 1 − e^Σiβba_i, where a_i represents the age group of neighbor i and the sum goes over all neighbors. The values in the matrix used for these simulations were derived from [19], using their mixing matrix structure for measles. Infected individuals recover after two weeks; recovered individuals are immune to the disease.

Maintaining epidemics: “sparking”

Particularly in the case of smaller populations, fadeouts (periods during which no one is infected, and after which further epidemics would be impossible without reintroduction of the disease) are frequent. To ensure that there is always some chance of infection at each weekly update of the disease algorithm, we introduce a sparking process, whereby a susceptible individual will become infectious without contact with an already infected individual in the population. The implicit assumption is that the “spark” has had contact with an infected individual from outside the native population, has become infected, and has introduced the disease into the native population. The spark is chosen at random from all current susceptibles in the population with probability P(t) ∼ ln(N(t)), where N(t) is the total population size at time step t. The increase of the sparking probability with population size is supported by the fact that epidemics will fade out for long time periods in small populations unless the disease is reintroduced, and that disease becomes endemic as population size increases. We have evaluated several functional forms and found that the slow increase of a logarithmic function works best.

Results

Social network topology

As described above, we simulate a dynamic contact network, meaning that the individuals comprising the underlying social population are represented by vertices (nodes) in a network, their most salient social interactions (familial, work, and (pre)school) are indicated by edges; and that the vertices and edges change over time with rates based on statistical data, such as age distributions, birth rates, marriage rates, immigration rates, etc. The network is dynamic in that (1) the number of nodes grows in time, (2) the age of each node changes yearly, and (3) the nodes' social edges change in number and type over time. In addition, a disease algorithm propagates a disease with specific transmission and recovery parameters through the evolving social network.

In order to explore the social topology of our networks, we simulated multiple replicates (between 50 and 100 replicates for each starting size) whose initial populations ranged from 10,000 nodes to ∼250,000 nodes. Each of these networks was allowed to evolve according to the social algorithm (but without disease propagation) for 25 years, such that given a 0.6% annual population growth rate, a 15% increase in population was experienced. At five year increments, salient topological characteristics and distributions of each social network, as well as of the work, family, and (pre)school subnetworks were recorded. Remarkably, regardless of network size, we found that after a period of roughly 10 years, the statistical distributions in the macroscopic topology of our networks stabilized, even though the topology continued to change on an individual-based level. For this reason, all results on large-scale social topology reported herein are formed from data that has been aggregated over multiple replicates and for a series of years.

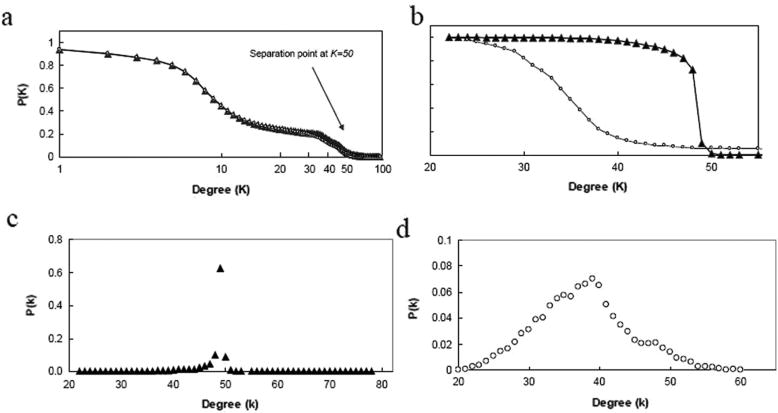
One of the most important topological quantities dictating the manner in which a disease will spread from one individual (node) to others is the degree (k) – the number of edges adjacent to a node—that each individual has. For our simulations, when the entire network is looked at in terms of a cumulative degree distribution (the probability that a given individual will have degree higher than degree K), regardless of the total population size, the degree distributions for the full populations are quite similar (Figure 1a). All networks exhibit nodes with between 0 and 100 connections (some of these may be multiple connections to the same person), and the majority of nodes in the network do not have degree much greater than ∼40, since the probability of having K>40 is only about 20%. The shallow slope of the region between K=15 and K=35 is due predominantly to (pre)school connectivity and secondarily to work connectivity. This shallow sloped region is followed by a steeper segment (between K=35 and K=50) that becomes increasingly switch-like as population size grows. The behavior of the distribution in this segment is a function of school connectivity. Specifically, the cumulative school degree distribution is switch-like in appearance for populations, but decreases more gradually for smaller populations (Figure 1b), and can be superimposed on the transition region between 40<K<55 in the total cumulative degree distribution if the preschool subgraph is excised from the network.

Figure 1.

(a) Total cumulative degree distribution (plotted on a log-linear scale) and (b) cumulative school degree distribution for populations of size ∼10⁵ (▲) and ∼10⁴ (○). The probability P(k>K) is plotted for each degree in an averaged set of typical simulated networks. The switch-like behavior of the cumulative distribution for the larger graph is a reflection of a delta function-like non-cumulative distribution around K=50. (c,d) Non-cumulative school degree distributions. The probability, P(k), is plotted for each degree in an averaged set of typical simulated networks of (c) ∼10⁵ (▲) and (d) ∼10⁴ (○) nodes. The larger population exhibits a delta function-like peak at k=50, while the degree distribution of the smaller population is more normally-distributed.

The difference in behavior between the school degree distribution of large populations and that of small populations is a result of a combination of factors. Large populations have far more classes than small populations, and these classes are also far more likely to be filled to capacity (40 students). Therefore the average school-aged child will have more school links in a larger population than will a comparably-aged child in a smaller population, both because of a larger average class size, and a higher average inter-class degree ( $<k_{\text{inter}}^{\text{large}}>\approx \mathit{12}$ and $<k_{\text{inter}}^{\text{small}}>\approx \mathit{3}$, respectively). The net effect of population size on school degree is to cause the school degree distribution (non-cumulative) to become more and more sharply peaked around k=50, during the season of highest connectivity (transmissivity); during seasons of lower, but non-zero connectivity, the distribution shifts slightly to the left. The corresponding non-cumulative school degree distribution resembles a delta-function (at k=50) for large populations (Figure 1c), but is more normally-distributed for small populations (Figure 1d).

As with the cumulative degree distribution, the average clustering coefficient of each of our networks—a topological quantification of the degree of interconnectedness of the neighbors of each node in the graph—is largely independent of network size. The average clustering coefficient of populations ranging in size from 10,000 nodes to ∼250,000 nodes falls in a narrow range between 0.52<C<0.61. The relatively large average clustering coefficient indicates that most nodes in the network belong to tightly-knit social subgroups, in agreement with real-world social networks [12]. This high clustering coefficient of the simulated social networks has a direct impact on the facility with which disease will propagate through the population.

Comparison of simulated measles dynamics to observed dynamics

We validate our framework by extensive tests and comparisons between the output from the simulations and comparable features or plots of real-world data for a well-studied disease—measles. Measles is a highly-contagious, airborne Morbillivirus that is spread by respirating viral particles from the nose or mouth of an infected individual, either through direct contact or through aerosol transmission. Over 90% of people without immunity to measles who share a living space with an infected individual will contract the disease. In most cases, the disease in not fatal, and usually has a recovery time of about two weeks. An abundance of public health data, particularly for towns and cities in England and Wales in the period beginning just after World War II and continuing to the present, documents case counts and vaccination reports for measles, providing a wealth of information for time series studies at multiple population sizes. In this subsection, we report comparisons for both small (∼10⁴) and large (∼10⁵) simulated populations, demonstrating not only that their dominant epidemic features are in excellent agreement with real data, but also that our simulations capture more subtle, yet measurable features of measles epidemics that relate topological dynamics to disease dynamics. We determined the average number of individuals infected during a given epidemic <I(t)>, the average interepidemic period <T_inter>, and the average epidemic duration <τ>. Additionally we calculated the distributions of other epidemiological quantities, including the time spent in fadeout (when no one is infected) as a function of population size, the force of infection by age cohort λ (the by-age likelihood of acquiring an infection), the basic reproductive ratio R_o, (the expected number of secondary cases due to one infectious individual in a fully-susceptible population) and responses of the epidemic attractor both to changes in birth rate and to seasonal influences.

Infection profiles, interepidemic periods, and epidemic lengths

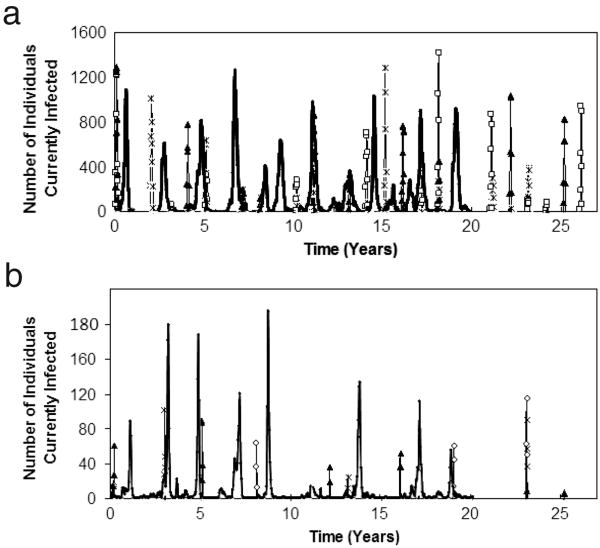
The infection profiles of a sampling of simulated populations of starting size N=107,000 over a time span of 25 years (Figure 2a) agree qualitatively with data from [2] for the city of Blackburn (heavy line), also with population of 107,000. Similarly, profiles for a simulated population 10 times smaller (Figure 2b) concur with data from [2] for the city of Teignmouth (heavy line), whose population is N=10,700. The disease trajectories are more reproducible (i.e. multiple trajectories overlap) for the larger population, since fadeouts become less and less frequent. We note that if the trajectories are plotted on a weekly timescale, variation among the trajectories at all population sizes becomes apparent.

Figure 2.

Infection profiles for a sampling of 3 replicate simulated populations (Replicate 1=*; Replicate 2=□; Replicate 3=▲) of starting size N=107,000 (a) and N=10,700 (b) over 25 years. Counts are aggregated monthly. Peaks that contain two or more symbols indicate reproducible epidemics that occur at identical times in two or more replicate simulated populations. In figure 2a, the heavy line indicates pre-vaccine era data obtained for the city of Blackburn, England for a period of 20 years; in figure 2b, the heavy line indicates pre-vaccine era data for the city of Teignmouth, England for a period of 20 years.

Table 1 compares the average number of infected individuals per unit time <I(t)>, the average interepidemic period <T_inter>, and the average epidemic duration <τ> for the simulated populations and the real data from [2], and demonstrates that simulation and data agree quantitatively, as well as qualitatively.

Table 1.

Comparison of epidemic features in large and small populations in simulation versus real data. <I(t)> indicates the average number of infected individuals per unit time, <T_inter> represents the average inter-epidemic period and <τ> is the average epidemic duration. The simulation results were averaged are over 50 simulations for N=107,000 and 100 simulations for N=10,700. Each simulation represents a different contact network and transmission timecourse.

Data Set	<I(t)>	<Tinter>	<τ>
Blackburn	∼500	1-2 years	41 weeks
107,000	∼413	2.02 ± 1 years	40 ± 2 weeks
Teignmouth	∼81	1-4 years	38 weeks
10,700	∼88	4 ± 3.31 years	40 ± 2 weeks

Time spent in fadeout as a function of population size

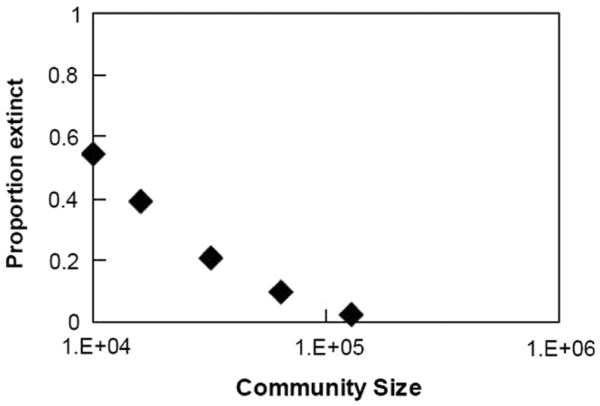
It is well documented for towns and cities in England and Wales that the amount of time a population spends in fadeout—i.e. without any infected individuals— decreases as the size of the population increases [2]: as the population size grows from N ∼10⁴, time spent in fadeout quickly decreases from 60% to 0%. We find a similar trend for population sizes between N ∼10⁴ and N ∼10⁵ (Figure 3).

Figure 3.

Proportion of time a community is in fadeout, as a function of community size. The data points are averaged values for five simulations at each population size.

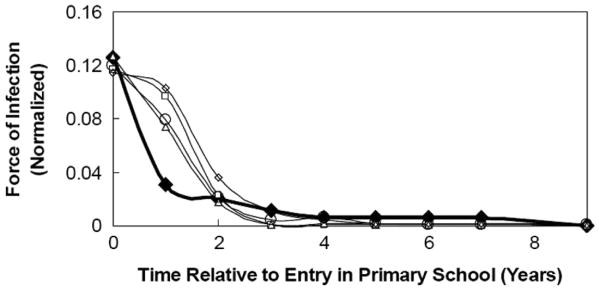
Force of infection by age cohort (λ)

The interplay between population dynamics and disease dynamics in our simulations produces a force of infection profile—i.e. the by-age likelihood (λ) of acquiring an infection—that peaks for children in their first year of primary school, and that is independent of population size (Figure 4). For an individual simulation, a force of infection profile was generated by recording, for each individual in the population that contracted the disease during the simulation, the age at which the individual became infected. These ages at first infection were then tallied, and a distribution of normalized, by-age probabilities of infection was generated. In order to better illustrate this distribution's relationship to contact network topology, Figure 4 depicts the dominant trend of the distribution—the peak at what would be 6 years of age—not in terms of individuals' raw ages at first infection, but, instead, in terms of time relative to their entry into primary school. We have chosen to depict the force of infection profile in this manner for two main reasons: (1) similar trends have been noted in [4, 5], and thus serve as benchmarks for measles simulations, and (2) we find that the force of infection profiles are not robust to dramatic changes in the contact network topology (assuming that disease parameters, namely recovery rate and WAIFW matrix, remain the same); specifically, if we substantially increase or decrease the interconnectivity among classrooms, the force of infection profile will change. A substantial increase in connectivity among classrooms tends to broaden the peak in the force of infection profile across those age groups for which the probability of infection is largest in the WAIFW matrix (i.e. 5-9 years), while a substantial decrease in connectivity among classrooms tends to leave peaks in the force of infection profile only in those age groups in which the disease was sparked. The force of infection profile, derived from measles epidemics in England and Wales [19], is plotted as a heavy line in Figure 4. The deviation between the simulated force of infection profiles and the real profile for children in their second year of school (i.e. the fact that simulations overestimate the real value) can be attributed to an oversimplification in the simulated population: while it is likely that real first-grade classrooms consist of a mixture of 5 and 6-year olds, for computational ease we have chosen both to segregate classrooms by age, as well as to consider 6 years to be the minimum age for entry into classrooms. These modeling simplifications decrease the connectivity among 5-year olds and children between the ages of 6 and 13, and subsequently lower the probability of transmission (and, thus, the force of infection) between 5-year olds and 6-13 year-olds. The lower probability of infection among 5-year olds creates a larger-than-expected reservoir of children who can still acquire the infection when they turn 6, and while many of these children will become infected at 6 years of age, others will not contract the infection until the following year; hence the larger-than-expected force of infection for children in their second year of school. If children are aggregated in five-year age groups as is often done for simplification (see, for example, [5]), the maximum deviation (for 1 to 4 year olds) is less than 3% between the simulations and the real data.

Figure 4.

Force of infection profile. Data markers differentiate among population sizes; filled diamonds (◆) denote the real data, open diamonds (◇) indicate N=10,000, open circles (○) denote N=20,000, open squares (□) indicate N=50,000, and open triangles (Δ) denote N=100,000. Real data, derived from epidemic counts in England and Wales [19] is indicated by the heavy line in the plot. The distributions peak during the first year of primary school and are robust to changes in population size.

Basic reproductive ratio (R_o) and population size

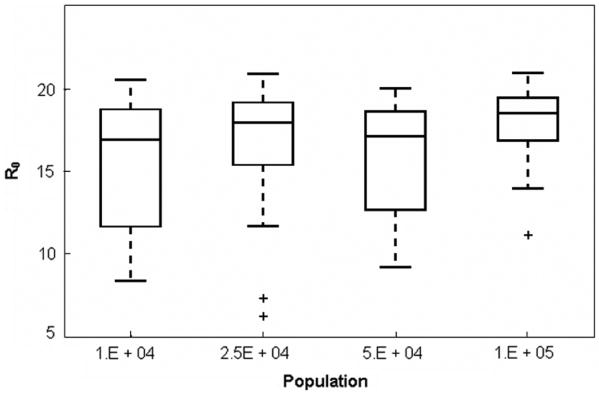
The basic reproductive ratio, R_o, is the expected number of secondary cases of a disease following the introduction of one infectious individual into a fully-susceptible population. The exact value of R_o cannot usually be determined from incidence data, and various approximate theoretical methods are used to estimate it. To provide an estimate not directly dependent on the WAIFW matrix, we have used the approximate relationship R₀ = L/<a> [2, 20], where L is the life expectancy of the population and <a> is the mean age at first infection. We used the reported life expectancy of females and males in England from 1940-1960, i.e. L_f=73.2 years and L_m=66.8 years, respectively [21]. At each update of the disease algorithm, we polled the number of individuals who had become infected at that time step, and recorded both their genders and their ages. From this information we calculated the R_o values at that time step as R₀ = f L_f/<a>_f + (1 − f)L_m/<a>_m, where f is the fraction of females in the newly infected population, <a>_f is the average age of newly infected females and <a>_m the average age of newly infected males. At the end of each complete simulation, an average over all timestep-specific R_o values was obtained, and this was taken to be the R_o value for the complete simulation. Our simulations demonstrate an R_o value (R₀ =17.6 ± .75) that is independent of population size and that falls within the range of generally-accepted reproductive ratio values for measles, 14< R_o<18 (as was also found in [1]). The data plotted in Figure 5 are aggregate values from time series data, which, itself, shows little variation from one year to the next, suggesting that R_o is not affected by the underlying dynamics of the social network (on an annual timescale).

Figure 5.

Basic reproductive ratio as a function of population size. For each population size, the box plot has been aggregated over 10 simulations, each spanning 30 years. The bars (lowest and highest) extending from the dashed lines in each plot indicate the 5^th and 95^th percentiles for R_o values at a given population size, while the lower and upper bounds of each box indicate the first and third quartiles, respectively. Datapoints outside the whiskers are considered to be outliers (and therefore, not of statistical significance). The bar within each box gives the median value for each data set.

Baby booms and epidemic period

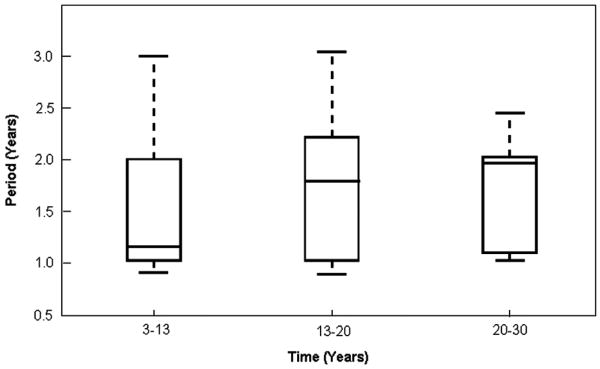
As has been well documented in [2], a sudden and dramatic change in the birth rate of a population, such as that experienced in England and Wales in the late 1940's, will cause the period attractor for measles epidemics in large populations to shift from biennial to annual. Over a ten year period (beginning at year 3 and terminating at year 13 of the simulations) we increased the overall birthrate by 30% and monitored the epidemic period during this simulated “baby boom”, between years 13 and 20, and between years 20 and 30. The simulations indicate that the median epidemic period is strongly annual during the baby boom era, but quickly returns to a biennial attractor once the boom has terminated. The biennial attractor stabilizes as time progresses (Figure 6).

Figure 6.

Epidemic periods in a population of size N>10⁵ during a simulated baby boom (years 3-13), following the termination of the boom (years 13-20) and long after the termination of the boom (years 20-30). During the baby boom the birthrate has been increased by 30%. The bars (lowest and highest) extending from the dashed lines in each plot indicate the 5^th and 95^th percentiles for epidemic periods at the given population size, while the lower and upper bounds of each box indicate the first and third quartiles, respectively. The bar within each box gives the median value for each data set.

Seasonal dynamics of recurrent epidemics

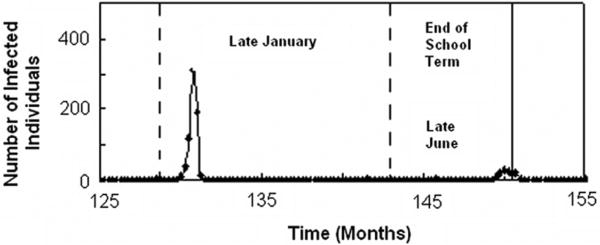
Recent work by Stone et al. [3] has shown that for seasonally-driven diseases, such as measles, seasonal changes—and therefore, the time of year at which an outbreak begins or ends—can play a crucial role in determining whether an outbreak will develop into a full-scale epidemic, or whether it will be curtailed and result in a “skip” [3]. Stone et al. demonstrate that, in general, if an epidemic peaks early in a given year (during months 0-3), the following year will usually experience a skip; that is, there will either be no epidemic, or the epidemic will occur late and be curtailed by the changing of seasons from high transmissibility to low transmissibility. As can be seen in Figure 7, we observe similar trends in our simulations: for example, we see epidemics that peak early in the high-transmissibility season of one year, followed by a late outbreak, which is ultimately curtailed in the following year, due to the decrease in transmissibility with the onset of summer vacation. Furthermore, we find that in all cases for which a potential epidemic has been interrupted by a change in seasonal transmissibility, we can clearly differentiate skips from continued, but decreased epidemics, since for the former, the number of susceptible individuals continues to increase immediately following the epidemic peak, while for the latter, this is not the case. Additionally, the mathematical criterion put forth in [3] to differentiate these seasonally-induced skips from seasonally-weakened epidemics (namely that if a skip occurs, the fraction of the population that is infected should be less than or equal to the local per capita replenishment rate), is satisfied for each occurrence in our simulations.

Figure 7.

An example of seasonally-driven dynamics. Dashed lines indicate the beginnings of years; solid line indicates the end of term. The early-peaking outbreak in the first year causes a late-breaking epidemic in the following year. Although this outbreak begins to gain footing, it is curtailed by the end of the school term, and the subsequent drop in transmissivity in late June.

R₀ and school subgraph topology

Recall that the cumulative degree distribution of school-aged children becomes increasingly switch-like around k=50 as population size grows (see Figure 1). We previously noted that the reason for this effect is a combination of fuller classrooms and more interclass connections in larger populations. Simply put, a child attending a school in a large city is more likely to be in a full or overcrowded classroom, and will probably contact more people in the course of his or her day in the hallways and lunchroom, on the playground and bus, etc., than will the average student in a small, rural setting. Thus, there is heterogeneity in connectivity that differentiates urban schools from rural schools. However, we surprisingly still see an R₀ value that is essentially independent of population size. Compartmental modeling has assumed homogeneity in connectivity between schools in large populations and schools in small populations as the root cause behind the size-independent value of R₀ [2]. The results of our simulations suggest that this may not be the case, and that, instead, the mean age at first infection may have more to do with the independence of R₀ across population sizes.

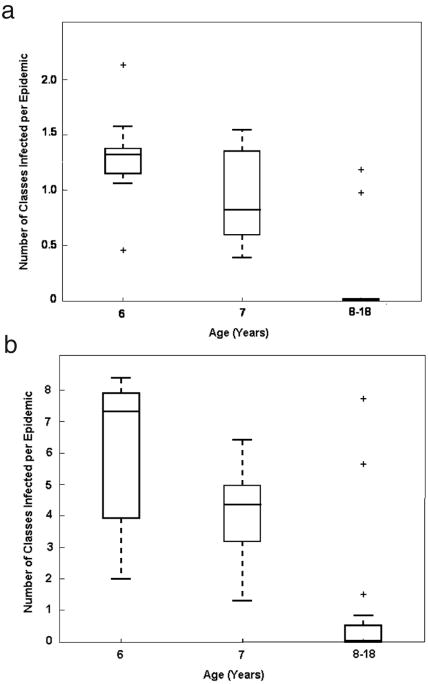
We find that regardless of population size, infection is most likely to gain initial footing in a classroom of median age six years old, in part because this is where transmission rates are highest. In smaller populations, where the interclass links are sparse and where the number of classes within a given age group tends to be small, infection of one class will not necessarily lead to infection of more classes (Figure 8a) and therefore the mean age at first infection in smaller populations will generally show a strong bias towards six years of age (as is indicated by the peak in the force of infection profile at age six). On the other hand, in larger populations, we observe a “class-hopping” effect in epidemic dynamics, whereby if one classroom in a large population becomes infected, the high density of interclass links ensures that other classes of the same age will also immediately become infected (Figure 8b). Since the transmission rate among six-year olds dominates other transmission rates, we again see a strong biasing of the mean age at first infection towards six years of age. Thus a simple explanation for why R₀ remains independent of population size lies in the fact that as population size grows, the mean age at first infection does not deviate—it is (on average) six years old, regardless of population size.

Figure 8.

Box plot of the number of classes, by age, infected over the course of an epidemic in a population of (a) 10,000 individuals, and (b) 100,000 individuals. Due to the sparse observations of infected classes of age >7 the data for ages 8-18 was aggregated. The bars (lowest and highest) extending from the dashed lines in each plot indicate the 5^th and 95^th percentile for average number of classes infected in a given epidemic, while the lower and upper bounds of each box indicate the first and third quartiles, respectively. Datapoints outside the whiskers are considered to be outliers (and therefore, not of statistical significance). “Class-hopping” is evident in the larger population, where the median number of classes infected per epidemic is above one; this trend is not present in the smaller population.

We also find that transmissibility between children of elementary school age (6-13 years) and children of high school age (14-18 years) is sufficiently low so as to prevent jumping of the disease between elementary schools and high schools in both small and large populations, even though the density of elementary-high school links is higher in larger populations. Thus, unless an outbreak initiates in a high school, it will almost certainly be restricted to elementary-aged children, ultimately preventing the R₀ value from changing with population size. We can predict that this behavior would not be observed in a disease with a higher transmissibility between age groups and instead the disease will have a higher spread in large populations, and therefore a higher R₀ value.

Large-scale epidemic occurrence and school edge distributions

We define global epidemics to be those epidemics whose size is at least half of the maximum size of all observed epidemics for a given simulation. We also define nonrecovered intraclass edges as those edges that connect infected or susceptible schoolchildren within the same class, and we form the degree distribution for these edges. This distribution changes in time both as the disease propagates through the school network and as the topology of the school network changes due to social dynamics. Remarkably, we find that a peak at a high degree in this nonrecovered intraclass degree distribution during a given year is a strong predictor of a global epidemic's occurring during that year.

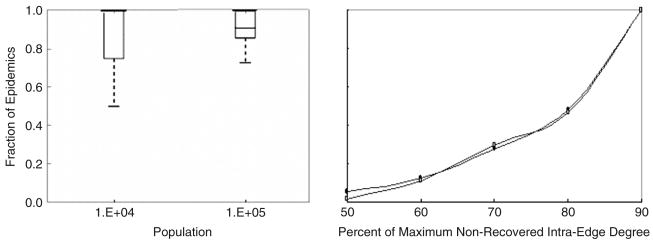
We find that nearly all global epidemics in small and large populations (N=10⁴ and N=10⁵, respectively) are correlated with high-degree peaks in this type of non-recovered distribution (Figure 9a). When this condition is met, the majority of susceptible and infected schoolchildren in large and small populations will have a school degree close to the degree at the peak of the distributions in Figures 1c,d, respectively. Interestingly, the median fraction of epidemics correlated with a high-degree intraclass peak is significantly lower for larger populations. For small populations, the complete infection of a single, full classroom of susceptibles—i.e. a subgraph for which the nonrecovered intraclass degree is maximal-- is an outbreak that is oftentimes large enough to be considered a global epidemic. Since infection of only one or two classrooms is the most common type of outbreak in small populations, if most of these outbreaks can be classified as global epidemics, most global epidemics will be strongly correlated with a peak in the nonrecovered intraclass degree distribution. In large populations, where the pathogen is able to invade multiple classrooms, it is still possible to generate a global epidemic even if classrooms contain some number of recovered individuals—i.e. if the nonrecovered intraclass degree is not maximal.

Figure 9.

Fraction of all global epidemics correlated with a peak in the distribution of nonrecovered intraclass degrees in small and large populations (given by population in Figure 9a). (b) The cumulative fraction these epidemics associated with peaks for which the ratio of the peak degree (k_peak), to the maximum degree in the distribution, (k_max), attains the value indicated on the x-axis. The relationship is independent of population size and increases abruptly as this ratio increases from 80% to 90%. Values for a population of 10⁴ individuals (○) and 10⁵ individuals (■) have been plotted.

A closer inspection of the relationship between global epidemic occurrence and high-degree peaks in the nonrecovered intraclass degree distribution reveals that the ratio of the degree at which the peak occurs (k_peak) to the maximum degree in the distribution (k_max), is always greater than 0.5 (regardless of the population size) for epidemics that are correlated with peaks in the nonrecovered intraclass degree distribution. Moreover, the fraction of all global epidemics that can be correlated with peaks in the nonrecovered intraclass degree distribution increases from ∼.01 to ∼.18 as the ratio k_peak/k_max increases from 0.5 to 0.8, and then jumps to ∼0.5 as the degree ratio reaches 0.9 (Figure 9b). The fact that both small and large populations exhibit this trend suggests that the ratio k_peak/k_max serves as a threshold condition for large-scale epidemic occurrence: namely, if k_peak/k_max ≥0.9, populations are likely to experience global epidemics. Thus a network property of the contact network, more precisely of the contact network that is still visible to the disease, predicts the future dynamic behavior of the network.

Conclusions

Computer simulation of detailed, evolving social networks and disease dynamics promises to bring to light many questions, such as the previously-mentioned R₀ mystery, that may prove extremely valuable to epidemiological modeling, because such simulation affords us the opportunity to explore (on multiple scales) changes in topology concurrently with disease dynamics. Synthesizing the contact network data and some of the information gleaned from our disease dynamics simulations provides a layer of insight into the interrelationships between the dynamics of the social contact network and the dynamics of the disease propagating on that network that cannot be readily obtained via compartmental modeling. In particular, this network-based model facilitates a detailed understanding of the causal social-topological mechanisms behind disease propagation in cases for which fully-mixed models cannot be employed because of a high degree of heterogeneity in social contacts. Our results for a fairly simple set of algorithms reproduce the dominant dynamic trends for measles in populations that span two orders of magnitude, suggesting that the algorithms can be successfully tailored to less well-studied diseases, or to well-studied diseases in novel social settings. For example, by changing the disease parameters (the recovery rate and the input matrix of transmission rates by age cohort), pathogens such as flu or SARS could be studied. On the other hand, input distributions for the social networks' formative algorithms could be changed to create a population that resembles a large Third World city; simulations for measles propagation in this type of social network could shed light on how and why the age strata of Third World populations affected by measles are markedly younger than their First World counterparts.

A critical next step for network-based epidemiology in general (and, perhaps for this model, in particular), will be to parameterize network models and update the formative algorithms as real-world social network interaction data becomes available—i.e. as the real-world edge (who-is-connected-to-whom) data becomes available—for different social networks. Having real-world edge data for large social networks will add to our social network models quantitative precision that is, at present, not achievable. Various groups around the world are beginning to use detailed census data in tandem with mapping human mobility patterns[22-28] to acquire this type of edge information for school and work groups, making such advances a distinct possibility within the next few years.