Comparison of methods for evaluating drug-drug interaction

Abstract

This study was to compare several published methodologies for evaluating the nature of drug-drug combination, i.e., curve-shift analysis, isobologram, combination index, and universal surface response analysis. The comparison used the literature data on the combination of a glycinamide ribonucleotide formyltransferase inhibitor AG2034 and trimetrexate in cultured tumor cells and the published analysis results for the universal surface response method. All four methods provided similar major conclusions: (a) the nature of interaction between AG2034 and trimetrexate depended on the level of folic acid added to the culture medium (i.e., 2.3 or 78 μM), (b) at high folic acid, the interaction was universally synergistic for all tested combination ratios and over the full range of drug effect levels, and (c) at low folic acid, synergism was present but less extensive. Additional information provided by the different methods is as follows. The curve shift analysis enabled the inspection of the experimental data and visual evaluation of the approximate parallelism between the dose response curves. Isobologram analysis provided the range of concentration ratios where maximal synergy was obtained. The combination index analysis readily provided quantitative estimation of the extent of synergy or antagonism. The universal surface response method summarized drug-drug interaction in a single parameter, facilitating comparison of larger arrays of combinations. Only the curve shift analysis and the universal surface response method yielded a statistical estimate of differentiation between synergy, additivity, and antagonism. In summary, curve shift analysis, isobolograms, combination index analysis, and the universal response surface method are useful methods for analyzing drug-drug interaction, and provide complimentary information.

2. INTRODUCTION

Evaluation of drug-drug interaction is important in all areas of medicine. The nature and the extent of drug interaction are usually determined in in vitro studies. Computational approaches have been used to analyze experimental data for the nature of interaction, i.e., synergistic, additive or antagonistic. In situations where the mechanisms of drug actions and drug-drug interactions are well understood, mechanism-based pharmacodynamic modeling is a valuable tool (1). However, in the more common situations where there are insufficient mechanistic understandings to allow a well defined method, empirical methods based on Loewe additivity can be applied (2–4). The theoretical basis and methods for analyzing drug-drug interaction have been reviewed previously (5, 6).

Loewe additivity has become the basis for the following contemporary methods used to analyze drug-drug interaction. The isobologram analysis (7) evaluates the nature of interaction of two drugs, i.e., drug A and drug B, at a given effect level. Operationally, the concentrations required to produce the given effect (e.g., IC₅₀) are determined for drug A (IC_{x, A}) and drug B (IC_{x, B}) and indicated on the x and y axes of a two-coordinate plot, forming the two points (IC_{x, A}, 0) and (0, IC_{x, B}). The line connecting these two points is the line of additivity. Then, the concentrations of A and B contained in combination that provide the same effect, denoted as (C_{A, x}, C_{B, x}), are placed in the same plot. Synergy, additivity, or antagonism is indicated when (C_{A, x}, C_{B, x}) is located below, on, or above the line, respectively.

Combination index (CI) is calculated by Eq. 1.

$$CI=\frac{C_{A,x}}{I{C}_{x,A}}+\frac{C_{B,x}}{I{C}_{x,B}}$$ (1)

A CI of less than, equal to, and more than 1 indicates synergy, additivity, and antagonism, respectively.

Our laboratory recently described the curve-shift analysis and proposed the simultaneous use of isobologram, combination index, and curve-shift analyses for the evaluation of interaction in anticancer agents (8). Curve-shift analysis is a two-dimensional graphical data representation that directly compares the concentration-effect curves obtained for each of the dilution series associated with the selected concentration ratios in the typical experimental design. Concentrations of single agents and combinations are normalized to the corresponding IC₅₀ equivalents of single agents, as previously introduced (5, 9–11), and analyzed by nonlinear regression using the Hill equation. A leftward shift of combination concentration-effect curves relative to the curves for both of the single agents indicates Loewe synergy and a rightward shift indicates Loewe antagonism. Because of the two-dimensional format, visual inspection of goodness of fit of experimental data points, and of differences in slopes of the family of the dose response curves is facilitated.

We showed that non-linear regression analysis in the fitting of effect data to model equations represented an improvement over the linear regression fitting to transformed equations frequently used for the combination index analysis (8).

An additional analysis method, proposed and applied by Greco et al. (6,12–13), is the “universal response surface method”. This method assumes that the concentration-effect relationship for each drug separately follows the Hill equation and is designed to simultaneously fit all combination data to a single function. The fitting function (Eq. 2) defaults to Loewe additivity when the “synergism-antagonism parameter” α has a value of zero. Deviation from additivity results in a positive fitted value of α for synergistic interaction, and a negative value of α for antagonistic interaction.

$$1=\frac{C_{A,E}}{{IC}_{50,A}{(\frac{E}{E_{max}-E})}^{1/n_A}}+\frac{C_{B,E}}{{IC}_{50,B}{(\frac{E}{E_{max}-E})}^{1/n_B}}+\alpha \frac{C_{A,E}{C}_{B,E}}{{IC}_{50,A}{IC}_{50,B}{(\frac{E}{E_{max}-E})}^{1/(2n_A)+1/(2n_B)}}$$ (2)

Considerable debate remains with respect to the method-of-choice for analyzing drug-drug interaction data (14). The goal of the present report is to compare several methods of data analysis. The comparison used the literature data on the combination effect on tumor cell growth of two anti-folate agents, i.e., the dihydrofolate reductase inhibitor trimetrexate and the glycinamide ribonucleotide formyltransferase inhibitor AG2034 (12). The anti-proliferation effects of these agents, alone or in combination, were studied in the presence of low and high concentrations of folic acid to determine the effect of folates on the interaction between the two agents acting through inhibition of different members of the de novo purine and thymidylate synthesis pathways; the results were analyzed using the universal response surface method. The current study compared the results of curve shift analysis, isobolograms and combination index analysis to the results of the universal response surface method.

3. MATERIALS AND METHODS

3.1 Experimental data

The experimental data was provided by Dr. William Greco (Roswell Park Cancer Institute, Buffalo, NY) and was previously reported by Faessel et al. (12). In brief, exponentially growing mycoplasma-free HCT-8 human ileocecal adenocarcinoma cells were treated with AG2034 alone, trimetrexate alone, and their combinations, for 96 h. The trimetrexate -to-AG2034 concentration ratios were 1:0.1, 1:0.2, 1:0.5, 1:1.25, 1:2.5, 1:5, 1:10, 1:20, 1:50, 1:125, and 1:250 in the presence of 2.3 μM folic acid, and 1:1, 1:2, 1:5, 1:12.5, 1:25, 1:50, 1:100, 1:200, 1:500, 1:1250, and 1:2500 in the presence of 78 μM folic acid (5 replicates per data point). To examine the effects of folic acid, the culture medium was supplemented with either low or high concentrations of folic acid (i.e., 2.3 or 78 μM).

Drug activity was measured by the sulforhodamine B (SRB) method; the absorbance readings (OD values) were corrected for the reported, extrapolated background reading of 0.133 (12). We usually correct with the asymptotic minimum OD value for each dilution series (8), but deviated slightly from this practice for a more direct comparison with the data analysis presented in Faessel et al. (12), which used a single background value for correction. The deviation was minimal, averaging 0.9 % of the OD reading for control cells. All SRB absorbance readings at zero drug concentration are averaged and the mean is used as OD at control. The drug effect is measured by (OD at control-OD after treatment)/OD at control *100%.

3.2 Data analysis

Isobologram, combination index, and curve shift analysis are derivatives of Loewe additivity model (5–6), which is based on the assumption that a drug cannot interact with itself.

3.2.1 Isobologram analysis

The isobologram analysis provides a graphical presentation of the nature of interaction of two drugs, i.e., drug A and drug B (7). First, in a two-coordinate plot with one coordinate representing concentration of drug A and the other representing concentration of drug B, the concentrations of drugs A and B required to produce a defined effect x (e.g., IC_{50, A} and IC_{50, B} when x=50%), when used as single agents, are placed on the x and y-axes, respectively. The line of additivity is constructed by connecting these two points (e.g., (IC_{50, A}, 0) and (0, IC_{50, B}) for a 50% effect isobologram plot). Second, the concentrations of the two drugs used in combination to provide the same effect x (e.g., x=50%), denoted by point (C_{A, x}, C_{B, x}), are placed in the same plot. Synergy, additivity, or antagonism is indicated when this point is located below, on, or above the line, respectively.

3.2.2 Combination index analysis

Combination index provides a quantitative measure of the extent of drug interaction at a given effect level (5, 6, 15). That is, the combination concentrations of drug A and drug B to produce a effect x, C_{A, x} and C_{B, x}, are normalized by their corresponding concentrations that produces the same effect as a single agent, IC_{x, A} and IC_{x, B}, respectively. The sum of C_{A, x}/IC_{x, A} and C_{B, x}/IC_{x, B} is defined as the combination index at effect x as indicated by Eq. 1. If not available from experimental data, predicted concentrations of C_{A, x} and C_{B, x}, based on regression-derived Hill parameters of the studied combination ratio, were used to calculate combination index at any effect x (8, 15). Therefore, combination index curves can be generated by plotting combination indices against a series of effect levels. It is worth noting that combination index curves generated by Zhao et al (8) did not use the CALCUSYN program made available by Chou and Talalay (15), and instead were obtained by performing data fitting using nonlinear regression without logarithmic transformation.

3.2.3 Curve shift analysis

Curve shift analysis allows simultaneous presentation of the studied concentration-effect curves of singe-agent and combination treatments in a single plot.

Single agent dose-response relationships were analyzed using the Hill equation (Eq. 3).

$$E=Emax·\frac{C^n}{{IC}_{50}^n+C^n}$$ (3)

Where E is the measured effect; C is the drug concentration; Emax is the full range of drug effect, and was set at 100%; IC₅₀ is the drug concentration producing the median effect of 50%; and n is the curve shape parameter describing the steepness of the concentration-effect relationship.

The combination concentrations of drugs were normalized to their respective single agent IC₅₀. Eq. 4 states the IC₅₀-equivalent concentration of Drug A or Drug B, used alone or in combination with each other, required to produce x% effect. Note that for single agent, one of the two terms (C_A,x or C_B,x) on the right hand side of the equation becomes zero.

$${IC}_{50}\mathit{Equivalent}\mathit{Concentration}=\frac{C_{A,x}}{{IC}_{50,A}}+\frac{C_{B,x}}{{IC}_{50,B}}$$ (4)

Where IC_{50, X} is the IC₅₀ value of drug X. Substituting Eq. 4 into Eq. 3 yielded Eq. 5, which describes the effects of combination therapy as a function of IC₅₀-equivalent concentrations. IC_50,combo and n_combo are the values for the combination therapy.

$$\mathit{Combination}\mathit{Therapy}\mathit{Effect}=\frac{E_{max}{\left(\frac{C_{A,x}}{{IC}_{50,A}}+\frac{C_{B,x}}{{IC}_{50,B}}\right)}^{n_{\mathit{combo}}}}{{\left(\frac{C_{A,x}}{{IC}_{50,A}}+\frac{C_{B,x}}{{IC}_{50,B}}\right)}^{n_{\mathit{combo}}}+{({IC}_{50,\mathit{combo}})}^{n_{\mathit{combo}}}}$$ (5)

Plotting the effects of single agents and combinations against IC₅₀-equivalent drug concentrations enables the simultaneous presentation of these concentration-effect curves in a single plot. Due to the normalization, the curves for the single agents will have an IC₅₀ value of one “ IC₅₀ equivalent”, while synergistic combinations will have a lower IC₅₀ value resulting in a leftward shift, and antagonistic combinations will show a rightward shift.

3.3 Computer software packages and procedures

All programming codes and calculations used SAS language and procedures (SAS, Cary, NC). Nonlinear regressions were performed using the SAS/STAT Proc NLIN routine with the unweighted Marquardt iteration method. Graphical presentations were generated by S-plus (Insightful, Seattle, WA).

4. RESULTS

4.1 Results of curve-shift analysis

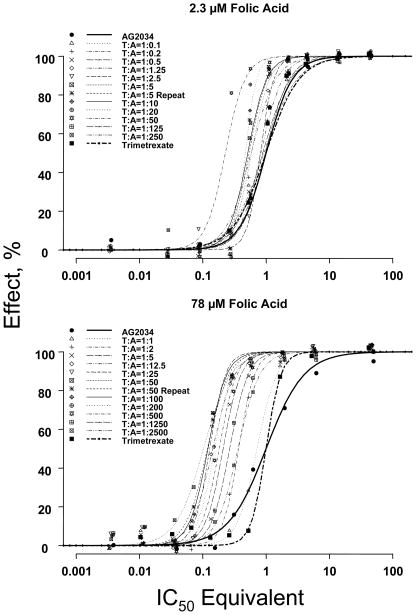
Figure 1 shows the dose response curves for trimetrexate, AG2034, or their combinations, in the presence of 2.3 or 78 μM folic acid. Table 1 summarizes the nonlinear fitting results.

Figure 1. Curve shift analyses.

The experimental combination concentrations were normalized to IC₅₀-equivalents of single agents. Data were analyzed using nonlinear regression without weighting. The data points are mean values of five replicates. The lines are best-fitted regressed lines. A leftward shift of concentration-effect curves for combinations when compared to single agent curves indicates synergism, and a rightward shift indicates antagonism. T:A indicates trimetrexate-to-AG2034 ratios in their molar concentration. Experiment with ratio of T:A=1:50 has been performed twice; the second experiment is labeled T:A=1:50 repeat. Note that the legend gives the molar concentration ratios of the trimetrexate:AG2034 mixtures. However, the X axis (logarithmic scale) is the total concentration of trimetrexate plus AG2034 expressed in IC_{50, equivalents} as calculated by Eq. 4.

Table 1. Results of curve shift analysis.

Experiments were conducted at two levels of folic acid. Combination ratio indicates the trimetrexate-to-AG2034 ratio in their actual concentrations (μM). Initial concentrations are the starting concentrations, which were subsequently diluted at fixed concentration ratios. IC_{50, combination} is the combination concentration in IC₅₀ equivalents, as calculated by Eq. 4. SE is the corresponding standard error. The critical value for the inverse cumulative T-distribution (type I error rate = 0.025, two sides, degrees of freedom = 53) is equal to 2.01. IC_{50, combination} +2.01 SE <1, IC_{50, combination} −2.01 SE <1< IC_{50, combination} +2.01 SE, and IC_{50, combination} −2.01 SE >1 indicate synergy, additivity, and antagonism, respectively. Parameter n is the curve shape parameter describing the steepness of the concentration-effect relationship. IC₅₀ values for pure agents are as follows. AG2034 in 2.3 μM folic acid: 0.0063±0.0004 μM, in 78μM folic acid: 0.56±0.08 μM (universal response surface estimates: 0.0035 and 0.414μM, respectively). Trimetrexate in 2.3 μM folic acid: 0.0014±0.0009 μM, in 78 μM folic acid: 0.013±0.001 μM (universal response surface estimates: 0.0015 and 0.013 μM, respectively).

PteGlu, μM	Combination Ratio	Initial concentration before dilution		IC50, combination, IC50 equivalents	n	Evaluation at 50% Effect Level
	Trimetrexate:AG2034	Trimetrexate, μM	AG2034, μM	Mean±SE	Mean±SE
2.3	AG2034 alone	0.00	2.78	1.00±0.06	3.12±0.53
	1:0.1	0.55	0.05	0.96±0.06	2.29±0.28	Additive
	1:0.2	0.54	0.11	0.91±0.08	2.26±0.42	Additive
	1:0.5	0.51	0.25	0.90±0.10	2.82±0.77	Additive
	1:1.25	0.45	0.56	0.89±0.03	3.81±0.31	Synergy
	1:2.5	0.37	0.93	0.89±0.06	5.00*	Additive
	1:5	0.28	1.39	0.63±0.02	5.00*	Synergy
	1:5 repeat	0.28	1.39	0.58±0.02	5.00*	Synergy
	1:10	0.19	1.85	0.56±0.01	4.92±0.43	Synergy
	1:20	0.11	2.22	0.53±0.03	5.00*	Synergy
	1:50	0.05	2.53	0.26±0.01	5.00*	Synergy
	1:125	0.02	2.67	0.99±0.07	3.19±0.59	Additive
	1:250	0.01	2.73	0.60±0.02	3.87±0.57	Synergy
	Trimetrexate alone	0.56	0.00	1.00±0.64	2.32±0.33
78	AG2034 alone	0.00	27.78	1.00±0.14	1.45±0.23
	1:1	0.55	0.54	0.72±0.05	2.80±0.43	Synergy
	1:2	0.54	1.07	0.37±0.02	3.53±0.49	Synergy
	1:5	0.51	2.53	0.21±0.01	3.12±0.52	Synergy
	1:12.5	0.45	5.56	0.14±0.01	2.54±0.35	Synergy
	1:25	0.37	9.26	0.13±0.01	3.55±0.74	Synergy
	1:50	0.28	13.89	0.10±0.01	2.00±0.10	Synergy
	1:50 repeat	0.28	13.89	0.12±0.01	2.59±0.42	Synergy
	1:100	0.19	18.52	0.12±0.01	2.96±0.34	Synergy
	1:200	0.11	22.22	0.15±0.01	3.21±0.54	Synergy
	1:500	0.05	25.25	0.18±0.02	3.16±0.82	Synergy
	1:1250	0.02	26.71	0.27±0.02	3.03±0.69	Synergy
	1:2500	0.01	27.24	0.36±0.04	2.55±0.61	Synergy
	Trimetrexate alone	0.56	0.00	1.00±0.08	3.73±0.62

^*The fitted value of n is limited to 5.00. At this value, effect declines over the effect range (e.g. from 90% to 3% effect) between adjacent data points at the employed $\sqrt{10}$ or 3.16-fold sequential dilution, and higher values cannot be accurately estimated.

In general, the plots showed well-spaced concentration points, with several data points near the IC₅₀ value. The experimental design used approximately three-fold steps in concentration dilution; this practice provided, in most curves, at least two points in the middle range of approximately 20 to 80% effect. All concentration-effect curves for various trimetrexate and AG2034 combinations were situated close to or to the left of the curves for the two single agents, indicating additivity or synergy. Differences were observed for the curves obtained at low and high folic acid concentrations.

At the high folic acid concentration (78 μM), all concentration-effect curves for the combinations exhibited a strong leftward shift compared to single-agent curves, indicating synergistic interaction between trimetrexate and AG2034. The IC₅₀ equivalents for the combinations ranged from 0.1 to 0.72. The corresponding extent of synergy ranged from a 1.5- to 10-fold leftward shift in the concentration-effect curves. The maximal 8- to 10-fold synergy was observed at about 1:50 trimetrexate:AG2034 molar concentration ratio. Note that most of the concentration-effect curves were in parallel, with the exception that AG2034 showed a shallower slope. The analysis of nonparallel curves for drug-drug interaction is considered more challenging compared to parallel curves (4, 5).

At low folic acid concentration (2.3 μM), several differences were observed. First, the IC₅₀ values for single agents AG2034 and trimetrexate were about 10 and 100 fold lower compared to their IC₅₀ values at high folic acid concentration. Second, not all concentration-time curves for the combinations showed an apparent leftward shift; five of the twelve combinations overlapped with the curves of single agents. This indicates additivity, which is in agreement with the finding that their combination concentrations expressed in IC₅₀ equivalents (as calculated by Eq. 4) were not statistically different from 1.0 at 50% effect level (Table 1). A second cluster of six curves showed a shift to the left; the combination concentrations expressed in IC₅₀ equivalents were between 0.5 and 0.6 at 50% effect level, indicating a synergy of about two-fold at this level. Finally, one combination (trimetrexate:AG2034 ratio of 1:50) showed the furthest shift to the left, which appeared to be largely the result of a single data point.

4.2 Results of isobologram analysis

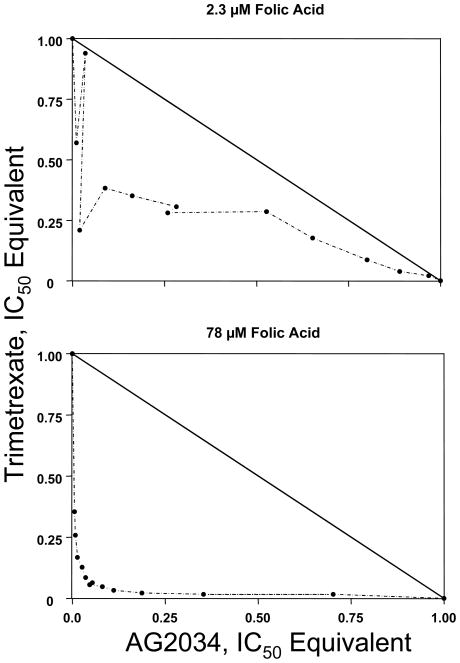
In contrast to curve shift analysis which provides the entire spectrum of effect levels, isobologram analysis is typically conducted for single effect levels, e.g., 50% effect level. Figure 2 shows the isobolograms at 50% effect level, and Table 2 summarizes the results. At the high folic acid concentration, the isobologram analysis showed extensive synergy, with the maximum extent of about 10-fold synergy occurring at a fairly broad range of concentration ratios (the median ratio was slightly higher than 1.0).

Figure 2. Isobologram analysis.

The diagonal line is the line of additivity. Experimental data points, represented by dots, located below, on, or above the line indicate synergy, additivity, or antagonism, respectively.

Table 2. Results of isobologram analysis.

Experiments were conducted at two levels of folic acid. Combination ratio indicates the trimetrexate-to-AG2034 ratio in their actual concentrations (μM). Concentration in IC₅₀ equivalents is the normalized concentration that is calculated by dividing the actual concentration used in combination treatment with its corresponding single-agent IC₅₀. Combination index at 50% effect level is the sum of trimetrexate and AG2034 IC₅₀-equivalent concentrations used in combination according to Eq. 1.

PteGlu, μM	Combination Ratio	Concentration, IC50 Equivalent		Combination Index at 50% effect level	Evaluation at 50% Effect Level
	Trimetrexate:AG2034	Trimetrexate	AG2034
2.3	1:0.1	0.57	0.01	0.58	Synergy
	1:0.2	0.94	0.03	0.97	Synergy
	1:0.5	0.21	0.02	0.23	Synergy
	1:1.25	0.38	0.09	0.47	Synergy
	1:2.5	0.35	0.16	0.51	Synergy
	1:5	0.31	0.28	0.59	Synergy
	1:5 repeat	0.28	0.26	0.54	Synergy
	1:10	0.29	0.53	0.81	Synergy
	1:20	0.18	0.65	0.83	Synergy
	1:50	0.09	0.80	0.89	Synergy
	1:125	0.04	0.89	0.93	Synergy
	1:250	0.02	0.97	0.99	Synergy
78	1:1	0.35	0.01	0.36	Synergy
	1:2	0.26	0.01	0.27	Synergy
	1:5	0.17	0.01	0.18	Synergy
	1:12.5	0.13	0.03	0.15	Synergy
	1:25	0.08	0.04	0.12	Synergy
	1:50	0.06	0.05	0.10	Synergy
	1:50 repeat	0.06	0.05	0.12	Synergy
	1:100	0.05	0.08	0.13	Synergy
	1:200	0.03	0.11	0.14	Synergy
	1:500	0.02	0.19	0.21	Synergy
	1:1250	0.02	0.35	0.37	Synergy
	1:2500	0.02	0.70	0.72	Synergy

At the low folic acid concentration, all data points for trimetrexate and AG2034 combinations were below the line of additivity, indicating synergy. Maximal synergy of approximately 2-fold was achieved at a trimetrexate-to-AG2034 IC_{50, equivalent} concentration ratio close to one.

4.3 Results of combination index analysis

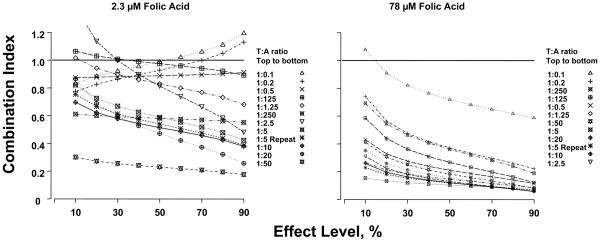
Figure 3 shows the CI values, and Table 3 summarizes the results. At the high folic acid concentration, the CI values were consistently below 1, indicating synergy. CI decreased at increasing effect levels, indicating increasing degree of synergy at higher effect levels. Synergy of greater than 5- fold at the 50% effect level was observed for the curves with trimetrexate:AG2034 concentration ratios of 1:12.5, 1:25, 1:50, 1:100, 1:200, and 1:500 (Table 3).

Figure 3. Combination index curve analysis.

CI values less than, equal to, or greater than 1 indicates synergy, additivity, or antagonism, respectively. The horizontal line at Combination Index=1 is the line of additivity. T:A ratio indicates trimetrexate to AG2034 ratio in their molar concentrations.

Table 3. Combination indices: Effects of folic acid concentrations, combination concentration ratios and effect levels.

Experiments were conducted at two levels of folic acid. Combination ratio indicates the trimetrexate-to-AG2034 ratio in their actual concentrations (μM). Effect level indicates the effect level at which the combination index was calculated (using Eq. 1).

PteGlu, μM	Combination Ratio	Combination Index at Effect Level (%) of
	Trimetrexate:AG2034	10	20	30	40	50	60	70	80	90
2.3	1:0.1	0.83	0.89	0.92	0.96	0.99	1.02	1.06	1.11	1.19
	1:0.2	0.77	0.83	0.86	0.90	0.93	0.96	1.00	1.05	1.13
	1:0.5	0.87	0.88	0.88	0.88	0.89	0.89	0.90	0.90	0.91
	1:1.25	1.02	0.94	0.90	0.86	0.83	0.80	0.77	0.73	0.68
	1:2.5	1.38	1.14	1.00	0.90	0.81	0.74	0.66	0.58	0.48
	1:5	0.82	0.73	0.67	0.63	0.59	0.55	0.52	0.48	0.42
	1:5 repeat	0.75	0.67	0.61	0.57	0.54	0.51	0.47	0.44	0.39
	1:10	0.70	0.62	0.58	0.54	0.51	0.49	0.46	0.42	0.38
	1:20	0.86	0.69	0.60	0.53	0.47	0.42	0.37	0.32	0.26
	1:50	0.30	0.27	0.25	0.24	0.23	0.22	0.21	0.19	0.17
	1:125	1.06	1.03	1.01	0.99	0.97	0.96	0.94	0.92	0.89
	1:250	0.61	0.60	0.59	0.59	0.58	0.57	0.57	0.56	0.55
78	1:1	1.08	0.91	0.82	0.76	0.72	0.68	0.65	0.62	0.59
	1:2	0.74	0.56	0.48	0.42	0.37	0.33	0.30	0.26	0.22
	1:5	0.43	0.33	0.27	0.24	0.21	0.19	0.16	0.14	0.11
	1:12.5	0.27	0.21	0.18	0.16	0.14	0.13	0.12	0.10	0.08
	1:25	0.31	0.22	0.18	0.15	0.13	0.11	0.09	0.08	0.06
	1:50	0.15	0.13	0.12	0.11	0.10	0.10	0.09	0.08	0.07
	1:50 repeat	0.23	0.18	0.15	0.13	0.12	0.11	0.09	0.08	0.06
	1:100	0.26	0.20	0.16	0.14	0.12	0.10	0.09	0.07	0.06
	1:200	0.35	0.26	0.21	0.18	0.15	0.13	0.11	0.09	0.07
	1:500	0.41	0.30	0.25	0.21	0.18	0.16	0.13	0.11	0.08
	1:1250	0.59	0.44	0.36	0.31	0.27	0.23	0.20	0.16	0.12
	1:2500	0.69	0.54	0.46	0.41	0.36	0.32	0.28	0.24	0.19

At the low folic acid concentration, the results were more complex. First, the CI-vs-effect lines showed inconsistent trends. Six of twelve CI-vs-effect lines showed CI values between 0.23 and 0.6 at the 50% effect levels, indicating a 1.7- to 4-fold synergy. The remaining six curves showed higher CI values that at times were close to or greater than 1. Second, very different CI-vs-effect lines were observed for combinations consisting of similar trimetrexate-to-AG2034 concentration ratios. For example, the lines for sequential trimetrexate:AG2034 concentration ratios increasing from 1:0.1 to 1:2.5, showed increasing CI values with increasing effect levels (trimetrexate:AG2034 = 1:0.1, 1:0.2), a horizontal relationship (trimetrexate:AG2034 = 1:0.5), and decreasing CI values with increasing effect (trimetrexate:AG2034 = 1:1.25, 1:2.5). This trend was not easily noted in the curve shift analysis, but was shown previously based on isobologram analysis at effect levels ranging from 0.1 to 0.9 (12). The pattern was described as a highly reproducible “snaking” of the isobolograms around the line of additivity and was observed for several of the combinations.

4.4 Results from universal surface response analysis

This was obtained from the previous publication (12). The conclusions were as follows. (a) The combination of trimetrexate and AG2034 showed synergy at high and low folic acid levels; the value for the interaction parameter α was 1.50±0.25 (mean ± SE) at 2.3 μM and 146±20 at 78 μM. (b) The combination consistently showed the highest degree of synergy at high folic acid concentration. (c) The extent of synergy at high folic acid level was significantly higher than at low folic acid level. (d) The extent of synergy was lower at very low and high effect levels compared to medium effect levels. These general findings are consistent with the results of isobologram, combination index and curve-shift analyses.

It is noted that the IC₅₀ values for single agents AG2034 and trimetrexate determined using Eq. 3 differed from the values obtained using the universal response surface method by 0–44% (Table 1). This may be due to the different ways of fitting the parameter value, including the manner of background correction for absorbance at infinite drug concentration, the manner of handling control absorbance under drug-free conditions, the manner of weighting, and the fitting of a whole response surface vs fitting of individual single agent curves.

5. DISCUSSION

This report compared different methods of evaluating drug-drug interaction, using the published results for the combinations of trimetrexate and AG2034. The results indicate that isobologram, combination index, curve-shift and universal surface response analyses yielded similar conclusions, i.e., (a) the degree of synergistic interaction between AG2034 and trimetrexate depended on the level of folic acid added to the culture medium (i.e., 2.3 or 78 μM) and (b) at the high folic acid level, the interaction was universally synergistic for all tested combination ratios and over the full range of drug effect levels.

It is noted that the four methods offer complimentary information. The curve shift analysis method allows direct inspection of the experimental data, evaluation of whether the selected concentration points were appropriate, and visual inspection of approximate parallelism between the dose response curves. The latter enables an investigator to determine whether equal or dissimilar effects are observed at low and high effect levels. However, the curve shift analysis method is not well suited for evaluating the range of combination ratio values that yield maximal or near maximal synergy. For the latter, the isobologram analysis provides the changes in the extent of interaction as a function of trimetrexate-to-AG2034 concentration ratios; the points that are located furthest away from the line of additivity correspond to the maximal synergy or antagonism. For example, the current example showed the maximal synergy at the concentration ratio of approximately 1:1 expressed in IC₅₀ equivalents. On the other hand, the isobologram analysis does not provide the exact extent of synergy, nor statistical differentiation between synergy, additivity, and antagonism.

The combination index analysis provides an easy presentation of quantitative synergy data, with some caveats. The method lends itself well to evaluation of trends between effect levels, such as the increasing extent of synergy with increasing effect level for all combinations at high folic acid concentrations, and the more complex trends at low folic acid concentration. However, as we have shown previously (8), the combination index analysis is highly sensitive to small changes in effect measurements at low and high concentrations (i.e. at low and high effect levels). A further shortcoming is the lack of statistical evaluation of synergy, additivity, or antagonism.

The universal surface model approach provides a single value summarizing the nature of interaction for the totality of data on the combinations. As this method employs a simultaneous fit of all combination data to a single function, it circumvents the interaction analysis at multiple levels of effect (e.g., IC₁₀ to IC₉₀), or for multiple (drug A-to-drug B) concentration ratios needed for 2-dimensional models. The method provides the convenience of a single value of α to represent the extent of synergy. An excellent application of this method is in large screening exercises, searching for the most highly synergistic drug combinations, where the single parameter representing synergistic/antagonistic interaction allows the investigator to rank drug combinations from least to most synergistic. The model further provides a statistical indication of deviation from additivity. The method is, however, not suited to scrutinize the synergy of a single combination in detail. A further limitation is that the model equation defining the interaction surface is designed to describe interactions yielding smoothly bowing isobolograms, and is not versatile for evaluating interactions with a more complex pattern, such as the combination of LY231514 with trimetrexate, which shows synergy at certain concentration ratios and antagonism at other ratios (12). Consequently, the value of α is not indicative of the extent of interaction. A final limitation of the universal surface method is that the value of α cannot be easily converted to an estimate of the extent of synergy. In summary, the four methods of synergy evaluation presented here have their utility and limitations, and analysis of synergy by multiple methods is recommended. Further development of methods that allow statistical differentiation between synergy, additivity, and antagonism is warranted.

Abbreviations

C_A,x and C_B,x

concentration of drugs A and B used in a combination that generates x% of the maximal combination effect

CI

combination index

IC_x

drug concentration needed to produce x% of the maximal effect

SRB

sulforhodamine B