Cone beam CT dosimetry: A unified and self-consistent approach including all scan modalities—With or without phantom motion

Abstract

Purpose: This article describes a common methodology and measurement technique, encompassing both conventional (helical and axial) CT scanning using phantom translation and cone beam (or narrow fan beam) CT scans about a stationary phantom. Cone beam CT systems having beam widths along the z-axis wide enough to cover a significant anatomical length (50–160 mm) in a single axial rotation (e.g., in cardiac CT) are rapidly proliferating in the clinic, referred to herein as stationary cone beam CT (SCBCT). The integral format of the CTDI paradigm is not appropriate for a stationary phantom, and is not useful for predicting the dose in SCBCT, nor for perfusion studies or CT fluoroscopy. Likewise, the pencil chamber has limited utility in this domain (even one of extended length).

Methods: By demonstrating, both experimentally and theoretically, the match between the dose distribution f(z) for a wide cone beam and that due to an axial scan series $\tilde{D}\left(z\right)$, it is shown that the dose on the central ray of the cone beam f(0) is both spatially colocated and numerically equal to the dose predicted by CTDI for the axial series; and thus f(0) is the logical (and unique) choice for a SCBCT dose-descriptor consistent with the CTDI-based dose of conventional CT. This dose f(0) can be readily measured using a conventional (short) ionization chamber. Additionally, Monte Carlo simulations of Boone [J. M. Boone, “Dose spread functions in computed tomography: A Monte Carlo study,” Med. Phys. 36, 4547–4554 (2009)], expressed as a scatter LSF (or DSF), allow the application of a convolution-based model [R. L. Dixon, M. T. Munley, and E. Bayram, “An improved analytical model for CT dose simulation with a new look at the theory of CT dose,” Med. Phys. 32, 3712–3728 (2005)] of the axial dose profile f(z) for any primary beam width a (anyn×T), fan beam and cone beam alike, from a single LSF kernel; its simple form allows the results to be expressed as simple analytical equations. The experimental data of Mori et al. [S. Mori, M. Endo, K. Nishizawa, T. Tsunoo, T. Aoyama, H. Fujiwara, and K. Murase, “Enlarged longitudinal dose profiles in cone-beam CT and the need for modified dosimetry,” Med. Phys. 32, 1061–1069 (2005)] from a 256 channel cone beam scanner for a variety of beam widths (28–138 mm) are used to corroborate the theory.

Results: Useful commonalities between SCBCT and conventional CT dose are revealed, including a common equilibrium dose parameter A_eq, which is independent of z-collimator aperture a (orn×T), and a common analytical (exponential growth) function H(λ) describing the relative approach to scatter equilibrium at z=0 for both modalities (with λ=a or λ=scan length L). This function exhibits good agreement with the above-mentioned cone beam data of Mori et al. for H(a) as well as with data H(L) obtained from conventional CT scanning [R. L. Dixon and A. C. Ballard, “Experimental validation of a versatile system of CT dosimetry using a conventional ion chamber: Beyond CTDI₁₀₀,” Med. Phys. 34(8), 3399–3413 (2007)] for the same directly irradiated, phantom length L=a.

Conclusions: This methodology and associated mathematical theory provide a physically self-consistent description of dose between stationary phantom CT and conventional CT, and has predictive capabilities which can be used to effect a substantial reduction in data collection; provide a bridge between modalities; and predict the relevant peak doses f(0) for perfusion studies.

INTRODUCTION

CT systems having beam widths along the z-axis wide enough to cover a significant anatomical length in a single axial rotation are rapidly proliferating in the clinic. Some utilize a conventional CT platform and can provide both conventional helical or axial scanning motions involving patient∕table translation, as well as single (or multiple) rotation acquisitions at a fixed z location without table motion (used, for example, in acquiring cardiac images using subsecond scans), having selectable nominal cone beam widths of 40–160 mm in one 320 channel system recently introduced. The methodology introduced herein for stationary phantom cone beam CT (SCBCT) also applies to any CT scan without table motion (whether wide cone beam or narrow fan beam) in applications ranging from CT fluoroscopy, brain perfusion, and multiphasic liver scans.

A primary objective of this paper is the description of a self-consistent methodology which can bridge the gap between the dose accrued in conventional helical or axial scan modes in which the phantom is translated through a distance L; and CT operation without table∕phantom motion, usually (but not necessarily) utilizing wider “cone beams” having variable lengths of 40–180 mm along z.

The experimental data of Mori et al.¹ obtained on a 256 channel cone beam CT scanner (the prototype of the abovementioned 320 channel scanner) are used to corroborate the theory and conclusions. This system and data set are also representative of the commercially available 320 channel system; the basic principles are unchanged.

For brevity, the two modalities are referred to as

• A. “Conventional CT.” Axial or helical scan acquisitions using multiple rotations, regularly spaced along z due to table∕phantom translation over (−L∕2,L∕2).

• B. “SCBCT.” Image data are acquired using single or multiple axial rotations about a stationary phantom (table advance b=0, scan length L=0). (The results are also applicable to narrow “fan beam” CT using a stationary phantom as used in perfusion studies).

It will be shown in Sec. 2 that the dose on the central ray of the cone beam f(0) is both spatially colocated and numerically equal to the dose predicted by CTDI for a conventional scan series; and thus f(0) is the logical (and unique) choice for a SCBCT dose-descriptor consistent with the CTDI-based dose used in conventional CT. In addition to a common mathematical formalism which describes the dose for both modalities, there is an identical measurement technique applicable to both cases utilizing a short ionization chamber.²

Both modalities are shown to possess a common equilibrium dose parameter A_eq which is independent of z-collimator aperture a (or n×T), and a common analytical function H(λ) is derived describing the relative approach to scatter equilibrium at z=0 (with λ=a for the stationary phantom or λ=scan length L). This commonality provides a crossover or bridge between conventional and stationary phantom CT, such that one can predict the complete data set for both modalities from a single measurement of the central (peak) dose f(0) resulting from a single axial rotation at a given aperture setting a. From this, one can predict the SCBCT or fan beam peak dose f(0) for any beam width a, and the conventional CT dose (as predicted by CTDI) for any scan length L (including the limiting equilibrium dose) for any collimator aperture setting a and any pitch p. Although the crossover between modalities is an interesting aspect of the theory developed, it is by no means the only application or goal of the theoretical development to follow.

The glossary of parameters in the Appendix is provided as a quick reference for the following development and throughout.

The following development concentrates on the actual in-phantom dose for both conventional CT involving phantom translation, and stationary phantom CT such as SCBCT, directed toward creating a consistent approach to CT dose assessment which provides continuity of dose and physical interpretation between these two modalities. To that end, it is necessary to review the dose-descriptors used in conventional CT (and the CTDI paradigm).

THEORY

Conventional CT scanning using table∕phantom translation

Accumulated dose equations for helical or axial scan trajectories utilizing table∕phantom translation along z

The best way to establish the correct and unequivocal physical interpretation (and limitations) of the CTDI equation and its related dose equations is to derive it. A simpler derivation³ (compared to the original⁴) using convolution methods is outlined below (the resulting equations are also necessary and pertinent to this paper).

Axial scanning

One assumes a series of N=2J+1 rotations, each producing an identical axial dose profile f(z) centered at z^′=kb (where k denotes the k_th rotation); spaced at equal intervalsb; and dispersed over a total phantom length L=Nb along z as a result of translating the table (and phantom) by a distance b between each rotation (“step and shoot”). This results in a quasiperiodic (or oscillatory) dose distribution³ of fundamental period b, given by the superposition of displaced profiles shown below

$${\tilde{D}}_N\left(z\right)=\sum _{k=-J}^{J}f\left(z-kb\right)=f\left(z\right)\otimes \sum _{-J}^J\delta \left(z-kb\right),$$ (1)

also expressed above as the convolution of f(z) with a finite “comb” of δ-functions, which replicate f(z) at each location z^′=kb. This assumes “shift-invariance” along z (identical dose profiles at each z^′=kb spaced at equal intervals b), which also requires a shift-invariant phantom having a constant cross-section and composition along z (including, but not restricted to, uniform cylindrical or elliptical phantoms). The pencil chamber measurement method is likewise foiled by any loss of shift-invariance.

This dose can be smoothed³ by taking the “running mean” (averaging over z±b∕2 at each z), which is equivalent to convolving Eq. 1 with the unit-area rect function b⁻¹ Π(z∕b), which in turn collapses the δ-function comb into the longer rect function Π(z∕L) of length L=Nb; resulting in the convolution equation³ for the smoothed dose D_L(z) accumulated at each value of z for a scan length L and given by Eq. 2 below

$$D_L\left(z\right)=\frac{1}{b}f\left(z\right)\otimes \Pi \left(z∕L\right)=\frac{1}{b}{\int }_{-L∕2}^{L∕2}f\left(z-z^{\prime }\right)d{z}^{\prime },$$ (2)

where f(z) includes both the primary beam and scatter contributions f(z)=f_p(z)+f_s(z) and is therefore much broader than the primary beam width (FWHM) a, where a is equal to the z-collimator aperture geometrically projected onto the axis of rotation (AOR).⁵ MDCT requires that a>nT in order to keep the penumbra beyond the active detector length nT. Evaluation of Eq. 2 at z=0 results in the accumulated dose D_L(0) at the center of the scan lengthL as given by Eq. 3 below

$$D_L\left(0\right)=\frac{1}{b}{\int }_{-L∕2}^{L∕2}f\left(z^{\prime }\right)d{z}^{\prime },$$ (3)

which (for axial scans) represents an average dose over the small interval ±b∕2 about z=0, where b is typically small compared to the total scan length L=Nb.⁶ Note, however, the implicit dependence of the integration limits ±L∕2 and the divisor b, physically related by L=Nb. We are now done. These three equations provide the complete physical basis for conventional CT dosimetry. The derivation of Eq. 3 outlined above is equivalent to the original derivation,⁴ which led to the definition of MSAD and CTDI.

Equation 3 for D_L(0) represents the basic equation upon which the CTDI methodology is based, in which the divisor b of the integral physically represents a table advance per rotation, with CTDI_L itself defined⁴ as the value of D_L(0) in Eq. 3, resulting from a specific table increment (scan interval) b=nT, which interval produces “contiguous” axial scans in the image domain (leaving no gaps in the acquired image data). Thus, physically, CTDI_L is equal to the accumulated dose at the center (z=0) of the scan length (−L∕2,L∕2), for a table advance b=nT=“N×T” (a generalized pitchp=b∕nT=1). Substituting b=nT into Eq. 3 gives the familiar CTDI equation

$${\text{CTDI}}_L=\frac{1}{nT}{\int }_{-L∕2}^{L∕2}f\left(z^{\prime }\right)d{z}^{\prime },$$ (4)

which one can also express in terms of D_L(0) from Eq. 3 and pitch p as CTDI_L=(b∕nT)D_L(0)=pD_L(0).^{6, 7, 8}

There is actually no imperative to have a separate equation for CTDI_L, since it simply represents a special case of Eq. 3, namely, a particular value of D_L(0) corresponding to a specific table increment b=nT (a pitch of unity), and thus nT in the CTDI equation physically represents a table increment.

Measurement of the integral in Eqs. 3, 4 using a pencil chamber of fixed-length ℓ only allows prediction of the accrued dose at z=0 for a scan length L=ℓ (e.g.,L=100 mm as for CTDI₁₀₀). Additionally, assigning a fixed integration length L (e.g., 100 mm) to CTDI_L breaks the required coupling L=Nb between the divisor b and the integration limits ±L∕2. For conventional CT, as L becomes large enough to completely span the very long scatter tails of f(z) at L=L_eq, such that no additional scatter can reach z=0 for L≥L_eq (symbolically L→∞), then D_L(0) approaches its limiting value, the equilibrium dose D_eq, written as

$$D_{\text{eq}}\left(a∕b\right)=\frac{1}{b}{\int }_{-\infty }^{\infty }f\left(z^{\prime }\right)d{z}^{\prime }\propto \left(a∕b\right).$$ (5)

Since D_eq depends (explicitly) on the inverse of table increment b, and is directly proportional to the collimator aperture a implicitly through the infinite integral of f(z) (as shown in Sec. 3B), then D_eq is directly proportional to a∕b.

Helical scanning

Equations 2, 3, 4, 5 have likewise been shown³ to apply to helical scanning at a pitch p=b∕nT if an angular average over 2π at a fixedz is used to smooth (average) the peripheral axis dose distribution rather than the longitudinal running mean used for axial scans [the dose for helical scans on the phantom central axis is nonoscillatory, requiring no averaging, and is given by Eq. 2]. The longitudinal and angular averages have been shown⁵ to converge at values of z where dose equilibrium has been established.

The derivation of Eqs. 2, 3, 4, 5 for helical scanning³ is briefly outlined below, since it more clearly illustrates some important properties of D_L(0) and CTDI_L. The dose rate on the central axis is independent of beam (gantry) angle θ, hence the dose rate profile is $\dot{f}\left(z\right)={\tau }^{-1}f\left(z\right)$, where τ is gantry rotation time. Translation of the table and phantom at velocity v produces a dose rate profile in the phantom reference frame expressed as a traveling wave $\dot{f}\left(z,t\right)={\tau }^{-1}f\left(z-vt\right)$, thus the dose accumulated at a given z as the profile travels by is given by the time integral of $\dot{f}\left(z,t\right)$ over the total “beam-on” time t₀, namely, $D_L\left(z\right)={\tau }^{-1}{\int }_{-t_0∕2}^{t_0∕2}f\left(z-vt\right)dt$. Conversion to the spatial domain using z^′=vt, scan length L=vt₀, and a table advance per rotation b=vτ (a pitch of p=b∕nT), leads directly to the same convolution equation for D_L(z) [Eq. 2] previously derived for axial scans, and from which Eqs. 3, 4, 5 also follow as before; however, D_L(0) and CTDI_L in the helical mode both refer to the dose precisely at z=0 (and likewise on the peripheral axis where an angular average³ is used).

If the table and phantom remain stationary (v=0), the time integral of the dose rate $\dot{f}\left(z\right)={\tau }^{-1}f\left(z\right)$ is simply D_L(z)=(t₀∕τ)f(z)=Nf(z); likewise, in the limit v→0,L=vt₀→0, the integration limits ±L∕2→0; thus the integral format of Eqs. 2, 3, 4 collapse, and all converge smoothly to Nf(z) or Nf(0). Likewise, for axial scanning, setting the table increment to b=0 in Eq. 1 reduces the summation to ${\tilde{D}}_N\left(z\right)=Nf\left(z\right)$, and the integral format of Eqs. 2, 3, 4 for axial scanning [including Eq. 4 for CTDI_L] also collapse, converging to Nf(z) or Nf(0) in the limit b→0, L=Nb→0. This convergence is readily seen using Eq. 3. As L becomes very small, the integral can be approximated by f(0)L, thence D_L(0)≈(1∕b)f(0)L=Nf(0), or formally as $\underset{L\to 0}{\text{lim}}{D}_L\left(0\right)=Nf\left(0\right)$.

The quantities b and L=Nb are dynamic variables of table∕phantom motion (and intimately coupled thereby); therefore, artificially constraining one or both in Eqs. 2, 3, 4 (such as fixing L in CTDI₁₀₀) will foil the convergence to Nf(0) as b→0, and thus negate its relevance to SCBCT. Neither Nf(z) nor Nf(0) contain nT, which has no relevance in SCBCT dosimetry.

The following important points are clear from the foregoing:

• (1)The integral of f(z) over (−L∕2,L∕2) for D_L(0)) in Eq. 3 and for CTDI_L in Eq. 4is solely the result of phantom translation over the distance L=vt₀=Nb; moreover, the integration limits ±L∕2 and the divisor of the integral (the table increment b=vτ) are necessarily coupled via L=vt₀=Nb (coupled by couch velocity v for helical scans).
• (2)The integral of f(z) over (−L∕2,L∕2) does not imply any averaging of the dose over the scan length L, but rather CTDI_L predicts the dose precisely at z=0 [at the center of the scan length (−L∕2, L∕2)] for helical scans at a pitch of unity.
• (3)Physically, this integral represents a summation of the decreasing incremental contribution to the dose at z=0 by the scatter tails of the traveling profile as it gets further from the origin. And it is this lateral dispersal of the dose profiles due to phantom translation which results in the central dose at z=0 reaching a limiting equilibrium value D_eq for large scan lengths.
• (4)CTDI always predicts the dose at (or about) the center of the scan interval (−L∕2,L∕2) at z=0.
• (5)For a stationary phantom (v→0, and b=vτ→0,L=vt₀→0), and since the integration length L→0, the integral format of Eqs. 2, 3, 4 “collapses,” smoothly converging in this limit to the nonintegral formD_L(z)=Nf(z), or D_L(0)=Nf(0), which increase without bound with N, since the individual dose profiles (deprived of lateral dispersal due to phantom translation) simply pile up on top of each other.

The properties (1)–(5) listed above also apply to axial scanning, which can be understood if one realizes that in this case, the integral over (−L∕2,L∕2) in Eqs. 3, 4 represents the smoothed version of the discrete summation ${\tilde{D}}_N\left(0\right)$ in Eq. 1.

In summary, for conventional CT scanning, CTDI_L [or any dose D_L(0)=p⁻¹CTDI_L derived from it] always represents the accumulated dose at (or about) the center of the scan length (−L∕2,L∕2) at z=0. This also applies to MSAD,⁴ CTDI_w (Ref. ⁹), and CTDI_vol, the latter two are essentially planar averages over the area of the central scan plane atz=0, since no averaging over the scan length L has been performed.

The case of the stationary phantom

The dose distribution produced by a single axial rotation of a wide cone beam or a narrow fan beam having a primary beam width (FWHM)=a (where a is also the projected z-collimator aperture setting) is denoted by f(z) as before, and by Nf(z) for N rotations without table translation, with a central ray peak dose Nf(0).

Relating the dose and the dose distribution in SCBCT to that of conventional CT,

• (1)The fact that CTDI_L represents the dose at the center (z=0) of the scan length (−L∕2,L∕2) in conventional CT suggests that its direct analog in the case of SCBCT would likewise be the dose Nf(0) at the center z=0 of the beam (−a∕2,a∕2) (on the “central ray” of the cone beam); corresponding to the location of the maximum or “peak” dose for both modalities.
• (2)This conclusion is further supported by the physics which suggests that there should be little difference in the dose distribution f(z) produced by a wide primary beam of width a (a cone beam) and the axial dose distribution ${\tilde{D}}_N\left(z\right)$ produced by a series of N adjacent, narrow primary beams of width $\widehat{a}=a∕N$, spaced at intervals $b=\widehat{a}=a∕N$, resulting in the same total energy deposition in the phantom as the cone beam, while “directly irradiating” (with the primary beam) the same length of phantom L=Nb=a.
• (3)Using the beam model of Eq. 7 and ${\tilde{D}}_N\left(z\right)$ in Eq. 1, it is straightforward to show that the dose distribution ${\tilde{D}}_N\left(z\right)$ for the axial scan series described in (2) above for $b=\widehat{a}=a∕N$ and L=a is equal to that for the cone beam of width a$\left[f\left(z\right)={\tilde{D}}_N\left(z\right)\right]$; moreover, since ${\tilde{D}}_N\left(z\right)$ is smooth (since $b=\widehat{a}$), the peak doses at z=0, $D_L\left(0\right)={\tilde{D}}_N\left(0\right)=f\left(0\right)$ are all equal.
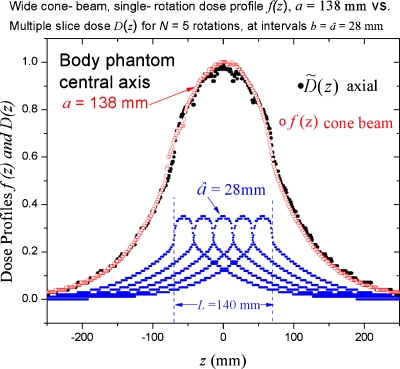
• (4)This correspondence is directly confirmed using the experimental data of Mori et al.¹ from a 256 channel cone beam CT system for which dose profiles for all available cone beam widths (apertures) a ranging from 28 mm (rounded up from 27.5 mm), up to a=138 mm were measured. Figure 1 depicts the comparison described in (2) and (3) above in which the axial dose distribution ${\tilde{D}}_N\left(z\right)$ produced by the superposition (summation) of N=5 axial profiles of width $\widehat{a}=28\text{\hspace{0.5em}mm}$, spaced at like intervals $b=\widehat{a}=28\text{\hspace{0.5em}mm}$, where L=Nb=140 mm is seen to be coincident with the a=138 mm cone beam distribution f(z) having a=L. (L=5×27.5 mm=138 mm exactly).
• (5)This provides a direct physical connection between the dose D_L(0)=p⁻¹CTDI_L in conventional CT (described using CTDI_L) and the corresponding dose f(0) in SCBCT, these doses being not only spatially colocated at z=0 but also equal in magnitude D_L(0)≈f(0), representing peak doses at z=0 in both cases as illustrated in Fig. 1.
• (6)Therefore, f(0) [or Nf(0) for multiple rotations] is the obvious choice to represent the dose for stationary phantom CT for wide cone beams (SCBCT) and narrow fan beams alike. In fact, f(0) is the only choice producing continuity between the two modalities. Use of any other “cone beam dose index” which predicted a dose other than f(0) would amount to the paradoxical assignment of different “dose values” to the same dose distribution [i.e., for the same length of anatomy imaged using the same x-ray technique].
• (7)It is also satisfying to note that the mathematics automatically forces the same conclusion, with the basic equations [Eqs. 1, 2, 3, 4], derived for conventional CT, all converging to the proper dose Nf(z) for a stationary phantom in the limit as table advance b→0 as previously shown, thereby losing their integral format [including CTDI_L→Nf(0), since b=nT is a table advance and likewise this b→0].

Figure 1.

The axial dose profile f(z) for a wide cone beam of widtha=138 mm generated by a single rotation about a stationary phantom (○) exhibits little difference from the accumulated dose distribution ${\tilde{D}}_N\left(z\right)$ (●) due to the superposition of N=5 axial profiles $\widehat{f}\left(z\right)$ having $\widehat{a}=28\text{\hspace{0.5em}mm}$ spaced at intervals (a table increment of) $b=\widehat{a}=28\text{\hspace{0.5em}mm}$, with a resulting a scan length $L=N\widehat{a}=140\text{\hspace{0.5em}mm}$; giving essentially the same directly irradiated length (L=a) as the cone beam having a=138 mm. The peak doses atz=0 are essentially equal, ${\tilde{D}}_N\left(0\right)\approx f\left(0\right)=1.0$, thereby corroborating the choice of f(0) to represent the dose for SCBCT.

Measurement of the central ray dose f(0) for a wide cone beam and a stationary phantom in SCBCT

• Since f(0) is the dose on the central ray of the cone beam at depth in the phantom, the obvious (and simplest) method is to directly measure f(0) at that point using a small ionization chamber (such as a 0.6 cc Farmer-type chamber), the same method used for decades to measure depth-dose in a stationary phantom.

• This same measurement method^{2, 3, 10, 11, 12} has also been utilized in conventional CT to directly measure the accumulated dose D_L(0) at z=0 during phantom translation over (−L∕2,L∕2); its validity and robustness having been thoroughly demonstrated;² and which method also offers considerable advantages over the fixed-length pencil chamber, namely, unrestricted integration length (scan length) L, as well as broad applicability to shift-variant phantoms and techniques since it represents a direct dose measurement rather than a dose inferred from an integral acquired by irradiation of a pencil chamber.

• A pencil chamber cannot be used to measure f(0) since it can only measure the integral of f(z), and thus cannot distinguish between dose profiles having the same area but differing peak (or central ray) doses f(0).

The equilibrium dose constant A_eq: A useful simplification obtained by setting the table advance b equal to the aperture a (b=a)

Returning to conventional CT scanning with phantom translation, an interesting and useful shortcut is described. Setting the scan interval b=a (where a closely approximates the primary beam FWHM) produces scan contiguity in the dose domain. Since D_eq is proportional to (a∕b), the equilibrium dose approached when b=a, denoted by A_eq=(b∕a) D_eq will depend on neither b nor a; and [using Eq. 5] A_eq can be written as

$$A_{\text{eq}}=\frac{1}{a}{\int }_{-\infty }^{\infty }f\left(z^{\prime }\right)d{z}^{\prime }=\text{constant}.$$ (6)

A_eq is a constant, independent of aperture a (and thence nT), since the integral is directly proportional to a as previously noted. For conventional CT, D_eq=(a∕b)A_eq, thus A_eq is the equilibrium dose for a table advance b=a (or a pitchp=a∕nT).

The equilibrium dose constant A_eq=(a∕nT)⁻¹CTDI_∞, although related to CTDI_∞, is not a proper CTDI, since b=a represents a detector pitch p=a∕nT>1 in MDCT for which a primary beam width a>nT is required to keep the penumbra beyond the active detector length nT (referred to as “overbeaming”) thus A_eq<CTDI_∞.

For conventional CT, overbeaming produces an increase in CTDI and accumulated dose by the factor a∕nT (as compared to a≈nT for single slice scanners); however, overbeaming has less significance in SCBCT, producing a smaller dose increase since there are no overlapping, adjacent dose profiles.

Note that the aperture a corresponding to a given nT can be calculated from the dose efficiency, which is essentially equal to the inverse of the overbeaming factor (a∕nT)⁻¹, and IEC standards¹³ now require the dose efficiency to be supplied in the scanner technical documents (the dose efficiency may also be provided on the scanner monitor for some models). Typical apertures have also been published^{2, 5} for the GE Lightspeed family of scanners. However, as noted above, (a∕nT)⁻¹ does not actually represent dose efficiency for stationary phantom CT (such as SCBCT). Use of A_eq allows a considerable reduction in data collection as will be illustrated, since its value can be fixed by making a measurement at single value of the aperture a.

Numerical analysis of experimental SCBCT dose data

The experimental data of Mori et al.¹ obtained on a 256 channel cone beam CT scanner includes a direct measurement of both the central ray dose f(0) as well as the infinite integral of the dose profile f(z) denoted by DPI_∞; whose data can be used to illustrate the magnitude by which the actual dose f(0) is overestimated should one attempt to apply CTDI_∞ to the problem (or by using CTDI₃₀₀, measured using a 300 mm long pencil chamber, to approximate CTDI_∞). As previously noted, nT has no relevance to the dose in stationary phantom CT (contiguity has no meaning and pitchp=b∕nT=0).

The analysis is both simplified and made considerably more interesting if one uses A_eq from Eq. 6 as a “surrogate” for CTDI_∞, where A_eq=(a∕nT)⁻¹CTDI_∞<CTDI_∞.

Table 1 illustrates the relationship between the measured central ray dose f(0) and A_eq for various beam widths (aperture values) ranging from a=28–138 mm, resulting from a single axial rotation about the center (z=0) of a 900 mm long, 32 cm diameter, stationary PMMA body phantom.¹

Table 1.

Measured cone beam doses and dose integrals resulting from a single axial rotation about a stationary phantom (no table advance) for a 256 channel scanner (SCBCT) based on the data of Mori et al. (Ref. ¹), where f(z) denotes the axial dose profile corresponding to a primary beam width a on the central axis of the PMMA body phantom (32 cm diameter, 900 mm length), integrated over 900 mm to obtain the dose profile integral DPI_∞, all data being normalized per 100 mAs [measured data (Ref. ¹)–central axis, body phantom].

Primary beam aperture a or FWHM (mm)	Dose profile integral${\text{DPI}}_{\infty }={\int }_{-\infty }^{\infty }f\left(z\right)dz$	Equilibrium dose constantAeq=DPI∞∕a$=1∕a{\int }_{-\infty }^{\infty }f\left(z\right)dz$	Measured central ray dosef(0)	RatioAeq∕f(0)
138 mm	848 mGy  mm	6.14 mGy	4.37 mGy	1.43
111	686	6.18	3.90	1.58
80	498	6.22	3.19	1.95
49	303	6.18	2.27	2.72
28a	169	6.15	1.53	4.02

^aRounded off from 27.5 mm.

The original raw data¹ were reanalyzed to deduce the effective apertures a using the equivalent width¹⁴ of the primary beam profiles as measured free-in-air¹ [a≈width at 1∕2f(0)].

Thus the equilibrium dose constant A_eq=(b∕a)D_eq is indeed seen to be independent of aperture a as previously postulated, remaining constant to better than ±0.7% over the entire range of apertures from a=28–138 mm; whereas CTDI_∞=(a∕nT)A_eq varies by a factor of 2.5 over the same range (corresponding nT values are 10, 32, 64, 96, and 128 mm); however, the important point is that A_eq significantly overestimates the relevant SCBCT dose f(0) by the factor shown in the last column of Table 1, viz., by a factor of 4 for a beam width of a=28 mm, by a factor of 2 fora=80 mm, and by a factor of 1.4 for a=138 mm, with CTDI_∞ giving an even larger overestimate (since a>nT). This result was previously anticipated since neither A_eq nor CTDI_∞ (described by integral equations) are relevant to the dose in stationary phantom CT (e.g., SCBCT).

The data in Table 1 are also illustrative of the magnitude of the error obtained in SCBCT when using a pencil chamber of length ℓ=300 mm to measure CTDI₃₀₀ (as an approximation to CTDI_∞) as illustrated by the following Gedanken experiment. Assume a cone beam width a=115 mm corresponding to nT=100 mm. By definition, CTDI₃₀₀ is equal to the dose at the center of three contiguous axial scans, each with nT=100 mm, stitched together using an interval (a table advance) of b=nT=100 mm, for a total scan length of L=Nb=300 mm. In this case CTDI₃₀₀ overestimates the SCBCT peak dose f(0) by about 60%, due to scatter from the two additional contiguous scans which augment the dose f(0) at z=0 [CTDI₃₀₀=1.6f(0)].

The notion that the integral equations for CTDI_∞ or A_eq might predict some useful average dose for SCBCT is readily dispelled; since it is clear from the data in Table 1 and Fig. 1, that A_eq and thus CTDI_∞ (and CTDI₃₀₀) are both larger than the peak dose f(0) for every available aperture setting, i.e., their associated dose values do not exist anywhere in the phantom. Mathematically, in order to obtain f(0) from ${\int }_{-\infty }^{\infty }f\left(z\right)dz$, one must divide the integral by the equivalent width¹⁴a_w of the function; however, since f(z) contains a broad scatter component, a_w is larger than the primary beam widtha (or nT) used as divisors in computing A_eq (or CTDI_∞) [e.g., for the a=28 mm profiles shown in Fig. 1, a_w=112 mm, for which A_eq overestimates f(0) by a factor of (a_w∕a)=4.]. Thus A_eq (or CTDI_∞) will always overestimate f(0). So why do we divide the integral by the primary beam width? We do not—These divisors represent table incrementsb=a for A_eq (or b=nT for CTDI) and not primary beam widths (actual or nominal). The CTDI paradigm was never intended to predict the dose f(0) for a single axial rotation, but rather the accumulated dose D_L(0) at z=0 for N multiple scans, spaced at intervals b due to table translation over a length L=Nb.

A small ion chamber can precisely measure the desired peak dose f(0)=1.0 in Fig. 1, whereas the “dose” values given by the “CTDI types” are A_eq=1.4, CTDI_∞=1.5, and CTDI₃₀₀=1.4, all lying well above the peak dose f(0)=1.0 (even above the top of Fig. 1).

Since A_eq is independent of aperture a, a narrow beam can be used to measure A_eq if the aperture a is known; however, this is small consolation since the values of both A_eq and CTDI_∞ overestimate the dose f(0) in SCBCT for clinically relevant cone beam widths (see Table 1). The SCBCT dose f(0) would exhibit a variation of more than 200% (a factor of 2.3) over the range of beam widths a=50–180 mm available for clinical use on the aforementioned 320 channel SCBCT scanner (corresponding to nT=40–160 mm); and a much larger variation in the case of narrow fan beams also used in stationary phantom CT such as in CT fluoroscopy or perfusion studies [for which the peak dose f(0) may be significantly overestimated¹⁵ by attempting to apply the dose paradigm based on CTDI₁₀₀ [we note that the IEC definition¹³ of CTDI_vol utilizes N×CTDI₁₀₀ compared to the actual dose Nf(0)].

It is therefore important to determine f(0) over the complete range of apertures used clinically in the SCBCT acquisition mode, e.g., for (40 mm≤nT≤160 mm). A useful theoretical function is derived in Sec. 3 describing the variation in f(0) with a, which closely matches the data in Table 1; and which can be used to extrapolate a measurement of f(0) at a single value of aperture a to any other aperture; thus allowing the prediction of the peak doses f(0) for narrow fan beams which would require an ion chamber length ℓ<nT for the central axis measurement.

The approach to scatter equilibrium

From the data in Table 1, it appears that f(0) is increasing towardA_eq as the cone beam width a increases, and such a convergence does indeed occur, but only for very wide (and thus clinically irrelevant) cone beam widths of a≥470 mm. Like the accumulated dose D_L(0) in conventional CT, the SCBCT dose f(0) will also asymptotically approach a maximum equilibrium value f_eq(0) when the cone beam width a becomes wide enough to achieve scatter equilibrium on the central ray at z=0, such that scatter produced from any further increases in primary beam width can no longer reachz=0, and thus no longer affect f(0). Attainment of equilibrium at z=0 depends only on the distance of the outermost primary beam photons from the origin. When the probability becomes negligible that primary photons scattered at the far-flung primary beam edges (at z^′=±a∕2 for the cone beam or at z^′=±L∕2 in conventional CT) can reach the origin, then equilibrium is achieved for cone beam widths a≥a_eq, and likewise for scan lengths L≥L_eq for conventional CT, thus it follows that a_eq=L_eq. Likewise, the magnitude of the equilibrium dose constant A_eq is the same for both modalities. (These results follow from our previous arguments demonstrating the equality of the dose at z=0 for the two modalities for the case L=a.)

Since L_eq≈470 mm in conventional CT,¹⁶ scatter equilibrium at z=0 will therefore occur for cone beam widthsa≥470 mm in the 32 cm PMMA body phantom. However, since such wide cone beams are not utilized (nor likely to be) in this modality, the cone beam equilibrium dosef_eq(0)=A_eq is not clinically relevant for SCBCT; whereas, for conventional CT scanning, typical body scan lengths ofL≥250 mm produce doses which closely approach D_eq; therefore D_eq or CTDI_∞ [and likewise A_eq=(b∕a) D_eq)] is a considerably more relevant dose for this modality. However, the value of A_eq can serve as a convenient, common normalization constant for both modalities.

The approach to equilibrium function H(λ)

The variation in the relative approach to equilibrium function H(a)=[f(0)∕f_eq(0)] is conceptually quite similar to the increase in dose at a given depth with increasing field size observed for a stationary x-ray beam incident on a phantom (except only one field dimension a is varied in this case). In fact, the SCBCT equilibrium dose is the same as A_eq for conventional CT, viz. f_eq(0)=A_eq; and the relative approach to equilibrium curves H(L)=D_L(0)∕D_eq and H(a)=f(0)∕A_eq should be the same using the correspondence a=L, based on our previous analogy between a cone beam and a juxtaposition of adjacent narrow fan beams.

MODELING THE CONE BEAM

For definiteness and simplicity, all numerical examples and derivations refer to the dose on the central axis of the 32 cm diameter cylindrical PMMA body phantom at 120 kVp using a bow-tie filter unless otherwise noted. The peripheral axis is dealt with in Sec. 4.

General considerations

As previously seen in Fig. 1, there is nothing particularly mysterious about the SCBCT axial dose profile f(z) for a wide cone beam of width a, being quite similar to the cumulative dose distribution D_L(z) in conventional CT at a pitch near unity $\left(p=\widehat{a}∕nT\right)$ for the same directly irradiated phantom length L=a. Differences in beam divergence between the narrow beams and wide cone beam are quite small (only about ±7° deg from the central ray at the extreme edgesz=±a∕2 of the widest cone beam, a=138 mm).

The heel effect

The only real difference is that the wider collimator aperture of the cone beam enhances the heel effect; however, neither its odd nor its even components⁵ have any significant effect on the central ray dose f(0) [the SCBCT dose-descriptor of interest], with both the primary and the scatter components at z=0 being essentially unaffected. Thus, a simple model which ignores anode tilt and the heel effect should do quite nicely for predicting the relevant SCBCT dose f(0), but may do somewhat less well in reproducing the entire dose distribution f(z), particularly near the beam edges for wide cone beams on the peripheral axes. It also produces the same results as a more complex model⁵ (including anode tilt and the heel effect) for the integral theorems involving A_eq and D_eq.

A simple beam model predicting the observed dose data

The primary beam LSF is the focal spot emission intensity⁵ (as slit-projected by the z-collimators onto the AOR), and expressed as a scaled function lsf(z)=c⁻¹g(−z∕c) having unit area, where c represents the slit-projected focal spot length (c∼3 mm).

The scatter LSF (z−z^′) is the much broader scatter response function to a unit-strength primary beam impulse δ(z^′) (or “knife edge”) applied at z=z^′, where η is the scatter to primary ratio S∕P, where η is equal to the ratio of scattered to primary energy deposited along z as expressed by the ratio η=S∕P, where $S={\int }_{-\infty }^{\infty }{f}_s\left(z^{\prime }\right)d{z}^{\prime }$ and$P={\int }_{-\infty }^{\infty }{f}_p\left(z^{\prime }\right)d{z}^{\prime }$. Thus ${\int }_{-\infty }^{\infty }\text{LSF}\left(z\right)dz=\eta$, and it is convenient to express LSF(z)=ηlsf(z) where lsf(z) is a unit-area scaled function, symbolically represented as lsf(z)=d⁻¹h(z∕d), where d represents the width of the broad scatter LSF (d∼100 mm) and where d⪢c.

The model generates the primary beam component f_p(z) and the scatter component f_s(z) of the axial dose profile f(z)=f_p(z)+f_s(z) by the convolution shown below

$$f\left(z\right)=\left[\frac{1}{c}g\left(\frac{-z}{c}\right)+\eta \frac{1}{d}h\left(\frac{z}{d}\right)\right]\otimes A_0\Pi \left(\frac{z}{a}\right),$$ (7)

where A₀Π(z∕a) represents the core primary beam function (without penumbra). The convolution of the focal spot lsf[c⁻¹g(−z∕c)] with A₀Π(z∕a) produces the primary beam function f_p(z) by adding a penumbra of width c to Π(z∕a), and the convolution of the scatter LSF(z)=ηlsf(z)=ηd⁻¹h(z∕d) with the primary beam core A₀Π(z∕a) gives the scatter component f_s(z), where the negligible effect of the primary beam penumbra on the scatter distribution has been ignored (its effect is truly nil).

Since in MDCT the penumbra c is necessarily small compared to the aperture setting a, the width c of the penumbra added to Π(z∕a) by its convolution with c⁻¹g(−z∕c) is small compared to a (c⪡a), in which case A₀=f_p(0) which is the “point dose” on the central ray (z=0) contributed by the primary beam at isocenter (at a depth of 16 cm in the body phantom) [as the aperture a is decreased to a value comparable to the penumbra c, the beam FWHM actually increases, becoming larger than a and its peak intensity f_p(0) decreases below the emitted intensity A₀ due to narrow slit effects⁵. This effect required postpatient collimation to achieve narrow slice widths for single slice scanners].

The integral theorem

The expression for the infinite integral of f(z), and thence the equilibrium dose constant A_eq in Eq. 6 (or CTDI_∞), immediately follows from Eq. 7 without requiring any detailed knowledge of the functional form of f(z) (or that of either lsf); the infinite integral of the convolution in Eq. 7 being obtained by inspection as

$${\int }_{-\infty }^{\infty }f\left(z^{\prime }\right)d{z}^{\prime }=A_0\left(1+\eta \right)a=f_p\left(0\right)\left(1+\eta \right)a,$$ (8)

which shows the important proportionality of the infinite integral of f(z) to the aperture a, and also providing the theoretical formula for A_eq shown below

$$A_{\text{eq}}=\frac{1}{a}{\int }_{-\infty }^{\infty }f\left(z^{\prime }\right)d{z}^{\prime }=A_0\left(1+\eta \right)=f_p\left(0\right)\left(1+\eta \right),$$ (9)

thereby confirming the constancy of A_eq, namely, its independence of aperture setting a (and also of nT). Equation 9 shows that A_eq depends only on the primary beam intensity f_p(0) on the central ray, which is well-known to be independent of collimator setting (assuming a>c), and on the S∕P ratio η (since η is also the impulse-response amplitude, it cannot depend on a); and also confirms that A_eq is the same for conventional CT and SCBCT.

The equilibrium dose for conventional CT can be written as D_eq=(a∕b) A_eq, which is directly proportional to (a∕b) since A_eq is a constant (physically, opening the collimator aperture a deposits more energy per rotation, and reducing b packs the dose profiles into a smaller length, both leading to an increase in dose). Thus D_eq for conventional CT can have different values, depending on both the aperture a (and thence nT) and the table increment b (or helical pitchp=b∕nT), and D_eq=A_eq only for a table advance of b=a; however, for SCBCT the scatter equilibrium limit for the dose f(0) is always A_eq (a constant).

The constancy of A_eq predicted by this model remains valid even for wide cone beams, as clearly illustrated by the experimental data in Table 1. This broad general result follows physically from the conservation of energy, the total amount of energy escaping the collimator, impinging on the phantom, and absorbed in the phantom is directly proportional to the aperture a which acts as an energy gate; thus the constancy of A_eq holds along any phantom axis, central or peripheral. Note also that the infinite integrals of the primary beam and scatter components are both (separately) proportional to aperture a, thus a free-in-air measurement² of CTDI_∞ (air) is proportional to a and thus can provide the relative variation of aperture a with nT.

Relation between A_eq and the total energy deposited in the phantom (integral dose)

For an axial or helical scan series, the total energy E deposited (absorbed) in the phantom along a given z-axis is represented by the infinite integral of $\tilde{D}\left(z\right)$ in Eq. 1, or of D_L(z) Eq. 2, either resulting in $E=N{\int }_{-\infty }^{\infty }f\left(z\right)dz=N{A}_{\text{eq}}a$; the same formula as for the total energy deposited by N rotations about a stationary phantom (as for SCBCT) for which the dose distribution is Nf(z). With good reason, the total energy deposited by N rotations is independent of their spread or distribution along z and depends (for a given kVp and bow-tie filter) only on the product of N×(mAs per rotation)×(aperture a), or simply on the product of (total mAs)×(aperture a); and the total energy E deposited is the same whether the table moves or not (which likewise applies to the DLP⁹).

Calculation of the relevant stationary phantom peak dose f(0) using this model

To obtain the desired dose f(0), we evaluate f(z) in Eq. 7 at z=0, which is a simple task for the primary beam intensity A₀ which is given by f_p(0)=A₀ for the case where a>c; however, for the scatter component, neither d nor a dominate sufficiently, and the convolution gives a scatter component of

$$f_s\left(z\right)=A_0\eta {\int }_{-\infty }^{\infty }{d}^{-1}h\left(\frac{z-z^{\prime }}{d}\right)\Pi \left(\frac{z^{\prime }}{a}\right)d{z}^{\prime }=A_0\eta {\int }_{-a∕2}^{a∕2}{d}^{-1}h\left(\frac{z-z^{\prime }}{d}\right)d{z}^{\prime }.$$ (10)

Since our goal is to determine the central ray dose f(0) in the stationary phantom which is used as the dose-descriptor for SCBCT, setting z=0 in Eq. 10 to obtain f_s(0) and adding the primary beam component f_p(0)=A₀ to the scatter component, f(0)=f_p(0)+f_s(0), the total central ray dose is given by

$$f\left(0\right)=f_p\left(0\right)\left[1+\eta \frac{1}{d}{\int }_{-a∕2}^{a∕2}h\left(\frac{z}{d}\right)dz\right].$$ (11)

If a⪢d, the above integral is essentially infinite, and f(0)=f_p(0)(1+η)=A_eq, corresponding to scatter equilibrium being attained at z=0.

The scatter LSFs exhibit surprising simplicity

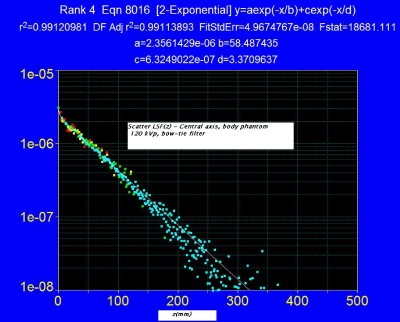
Further results from this model require a more detailed knowledge of the scatter LSF(z)=ηlsf(z) on the phantom axis. To that end, Boone¹⁷ has recently performed Monte Carlo (MC) dose simulations in a variety of cylindrical phantoms (with and without bowtie filters); and more importantly has provided the data in their most useful and concise form, namely, as a scatter LSF which can be used as a “kernel” in the integral expressions derived above to calculate f(0) [as well as f(z)] for any beam width a, without requiring any additional MC simulations. Moreover, these scatter LSFs exhibit a surprising simplicity, asymptotically approaching a pure, single-exponential of the form exp(−μ_rz) a few cm beyond z=0, thus allowing the theoretical results to be expressed as simple analytical functions.

Figure 2 shows the scatter LSF(z) obtained by Boone¹⁷ for the central axis of a 32 cm diameter PMMA phantom of infinite length at 120 kVp with bow-tie filter, this function being readily fit by a double-exponential decay as shown. Only half of the even function LSF(z)=LSF(−z) is shown.

Figure 2.

Scatter LSF, central axis 32 cm diameter PMMA body phantom with double-exponential fit function (arbitrary units). Data from a Monte Carlo simulation (Ref. ¹⁷) at 120 kVp with a body bow-tie filter.

Renormalizing the scatter LSF function fit parameters shown in Fig. 2 to conform to our notation (using scaled, unit-area lsf functions), where LSF=η×lsf(z), it becomes

$$\text{lsf}\left(z\right)=\left(1-\epsilon \right)\frac{1}{d}\text{exp}\left(-2\left|z\right|∕d\right)+\epsilon \frac{1}{\delta d}\text{exp}\left(-2\left|z\right|∕\delta d\right),$$ (12)

where d=117 mm, δd=6.74 mm=.0576d, and where (1−ε)=0.985 and ε=0.015 are the respective areas of the asymptotic first term, and the transient second term; and where the S∕P ratio¹⁷ is η=13 for the central axis of the body phantom. The transient second term in Eq. 12 becomes negligible for z>10 mm, after which the lsf reaches its single-exponential asymptotic form, which when written as exp(−μ_rz), corresponds to a value of μ_r=0.17 cm⁻¹.

The transient second term in Eq. 12 produces little effect for cone beams (or beams having widths a>20 mm), and the lsf can be approximated quite well in this case by the first term of Eq. 12 as a single-exponential (renormalized to unit area), namely, as

$$\text{lsf}\left(z\right)=d^{-1}h\left(z∕d\right)\cong d^{-1}\text{\hspace{0.17em}exp}\left(-2\left|z\right|∕d\right)$$ (13)

in which d=117 mm.

Derivation of the equation for the peak dose f(0) using the scatter LSF

Substitution of the simplified Eq. 13 into Eq. 11 and integrating yields

$$f\left(0\right)\cong f_p\left(0\right)\left[1+\eta \left(1-e^{-a∕d}\right)\right].$$ (14)

Using the more accurate double-exponential fit to the lsf given by Eq. 12, which is more appropriate (more accurate) for narrow fan beams, gives

$$f\left(0\right)=f_p\left(0\right)\left\{1+\eta \left[\left(1-\epsilon \right)\left(1-e^{-a∕d}\right)+\epsilon \left(1-e^{-a∕\delta d}\right)\right]\right\}.$$ (15)

Both Eqs. 14, 15 approach the same limiting dose value for a⪢d, f(0)→f_p(0)[1+η]=A_eq, and for all practical purposes (within 2%) when a≥a_eq=4d=470 mm [from e^−a∕d=e⁻⁴=0.018 in Eqs. 14, 15]. Although this expression for A_eq=f_p(0)[1+η] was previously obtained in Eq. 8 using the convolution integral theorem, this model provides a clear physical insight and a functional form (an exponential growth function) describing the approach of f(0) toward its (unattainable) equilibrium value A_eq, clearly illustrating that this occurs only in the limit where the cone beam width a itself becomes large with respect to the widthd=117 mm of the scatter LSF, namely, for a≥4d=470 mm. For a primary beam width a=4d, a primary photon scattered at the extreme edges of the beam z=±a∕2 has only a negligible chance of getting back to z=0 to contribute to the center dose f(0) [a survival probability of exp(−μ_ra∕2)=e⁻⁴]. The same LSF and thus the same argument applies to conventional CT; a primary photon scattered from the extremes of the scan length at z=±L∕2 whereL=4d has exactly the same chance (e⁻⁴) of making it back to z=0 to contribute to D_L(0); therefore, the equilibrium lengths are identical for the two modalities, i.e., L_eq=a_eq=4d=470 mm on the central axis.

Although A_eq (like CTDI) does not represent a meaningful or relevant dose value for SCBCT, it has utility as a convenient normalization constant for the common approach to equilibrium function H(λ), which becomes H(L) for conventional CT and H(a) in stationary phantom CT.

The approach to equilibrium function H(a)

The relative “approach-to-equilibrium” function H(a)=f(0)∕A_eq for the stationary phantom using the more general Eq. 15 is given by

$$H\left(a\right)=\frac{1}{1+\eta }+\frac{\eta }{1+\eta }\left[\left(1-\epsilon \right)\left(1-e^{-a∕d}\right)+\epsilon \left(1-e^{-a∕\delta d}\right)\right].$$ (16)

The first term 1∕(1+η) represents the relative primary beam contribution and the second term the relative scatter contribution; however, since δd=6.74 mm, the transient scatter term grows very quickly to its small limiting value ε=0.015 for a>25 mm, representing only 1.5% of the total scatter at equilibrium.

A simplified form of H(a) applicable to the wider beams of SCBCT is obtained using the single-exponential scatter lsf in Eq. 13 which produces f(0) in Eq. 14, and which in turn gives.

$$H\left(a\right)\cong \frac{1}{1+\eta }+\frac{\eta }{1+\eta }\left(1-e^{-a∕d}\right).$$ (17)

The second term in both equations represents the scatter contribution which has the form of an exponential growth curve, increasing with beam width a until reaching its asymptotic (equilibrium) limit H(a)→1 for a≥4d≈470 mm, the fractional scatter contribution at equilibrium being η∕(1+η) and the relative primary contribution 1∕(1+η).

The commonality of the approach to equilibrium function H(a) for both stationary phantom scanning (e.g., SCBCT) and conventional CT scanning

Note that the same scatter LSF function applies both to stationary beam CT and conventional axial or helical CT [usable in both cases to create an axial dose profile f(z) in Eq. 7]; however, this profile must additionally be integrated over (−L∕2,L∕2) for conventional CT to obtain the accumulated dose D_L(0) at z=0 [Eq. 3] or CTDI_L [Eq. 4], resulting in the additional dependence of the equilibrium dose D_eq in conventional CT on the table increment b (or pitchp=b∕nT) and aperture a, i.e., D_eq=(a∕b)A_eq is proportional to (a∕b) as noted previously. The integral theorem [Eq. 9] shows that the equilibrium dose constant A_eq=(b∕a)D_eq=f_p(0)(1+η) has the same value for both SCBCT and conventional CT, being independent of aperture a (and scan length L).

The cone beam dose f(0) necessarily approaches the same equilibrium dose value f_eq(0)=A_eq with increasing aperture setting a (although it will never get there for practical cone beam widths).

Comparing SCBCT with aperture a to conventional CT with N rotations of aperture $\widehat{a}=a∕N$ and $b=\widehat{a}$ for whichL=Nb=a, it was previously shown (and observed in Fig. 1) that D_L(0)=f(0). Therefore, since f(0)_a=D_L(0) for L=a, then H(L)A_eq=H(a)A_eq, thus H(L)=H(a) for L=a; hence a common function H(λ) applies to both modalities with λ=L or λ=a.

The function H(L) is essentially independent of aperture,^{5, 16} since both D_eq and D_L(0) are proportional to $\widehat{a}$ [rigorously in the case of D_eq and approximately⁵ for D_L(0)] at least over an aperture range corresponding to (2.5 mm≤nT≤40 mm). Boone¹⁶ has shown that H(100 mm)=[CTDI₁₀₀∕CTDI_∞]=[D₁₀₀(0)∕D_eq] varies by less than 1% over this range of apertures.

Comparison of the theoretical equation for H(a) with experiment

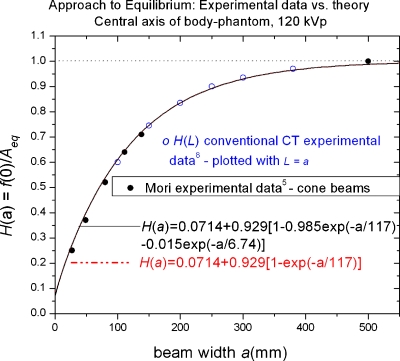
Does our mathematical model of the dose profilef(z), correctly predict the measured¹ variation in f(0) with aperture a given in Table 1? Or equivalently, does the derived analytic function H(a)=f(0)∕A_eq given by Eq. 16 [or approximated by Eq. 17 for cone beams] agree with the observed ratio computed from the experimental data¹ in Table 1? Figure 3 answers this affirmatively illustrating the excellent agreement between the theoretical predictions of Eqs. 16, 17 (the curves) and the experimental values¹ of the relative, stationary phantom peak doses f(0)_a shown by the solid data points (•)It should be emphasized that this is not empirical curve fitting, but rather comparing a physical theory having no adjustable parameters as embodied by Eq. 16 to the observed experimental data, thereby giving added confidence in its general applicability.

Figure 3.

Approach to scatter equilibrium theory vs experiment. Relative approach to equilibrium function H(a)=f(0)∕f_eq(0)=f(0)∕A_eq on the central axis of a stationary phantom (e.g., SCBCT). The solid circles (●) are the experimental data of Mori¹ presented in Table 1. The solid and dashed lines representing H(a) are not empirical fits but rather theoretical predictions obtained from the mathematical model; the solid black line representing the full double-exponential scatter lsf Eq. 16, and the essentially congruent dotted-dashed line using the simpler single-exponential approximation of the scatter lsf Eq. 17. Also plotted is the experimental approach to equilibrium data for conventional CT scans measured² on GE 16 channel and 64 channel scanners for scan lengths L from 100 to 400 mm, and plotted (○) using the correspondence L=a; thus validating the same functional form for both modalities, H(L)=H(a) with the correspondence a=L.

The single-exponential approximation of the lsf in Eq. 13 leading to the simple growth curve H(a) of Eq. 17 is indistinguishable from the double-exponential form of the lsf which produces H(a) in Eq. 16 also shown in Fig. 3.

The premise that the same function H(a) can also predict the variation in the accumulated dose D_L(0) at z=0 with scan length L for conventional CT simply by making the substitution L=a in Eq. 17 is also confirmed by plotting experimental values² of H(L) measured using helical scans on 16 and 64 channel GE scanners (open circles in Fig. 3), which data also fall on the theoretical curves, thereby confirming this premise, at least over the measurement range used (100 mm≤L≤400 mm). It should be noted, however, that H(L) refers to the variation in dose in a phantom at least 500 mm long, and cannot be used without correction to extrapolate CTDI₁₀₀ measured in a standard 140 mm long body phantom to predict CTDI_∞, or D_eq=p⁻¹CTDI_∞ (e.g., an increase in body phantom length from 150 to 400 mm was observed² to produce an increase in the measured value of CTDI₁₀₀ by 7.3% on the central axis and by 1.3% on the peripheral axis at 120 kVp).

Extension to peripheral axes

Due to the potential practical utility of the derived analytical functions, it behooves us to make a similar (but abbreviated) analysis for the peripheral axis of the same body phantom (a more complex problem).

That A_eq as defined in Eq. 6 is likewise a constant (independent of aperture a) on the peripheral axis is confirmed using the experimental data of Mori¹ as shown in Table 2.

Table 2.

Mori (Ref. ¹) data for the peripheral axis of the body phantom.

Primary beam aperture a or FWHM (mm)	Dose profile integral${\text{DPI}}_{\infty }={\int }_{-\infty }^{\infty }f\left(z\right)dz$	Equilibrium dose constantAeq=DPI∞∕a$=1∕a{\int }_{-\infty }^{\infty }f\left(z\right)dz$	Measured central ray dosef(0)	RatioAeq∕f(0)
138 mm	1520 mGy mm	11.0 mGy	9.60 mGy	1.14
111	1220	11.0	9.02	1.21
80	900	11.1	8.54	1.28
49	530	10.6	8.06	1.35
28a	290	10.6	7.34	1.49

^aRounded off from 27.5 mm.

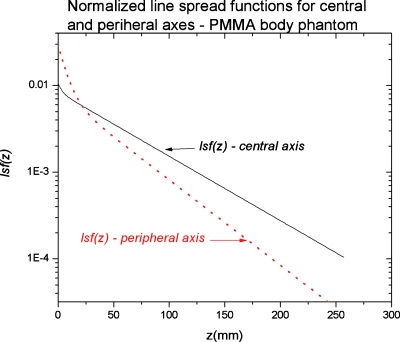
The normalized (to unit area) lsfs for the central and peripheral axes are both shown in Fig. 4 for comparison. The double-exponential fit proved reasonably successful for the peripheral axis, resulting in the lsf fit parameters of ε=0.304, δd=14 mm, and d=88 mm which, together with η=1.5, give a scatter LSF as described by Eq. 12.

Figure 4.

Scatter lsf for the central and peripheral axes in a 32 cm diameter PMMA phantom normalized to unit area. The actual LSF=η×lsf, where η=S∕P ratio with η=13 for the central axis and η=1.5 for the peripheral axis (Ref. ¹⁷); thus the absolute peripheral axis LSF falls below that for the central axis as expected.

Derivation of the expression for f(z) and f(0) on the peripheral axis using the LSF

As discussed previously,⁵ the convolution model [Eq. 7] strictly holds only for a fixed gantry angle θ on a peripheral axis, since the parameters η, a, c, the lsf, and A₀=f_p(0) are all functions of beam angle θ; thus Eq. 7 must be written as f(z,θ) and then averaged (integrated) over 2π in order to obtain the axial dose profile f(z) on the peripheral axis, thereby losing the convolution format for f(z) and possibly the applicability of the LSF (also mentioned by Boone¹⁷). However, as shown in Appendix A, if θ=0 denotes the gantry angle for which the beam is directly incident on the peripheral axis in question, then most of the dose on that axis is delivered for a small enough angular range ±Δθ about θ=0, such that a(θ) is slowly varying over ±Δθ and can be replaced by its average value ⟨a⟩, which is the FWHM of the axial dose profile a^′=⟨a⟩ on the peripheral axis [and which is only about 5% greater⁵ than the minimum value of a(θ) at θ=0]. Thus Eq. 15 for f(0) and Eq. 16 for H(a) also apply, with a replaced by a^′, and using the corresponding peripheral axis (double-exponential) fit parameters ε=0.304, d=88 mm, and δd=14 mm, and a S∕P ratio of η=1.5.

$$H\left(a^{\prime }\right)=\frac{1}{1+\eta }+\frac{\eta }{1+\eta }\left[\left(1-\epsilon \right)\left(1-e^{-a^{\prime }∕88\text{\hspace{0.5em}mm}}\right)+\epsilon \left(1-e^{-a^{\prime }∕14\text{\hspace{0.5em}mm}}\right)\right].$$ (18)

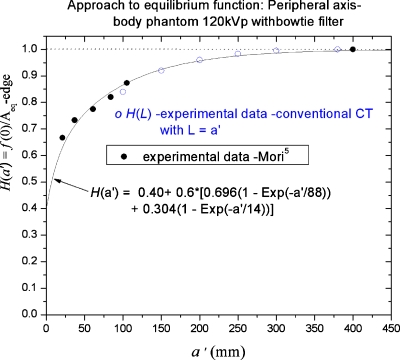
The parameter a^′, the FWHM of the peripheral axis profile f(z) which automatically appears in the peripheral axis equations for f(0) and in H(a), is the physically significant parameter for comparing modalities on the peripheral axis, i.e., an axial scan series using beams of width a^′∕N at a like scan interval b=a^′∕N with L=Nb=a^′ will produce a relatively smooth dose distribution (without gaps) on the peripheral axis which is comparable to a cone beam distribution f(z) of width a^′. Figure 5 shows the relative stationary phantom, peripheral axis peak dose experimental data¹ in Table 2 plotted vs a^′=0.76a compared to the theoretical curve H(a^′) in Eq. 18. Likewise, the experimental conventional peripheral axis CT data²H(L) is plotted using the correspondenceL=a^′, with both data sets exhibiting reasonably good agreement between experiment and the theoretical curve H(a^′) in Eq. 18.

Figure 5.

Approach to equilibrium function H(a^′) on the peripheral (edge) axis of the body phantom plotted vs the FWHM a^′ of the cone beam dose profile f(z) on that axis, together with the experimental data of Mori (Ref. ¹) and helical scan data (Ref. ²) plotted using L=a^′.

Since a^′ is proportional to the central axis aperture projection a, either could be used to evaluate A_eq as noted in Appendix A (it is independent of aperture), and it is more convenient to work with a and H(a) as was done in Table 2. By substituting a=a^′∕0.76 into H(a^′) we obtain

$$H\left(a\right)=\frac{1}{1+\eta }+\frac{\eta }{1+\eta }\left[\left(1-\epsilon \right)\left(1-e^{-a∕116}\right)+\epsilon \left(1-e^{-a∕18.4}\right)\right],$$ (19)

where now d=88∕0.76=116 mm, δd=14∕0.76=18.4 mm, with ε=0.305 and η=1.5 as before. (It is interesting thatd=116 mm which determines asymptotic equilibrium is essentially the same as on the central axis where d=117 mm.) Of course, H(a) in Eq. 19 is completely equivalent to H(a^′) in Eq. 18 in which d=88 mm and δd=14 mm.

For comparison with conventional CT we must still substitute L=a^′ into H(a^′) in order to obtain

$$H\left(L\right)=\frac{1}{1+\eta }+\frac{\eta }{1+\eta }\left[\left(1-\epsilon \right)\left(1-e^{-L∕88}\right)+\epsilon \left(1-e^{-L∕14}\right)\right],$$ (20)

where H(L)=D_L(0)∕D_eq and D_eq=(a∕b)A_eq.

The reason Eqs. 18, 19 differ in form but not substance is that the scan length L does not diverge (it is the same for the central and peripheral axes), whereas the beam width a does diverge. We have chosen to work with a rather than a^′ simply for convenience. Note that dose equilibrium is approached to within 2% on the peripheral axis (our central axis criterion) for $a_{\text{eq}}^{\prime }=L_{\text{eq}}=300\text{\hspace{0.5em}mm}$, and a_eq=400 mm (compared to L_eq=a_eq=470 mm on the central axis).

Generating the complete data set for conventional and stationary phantom CT from a single measurement of the peak dose f(0) resulting from a single axial rotation—An example

For added clarity, the peak axial profile dose f(0) is parametrized in the following with the aperture a (primary beam width) as f(0)_a and the experimental data of Mori¹ for a 32 cm diameter PMMA body phantom are utilized. We will presume for illustrative purposes that only a single measurement of f(0)_a has been made at a single aperture setting a, using a single axial rotation about a small ion chamber (e.g., a Farmer-type chamber) in a stationary phantom. The strategy is then to determine the value of A_eq by inverting the relation

$$f{\left(0\right)}_a=H\left(a\right)A_{\text{eq}}$$ (21)

and applying the analytical functions derived for H(a) in Eqs. 16, 19. Having obtained A_eq, we can then predict the desired stationary phantom dose f(0)_a for any aperture a from Eq. 21 for the wide cone beams of SCBCT and the narrow fan beams of perfusion studies (or for any procedures using a stationary phantom).

But recall, we also showed that the same equilibrium dose A_eq applies to conventional axial or helical CT using phantom∕table motion for a scan interval $b=\widehat{a}$ or a pitch $p=\widehat{a}∕nT$. Thus, we can parlay the peak dose f(0)_a value acquired using a single axial rotation about a stationary phantom with a conventional short ion chamber into the conventional CT equilibrium dose D_eq attained for any aperture setting $\widehat{a}$ (any nT) for any table increment b (or any pitch p=b∕nT) using $D_{\text{eq}}=\left(\widehat{a}∕b\right)$A_eq, and thence the dose for any scan length L from D_L(0)=H(L) D_eq using the same function expressed as H(L); the complete data set from a single axial rotation without ever scanning over L.

From an experimental point of view, it would be better to use several (N) rotations and measure Nf(0)_a (particularly on the peripheral axis) in order to minimize errors due to “end effects” (beam-on∕off ramp-up times and variable start∕stop angles); the extra acquisition time required is only seconds and inconsequential.

The following example using the data of Mori¹ in Tables 1, 2 for the central and peripheral axes of the body phantom, respectively, will be used to illustrate the feasibility of this somewhat ambitious plan. It is assumed that the scanner can be operated in both a conventional CT mode as well as the SCBCT mode. The key to success is an accurate determination of A_eq which suggests using a reasonably wide beam, such as a=111 mm. We therefore presume that only a single measurement of the peak axial dose f(0)_a=f(0)₁₁₁ is made on each phantom axis, these being the values shown in bold type in Table 3 for a=111 mm. We will then attempt to predict the other data from these [and then check our predictions (shown in italics) against the actual measured data]. This is best illustrated by displaying the results in tabular form as in Table 3.

Table 3.

Stationary phantom doses f(0)_a, as predicted from a measurement of peak dose for a single aperture setting. In this example, f(0)₁₁₁ was used as the measured value (shown in bold type) from which the values of A_eq shown in the last row were predicted using H(a). Predicted doses are given in italics, the actual measured doses (Ref. ¹) from Tables 1, 2 are also listed for comparison, and the % error is shown.

a (mm)	Central axis				Peripheral axis
	Eq. 16H(a)	Peak dose f(0)a			Eq. 19H(a)	Peak dose f(0)a
		PredictedH(a)Aeq	Measured Table 1	Error (%)		PredictedH(a)Aeq	Measured Table 2	Error (%)
138	0.715	4.35 mGy	4.37 mGy	0.5	0.873	9.38 mGy	9.60 mGy	−2.3
111	0.641		3.90		0.84		9.02
49	0.385	2.34	2.27	3.1	0.714	7.67	8.06	−5.1
28a	0.272	1.63	1.53	8.0	0.630	6.74	7.34	−9.0
7.8	0.140	0.85			0.490	5.26
∞	1.000	Aeq=6.08	Aeq=6.17	1.5	1.000	Aeq=10.7	Aeq=10.9	−1.5

^a28 mm rounded off from 27.5 mm.

The value of the aperture-independent constant A_eq is predicted using the measured peak dose for a=111 mm using A_eq=f(0)_a∕H(a)=f(0)₁₁₁∕H(111)=3.90∕0.641=6.08 mGy on the central axis, and A_eq=9.02∕0.84=10.74 mGy on the peripheral axis, which agree (within 1.5%) with the average experimental values of 6.17 and 10.86 from Tables 1, 2. Thence the value of the stationary phantom peak dose f(0)_a=H(a)A_eq can be predicted for any aperture a, and some representative values are given in Table 3 for comparison with the measured values where available.

It might also be prudent to measure f(0)_a for several values of a, since the additional acquisition time is minimal and of little consequence, and likewise to measure a CTDI_L to confirm a good crossover. The doses for a narrow aperture of a=7.8 mm (nT=5 mm) such as one might use in a stationary phantom perfusion study are also shown in Table 3, to illustrate that CTDI₁₀₀ overestimates the peak dose f(0) by factors of 6.9 and 2.7 on the central and peripheral axes, respectively, and the reported CTDI_vol (Ref. ¹³) overestimates the peripheral axis peak dose (comparable to the skin dose and pertinent to perfusion studies) by a factor of 4.1 (see Ref. 15).

This is not surprising since CTDI₁₀₀ represents the dose at the center of 20 contiguous 5 mm axial scans spaced at b=nT=5 mm, and thus includes significant scatter from the adjacent slices and over-beaming as well.

Crossover to conventional CT dose

We can also extend this single measurement of the SCBCT peak dose f(0)₁₁₁ to conventional CT and generate complete dose tables for that modality. We already have the predicted value of the quantity of greatest interest (and the most difficult to measure) in helical or axial scanning, namely, the equilibrium dose constant A_eq (with predicted values of 6.08 and 10.7 mGy from Table 3), which have the same value for conventional CT (assuming the same bow-tie filter) and from which the conventional CT equilibrium dose D_eq for any table increment b (or any pitch p=b∕nT) and for any aperture $\widehat{a}$ (or nT) can be obtained using $D_{\text{eq}}=\left(\widehat{a}∕b\right)$$A_{\text{eq}}=\left(\widehat{a}∕nT\right)p^{-1}{A}_{\text{eq}}$, and thence the dose for any scan length L can be obtained using D_L(0)=H(L) D_eq. For example, assuming the scanner is operated in a helical mode withnT=64×0.5 mm=32 mm (corresponding to an aperturea=49 mm), pitch p=0.78, τ=1 s, total beam-on timet₀=4.0 s, scan length L=vt₀=100 mm; then D_eq=(a∕b)A_eq=(a∕nT)p⁻¹A_eq=1.96A_eq=11.9 and 21.0 mGy on the central and peripheral axes, respectively, which, when corrected to L=100 mm using the values of H(L)=0.60 from Eq. 17 and H(L)=0.86 from Eq. 20, results in dose values of D_L(0)=H(L)D_eq=7.1 and 18.1 mGy on the two axes.

SUMMARY AND CONCLUSIONS

• For SCBCT scanning (without table∕phantom motion), it was shown that the peak dose f(0) on the central ray (z=0) of the cone beam is the logical (and unique) choice for a SCBCT dose-descriptor consistent with the CTDI-based dose used in conventional CT.

• This point dose f(0) can be directly measured using a single axial rotation about a small ion chamber located in the phantom on the central ray of the primary beam (z=0).

• A common measurement method can be utilized for both the stationary and moving phantom, viz., a conventional, short ionization chamber (such as a 0.6 cc Farmer-type chamber) located at the center z=0 of the directly irradiated length to measure the dose Nf(0) for SCBCT, or the accumulated dose D_L(0) at z=0 in conventional CT using a helical (or axial) scan series² to translate the phantom (and ion chamber) over (−L∕2,L∕2) where L=vt₀ (or L=Nb). This direct measurement method is actually more general than the theoretical equations, requiring neither shift-invariance of the phantom, the x-ray beam, nor the scan interval.

• The equilibrium dose constant A_eq=(b∕a)D_eq is independent of both pitch p=b∕nT and aperture a (thence nT), and was shown to have a common value for both SCBCT and conventional CT, and its constancy has been demonstrated over a wide aperture range (28 mm≤a≤138 mm); therefore it is sufficient to determine A_eq at a single known aperture value a (which need not be a wide beam).

• Many common features of the SCBCT dose f(0) as a function of cone beam width a and the conventional CT dose D_L(0) as a function of scan length L have been established, including a common equilibrium dose constant A_eq, a common scatter equilibrium lengtha_eq=L_eq, and a common function H(λ) which describes the relative approach to dose equilibrium for both modalities, where λ=a, or λ=L, such that f(0)_a=H(a)A_eq, and D_L(0)=H(L)D_eq=H(L)(b∕a)A_eq.

• Using the scatter LSF derived from the Monte Carlo simulation of Boone,¹⁷ analytic functions describing the variation in the peak dose of an axial dose profile f(0)_a and H(a)=f(0)_a∕A_eq as a function of collimator aperture a (primary beam width) were derived [e.g., see Eqs. 15, 16], which functions provided a good match to the experimental data,^{1, 2} and which have importance and utility for predicting the peak dose for the narrow fan beams used in perfusion studies¹⁵ as well as the relevant cone beam dose f(0) in SCBCT for any beam width (aperture) a.

• The commonality described above also suggests the possibility that a single measurement of the peak dose f(0)_a of an axial dose profile resulting from a single rotation about a stationary phantom for a single (arbitrarily chosen) aperture a setting using a small ion chamber is sufficient to predict the peak dose f(0)_a for any other aperture, for wide cone beams and narrow fan beams alike, including the scatter equilibrium dose constant A_eq using the function H(a) to obtainA_eq=f(0)_a∕H(a). The value of A_eq can then be used to predict the equilibrium dose D_eq for conventional axial or helical CT scans for any table increment b (or any pitch p=b∕nT) at any aperture setting a (any nT) using D_eq=(a∕b) A_eq, and thence to predict the dose for any desired subequilibrium scan length L usingD_L(0)=H(L) D_eq using the same analytical function H(λ) with λ=L; obtaining the complete data set without ever scanning over L. That is, the theory developed allows a “crossover” between stationary phantom and conventional (helical or axial) scanning modalities (assuming shift-invariance exists). In fact, one obtains the complete data set for both modalities, namely, f(0)_a for any a, A_eq, D_eq=(a∕b) A_eq, and D_L(0) for any L, all from a single measurement of the peak dose f(0)_a of an axial dose profile resulting from a single axial rotation about a stationary phantom.

• Inspection of Fig. 3 illustrates the rather remarkable confluence of an analytical, theoretical function based on a scatter LSF obtained from a Monte Carlo simulation, with axial profile peak doses f(0)_a measured on a Toshiba 256 channel cone beam scanner, with helical scan doses D_L(0) measured on conventional GE LS scanners, which speaks to the generality of these results.

• This work is based on Monte Carlo data¹⁷ obtained at 120 kVp in a 32 cm diameter PMMA phantom using a typical bow-tie filter, and is intended as a proof of concept exposition (which successfully matched the experimental data^{1, 2}); moreover, the theory and equations are quite general and can now be easily extended¹⁷ to any phantom diameter (for a variety of phantom materials) at a variety of kVp settings (with or without) bow-tie filters; and these systematics are to be developed in future work. It would also be useful to have further corroborative experimental measurements of peak doses f(0)_a for narrow axial profiles in the range of (5 mm≤nT≤40 mm).

NOMENCLATURE

MDCT

“Multidetector CT”

Fan beam

A nominal beam width of ≤40 mm along z (≥40 mm is typically called a cone beam)

Shift-invariance

Translational invariance (independent of location along the z-axis)

AOR

Gantry axis of rotation located at isocenter; F=source to isocenter distance

t₀

Total beam-on time for an axial or helical scan series (tube loading time)

τ

Time for a single 360° gantry rotation (typically τ=1 s or less)

N

(t₀∕τ)=total number of gantry rotations in an axial or helical scan series (N may not be an integer for helical scanning)

v

Table velocity for helical scans

b

Generalized table advance per rotation (mm/rot), or table index

b

vτ for helical scans; b=scan interval for axial scans (denoted elsewhere as Δd or “I”)

L

υt₀=definition of total helical scan length (the total reconstructed length is <L)

L

Nb=generalized definition of total scan length (axial or helical)

Π(z∕L)

rect function of unit height and width L spanning an interval (−L∕2,L∕2)

nT

Total slice width acquired in a single rotation (often denoted by “N×T”). Also equal to the total active detector length projected at isocenter for MDCT (e.g., nT=16×1.25 mm=20 mm)

a

Geometric projection of the z-collimator aperture onto the AOR (by a “point” focal spot). For MDCT a>nT (called “overbeaming”) to keep the penumbra beyond the active detector length nT

p

b∕nT=generalized “pitch”

Accumulated dose

Dose accrued at a given z (e.g., z=0) due to a complete series of N axial or helical rotations

f(z)

Single rotation (axial) dose profile acquired with the phantom held stationary

D_eq

Limiting value of accumulated dose approached in conventional CT for scan lengths L≥L_eq

L_eq

Scan length required for the dose to approach to within <2% of D_eq at z=0 (denoted symbolically as L→∞)

A_eq

The equilibrium dose constant, equal to D_eq for a table increment b=a (and independent of aperture a and nT)

R

Radius of cylindrical phantom

η

Scatter to primary ratio S∕P

APPENDIX A: DERIVATION OF THE LSF FORMULATION FOR THE PERIPHERAL AXIS

By analogy with Eq. 7

$$f\left(z,\theta \right)=A_0\left(\theta \right)\left[\frac{1}{c\left(\theta \right)}g\left(\frac{-z}{c\left(\theta \right)}\right)+\eta \left(\theta \right)\text{lsf}\left(z,\theta \right)\right]\otimes \Pi \left(\frac{z}{a\left(\theta \right)}\right),$$ (A1)

where A₀(θ)=f_p(0,θ) is the primary beam intensity (dose rate) on the peripheral axis, and is thus the appropriate weighting function to average various parameters over θ as related to the peripheral axis.⁵ For example, the average of A₀(θ)a(θ) can be written as A₀⟨a⟩ where A₀=f_p(0) is the total primary beam dose on the peripheral axis [the integral of A₀(θ)=f_p(0,θ) over all angles⁵], and ⟨a⟩ is the dose-weighted average of the projected aperture a(θ) on the peripheral axis, which is equal to the width (FWHM) of the primary beam profile f_p(z) on that axis. The presence of a(θ) in the rect function Π[z∕a(θ]) in Eq. A1 breaks the shift-invariant symmetry required by the convolution once the integration over θ is performed. Expressing the convolution in Eq. A1 in its integral form, illustrates the difficulty, namely,

$$f\left(z,\theta \right)=A_0\left(\theta \right)\left[1+{\int }_{-a\left(\theta \right)∕2}^{a\left(\theta \right)∕2}\text{LSF}\left(z-z^{\prime },\theta \right)d{z}^{\prime }\right].$$ (A2)

Fortunately the problem is solvable in closed form on the peripheral axis, since most of the dose on a given peripheral axis is contributed while the beam is directly incident on that axis (θ=0), due to the fact that phantom, bow-tie filter, and secondarily inverse square attenuation⁵ serve to rapidly “pinch off” the primary beam intensity A₀(θ) at angles beyond about ±50°, over which angular range a(θ) is slowly varying. This likewise applies to the peripheral axis of the head phantom,⁵ where the roll off of A₀(θ) is slower, but which is compensated by a smaller variation in a(θ). In fact, it was previously shown⁵ that ⟨a⟩=1.05 a(0) for the peripheral axes in both body and head phantoms, and only 5% above its minimum value a(0) at θ=0. This limited variation in a(θ) allows one to replace it in the above equations by its average value a^′=⟨a⟩ with negligible error, thereby preserving the convolution format (a^′ is equal to the FWHM of the axial dose profile on the peripheral axis). Indeed, this approximation is good on a z-axis located at any radius in either phantom.

Replacing a(θ) by a^′=⟨a⟩ in Eq. A2 and setting z=0 gives

$$f\left(0,\theta \right)=A_0\left(\theta \right)\left[1+{\int }_{-a^{\prime }∕2}^{a^{\prime }∕2}\text{LSF}\left(z^{\prime },\theta \right)d{z}^{\prime }\right],$$ (A3)

which, when averaged (integrated) over θ, gives

$$f\left(0\right)=A_0+{\int }_{-a^{\prime }∕2}^{a^{\prime }∕2}d{z}^{\prime }\frac{1}{2\pi }{\int }_{-\pi }^{\pi }{A}_0\left(\theta \right)\text{LSF}\left(z^{\prime },\theta \right)d\theta =A_0+A_0{\int }_{-a^{\prime }∕2}^{a^{\prime }∕2}⟨\text{LSF}\left(z^{\prime }\right)⟩d{z}^{\prime },$$ (A4)

where ⟨LSF(z^′)⟩ denotes the dose-weighted angular average of LSF(z,θ)=η(θ)lsf(z,θ) over a complete rotation.

Equation A4 is seen to have the same form as Eq. 12 for the central axis [recognizing the scaled form of the LSF previously used LSF(z)=ηd⁻¹h(z∕d)], thus Eq. 17 for f(0) and Eq. 18 for H(a) also apply, if one replaces a with the FWHM of the axial dose profile on the peripheral axisa^′=⟨a⟩≈1.05a(0)≈0.76a, where a(0)=a(F−15 cm)∕F, and where F is the focal to AOR distance, and uses the values of the (double-exponential) fit parameters (ε,d,δd) appropriate to the peripheral axis and η=1.5.