3-D Localization of Virtual Sound Sources: Effects of Visual Environment, Pointing Method, and Training

Abstract

The ability to localize sound sources in three-dimensional space was tested in humans. In experiment 1, naive subjects listened to noises filtered with subject-specific head-related transfer functions. The tested conditions included the pointing method (head or manual pointing) and the visual environment (VE) (darkness or virtual VE). The localization performance was not significantly different between the pointing methods. The virtual VE significantly improved the horizontal precision and reduced the number of front-back confusions. These results show the benefit of using a virtual VE in sound localization tasks. In experiment 2, subjects were provided sound localization training. Over the course of training, the performance improved for all subjects, with the largest improvements occurring during the first 400 trials. The improvements beyond the first 400 trials were smaller. After the training, there was still no significant effect of pointing method, showing that the choice of either head- or manual-pointing method plays a minor role in sound localization performance. The results of experiment 2 reinforce the importance of perceptual training for at least 400 trials in sound localization studies.

Testing the localization of sound sources requires accurate methods for the presentation of stimuli and the acquisition of subjects’ responses. The acquisition method may affect the precision and accuracy of the response to the perceived sound direction and change the efficiency of the localization task. Many methods have been used in localization tasks: verbal responses (Wightman and Kistler-1989#2; Mason et al. 2001); rotating a dial or drawing (Haber et al. 1993); pointing with the nose (Bronkhorst 1995; Pinek and Brouchon 1992; Middlebrooks 1999); pointing with the chest or finger (Haber et al. 1993); pointing with extensions of the body, like a stick, cane, or gun (Haber et al. 1993; Oldfield and Parker 1984); pointing with a laser pointer (Lewald and Ehrenstein 1998; Seeber 2002); and using sophisticated computer interfaces (e.g., Begault et al. 2001). [Haber et al. 1993] compared nine different response methods and showed the best precision for pointing methods. They compared the methods in blind subjects using pure-tones and tested in the horizontal plane only. The difference between the head-pointing method and manual-pointing method (finger, gun, or stick) remains unclear for 3D-sound localization in sighted subjects. For sound localization in 3D, the manual pointer may promise a better ability to point to high elevations, which can be difficult to access by lifting the head and pointing with the nose. On the other hand, using the manual pointer may cause a bias in the responses in the horizontal plane because holding the pointer in one hand creates an asymmetric pointing situation. [Pinek and Brouchon 1992] found such an effect in a horizontal-plane localization task for right-handed subjects holding the manual pointer in their right hand. This disadvantage could counteract the potential advantage of manual pointing in vertical planes. A direct comparison between head- and manual-pointing methods has not been investigated for sound localization including the vertical planes. Thus, we investigated the effect of head and manual pointing on sound localization ability in 3-D space.

Many studies investigated the link between the visual and auditory senses with respect to sound localization (e.g., Lewald et al. 2000; May and Badcock 2002; Shelton and Searle 1980). The general finding is that the addition of visual information improves sound localization when the auditory and visual inputs provide congruent information (Jones and Kabanoff 1975). Also, localization of visual targets has been found to improve when spatially correlated audio information is provided (Bolia et al. 1999; Perrott et al. 1996). There are, however, differences in the processing of the auditory and visual information. In principle, the auditory system encodes a sound location primarily within a craniocentric frame of reference. This is defined for each subject individually by the position of the ears and acoustic properties of the head, torso, and pinna. In contrast, the visual system encodes positions within an oculocentric frame of reference, which changes with eye movements (Konishi 1986). The difference in the frames of reference can be a potential source of error and confusion when localizing sounds with visual feedback, and is the reason for the investigations of visual effects and after-effects on sound localization (for a review see Lewald and Ehrenstein 1998). Generally, when a subject has to point at a required position in the presence of visual feedback, visuomotor recalibration between the proprioceptive and the visual information can reduce the pointing bias. For example, [Redon and Hay 2005] found that using a visually-structured background reduces pointing bias to visual targets. [Montello et al. 1999] tested pointing accuracy to remembered visual targets. They found that when blindfolded, the subjects showed higher bias and worse precision compared to the condition where the subjects were provided visual information about the background. A visual environment (VE) may also help subjects to respond accurately in sound localization tasks.

The purpose of experiment 1 was to systematically investigate the effects of using a virtual VE and different pointing methods with naive listeners. It was hypothesized that for elevated targets, subjects would be able to point more accurately with the manual-pointing method. Further, it was hypothesized that using a virtual VE would improve sound localization. We used virtual acoustic stimuli generated with individualized head-related transfer functions (HRTF, Møller et al. 1995), which are known to provide both good horizontal and vertical localization cues.

Comparing previous sound localization studies is difficult because of differences in the amount of training the subjects received prior to the data collection. There are several studies with naive subjects (Begault et al. 2001; Bronkhorst 1995; Djelani et al. 2000; Getzmann 2003; Lewald and Ehrenstein 1998; Seeber 2002) and several with trained subjects (Carlile et al. 1997; Makous and Middlebrooks 1990; Martin et al. 2001; Middlebrooks 1999; Wightman and Kistler 1989#2). In addition, some of those studies provided visual feedback during the testing, which may be considered as additional perceptual training. A standard localization training protocol seems to be non-existent. Thus, we explored the effects of training in experiment 2. The training was performed using the virtual VE and the two pointing methods. This allowed for an extensive comparison of our study to previous sound localization studies and for an explicit investigation of the training effect.

EXPERIMENT 1

Methods

Subjects

Ten listeners participated in the experiments (six male and four female). The age range was 23 to 36 years. All subjects had normal audiometric thresholds and normal or corrected-to-normal vision. The listeners were naive with respect to localization tests. All listeners were right-handed.

Apparatus

The virtual acoustic stimuli were presented via headphones (HD 580, Sennheiser) in a semi-anechoic room. The subjects stood on a platform enclosed by a circular railing. The A-weighted sound pressure level (SPL) of the background noise in this room was 18 dB with reference to 20 μPa on a typical testing day. A digital audio interface (ADI-8, RME) with a 48-kHz sampling rate and 24-bit resolution was used. The VE was presented via a head-mounted display (HMD; 3-Scope, Trivisio). The HMD was mounted on the subject’s head and provided two screens with a field of view of 32° × 24° (horizontal × vertical dimensions). The HMD housing surrounding the screens was black. The HMD did not enclose the complete field of view. Thus, for the tests in darkness, it was necessary for the room to be darkened to provide no visual information. The virtual VE was presented binocularly with the same picture for both eyes. This induced a visual image without stereoscopic depth, which was intended in order to reduce potential binocular stress (May and Badcock 2002). The subjects could adjust the interpupillary distance and the eye relief to achieve a focused and unvignetted image. The resolution of each screen was 800 × 600 (horizontal × vertical). The position and orientation of the subjects’ head were captured via an electromagnetic tracker (Flock of Birds, Ascension) in real-time. One tracking sensor was mounted on the top of the subjects’ head. In conditions where the manual hand pointer was used, the position and orientation of the pointer were captured with a second tracking sensor mounted on the pointer. The tracking data were used for the 3D-graphic rendering and response acquisition. The tracking device was capable of measuring all 6 degrees of freedom (x, y, z, azimuth, elevation, and roll) at a rate of 100 measurements per second for each sensor. The tracking accuracy was 1.7 mm for positions and 0.5° for orientation.

Two personal computers were used to control the experiments in a client-server architecture. The machines communicated via Ethernet using TCP/IP. The client machine acquired the tracker data, created and presented the acoustic stimuli, and controlled the experimental procedure, while the server machine handled the 3D graphic rendering upon client’s requests. This architecture allowed a balanced distribution of computational resources. The latency between the head movements and the updated visual information was less than 37.3 ms.

HRTF measurement

Individual HRTFs were measured for each subject in the semi-anechoic chamber. Twenty-two loudspeakers (custom-made boxes with VIFA 10 BGS as drivers; the variation in the frequency response was ±4 dB in the range from 200 to 16000 Hz) were mounted at fixed elevations from −30° to 80°. They were driven by amplifiers adapted from Edirol MA-5D active loudspeaker systems. The loudspeakers and the arc were covered with acoustic damping material to reduce the intensity of reflections. The total harmonic distortion of the loudspeaker-amplifier systems was on average 0.19 % (at 63-dB SPL and 1 kHz). The subject was seated in the center of the arc and had in-ear-microphones (Sennheiser KE-4-211-2) placed in his/her ear canals. The microphones were connected via amplifiers (RDL FP-MP1) to the digital audio interface. A 1728.8-ms exponential frequency sweep beginning at 50 Hz and ending at 20 kHz was used to measure each HRTF.

The HRTFs were measured for one azimuth and several elevations at once (see below) by playing the sweeps and recording the signals at the microphones. Then the subject was rotated by 2.5° to measure HRTFs for the next azimuth. In the horizontal interaural plane, the HRTFs were measured with 2.5° spacing within the azimuth range of ± 45° and with 5° spacing outside this range. The positions of the HRTFs were distributed with a constant spherical angle, which means that the number of measured HRTFs in a horizontal plane decreased with increasing elevation. For example, at the elevation of 80°, only 18 HRTFs were measured. In total, 1550 HRTFs were measured for each listener. To decrease the total time required to measure the HRTFs, the multiple exponential sweep method (MESM) was applied (Majdak et al. 2007). This method allows for a subsequent sweep to be played before the end of a previous sweep, but still reconstructs HRTFs without artifacts. The MESM uses two mechanisms, interleaving and overlapping and both depend on the acoustic measurement conditions (for more details see Majdak et al. 2007). Our facilities allowed the interleaving of three sweeps and overlapping of eight groups of the interleaved sweeps. During the HRTF measurement, the head position and orientation were monitored with the same tracker as used in the experiments. If the head was outside the valid range, the measurements for that particular azimuth were repeated immediately. The valid ranges were set to 2.5 cm for the position, 2.5° for the azimuth, and 5° for the elevation and roll. On average, measurements for three azimuths were repeated per subject and the measurement procedure lasted for approximately 20 minutes.

Equipment transfer functions were measured. They were derived from a reference measurement in which the in-ear microphones were placed in the center of the arc and the room impulse response was measured for all loudspeakers. The room impulse responses showed a reverberation time of approximately 55 ms. The level of the largest reflection (floor reflection) was at least 20 dB below the level of the direct sound and delayed by at least 6.9 ms. The equipment transfer functions were cepstrally smoothed and their phase spectrum was set to the minimum phase. The resulting minimum-phase equipment transfer functions were removed from the HRTFs by spectral division. We assume that after this equalization, the room reflections and the equipment had only a negligible effect on the fidelity of HRTFs.

Directional transfer functions (DTFs) were calculated using a method similar to the procedure of [Middlebrooks 1999]. The magnitude of the common transfer function (CTF) was calculated by averaging the log-amplitude spectra of all HRTFs for each subject. The phase spectrum of the CTF was set to the minimum phase corresponding to the amplitude spectrum of the CTF. The DTFs were the result of filtering the HRTFs with the inverse complex CTF. Finally, the impulse responses of all DTFs were windowed with an asymmetric Tukey window (fade in of 0.25 ms and fade out of 1 ms) to a 5.33-ms duration.

Stimuli

The acoustic targets were uniformly distributed on the surface of a virtual sphere centered on the listener. To describe the acoustic target’s position, lateral and polar angles from the horizontal-polar coordinate system were used (Morimoto and Aokata 1984). The lateral angle ranged from −90° (right) to 90° (left). The polar angle of the targets ranged from −30° (front, below eye-level) to 210° (rear, below eye-level). The target distribution was achieved by using a uniform distribution for the polar angle and an arcsine-scaled uniform distribution for the lateral angle. In the vertical dimension, positions from −30° to +80° relative to the eye-level of the listener were tested. In the horizontal dimension, the entire 360° were tested.

The auditory stimuli were Gaussian white noises with a duration of 500 ms, which were filtered with the subject-specific DTFs. Prior to filtering, the position of the acoustic target was discretized to the grid of the available DTFs. The filtered signals were temporally windowed using a Tukey window with a 10-ms fade.

The level of the stimuli was 50 dB above the individual absolute hearing threshold. The threshold was estimated in a manual up-down procedure using a target positioned at azimuth and elevation of 0°. In the experiments, the stimulus level for each presentation was randomly roved within the range of ±2.5 dB to reduce the possibility of localizing spatial positions based on overall level.

Procedure

Prior to the main tests, subjects performed a procedural training, where they played a simple game in the first-person perspective. The subjects were immersed in a virtual VE, finding themselves inside of a yellow sphere with a diameter of 5 m. Grid lines every 5° and 11.25° (horizontal and vertical, respectively) were used to improve the orientation in the sphere. The eye-level and the meridian were marked with small blue balls. The reference position (azimuth and elevation of 0°) was marked with a larger red ball. Instructions were presented at the top of the field of view. The lighting in the sphere was evenly tempered with more light at the front and back than at the sides. The subjects could see the visualization of the hand pointer as shown in Fig. 1. Rotations in azimuth and elevation were rendered in the VE. Rolls and translations were not rendered.

Figure 1.

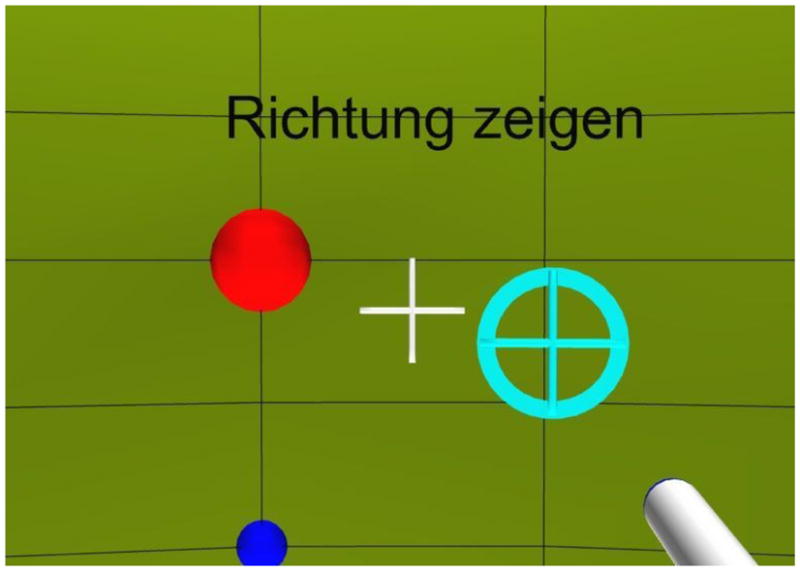
(color online). VE from the subject’s point of view. The large (red) ball denotes the reference position. The small (blue) ball denotes the meridian. The (white) cross-hair represents the center of the display. The (white-shaded) cylinder in the right-bottom corner is the visualization of the manual pointer. The (cyan) circle with a cross-hair shows the projection of the pointer on the sphere. Instructions were presented at the top of the field of view (“Point to the direction” in this example).

In the procedural training, at the beginning of each trial, the subjects were asked to look at the reference position. By clicking a button, a visual target in form of a red rotating cube was presented on the surface of the sphere at a random position. The subjects had to find the target, point at it, and click a button within four seconds, which was considered a “hit”. Otherwise, the trial was considered a “miss”. If the trial was a hit, then the subjects heard a short confirmation sound. To avoid any auditory training effects, acoustic information about the target position was not provided during the procedural training. Subjects were trained in blocks of 100 targets in a balanced block order. The procedural training was continued until 95% of the targets were hit with a root-mean-square (RMS) angular error smaller than 2° measured in three consecutive blocks. On average, the subjects required 590 and 710 targets to reach the procedural training requirements for the head- and manual-pointing methods (see below), respectively.

In the main experiment, the effect of the VE was studied under two different conditions. In the condition “HMD”, the subjects were immersed in the VE, as used in the procedural training. In the condition “Dark”, the subjects were tested in darkness. In this condition, the VE was turned black and only the reference position was shown for calibration purposes. Also, the room lights were switched off. Thus, the subjects had no visual information regarding their orientation except for the reference (which was removed after acoustic presentation, see below).

Two response methods were investigated: head and manual pointing. In the head-pointing method, the subjects were asked to turn their body, head, and nose to the perceived direction of the target. The subjects were asked to avoid using eye-movements to indicate the perceived position. In tests with the HMD, the subjects were asked to use the cross-hair on the screen to indicate the perceived position. In the head-pointing method, the orientation of the head was recorded as the perceived target position. In the manual-pointing method, subjects had the pointer in their right hand and were asked to point to the direction of perceived target. The projection of the pointer direction on the sphere’s surface, calculated from the position and orientation of the tracker sensors, was visualized as a cross-hair and recorded as the perceived target position. The pointer was also visualized whenever it was in the subjects’ field of view.

At the beginning of each trial, the subjects were asked to look at the reference position. The head position was monitored and when it was at the reference position, subjects were allowed to confirm their readiness by clicking a button. After confirmation, the acoustic target was presented. The subjects were instructed to remain in the reference position during the acoustic presentation. After the acoustic presentation, the subjects were asked to point to the perceived position with the head or the manual pointer, depending on the test condition. In the condition “Dark”, the reference marker was removed after the acoustic presentation. No information about the target’s position was provided during the tests.

The tests were performed in blocks. Each block consisted of 100 acoustic targets with random positions and lasted for approximately 30 minutes. All combinations of VE and pointing method were tested for all the subjects; however, the condition did not change within one block. The block order was random and different for each subject. In total, four blocks were tested per condition and subject.

Data analysis

In the lateral dimension, the localization ability was investigated separately for each subject, condition, hemifield (front and back), and for different groups of lateral positions. [Makous and Middlebrooks 1990] reported a larger response variability in the rear hemifield compared to the front hemifield. [Carlile et al. 1997] pointed out that this may be due to some motor or memory related issues. Thus, our lateral errors were analyzed separately for these two hemifields. The data separation for the two hemifields was done on the basis of the polar response angle. In addition, different lateral positions were analyzed by grouping target positions. For the right hemifield, the groups were: 0° to −20°, −20° to −40°, and −40° to −90°. For the left hemifield, the groups were: 0° to 20°, 20° to 40°, and 40° to 90°. These groups contained approximately the same number of tested positions.

The errors were calculated by subtracting the target angles from the response angles. Following the conventions of [Heffner and Heffner 2005], we distinguish between the localization bias, which is the systematic error, and localization precision, which is the statistical error. The lateral bias is the signed mean of the lateral errors. The bias is sometimes called the localization accuracy. The lateral precision error is the standard deviation of the lateral errors. It represents the consistency of the localization ability and is sometimes called localization blur.

In the polar dimension, the quadrant errors were analyzed. The quadrant error represents the percentage of confusions between the front and back hemifields. [Makous and Middlebrooks 1990] defined a quadrant error as a response at the hemifield opposite to the target. This definition is questionable for targets near the frontal plane. To avoid such problems, [Carlile et al. 1997] counted the number of responses in the wrong hemifields while excluding those on or close to the vertical plane containing the interaural axis (i.e. frontal plane). [Middlebrooks 1999] treated absolute polar errors greater than 90° as quadrant errors. He included only median targets (within lateral angles of ±30°) in the calculation. This was intended to reduce the problem that the spherical angle, corresponding to a given polar angle is compressed at large lateral angles near the poles. In our study, this method would have excluded almost half of the data. Thus, we used a method where all the targets within lateral angles of ±60° were included and we compensated for the compression in the polar angle. We define the quadrant error as the percentage of responses where the weighted polar error exceeds ±45°. The weighted polar error is calculated by weighting the polar error with w = 0.5·cos (2·α) + 0.5, where α is the lateral angle of the corresponding target. For targets in the median plane (α=0°), w=1 and the polar error must exceed ±45° to be considered a quadrant error. For targets at α=±45°, w=0.5 and the polar error must exceed ±90° to be considered a quadrant error. For targets at α=±60°, w=0.25 and the polar error must exceed ±180° to be considered a quadrant error, which cannot be achieved in this coordinate system. Thus, targets beyond a lateral angle of ±60° cannot have a quadrant error. In other words, the quadrant error was based on responses within the ±60° lateral range only. Our weighting procedure is comparable to the procedure of [Martin et al. 2001], who used the weighted elevation angle to determine the occurrence of front-back confusions. The quadrant errors were calculated for four regions, resulting from the combination of two elevations (eye-level and top) and two hemifields (front and rear). The elevation “eye-level” included all targets with elevations between −30° and 30°. The elevation “top” included all targets with elevations between 30° and 90°. For targets in the median plane, this corresponded to grouping based on polar angles of 0° (front/eye-level), 60° (front/top), 120° (rear/top), and 180° (rear/eye-level).

Circular statistics (Batschelet 1981) were used to analyze the errors in the polar dimension (Montello et al. 1999). The bias in the polar dimension is the circular mean of the polar errors and is referred to as polar bias. The polar bias does not need to be weighted with the lateral angle, as only the variance, not the mean of the responses, is assumed to be affected by the transformation to the horizontal-polar coordinate system. In conditions with a large percentage of quadrant errors, the polar bias is highly correlated to the quadrant error, showing the dominant role of the quadrant error in this metric. The analysis shown in the Results section is based on the local polar bias, which is the polar bias after quadrant errors have been removed. The precision in the polar dimension, referred to as the polar precision error, is the circular standard deviation of the weighted polar errors. As for the quadrant errors, the weighted polar errors are used to reduce the problem of the spherical angle compression when including all targets. Comparable to the polar bias, the polar precision error is also correlated to the quadrant error and the analysis shown in the Results section is based on the local polar precision error, which is the polar precision error after quadrant errors have been removed. Both local polar bias and local polar precision error were analyzed separately for four position groups. The data were separated by target polar angle, with ranges −30° to 30°, 30° to 90°, 90° to 150°, and 150° to 210°. This grouping corresponds to the grouping in the analysis of the quadrant error.

The quadrant errors and local polar precision errors for random responses (i.e., guessing) were estimated. The estimations were done by replacing the polar angles of the responses by random polar angles (equally distributed between −30° and 210°) and calculating the metrics. The results indicate the chance rate and are shown in the relevant figures.

Repeated-measures analyses of variance (RM ANOVA) were performed on each of the described metrics. Each error metric was calculated four times (once per block of 100 trials). This resulted in four values per metric, subject, and condition. Differences between conditions were determined by Tukey-Kramer post-hoc tests using a 0.05 significance criterion.

Results

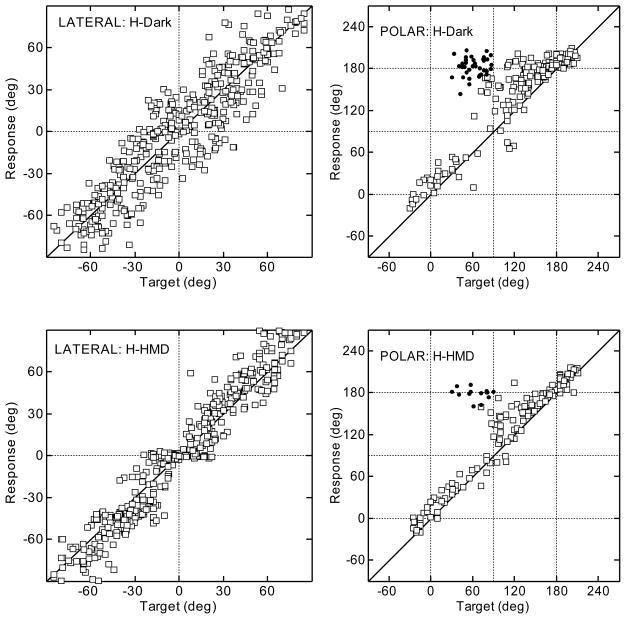
Figures 2 and 3 show typical results for the head- and manual-pointing methods, respectively, for a typical subject. The top and bottom rows show the results for the conditions “Dark” and “HMD”, respectively. Left and right panels show the results for the lateral and polar angle, respectively, following the layout of [Middlebrooks 1999]. For all panels, the target angles are shown on the x-axis and the response angles are shown on the y-axis. The quadrant errors are plotted as filled circles. All other responses are plotted as open squares. The results for the polar angle are shown for targets with lateral angles up to ±30° only.

Figure 2.

Results for a typical subject using the head-pointing method in darkness (top row) and with the HMD (bottom row). Lateral and polar dimensions are shown in the left and right panels, respectively. Filled circles represent quadrant errors.

Figure 3.

Results for the same subject as shown in Fig. 2 using the manual-pointing method. All other conventions are as in Fig. 2.

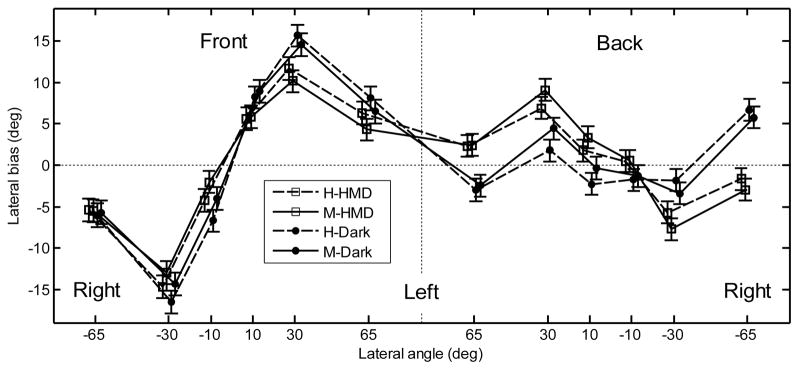
The lateral bias averaged over subjects is shown in Fig. 4. The data left of the central vertical dashed line represent responses to the front, those to the right represent responses to the rear. For the front hemifield, the bias shows an overestimation of the lateral positions. For the rear hemifield, the bias shows no clear effect. A repeated-measures ANOVA with the factors position (±65°, ±30°, and ±10°), hemifield (front, back), pointing method (head, manual), and VE (Dark, HMD) was performed. The effect of the position was significant [F(5,1812) = 122, p < .001] and the effect of the hemifield was not significant [F(1,1812) = .1, p = .75]. There was a significant interaction between position and hemifield [F(5,1812) = 44.6, p < .0001]. A post-hoc test showed a significant effect of position for the front targets and non-significant effect of position for the rear targets. The effect of the pointing method was not significant [F(1,1812) = .41, p = .52]. The effect of the VE was not significant [F(1,1812) = .07, p = .80]; however, there was a significant interaction between position, hemifield, and VE [F(5,1812) = 9.83, p < .0001]. A post-hoc test showed that for most positions tested in darkness, the bias was significantly lower for the rear hemifield than for the front hemifield. For tests with the HMD, the bias did not vary significantly across the hemifields.

Figure 4.

Lateral bias for the naive subjects for the front hemifield (left panel) and rear hemifield (right panel). Data labeled as “H” and “M” represent the results for head- and manual-pointing methods, respectively. Data labeled as “HMD” and “Dark” represent the results for tests with the HMD and in darkness. The error bars show the standard errors.

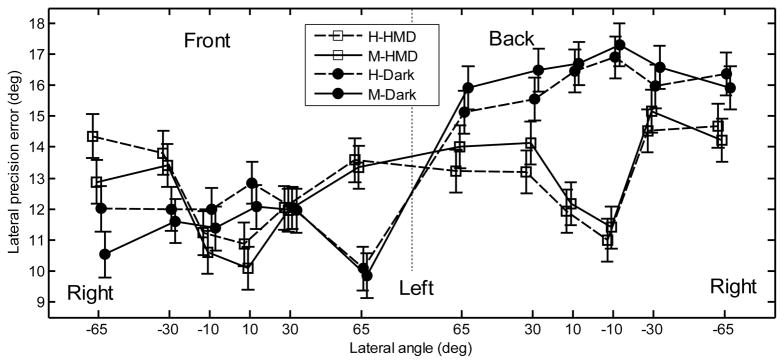
The lateral precision error averaged over subjects is shown in Fig. 5. When tested with the HMD, the central positions showed low precision errors. When tested in darkness, the difference across lateral positions is not evident. For the rear hemifield, the effect of the VE is evident: with the HMD, subjects showed lower precision errors. For the front hemifield, the effect of the VE seems to be marginal. A repeated-measures ANOVA with the factors lateral position, hemifield, pointing method, and VE was performed. The effect of the position was significant [F(5,1817) = 2.71, p = .019]. The effect of the hemifield was also significant [F(1,1817) = 106.7, p < .0001], showing a lower precision error for the front hemifield (11.9°) than for the rear hemifield (14.8°). The effect of the pointing method was not significant [F(1,1817) = .1, p = .75]. The lack of a pointing method effect was consistent across all positions and planes as shown by the lack of a significant interaction between position and pointing method [F(5,1817) = .55, p = .74] or between hemifield and pointing method [F(1,1817) = 3.4, p = .065]. The effect of the VE was significant [F(1,1817) = 15.2, p = .0001], showing a higher precision error in darkness (13.9°) than with the HMD (12.8°). The interaction between VE and hemifield was significant [F(1,1817) = 47.2, p < .0001]. A post-hoc test showed that for tests in darkness, the precision error was significantly higher for the rear hemifield than for the front hemifield. In contrast, for tests with the HMD, the lateral precision error did not vary significantly across the hemifields. The interaction between VE and lateral position was also significant [F(5,1817) = 7.49, p < .0001]. A post-hoc test showed that for tests with the HMD, the precision error was significantly lower for the central positions. For tests in darkness, the precision error did not vary significantly across the positions.

Figure 5.

Lateral precision error for the naive subjects. All other conventions are as in Fig. 4.

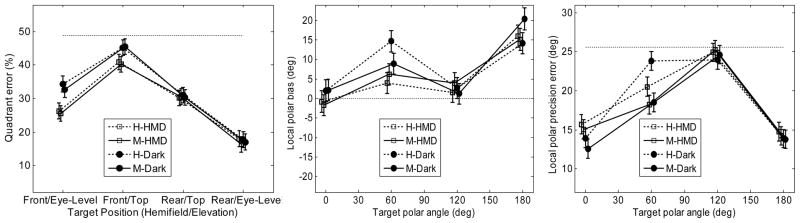
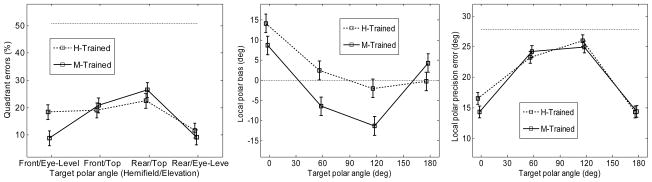
The quadrant error averaged over subjects is shown in the left panel of Fig. 6. The quadrant errors are consistently lower than chance for all but one position: for the front-top targets the quadrant error appears to approach the range of guessing. A repeated-measures ANOVA with factors elevation, hemifield, pointing method, and VE was performed. The effect of the elevation was significant [F(1,621) = 80.6, p < .0001], showing a lower quadrant error for the eye-level positions (23.5%) than for the top positions (36.7%). The effect of the hemifield was significant [F(1,621) = 71.5, p < .0001], showing a lower quadrant error for the rear hemifield (23.9%) than for the front hemifield (36.4%). The effect of pointing method was not significant [F(1,621) = .19, p = .66]. The factor VE was significant [F(1,621) = 4.66, p = .031], showing a lower quadrant error with the HMD (28.5%) than in darkness (31.7%). The VE did not interact with the elevation [F(1,621) = .23, p = .63], but it interacted with the hemifield [F(1,621) = 4.07, p = .044]. A post-hoc test showed that for the front hemifield, the quadrant errors were significantly lower for tests with the HMD (33.3%) than in darkness (39.4%). For the rear hemifield, the difference between the quadrant errors for tests with the HMD (23.8%) and in darkness (24.0%) was not significant.

Figure 6.

Results for the naive subjects. Left panel:quadrant errors. Middle panel: local polar bias. Right panel: local polar precision error. The thin dotted lines represent the chance rate. The error bars represent the standard errors.

The local polar bias averaged over subjects is shown in the middle panel of Fig. 6. A repeated-measures ANOVA with factors position, pointing method, and VE was performed. The effect of position was significant [F(3,596) = 27.2, p < .001]. The effect of the pointing method was not significant [F(1,596) = .05, p = .83]. The effect of the VE was significant [F(1,596) = 3.99, p = .046], showing a lower bias for tests with HMD (5.6°) than for tests in darkness (8.3°).

The local polar precision error averaged over subjects is shown in the right panel of Fig. 6. A repeated-measures ANOVA with the factors position, pointing method, and VE was performed. The effect of the position was significant [F(3,596) = 72.3, p < .0001], showing lower precision errors for the eye-level positions. The effect of the pointing method (17.8° vs. 18.3°) was not significant [F(1,596) = 3.7, p = .055]. The interaction between position and pointing method was also not significant [F(3,596) = 2.44, p = .064]; however, a post-hoc test showed that for the front-top positions, the precision error was significantly lower for the manual-pointing method (18.3°) than for the head-pointing method (22.2°). The effect of VE was not significant [F(1,596) = .54, p = .46].

Lateral bias, lateral RMS errors, local RMS polar errors, elevation bias, and quadrant errors were calculated according to [Middlebrooks 1999], who tested trained subjects with the head-pointing method in darkness. His and our results are shown in Tab. 4. These results are discussed in the Discussion section of experiment 2.

Table 4.

Results Using the Metrics from [Middlebrooks 1999].

	Middlebrooksa	HMDb		Darkb		Trainedc
		Head	Manual	Head	Manual	Head	Manual
lateral bias (deg)	3.1 ± 3.9	0.4	0.7	0.8	1.0	0.7	−0.2
lateral RMS error (deg)	14.5 ± 2.2	14.4	15.1	17.9	18.6	12.4	12.3
local RMS polar error (deg)	28.7 ± 4.7	37.3	37.5	37.6	37.9	30.9	32.7
elevation bias (deg)	10.2 ± 6.6	7.7	8.3	10.9	11.6	2.5	4.6
quadrant error (%)	7.7 ± 8.0	20.8	19.2	22.2	20.7	11.1	7.8

Note.

^aMiddlebrooks shows the data (± standard deviation over subjects) from [Middlebrooks 1999], his Table I.

^bHMD and Dark show the results from experiment 1.

^cTrained shows the results from experiment 2.

Discussion

General effects

For all conditions, the target position had a significant effect on localization performance. Also, our naive subjects show similar trends to trained subjects in other studies. For example, [Makous and Middlebrooks 1990] showed a better precision for targets in the front compared to targets in the rear. Our results show a similar precision pattern, although, in the horizontal plane, the differences strongly depend on the tested conditions. Also, [Makous and Middlebrooks 1990] and [Carlile et al. 1997] showed a better precision for more central positions, which is consistent with our data.

In the horizontal plane, our subjects overestimated the actual lateral position. This is in agreement with the results of [Lewald and Ehrenstein 1998], who reported a lateral bias of 10° for targets at a lateral angle of 22°. In our study, the lateral bias is 12° for targets at a lateral angle of 30°. [Seeber 2002] reported a lateral bias of 5° for targets at 50° (compared to our bias of approximately 10°). [Begault et al. 2001] tested for front and back positions and reported an unsigned azimuth error of approximately 24°. This is higher than our lateral precision error of 15°. [Oldfield and Parker 1984] and [Carlile et al. 1997] reported a pattern of lateral bias similar to our pattern, even though they used real sound sources and tested trained subjects: small lateral overestimation of the central positions and large lateral overestimation of the non-central positions (±30°). Our lateral bias is not in agreement with [Lewald et al. 2000], whose subjects tended to underestimate the lateral position, with an increasing deviation for increasing lateral positions.

In the polar dimension, our subjects made numerous quadrant errors, especially when tested in darkness. This is in agreement with the results of [Begault et al. 2001], who reported a quadrant error of 59%, approaching their chance rate of 50%. Their quadrant error is much larger than our quadrant error of approximately 30% (our chance rate: 48%), even though both studies tested naive subjects. [Bronkhorst 1995], who also tested naive subjects, found quadrant errors of 28% (chance rate: 50%), which is more consistent with our results. Interestingly, in our study, for elevated targets, the local polar precision errors and quadrant errors were almost in the range of chance. In contrast, the eye-level positions showed a local polar precision error and a quadrant error much better than chance. This indicates that subjects had difficulty localizing the elevated positions, independent of pointer and VE.

Effect of the visual environment

The virtual VE had a profound effect on the localization ability. In the horizontal plane, lateral precision improved when tested with the HMD. In particular, significant improvements were found for the central positions and for the rear hemifield. In the vertical plane, the HMD reduced the quadrant errors and the local polar bias, particularly, in the front hemifield. This is in agreement with [Shelton and Searle 1980], who showed that for targets located in the front, subjects localized sounds more accurately with vision than when blindfolded. They concluded that vision improved sound localization by visual facilitation of spatial memory and providing an adequate frame of reference. It may be that the presence of the structured VE helped our subjects in the direct visualization of targets that were in the field of view.

The better precision in the horizontal plane but not in the vertical plane indicates that the VE effect is neither due to generally better orientation in the HMD condition, nor due to generally higher confusion when tested in darkness. In summary, our results show evidence for better sound localization when tested with a virtual VE.

Effect of pointing method

Generally, both pointing methods resulted in similar localization performance. In the horizontal plane, we did not find a significant difference between the head- and manual-pointing methods. For the manual-pointing method, our results are in agreement with the results of [Pinek and Brouchon 1992], who found an overestimation of the lateral positions when the right-handed subjects used the manual pointer in their right hand. All our subjects were right-handed and held the pointer in their right hand. For the head-pointing method, [Pinek and Brouchon 1992] found an underestimation of the lateral positions. This is contrary to our results, which show an overestimation of lateral positions independent of the pointing method. We have no explanation for this discrepancy. [Pinek and Brouchon 1992] also found no general difference in the precision between the two pointing methods, which is in agreement with our results. [Haber et al. 1993] compared the effects of the head- and manual-pointing methods on sound localization and reported similar performance for these pointing methods, which is in agreement with our results.

In the vertical plane, our results show a slightly better precision when subjects used the manual-pointing method to indicate the elevated targets in the front hemifield. This is in agreement with our hypothesis of subjects having difficulty pointing with the head to the elevated positions. We expected a consistently larger bias and not a worse precision when the head-pointing method was used. The very small difference in the polar precision error between the head-pointing (22.2°) and manual-pointing (18.3°) methods and the lack of significance of this difference (p = .055) indicate that the choice of the pointer in sound localization tasks has only a minimal effect on the results. This finding is consistent with the results of [Djelani et al. 2000], who tested sound localization using virtual acoustic stimuli with head movements allowed and also found no difference between the head-pointing and manual-pointing methods.

The lack of a significant difference between head- and manual-pointing methods may be explained by the extensive procedural training our subjects received for both pointing methods. In the procedural training, our subjects were trained to use both pointing methods until they reached an equal performance for both. This could reduce the potential pointer effect in subsequent tests. However, the lack of a significant pointer effect may also result from testing naive subjects. It may be that lack of experience in localizing virtual sounds (hence, large variance in response metrics) has obscured the difference between the pointing methods. In a second experiment we intended to investigate how perceptual training changes localization ability. By investigating the training effect separately for both head- and manual-pointing methods, we would be able to dismiss that the lack of difference between pointing methods found in this experiment is due to testing naive subjects.

EXPERIMENT 2

In this experiment, the effect of training on localization ability was investigated. The training was performed by providing visual information about the spatial position of the virtual sound source. Thus, the conditions in darkness could not be tested, thus, all blocks are equivalent to the HMD blocks in experiment 1. The effect of the pointing method was tested using the HMD.

Two hypotheses were tested. First, we hypothesized that performance would generally improve with training, resulting in lower localization errors. Second, we hypothesized that the lower localization errors as a result of training would allow us to identify one of the pointing methods as the preferable one.

Method

Subjects, apparatus, and stimuli

The subjects from experiment 1 also participated in experiment 2. They were grouped so that five subjects were trained using head pointing and five subjects were trained using manual pointing. The subjects were ranked according to their quadrant errors from experiment 1 and assigned to the two groups with the goal of having groups with similar quadrant errors. The head-pointing group consisted of NH08, NH11, NH13, NH14, and NH19 and had an average quadrant error of 27.5%. The manual-pointing group consisted of NH12, NH15, NH16, NH17, and NH18 and had an average quadrant error of 28.8%. The stimuli and the apparatus were the same as in experiment 1.

Procedure

At the beginning of each trial, the subjects were asked to orient themselves to the reference position and click a button. Then, the acoustic stimulus was presented. The subjects were asked to point to the perceived position and click the button again. This response represents the test condition without feedback, and it was recorded for the analysis of the localization ability. Then, visual feedback was provided by showing a visual target at the position of the acoustic stimulus. The visual target was a red rotating cube, as in the procedural training of experiment 1. In cases where the target was outside of the field of view, an arrow pointed towards its position. The subjects were asked to find and point at the target, and click the button. At this point in the procedure, the subjects had both heard the acoustic target and seen the visualization of its position. To stress the link between visual and acoustic location, the subjects were asked to return to the reference position and listen to the same acoustic target once more. Then, while the target was still visualized, the subjects had to point at it and click the button again.

With this procedure we intended to teach the subjects to associate the visual and acoustic spatial positions of targets. Additionally, by recording the response during the first phase of the trial, we were able to directly collect data about the localization performance within the training block. Hence, additional test blocks between the training blocks were not required.

The subjects were trained in blocks of 50 trials, reduced from 100 trials because each trial lasted at least twice as long as in experiment 1. Subjects completed one block within 20 to 30 minutes, after which they took a break. Up to six blocks were performed per session, with one or two sessions per day. Depending on the availability of the subjects, 600 to 2200 trials were completed, over a span of 2 to 32 days (20 days on average).

Results

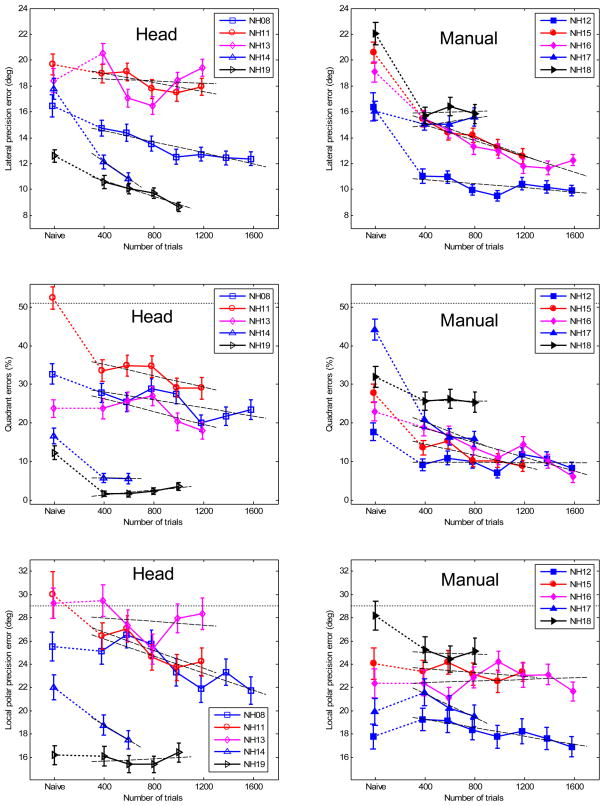
Figure 7 shows the lateral precision error, quadrant error, and local polar precision error as a function of trials and averaged over position. Each line shows the performance of an individual subject with the identification code shown in the legend. The data shown at “Naive” represent the results from experiment 1. The other data show the progress of training in steps of 200 trials. In the two top panels, each point represents a lateral precision error as an average over 400 trials. The variance of each average was estimated by bootstrapping (Efron and Tibshirani 1993). For each point, 200 lateral precision errors were calculated. Each lateral precision error was calculated from 400 bootstrapped samples that were randomly drawn with replacement from the pool of the last 400 collected trials. The standard deviation of the 200 lateral precision errors is shown in Fig. 7 as vertical bars at the data points. For the lateral bias and polar bias, the data showed no consistent trends as a function of trials and therefore were omitted. In the middle and bottom panels of Fig. 7, the quadrant errors and local polar precision errors, respectively, were calculated similarly.

Figure 7.

(color online). Training results for each subject. Left panels: head-pointing method; Right panels: manual-pointing method. Top panels: lateral precision errors; Middle panels: quadrant errors; Bottom panels: local polar precision errors. The data shown at “Naive” represent the results from experiment 1. The other data show the averages of the progress of training in steps of 200 trials, 400 trials for each point. The error bars show the standard deviation of the bootstrapped errors (see text). The dashed lines represent the regression line fitted to the training data. The horizontal dotted lines represent chance rate.

The short-term training effect was investigated by comparing the data from experiment 1 (at “Naive”) to the data from experiment 2 for the first 400 training trials for the two pointing methods separately. Repeated-measures ANOVAs were performed with the factor mode (naive and trained) for the one-sided lateral bias, lateral precision, quadrant error, local polar bias, and local polar precision error. For the one-sided lateral bias, the right-side data were flipped to the left side and pooled with the left-side data. The results are presented in Tab. 1 and show significant improvements in all but one condition: the local polar precision error for the manual-pointing method. On average, subjects showed substantially reduced systematic biases after the training.

Table 1.

Results for the Short-Term Training Effects

Pointing Method	Condition	One-sided lateral bias	Lateral precision error	Quadrant error	Local polar bias	Local polar precision error
Head	Naive	3.7°	17.1°	27.5%	4.6°	24.4°
	Trained	0.0°	15.4°	18.3%	2.9°	23.2°
	p-value	< .0001	.0023	< .0001	.048	.007
Manual	Naive	6.8°	18.8°	28.8%	5.8°	22.4°
	Trained	0.2°	14.4°	18.4%	−0.7°	22.0°
	p-value	< .0001	< .0001	< .0001	< .0001	.27

Note. The p-values show the significance of differences between “Naive” and “Trained”.

The long-term training effect was investigated by fitting the individual data shown in Fig. 7 to a linear model. The data from experiment 1 were not included in the model. The linear model assumes that subjects continue to improve beyond being perfect, while in reality the improvement stagnates at some point. Our subjects did not show any marked stagnation of the improvement and thus, the linear model seems to be an adequate approximation for this analysis.¹ The model results are represented by the linear regression lines, which are shown in Fig. 7 . The slopes of the regression lines represent the amount of improvement over time. The offset of the regression lines represent the absolute performance of a subject at the beginning of the training. The slopes are given in Tab. 2 for individual listeners and for each subject group. The slopes for the lateral precision and local polar precision errors are given in degrees per 100 trials. The slopes for the quadrant errors are given in % per 100 trials. All values which are different from zero with 95%-confidence are shown in bold.² The average slopes were calculated by fitting regression lines to the data pooled from all subjects. Before pooling, the subject-dependent offsets (representing individual performance before training) were removed from the data. The results show that all but one of the average slopes were significantly negative. The exception was the local polar precision for the manual-pointing method, which had a non-significant negative slope.

Table 2.

Slopes of the Linear Regression Model for the Errors as a Function of Training Progress

Pointing method	Subject	Slope of the lateral precision errors (Degrees per 100 trials)	Slope of the quadrant errors (% per 100 trials)	Slope of the local polar precision errors (Degrees per 100 trials)
Head	NH08	−0.21	−0.52	−0.37
	NH11	−0.18	−0.74	−0.39
	NH13	−0.04	−0.78	−0.08
	NH14	−0.66	−0.06	−0.64
	NH19	−0.30	+0.34	+0.05
	Average	−0.18	−0.57	−0.26
Manual	NH12	−0.08	−0.01	−0.18
	NH15	−0.35	−0.75	−0.09
	NH16	−0.30	−0.91	+0.04
	NH17	+0.14	−1.33	−0.51
	NH18	+0.67	−0.13	−0.04
	Average	−0.24	−0.45	−0.06

Note. The slopes which are different from zero within the 95%-confidence interval are shown in bold.

With the help of the regression line slopes, the short-term and long-term training effects were compared quantitatively. The short-term improvements due to training are represented by the error differences between the naive and the first 400 trials of training. The long-term improvements are represented by the improvements predicted by the linear model for a training period of 400 trials. Both the short-term and the long-term improvements are shown in Tab. 3. The improvements from the short-term training were substantially higher than the improvements from the long-term training. This indicates that most of the training effect took place within the first 400 trials of training.

Table 3.

Comparison of the Short-Term and Long-Term Training Effects.

Pointing Method	Condition	Lateral precision error	Quadrant error	Local polar precision error
Head	Short-terma	1.7°	8.8%	1.2°
	Long-termb	0.7°	2.3%	1.0°
Manual	Short-terma	4.4°	10.7%	0.4°
	Long-termb	1.0°	1.8%	0.2°

Note.

^aShort-term shows improvements in results between naive subjects and the first 400 trials of training. The bold values represent significant (p < .05) differences between the naive and training data.

^bLong-term shows improvements predicted by the linear model for a training of 400 trials. The bold values represent error differences with a significant long-term training effect, as given by the significantly-negative (within the 95%-confidence interval) regression lines.

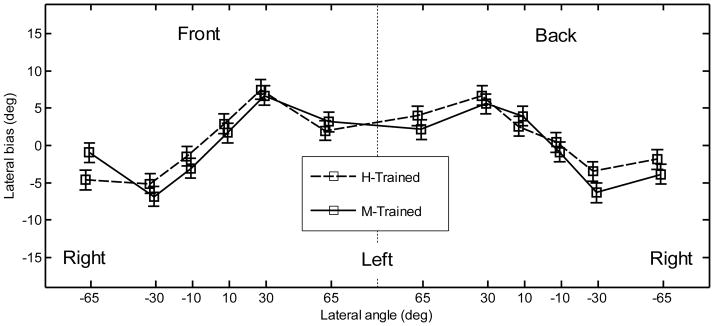
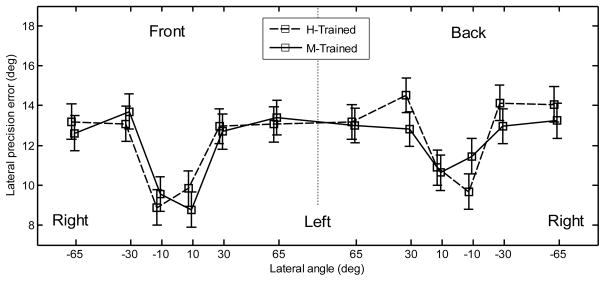
Pointing method and position effects were investigated by using all the data from experiment 2. The lateral bias for the two pointing methods is shown in Fig. 8 as a function of position. Note that each point represents data from five subjects, whereas in experiment 1 the corresponding points represent data from all ten subjects. The lateral bias showed a similar trend to that found in experiment 1; however, its magnitude was much smaller (largest overshoot of approximately 7°). An ANOVA with factors position, hemifield, and pointing method was performed. The positions corresponded to those used in experiment 1. The effect of position was significant [F(5,456) = 44.8, p < .0001]. None of the other main effects or interactions were significant [F(1,456) < 1.59, p > .21 for all]. The lateral precision error is shown in Fig. 9. The lateral precision error had a similar trend to that found in experiment 1; however, in experiment 2, the errors were smaller for most positions. An ANOVA with factors position, hemifield, and pointing method was performed. The effect of position was significant [F(5,456) = 15.2, p < .0001]. A post-hoc test showed that subjects performed significantly better for the central positions (9.9°) than for other positions (13.3°). The effect of hemifield was significant [F(1,456) = 4.15, p = .042], showing a significantly lower precision error for the targets located in the front (11.8°) than for targets located in the back (12.5°). The effect of pointer was not significant [F(1,456) = .38, p = .54]. None of the interactions were significant (p > .53).

Figure 8.

Lateral bias after training for the two pointing methods. The error bars represent the standard errors.

Figure 9.

Lateral precision error after training for the two pointing methods. The error bars represent the standard errors.

The quadrant errors for the two pointing methods are shown in the left panel of Fig. 10. An ANOVA with factors elevation (eye-level, top), hemifield (front, rear), and pointing method was performed. The effect of hemifield was not significant [F(1,152) = .12, p = .73], but the effect of elevation [F(1,152) = 28.1, p < .0001] was significant. Also, the interaction between elevation and hemi-field was significant [F(1,152) = 4.06, p = .046], showing that subjects had different quadrant errors for different positions. The effect of pointing method was not significant [F(1,152) = .65, p = .42]; however, the interaction between elevation and pointing method was significant [F(1,152) = 5.37, p = .022]. Post-hoc tests showed that the manual-pointing method yielded significantly less quadrant errors for the eye-level positions (9.0%) than for the top-positions (23.7%) while the head-pointing method did not yield significantly different quadrant errors between the eye-level positions (15.0%) and the top positions (20.8%).

Figure 10.

Results after training for the two pointing methods. Left panel:quadrant errors. Middle panel: local polar bias. Right panel: local polar precision error. The horizontal dotted lines represent the precision errors for random responses. The error bars show the standard errors.

The local polar bias is shown in the middle panel of Fig. 10. An ANOVA with factors position and pointing method was performed. The effect of position was significant [F(3,152) = 21.9, p < .0001]. The effect of pointing method was also significant [F(1,152) = 8.5, p = .0041]. For the head-pointing method, the average bias was 3.5°. For the manual-pointing method the average bias was −1.7°. The interaction between elevation and pointing method was significant [F(3,152) = 3.9, p = .010], showing that the effect of pointing method depended on the elevation. A post-hoc test showed that for the top positions, the bias was significantly higher for the head-pointing method (0.10°) than for the manual-pointing method (−8.7°). For the eye-level positions, the bias was not significantly different between the head-pointing (6.4°) and the manual-pointing (5.0°) method.

The local polar precision errors are shown in the right panel of Fig. 10. An ANOVA with factors position and pointing method was performed. The effect of the position was significant [F(3,152) = 69, p < .0001]. A post-hoc test showed significantly lower precision errors for the eye-level positions (14.9°) than for the top positions (24.6°). Neither the effect of the pointing method [F(1,152) = .71, p = .40] nor the interaction between position and the pointing method [F(3,152) = 1.04, p = .38] were significant.

The lateral bias, lateral RMS errors, local RMS polar errors, elevation bias, and quadrant errors were calculated according to [Middlebrooks 1999]. A summary of his and our results is given in Tab. 4.

Discussion

General

With respect to the effect of position, the results from experiment 2 confirm the results from experiment 1. Listeners overestimated the lateral position and were more precise for central positions. The quadrant errors are still lower for the eye-level positions compared to the top positions. Hence, even though the absolute performance significantly improved during the training, the results with naive and trained subjects show similar position dependence.

Our results for tests in darkness with the head-pointing method in experiment 1 can be compared to the results of [Middlebrooks 1999], who tested trained subjects. The results are shown in Tab. 4. Compared to his results, the lateral bias and elevation bias from our experiment 1 are similar. The lateral RMS error, local RMS polar error, and quadrant error were higher in our study, which probably resulted from testing naive subjects. When tested with the HMD, our lateral RMS error was in the range of Middlebrooks’ lateral RMS error, which shows that the visual information from the HMD compensated for the lack of training. This was not the case for the local RMS polar error and quadrant error, which did not decrease when testing with the HMD. During the training, however, these errors decreased, which indicates that sufficient training may help vertical-plane localization. Interestingly, during the training, the lateral RMS error, lateral bias, and elevation bias decreased further, becoming even lower than in [Middlebrooks 1999]. This shows the importance of both the training and the VE when measuring human sound localization ability.

Pointing method effect

In tests with naive subjects, the pointing method had a small effect on the polar precision. After training, this effect was reduced further, i.e., for quadrant errors, the pointing method did not show an effect when averaged over positions. When looking at particular positions, the manual-pointing method yielded more quadrant errors for the top positions, while the head-pointing method yielded more quadrant errors for the eye-level positions. With respect to the local polar bias, the two pointing methods showed significantly different patterns. The head-pointing method showed an overestimation of the elevation for only the front eye-level positions. The manual-pointing method showed no clear pattern across positions. On average, the bias was smaller for the manual-pointing method than for the head-pointing method. Even with the smaller average bias, the results of experiment 2 do not support our hypothesis that the elevated positions can be more easily reached with the manual-pointing method. We conclude that differences between the pointing methods are negligible even after training, and the choice of the type of pointer plays a minor role in sound localization tasks.

Effect of the training

Our data show a substantial effect of training. Subjects could learn to better localize sounds in terms of precision, bias, and quadrant error. After the short-term training (within the first 400 trials), subjects showed almost no bias in the responses. The subjects also showed a large reduction in quadrant errors for the eye-level targets, where there is a large spectral difference between front and rear HRTFs (Macpherson and Middlebrooks 2003). For the top positions, the improvements in quadrant errors were smaller, indicated by a more shallow learning curve. This may be a consequence of a smaller spectral difference between the front and rear HRTFs for the top positions, making the distinction between front and back positions more difficult (Langendijk and Bronk- ). Subjects showed dramatically improved localization performance within the first 400 trials. The subsequent training showed smaller improvements. This indicates that a training period of 400 trials is very efficient in obtaining reliable subject performance in localization tasks. Interestingly, the localization performance did not completely saturate even when subjects were trained for up to 1600 trials.

These results are in agreement with [Makous and Middlebrooks 1990] who tested localization ability after training subjects for only a few hours. The amount of training as well as their localization results are comparable to ours; however, they reported a lower quadrant error (their percentage of front-back confusions was 6%). This may be due to their use of real sound sources or their slightly different definition of quadrant errors. [Carlile et al. 1997] also used real sound sources in a sound localization training paradigm. They found an improvement in performance that saturated after 7 to 9 blocks, each block containing 36 trials. This is roughly comparable with the substantial improvements in localization ability within the first 400 trials of training of our experiment. Our training results are comparable to [Middlebrooks 1999], who trained subjects for 1200 trials (see Tab. 4). The comparison of our results to [Middlebrooks 1999] also shows that despite the differences between the studies (different equipment, testing different subjects and having small differences in the procedure), a similar localization performance can be achieved as long as a sufficiently long training period is provided. [Martin et al. 2001] tested localization ability using virtual sound sources with highly trained subjects. They obtained a remarkably low percentage of front-back confusions (2.9%), which is lower than ours and that of [Middlebrooks 1999]. The absence of level roving during their test may explain their superior performance because it could have allowed loudness cues to be used to resolve front-back confusions. [Zahorik 2006] investigated training effects in sound localization and provided visual feedback via a virtual VE, which was similar to ours. They used non-individualized HRTFs to create virtual acoustic stimuli. They found a significant reduction of front-back confusions in the trained subject group, but their precision was not affected by the training. This is contrary to our results, because we found improvements in both quadrant errors and precision. Zahorik et al. interpreted the lack of larger improvements as effects of the considerable differences between the applied and listeners’ HRTFs, and the relatively short training period of only 30 minutes.

Generally, our training paradigm may be considered as perceptual training on a specific stimulus cue in terms of supervised learning where one neural network controls the plasticity over another network (Knudsen 1994). In one condition of experiment 1, the subjects were tested in darkness, having only proprioceptive cues for orientation. This condition led to the worst localization performance of this study. Using the HMD, the localization performance improved, which can be explained by an integration of the proprioceptive and visual cues for orienting and pointing. This is consistent with the results of [Redon and Hay 2005], who showed that pointing bias decreased when access to a visual background was provided. In experiment 2, an additional cue was provided: visual information about the target’s position and it was hypothesized that this would improve localization performance by initiating perceptual training. In fact, our training resulted in an improved localization performance, suggesting that by providing sufficiently congruent information in audio and visual channels perceptual training can be achieved.

In the short-term training (within the first 400 trials), the quadrant error substantially improved. In our study, the quadrant error represents the number of front-back confusions. In reality, front-back confusions can be easily resolved by small head rotations for sufficiently long signals (Perrett and Noble 1997-Percept). In our experiments, head rotations were not allowed. To resolve front-back confusions, subjects were forced to rely solely on the acoustic properties of the stimuli such as the spectral profile. Note that the stimulus level was disrupted as a spatial cue by randomly roving the level from trial to trial. Thus, it is likely that the learning process that occurred during our training was learning to focus on the spectral profile as a cue for the spatial position of the sound. The subjects obviously improved their localization performance on a rapid time-scale. There is strong evidence that selective attention facilitates sound localization (Ahveninen et al. 2006). The important role of attention has also been shown on the neural level (for a review see Fritz et al. 2007). Hence, the increased attention to static cues like spectral profile may, in addition to the perceptual training, explain the rapid short-term improvements.

With respect to long-term training, it has been shown that a recalibration of the auditory spatial map, guided by visual experience, is possible (Hyde and Knudsen 2001). In our case, the daily training of the experiment-specific spectrum-position mapping may have led to such a recalibration of the original audio-visual spatial map, resulting in a continuous improvement of the precision, bias, and quadrant error. Such plasticity of the auditory system has been shown in studies on different time scales with humans (Hofman et al. 1998; Shinn-Cunningham et al. 1998-1; Wright and Sabin 2007), ferrets (Kacelnik 2006), and owls (Knudsen 2002). In all of those studies, the localization cues were substantially changed, forcing a recalibration of the perceptual map. In our study, however, we used individualized HRTFs, and given our subjects’ moderate improvements in the long-term training, it seems that such a substantial recalibration was unlikely.

Improvements due to training could also have been based on procedural learning (Hawkey et al. 2004). During the training subjects might have calibrated their pointing strategy to the testing environment. For example, for the head-pointing method, at the beginning of the training subjects might have used their eyes to point to the more elevated positions and during the training they might have learned to use their head and nose. Analogous, for the manual-pointing method, because of a potential horizontal bias due to the handedness, subjects might have calibrated to the visual environment over the course of training. To reduce such an effect, we performed extensive procedural training prior to data collection in experiment 1. Subjects completed this training with RMS errors smaller than 2° (independent of direction). In the subsequent acoustic tests, naive subjects had lateral and polar precision errors of 18° and 23.3°, respectively. After the training they had lateral and polar precision errors of 12.2° and 19.8°, respectively. Assuming the procedural skills learned in the pretest generalize to the succeeding acoustic tests, the procedural learning most likely played a minor role during the acoustic tests and training.

In summary, our results reinforce the importance of training in sound localization studies. Improvements during the acoustic training were observed in the percentage of quadrant confusions, response precision, and response bias. The results indicate that the first 400 trials of training were essential to obtain substantial improvements in localization ability. Further training resulted in relatively much smaller improvements. The pointing method (head or manual) had a negligible effect on sound localization performance.